Mostrando artículos por etiqueta: espirales
Proporcionalidad. Las Espirales X
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades al subproyecto TELESECUNDARIA.
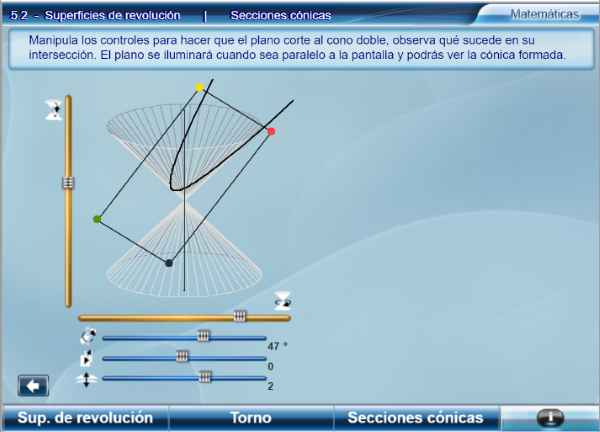
Como muestra, enlazamos la unidad sobre superficies de revolución
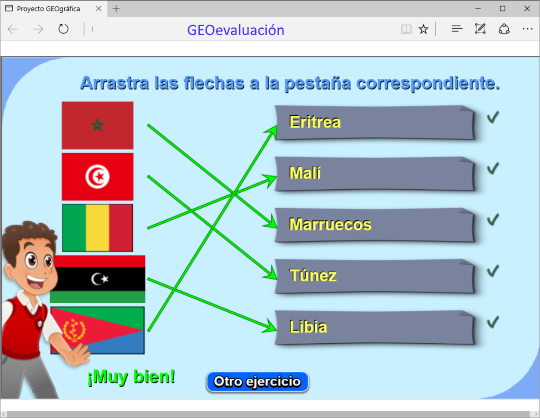
También es continuo el flujo de aportación de unidades al apartado GEOevaluación del subproyecto GEOgráfica
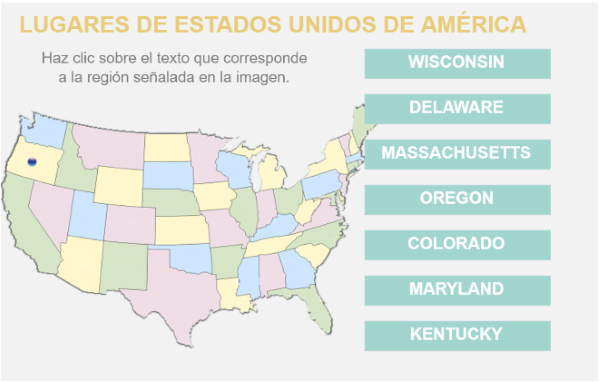
En esta ocasión enlazamos la Evaluación de los Estados Unidos de América
Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos lugares geométricos aunque, en particular, es de especial interés la creada por Ángel Cabezudo Bueno ya que, además de ser la primera de la serie actual, entronca directamente con la fuente origen de dicha serie, el trabajo de José R. Galo Sanchez sobre las proporciones, la belleza en las Matemáticas y la espiral Cordobesa y es consecuencia de la acertada propuesta de espiral gnomónica Cordobesa, ambas: propuesta y miscelánea se muestran y/o enlazan a continuación.
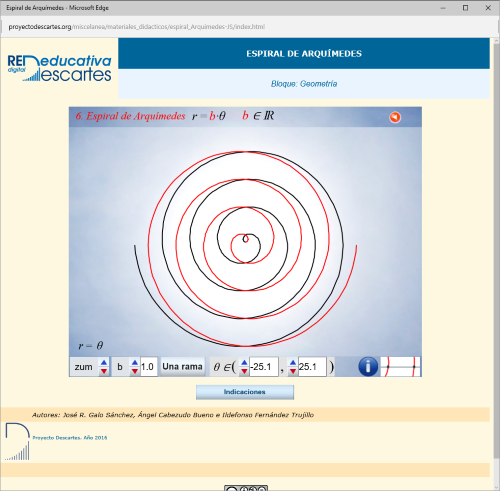
El artículo anterior mostraba, paso a paso y exhaustivamente escenas interactivas con la creación de un lugar geométrico (l.g.) por un punto común a dos segmentos y por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos, el actual vuelve a construir la espiral de Arquímedes y también paso a paso e interactivamente muestra como trisecar un ángulo cualquiera y como hallar la cuadratura de cualquier círculo.
A continuación se exponen las escenas interactivas.
- Generación del lugar geométrico conocido como espiral de Arquímedes.
- Trisección de un ángulo mediante la espiral de Arquímedes.
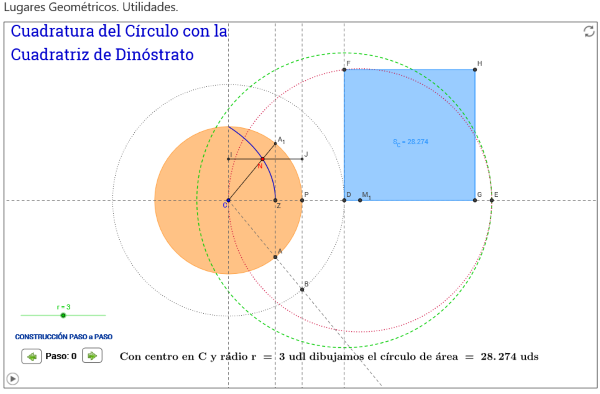
- La cuadratura del círculo mediante la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la relación de la espiral con la orografía y la interpretación de las señales cosmológicas por las diferentes culturas con objeto de apreciar distintas formas de enfocar el tema que nos ocupa.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Hiperbólica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral Hiperbólica
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto. Dejamos para los lectores interesados la inclusión total y/o personalizada de esta opción.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Hiperbólica incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido los siguientes trabajos realizados con el programa GeoGebra: en el primero se muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el segundo para la cuadratura del círculo.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales IX
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca el subproyecto TELESECUNDARIA.
En palabras del encargado de la presentación del subproyecto en el Blog, Ángel Cabezudo Bueno, "Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.
Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.
En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5." los primeros materiales pueden verse y descargarse siguiendo el enlace gráfico siguiente.
Dentro de nuestro ámbito local queremos destacar, entre otros, los siguiente materiales:
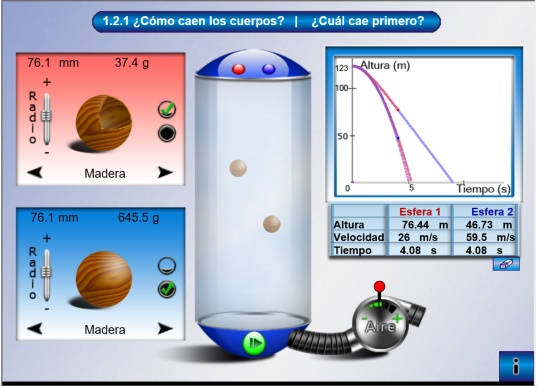
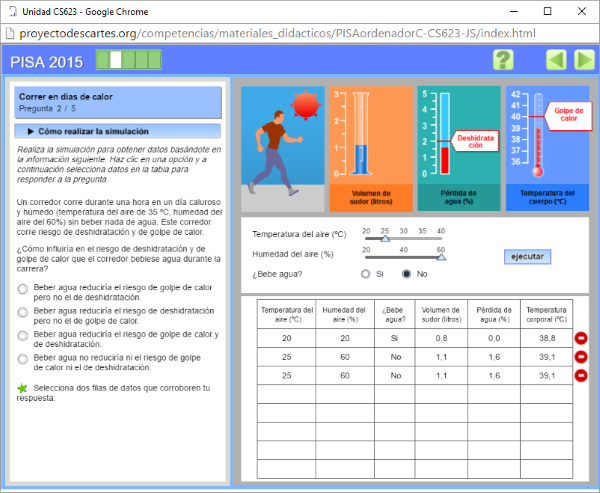
- Todos los creados para el subproyecto COMPETENCIAS. Debido a la creciente internacionalización de nuestro sistema educativo, progresiva integración en la comunidad europea, conviene que la manera de evaluar competencias en los ámbitos externos sea conocido con objeto de participar en igualdad de condiciones. Un acercamiento a estos procedimientos lo ofrecen los materiales del proyecto Competencias.
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente; no obstante en esta ocasión queremos enfocar el proceso de creación de la espiral desde el punto de vista de la definición de un lugar geométrico.
La miscelánea anterior muestra, paso a paso, la creación de un lugar geométrico (l.g.) por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos. Existen otros muchos lugares geométricos, entre los clásicos y más conocidos destaca la Trisectriz de Hipias que junto con la espiral de Arquímedes se ha usado, además de para otras utilidades, para la trisección de cualquier ángulo. A la Trisectriz de Hipias también se la llama Cuadratriz de Dinóstrato debido a que este geómetra usó el l.g. para la cuadratura del círculo. La Trisectriz (o Cuadratriz) es el l.g. generado por el punto común a dos segmentos uno de los cuales gira alrededor de uno de sus extremos y el otro se desplaza horizontalmente según muestran las siguientes escenas:
- La Trisectriz de Hipias que muestra, mediante una animación, la definición de la curva
- La trisección de un ángulo mediante la Trisectriz de Hipias. También se basa en una animación, en la primera parte se dibuja la curva y a continuación se muestra y explica, de forma dinámica, la trisección de un ángulo. La animación puede detenerse/reanudarse en cualquier instante.
- La cuadratura del círculo mediante la Cuadratriz de Dinóstrato (Primera Parte). Esta escena se basa en un pulsador que muestra, según se pulsa, la explicación del proceso para cuadrar el círculo. También tiene una animación que vuelve a construir la curva. La animación puede activarse/detenerse en cualquier instante.
Conviene analizar las escenas anteriores, reproducirlas y/o mejorarlas y ver la forma de integrarlas en la miscelánea sobre las espirales.
En próximas entradas en el Blog completaremos el estudio de uso de la Cuadratriz y veremos la manera de trisecar un ángulo y cuadrar el círculo con la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno muy particular que muestra la manera de dibujar la Trisectriz de Hipias (Cuadratriz de Dinóstrato) con ¿regla y compás? con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa. Buscando en internet se pone de manifiesto el enorme interés que suscitan, aún hoy en día, los problemas clásicos de la Geometría Griega.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fermat" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fermat
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Y desde este enlace descargar el proyecto con la espiral de Fermat incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades hemos incluido dos trabajos, realizados con el programa GeoGebra, uno muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el otro, enlazado en la imagen que sigue a la trisección, se lleva a cabo la cuadratura de un círculo de forma dinámica.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Bibliografía.- Para la realización de esta entrada y siguientes ha sido de gran ayuda la siguiente información:
- El trabajo sobre las TRISECTRICES de Pedro González Enríquez.
- Cuadratura de un círculo con la Cuadratriz de Dinóstrato
- Cuadratura de un círculo
Ildefonso Fernández Trujillo. Blog ReDescartes 2016
Un grillo está sobre una superficie, que gira a una velocidad angular constante, y se está desplazando dando saltos siguiendo una línea recta que pasa por el centro de giro. Ha dado un salto inicial y posteriormente cada salto es c veces mayor que el anterior. ¿En qué posición está en cada instante? ¿Cuál es la trayectoria que sigue?
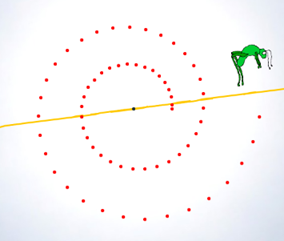
Este planteamiento dinámico conduce a una curva, ampliamente estudiada, la cual es el objeto de este artículo de difusión. En la miscelánea que hemos publicado en nuestro servidor de contenidos puedes ver el camino que sigue nuestro grillo saltarín, pudiendo seleccionar el salto y la velocidad de giro que desees y observando en qué influye tu elección.
Es bien conocido que la circunferencia es una curva equiangular, es decir, que en cualquier punto de la misma, el ángulo que forma el radio con la tangente es siempre constante e igual a un ángulo recto.
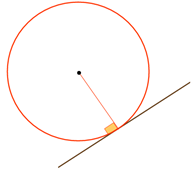
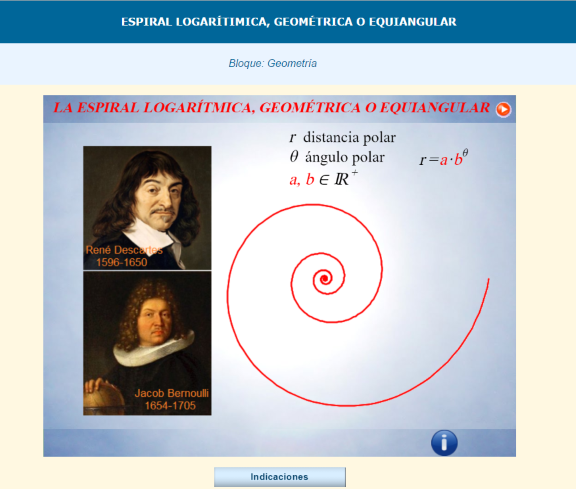
Inicialmente René Descartes (1596-1650) fue quien se planteó la determinación de una curva que también fuera equiangular, pero que el ángulo fuera el que previamente se deseara, es decir, una generalización de lo que acontece en la circunferencia. Jakob Bernoulli (1654-1705) también la analizó y la denominó “Spira mirabilis” o espiral maravillosa, y de acuerdo con sus propiedades, en su epitafio hizo poner “Eadem mutata resurgo”, es decir, “Mutante y permanente vuelvo a resurgir siendo el mismo”. En este recurso podrás comprobar el significado de esta expresión y experimentar que:
¡Ciertamente es maravillosa!
Para ello, planteamos un camino en varias fases, un total de doce, y en cada una de ellas se avanza en el análisis de esta espiral, en sus propiedades. Pulsa sobre la imagen siguiente para acceder al recurso.
En las tres primeras fases se aborda su construcción dinámica —dependiente del tiempo— y se inicia su análisis con la obtención de la relación —digamos estática o atemporal— entre la distancia y el ángulo polar. Ésta, es la ecuación algebraica en coordenadas polares de la espiral y nos permite identificar el significado físico de los parámetros específicos de la misma.
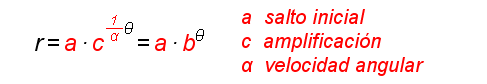
La expresión justifica su denominación como espiral logarítmica, pues se observa que el ángulo polar se puede expresar en función del logaritmo del radio polar. Y en la fase cuarta del recurso se observa y justifica que a es un factor de escala, que para b=1 obtenemos como caso particular la circunferencia y que las espirales de base b y 1/b son simétricas respecto del eje polar.
Una quinta fase permite ver y justificar por qué también se le denomina espiral geométrica ya que los puntos de ella situados sobre una misma semirrecta siguen la relación de una proporción geométrica (aquí se aplica una analogía con la que acontece en la espiral de Arquimedes o espiral aritmética). Y en la sexta se visualiza y demuestra el carácter equiangular que motivó a Descartes.
El hecho de ser equiangular es lo que le confiere a esta espiral su carácter tan especial. Y en base a ello, las últimas fases del recurso se centran en mostrar y demostrar el carácter maravilloso que marcó Bernoulli y que sintetizó en la citada expresión: “Eadem mutata resurgo”. Para una circunferencia es fácil de intuir y ver que su forma es tal que siempre surge o resurge siendo la misma, crece y crece siempre siendo la misma. Y lo maravilloso es que este surgir y resurgir siendo la misma se verifica también en esta “circunferencia generalizada” o espiral logarítmica, es decir, la razón de su crecimiento instantáneo es la unidad. Sintetizando el planteamiento que se realiza en el recurso, pues el detalle lo puedes comprobar interactuando con él, tenemos que:
- Inicialmente el análisis del crecimiento se aproxima mediante rectángulos semejantes circunscritos a la espiral, que siguen un patrón de crecimiento gnomónico en el sentido euclídeo (según lo definido en “Los elementos de Euclides”), que puede interpretarse como el patrón de crecimiento en pasos discretos de π radianes.
- Posteriormente se aborda el crecimiento, pero en el sentido establecido por Aristóteles cuando decía: «Hay ciertas cosas que no sufren alteración salvo en magnitud, cuando crecen...».

Y aquí, esto se aborda planteando el crecimiento con polígonos semejantes construidos sobre radios vectores, correspondientes a puntos de la espiral, que difieren:
-
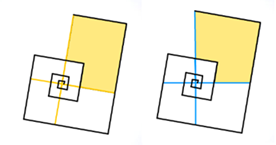
- En π/2 radianes, lo que conduce a una razón de semejanza b^(π/2):
-
- O, en general, con paso 2π/n y razón de semejanza b^(2π/n):
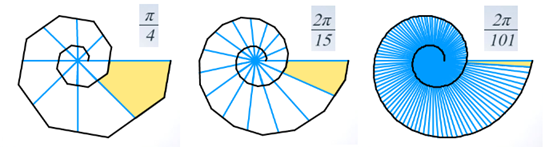
Como ejemplo, sobre la concha del Nautilus pompilius, se muestra un crecimiento gnomónico discreto de paso 2π/16 en una espiral logarítmica cordobesa (b=1.186):

- Finalmente cuando el crecimiento es instantáneo, es decir, si n->infinito y el paso entre radios vectores es por tanto 2π/n->0, la razón de semejanza b^(2π/n) tiende a la unidad: “Eadem mutata resurgo”.
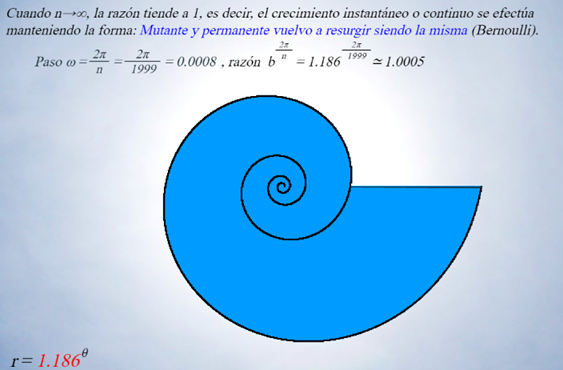
¡Te deseamos un buen aprendizaje siguiendo a nuestro grillo!
Título: La espiral logarítmica, geométrica o equiangular
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Proporcionalidad. Las Espirales VIII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destacan las aportadas por la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes España que, coordinadas por el profesor Juan Guillermo Rivera Berrío, han añadido al subproyecto GEOgráfica una importante cantidad de contenidos, lo que ha hecho necesario dividir el subproyecto inicial en varios subproyectos: GEOcapital, GEOdiver, GEOcolor y GEOevaluación (en estado muy avanzado), estando en fase de desarrollo los de: GEOmontañas y GEOrios, los tres primeros pueden verse y descargarse siguiendo el enlace gráfico siguiente.
El carácter evaluativo - formativo de estas unidades es extraordinario según se manifiesta en la escena anterior y en las que enlazamos a continuación.
También cabe señalar el desarrollo de todo un nuevo subproyecto "PLANTILLAS CON DESCARTES-JS que proporciona herramientas para la creación de contenidos lúdico-didácticos."
Dentro de nuestro ámbito local destacan, entre otras muchas, las siguientes aportaciones:
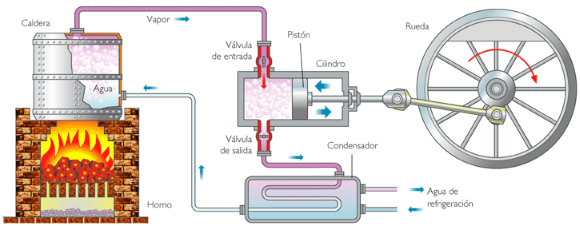
- Dos libros digitales e interactivos en el apartado de Física y Química del subproyecto iCartesiLibri: Teoría de la relatividad y Máquinas térmicas.
- La sorprendente y hermosa Miscelánea La espiral Logarítmica
- Dentro del subproyecto "Unidades Didácticas" la extensa e instructiva unidad Puzles Descartes que dota a la creación de escenas con el editor DescartesJS de una herramienta versátil y potente para la elaboración de objetos educativos lúdicos e interactivos.
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la manera de dibujar la espiral áurea con regla y compás con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fibonacci" tal y como anunciamos en el artículo del mes pasado.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fibonacci
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Fibonacci incluida.
También, relacionando, mediante el programa GeoGebra, la espiral con el Fenaquistiscopio, quisiera enlazar el siguiente trabajo de Nicolas Erdrich.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Una hormiga está sobre una superficie que gira a una velocidad angular constante y se está desplazando, también a una velocidad constante, siguiendo una línea recta que pasa por el centro de giro. ¿En qué posición está en cada instante? ¿Cuál es la trayectoria que sigue?
Este planteamiento dinámico conduce a una antiquísima curva estudiada por Arquímedes y que describió, en torno al 225 a. C., en su libro "Sobre las espirales". Por ello lleva su nombre: "La espiral de Arquímedes.

( gif animado descargado desde http://gifsanimados.de/hormigas )
Y en la miscelánea que hemos publicado en nuestro servidor de contenidos puedes ver el camino que sigue nuestra laboriosa hormiga seleccionando las velocidades que desees y observando en qué influyen éstas.
A partir de la construcción dinámica --dependiente del tiempo--, se procede al análisis de esta curva que se inicia con la obtención de la relación --digamos estática o atemporal-- entre la distancia y el ángulo polar. Ésta es la ecuación algebraica en coordenadas polares de la espiral de Arquímedes y nos permite identificar el significado físico de los dos parámetros específicos de la misma. El primero es la posición o distancia inicial al centro de giro o polo y el segundo es la relación entre la velocidad lineal y la angular:

Interactuando con la escena y manteniendo inicialmente el parámetro b fijo, podremos observar como la variación del parámetro a lo que se produce es un giro en la curva, y podremos ver dos ramas que tienen simetría especular.
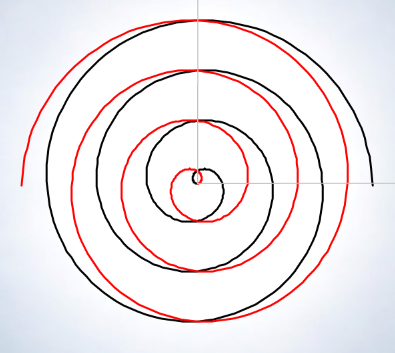
En el caso particular que b sea cero la espiral degenera en una circunferencia e incluso en un punto si también se tiene que a es cero.
En una última instancia se puede verificar analítica y experimentalmente como todos los puntos de la espiral que están situados sobre la recta de ecuación q = constante son equidistantes entre sí y, por tanto, sus distancias al polo constituyen una progresión aritmética de diferencia 2pb. Por esta razón, a la espiral de Arquímedes, también se le denomina espiral aritmética.
Pulsando sobre la imagen siguiente puedes acceder al contenido de esta miscelánea:
¡Te deseamos un buen aprendizaje siguiendo a nuestra hormiga!
Título: La espiral de Arquímedes
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Proporcionalidad. Las Espirales IV
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio de colaboración con la Facultad Regional Santa Fe de la Universidad Tecnológica Nacional de Argentina, está la miscelánea: Simulador de Sistemas diferenciales autónomos y no autónomos creada por la profesora Valeria Bertossi. La siguiente imagen enlaza con la miscelánea.
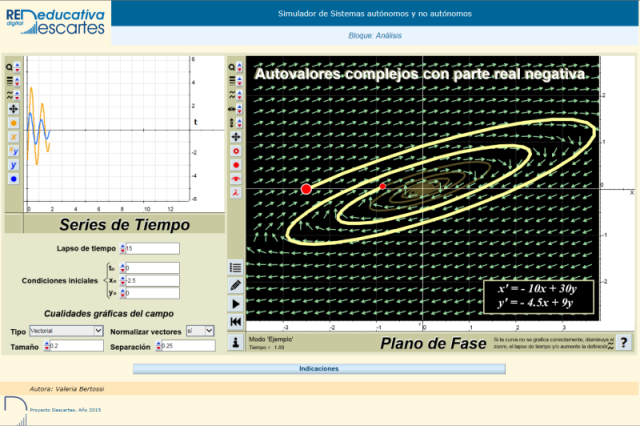
También cabe destacar la aportación del profesor José R. Galo Sánchez con su trabajo sobre Geometría tridimensional, también disponible en catalán gracias a la profesora Monserrat Gelis Bosch, que enlazamos a continuación.
En próximos artículos comentaremos y/o enlazaremos la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis. Por su indudable interés se aconseja visitar dicho subproyecto al igual que el recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, y que con el nombre @prende proporciona a los alumnos un material lúdico e interactivo que facilitará de forma notable la asimilación de conceptos matemáticos.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las familias 3D, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de la escena de la espiral de Teodoro para incluirla en la miscelánea sobre las espirales en estudio, vamos a mostrar un vídeo que relaciona la música y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea tal como está en la actualidad, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
La escena de la espiral de Teodoro, que vemos a continuación
Está formada por:
- dos controles tipo pulsador
- un texto
- un punto rojo de referencia
- una familia de 139 puntos
- otra de 138 segmentos.
Los pulsadores controlan, respectivamente, la cantidad de puntos y segmentos que están presentes en la escena. Inicialmente son visibles 0 segmentos y 29 puntos.
Con objeto de que puedan verse varias vueltas de la espiral, la escala del espacio donde se representa tiene un valor de 15 en lugar de 48 que es el que viene por defecto.
Para poder dibujar la colección de puntos, y posteriormente los respectivos segmentos, hemos definido:
- Un vector de 140 de tamaño para albergar los arcos que los segmentos que unen los sucesivos puntos con el de referencia forman con la horizontal.
- Una función, x1, para controlar la abscisa de los puntos.
- Otra función, y1, para controlar la ordenada de los puntos.
Los gráficos siguientes muestran como se ha hecho lo anterior.
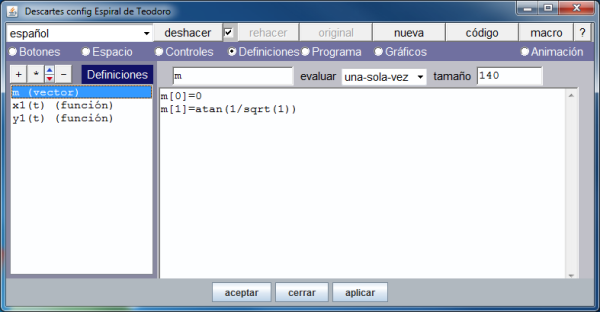
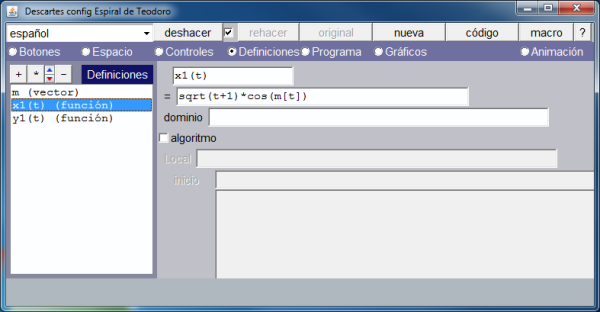
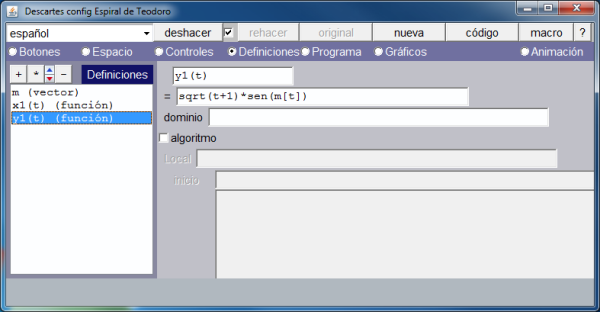
En la imagen que muestra la definición del vector se ve que únicamente se asignan valores a sus dos primeras componentes. Activando la opción de menú: Programa, vemos, en la siguiente imagen, como se han definido el resto de los arcos.
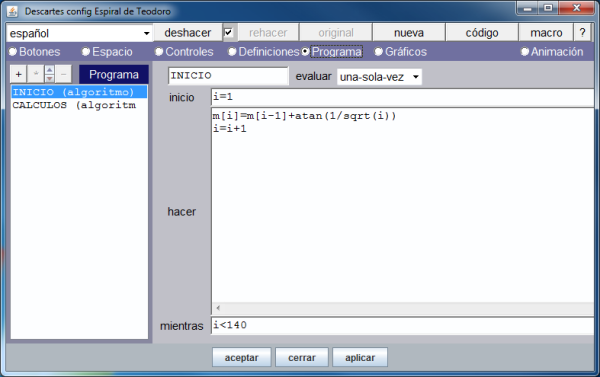
La siguiente imagen muestra los gráficos de la escena, en concreto despliega la forma en que se ha definido la colección de puntos.
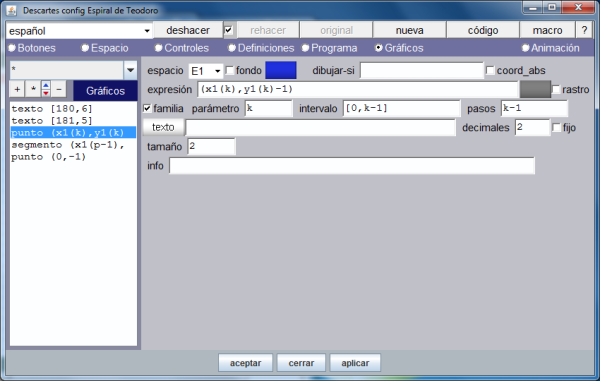
Observamos que los 139 puntos de la espiral se han definido mediante una familia que depende del parámetro k (identificador del pulsador de nombre: puntos presente en la pantalla).
La cantidad de puntos en pantalla depende del valor de este pulsador, el cual podemos manipular a nuestra conveniencia.
Analizada la escena de la espiral de Teodoro podemos pasar a incluirla en la miscelánea que estamos elaborando, acción que dejamos para el siguiente artículo. Aunque, insistimos, es conveniente que, para practicar con el editor de escenas, cada cual lo intente por su cuenta ya que disponiendo de las escenas se puede analizar cada uno de los cambios que se hagan y observar el efecto de cualquier modificación y así aprender a configurar escenas con el editor.
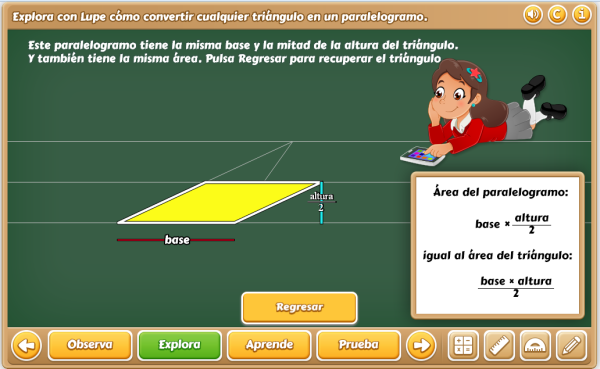
Como aplicación de la proporción Humana hemos elaborado la siguiente escena donde se hace una breve introducción al estudio del Triángulo Cordobés.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un cuadrado con triángulos cordobeses.
Acceso al recurso en GeoGebra
Conviene desplazar el deslizador tesela con las flechas del teclado.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales III
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes caben destacar, entre otras, la creación del subproyecto Pisa con ordenador por parte de Mª José García Cebrian y José R. Galo Sánchez, documentado en este Blog por Santos Mondéjar López y la herramienta creada por el profesor Ángel Cabezudo Bueno que nos ha dotado de la posibilidad de analizar un crecimiento espiral y hallar la expresión matemática que mejor lo ajusta. La siguiente imagen enlaza con la miscelánea que explica el proceso de creación de dicha herramienta y el uso de la misma.
En el proceso de recuperación y adaptación de materiales de la Red Descartes que habían quedado obsoletos y en el de creación de nuevos recursos son varios los trabajos que merecen mención especial que ya está reflejada en el Blog, no obstante animamos a los socios y visitantes de nuestra web a usar y estudiar dichos trabajos y emprender tareas de adaptación-creación de: Unidades, Misceláneas, Discursos... para recuperar todo el esfuerzo e ilusión que en su día se invirtió y dotar a la aldea global de herramientas útiles para la enseñanza y el aprendizaje.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información de las funciones matemáticas disponibles para la construcción de escenas.
Antes de comenzar con el análisis de los gráficos incluidos en la escena en estudio vamos a mostrar un vídeo que relaciona los fractales y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
- Espirales de Antonio Pérez Sanz
- Real Sociedad Matemática Española
- Espirales, fractales, Fibonacci,...
- Visión más espiritual
- Espirales y Laberintos
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior nos quedamos estudiando los gráficos introducidos en la escena: puntos, segmentos, líneas, polígonos, textos... etc. Para lo cual abrimos la opción de menú Gráficos y observamos los 26 objetos creados y que muestra la siguiente imagen.
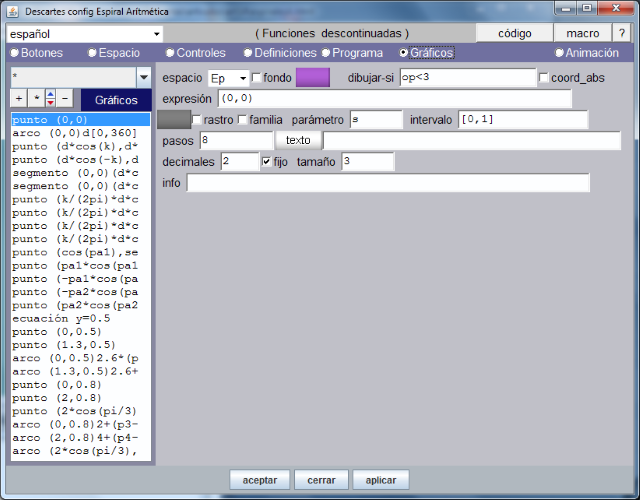
Insistimos en la conveniencia de descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada gráfico. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los gráficos se puede examinar y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos gráficos son las que comienzan por: <param name="G_x" que en nuestro caso llegan hasta <param name="G_26". Recordamos que se debe tener mucha precaución al editar directamente el código.
Observando la imagen vemos que, en primer lugar, se ha definido un punto en el origen de coordenadas (0,0) que, en esta ocasión, está centrado en la escena. Conviene, si no se tiene práctica, estudiar y probar las diferentes maneras de situar el origen de coordenadas de un espacio y el espacio en si mismo, dentro de la escena. También vemos el espacio donde se representará el punto, su color, tamaño y otra serie de parámetros autoexplicativos y de facil uso.
De los parámetros que ayudan a manejar un punto en la escena uno muy interesante es el de 'familia' que mediante un parámetro (variable) que se introduce en la/s coordenada/s y que se declara en el cuadro de texto "parámetro" (o se acepta el ofrecido por el editor 's') permite introducir simultáneamente tantos puntos como se precise en los lugares definidos por las coordenadas.
La siguiente imagen muestra como se han definido la colección de puntos azules que dibujan la espiral de Aquímedes según la definió el geómetra griego, donde se usa el parámetro global 'familia' con el parámetro o variable 'k '. Recordamos que en su momento definimos el control 'k ' y le asignamos un valor inicial y un valor final. Esta manera de proceder hace que la escena sea interactiva ya que el conrol k puede manipularse al estar presente en la escena en forma de pulsador.
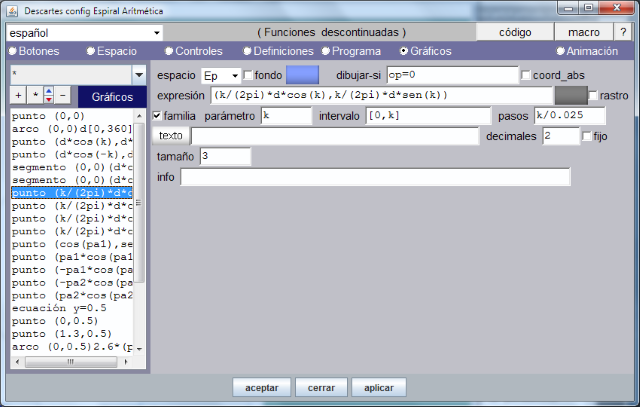
Puesto que disponemos de la escena podemos analizar cada uno de los gráficos cambiando los valores de sus parámetros y observando el efecto de las modificaciones para así aprender a configurar escenas con el editor de código.
Con objeto de practicar con los condicionales hemos elaborado la siguiente escena para su análisis. Es una pequeña aplicación donde se hace una breve introducción al estudio de la distribución de la proporción humana en superficies lisas mediante triángulos, rectángulos, rombos y otras figuras derivadas.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como obtener dos triángulos cordobeses a partir de un folio DIN A4.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral de Teodoro entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales II
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes cabe destacar el impresionante impulso que ha tenido el estudio generalizado de las espirales logarítmicas y la particularización al caso de las gnomónicas entre las que se han destacado las de proporción Divina y Humana. En esta línea el profesor Ángel Cabezudo Bueno ha dotado a la espiral humana de una nueva envoltura aproximándola gnomónicamente mediante funciones exponenciales. Estas son, con sus propias palabras, las razones que aporta para llevar a cabo la acción a la vez que ofrece unas instrucciones de uso de la escena que ha creado.
Espiral gnomon-exponencial y su correspondiente espiral logarítmica
Aparte de la proporción áurea o divina hemos venido trabajando con la proporción cordobesa por ser más natural o humana.
Nos llamó la atención la proporción cordobesa e investigamos de ella algunas cuestiones:
- ¿Cuál es su espiral obtenida al modo con que se obtiene la espiral de Durero en relación a la proporción Áurea?
- El gnomon áureo es un cuadrado y la espiral puede construirse fácilmente con regla y compás, pues basta dibujar un cuadrante de circunferencia haciendo centro en un vértice y conectando los dos vértices opuestos. Repitiendo este proceso sobre los sucesivos gnómones podemos obtener una versión muy aproximada de la espiral logarítmica correspondiente.
Queriendo hacer extensivo este procedimiento con el gnomon cordobés de lados desiguales nos fijamos en la elipse como curva que nos aproxima a la logarítmica correspondiente. El único inconveniente es que no se puede construir fácilmente, aunque sea de forma aproximada, con regla y compás. Además, piénsese que hay que dibujar cuatro arcos de elipse para cada vuelta de espiral. No obstante pudimos ver su dibujo utilizando DescartesJS, nuestra habitual herramienta matemática. - Otras espirales basadas en el modelo gnomon-elipse se han podido así mismo dibujar y aunque su estética no nos ha disgustado además de cumplir con la condición de ser derivables en los puntos de enlace de los arcos de elipse, hemos querido probar otras aproximaciones.
Pensando que el modelo gnomon-exponencial, que consiste en trazar arcos de exponencial en vez de arcos de elipse, debería de dar resultados mejores me he puesto a hacer unos cálculos y al ver que la cosa iba saliendo bien pasé a programar una escena con Descartes.
Debo advertir que esta escena ha estado orientada a hacer algunas averiguaciones en relación con este modelo gnomo-exponencial y hacer algunas comparaciones con lo que ya teníamos, es decir la construcción con el modelo gnomon-elipse y la espiral logarítmica. Por tanto he descuidado, en esta ocasión, la utilización de recursividad para obtener vértices y longitudes de los lados de los sucesivos gnómones dado que este problema ya lo tenemos resuelto (sendas escenas una del profesor José Galo Sánchez y otra mía) y queriendo ver enseguida resultados he trabajado con los valores de estos elementos en los cuatro primeros gnómones (de 0 a π/2, de π/2 a π , de π a 3π/2 y de 3π/2 a 2π), completando así una vuelta de espiral. Bien es cierto que han bastado estos cuatro gnómones para observar la recurrencia al calcular los parámetros de la exponencial en cada gnomon:
![]()
A esta, en coordenadas polares, que formalmente es la misma que la de la correspondiente espiral logarítmica, le aplicamos las condiciones de contorno al gnomon donde va a ser trazada. Es decir para un gnomon de lados a y b cuyo radio vector debe de rotar entre Θ y Θ+Π/2 le imponemos las siguientes dos condiciones:
- Para el ángulo Θ se debe cumplir que r = a
- Para el ángulo Θ+π/2, se debe cumplir que r = b
Con estas dos condiciones podemos determinar los parámetros m y n. Resulta que
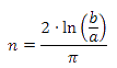
es una constante para todos los gnómones puesto que 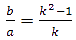 para cualesquiera a y b siendo k=razón de proporcionalidad (k=1,307 para la cordobesa, k=1,618 para la áurea, etc.)
para cualesquiera a y b siendo k=razón de proporcionalidad (k=1,307 para la cordobesa, k=1,618 para la áurea, etc.)
Los valores de m siguen esta ley de recurrencia: 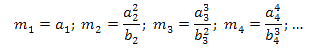 .......
.......
O bien teniendo en cuenta que 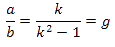 podemos escribir
podemos escribir![]() ........
........
La curva resultante es derivable en los puntos de empalme.
Un cambio de base c ≠ e en la exponencial es posible
r= m0·cn0·θ (2)
verificándose que ![]()
Para el caso k=1,618 (áurea), tenemos a = b (gnomon cuadrado) y la exponencial se convierte en circular pues ![]() con lo que la ecuación polar ahora es
con lo que la ecuación polar ahora es
r = m (3)
Con el modelo gnomon-elipse la traza circular era un caso de elipse y con el modelo gnomon-exponencial la traza circular es un caso de exponencial.
Veamos algunas imágenes captadas de la escena que nos permite hacer algunos comentarios y de paso explicar algo de la funcionalidad de la misma:
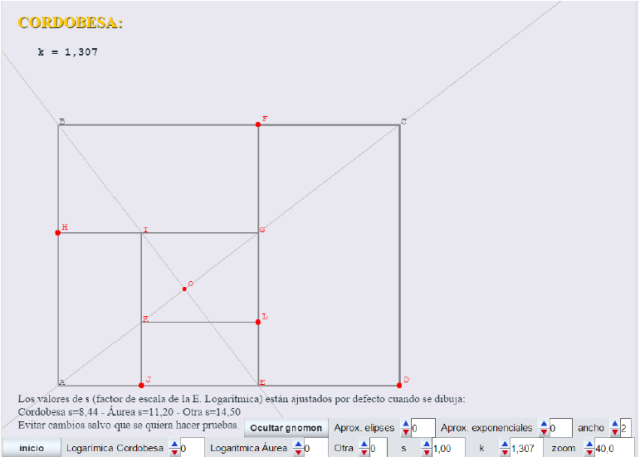
- EDCF (polo en E)
- GFBH (polo en G)
- IHAJ (polo en I)
- FJEL (polo en F)
-
-
- El control k proporciona sucesivamente K=1,307 (cordobesa), k=1,618 (áurea), k=1,929 (otra).
- Las correspondientes espirales logarítmicas a estos tres valores de k se obtienen poniendo a 1 su control que excluye al resto: Logarítmica Cordobesa, Logarítmica áurea y Otra logarítmica
- Se pueden representar para cierto valor de k, sus aproximadas espirales gnomónica-con-elipses y gnomónica-con-exponenciales.
- Las espirales para cierto k se pueden superponer para hacer comparaciones.
-
- Se representan sólo cuatro gnómones a partir del rectángulo ABCD:
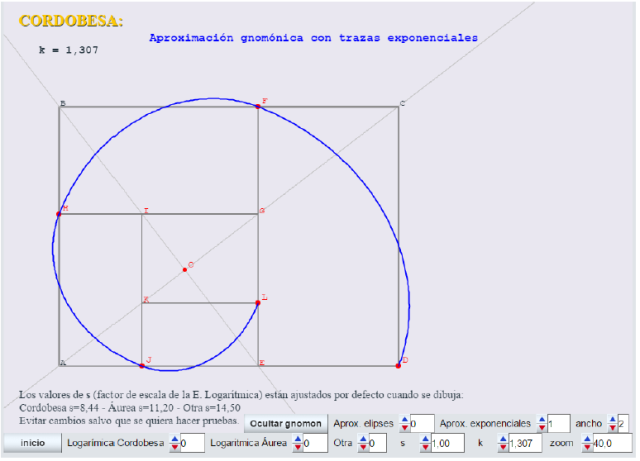
-
-
- El control ancho permite tres anchos de punto (1, 2, 3) de las curvas aproximadas. El ancho de la logarítmica es 1 fijo (se observa mejor la diferencia con ancho 1).
- El parámetro s es un factor de escala de la espiral logarítmica, que facilita el ajuste a los vértices de los gnómones. Están fijados por defecto para cada una de las tres espirales.
-
Observar la buena aproximación que se consigue con el modelo gnomon-exponencial para la cordobesa.
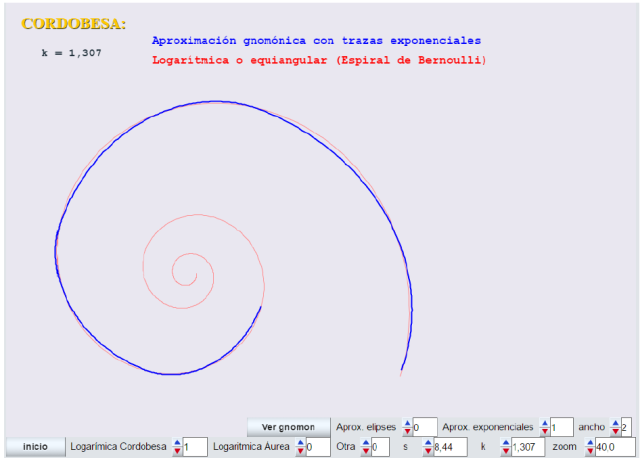
El modelo gnomon-elipse para valores de k menores que 1,618 (áurea) no es muy bueno. Este es el caso de la cordobesa.
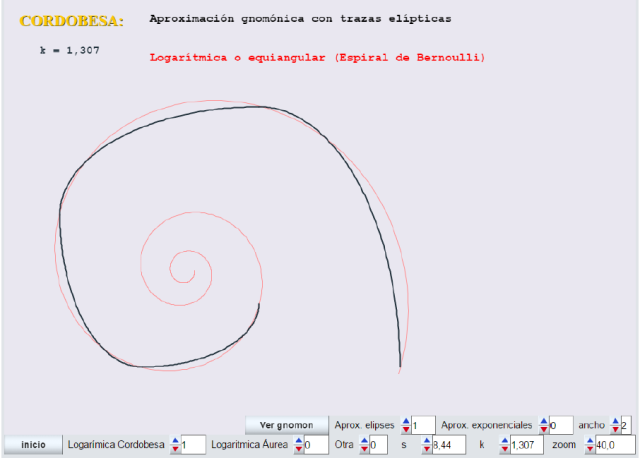
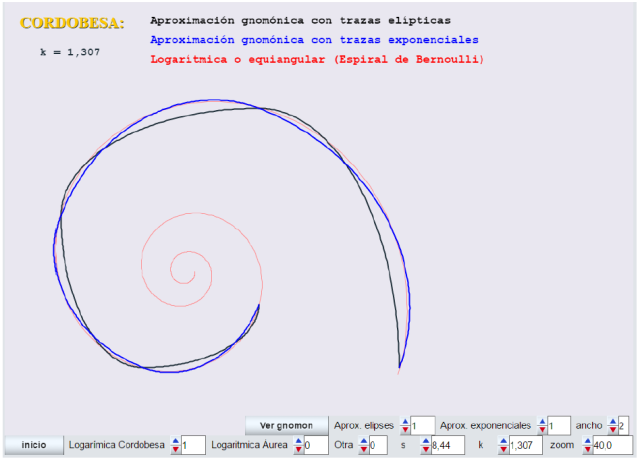
En la siguiente imagen podemos ver una comparativa de las tres espirales para el caso k=1,307 (cordobesa) al dibujarlas juntas.
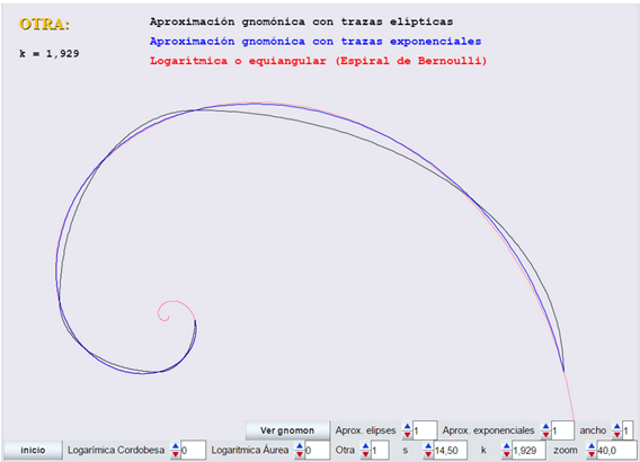
Ver el buen acoplamiento de las trazas exponenciales para k=1,929 (otra)
Animamos a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que están elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos que llevan a la información de cómo crear animaciones y juegos interactivos para el aula.
Antes de comenzar con el desarrollo de las aplicaciones de la Proporcionalidad vamos a mostrar el vídeo que el profesor Antonio Pérez Sanz elaboró para el programa + por - de TVE.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales:
Recordamos que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad, el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales, las ecuaciones paramétricas de una curva, la ecuación polar, las aplicaciones de la derivada y cualquier otro relacionado con el tema de estudio.
No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.
También recordamos que al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.
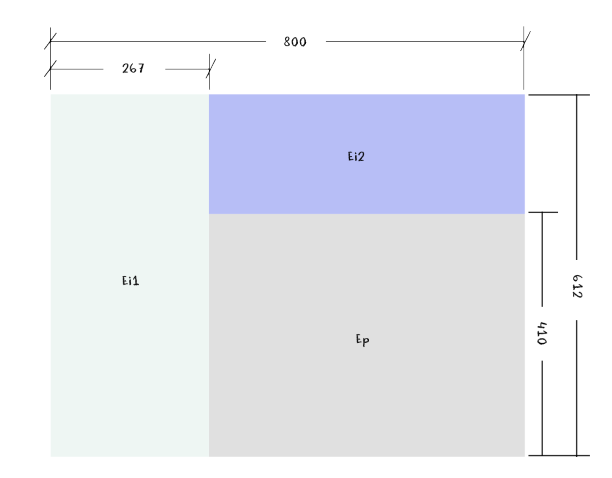
En el artículo anterior se mostró la manera en que se había realizado la siguiente escena
hasta la creación, configuración y posicionamiento del control de tipo menú y de nombre "Espiral". La siguiente imágen muestra todos los controles necesarios para hacer que la escena funcione.
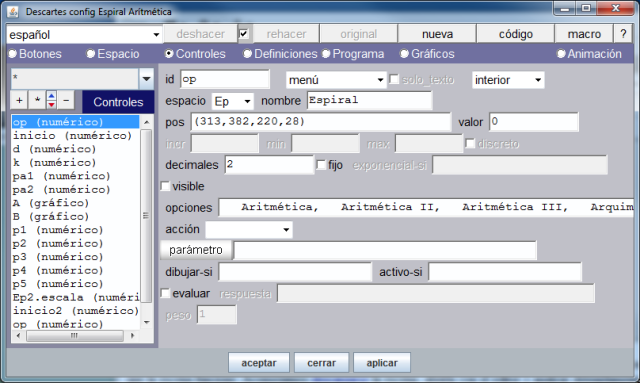
Aconsejamos descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada control. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los controles se puede examinar, y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos controles son las que comienzan por: <param name="C_x" que en nuestro caso llegan hasta <param name="C_16". Recordamos que se debe tener mucha precaución al editar directamente el código.
Ahora, seleccionando en el editor de código la opción Definiciones, observamos
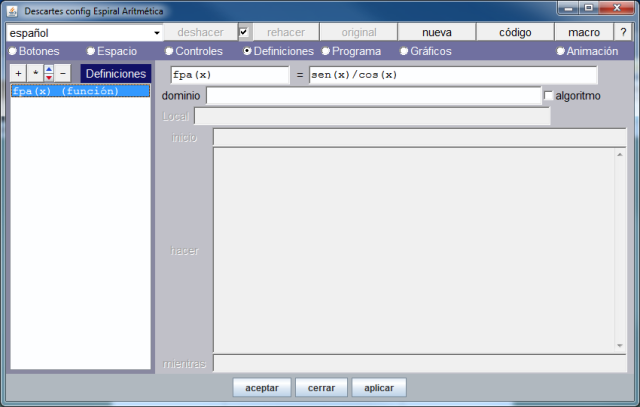
Se ha definido la función fpa que calcula la tengente de un ángulo dado en radianes para facilitar el dibujo de las familias de puntos.
En la opción Programa aún no se ha definido nada y en Gráficos se han definido varios puntos, segmentos etc... como puede comprobar el lector si abre dichas opciones de menú. En el próximo artículo explicaremos cada uno de los gráficos definidos.
Más adelante, cuando la primera fase esté completa, implementaremos los espacios informativos con los detalles de cada espiral y veremos la manera de sincronizar las distintas partes de la información.
Queremos adelantar, por si el lector desea hacer prácticas por su cuenta y luego comprobar los resultados, que una vez analizada la escena tal como está ahora, vamos a integrar en ella esta otra.
dedicada a la espiral de Teodoro

Pitágoras
En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo