Una hormiga está sobre una superficie que gira a una velocidad angular constante y se está desplazando, también a una velocidad constante, siguiendo una línea recta que pasa por el centro de giro. ¿En qué posición está en cada instante? ¿Cuál es la trayectoria que sigue?
Este planteamiento dinámico conduce a una antiquísima curva estudiada por Arquímedes y que describió, en torno al 225 a. C., en su libro "Sobre las espirales". Por ello lleva su nombre: "La espiral de Arquímedes.

( gif animado descargado desde http://gifsanimados.de/hormigas )
Y en la miscelánea que hemos publicado en nuestro servidor de contenidos puedes ver el camino que sigue nuestra laboriosa hormiga seleccionando las velocidades que desees y observando en qué influyen éstas.
A partir de la construcción dinámica --dependiente del tiempo--, se procede al análisis de esta curva que se inicia con la obtención de la relación --digamos estática o atemporal-- entre la distancia y el ángulo polar. Ésta es la ecuación algebraica en coordenadas polares de la espiral de Arquímedes y nos permite identificar el significado físico de los dos parámetros específicos de la misma. El primero es la posición o distancia inicial al centro de giro o polo y el segundo es la relación entre la velocidad lineal y la angular:

Interactuando con la escena y manteniendo inicialmente el parámetro b fijo, podremos observar como la variación del parámetro a lo que se produce es un giro en la curva, y podremos ver dos ramas que tienen simetría especular.
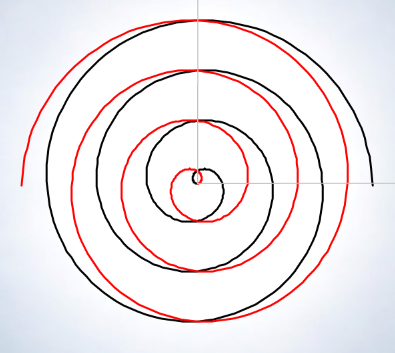
En el caso particular que b sea cero la espiral degenera en una circunferencia e incluso en un punto si también se tiene que a es cero.
En una última instancia se puede verificar analítica y experimentalmente como todos los puntos de la espiral que están situados sobre la recta de ecuación q = constante son equidistantes entre sí y, por tanto, sus distancias al polo constituyen una progresión aritmética de diferencia 2pb. Por esta razón, a la espiral de Arquímedes, también se le denomina espiral aritmética.
Pulsando sobre la imagen siguiente puedes acceder al contenido de esta miscelánea:
¡Te deseamos un buen aprendizaje siguiendo a nuestra hormiga!



 CONTACTO
CONTACTO


