Mostrando artículos por etiqueta: espirales
La esencia del Nautilus es ostensiblemente cordobesa, pero al analizar su ontogenia biológica se detecta un comportamiento diferente en cada uno de los tres verticilos que pueden contabilizarse en la concha de todo animal adulto. Esta diferencia es especialmente manifiesta y significativa en el primero de ellos. En este artículo, nos ponemos nuestras gafas matemáticas para tratar de localizar la causa y así poder mejorar el modelo matemático uniforme que previamente habíamos compartido. Aquí, nos adentramos plenamente en la ontogenia matemática del Nautilus. Toda espera queda satisfecha para quienes son pacientes y están interesados.
En los artículos previos (Ontogenia I y Ontogenia II) llegamos a detectar la necesidad de una revisión del modelo cordobés uniforme del Nautilus, en especial en el primer verticilo. Y para lograr modelar la ontogenia matemática citada, tendremos que apoyarnos en la ontogenia biológica detectando en ésta los diferentes detalles y particularidades que determinan las características esenciales en cada momento y etapa, y tendremos que concretar cada una de ellas para su adecuada traslación al modelo matemático final. Esto es lo que abordaremos a continuación.
Observando la ontogenia biológica del Nautilus con gafas matemáticas
Concha embrionaria
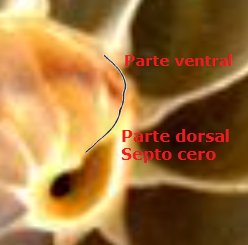
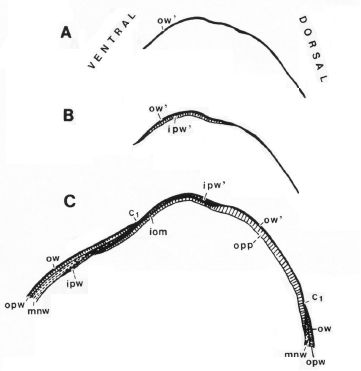
La concha embrionaria inicial, aquella que no tiene ninguna cámara y septo, y de ahí que se le denomine preseptal, tiene aspecto de lapa (Figuras 7 y 10). Su perfil (imagen A de la Fig. 11 y Fig. 15) queda modelado por dos curvas: una que se corresponde con la parte ventral, aquella que tendrá continuidad en la pared ventral de la concha, y otra dorsal que podría considerarse como el septo inicial o septo cero (Mutvei & Doguzhaeva, 1997). Esta característica primigenia se traslada y mantiene permanente en todas la etapas vitales, es un invariante, pues como conocemos se verifica que todo punto interior a la concha o sobre ella se obtiene como la intersección de dos curvas espirales, una longitudinal similar a la ventral y otra transversal similar a la septal.
Curvatura ventral
La constricción de la cicatriz, coincidente con la intersección de la concha embrionaria con el primer septo, es la que marca el inicio del patrón de crecimiento correspondiente a la sección de la concha ventral. A partir de la imagen correspondiente a la fase del primer septo (ver Fig. 16) podemos observar claramente la curvatura de la parte ventral y verificar cómo ésta se ajusta a una espiral cordobesa, ajuste que permanece durante toda la vida del animal (Fig. 17). Consecuentemente, ésta es una característica intrínseca y permanente, un segundo invariante, en toda la ontogenia del Nautilus desde el periodo embrionario septal a la madurez.
 |
 |
 |
| Fig. 15. Perfil de la concha embrionaria o preseptal | Fig. 16. Ajuste de la pared ventral en la fase del primer septo. C1: Constricción |
Fig. 17. El perfil ventral es cordobés en toda la etapa vitall |
Tangencialidad de los septos con la pared ventral de la concha
En las imágenes de las figuras 12, 13 y 14 puede intuirse que las paredes septales confluyen con la pared ventral de la concha tangencialmente, lo cual a priori parece lógico que acontezca para que el cuerpo del animal pueda asentarse de manera uniforme en la zona de unión de ambas paredes. Eso se visualiza claramente a nivel microscópico (Fig. 18), donde en la parte apical (parte izquierda en esa imagen) también puede observarse un cemento de unión entre ambas paredes que a nivel macroscópico difumina esta tangencialidad y puede inducir a interpretar inadecuadamente la forma en que ambas capas confluyen. Esta tangencialidad se da en toda la ontogenia del Nautilus, tercer invariante, y necesitamos destacarla y fijarla porque es básica para el modelo matemático buscado.
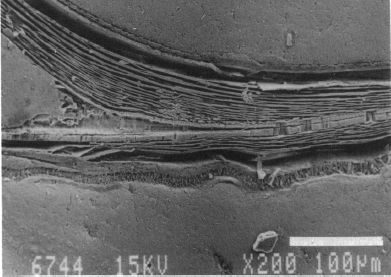
Fig. 18. Detalle de la unión del segundo septo y la parte ventral de la concha en la fase de dos cámaras. Ampliación de la imagen de la Fig. 13. Entre ambas paredes en la parte apical se observa un cemento de unión. (Procedente de Landmam et al.1989).
Incidencia de los septos con la pared dorsal de la concha
La modelación de la incidencia de los septos con la pared dorsal requiere un análisis detallado ya que presenta variaciones destacables en cada verticilo y, por tanto, habrá que localizar la causa de las mismas. Así pues, observando la unión de los dos primeros septos con dicha pared dorsal (Fig. 19) podemos constatar que aquí no acontece, no se reproduce, la indicada tangencialidad ventral y se detecta cemento de unión en la parte apical (en esta imagen ubicada a la derecha) y en la adoral (izquierda). Matemáticamente, si partimos de que la forma del septo sigue una determinada curva prefijada (en el modelo global uniforme indicamos, mostramos y asumimos que es un arco de espiral) y considerando la tangencialidad indicada de éste con la pared ventral, entonces se concluye que la incidencia que acontece con la pared dorsal viene dada, está preestablecida, es forzada y tiene que asentarse según el ángulo que corresponda en cada momento, y quizás ello es lo que constructivamente obliga a que la unión se tenga que reforzar para obtener una consistencia adecuada (de ahí el cemento indicado). Algebraicamente, detectada la forma de la de la pared dorsal, la determinanción del ángulo y punto de incidencia quedan reducidos a intersecar la ecuación del septo con la de la pared dorsal, y eso es lo que haremos en su momento y en cada una de las fases del crecimiento, las cuales hemos asociado a cada verticilo.

Fig. 19. Detalle de la unión de los dos primeros septos (1 y 2) y la parte dorsal de la concha en la fase de dos cámaras. Ampliación de la imagen de la Fig. 13. Entre ambas paredes se observa un cemento de unión. (Procedente de Landmam et al.1989).
Adicionalmente, dado que la parte dorsal de la concha es diferente en el primer verticilo (lo analizaremos posteriormente en un apartado específico), la amplitud del arco del septo parece ser variable y ,si es así, tendrá que acortarse o alargarse hasta encontrar el punto de apoyo necesario para el cierre de cada cámara. Acorde con ello, el ángulo de incidencia observado parece ser diferente en los septos del primer verticilo (observar detenidamente la Fig. 20, imagen A). En esa misma figura se observa que en el segundo verticilo, en el área dorsal media (mda), son ostensibles las depresiones septales dorsales (dsd), ver detalle de su forma en las imágenes B, C y D, y éstas se vuelven menos notables en el tercer verticilo. La ontogenia biológica parece mostrarse esquiva con la matemática o simplemente gusta de marcarnos retos adicionales sobre los que dilucidar.
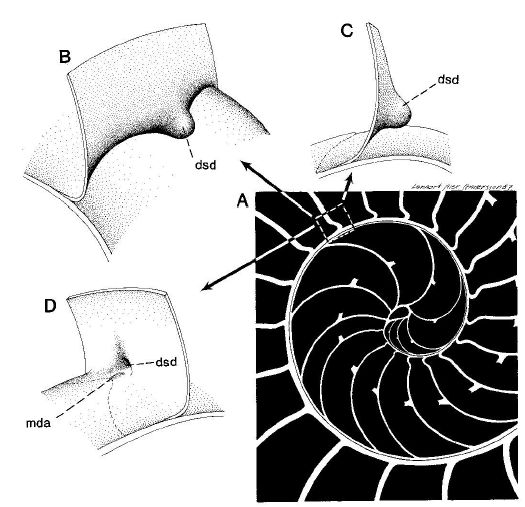
Fig. 20. Sección de la concha del Nautilus. Diferentes vistas de la depresión septal dorsal (dsd) en el área dorsal media (mda). (Procedente de Mutvei & Doguzhaeva, L. 1997).
Labio dorsal y ombligo
Como indicamos con antelación (ver la figura 10) es en la constricción dorsal, que es también el punto de incidencia del primer septo, donde el perfil de la concha en su parte dorsal cambia su concavidad y adopta la misma que la pared ventral, si no fuera así, la cavidad se cerraría. Y al confluir la pared dorsal de este primer verticilo con la concha embrionaria preseptal es como se forma el ombligo.
A priori, no es fácil poder modelar con certeza la forma que adopta este labio dorsal dado que su recorrido es inferior a una vuelta y, consecuentemente, las referencias sobre las que apoyarse puede que no sean suficientes. Lo que sí puede observarse es un posible crecimiento en espiral, es esperable que sea así ¿verdad?, y además que ésta sea una espiral geométrica para que el crecimiento sea gnomónico; por tanto, planteamos y establecemos esta hipótesis. Adicionalmente, por uniformidad, consideraremos que el tipo de crecimiento sea también cordobés ya que la pared dorsal en el segundo y tercer verticilo tiene esa forma (las paredes dorsales en estos verticilos eran previamente, en la vuelta anterior, sendas paredes ventrales ) y es lógico que ésta se mantenga en el primero o mejor dicho que ésa sea la tendencia original que continúa posteriormente. Es esperable y lógico que la curvatura del dorso del animal se mantenga en toda su existencia. Bajo esa consideración, lo que sí es obvio (observar la Fig. 16) que:
- La espiral que modela la pared ventral no modela al labio dorsal. Observad como la parte correspondiente a esta espiral que se ha dibujado en la imagen mediante puntos no se ajusta a dicho labio.
- El polo de la espiral del labio no puede coincidir con el polo de la espiral de la pared ventral ya que el primero ha de ubicarse en el interior del ombligo y el segundo según lo ya modelado se sitúa sobre su borde (ver Fig. 21). Estamos hablando de una distancia entre esos dos polos que estará en el entorno de un milímetro y que puede parecer una diferencia no significativa, sin embargo, como veremos, ésta es realmente la clave diferenciadora y la causa de las variaciones que se observan en el crecimiento durante el primer verticilo respecto al de los restantes. Sí, ¡así es de simple!. A nivel global, a la escala de la concha de un ejemplar maduro, no hay una diferencia visual entre ambas (ver en la esquina superior derecha en la figura 21 que la espiral ventral, en color azul, y la dorsal en rojo se "solapan"), pero a nivel local se contempla un comportamiento muy diferenciado (ver la parte central en esa figura 21), ¡esas son las maravillas de la espiral logarítmica o geométrica o "Spira mirabilis" como la bautizó Jacob Bernoulli.
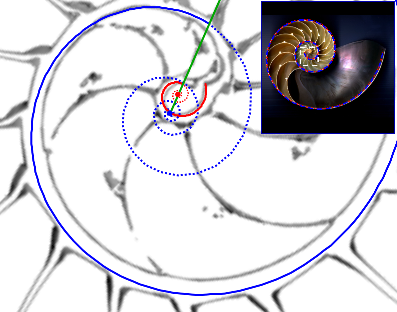
Fig. 21. Modelización de la concha en el primer verticilo. Espirales cordobesas con diferente polo. En rojo el labio dorsal y en azul la pared ventral. Diferenciado a nivel microscópico (imagen central) y "coincidente" a nivel macroscópico (esquina superior derecha).
¡Vaya! Ya lo había adelantado literariamente antes, pero ahora ¡se me hizo irresistible mostrarles gráficamente, en esta figura 21, la causa o germen que permitirá comprender mejor al Nautilus! Bien sabe quien se dedica a investigar que no puede ocultarse la satisfacción cuando en el interior de nuestra mente surge la inspiración ¡Ajá! que sublimó Martin Gardner y la que llevó a Arquimedes a correr desnudo, insconcientemente, a la par que gritaba ¡Eureka! a sus paisanos de Siracusa. Y salvando las distancias y comparaciones, estaba deseoso de que lo vieran. Pero esa inspiración inicial, que esporádicamente regalan las musas generalmente sólo a quien está trabajando, no es más que la piedra angular que asienta y modula la futura estructura global, pero habrá que seguir construyendo sobre ella en base a nuevas inspiraciones y deducciones lógicas. Así pues, hemos de asentar esa piedra base y aplicar todos los detalles detectados, analizados y descritos en la particular revisión que hemos realizado de la ontogenia biologica del Nautilus, para así llegar con paso firme a nuestro objetivo que es poder comunicarles lo que sotto voce nos cuenta el Nautilus acerca de su ser y crecer, y poder hacerle de traductor al lenguaje que muchos catalogan como el criptográfico o secreto de la Naturaleza: el matemático. Ahora sí, llegó el momento esperado, o al menos anunciado, de formular detalladamente la Ontogenia matemática del Nautilus. Gracias por ser pacientes, considero que se verán gratificados por haber llegado aquí y por continuar conmigo.
Ontogenia matemática del primer verticilo del Nautilus
Para realizar el análisis matemático en este primer verticilo utilizaremos el siguiente recurso interactivo (escena interactiva 2):
Escena interactiva 2. Concha y sifúnculo del Nautilus en el primer verticilo.
Puede interactuar libremente con ella. Si posiciona el ratón sobre los botones tendrá una breve información o consulte las instrucciones.
Modelando el labio dorsal
Para mostrar la modelización del labio dorsal y el primer verticilo hemos elegido la concha digitalizada por el Museo de D’Arcy Thompson (Fig. 22) en la Universidad de Dundee y, en particular, los datos tridimensionales aportados por dicho museo correspondientes a esa digitalización. A partir de ellos, González-Restrepo (2019) obtuvo la sección sagital y las parasagitales (Fig. 23), así como las radiales. Realizamos esta elección porque en esta fuente gráfica el corte con los septos del primer verticilo y con los restos del canal sifuncular es más visible que los que pueden observarse en la concha que hemos utilizado, hasta ahora, como soporte de referencia para mostrar el modelo uniforme y las propiedades observadas. Aquí se puede ver que los septos del primer verticilo están incompletos y consecuentemente tampoco se visualiza el rastro del canal del sifúnculo, por tanto, no es posible modelar lo que no es visible. Esta es la razón de cambiar la referencia gráfica que utilizamos como muestra.
| Modelo tridimensional de la sección de la concha de un Nautilus pompilius. |  |
|
Fig. 22. Nautilus Shell (sectioned) by University of Dundee Museum Collections on Sketchfab |
Fig. 23. Cortes por planos paralelos al plano medio obtenidos por González-Restrepo (2019) a partir del modelo 3D del Museo Dundee. |
Partamos de que la espiral logarítmica cordobesa[1] que modela la pared ventral (representada en color azul en las imágenes y escenas) viene dada en coordenadas polares por:
![]() (1)
(1)
o en coordenadas cartesianas en función del parámetro θ :
 (2)
(2)
es decir, que ubicamos su polo en el origen de coordenadas. Adicionalmente denotaremos el ángulo inicial de la espiral como θi, y como θf el ángulo final correspondiente a la boca de la concha.
Con la notación anterior, entonces el polo de la espiral cordobesa que aproxima al labio dorsal se situaría en D(0.035, 0.080) y su ecuación paramétrica sería:
 (3)
(3)
Donde el coeficiente ![]() , verificaría que
, verificaría que ![]() .
.
De los valores posibles el que teóricamente podría ser más certero se correspondería con:
![]() (4)
(4)
pues matemáticamente representaría que el labio dorsal tiene un retraso de dos vueltas (un ángulo de retardo de 4π) respecto a la pared ventral inicial. Sería de esperar que el retraso fuera de 2π, pues ésta es la relación que acontece en los siguientes verticilos cuando la que antes era pared ventral pasa a ser la nueva pared dorsal en la siguiente vuelta (de ahí lo de 2π), pero lo esperado no es siempre lo encontrado.
Geométricamente, si el labio dorsal en el primer verticilo tuviera sólo el retardo de 2π se generaría un ombligo de mayor tamaño al que se observa en la concha del Nautilus. Esto representaría al animal un esfuerzo constructivo mayor, pues tendría que cubrir una superficie más amplia (en este caso más longitud dado que estamos trabajando con la sección) ya que este labio dorsal bordearía a la concha embrionaria. En la escena interactiva 3, espacio izquierdo, puede verse cuál sería la forma del labio dorsal, ombligo y concha en el supuesto de un retardo de 2π y en el espacio derecho el caso de retardo 4π. Entre las dos alternativas la correspondiente a 4π parece la más eficiente. Podrían plantearse retardos que no tuvieran que ser múltiplos de 2π, pero de partida ello no se observa como biológicamente adecuado, pues estaría considerándose que la parte dorsal del cuerpo del animal tendría un crecimiento descompensado, al menos en algún instante o periodo temporal, respecto a la ventral. Pudiera acontecer, pero el deslizamiento que realiza a lo largo del fragmacono al crecer, inspira más una situación más regular. Si en el periodo evolutivo acontecido en la larga historia de este animal han ocurrido retardos de otro tipo, al menos parece que la selección natural ha conducido al retardo de 4π que hemos detectado y que consideramos en nuestro modelo del primer verticilo.
Escena interactiva 3. Modelando el labio dorsal del Nautilus en el primer verticilo.
Puede interactuar libremente con ella. Si posiciona el ratón sobre los botones tendrá una breve información o consulte las instrucciones.
Ambas espirales comparten el mismo eje polar (en color verde en la escena), es decir, el eje de cada una de ellas está incluido en la semirrecta que pasa por el polo ventral y por el polo dorsal. Adicionalmente, esta semirrecta interseca a la concha en la constricción dorsal y la ventral que son los puntos de intersección y tangencia, respectivamente, del primer septo con la pared dorsal y la ventral de dicha concha. Esto cuadra con la ontogenia biológica descrita antes y matemáticamente aporta también una pauta común de crecimiento al compartir ambas espirales el mismo parámetro angular. El ángulo inicial común para ambas espirales indicamos que lo denotaríamos como θi y entonces el recorrido total de la espiral dorsal termina en ![]() .
.
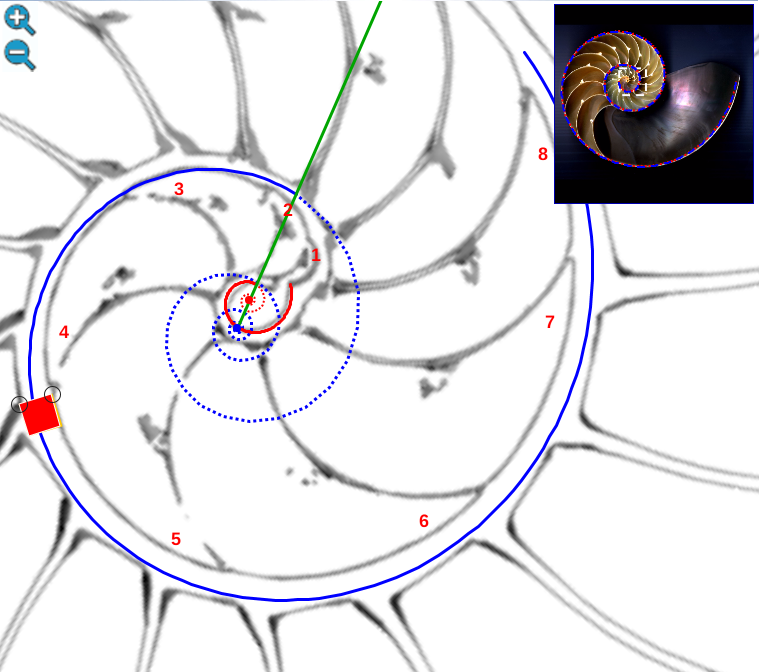
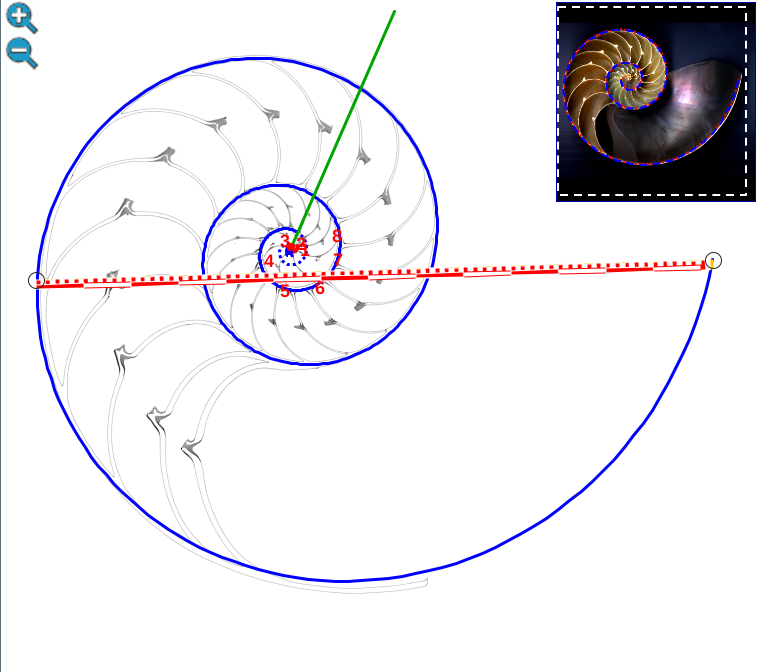
La pequeña variación existente entre los polos de ambas espirales (aproximadamente un milímetro) conduce a que el labio dorsal no finalice su recorrido siendo tangente a la concha embrionaria preseptal, sino que este labio incide e interseca a dicha concha primigenia cuando se cierra el primer verticilo y se genera el ombligo. Consecuentemente, el enlace con la parte ventral inicial no es suave, sino que se produce a través del séptimo y octavo septo. Son estos últimos septos del primer verticilo los que al apoyarse en la concha primigenia se adaptan para dar continuidad con la pared ventral inicial. El hecho de que no se produzca esa tangencialidad entre la pared ventral inicial y la finalización del labio dorsal refuerza y muestra la necesidad de considerar la existencia de dos polos diferenciados en el modelo teórico y, también, que no se pueda atribuir esta diferencia a un error en la precisión del ajuste gráfico realizado[2]. Ver detalle del modelo a nivel local en la figura 22 y a nivel global en la figura 23.
 |
 |
|
Fig. 22. Ajuste del labio dorsal (espiral en rojo) y de la pared ventral en el primer verticilo (espiral azul)). La sección gráfica de referencia se debe a González-Restrepo (2019). En rojo la regla de medida que marca 1 mm. |
Fig. 23. Ajuste global de la concha del Museo de D’Arcy Thompson, en base al corte realizado por González-Restrepo (2019). La regla de medida marca 143 mm. |
El canal sifuncular en el primer verticilo
En nuestro primigenio modelo uniforme detectamos que el canal sifuncular actuaba como el eje del fragmacono, es decir, que es equidistante de la pared ventral y dorsal. En este supuesto uniforme ambas paredes describen sendas espirales cordobesas con igual polo, de manera que si la ecuación en coordenadas polares de la primera es ![]() , la de la segunda sería
, la de la segunda sería ![]() (realmente es la misma espiral, pero la segunda con un ángulo de retardo de 2π o coeficiente 0,3431...) y, entonces, el sifúnculo tiene de ecuación
(realmente es la misma espiral, pero la segunda con un ángulo de retardo de 2π o coeficiente 0,3431...) y, entonces, el sifúnculo tiene de ecuación
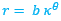 (5)
(5)
donde 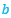 toma el valor medio de los respectivos coeficientes 1 y
toma el valor medio de los respectivos coeficientes 1 y 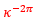 de las espirales anteriores, es decir,
de las espirales anteriores, es decir,
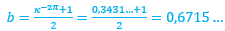 (6)
(6)
lo que se corresponde con una espiral cordobesa con un ángulo de retardo de ![]() . Pero, ya comprobamos que el ajuste anterior es adecuado en el segundo y tercer verticilo, pero no así para el primero. No obstante, ahora sí, estamos en condiciones de determinar cómo queda modelado el sifúnculo en esta primera vuelta.
. Pero, ya comprobamos que el ajuste anterior es adecuado en el segundo y tercer verticilo, pero no así para el primero. No obstante, ahora sí, estamos en condiciones de determinar cómo queda modelado el sifúnculo en esta primera vuelta.
El fragmacono en el primer verticilo está delimitado por dos espirales cordobesas cuyas ecuaciones son (2) y (3), ambas con un ángulo polar común, pero con distinto polo. Si consideramos que el sifúnculo en este verticilo tiene un comportamiento similar a los dos posteriores, entonces éste sería el eje de ese fragmacono y, para determinarlo, procedamos a determinar el lugar geométrico de los puntos del plano que equidistan de ambas y obtendremos que viene determinado por la ecuación:
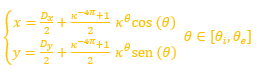 (7)
(7)
que se corresponde con una espiral cordobesa, cuyo polo![]() es el punto medio de segmento determinado por el polo de la pared dorsal
es el punto medio de segmento determinado por el polo de la pared dorsal ![]() y el de la ventral
y el de la ventral ![]() , y su coeficiente es la media aritmética de los coeficientes respectivos[3]
, y su coeficiente es la media aritmética de los coeficientes respectivos[3]
![]() (8)
(8)
Al representar gráficamente esta espiral (ver en la imagen derecha de la fig. 24 la línea discontinua en color naranja o interactuar en la escena interactiva 3) observamos que realmente no modela adecuadamente a dicho sifúnculo en ese verticilo. Sin embargo, si observamos en esa figura 24 la espiral trazada en una línea continua, también de color naranja, ésta sí se ajusta al los restos del canal sifuncular.
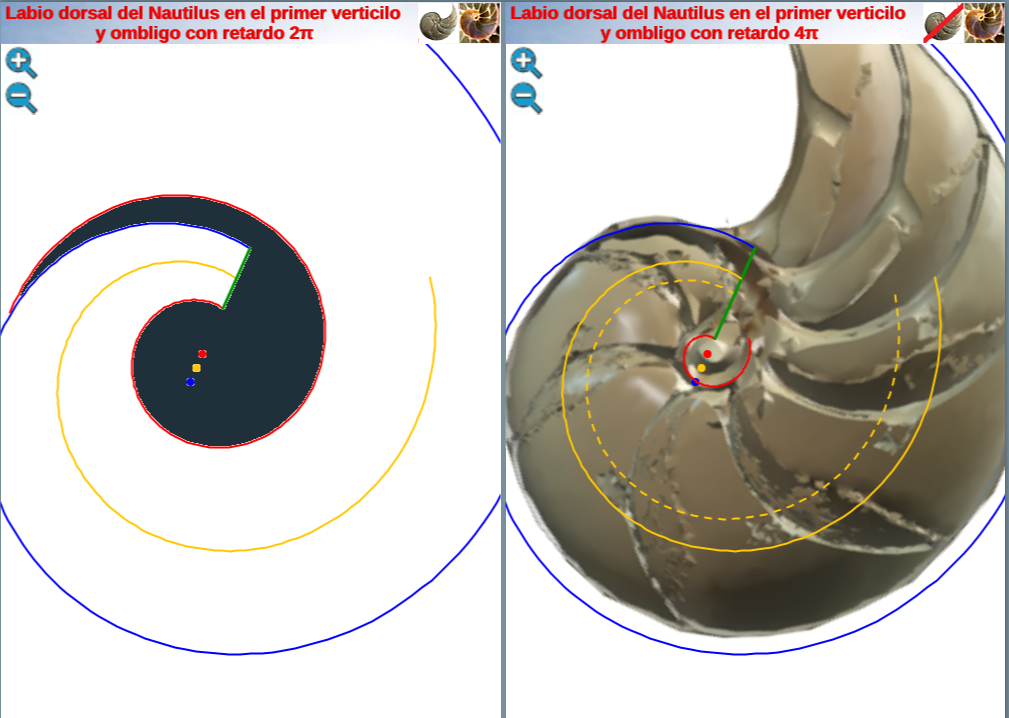
Fig. 24. En la imagen de la izquierda y de la derecha eje del fragmacono en el primer verticilo cuando el labio dorsal tiene un retardo de 2π (espiral continua de color naranja). A la derecha en línea discontinua eje del fragmacono en el primer verticilo cuando el labio dorsal tiene un retardo de 4π. La primera se ajusta al canal sifuncular.
La ecuación de esa espiral y sifúnculo es la siguiente:
 (9)
(9)
donde
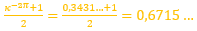 (10)
(10)
y se correspondería con el eje del fragmacono, pero en el caso de que el labio dorsal tuviera sólo un retardo de 2π (ver imagen izquierda en la figura 24 o interactuar en la escena 3). Ese coeficiente o retardo en el sifúnculo es el mismo que acontece en el segundo y tercer verticilo, pero aquí el polo es diferente. En la figura 25 podemos ver una comparativa de la espiral sifuncular aquí determinada (en color naranja) y la del sifúnculo en el modelo uniforme (en turquesa).
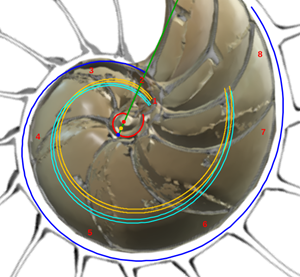
Fig. 25. Comparativa de la espiral sifuncular del primer verticilo (naranja) y la del sifúnculo en el modelo uniforme (turquesa).
Así pues, la causa de que el sifúnculo tenga un comportamiento diferenciado en el primer verticilo se centra en el hecho de que el labio dorsal y la pared ventral tienen diferente polo. La explicación de cuál es la causa de su desviación respecto al eje del fragmacono queda abierta...
Pienso que hemos dado un gran paso en la comprensión y explicación de la ontogenia matemática del Nautilus. En ella, sigue imperando su carácter netamente cordobés, introduciendo bonitos matices matematicos que explican los matices biológicos observados. Pero D. Antonio Machado nos indicó que se hace camino al andar y para ello, después del primer paso dado, han de llegar otros y en nuestro estudio, ahora, tendremos que centrarnos especialmente con las paredes septales y, ¿por qué no?, quizás tratar de localizar cuál es el germen de la esencia cordobesa de este entrañable, al menos para mí, animalito. Así pues, tendré que preparar un nuevo artículo. ¿Será el último de esta serie o no será? El tiempo y la inspiración lo dirá... Les estaré esperando por aquí... ¡pronto!
[1] Para saber por qué esa espiral es una espiral cordobesa, por qué la razón de que la base de esa exponencial sea κ = 1,18558… y su significado, puede consúltarse: Galo et al (2016).
[2] De nuevo, hemos de recordar que el paso de la yocto-yotta realidad al modelo teórico requiere de la consideración de cierta tolerancia, pero que hay que saber distinguirla de la existencia de una diferencia que provoque cambios en el modelo. Si la toma en consideración de esa tolerancia no cambia el modelo podremos aceptarla y admitirla, pero habrá que evitarla cuando se provoque un cambio en él. Así pues, en este caso es obligado considerar que los polos son diferentes. Por el contrario, por ejemplo, en las espirales que hemos considerado para ajustar el perfil del labio dorsal y de la pared ventral, en especial ésta, podría aducirse que necesitarían una mejora en su ajuste a la imagen de la concha en ese primer verticilo, pero realmente no es necesario ya que tal y como se ha considerado es suficientemente adecuado para determinar el modelo global que caracteriza al genus Nautilus. Esto ya lo mostramos en la fig. 21, y lo detallamos ahora, pues al observar el ajuste de la pared ventral (espiral azul) en el primer verticilo y su ajuste global en la toda la concha, se marca de manera evidente que la tolerancia considerada es admisible para determinar el modelo a nivel tanto local como global (el grosor de la pared es inferior a un mm, lo puede medir en la escena y el ejemplar considerado tiene unos 143 mm en su etapa adulta, figuras 22 y 23) . Sin embargo, si modificásemos la posición del polo de la pared dorsal, es decir, ignorásemos la pequeña distancia que existe entre ambos polos obtendríamos variaciones no admisibles a nivel local, es decir, cambiaría el modelo y no se ajustaría a la ontogenia del Nautilus.
[3] En general puede comprobarse que dadas dos espirales logarítmicas con igual base, con el mismo ángulo polar y con diferentes polos; si se halla el lugar geométrico de los puntos de plano obtenidos mediante una combinación lineal de las mismas se obtiene que es una espiral logarítmica del mismo tipo, es decir, de igual base y ángulo polar, y con polo la combinación lineal de los polos y coeficiente la combinación de los coeficientes.
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016 a) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
González-Restrepo, F. (2019): Cortes del Nautilus a partir de la digitalización 3D del museo Dundee. Red Descartes Colombia.
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
En su primer verticilo, la concha del Nautilus tiene un crecimiento diferenciado del que acontece en el segundo y tercero. Su esencia, implícita y explicitamente, es siempre cordobesa, pero de partida el número de cámaras en ese primer verticilo son ocho y consecuentemente con paso π/4 entre ellas, frente a las diecisés y paso π/8 del segundo, paso que también ocurre en el tercero. ¿Qué acontece en la ontogenia del Nautilus que sea la causa productora de esa distinción? En este segundo artículo (desde aquí puede acceder al primero) nos adentraremos en la biología de este animal, o más precisamente en el rastro calcáreo que deja y que conforma su concha, para tratar de dar respuesta matemática a esta pregunta. Procedamos a iniciar y a adentrarnos en la ontogenia del Nautilus y desde ahí trascender a su ontogenia matemática.
La concha embrionaria y el primer verticilo
A primera vista la concha embrionaria del Nautilus (Fig. 6), en su periodo pre-cameral, aparenta una forma similar a la concha de una lapa (Fig. 7) (MolluscaBase eds., 2021), pero a diferencia del crecimiento que sigue ésta, que simplificadamente podemos decir que es radial y anular, el Nautilus aborda un cambio de concavidad en la parte dorsal y adopta una curvatura similar tanto en la parte ventral como en la dorsal (Fig. 8) y eso es lo que marca la tendencia a la forma enrollada que adquirirá con posterioridad. La parte dorsal embrionaria es inicialmente casi plana, pero en la denominada constricción de la cicatriz (Fig. 11), coincidiendo con el inicio de la formación de las primeras cámaras y septos, es cuando se produce ese cambio de concavidad que forma el labio interior dorsal (observar en la parte inferior de la Fig. 6-D el piquito que está formándose y en las figuras 12 a 14 cómo se va desarrollando ese labio). Si no se produjera ese cambio de concavidad, irremediablemente la concha se cerraría al intersecar consigo misma. Cuando al crecer, el labio llega a confluir con la parte dorsal inicial de la concha se produce la formación del espacio umbilical u ombligo (Figura 10), momento en el que se completa el primer verticilo y, consecuentemente, la parte ventral inicial de la concha pasa ahora a ser interior a la misma y comienza a actuar como nueva parte dorsal de la cámara habitacional en el segundo verticilo.
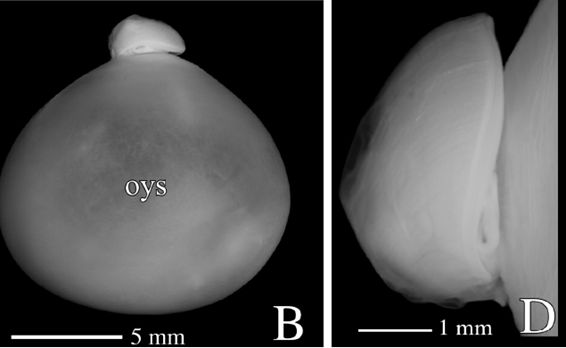
Fig. 6. Embrión de 4 meses del Nautilus pompilius. Imagen B: Perfil con el saco vitelino exterior (oys: outer yolk sac). Imagen D: Detalle de la concha embrionaria. (Procedente de Sasaki, et al., 2010).

Fig. 7 Lapa (Patella). Muséum national d’Histoire naturelle, Paris (France).
 |
 |
|
Fig. 8. Embrión del Nautilus belauesis dentro de la cápsula del huevo (éste ha sido recortado en la parte superior. El embrión contaba con una cámara septal. Procedente de Saunders and Landman (2010: pl. IV, p. xxxiv) |
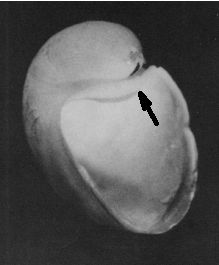
Fig. 9. Labio dorsal (señalado por la flecha) en la concha del Nautilus en la fase de dos cámaras. (Procedente de Landmam et al.1989). |
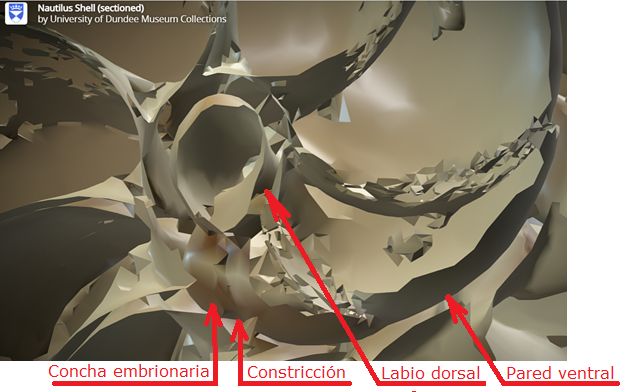
Fig. 10. Detalle del ombligo y de las primeras cámaras. Se observa la concha embrionaria inicial tipo lapa, la constricción que marca el inicio de la pared ventral y el cambio de curvatura en la pared dorsal.
(Procedente de la imagen 3D de la Universidad de Dundee).
Así pues, el perfil de la concha embrionaria preseptal del Nautilus (Fig. 6) puede simplificarse o sintetizarse en dos líneas curvas: la que delimita la parte dorsal y la correspondiente a la ventral (parte izquierda y derecha respectivamente en la figura 6.B). Esta simplificación nos recuerda y hace pensar en la conjunción, antes señalada, entre la espiral longitudinal y la transversal observada en el análisis resumen expuesto en la introducción. Y esa perspectiva se refleja claramente en la sección de dicha concha embrionaria correspondiente a esa fase preseptal (Fig. 11) donde la parte dorsal embrionaria bien podremos catalogarla como el septo cero o inicial (Mutvei & Doguzhaeva, 1997, indican que el protosepto o capa interior sobre la concha inicial es un septo que carece de tubo sifuncular).
Precisamente es en la constricción de la cicatriz (C1 en la Fig. 11) donde la concha adopta la curvatura cordobesa en la pared ventral e inicia el cambio de concavidad en la pared dorsal, iniciándose el labio dorsal. Las figuras 12 a 14 muestran el desarrollo durante la formación de los tres primeros septos.
 |
 |
|
Fig. 11. Desarrollo sucesivo de diferentes capas inorgánicas en la concha preseptal del Nautilus. |
Fig. 12. Sección media dorsoventral de la concha embriónica del Nautilus macromphalus en la etapa del primer septo (S1) y engarce del sifúnculo (Procedente de Tanabe, and Uchiyama, 1997). |
 |
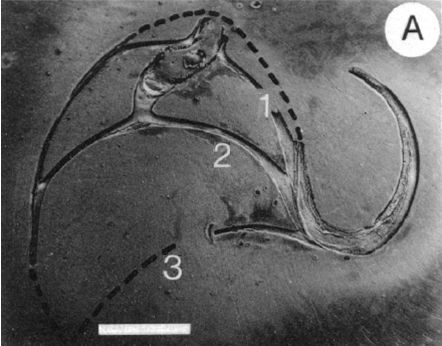 |
| Fig. 13. Sección media dorsoventral de la concha embriónica del Nautilus belauensis en la fase de dos cámaras (Procedente de Landmam et al.1989. Se corresponde con el ejemplar de la Fig. 9). | Fig. 14. Sección en la concha del Nautilus belauensis en la fase de tres cámaras. Las líneas discontinuas señalan las partes fragmentadas y perdidas al efectuar el corte. (Procedente de Landmam et al.1989). |
En la discusión que realizan en su artículo, Landman et al. (1989) exponen que la concha del Nautilus sufre marcados cambios durante la embriogénesis, en particular indican que durante la etapa de dos y tres cámaras, en el fragmacono, las proporciones que acontecen entre el volumen de las cámaras septales y el de la cámara habitacional son pequeñas y difieren de las alcanzados en etapas ontogénicas posteriores, ello es debido a que la longitud de la cámara habitacional es mucho mayor en la primera etapa vital que en la fase juvenil y adulta. Sin embargo, el perfil de la concha sí se asemeja en todas las fases.
Con la base y los detalles aportados hasta ahora, nos surge el interrogante acerca de: ¿qué acontece con nuestro modelo cordobés uniforme (con igual forma durante todas las etapas vitales) del Nautilus —un modelo bien adaptado a nivel global y macroscópico, como ya hemos mostrado en detalle— si lo confrontamos con esa fase inicial, que biológicamente está indicada como diferenciada? Pues, de partida, lo que ocurre es que se inicia una nueva etapa investigadora, un nuevo camino que recorrer a hombros de estos gigantes biológos, antes explícitamente citados, y de otros muchos más omitidos por economia literaria, pero por supuesto no olvidados, y junto a los de numerosos gigantes matemáticos poder modestamente contribuir a la "Ontogenia matemática del Nautilus". ¡Avancemos, pues!
Para poder adentrarnos en este análisis y contraste, podemos aglutinar todo lo indicado en un recurso interactivo ( ver la escena interactiva 1) que nos permita tener una visión solapada comparativa y que ayude en la conceptualización de lo que acontece, es decir, partir de una agrupación de instantáneas para lograr extraer un continuo descriptivo matemático. Es obvio, de nuevo es necesario indicarlo aunque pueda ser reiterativo, que la superposición de las fotos anteriores mostrará variaciones, algunas debido a que proceden de diferentes ejemplares y especies de Nautilus, otras serán consecuencia de la variabilidad que intrínsecamente acontece en todo espécimen o individuo concreto dentro de las características comunes e identificadoras que comparten y que definen a esa especie; o quizás que estén generadas por posibles desviaciones angulares al realizar los cortes sobre la concha para obtener su sección o perfil. En definitiva, errores comunes e implícitos en cualquier estudio y que aquí, adicionalmente, se ven magnificados gracias a la amplificación visual que nos aporta la técnica. Pero en esa escena, si alguien tiene un empeño cuantificador especial, puede verificar ―con la regla interactiva que se dispone― que nos adentramos en variaciones en el entorno de la décima de milímetro. Estos son detalles con los que se ha de convivir y que han de ponderarse en su justa magnitud para lograr esa visión global y poder encuadrarse en la perspectiva de búsqueda de un modelo o patrón conceptual y así lograr encontrarlo.
A continuación puede interactuar con dicho recurso interactivo y podrá abordar, si lo desea, su investigación personal a través de las diferentes herramientas que ahí se incluyen:
Escena interactiva 1. El modelo cordobes uniforme del Nautilus (revisión)
Nuestra reflexión la dejamos reflejada en la siguiente presentación y puede también usarse como guía a reproducir en la escena interactiva anterior.
Así pues, el análisis realizado nos marca varias necesidades:
- Necesidad de modelar el labio dorsal y el ombligo.
- Necesidad de estudio específico de la concha del Nautilus en el primer verticilo y su ontogenia en general.
- Necesidad de mejorar el modelo de confluencia de septos y paredes en el segundo y tercer verticilo.
En definitiva, contemplamos y concluimos que es obvia la necesidad de abordar la citada "Ontogenia matemática del Nautilus"... Y a ello nos dedicaremos en el siguiente artículo. Para no impacientarse "juegue" con el recurso interactivo aportado y adéntrese en los artículos indicados en la bibliografía descrita.
Bibliografía
MolluscaBase eds. (2021). MolluscaBase. Patella vulgata Linnaeus, 1758. Accessed through: World Register of Marine Species at: http://www.marinespecies.org/aphia.php?p=taxdetails&id=140685 on 2021-08-22
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Sasaki, T., Shigeno S. & Tanabe K. 2010. Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea (2010) in Tanabe, K., Shigeta, Y., Sasaki, T. & Hirano, H. (eds.) 2010. Cephalopods - Present and Past, Tokai University Press, Tokyo, p. 35-66.
Saunders, W. B., and N. H. Landman (eds.) 2010. Nautilus: the biology and paleobiology of a living fossil. (Springer. First edition New Y 1987) Plenum Press, New York.
Tanabe K. & Uchiyama, K. 1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Hace unos años mostramos que la forma y el crecimiento del Nautilus, prototipo de belleza natural y matemática, era neta y completamente cordobés. No obstante, manteniéndose dentro de ese canon, el desarrollo no es uniforme en todas sus etapas vitales y, en particular, en su etapa inicial marca diferencias que son dignas de modelar. Así pues, nos planteamos trasladarles en varios artículos de este blog la ontogenia matemática del Nautilus y le mostraremos que en la primera etapa el modelo se corresponde con un patrón de dos espirales cordobesas con diferente polo y, sin embargo, en la etapa juvenil y adulta éstas comparten el mismo polo. Un mínimo detalle que hay que añadir al buen hacer matemático de este animalito y que da explicación a su acontecer vital, permiténdonos comprender nuevos detalles de su ser.
Quedan invitados a su lectura y quedamos deseosos de sus comentarios y observaciones
Introducción
El Nautilus, usualmente catalogado como un fósil viviente ―si bien Ward (1984) lo encuadra en una estasis aparente[1]―, ha llamado siempre la atención no sólo por la belleza exterior de su concha, quizás no excesivamente destacable frente a la de otros moluscos, sino por aquella que esconde en su interior, ¡que es sorprendente!, y no deja indiferente a nadie. Por ello, ha sido ampliamente estudiada desde el punto de vista paleontológico, zoológico, biológico u ontogénico, pero también en el mundo artístico, el arquitectónico, el ingenieril, el físico-químico y, por supuesto, en el matemático. Incluso ha llegado a ser idealizada en estos entornos científicos, sin olvidar el contexto literario donde también se ha adentrado en lugares preminentes. Aupada como prototipo de belleza ha sido continuamente encajonada de manera forzada en el canon de belleza o proporcionalidad divina o áurea, a pesar de su resistencia y continuo grito de: ¡No!, ¡No soy áureo!, clamor que puede ser inaudible para legos, pero no debería serlo para eruditos. Más fácil hubiera sido haber creado la proporción nautílica, como referente o neotipo de belleza, que con rocambolescas maneras tratar de estirar, contraer o moldear su fina superficie calcárea, pues ello es una suerte imposible de lograr con tan frágil soporte.
En el artículo “Sobre la forma y el crecimiento cordobés del Nautilus pompilius” (Galo, Cabezudo y Fernández, 2016 a) detectamos y expusimos que la espiral logarítmica que se ajusta al perfil de la concha del Nautilus se corresponde con una espiral cordobesa (Fig. 1).

Fig. 1. Ajuste del Nautilus por una espiral logarítmica cordobesa (Galo et al. 2016 b).
Este hallazgo coyuntural que no deja de ser una mera coincidencia numérica, aunque para nosotros muy agradable, con la razón denominada cordobesa y que consecuentemente nos permite asociar su nombre al de Nautilus, hubiera quedado como una curiosidad anecdótica si no fuera porque ahí señalamos y detallamos (ver Fig. 2 y 3) que todo en el Nautilus se muestra cordobés ―sí, nosotros estuvimos silenciosos y atentos y le oímos decir: ¡Qué soy cordobé![2] (ver Fig. 4) ―:
- El rastro calcáreo del sifúnculo (órgano que vacía las cámaras y actúa en la consecución de la flotabilidad del animal) muestra que éste crece siguiendo la forma de esa espiral cordobesa y que es el eje de simetría del teórico cono topológico que forma la cavidad que ha ido construyendo y recorriendo el animal en su ciclo vital.
- Los septos (tabiques que conforman las cavidades de flotación) son arcos de una espiral que es también cordobesa.
- El polo de esos arcos septales se desplaza siguiendo una espiral del mismo tipo, cordobesa, que es la mediatriz de todos los radios vectores de la espiral de la concha.
- Todo punto de la concha o interior es la intersección de dos espirales cordobesas, una longitudinal (tipo a la del perfil de la concha, pero con un factor de escala) y otra transversal (tipo septal).
 |
 |
|
Fig. 2. Espiral que aproxima perfil de la concha (azul), la de los septos (amarilla) y la que describe el polo de los arcos septales (magenta). |
Fig. 3. Detalle de la espirales sobre las que se aproximan los septos: perfil de la concha (azul ),septos (amarilla) y la que describe el polo de los septos (magenta). |
 |
|
Fig. 4. El Nautilus es “cordobé”. |
Así pues, en el artículo citado ” (Galo, Cabezudo y Fernández, 2016 a) se buscó y se logró captar la esencia nautílica matemática a nivel conceptual global: “todo en el Nautilus se muestra cordobés”, y el modelo matemático que ahí se consideró fue único e indiferenciado en todo el crecimiento. Se aplicó la consideración de que dado que el crecimiento del Nautilus es gnomónico, es decir, que mantiene su forma cambiando su escala, se puede hacer una lectura atemporal esperando que el modelo sea aplicable en toda la fase vital desde su germen a su madurez. No obstante, esto, no es más que un útil deseo purista matemático que se mostrará débil para cualquier detenido observador que aborde su confrontación con la realidad, pues somos conscientes por experiencia vital personal que en el desarrollo de un ser vivo acontecen diferentes fases o etapas que introducen matices distintivos dentro de una esencia identificadora que permanece. Y siguiendo esta línea diversificadora, en este artículo lo que se persigue es abordar la ontogenia matemática del Nautilus, desde su periodo embrionario hasta la madurez y determinar cuál es el modelo matemático diferenciado en cada una de las etapas de crecimiento en correlación con los estudios biológicos micro y macroscópicos existentes. Y, de hecho, aquí veremos que se pueden diferenciar tres etapas que esencialmente se corresponden con cada uno de los tres verticilos (un verticilo es una revolución de 360° en el crecimiento en espiral de la concha de un molusco) que se contabilizan en la espiral de la concha de un ejemplar adulto, tres etapas que encierran ciertas diferencias y matices dentro del citado modelo cordobés global. Todo, sin olvidar y teniendo siempre presente, siendo conscientes, que cuando atravesamos el canal que enlaza la discreta yocto-yotta realidad, en la que vivimos, con la idealizada continuidad del mundo matemático siempre surgen interferencias (“aliasing”) que trataremos de mitigar y/o detallar, aunque hay que asumirlas.
La referencia zoológica de la que partiremos es: “Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea” de Sasaki, Shigeno & Tanabe (2010) donde, aportando unas magníficas fotografías, se aborda una revisión de la anatomía del Nautilus, que si bien se centra principalmente en los órganos y partes blandas, incluye también información sobre la forma embrionaria de la concha. Adicionalmente, en la introducción de ese artículo los autores detallan la literatura más significativa al respecto comenzando con el libro de Saunders and Landman (1987) que compila el conocimiento sobre el Nautilus hasta ese año y que posteriormente ha sido actualizado en la edición de 2010. Ladman et al. (1989) analizan la concha en el periodo embrionario y muestran su desarrollo hasta el tercer septo, estudio que se complementa en Mutvei and Doguzhaeva (1997), donde se muestran las curiosas depresiones dorsales septales en el segundo verticilo, y en Tanabe and Uchiyama (1997). Estos artículos nos servirán de soporte, guía y verificación en nuestro análisis matemático. También el modelo virtual tridimensional e interactivo de la concha del Nautilus del “D’Arcy Thompson Zoology Museum”, obtenido mediante escáner, es una magnífica fuente de observación visual interactiva, si bien hay que tener presente y es ostensible que el corte del ejemplar que se ha usado para su digitalización no coincide con el plano medio de simetría. Pueden consultarse otros modelos tridimensionales en Sketchfab.
| Modelo tridimensional de la sección de la concha de un Nautilus pompilius. |  |
|
Nautilus Shell (sectioned) by University of Dundee Museum Collections on Sketchfab |
Cortes por planos paralelos al plano medio obtenidos por González-Restrepo (2019) a partir del modelo 3D del Museo Dundee. |
La concha embrionaria y el primer verticilo
Landman et al. (1989) exponen que la forma de la concha del Nautilus sufre marcados cambios durante la embriogénesis y que los perfiles en la etapa de dos y tres cámaras difieren de los alcanzados en etapas ontogénicas posteriores. En nuestro artículo (Galo et al., 2016 a) ya pusimos de manifiesto (Fig. 5) que en el primer verticilo se contabilizaban ocho cámaras, frente a las dieciséis del segundo, es decir, cambia el paso interseptal teórico que en un primer momento es π/4 y posteriormente pasa a ser π/8. Este paso se mantiene también en el tercer verticilo, si bien en esta fase adulta pueden acontecer ciertos cambios morfológicos que influyen en los últimos septos y ése paso puede ser algo menor. En la imagen de la fig. 5 son ocho los septos en el tercer verticilo, pero este número es variable. A pesar de indicar estas diferencias, allí, optamos por presentar un modelo matemático teórico uniforme considerando un crecimiento idéntico en toda la vida del animal y ello permitió fijar los comportamientos globales antes citados como que el sifúnculo sigue el eje de simetría topológico de la cámara habitacional o que los polos de los septos se ubican en la espiral mediana, propiedades que ahora, en un proceso inverso, nos serán de utilidad para analizar y comprender lo que acontece en ese diferenciado primer verticilo. Y ese estudio es el que abordaremos en esta sección donde nos detendremos en la fase embrionaria precameral, en la fase de formación de las primeras cámaras y en lo que acontece en el resto de este primer verticilo.
 |
|
Fig. 5. Recuento de verticilos y cámaras en el Nautilus. |
En el análisis de ese primer verticilo nos adentraremos en un próximo artículo de este blog... no tardará en llegar.
[1] “Rather than being a prime example of a living fossil, the nautiloids may be examples of rapidly speciating organisms that change only slightly during each event, and return to the same form over and over. The result would be apparent stasis, but the actual history would be similar to that of any other rapidly speciating group-except that the net morphologic change over time would be small, rather than large” (Ward, 1984).
[2] En Córdoba (España) la pronunciación de las eses a final de palabra suele ser muy débil y para los oídos no habituados a esa tonalidad, éstas quedan como omitidas.
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016 a) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
Galo J.R., Cabezudo A. y Fernández I.(2016 b) : Recurso interactivo Sobre el crecimiento cordobés del Nautilus Pompilius. Red Educativa Digital Descartes.
González-Restrepo, F. (2019): Cortes del Nautilus a partir de la digitalización 3D del museo Dundee. Red Descartes Colombia.
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Sasaki, T., Shigeno S. & Tanabe K. 2010. Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea (2010) in Tanabe, K., Shigeta, Y., Sasaki, T. & Hirano, H. (eds.) 2010. Cephalopods - Present and Past, Tokai University Press, Tokyo, p. 35-66.
Saunders, W. B., and N. H. Landman (eds.) 2010. Nautilus: the biology and paleobiology of a living fossil. (Springer. First edition New Y 1987) Plenum Press, New York.
Tanabe K. & Uchiyama, K. 1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.
Ward P. (1984) Is Nautilus a Living Fossil?. In: Eldredge N., Stanley S.M. (eds) Living Fossils. Casebooks in Earth Sciences. Springer, New York, NY. https://doi.org/10.1007/978-1-4613-8271-3_31

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo.
Como prólogo a un breve estudio sobre la cuadratura del círculo, hemos analizado la manera de cuadrar algunos polígonos y hecho una breve reflexión sobre los teselados. En particular se ha visto, entre otros asuntos, el método general de cuadrar los polígonos regulares y referente a las teselaciones se ha mostrado, entre otras, la manera de teselar un triángulo cordobés con una sucesión de triángulos cordobeses.
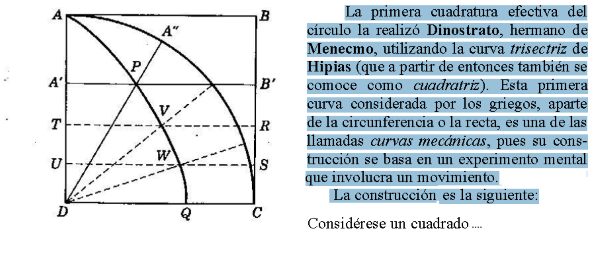
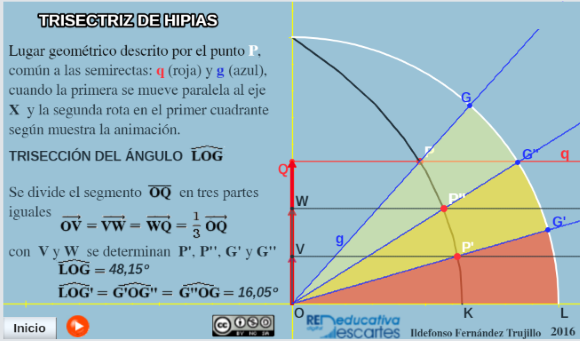
Dentro del tema que nos ocupa: los Lugares geométricos también, en su día, estudiamos las Trisectrices de Hipias y Nicomedes y en otros artículos se han expuesto misceláneas y escenas que desarrollan la espiral de Arquímedes y la cuadratriz de Dinostrato; no obstante en la presente entrada volvemos a insistir en el estudio de las primeras curvas mecánicas o lugares geométricos creados por estos autores por su evidente interés y para animar a la conversión en misceláneas de las escenas que aún no lo son.
Anteriormente hemos enlazado el extraordinario trabajo del profesor Fernando Bombal sobre la cuadratura del círculo, volvemos a hacerlo y en el leemos:
Recomendamos la lectura completa del documento así como el análisis de su extensa bibliografía.
También en entradas anteriores hemos enlazado con el blog de Miguel Ángel Morales Medina, en esta ocasión lo hacemos al básico pero minucioso artículo sobre la cuadratura del círculo: ¿Quién dijo que la cuadratura del círculo era imposible?.
A continuación y también como prolegómeno al estudio de la cuadratura del círculo enlazamos con dos pequeños trabajos sobre la cuadratura de las lúnulas: el primero de ellos creado con DescartesJS y el segundo con el programa GeoGebra.
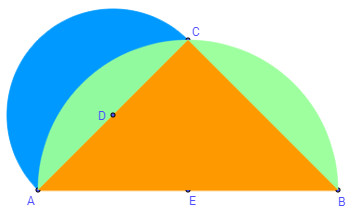
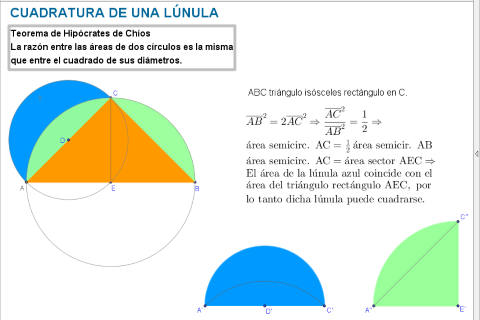
- Cuadratura de una lúnula I: Con la ayuda de dos semicírculos creamos una lúnula y aplicando el teorema de Hipócrates de Chios encontramos, según se muestra en la siguiente escena interactiva, un triángulo de igual área que dicha lúnula. Cuadrando el triángulo obtenemos la cuadratura de la lúnula.
Escena desarrollada con DescartesJS.
- Cuadratura de una lúnula II: actuando de forma análoga a como hemos hecho en la escena anterior obtenemos la cuadratura de una lúnula con el programa GeoGebra
Las escenas que se exponen a continuación son recreaciones de otras ya expuestas en este blog y tienen como objetivo refrescar la memoria sobre las curvas mecánicas mencionadas anteriormente.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
La trisectriz de Hípias
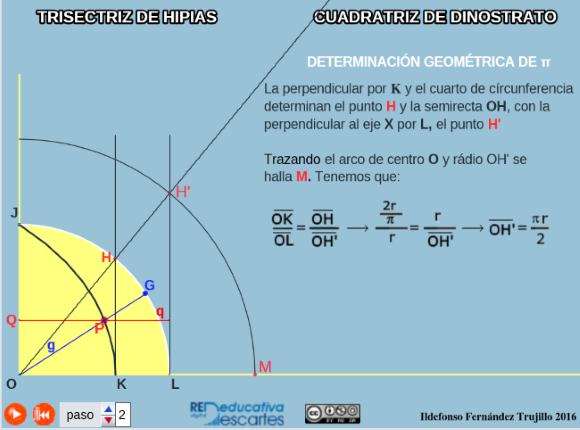
La trisectriz - cuadratriz de Hípias - Dinostrato
En la siguiente escena se determina un segmento relacionado directamente con el número π utilizando la trisectriz - cuadratriz de Hípias - Dinostrato
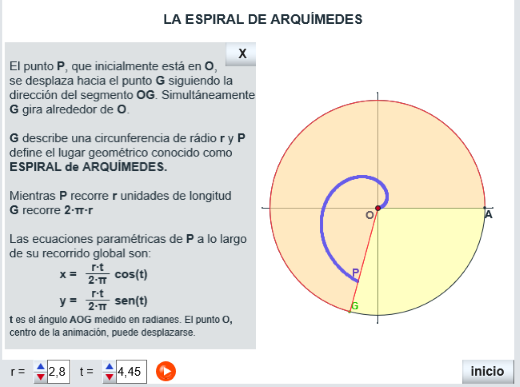
Las siguientes utilidades muestran: la primera, además de las ecuaciones paramétricas de la espiral, la manera como se genera el lugar geométrico conocido como espiral de Arquímedes y la otra la determinación de un segmento de longitud raiz cuadrada de π, en esta ocasión mediante la mencionada espiral de Arquímedes y la ecuación cartesiana de dicho lugar geométrico.
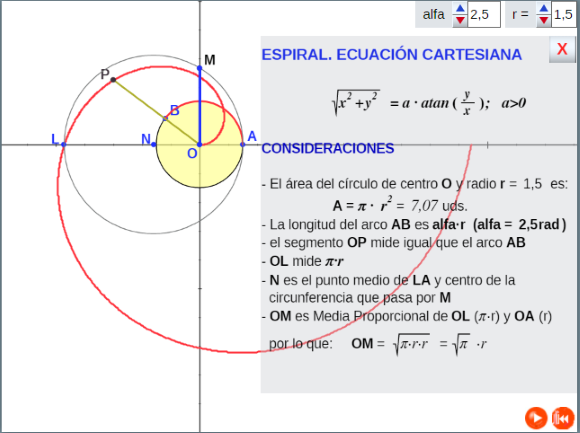
deducción de raiz de π con la espiral de Arquímedes
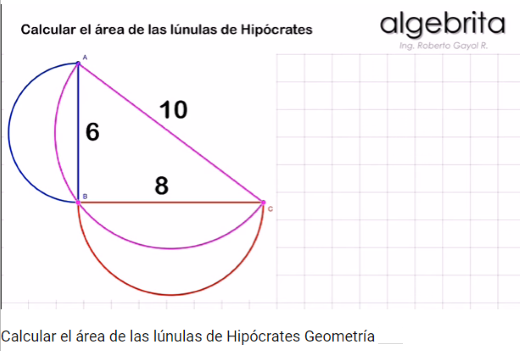
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, del área de las lúnulas de Hipócrates.
,Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadas para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
En el número 94 de la revista Epsilon de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Sobre la forma y el crecimiento cordobés del Nautilus pompilius". Un detallado trabajo de investigación desarrollado dentro de nuestra RED Descartes, reflejándose así en la autoría, por los socios José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo.
Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.
Hay una tendencia a tratar de asociar o encontrar en todo aquello que es bello la proporción áurea o divina, o a construir objetos a partir de esta razón porque se presuponen serán apreciados como bellos por el simple hecho de seguir dicha pauta. Esto, como no, también ha acontecido con la modelación matemática de la concha del Nautilus pompilius sobre la que suele afirmarse que su forma y crecimiento es áureo. Sin embargo, en este artículo se muestra y se analiza en detalle cómo dicha concha lo que realmente sigue es un patrón ubicado en la denominada proporción cordobesa o humana. Con apoyo en un recurso interactivo desarrollado con la herramienta Descartes se motiva el análisis y comportamiento y se procede a partir de la yocto-yotta realidad observada a construir el modelo matemático, el cual se detalla ampliamente.
Pulsando sobre la siguiente imagen se accede a dicho recurso interactivo que se aborda o plantea en seis fases:
- Ajuste de la concha por una espiral logarítmica.
- Ajuste del sifúnculo por una espiral logarítmica.
- Ajuste global por una familia de espirales cordobesas.
- Mejora del modelo discreto.
- Aproximación de los septos.
- Modelo matemático del Nautilus pompilius.
|
|
En cada fase se dispone de un botón de información que, al pulsarlo, da acceso a un detalle de las propiedades que pueden inducirse a partir de la interacción con la escena. |
 |
| Y en el botón de indicaciones se aborda una introducción, los objetivos, las instrucciones de uso en cada fase y finalmente se enlaza un artículo donde se detalla el análisis matemático realizado. Este artículo está embebido a continuación o bien puede abrirse y/o descargarse desde este enlace. |
En las conclusiones del artículo anterior afirmamos:
A través del detallado y progresivo análisis realizado hemos ido construyendo la base teórica o modelo matemático que soporta a la bella morfología del Nautilus Pompilius y hemos tratado del encontrar el modelo de crecimiento que conduce a poder explicar y a comprender por qué adquiere esa forma. Desde su inicio la espiral logarítmica cordobesa tomó presencia y a medida que la mirada se deslizaba hacia algún nuevo detalle esta espiral ha vuelto a imponer su presencia marcándonos y alumbrándonos el camino del descubrimiento y de la adquisición del conocimiento. La belleza del Nautilus pompilius se sustenta en la proporción cordobesa o humana y todo punto de su concha o del interior ha quedado determinado por la intersección de dos espirales cordobesas. El germen o base inicial matemática que explica el por qué acontece todo lo observado, se ha ubicado en el crecimiento gnomónico de un triángulo cordobés, las propiedades de éste se trasladan al desarrollo y comportamiento global detectado y modelado.
Deseamos que nuestro trabajo de investigación satisfaga tu curiosidad y te animamos a interactuar con nosotros bien realizando algún comentario en este blog (los comentarios no se publicarán directamente sino que pasan por una moderación previa a su publicación) o bien escribe al correo de nuestra RED Descartes: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Título: Sobre el crecimiento cordobés del Nautilus Pompilius
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Proporcionalidad. Las Espirales XIV
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación e iCartesiLibri.
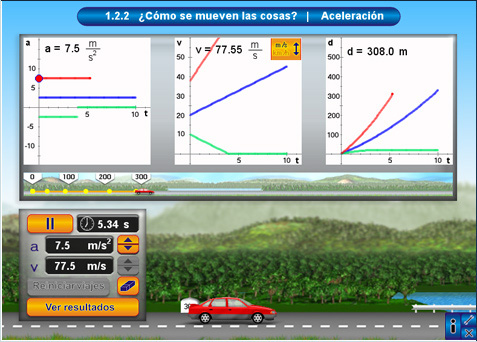
Como muestra enlazamos la unidad sobre Como se mueven las cosas. Aceleración, del subproyecto TELESECUNDARIA,
la GEOevaluación de SurAmérica,
y el libro interactivo Paletización y Empaque.
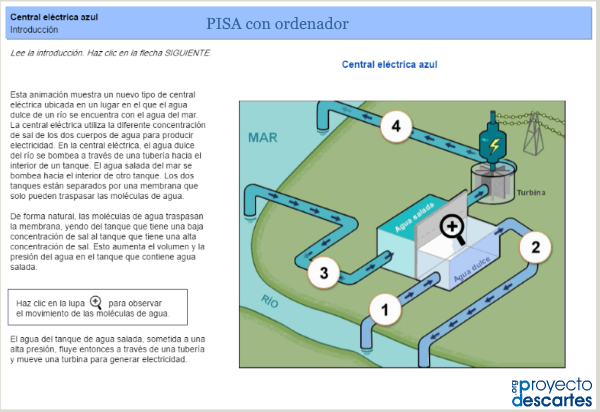
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D cuyos materiales pueden enlazarse desde este espacio web mediante los botones MATEMÁTICAS y FÍSICA Y QUÍMICA y los contenidos del subproyecto Competencias en general y en particular los referidos como PISA con ordenador. De entre ellos enlazamos, con la siguiente imagen, el extraordinario trabajo sobre la generación de energia Central eléctrica azul
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el instrumento ideado por la escuela platónica para duplicar un cubo, esto es, dado un cubo de arista a y volumen V halla de forma mecánica y basandose en los razonamientos de Hipócrates, el segmento de longitud a'= a·21/3 que será la arista del cubo de volumen V' = 2·V.
La escena permite, con cierta facilidad, determinar el segmento OD pero si el usuario no está familiarizado con el uso del instrumento puede pulsar el botón de información, ![]() , que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la construcción de Platón, o atribuida a la escuela platónica, del hecho de la duplicidad.
, que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la construcción de Platón, o atribuida a la escuela platónica, del hecho de la duplicidad.
La utilidad es facilmente adaptable y admite las modificaciones y/o ampliaciones que el usuario considere convenientes para su uso personal.
En el siguiente trabajo presentamos el instrumento conocido como Mesolabio de Eratóstenes y la manera de encontrar, con su uso virtual, el segmento que sirva de arista al cubo que doble en volumen a uno inicial dado.
Repetimos lo dicho anteriormente: la escena permite, con cierta facilidad, determinar la arista del cubo con volumen doble a uno dado, pero si el usuario no está familiarizado con el uso del instrumento puede pulsar el botón de información, ![]() , que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la semejanza de triángulos, del hecho de la duplicidad.
, que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la semejanza de triángulos, del hecho de la duplicidad.
En esta ocasión, en la sección de vídeo, hemos elegido la tercera parte de los que se han mostrado en las últimas entradas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales".
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Compleja" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Se ha creado la siguiente escena: Espiral compleja. El crecimiento de esta espiral, tal y como se ha construido, es extremadamente rápido debido al factor rn el lector puede modificar facilmente el comportamiento de la escena añadiendo más controles y/o modificando el rango de valores de los actuales.
La demostración de las fórmulas (teoremas) de Moivre y Euler están disponibles en la wikipedia. - Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Compleja incluida.
Con el siguiente trabajo realizado con GeoGebra, tendremos la oportunidad de manejar, virtualmente, un mesolabio para hallar la arista de un cubo que tenga doble volumen que uno dado. Esto es, partiremos de esta situación
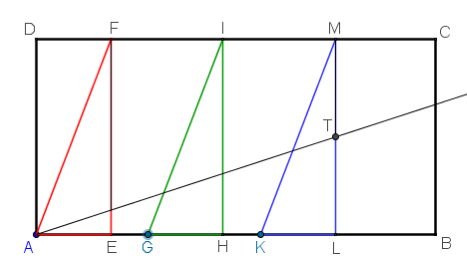
y trataremos de llegar a esta otra
solución
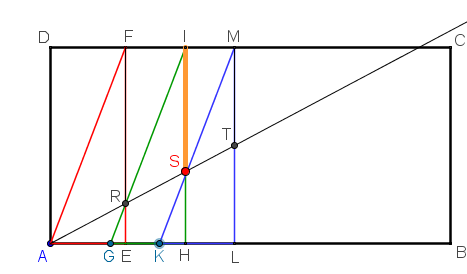
al manipular los controles gráficos G y K y conseguir el objetivo, se muestran las dos medias proporcionales, FR e IS, propuestas por Hipócrates, entre dos segmentos, MT y DA, de longitudes a y 2·a respectivamente, donde a es la longitud de la arista del cubo inicial. La recta determina el segmento que se usará de arista del cubo de volumen doble al primero.
Con ayuda de los cursores y seleccionando alternativamente con el ratón los puntos G y K el ajuste puede ser bastante exacto tal y como muestra la imagen solución.
Se ha creado el recurso en la web de GeoGebra: 'Las espirales complejas.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografia:
- Documentación de Yuli Andrea Rodríguez Rodríguez y Benjamin R. Sarmiento Lugo
- El problema de la Duplicación del cubo de Juana Contreras S. y Claudio del Pino O. Instituto de Matemática y Física. Universidad de Talca.
- Una aproximación a la curva de transición Clotoide vista desde Mathematica de:
Luís Blanch, Emilio Checa, Josefa Marín
Universitat Politecnica de Valencia
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. - Problema de la duplicación del cubo de Juan Pablo Mora.
- Consideraciones sobre los complejos y las espirales de:
Miguel Ángel Morales Medina - Otros documentos buscados en Internet.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales XII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
Como muestra enlazamos la unidad sobre Crecimiento Exponencial, del subproyecto TELESECUNDARIA,
la GEOevaluación de los estados y ciudades de México.
y el ejemplo de: Asocia parejas de imágenes y textos (2).
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y las adaptaciones de los trabajos de Javier de la Escosura Caballero: "Geometría dinámica del trángulo" que enlazamos a continuación
y el de Cuadrilateralia, donde se fomenta el estudio y conocimiento de las características matemáticas de los objetos mediante la manipulación virtual de los mismos y que enlazamos con la imagen siguiente.
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para trisecar un ángulo con la Concoide de Nicomedes. El ángulo a trisecar es el formado por el eje polar y la recta que une el polo con el punto que se desplaza por la directriz.
El análisis de la escena y su modificación, fundamentalmente en la situación del tercio del ángulo mencionado anteriormente, nos lleva a descubrir interesantes características de la Concoide. También son interesantes las modificaciones funcionales que mejoren las prestaciones de la utilidad.
Mencionar, por último, que la escena es copia de la que en su día publicó el profesor Pedro González Enríquez en su trabajo sobre las trisectrices.
Entradas anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por uno y dos puntos y algunas de las utilidades de los l.g. generados por un punto, en la actual comenzamos a mostrar algunos de los usos de la Concoide.
En esta ocasión, en la sección de vídeo, hemos elegido, debido a su calidad e interés, el mismo que en la entrada anterior, que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografías y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Lituus" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Lituus
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Lituus incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y la trisección del ángulo, hemos incluido los trabajos realizados con el programa GeoGebra donde se muestran dos metodos para trisecar un ángulo con la Concoide de Nicomedes.
Método 1.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales XI
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
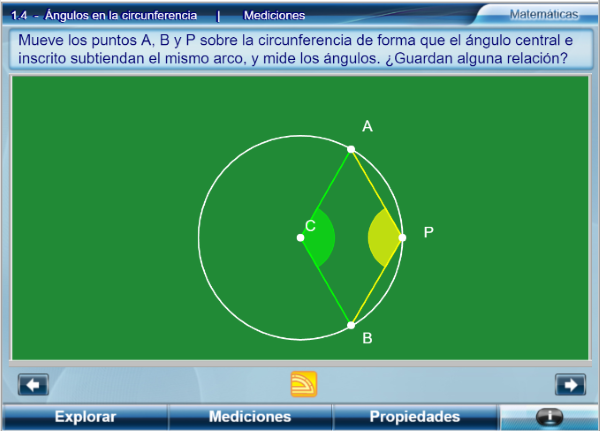
Como muestra enlazamos la unidad sobre Ángulos en la circunferencia, del subproyecto TELESECUNDARIA,
la GEOevaluación de Asia
y los ejemplos de Puzle de intercambio de imágenes tipo 2 donde Descartes realiza directamente el troceado en 4x4 de las imágenes, del subproyecto PLANTILLAS.
Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales y los lugares geométricos, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos objetos matemáticos. Se muestran y/o enlazan a continuación: una escena prolegómeno del estudio del l.g. "Concoide de Nicomedes" para más adelante ver su uso en la trisección de un ángulo, una miscelánea, que es un estudio riguroso y completo sobre las espirales logarítmicas y una segunda que complementa a la anterior. La excelente documentación aportada por ambas es una extraordinaria introducción a estudios más complejos de estos objetos y a la creación de utilidades educativas, dinámicas e interactivas.
Artículos anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por un punto, el actual muestra, según hemos visto, la creación de la Concoide de Nicomedes que es un l.g. definido por dos puntos, cuya posición depende del desplazamiento de un tercer punto por un eje. En próximas entradas se mostrará como trisecar un ángulo agudo con la Concoide.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografias y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Logarítmica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral Logarítmica
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Logarítmica incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido el trabajo realizado con el programa GeoGebra donde se muestra la construcción de la Concoide de Nicomedes para, más tarde, usarla en la trisección de un ángulo.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo