Los juegos didácticos del Proyecto AJDA cuentan con efectos sonoros, que pueden activarse o desactivarse en cualquier momento del juego a través del correspondiente control situado en la parte superior derecha:
Al ser pulsado este control el valor de la variable MUS cambia de 0 a 1 y viceversa a través del siguiente cálculo:
Características físicas y atmosféricas de la Tierra y de nuestro satélite
Escrito por Montserrat Gelis BoschEl subproyecto Miscelánea de la Red Educativa Digital Descartes, está formado por una serie de materiales digitales interactivos con contenidos muy variados del currículo de matemáticas. Se trata de escenas aisladas que se pueden utilizar para introducir, reforzar, ampliar o consolidar la temática que se esté trabajando en el aula.
En este artículo hemos seleccionado dos unidades de astronomía que pertenecen a este grupo:
- La Tierra y la Luna en cifras: Información sobre las principales características físicas y atmosféricas de la Luna y de la Tierra. En algunos apartados se proponen ejercicios de pasar a notación científica con autocorrección.
- Curiosidades sobre la Luna: En esta unidad se tratan algunas curiosidades relacionadas con la misión espacial Apolo11, que logró que por primera vez un hombre caminara sobre la superficie lunar.
Abierto el plazo de inscripción en el curso para el diseño de libros interactivos
Escrito por José Antonio Salgueiro GonzálezSe encuentra abierto el plazo de inscripción en el curso para el diseño de libros interactivos, acción que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana y portuguesa. Este curso tiene como objetivo principal abordar la conceptualización y el diseño, desarrollo y experimentación de nuevos recursos educativos abiertos en formato libro del s. XXI y basados en la interactividad, que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente.
Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación, utilizando una metodología activa, pues desde la primera sesión cada participante comenzará a diseñar y editar su proyecto de libro interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.
El curso comienza el día 16 de julio y finaliza el 15 de octubre de 2021, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:
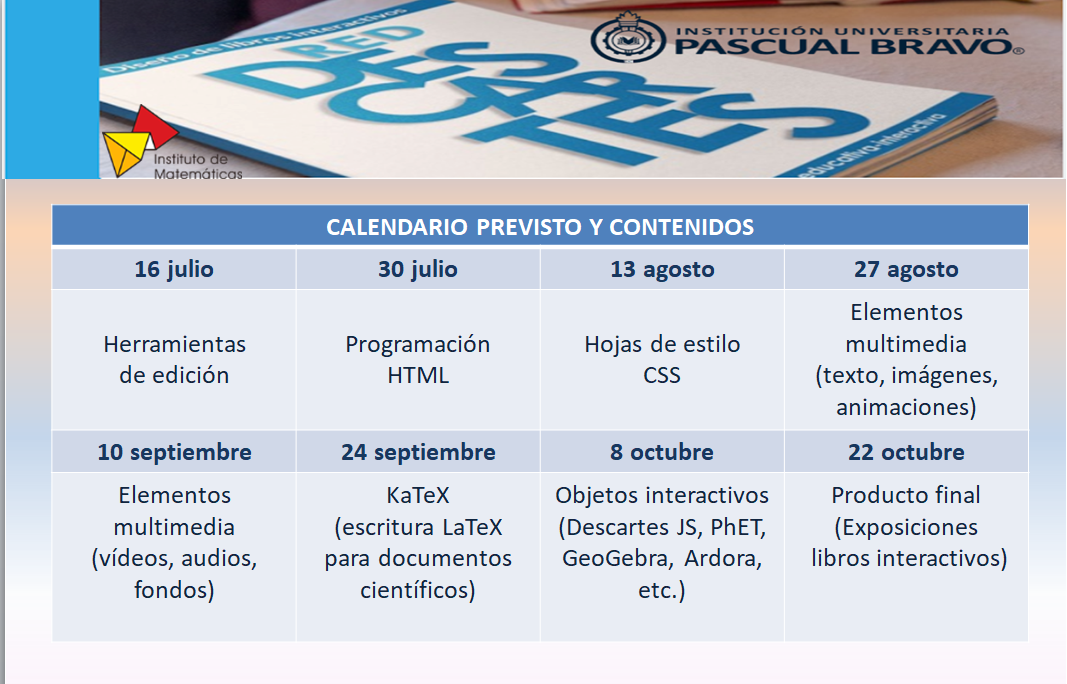
Según las necesidades y proyectos de cada participante, el producto final podrá ser como los mostrados a continuación:
- Libro digital interactivo: artes visuales, ciencias computacionales, ciencias administrativas y económicas, ciencias sociales y humanas, formación en Descartes JS, matemáticas, física, química, ingeniería, lengua inglesa, ...
- Revista digital interactiva
También puedes ampliar información en el artículo titulado "El libro interactivo al alcance de cualquier docente, etapa educativa y materia".
Recursos que utilizaremos:
- Descarga tu plantilla inicial
- Ejemplo básico de uso
- Descarga del libro de ejemplo básico de uso
- Ejemplo de libro interactivo con fórmulas con KaTeX, específico para el lenguaje científico
- Descarga del libro con fórmulas con KaTeX
- Tutorial para el diseño de libros interactivos
- Lista en Youtube con vídeos de apoyo
Artículo publicado en la revista Epsilon de la SAEM Thales
Escrito por Ángel Cabezudo BuenoEn el número 106 de la revista Epsilon (ISSN: 2340-714X) de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Congruencias en el triángulo de Pascal y el rectángulo de Newton" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se refleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.
Este trabajo fue prepublicado en nuestro blog en tres artículos en los que el autor divulgaba la investigación realizada:
- El paralelogramo de Newton el 6 de marzo de 2020.
- El rectángulo de Newton como "simétrico" del triángulo de Pascal el 27 de marzo de 2020.
- Congruencias en el triángulo de Pascal el 24 de abril de 2020.
y, posterioriormente compiló el artículo que sometido a revisión por pares se ha publicado en la revista indicada.
En el resumen se indica :
"El rectángulo de Newton surge como extensión del actualmente denominado triángulo de Pascal partiendo de la versión escalonada de Stifel. Sin embargo, si se parte del esquema organizativo aportado por Pascal entonces el rectángulo de Newton se obtiene mediante una simple simetría signada. Así pues, basta estudiar las congruencias con cero de los números combinatorios y en su análisis aportamos que éstas se ubican en una sucesión de triángulos básicos que se distribuyen de manera periódica. En base a esa periodicidad se incluye un criterio que permite determinar directamente la congruencia de un número combinatorio."
El plantemiento conceptual que sigue, puede sintetizarse en:
- Presentación del conocido triángulo de Pascal en su representación actual como triángulo isósceles escalonado y como triángulo rectángulo que es la original de Pascal, y presentación del menos divulgado rectángulo de Newton.
- Reducción del rectángulo de Newton al de Pascal mediante una simetría signada.
- Muestra de las congruencias con cero en el triángulo de Pascal y revisión de resultados previos de otros autores. Esos resultados se presentan normalmente de manera algebraica y, en general, son oscuros y difíciles de interpretar por profanos dada la abstracción que suele introducir el Álgebra, pero aquí son visualizados geométricamente quedando mostrados de manera diáfana tanto para legos como para ilustrados.
- Finalmente se enuncian algebraicamente los resultados obtenidos por el autor, los cuales muestran la periodicidad de las congruencias módulo p de los números combinatorios y la regla que permite su determinación directa a partir de la descomposición p-ádica del índice superior e inferior, y se visualiza el porqué de ese resultado.
Todo está aderezado por numerosas escenas interactivas que permiten al interesado reproducir la investigación y cómo, apoyándose en ellas, puede potenciarse la reflexión que permite alcanzar la meta lograda. ¡Acceda pulsando sobre la siguiente imagen!
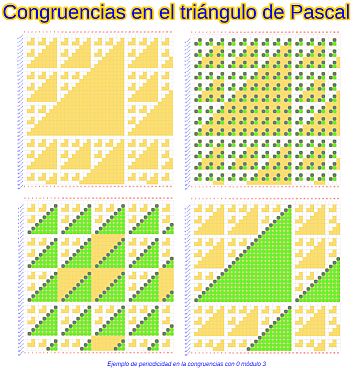 Pulsa sobre la imagen para abrir la escena
Pulsa sobre la imagen para abrir la escena
Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales. También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, abordéis actividades en vuestra aulas en las que divulgar el Triángulo de Pascal, el rectángulo de Newton y las curiosas congruencias que acontecen en ellos y a la vez que podáis promover en vuestro alumnado la inquietud básica, la chispa a partir de la cual se cataliza la vocación investigadora.
Más...
“El Cazador. A la caza de los secretos de la Alquimia”
Escrito por Jesús Manuel Muñoz CalleUna cuestión fundamental a la hora de utilizar juegos didácticos es la forma de ponerlos en práctica. El diseño, la preparación previa, la contextualización, los recursos, etc, son aspectos fundamentales para su buen funcionamiento. Pero podemos ir un paso más allá, utilizando los juegos aplicando metodologías de gamificación, sumergiendo a los participantes en un entorno, mecánicas y dinámicas que potencian y enriquecen el proceso de una forma significativa. En este artículo vamos a tratar cómo hemos realizado una actividad gamificada utilizando los juegos del Proyecto AJDA y presentaremos un vídeo donde se muestra su resultado, su título es:
“El Cazador. A la caza de los secretos de la Alquimia”
- Primera fase. Cada jugador, recibirá durante un minuto preguntas por parte del presentador, y por cada acierto conseguirá 1.000 puntos.
- Segunda fase. Con los puntos conseguidos el participante se enfrentará en un duelo de preguntas individual al “cazador o cazadora” (oponente experto/a). El cazador hará una oferta de puntos por encima y otra por debajo de los conseguidos por el concursante, que según la propuesta elegida estará a cuatro, cinco o seis casillas de llegar a “casa”. A continuación empieza “La caza”, concursante y cazador recibirán preguntas que deberán responder de forma simultánea e independiente. Por cada acierto avanzarán una casilla. El objetivo del jugador es llegar a “casa” y el del cazador atraparlo antes. Cada uno de los cuatro jugadores realizará de forma individual las dos primeras fases, los participantes que sean “cazados” en la segunda fase serán eliminados y los que lleguen “a casa” sumarán al bote común del equipo los puntos ganados en la segunda fase y se enfrentarán al cazador en la “caza final”.
- Tercera fase (“caza final”). Durante dos minutos los jugadores no eliminados recibirán preguntas por parte del presentador. Cada una deberá ser respondida por un solo jugador, el que primero dé al pulsador (si responde otro la respuesta se considerará fallada). Cada acierto dará al equipo de jugadores una casilla de ventaja. Además el equipo partirá con una ventaja inicial de tantas casillas como jugadores haya clasificados. Después llega el turno del “cazador”, que durante dos minutos recibirá preguntas. Si el cazador falla una pregunta habrá rebote para el equipo de jugadores, que de forma conjunta podrá responder, y si acierta hará retroceder una casilla al “cazador”. El equipo de jugadores gana si el cazador no logra igualar las casillas de ventaja que los jugadores han conseguido y el premio se reparte a partes iguales entre los participantes no eliminados.
Una característica del concurso es que cada día el programa adquiere como hilo conductor una temática de forma que concursantes, cazador y presentador adquieren los papeles de la misma a lo largo del programa, y en nuestro caso es la Alquimia.
La puesta en práctica se llevó a cabo en el laboratorio de Física y Química, utilizando tres juegos didácticos del Proyecto AJDA, cada uno de los cuales se corresponde con una de las etapas del concurso, para los que se elaboraron en torno a 300 preguntas de Física y Química de Bachillerato,contando con los siguientes participantes:
- Alquimistas aprendices (Concursantes): Paracelso Morandine, Willian Bacon, Blas Trimigesto y Javier Avicena (alumnos de la asignatura de Física de 2º Bachillerato).
- Gran Maestra alquimista (Cazadora): Vanessa León (Profesora de Química).
- Amo del Calabozo (Narrador y presentador): Jesús Muñoz (Profesor de Física).
- Sauron (Cámara y testigo omnisciente): Marcos Rodríguez (Profesor de Biología).
- Pueblo medieval: Alumnos de Biología.
Los alquimistas aprendices obtendrán por cada 1.000 puntos conseguidos una insignia de la asignatura de Física de cualquiera de las tres evaluaciones. El resultado de la experiencia se muestra en la siguiente composición:
La ecuación cuadrática. Proyecto Prometeo
Escrito por Montserrat Gelis BoschEntre los diferentes recursos de la RED para el estudio de ecuaciones cuadráticas, se propone en este artículo una serie de objetos de aprendizaje del subproyecto Prometeo, para el análisis de los diferentes tipos de ecuaciones de 2º grado. Se utilizan diferentes métodos de resolución según se trate de ecuaciones completas o incompletas.
Estas unidades están indicadas para los últimos cursos de la ESO y el bachillerato.
Las unidades seleccionadas pertenecen al grupo Recursos educativos interactivos de matemáticas para el bachillerato, una serie de recursos creados por el Equipo Descartes, que forman parte del proyecto Prometeo, promovido por el Departamento de Educación del Instituto de Matemáticas de la Universidad Nacional Autónoma de México.
Relación de los objetos seleccionados:
Ecuaciones de la forma ax² + c = 0.
Ecuaciones de la forma ax² + bx = 0.
Ecuaciones de la forma a(x+m)² = n.
Ecuaciones de la forma (ax+b)· (cx+d) = 0.
Ecuaciones cuadráticas completas: ax² + bx + c = 0.
En cada unidad se indica, en primer lugar, el procedimiento a seguir para su resolución y análisis del número de soluciones. A continuación se presenta una escena de ejercicios resueltos y finalmente, una escena de ejercicios para practicar con autocorrección.
Para su aplicación en el aula se propone insertar estos recursos en un aula Moodle.
En el siguiente vídeo se puede ver con detalle algunas de las actividades que contienen estos recursos:
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)












 CONTACTO
CONTACTO
