En junio de 1998 surge la herramienta de autor denominada Descartes que permitió el desarrollo de objetos educativos interactivos divulgables a través y mediante páginas web y, en base a ella, se organiza el proyecto educativo homónimo: "Proyecto Descartes". ¡Cumplimos 25 años! ¡Felicidades a todos los que han hecho posible este acontecimiento! y ¡felicidades a todos los que en algún momento han aprendido con el proyecto Descartes!
Todo instante, segundo, minuto,hora, día, semana, mes, año... es importante en la vida de cualquier persona, asociación o institución. Es más, incluso podríamos afirmar que los instantes son más trascendentes que los amplios periodos pues marcan bifurcaciones en el árbol vital a las que no se puede regresar. Pero, usualmente, lo que hacemos es elegir o marcar hitos en periodos más extensos para celebrar con mayor regocijo, en principio, el haber logrado alcanzarlos y aprovechar esos momentos para lanzar una mirada retrospectiva en la que recordar, rememorar, analizar y, por qué no, extraer conclusiones sobre lo experimentado. En el proyecto Descartes ya nos detuvimos en el décimo aniversario donde tuvimos un bonito juguete como regalo, un lindo trenecito con ruedas poligonales, y donde hicimos una reflexión sobre el camino recorrido y sobre los cambios metodológicos que podía facilitar el uso de los recursos interactivos de Descartes.
| Para acceder a la escena interactiva pulse sobre la imagen | Para acceder al artículo pulse sobre la imagen |
Transcurridos quince años adicionales, llegamos al vigésimo quinto aniversario y, a nivel personal, he pensado festejarlo aportando a nuestra asociación el modelo ontogénico de la concha del Nautilus, pues éste es el fruto de un análisis matemático en el que las escenas de Descartes han servido como herramienta básica, fundamental, sobre la que observar el crecimiento y a partir de ahí detectar las posibles regularidades hasta conseguir el salto de la "yocto-yotta realidad"[1] discreta al continuo matemático. Gracias Descartes y Descartes por vuestra ayuda; por una parte a René Descartes como promotor del estudio de la curva equiangular (generalización de la circunferencia) o espiral logarítmica y, por otra, gracias al proyecto Descartes por promover durante estos veinticinco años el cambio metodológico en el aprendizaje de las Matemáticas, y en cualquier área de conocimiento, usando objetos interactivos desarrollados con la herramienta homónima Descartes.
[1] En longitud, el orden de magnitud de aquello que es físicamente apreciable o medible en nuestro en-torno se ubica actualmente en el rango determinado por el intervalo [10-35, 1026] metros, es decir, desde la longitud de Planck al tamaño del universo observable. Pero en el Sistema Internacional el rango de prefijos para múltiplos y divisores se sitúa en el intervalo [yocto, yotta], es decir, [10-24, 1024], y de ahí surge nuestra denominación de yocto-yotta realidad que acuñamos en el artículo "Sobre la forma y el crecimiento cordobés del Nautilus pompilius" .
Para acceder a una animación pulsad aquí o sobre la imagen y para acceder a la escena interactiva pulse aquí
En el periodo transcurrido desde el décimo al vigésimo quinto aniversario acontecieron dos momentos críticos, casi simultáneos, en los que el proyecto Descartes pudo fenecer. Uno de carácter técnico provocado por el bloqueo de los applets de Java que se salvó con el desarrollo del editor e intérprete DescartesJS que patrocinó y sigue patrocinando el Instituto de Matemáticas de la UNAM. Otro, la terminación del patrocinio del Ministerio de Educación español al proyecto Descartes, lo cual solventamos constituyendo la organización no gubernamental "Red Educativa Digital Descartes" (RED Descartes), que hoy cumple diez años, y a partir de entonces desde nuestro portal educativo proyectodescartes.org damos un servicio altruista para la comunidad educativa de la aldea global.
La síntesis o resumen de todos estos años no es fácil de elaborar, es afortunadamente mucho el tiempo transcurrido y muchísimo más el tiempo acumulado que han empleado todos los colaboradores del proyecto en su planificación y desarrollo y, por tanto, es obvio que algo o bastante siempre quedará sin reflejar. Por ello, es de agradecer la línea de tiempo que ha elaborado José Antonio Salgueiro, usando una escena interactiva de Descartes, y que nos dejó accesible en su artículo: "25 años de historia en una línea de tiempo". La incluyo a continuación y puedes interactuar directamente con ella, pero si estás leyendo este artículo desde un dispositivo móvil es recomendable visitar la línea de tiempo en una ventana específica.
Cada uno de los que hemos intervenido en el proyecto Descartes contamos con nuestra propia línea de tiempo y con una visión personal del proyecto en la que se acumulan las remembranzas particulares. En el quinto número de la revista de RED Descartes algunos colegas cartesianos ya nos han detallado parte de las facetas que ellos han percibido al conocer y profundizar en Descartes. Con los artículos: "Proyecto Descartes en el tiempo", "Un encuentro que cambió mi vida", "Cómo conocí el editor DescartesJS", "Mi práctica docente en los orígenes del Proyecto Descartes", "La incidencia del proyecto Descartes en la labor como docente de Ciencias Básicas", "Desarrollo de Objetos Virtuales de Aprendizaje con Descartes. Una agradable experiencia", "Didáctica digital y procesos cognitivos: reflexiones pedagógicas del aprendizaje para la creación de contenido con la herramienta Descartes", "El Editor DescartesJS - Más allá de una herramienta de autor", "El proyecto Descartes y mi experiencia en la academia", estos colegas nos han invitado a mirar a través de sus ojos y al compartir sus percepciones seguro que han agitado las nuestras. Consecuentemente, es evidente que estáis deseosos de exponer vuestras vivencias en este blog o en un próximo número de la revista, ¡impacientes os siento!, por tanto no procrastinéis que tenemos suficientes bytes para acoger vuestros escritos, escenas, presentaciones, audiovisuales o multimedias en general. La vitalidad que pusiste y sigues poniendo en el proyecto, aquella que te satisfizo y aún te satisface, merece que nos la cuentes, ¡no dejes que viva sólo en tus neuronas!, ¡trasládala a las nuestras!
Y en las diferentes modalidades musicales y tonalidades que se usan por nuestro orbe y, en particular, en el panhispano-americano entonemos el ¡Cumpleaños feliz! o ¡Las mañanitas! y también ¡Happy birthday! y celebremos juntos este
25.º aniversario del proyecto Descartes
¡MUCHAS FELICIDADES!
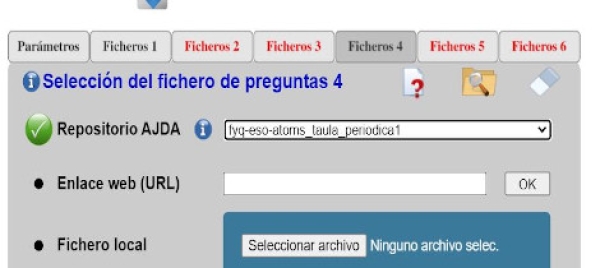
Hay juegos que necesitan cargar varios ficheros de preguntas al inicio de la partida, por ejemplo, juego "Minitrivial", que necesita cargar 6 ficheros, uno por cada uno de los seis temas que se utilizaran en el desarrollo de la partida.
Para mejorar este proceso de carga se ha diseñado un sistema para la selección de dichos ficheros al inicio de la partida (aunque también podrán ser cambiados durante el transcurso de la misma a través de la opción de configuración del menú superior desplegable).
Al inicio de la partida se presenta una pantalla con una pestaña de configuración de los parámetros de la partida y tantas pestañas para carga de ficheros como sean necesarias. A través de cada una de las pestañas se introducirán los correspondientes ficheros.
Se podrá pasar de una pestaña pulsando en las propias pestañas a otra a través de los menús inferiores de navegación anterior y siguiente.
Cada ventana de selección de ficheros presentará su propio sistema de selección de ficheros, los datos y requisitos del mismo y las opciones de configuración.
Las pestañas en las que aun no se haya realizado la selección del fichero se mostrarán en rojo y pasarán a color negro cuando ésta haya sido realizada. Hasta que todos los ficheros hayan sido seleccionados no se podrá comenzar la partida (si se selecciona la modalidad de juego con introducción de preguntas a través de ficheros).
Configuración de la entrada Etiquetas Uso de juegos, No hay sugerencias que coincidan Publicada el 4/5/23 11:24 Enlace permanente Ubicación Opciones
Bachillerato. Libros interactivos de Matemáticas
Escrito por Montserrat Gelis BoschEn este artículo presentamos una serie de libros interactivos, cuyos contenidos se han desarrollado a partir de las diferentes modalidades de matemáticas de 2º de bachillerato de España, si bien también pueden emplearse en estudios equivalentes de otros sistemas educativos.
Estos materiales pertenecen al subproyecto iCartesiLibri de la RED Descartes y ofrecen una amplia gama de recursos y herramientas que pueden ayudar a los estudiantes a comprender mejor los conceptos matemáticos, practicar habilidades y desarrollar un enfoque más activo y participativo hacia el aprendizaje de las matemáticas. Se presentan los conceptos de manera visual, interactiva y atractiva, con múltiples ejercicios y problemas para practicar, todos con sus correcciones. Al finalizar cada capítulo, se ofrece una Autoevaluación que permiten valorar los conocimientos adquiridos.
- Matrices
- Determinantes
- Sistemas de ecuaciones.
Análisis matemático para bachillerato
- Funciones: límites y continuidad
- Derivadas
- Aplicaciones de las derivadas
- Integrales
Geometría analítica del espacio
- Vectores
- El espacio afín
- Espacio métrico
Los contenidos de estos libros cubren el currículum de Matemáticas establecido por las universidades españolas en sus procesos selectivos. Para preparar dichas pruebas, al final de cada uno de estos libros, se incluye un apéndice con problemas propuestos en algunas de las Pruebas de Acceso a la Universidad (PAU), en los diferentes distritos universitarios de España.
En el siguiente vídeo se muestra con detalle el contenido y las actividades propuestas en el libro Geometría analítica del espacio:
Quinto número de la "Revista Digital RED Descartes"
Escrito por José R. Galo SánchezEn este mes de mayo de 2023 hemos publicado el quinto número de nuestra publicación periódica: "Revista Digital de la RED Descartes" —panhispánica, educativa e interactiva—. En la portada se refleja cual es nuestra celebración especialísima de este año: cumplimos 25 años como proyecto educativo y 25 años de la herramienta de autor que dio soporte a la creación de este proyecto. Algunos de los artículos incluidos tratan sobre este tema.
El proyecto Descartes fue creado en junio de 1998 y ahora, 25 años después, queremos celebrar esta efemérides con este número de la Revista Digital Red Descartes. Presentamos 12 artículos y ocho de ellos narran cómo el proyecto ha influido en los autores. Algunos han utilizado la herramienta desde hace muchos años, como José Antonio Salgueiro, quien en uno de sus artículos cuenta su experiencia de 24 años con ella. Otros, como Marisol Ramos, han descubierto el editor DescartesJS hace sólo tres años.
Para los amantes de las matemáticas, recomendamos leer y estudiar dos artículos interesantes. El primero se llama "Embaldosados nxn con L-Triominós" de Ángel Cabezudo, donde además de resolver un reto de embaldosar un tablero con L-Triominós, se explica cómo usar las opciones de guardar y recuperar el trabajo en cualquier momento. El segundo artículo es "El rectángulo de Newton como 'simétrico' del triángulo de Pascal" por José R. Galo , que muestra cómo el esquema organizativo con el que Pascal divulgó su triángulo es mejor que el que usó Newton. Además, Joel Espinosa contribuye con el artículo "Tipografías externas en escenas de DescartesJS", en el que brinda valiosas recomendaciones sobre cómo agregar otras tipografías en las escenas diseñadas con DescartesJS.
Finalmente se relacionan los últimos 19 libros del proyecto iCartesiLibri, que han sido publicados desde el último trimestre de 2022 hasta abril de 2023. Entre ellos, destacan "Mapas: lo que debes saber" de José M. Fernández, así como los primeros libros de ciencias naturales que nos enseñan sobre virus, ranas, arañas, mariposas, escarabajos y frutas. Además, podrás encontrar los dos primeros libros de Marisol Ramos, dos libros sobre lengua inglesa, cuatro nuevos libros de matemáticas y otros más que te invitamos a consultar en este número de la revista.
Confiamos en que este quinto número satisfaga algunos de tus focos de interés y que te parezca atractivo y variado. Puedes acceder a él sin más que clicar con el ratón o pulsar con tu dedo sobre la imagen que tienes un poquito más abajo.
Recuerda que puedes aportar tus comentarios y observaciones, tu retroalimentación es importante para nosotros. ¡Conecta con RED Descartes! Y si deseas compartir, tus artículos serán muy bienvenidos ¡queremos leer, interactuar y aprender contigo!
| Para acceder al quinto número pulse sobre la imagen |
¡Quedáis invitados a publicar vuestros artículos en nuestra revista! Como referencia para la composición de su contenido podéis consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Más...
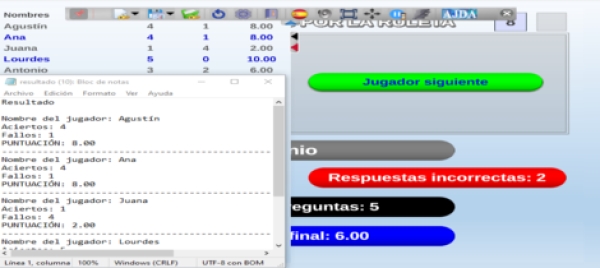
A continuación comentamos otra de las mejoras introducidas en los juegos didácticos y que afecta a la generación de ficheros de de texto con los resultados parciales o finales y que pueden ser solicitados en cualquier momento de la partida a través del menú de guardado de la barra superior desplegable, guardado de resultados (botón azul).
- Los datos de los ficheros de resultados se recuperan correctamente y de forma completa en partidas que han sido continuadas a partir de partidas guardadas en ficheros con anterioridad.
- Se ha mejorado la presentación y organización de los datos.
- Se han incluido nuevos datos de resultados en los ficheros.
- La opción de descargar el fichero de resultados está disponible en cualquier momento del juego.
- Se pueden descargar y archivar cuantos ficheros de resultados se quieran a lo largo de la partida.
PISA con ordenador. Evaluación por competencias
Escrito por Montserrat Gelis BoschPISA (Programme for International Student Assessment) es un estudio internacional de evaluación educativa que se realiza cada tres años para medir el rendimiento acadèmico de los estudiantes de 15 años en matemáticas, ciencias y comprensión lectora. Consiste en una serie de pruebas de evaluación por competencias que presentan diferentes niveles de dificultad, y pueden incluir preguntas de selección múltiple, respuestas abiertas y preguntas basadas en escenarios o situaciones.
Algunas de las preguntas utilizadas en los estudios PISA se han liberado para su difusión y uso convirtiéndose en unos excelentes recursos didácticos en el aula, dentro de las áreas de las Matemáticas, la Lengua y Literatura y las Ciencias, de cualquiera de los cursos de la Educación Secundaria Obligatoria.
En 2015, cuando estas pruebas se empezaron a realizar por medios informáticos, se liberaron una serie de unidades todas ellas relacionadas con la ciencia con el objetivo de dar a conocer el formato y tipología de las nuevas pruebas.
El subproyecto Competencias de la RED Descartes, contiene una serie de unidades realizadas a partir de estas pruebas liberadas. Se introduce dinamismo y aleatoriedad, para que el alumnado pueda reutilizar la misma unidad tantas veces como sea necesario para su aprendizaje. Se parte del concepto de evaluación como instrumento de mejora del proceso de enseñanza-aprendizaje.
En el siguiente vídeo se presentan dos unidades pertenecientes al grupo PISA con ordenador del proyecto Competencias:
- Casa de bajo consumo En esta unidad se presenta una simulación que permite estudiar cómo los diferentes colores del tejado influyen en el consumo de la energía.
- Central eléctrica azul En esta escena se presenta una animación que muestra un nuevo tipo de central eléctrica ubicada en un lugar en el que el agua de un rio se encuentra con el agua del mar. La central eléctrica utiliza la diferente concentración de sal de los dos cuerpos de agua para producir electricidad.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



















 CONTACTO
CONTACTO
