Ildefonso Fernández Trujillo, in memoriam
Escrito por Ángel Cabezudo Bueno
| Algunas personas jamás nos dejan, nunca se van
por completo aunque ya no estén. Su voz se escucha, vemos la expresión de su semblante, su huella existe, su esencia queda. Algunas personas jamás nos dejan… ¡están para siempre! |
|
 |
El pasado día 28 de julio, recibimos la fatal noticia del fallecimiento de nuestro colega cartesiano Ildefonso Fernández Trujillo. Nos sentimos conmovidos y trasmitimos desde aquí a sus seres queridos y familia nuestras condolencias. ¡Descansa en paz, amigo!
Ante todo fue un gran compañero y una excelente persona.
Los que tuvimos que tratar y trabajar junto a Ildefonso, estamos de acuerdo en ciertos aspectos de su personalidad. De apariencia sosegada trasmitía confianza, seguridad y sobre todo humanidad. Creativo, interesado en aprender, sabio y humilde. Confiable, ordenado y cumplidor con sus compromisos. Amable, cordial, respetuoso y cooperativo.
Desde muy joven mostró interés por la Ingeniería y la Medicina, de las que inició estudios, pero terminó decantándose por cursar Matemáticas.
Licenciado en Matemáticas por la Universidad Complutense (Madrid) en 1977, amplió su formación en esta universidad y también en la Universidad Carlos III realizando cursos complementarios en el ámbito matemático y en el estadístico. Adicionalmente se formó en la Universidad de otoño del Ilustre Colegio Oficial de Doctores y Licenciados en Filosofía y Letras y en Ciencias de la Comunidad de Madrid, colegio del que fue miembro; en la Universidad Menéndez Pelayo (Santander) y en la Universidad Nacional de Educación a Distancia (UNED).
Se adentró en la Electrónica a través de un curso del centro privado de formación a distancia CEAC y ello le sirvió de base para sus posteriores trabajos en informática, robótica, domótica y sistemas de control remoto y, también, en la seguridad informática.
Tuvo interés en el ámbito de la energía, realizando cursos en el Fórum Atómico Español y de manera autodidacta implementó en sus últimos años la energía solar a nivel doméstico.
Interesado por el conocimiento sobre las cosas, dedicó toda su vida al estudio autodidacta en general, instruyéndose permanentemente no sólo en aspectos científicos sino también en humanísticos.
Durante 33 años ejerció como profesor en la Administración Pública enseñando matemáticas en distintos Institutos de Educación Secundaria y localidades de la Comunidad Autónoma de Madrid. En ese periodo participó en numerosos cursos del Ministerio de Educación y Ciencia, como asistente y como ponente, tanto de matemáticas como de informática, en perfeccionamiento docente y en astronomía. Fue tutor de cursos a distancia y de profesores en prácticas para el Ministerio.
Desarrolló múltiples aplicaciones de Geometría en la herramienta digital GeoGebra, conoció el Proyecto Descartes y se entusiasmó enseguida con las posibilidades didácticas que le ofrecía, incorporándose en 2008 como colaborador del Proyecto y posteriormente en junio de 2013 como socio fundador de nuestra ong "Red Educativa Digital Descartes". Trabajó intensamente desde su incorporación formando equipo en el Proyecto Agrega y en la adaptación de escenas a DescartesJS, ha escrito numerosos artículos en el Blog de nuestra Web y ha elaborado sus propios materiales didácticos de gran calidad en distintos subproyectos de la "RED Descartes".
Se jubiló como docente en el año 2010, a los 60 años, ejerciendo en el IES Humanes (Humanes-Madrid) y siguió en RED Descartes contribuyendo con su buen hacer al Proyecto Descartes.
Es mucha la obra que nos deja Ildefonso y que se puede consultar en nuestro sitio web proyectodescartes.org y adelantamos que pronto disfrutaremos de la misma clasificada en un Libro Digital Interactivo que daremos a conocer en cuanto se publique.
Baste al menos dejar constancia en este “In Memoriam” de alguna muestra de su trabajo.
Empecemos por mencionar el subproyecto de la Red Educativa Digital Descartes titulado GEOgráfica: una colección de recursos educativos interactivos que ayudan al aprendizaje de la Geografía mundial con diferentes niveles de detalle --desde el contexto global al local--, y con diferentes ámbitos disciplinarios, es decir, la Geografía general, física y humana, y la Geografía regional. Fue precisamente Ildefonso el promotor de este proyecto basado en una aplicación que anteriormente había desarrollado en Visual Basic y después en html y que ahora podemos disfrutar en DescartesJS. La idea estaba en marcha y bastaba formar equipo de colaboradores para elaborar las plantillas y desarrollar los contenidos.
Podemos también desglosar otras colaboraciones:
 |
En el siguiente enlace recogemos su contribución al subproyecto Miscelánea de RED Descartes con interesantes trabajos sobre geometría, probabilidad
|
|
|
y los correspondientes a evaluación formativa (con los que empezó a colaborar con nosotros). |
||
 |
Ildefonso participó en el interesante subproyecto Competencias. Sus contenidos se basan en las unidades liberadas de PISA. Aunque el objetivo inicial y único de dichas unidades es la evaluación también pueden usarse en el contexto formativo al introducir aleatoriedad y autocorrección. | |
Habitual redactor de artículos para el Blog de RED Descartes nos permitió estar al día leyendo sus magistrales contenidos sobre diversos temas que iban apareciendo publicados en los diferentes subproyectos de la RED.
Otra faceta de Ildefonso es la de haber sido un profílico GeoGebrero, de la que ya hemos dado noticia. Hemos buscado estos trabajos en su antigua página personal en la Web de GeoGebra. Y se preocupó por la consecución de la comunicación entre GeoGebra y Descartes.
Y merece cerrar esta sentida reseña con la cita de un trabajo sobre el Nautilus que para Ildefonso fue muy especial y significativo, ¡tanto que su familia le vincula con él! Un proyecto en el que con paciente observación y análisis, pudimos no sólo oír lo que el Nautilus llevaba susurrando durante muchísimo tiempo y que nadie interpretó adecuadamente, sino escucharle gritar claramente: ¡Qué no soy áureo!, ¡Qué soy cordobés!
 |
 |
 |
| Sobre la forma y el crecimiento cordobés del Nautilus pompilius | ||
¡Muchas gracias, Ildefonso! Todos los socios de RED Descartes te echaremos de menos y te tendremos presente en nuestro día a día, trabajando altruistamente por la comunidad educativa de la aldea global como tú también lo has hecho con tan buen saber y hacer.
Nos quedamos muy tristes con tu partida, pero muy gratificados por lo que, entre otros sentidos comentarios, nos trasladaba tu esposa Alicia Isabel y tus hijos Diego, Homero, Antonio, Carlos y Adora: "Pertenecer a ésta, vuestra comunidad, le proporcionó desafíos, compañía, ilusión y alegría, por lo que no podemos estar más agradecidos con todos vosotros por haberle aportado felicidad a nuestro padre.".
Los socios de la Red Educativa Digital Descartes.
El proyecto Canals de la RED Descartes contiene una serie de objetos digitales interactivos que han sido creados a partir de una selección del material manipulativo creado por la reconocida profesora Mª Antònia Canals.
Durante su larga trayectoria docente, la profesora Mª Antònia Canals reunió una extensa colección de materiales manipulativos, que son referente y guía para el aprendizaje y la enseñanza de las matemáticas.
Los materiales están clasificados por temas o por niveles.
Índice temático:
Índice por nivel y curso:
Primaria
Secundaria
En el siguiente vídeo se presenta este proyecto y se muestra con detalle una selección de estos objetos pertenecientes al bloque de lógica y su inserción en un espacio moodle.
Asamblea general del 25º aniversario en el IES Alhakén II de Córdoba
Escrito por José Antonio Salgueiro GonzálezUn año más hemos celebrado nuestra Asamblea General Ordinaria en forma presencial, simultaneada con modalidad virtual para aquellos socios y socias que no han podido asistir físicamente, teniendo como punto de encuentro el IES Alhakén II de Córdoba. Por ello, nos desplazamos a la andaluza ciudad milenaria y crisol de civilizaciones desde diversos lugares y puntos geográficos de la península, como Burgos, Lebrija, Baza, Valladolid, Madrid, Santiago de Compostela, Logroño, Santomera, Zaragoza, Santander, Barcelona y Cádiz. Particularmente, para quien suscribe este artículo, y después de tantos años colaborando desde entornos virtuales, ha sido un placer conocer personalmente a nuestra compañera Elena Álvarez y reencontrarme con Paco Rodríguez y Luis Barrios.
No se trataba de una normal asamblea, pues conmemoramos la efemérides del 25º Aniversario del Proyecto Descartes y de la herramienta de autor Descartes, habiendo canalizado con anterioridad algunas acciones como el artículo enlazado, una especial línea de tiempo y la monotemática, para esta ocasión, Revista Digital de la RED Descartes. Así que, tras el desarrollo preceptivo en lo referente a tareas como gestión y organización, memoria y propuesta de actividades, cierre económico y propuesta de presupuestos, fuimos adentrándonos en nuestra historia, alternando con la situación actual en base a una pregunta como eje vertebrador: "¿Cuáles han sido las claves para que hoy, 25 años después, los recursos educativos abiertos creados con la herramienta de autor Descartes sigan siendo objeto de gran aceptación entre los profesionales del mundo de la enseñanza y educación?"
Hemos valorado las nuevas incorporaciones y actualizaciones que ofrecemos en el ingente repositorio de recursos educativos abiertos e interactivos validados en el aula, para todas las modalidades de enseñanza y etapas educativas, desde infantil a universidad, generados con dos potentes herramientas de software libre, constituyendo nuestra humilde aportación altruista a los Objetivos de Desarrollo Sostenible de la UNESCO, especialmente el denominado ODS4, Educación de Calidad: la educación es la base para mejorar nuestra vida y el desarrollo sostenible. Aún así, somos conscientes del importante número de estudiantes y centros que, desgraciadamente, se ven obligados a usar entornos de aprendizaje virtuales y recursos con una baja conectividad, por lo que ponemos a su disposición nuestra e-publicación, desde donde pueden descargarse todos los recursos y utilizarlos en modo local sin navegar por internet. A su vez, consideramos el rendimiento de la Editorial RED Descartes, que amplía constantemente el número de volúmenes en las estanterías de nuestra biblioteca gratuita, ofreciendo, además, el mismo libro en formato PDF con enlaces a los recursos multimedia, con el fin de facilitar el aprendizaje a las personas que disponen de una baja conectividad.
Queremos mostrar desde aquí nuestro más sincero agradecimiento al equipo directivo del IES Alhakén II, y muy especialmente a D. Antonio Jesús López Olmedo, secretario del mismo, por su cálida acogida y exquisito trato dispensado, así como por facilitar el desarrollo de la asamblea general de RED Descartes, como no puede ser de otra manera por nuestra profesión, en un entorno educativo y académico.
Aprovechando la estancia en Córdoba, primera ciudad con cuatro declaraciones de la Unesco de Patrimonio de la Humanidad, y con nuestro compañero Pepe Galo como anfitrión, pudimos conocer, en las estribaciones de Sierra Morena, las ermitas y la ciudad califal de Medina Azahara (visita nocturna guiada), el grandioso edificio, con trece siglos de historia, que constituye la Mezquita-Catedral (visitas diurna y nocturna), el patio de los naranjos y la torre de la catedral que encapsula al alminar árabe pudiendo verse parcialmente en su interior, así como el entorno de la mezquita, puerta del puente, puente romano y noria de la Albolafia. Sin embargo, la emoción te asalta cuando paseas por la judería y te encuentras frente a Maimónides o Al-Gafequi, continúas hacia la sinagoga, la muralla de la Medina con la puerta de Almodóvar y, nuevamente, te detienes frente a las estatuas de Séneca y Averroes, siendo un buen momento para recordar y reflexionar sobre esta ciudad que un día, como capital de Al Ándalus, concentró el conocimiento de la humanidad con estos grandes sabios, filósofos y científicos, y nos viene a la memoria que la obra los Elementos de Euclides (ver página 69 en este enlace) llegó a la península ibérica directamente a la Biblioteca de Alhakén II en Medina Azahara, ciudad natal de Abulcasis, «padre de la cirugía moderna», quien siguió los pasos del gran Euclides para recopilar todos los conocimientos sobre medicina en su época.
Para conocer o profundizar en el concepto de proporción cordobesa en las construcciones árabes de la ciudad, recomendamos los siguientes recursos interactivos:
- La proporción cordobesa o humana
- Rectángulos cordobeses y áureos en el frontal del Mihrab de la Mezquita de Córdoba
- Triángulo, rectángulo y diamante cordobés. Tesela.
También tuvimos la oportunidad de visitar el monumento a los enamorados en memoria del amor entre el poeta Ibn Zaydun y la poeta y princesa Wallada, el barrio de San Basilio, Alcázar de los Reyes Cristianos y Baños Califales, el casco histórico de Córdoba (la Medina y la Axerquía) y parcialmente la ruta de las Iglesias Fernandinas (construidas por Fernando III el Santo), la plaza y Posada del Potro y, como no podía ser de otra manera, la pintura cordobesa en el Museo de Julio Romero de Torres.
Obviamente, pudimos degustar la variada y extraordinaria gastronomía cordobesa, destacando por desconocimiento de la mayoría de asistentes el plato conocido como mazamorra, que recomendamos probar. A su vez, en uno de los establecimientos recibimos con mucho cariño, y mostramos desde aquí nuestro agradecimiento, un plato conmemorativo que compartimos:
También compartimos el vídeo editado por nuestra compañera Solín Ruiz con las aportaciones de todos los participantes desde nuestro grupo de WhatsApp, donde se recogen momentos de la reunión, visitas a los distintos monumentos del patrimonio cordobés e instantes de ocio y divertimento:
El uso de este tipo de presentadores permite evitar la dependencia con presentadores comerciales como el PowerPoint de Microsofot o el KeyNote de Apple que, además, restringen la incorporación de algunos objetos diseñados en JavaScript, como las escenas interactivas de DescartesJS, GeoGebra, entre otros. Otra ventaja de usar HTML5 es poder compartir nuestras presentaciones vía web.
Si tienes interés en usar alguno de estos presentadores, te recomendamos el libro digital interactivo homónimo "Presentadores de diapositivas HTML5", donde encontrarás toda la información necesaria.
Modelo ontogénico matemático del Nautilus
Escrito por José R. Galo SánchezLa concha del Nautilus, un prototipo de belleza natural ampliamente divulgado, es un icono que habitualmente se utiliza para mostrar cómo la Naturaleza hace matemáticas. Pero el canon aúreo en el que insistente y cansinamente se le encuadra es erróneo. ¡El Nautilus es cordobés!, así lo demostramos en nuestro modelo uniforme (Galo J.R., Cabezudo A. y Fernández I., 2016) —modelo donde se considera que el crecimiento que acontece en todas las etapas vitales es siempre el mismo—. No obstante, como es habitual en todo ser vivo, la ontogenia de este animal presenta alometrías que quedan reflejadas en su concha y que pedían ser matemáticamente desentrañadas. Esto es lo que se detalla en el "Modelo ontogénico matemático del Nautilus" que aquí les presento.
Le invito a conocer este modelo e inicialmente, para situarle, le mostraré el cuaderno de bitácora de la investigación (que sintetiza lo publicado en artículos anteriores en este blog de RED Descartes) y posteriormente le detallaré el modelo matemático ontogénico en sí.
Queda cubierta una etapa ardua, y simultáneamente muy gratificante, en la que el Nautilus ha ido progresivamente activando mis neuronas hasta lograr descodificar y comprender el porqué matemático del rastro vital que va esculpiendo a medida que conforma su concha. Pero todo nuevo conocimiento más que actuar como cierre lo que suele proceder es como catalizador de nuevos objetivos y, por ello, mis siguientes pasos se centrarán en atisbar qué acontece fuera del la sección sagital bidimensional del Nautilus analizada y descrita en este artículo. La concha del Nautilus es tridimensional y, de nuevo, mi oído y el resto de sentidos incluido el sentido matemático, quedan prestos a desentrañar los susurros de mi paisano cordobés. Les emplazo a que más adelante lean mis avances al respecto y a que compartan sus opiniones y observaciones... tengan paciencia. Hasta pronto.
Cuaderno de bitácora
En la siguiente presentación tiene reflejado, sintéticamente, el camino seguido en esta investigación. Se incluyen hiperenlaces a artículos en los que puede profundizar sobre algún aspecto concreto.
Cuaderno de bitácora (puede controlar este recurso con el menú ፧ ubicado en la parte inferior) o verlo en este pdf: ![]()
Modelo ontogénico matemático del Nautilus
A partir del análisis previo he llegado al Modelo ontogénico del Nautilus que se desglosa en la siguiente presentación.
Modelo ontogénico matemático del Nautilus. ![]()
Todo lo anterior puede observarse en el siguiente recurso interactivo, que por defecto se presenta como una animación, pero puede pasar a modo manual sin más que pulsar el botón inferior izquierda, que está etiquetado con la imagen de una mano, y usar el control "paso".
Recurso interactivo donde se describe el modelo ontogénico matemático del Nautilus. Acceso a ventana completa y a las indicaciones.
Este modelo ontogénico puede observarse en la siguiente imagen animada. Al no tener datos sobre la temporalización real del crecimiento del Nautilus se ha asignado el mismo tiempo a cada septo.

Imagen animada del modelo ontogénico matemático del Nautilus
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016 a) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
Greenwald L., Ward P.D. (2010) Buoyancy in Nautilus. In: Saunders W.B., Landman N.H. (eds) Nautilus. Topics in Geobiology, vol 6. Springer, Dordrecht.
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Tanabe K. & Uchiyama, K. 1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.
Thompson, D’A. W., (1917). On growth and Form. Cam. Univ. Press.
Ward, P. (1979). Cameral liquid in Nautilus and ammonites. Paleobiology, 5(1), pp. 40-49.
Ward, P., Greenwald, L., & Magnier, Y. (1981). The chamber formation cycle in Nautilus macromphalus. Paleobiology, 7(4), 481-493. doi:10.1017/S0094837300025537

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Más...
Otras mejoras introducidas en los juegos ha sido en el terreno estético y visual, algunas de ellas gracias a la implementación de nuevas funcionalidades de Descartes en estos aspectos y que repercuten en una mejor apariencia y vistosidad de los mismos. Pasamos a comentar las más significativas.
- Utilización de degradados de color en elementos. También se pueden introducir imágenes de fondo. A continuación mostramos varios ejemplos:
- Mejora y uniformización de fondos en espacios, barras de navegación, escaletas, marcadores. A continuación mostramos algunos de ellos.
- Utilización de efectos en textos (bordes de letras, sombras, colores, alineaciones y justificaciones). Esto se puede apreciar, por ejemplo, en el título de los juegos. Otros ejemplos son textos con nombres de participantes o en marcadores.
- Empleo de estilos en botones y otros elementos. Dichos estilos incluyen: redondeado de bordes, sombras, estilos de color, estilos de textos, efectos de borde, activación y desactivación, efectos de ratón...
- Uso de imágenes, espacios y elementos animados. Estos recursos dan viveza y dinamismo a los juegos.
Aprendiendo a usar monedas y billetes de euro
Escrito por Montserrat Gelis BoschEn este artículo se presentan dos unidades de introducción a las monedas y billetes de euro, que pertenecen al subproyecto Unidades Didácticas de la RED Descartes.
Las unidades que aquí se exponen son El euro 1 y El euro 2 para 2º y 3º de primaria. En cada unidad se proponen una serie de actividades de clasificación, comparación y cálculo con monedas y billetes y van dirigidas al alumnado de segundo y tercero de primaria.
El desarrollo de estas unidades con la herramienta Descartes facilita una experiencia interactiva y en tiempo real, de manera que el alumnado pueda realizar acciones y recibir respuestas instantáneas. En cada ejercicio los números se generan aleatoriamente, para que se pueda practicar indefinidamente hasta dominarlo.
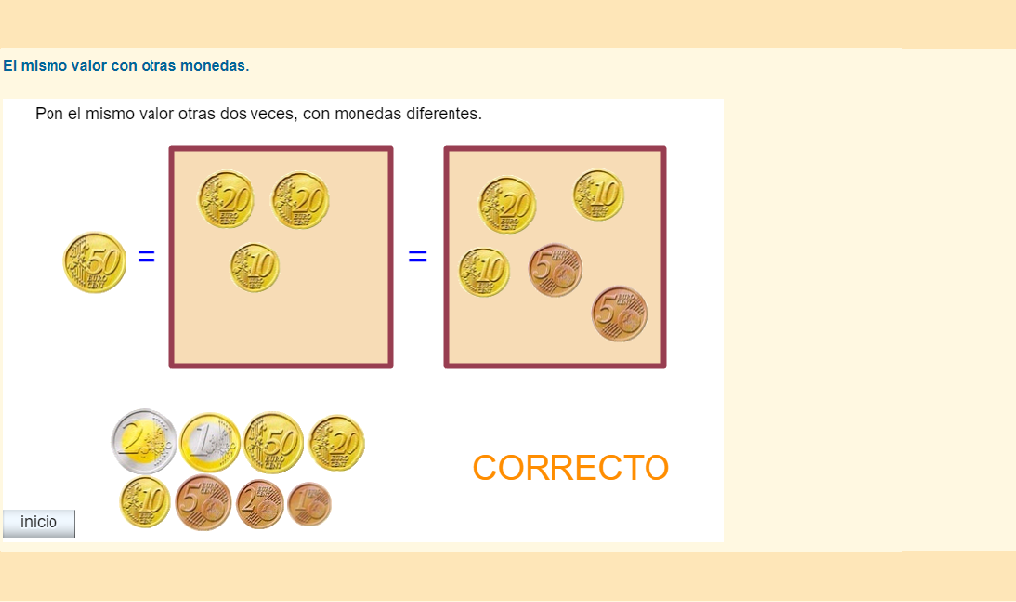
La primera de las actividades, El euro 1, contiene actividades de clasificación, conocimiento del valor de monedas y billetes, equivalencia entre monedas, contar billetes y monedas, pagar exacto en billetes y monedas y cobrar, dando "el cambio" en euros y céntimos.
 |
 |
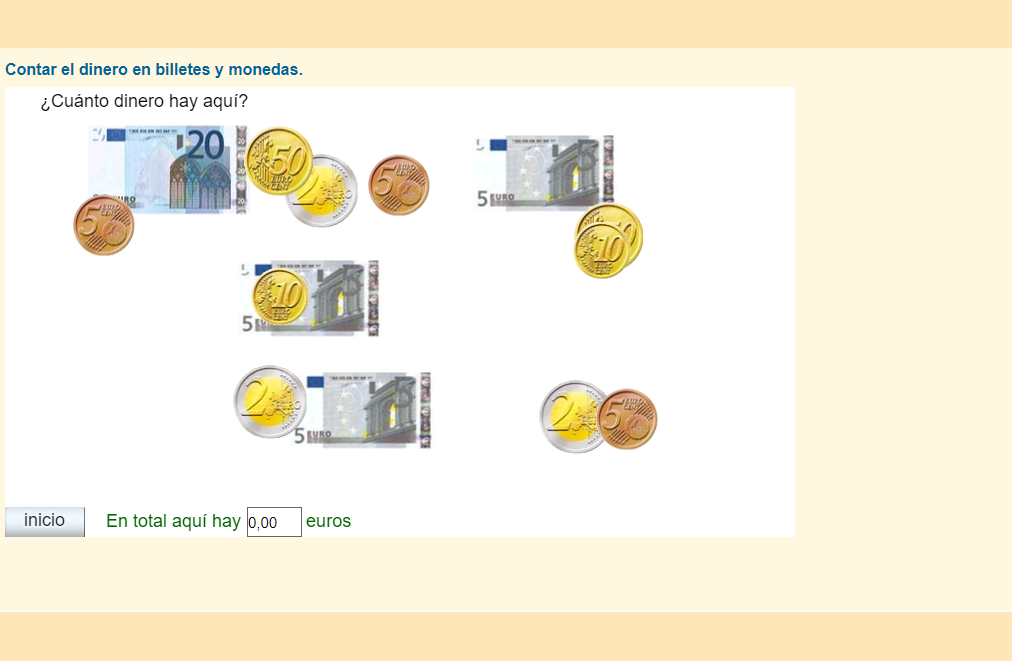
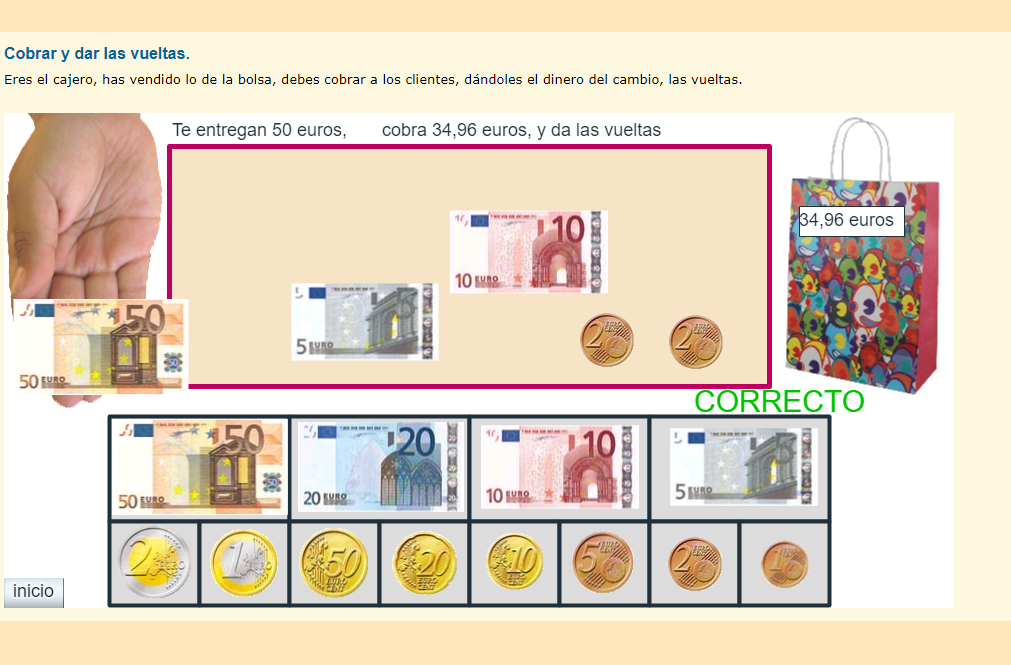
La segunda actividad, El euro 2, contiene actividades semejantes pero se introducen cálculos con decimales y cantidades mayores.
 |
 |
En el siguiente vídeo se puede ver con detalle los diferentes tipos de actividades que contienen estas unidades:
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
























 CONTACTO
CONTACTO
