Saludo inicial previo al curso "Edición de libros interactivos"
Escrito por José R. Galo SánchezSaludo inicial
|
0.
|
Primera sesión de la 2ª edición del curso "Edición de libros interactivos"
Escrito por José R. Galo SánchezPrimera sesión (16 de julio de 2021)
|
1A.
1B.
|
Vídeos de la 2ª edición del curso "Edición de libros interactivos" de RED Descartes
Escrito por José R. Galo SánchezLa segunda edición del curso "Edición de libros interactivos" de la RED Descartes (segundo semestre de 2021) se desarrolló según la siguiente planificación:
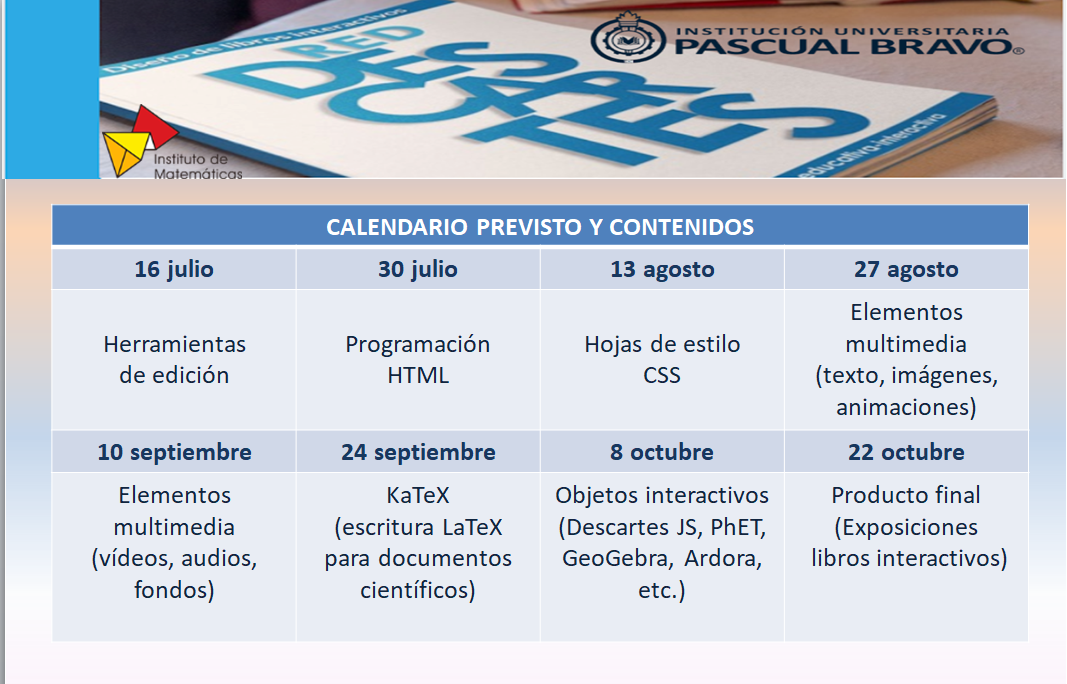
- Primera sesión (16 de julio de 2021).
- Segunda sesión (30 de julio de 2021).
- Tercera sesión (13 de agosto de 2021).
- Cuarta sesión (27 de agosto de 2021).
- Quinta sesión (10 de septiembre de 2021).
- Sexta sesión (24de septiembre de 2021).
- Séptima sesión (8 de octubre de 2021).
- Octava y última sesión (22 de octubre de 2021).
- Resultados de aprendizaje (5 de noviembre de 2021).
Página inicial curso "Edición de libros interactivos"
Curso "Edición de libros interactivos" de la RED Descartes (2ª edición en línea)
Escrito por José R. Galo Sánchez|
Curso de libros interactivos |
- La plantilla o plantillas del libro interactivo. Acceda, mire, observe y descargue la plantilla que vaya a usar.
En el curso se comienza con una plantilla básica (Mi_libro) que puede ver aquí y también descargarla desde acá. - Necesita un editor de texto plano para poder editar ficheros en código html, puede ser el bloc de notas de Windows o TextEdit de iOS, pero le recomendamos Notepad++ o Sublime text porque estos colorean las etiquetas y faclitan la edición. Por favor, descargue el que vaya a usar.
Comience su auto-formación
Lea e interactúe con el libro "Curso de libros interactivos", antes enlazado. También puede descargarlo.
¿Alguna ayuda adicional?
- Puede escribirnos a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
- Puede inscribirse a los cursos de formación en línea cuando se convoquen (ver convocatoria de la segunda edición).
- Puede consultar los vídeos grabados en las sesiones de la segunda edición del curso en línea que ha sido promovido por la Institución Universitaria Pascual Bravo (IUPB) de Medellín (Colombia), por RED Descartes de Colombia y RED Descartes España y que está dirigido e impartido por el Dr. Rivera, vicerrector de la IUPB y presidente de la RED Descartes de Colombia.
Vídeos de la segunda edición en línea del curso "Edición de libros interactivos"
Asamblea general ordinaria de RED Descartes 2021
Escrito por José R. Galo SánchezFin de curso lectivo e inicio de vacaciones, éste es el hito que da paso a la celebración de la "Asamblea General Ordinaria de RED Descartes". En este año 2021, en un siete de julio de "no San Fermín", de nuevo, hemos tenido que reunirnos de manera virtual a través de videoconferencia y con una segunda desilusión de no haber podido celebrarla en Zaragoza —no presiento que esté aquí, leyendo esto, algún anacoreta que de buena fe pregunte: ¿Y por qué?; ¿verdad?—. Tendremos que desmentir el dicho de "no hay dos sin tres" y conjurarnos para refrendar la certeza de que "a la tercera va a la vencida" y, tanto si se es creyente o ateo, poder acudir en 2022 a la Pilarica, vislumbrar la explanada basilicar, sentir reposadamente el fluir del Ebro y, ávidos, poder perdernos en el Tubo a festejar el altruismo cartesiano y verificar si es cierto que allí se profesa la exaltación de la amistad.
Pero regresemos del futuro al presente, aunque ya es pasado, y centrémonos en nuestra Asamblea virtual donde procedimos a abordar los temas estatutarios de obligado cumplimiento como la aprobación del acta de la asamblea anterior y de la memoria de actividades del finiquitado curso cartesiano; revisamos las inversiones y los gastos realizados, hicimos balance conjunto con los ingresos y efectuamos nuestra previsión para el próximo ejercicio. La Aritmética, ciencia tan temida por nos —sí, los matemáticos—, nos comunicó e hizo saber que RED Descartes goza de salud y que cuenta con un grado de inmunización suficiente para seguir dando servicio a nuestros usuarios durante bastantes anualidades. Estos podrán seguir haciendo clic con su ratón o dedo sobre los interactivos y recursos de nuestro espacio web y éste seguirá contabilizando sus aprendizajes e intereses, si bien reflejándolo en datos más banales como páginas servidas, Gb descargados u otras magnitudes más fáciles de cuantificar y medir. Cantidades que, en su momento, ya comunicamos aquí al inicio de este año 2021 y que ampliamos con los datos obtenidos hasta este pasado mes de junio: ¡Seguimos superando récords, mes a mes! No obstante, lo fundamental es que el servicio dado sea óptimo y éste principalmente se basa en la calidad de los recursos —que aporten satisfacción y aprendizaje a quien lo busca y necesita—, pero sin olvidar también su mantenimiento continuo, lo cual hacemos con interés, denuedo y vigilancia permanente.
Entre otros temas tratados en la reunión destacamos aquellos que versaron sobre:
- Recursos educativos y formación.
Son numerosos los recursos que se han desarrollado y publicado en este periodo. Recursos procedentes de Colombia, de España, de México y de Brasil. Y, en especial, destacamos los libros interactivos porque el avance innovador en este subproyecto cada vez es más significativo y diferenciador respecto a lo que usualmente se encuentra por ahí como libro interactivo, y cubriendo cualquier temática científica e incluso literaria. Pero, aunque seamos algo complacientes con lo logrado, aún nos queda bastante que andar para dar el salto distintivo de conceptualización de lo que sería ese nuevo libro que actualmente es inexistente. Sobre el desarrollo de estos libros interactivos —aquí se puede acceder al último modelo— se ha realizado un curso que se ha desarrollado a distancia y ha sido organizado por RED Descartes Colombia y la IUPB. Próximante se inicia una nueva edición del mismo.
- Editorial RED Descartes.
RED Descartes se ha constituido como editorial para publicar directamente con nuestro sello los libros interactivos que promocionamos. Ofrecemos nuestra editorial a todos aquellos interesados en satisfacer la ilusión de ver su libro interactivo publicado (obviamente tras un proceso de revisióny aceptación del mismo).
- Recursos en portugués.
Hemos iniciado una colaboración con colegas brasileños y actualmente se están abordando traducciones al portugués de libros interactivos y quincenas del proyecto ED@D.
- La herramienta Descartes.
En la herramienta Descartes continúan las mejoras gracias al mantenimiento soportado por el Instituto de Matemáticas de la UNAM a quien reiteramos desde aquí nuestro agradecimiento. La documentación actualizada puede consultarse en su web específica.
 Pulsa sobre la imagen para ampliarla
Pulsa sobre la imagen para ampliarla
También tratamos cuáles podrían ser las próximas actuaciones y/o líneas de trabajo en el próximo periodo que será el vigésimo cuarto del proyecto Decartes y el noveno de RED Descartes. Sobre ellos iréis tomando consciencia a medida que seamos capaces de transformar lo manifestado en una realidad.
¡La próxima Asamblea en Zaragoza en julio de 2022!
Allí no veremos y mientras tanto en la Red
Como se hizo. Envío de datos a un juego desde un iframe html embebido en él
Escrito por Jesús Manuel Muñoz CalleLos juegos del Proyecto AJDA y las escenas de DescartesJS en general, pueden contener páginas HTML integradas en ellos, de forma que un espacio del juego sea una página HTML. Vamos a analizar como se envían datos al juego desde el iframe HTML que está embebido en él,lo cual tiene diversas utilidades que trataremos en otros artículos
El iframe que está embebido será una sencilla página HTML, que llamaremos hijo.html y que contiene en su cuerpo dos elementos de entrada de datos, un campo de texto (con identificador CT) y un selector (con identificador SL):
<input name="textfield" type="text" id="CT" value="Campo de texto" >
<select name="selec" id="SL">
<option value="0" selected></option>
<option value="1">A</option>
<option value="2">B</option>
<option value="3">C</option>
<option value="4">D</option>
</select>
Para que se puedan enviar los datos al juego, en la cabecera del iframe embebido en el juego se debe incluir el siguiente código:
Autoevaluaciones del proyecto ed@d. Crear un paquete SCORM
Escrito por Montserrat Gelis BoschUn paquete SCORM (Sharable Content Object Reference Model) consiste en una lista de requisitos técnicos, que contiene una descripción detallada de la estructura de un objeto de aprendizaje y un conjunto de archivos y datos que hacen posible que sea interpretado por diferentes plataformas e-learning, como por ejemplo Moodle.
Si se dispone de un curso en una plataforma Moodle, se pueden crear paquetes SCORM con actividades de evaluación, de forma que las calificaciones obtenidas por el alumnado queden registradas en Moodle.
En los diferentes proyectos de la RED se dispone de muchas actividades con ejercicios de autoevaluación. En este artículo se propone la creación de un paquete SCORM a partir de la autoevaluación de una unidad del proyecto ed@d.
Para crear un paquete SCORM deberemos cumplir con una serie de requisitos previos:
En primer lugar será preciso crear una nueva carpeta, con el material necesario para el funcionamiento de la actividad. Para que la escena se comunique con Moodle, se deberán añadir también dos ficheros JavaScript y un archivo html llamado comunica.html. Este archivo contiene el código para enviar a Moodle la calificación (nota) obtenida en la actividad.
También se deberá modificar la escena del objeto interactivo con el editor DescartesJS, añadiendo un nuevo espacio html (cal), que carga la página comunica.html para la interacción con Moodle y un botón enviar, que al pulsar notificará la calificación de la actividad. También será preciso definir la variable nota, la suma de todas las respuestas correctas que quedará registrada en Moodle.
Finalmente, una vez modificada la escena, nos dispondremos a crear el contenedor SCORM usando un editor que permita crear estos paquetes. Hay varias herramientas para crear contenidos SCORM, en este caso se utiliza el programa RELOAD (Reusable eLearning Object Authoring & Delivery). Con RELOAD crearemos el paquete con los contenidos, los datos, la organización y la estructura de la actividad. El paquete con los archivos y carpetas necesarios se guardará en un fichero ZIP. Este es el fichero que se subirá a Moodle al crear una actividad del tipo SCORM.
Enlaces a los materiales:
Paquete SCORM (autoevaluación de la unidad de proporcionalidad)
En el siguiente vídeo, se muestra con detalle la creación y aplicación en Moodle de un paquete SCORM a partir de una autoevaluación del proyecto ed@d:
>
En parte de los juegos de AJDA es necesario utilizar y medir el tiempo de duración de las preguntas u otras acciones del juego.
El tiempo es un valor que se introduce en una o varias variables y cuya variación se controla normalmente a través del algoritmo de la pestaña Animación del editor de DescartesJS.
¿Cómo modificar plantillas Descartes y publicar los archivos desde nuestra cuenta de Google Drive?
Escrito por Montserrat Gelis BoschPlantillas Descartes JS es un libro del proyecto iCartesiLibri que contiene una recopilación de actividades que son fácilmente modificables, de modo que el profesorado pueda crear nuevos materiales que se adapten a sus objetivos.
Los libros digitales interactivos del proyecto iCartesiLibri abarcan muchas áreas de conocimiento y están diseñados con el fin de facilitar el autoaprendizaje, potenciando la autonomía del alumnado en su aprendizaje.
Pertenecen también a este grupo una serie de libros/tutoriales (Formación en Descartes JS) que contienen detalladas explicaciones y ejemplos para que el profesorado pueda elaborar sus propios libros digitales y la creación de escenas Descartes. Es dentro de este grupo donde encontramos el libro Plantillas Descartes JS. Este libro contiene muchas actividades (juegos de memoria, puzles, selección múltiple, emparejamientos…) que se pueden modificar para adaptarlas a nuestras necesidades.
En el siguiente vídeo elegimos una actividad de selección y vamos a ver la manera de cambiar las preguntas y respuestas de forma sencilla.
Una vez modificada la actividad necesitaremos un servicio de alojamiento que permita subir y publicar archivos html. Utilizaremos en este caso PoweredBy.Cloud un nuevo servicio gratuito desde nuestra cuenta de Google Drive.
Participantes de 14 países en el curso para el diseño de libros interactivos
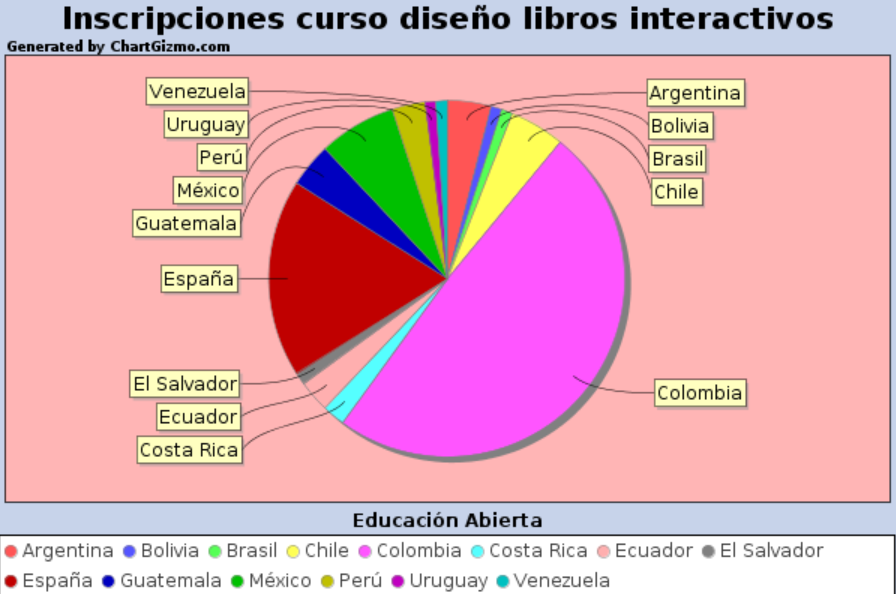
Escrito por José Antonio Salgueiro GonzálezDurante el mes de mayo se ha desarrollado el proceso de inscripción en el curso para el "Diseño de libros interactivos", que forma parte del programa de Educación Abierta de RED Descartes, con tal grado de aceptación que nos hemos visto comprometidos a incrementar el número de plazas previstas hasta alcanzar las cien. Una demanda de participantes procedentes de catorce países de habla hispana y portuguesa, con docentes y profesionales de la educación que comprenden las etapas educativas de primaria, secundaria, bachillerato y universidad, así como una amplia gama de especialidades, aunque destaca el profesorado de matemáticas.
Compartimos el siguiente diagrama de sectores con el porcentaje de participación por países:
Recordamos a todos los participantes que el curso comienza el día 16 de julio y finaliza el 15 de octubre de 2021, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:
Durante el mes de junio y, especialmente, la primera quincena de julio iremos proporcionando por correo electrónico la debida información al respecto. No obstante, ponemos a disposición de todos los participantes la dirección Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., donde pueden plantear cualquier tipo de consulta.
Agradecemos a todas las personas inscritas el interés mostrado y lamentamos no poder atender más demanda en esta convocatoria.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)




 CONTACTO
CONTACTO
