El "triángulo de Pascal o de Tartaglia" es ampliamente conocido tanto por las curiosas propiedades que en él pueden encontrarse como por su aplicación en el desarrollo algebraico de la potencia de un binomio. Suele aprenderse ligado a lo que usualmente se enseña con el nombre de "binomio de Newton" y que se identifica con la potencia de un binomio cuyo exponente es un número natural. Pero quien enunció o al menos divulgó este desarrollo particular, relacionándolo con ese triángulo, fue Pascal y de ahí que se denomine a dicho triángulo con su nombre. No obstante, el "triángulo de Pascal" ya era conocido, siglos antes, por matemáticos persas y chinos. Según Maor (1994) la aportación concreta de Newton en el contexto del desarrollo binomial se sitúa en el caso del desarrollo con  exponentes racionales y con exponentes enteros y únicamente llegó a conjeturarla sin llegar a abordar o al menos divulgar su demostración. Actualmente este resultado es un caso particular del denominado "Teorema binomial".

Newton abordó la extensión del triángulo de Pascal efectuando un cálculo hacia atrás, de manera que se mantuviera la misma propiedad recursiva de que un elemento de una fila sea el resultado de la suma de dos de la fila anterior siguiendo la propiedad que se verifica entre los números combinatorios.

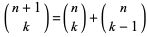
Con esta extensión recursiva en sentido inverso, Newton construye nuevas filas, cada una de las cuales tiene infinitos números y cuya escritura conduce a la forma de un "paralelogramo" (o si se desea puede mostrarse, en particular,  como un rectángulo) y cada una de ellas puede asociarse a filas que se corresponderían con números "combinatorios" cuyo índice superior serían números enteros negativos.

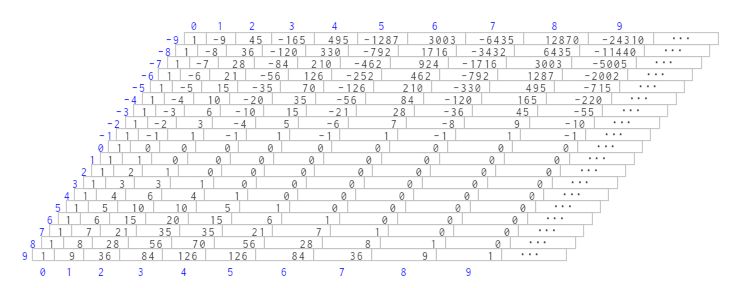
A su vez, Newton hace corresponder los números ubicados en cada fila con los coeficientes del desarrollo de la potencia de un binomio cuyo exponente ya no sólo sería un número natural, sino que en general puede ser un número entero. Y, consecuentemente, a todos los números del paralelogramo de Newton los denominaremos coeficientes binomiales (pierde sentido asociarlo con el número de combinaciones). El desarrollo del binomio conduce a un número finito de sumandos cuando el exponente es natural e infinitos (una serie) cuando es un entero negativo.

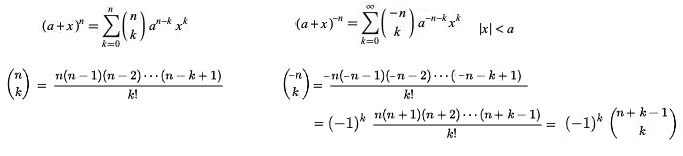
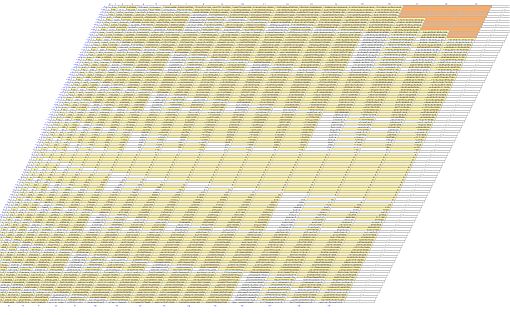
En la miscelánea "Extensión del triángulo de Pascal: El paralelogramo de Newton" se muestran los coeficientes binomiales de dicho paralelogramo. Pulsando el botón "indicaciones" de este recurso se pueden consultar algunos detalles adicionales. 

Pulsa sobre la imagen para abrir la escena

La representación de dicho paralelogramo numérico entraña dos dificultades principales a medida que se incrementa la cantidad de números a visualizar. Por un lado, el espacio que necesita ocupar la escritura de cada coeficiente binomial que progresiva y rápidamente va aumentando, al ser mayor el número de cifras que lo constituyen. Y, por otro, el tiempo de cálculo necesario para ubicar, desplazar y representar en la tabla dichos coeficientes y para poder escalarla (si se desea). Adicionalmente, el cálculo de los coeficientes conduce a números enteros que superan el número designado como MAX_SAFE_INTEGER y que en javascript es 2⁵³-1 (algo superior a 9 mil billones); así pues, en esos casos no se refleja el coeficiente y se colorea la casilla donde iría ubicada con un fondo rojizo.  

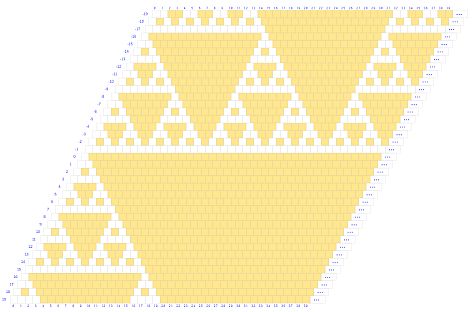
En dicha escena se pueden visualizar, mediante colores, pautas geométricas de cómo se distribuyen dichos coeficientes cuando se plantean congruencias numéricas respecto a un divisor y resto seleccionado. No obstante, estas distribuciones pueden observarse mejor si no se muestran los valores de los coeficientes y ello es lo que se aborda en la miscelánea: "Congruencias en el paralelogramo de Newton"

Pulsa sobre la imagen para abrir la escena

En este caso (ver las indicaciones incluidas en la miscelánea) la dificultades siguen centrándose en el espacio necesario para representar el paralelogramo cuando el número de filas y columnas considerado es elevado, pero al no reflejarse el número en sí, cada uno de estos coeficientes ocupa el mismo espacio y puede escalarse hasta el extremo de que ocupe un único píxel. Por otro lado, el cálculo de las congruencias puede hacerse de manera recursiva sin necesidad de calcular el coeficiente y consecuentemente no se ve afectado por lo indicado sobre el máximo entero admisible en javascript. Obviamente, las necesidades computacionales son elevadas y, por defecto, en la escena se ha limitado el número de filas y columnas a 400, pero editando la escena puede cambiarse.

Para evitar que cada interesado tenga que dedicar tiempo en la generación de las imágenes de las congruencias, he preparado un muestrario de consulta para las congruencias con los números primos hasta el treinta y uno, representando los coeficientes binomiales de índice superior en el rango desde -999 a 999 y de índice inferior de 0 a 999. Éste está accesible en la miscelánea: "Muestrario de congruencias en el paralelogramo de Newton", pudiéndose ampliar las imágenes ahí incluidas.

Pulsa sobre la imagen para abrir la escena

En un próximo artículo en este blog, mostraré que si retomamos el esquema organizativo original que Pascal (Traité du triangle arithmétique, 1665) utilizó al presentar y analizar las propiedades de este triángulo numérico, entonces los patrones de las congruencias que se observan en él son mas fáciles de identificar y pautar, y la extensión de estos a los coeficientes binomiales con índice superior un entero negativo se realiza de manera trivial.

Finalmente, quienes deseen aplicar los coeficientes binomiales y practicar con el desarrollo algebraico de potencias de un binomio pueden usar las siguientes misceláneas:

Ejercicios de desarrollo algebraico usando el "Binomio de Newton"

Pulsa sobre la imagen para abrir la escena

Ejercicios del "binomio de Newton" con exponente entero

Pulsa sobre la imagen para abrir la escena