Feliz Navidad con Descartes
Escrito por Juan Guillermo Rivera BerríoDesde RED Descartes Colombia y desde la Institución Universitaria Pascual Bravo os deseamos una Feliz Navidad para todos los cartesianos y pascualinos.
Escenas con DescartesJS: Técnicas y trucos (M06)
Escrito por Ángel Cabezudo BuenoEscenas con voz y sonido. Secuenciación temporal.

Introducción
El programa Descartes nos permite elaborar escenas incluyendo voces y sonidos. Podemos hacer que aparezcan en determinadas circunstancias según la actuación del alumno y pueden servir como explicación, como mensajes de ayuda o como felicitación cuando se ha resuelto bien una actividad.
También podemos hacer que sea el alumno quien ponga en marcha esos sonidos mediante controles, pero no trataremos con detalle en este artículo este tipo de controles de audio sino los eventos que darán origen a la reproducción de audio cuando se cumple cierta condición en el programa.
Hay que tener en cuenta que muchos ordenadores tienen deshabilitado el audio, por ello es conveniente que la actividad que se pide al alumno en la escena no dependa exclusivamente de los mensajes de voz que en ella se den.
Un programa interesante de uso libre que permite grabar voz y editar sonido para incorporar en las escenas de Descartes es Audacity. Puede exportarse el audio producido en diferentes formatos. Lo usual es el formato mp3 aunque en principio se puede utilizar cualquier formato compatible con HTML y el navegador Web utilizado.
Conviene tener en cuenta que el actual Editor de Escenas de Descartes no reproduce sonidos, aunque se puedan programar. Para comprobar que el sonido programado con Descartes funciona correctamente debemos guardar la escena en un archivo HTML y abrirla en un navegador Web – consultar este enlace sobre compatibilidad-.
Como se programan los sonidos en la escena
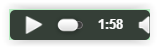
Podemos hacer que un sonido se escuche a través de un control de tipo audio.
 |
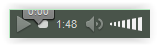 |
| Aspecto con Google Chrome | Aspecto con Mozilla Firefox |
Figuras 1a-b
Por ser de sobra conocido por todos no es necesario describir el funcionamiento de reproducción, pausa y parada proporcionado por este elemento multimedia.
La siguiente imagen muestra el panel Controles y los parámetros que se han establecido para el control de audio que se ha añadido en una escena. El control ha quedado identificado en este ejemplo por el nombre “sonido”.
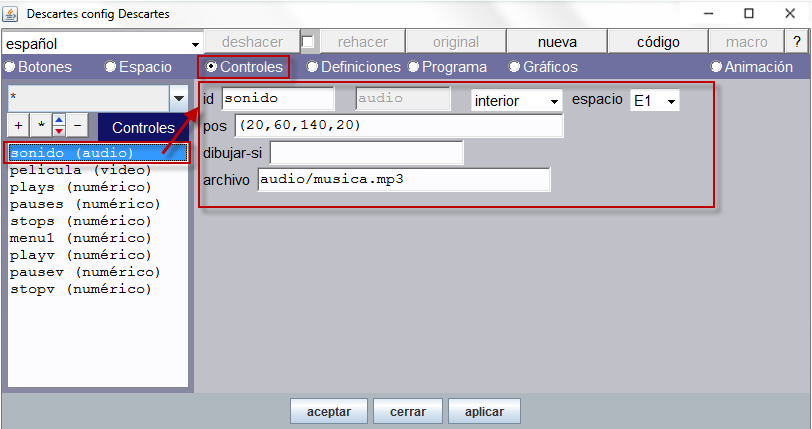
Figura 2
Los parámetros de este control son los referidos a la posición, el espacio, la condición dibujar-si y la trayectoria donde se encuentra el archivo de sonido p.e. "audio/musica.mp3" -ver documentación http://reddescartes.org/documentacion/audio-video/ -
Por lo general suele interesar que el sonido se escuche en situaciones especiales y por tanto se programa como auxiliar evento. En el artículo anterior, Escenas con DescartesJS: Técnicas y trucos (M05) - Adaptación de escenas. Librería de proyecto. Espacios HTMLIframe, se producía un sonido característico cuando un puzle quedaba armado correctamente. Este sonido se había programado como evento.
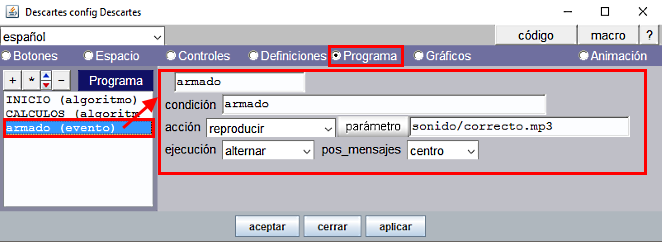
Figura 3
Verificar dicho sonido, desde este enlace, después de armar el puzle.
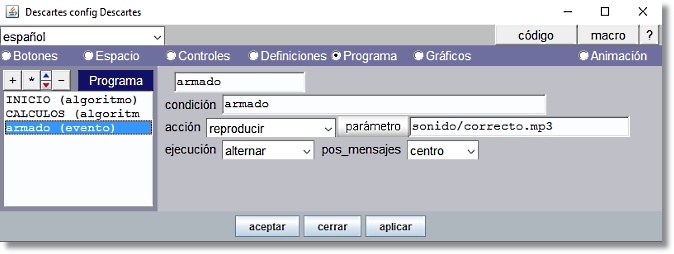
En la condición ponemos una expresión lógica que cuando es verdadera se reproduce el sonido. La acción que hay que seleccionar es "reproducir". El parámetro que se declara es la trayectoria donde se encuentra el archivo de audio, "sonido/correcto.mp3". En el apartado ejecución elegimos de entre las opciones "una-sola-vez", "alternar" o "siempre" que determina el modo de ejecución de la acción del evento, esto es:
- Una-sola-vez, sólo se ejecuta la primera vez que se cumple la condición.
- Alternar, se ejecuta la primera vez que la condición se cumple, pero si la condición deja de ser válida y vuelve a serlo luego, entonces vuelve a ejecutarse la acción.
- Siempre, se ejecuta siempre que se cumpla la condición.
El valor por defecto es "alternar".
Ejercicio práctico
Como práctica de la inclusión de sonidos te proponemos que selecciones una de tus escenas o bajes una de las cuatro escenas que ya han sido publicadas en esta sección del blog e incluyas en ella voz y sonido.
Los temas que hemos tratado son:
- Escenas con DescartesJS: Técnicas y trucos (B01) – Situar puntos en el plano cartesiano
- Escenas con DescartesJS: Técnicas y trucos (B02) – Identificar nombres en una imagen
- Escenas con DescartesJS: Técnicas y trucos (B03) – Distribución de nombres en un mapa
- Escenas con DescartesJS: Técnicas y trucos (M04) – Puzle de arrastre con efecto imán
Puedes grabar tu voz o buscar voz y sonido ya publicado, grabarlo y editarlo. También te aportamos los sonidos “correcto.mp3” y “Error.mp3” que se utilizan en las unidades “La suma 1” y “La resta 1” y que puedes descargar desde el enlace al final de este artículo.
- Primeramente, coloca la carpeta "audio", que contiene los sonidos, junto al archivo de la página HTML en la que está la escena donde vas a incluirlos.
- Vamos a poner un sonido para indicar que se ha resuelto bien la actividad de la escena.
- Abre el Editor de escenas y con él la página con la escena que vas a modificar.
- En el Panel programa haz clic sobre el signo + para añadir un auxiliar evento. En condición observa y pon lo mismo que hay en el mensaje de felicitación en el apartado dibujar-si.
- Puesto que con el Editor de escenas no se reproducen los sonidos, guarda los cambios y comprueba su funcionamiento abriendo la página con el navegador Web.
Sonido secuenciado
Cuando se incluyen varios sonidos que se deben de reproducir de forma sucesiva, si no queremos que se solapen uno con otro, tenemos que producir una secuenciación de los mismos y separarlos en el tiempo mediante una animación, asignando a cada uno de ellos el momento en el que debe comenzar a reproducirse.
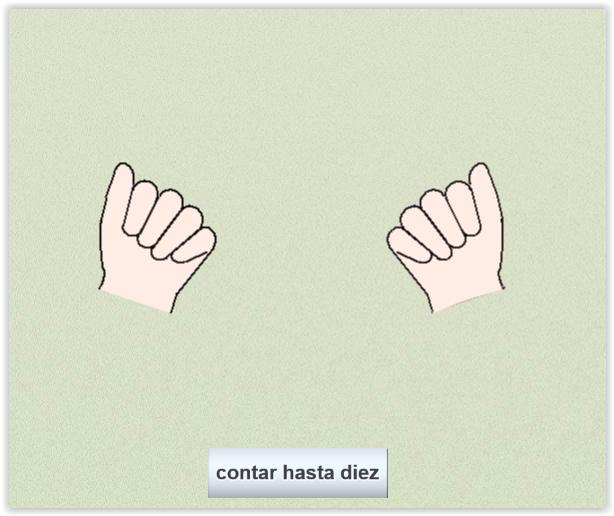
Vamos a utilizar un ejemplo muy sencillo de secuenciación programado para esta ocasión. El diseño está inspirado en la escena Sumando con los dedos de la unidad didáctica de Eduardo Barbero Corral titulada “La suma 1” para 2º curso de Primaria, que como se podrá observar atiende aspectos didácticos más amplios. Se utilizan los mismos sonidos de voz para contar (1a.mp3, 2a.mp3, 3a.mp3, …, 10a.mp3) y las imágenes de las manos han sido coloreadas. También puede consultarse, del mismo autor, la escena similar Restando con los dedos de la unidad didáctica “La resta 1”.
En la escena del ejemplo una animación ha hecho posible la secuenciación temporal de los distintos sonidos y también de la representación gráfica de los números 1 al 10.
Figura 4 (Abre la escena)
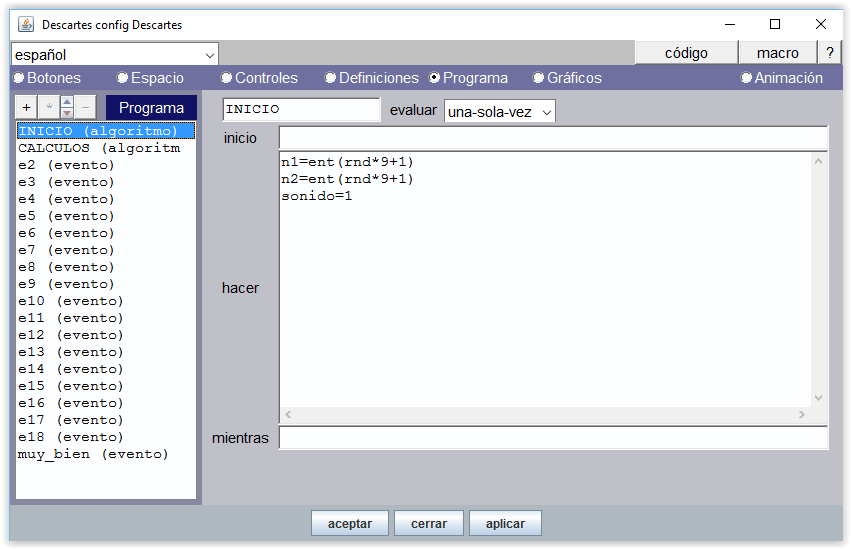
En el Editor de Descartes disponemos de un panel para configurar la animación. Una animación en Descartes es un algoritmo especial que refresca la escena cada vez que realiza un ciclo. Como todo algoritmo tiene la estructura inicio – hacer – mientras que se corresponde con la estructura de bucle “do… while” de los lenguajes C y Java y “repeat… while” de Pascal.
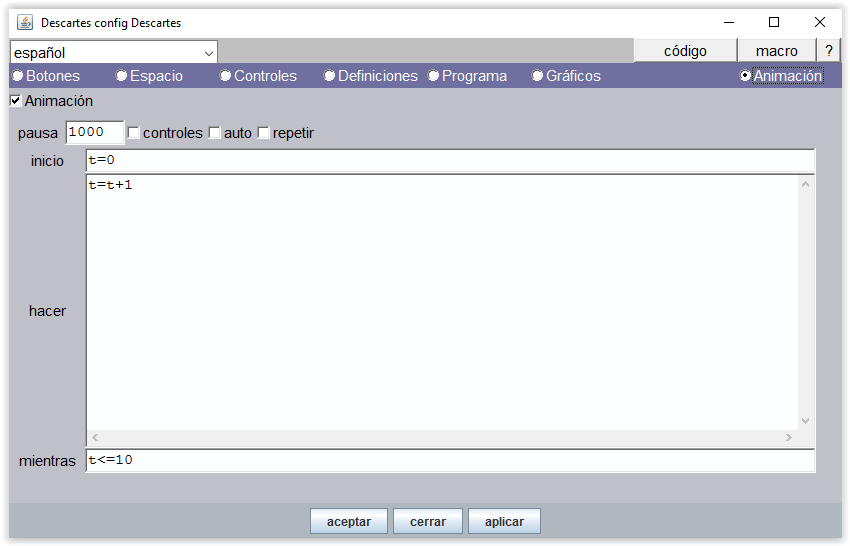
Figura 5
Interesa ver la documentación referida a Animaciones
Animación
La animación funciona como los algoritmos de Descartes, pero tiene sus propias singularidades. Se pone en marcha cuando se activa la acción de animar, ejecuta al principio las operaciones reflejadas en la casilla inicio, separadas por “;”, transforma sus valores según lo que se le indica en hacer y se detiene cuando deja de cumplirse la condición que se pone en mientras. Pero eso lo realiza no de forma instantánea, sino ralentizada por lo indicado en pausa. La pausa indica los milisegundos que espera el programa entre dos pasos sucesivos de la animación que por defecto vale 60.
La figura anterior es el panel animación de la escena de “contar hasta 10”.
Hay que seleccionar la casilla Animación para que esta esté activada y se puedan editar sus parámetros. Si esta casilla no se selecciona no se puede editar los campos del panel ni se puede activar la animación en el programa, aunque esté editada.
El bucle se inicia poniendo el contador a cero, t=0 y en cada ciclo o paso se incrementa en una unidad t=t+1. Cuando el contador supera el valor 10 la animación finaliza.
Es importante entender que una animación se puede poner en marcha de dos formas:
- De forma automática al iniciarse la escena. Para ello tiene que haberse seleccionado la casilla “auto”.
- Cuando se ejecuta la acción animar. Esta acción es una posible opción que tienen los controles numéricos en el panel Controles y también los eventos en el panel Programa.
En la siguiente imagen se muestra cómo se consigue poner en marcha la animación de la escena “contar hasta 10”
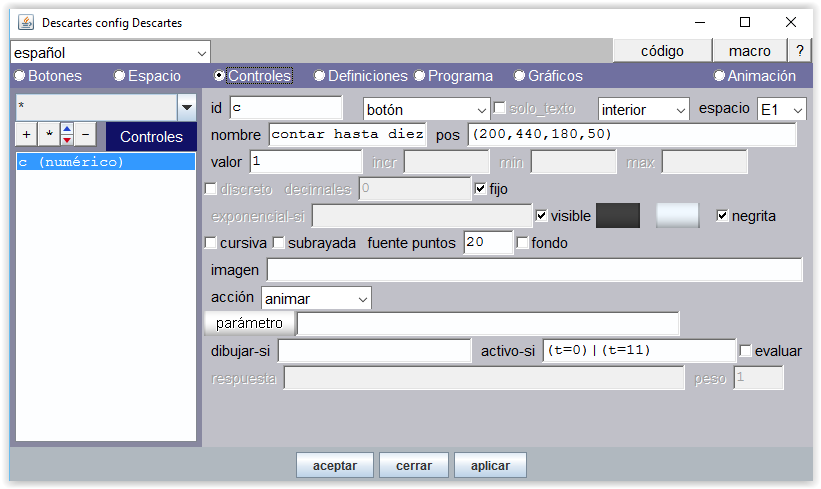
Figura 6
Se ha añadido a la escena un control numérico de tipo botón identificado por la variable c, rotulada con el nombre “contar hasta diez” y lleva la acción “animar” cuando se pulsa, en cuyo caso toma el valor 1 (este valor puede utilizarse para averiguar, p.e, si el control de botón ha sido pulsado).
En la ventana de activo-si se ha escrito la condición "(t=0)|(t=11)"; esto supone que el botón se puede pulsar y activar la animación cuanto t=0 ó t=11. En consecuencia, el botón queda desactivado a lo largo de la animación. Por defecto activo-si está en blanco.
Sonidos y gráficos secuenciados
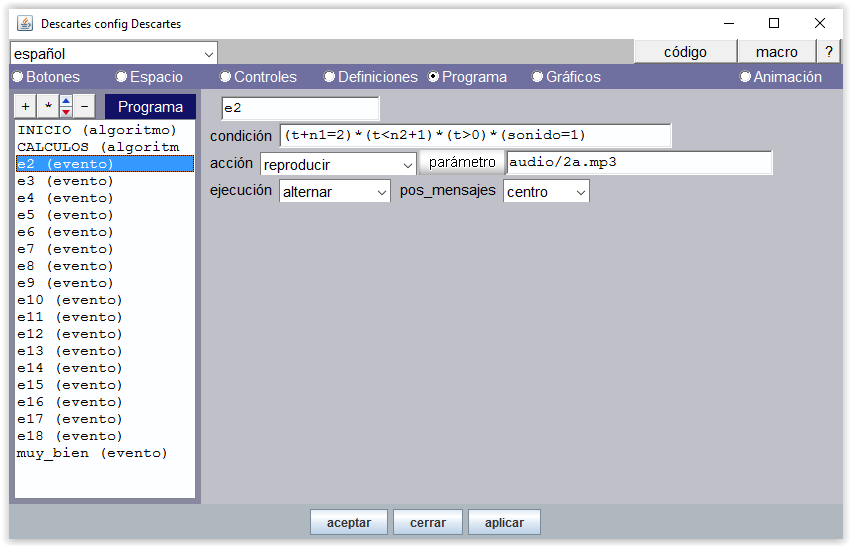
Sonidos
La animación lo que produce es que una variable t se incrementa cada cierto tiempo, indicado por el parámetro pausa. En nuestra escena del ejemplo, t es un contador que se incrementa cada 1000 ms (1 segundo). Este tiempo es suficiente para que se reproduzca de forma secuenciada (para cada valor de t) cada uno de los 10 archivos de voz independientes: “uno”, “dos”,…, “diez”. Cada sonido se reproduce para un valor determinado del contador. Un evento, en este contexto, consiste en reproducir un archivo de voz cuando el contador t toma cierto valor.
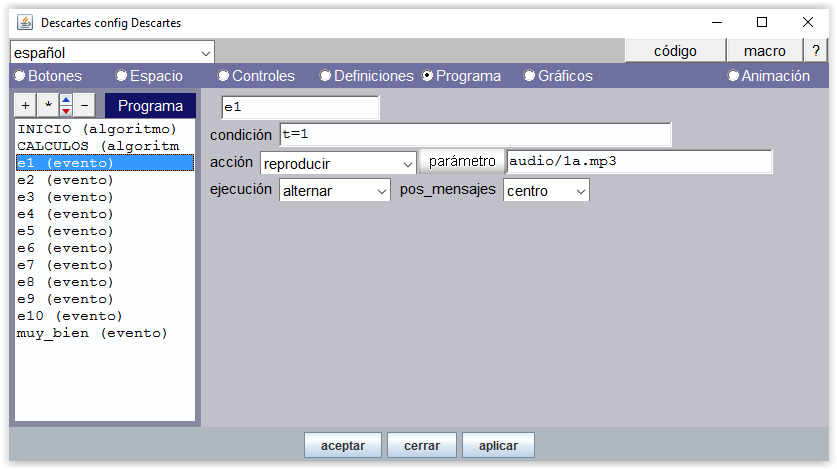
Figura 7
Un sonido de felicitación, "muy_bien.mp3" se reproduce cuando se termina de contar (condición t=11)
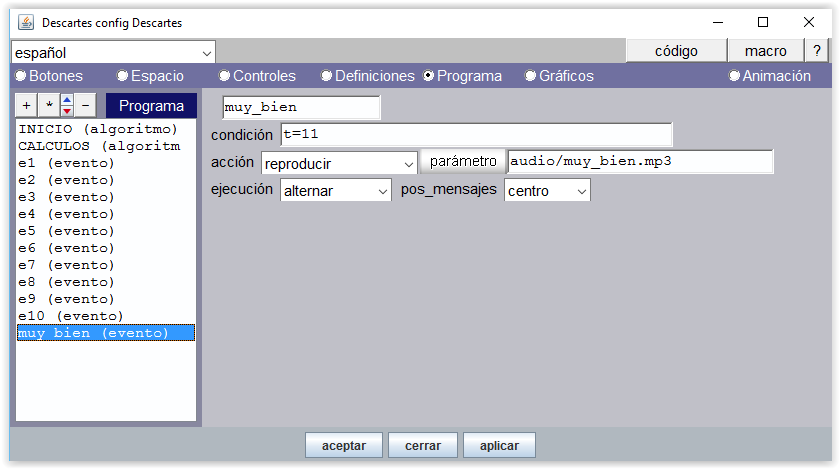
Figura 8
Gráficos
La misma animación que reproduce sonidos como eventos puede llevar aparejada la representación simultánea de gráficos de imágenes, textos, etc., que se vinculan con el valor del contador t.
En la escena de “contar hasta 10”, para cada valor de t, se representa la composición de las dos manos (derecha e izquierda) mostrando el número de dedos que señalan cada cantidad contada.
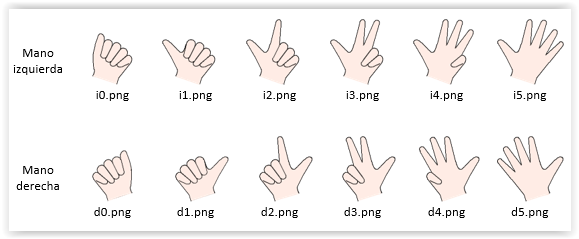
Figura 9
Así, para contar del 1 al 5, la mano izquierda tiene que estar cerrada, representada por "i0.png".
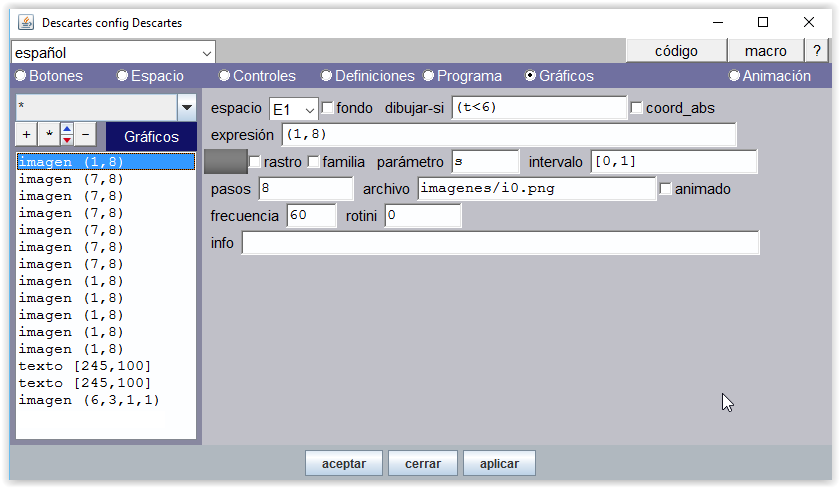
Figura 10
Antes de empezar a contar, t=0, la mano derecha está cerrada y queda representada por "d0.png".
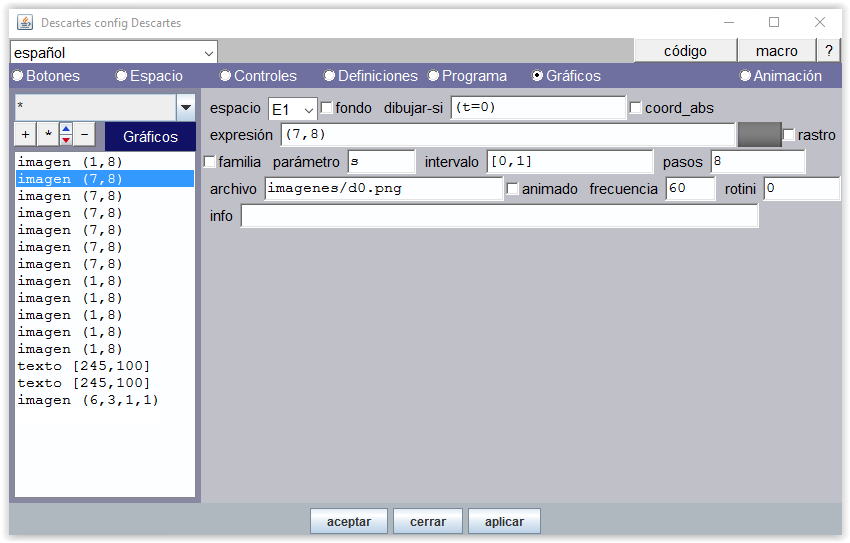
Figura 11
De t=1 a t=5 la mano derecha va mostrando sucesivamente el mismo número de dedos: d1.png,... , d5.png.
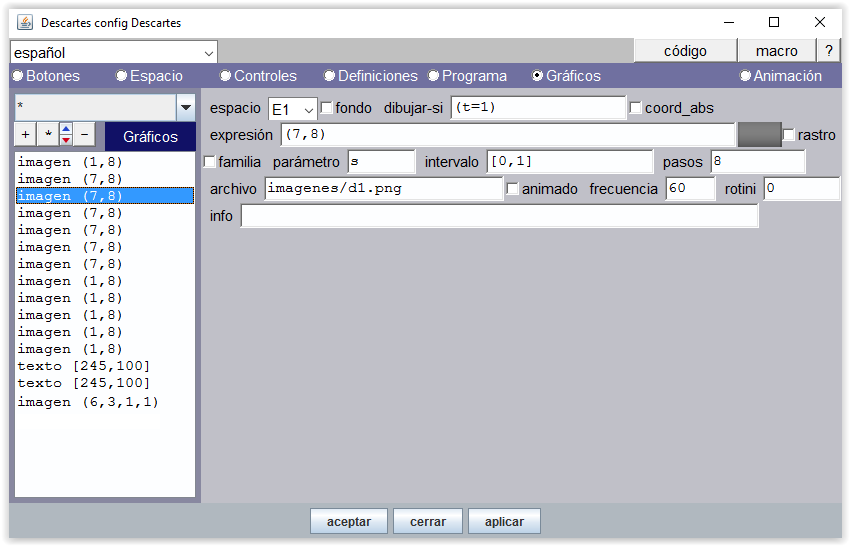
Figura 12
A partir de 5, la mano derecha tiene que mostrar los 5 dedos.
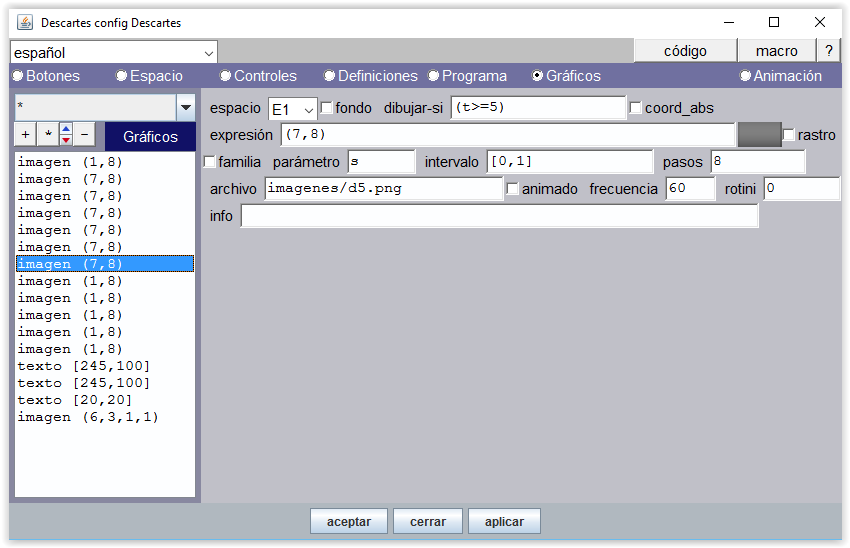
Figura 13
De t=6 a t=10, la mano izquierda va mostrando sucesivamente i1.png,... , i5.png.
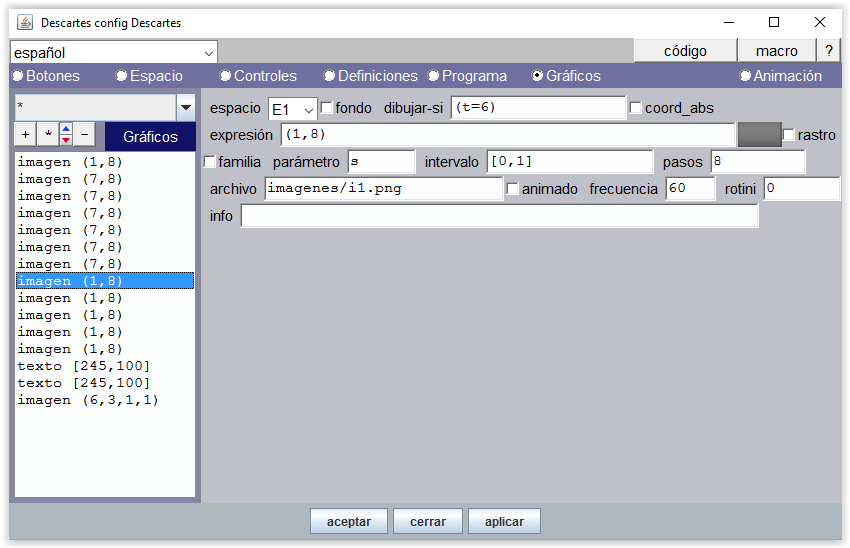
Figura 14
A partir de 10 la mano izquierda mostrará 5 dedos.
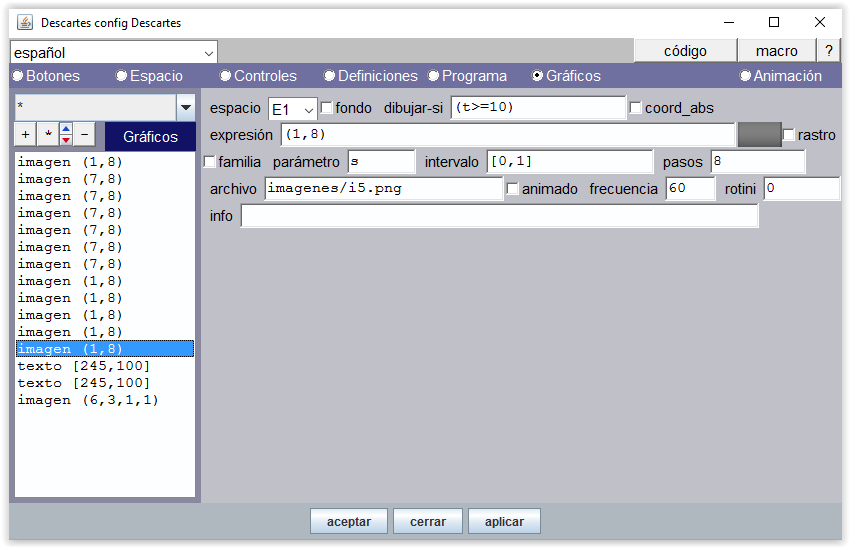
Figura 15
Un gráfico tipo texto reproduce el valor de la variable t en cada momento.
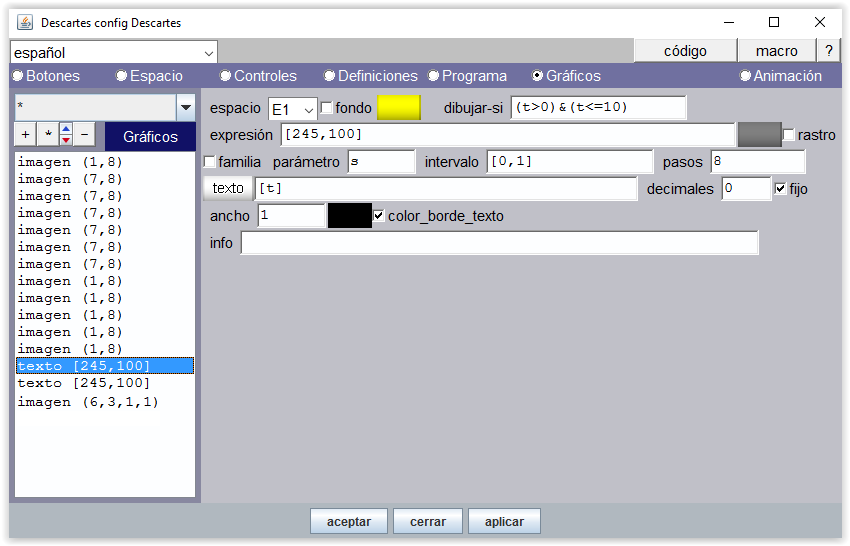
Figura 16
Cuando se termina de contar, t=11, por lo que hay que reproducir el valor de t-1 para mantener el valor 10 del texto.
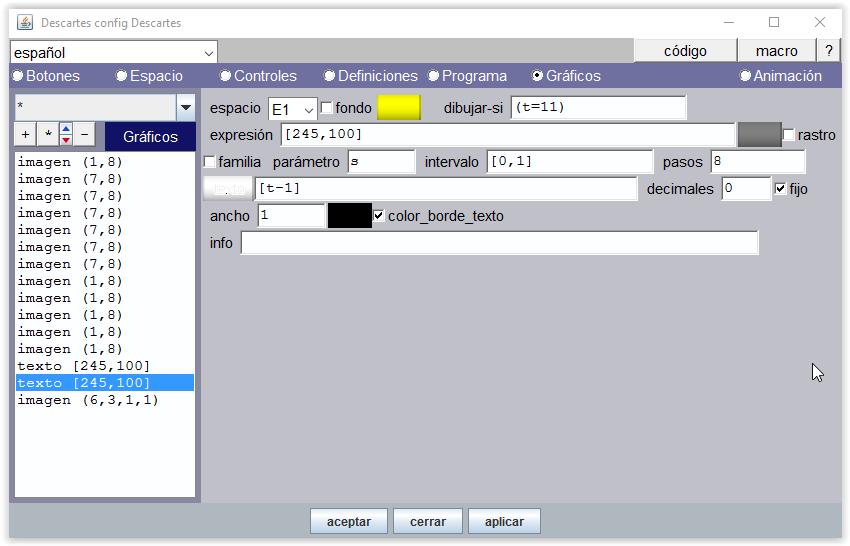
Figura 17
Una imagen acompaña al sonido de felicitación cuando se termina de contar (condición t=11).

Figura 18
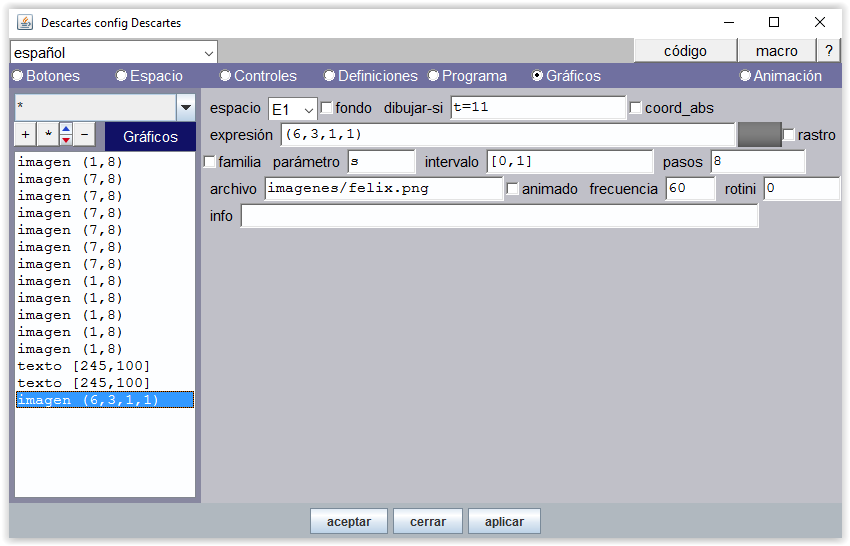
Figura 19
Proyecto
|
Escena_M06: Escenas con voz y sonido. Secuenciación temporal Como viene siendo habitual en esta serie de artículos vamos a proponer un proyecto relacionado con la secuenciación y el uso de la animación de Descartes para aquellos lectores que estén interesados en practicar y progresar un poco más en la programación con DescartesJS. Se trata de conseguir una escena lo más parecida a la siguiente. Figura 20 (Abre la escena) Como podrá observase está inspirada en la escena Sumando con los dedos de la unidad didáctica “La suma 1”. Pero se ha simplificado para quedarnos solo con los elementos de la programación relacionados con la secuenciación temporal de eventos producida por una animación, motivo de este artículo. He pretendido conseguir los mismos efectos de la escena original pero sin poner empeño alguno en que coincidieran sus respectivos códigos de programación. Se trata de practicar la suma de dos cantidades n1 y n2 que toman valores espectivos de 1 a 9. Para ello la escena tiene que contar con los dedos desde la composición con ambas manos para representar n1 hasta n1+n2: “Contar desde n1 otros n2 más”. Los sumandos n1 y n2 se generan aleatoriamente cada vez que se pulsa el control numérico de botón que lleva la acción de inicio (rotulado con el nombre “otra cuenta”). La expresión de DescartesJS que genera un número natural entre 1 y 9 es ent(rnd*9+1)
Figura 21-a Es decir, calcula la parte entera de rnd*9+1, siendo rnd una variable reservada en DescartesJS que cuando se invoca obtiene un valor real alatorio en el intervalo [0, 1). El control numérico de botón etiquetado con el nombre “contar” ejecuta la acción animar cuando se pulsa. La animación realiza un contador t=t+1 mientras t<n2+1. Los sonidos de voz se corresponden con los valores n1+1, n1+2, …, n1+n2 y en la práctica se utilizan desde 2a.mp3 (cuando n1=1) hasta 18a.mp3 (cuando n1=n2=9).
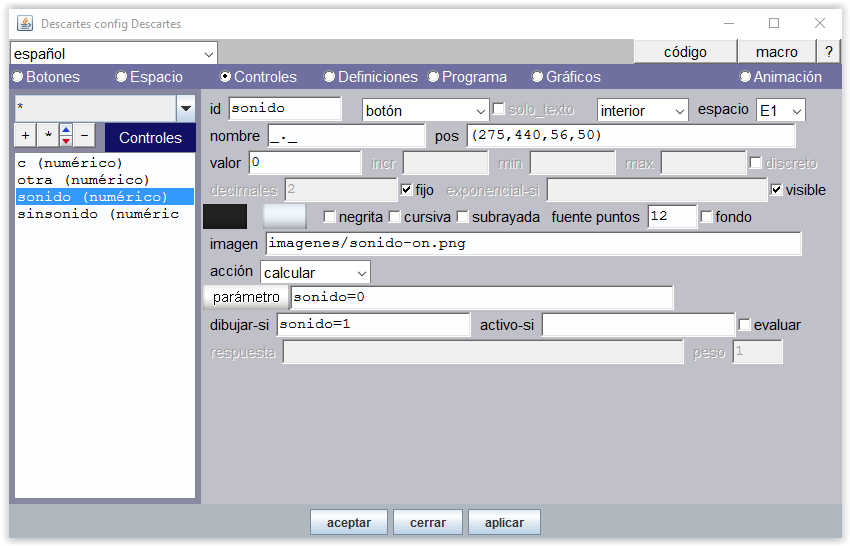
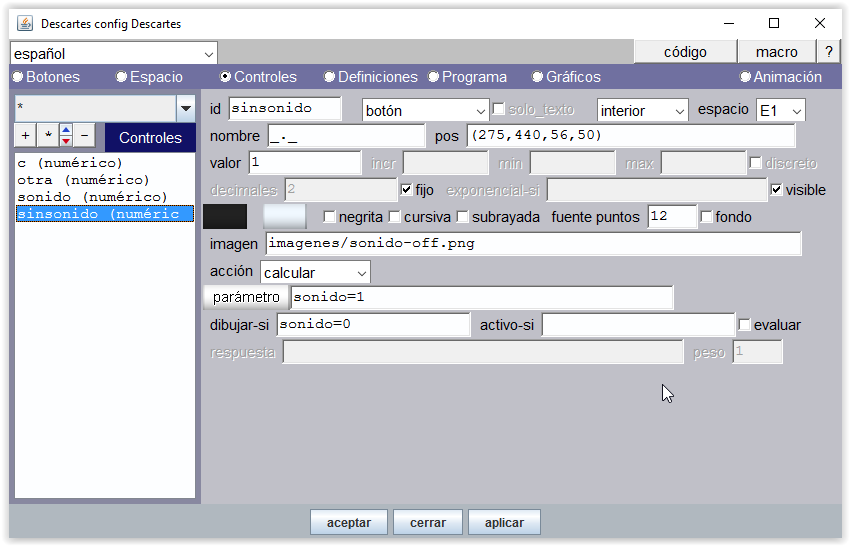
Figura 21-b Incluimos la posibilidad de contar sin reproducir la voz. Para ello se utiliza un control numérico de botón id="sonido", sin etiquetado de nombre “_._”, que lleva asociada la imagen de un altavoz "sonido-on.png". En la casilla pos de posición que ocupa el control se pone las dimensiones de la imagen 56x50 píxeles. Se muestra con la condición (dibujar-si) "sonido=1". Al pulsarlo toma el valor 0, acción calcular "sonido=0".
Figura 21-c Al pulsar el control id="sonido" se muestra en su lugar el control id="sinsonido", que lleva la imagen de un altavoz tachado "sonido-off.png". Este control al ser pulsado calcula "sonido=1", con lo que se activa la voz y se dibuja el control id="sonido".
Figura 22 El siguiente tríptico indica tres detalles que se deben de conseguir al programar la escena:
Figura 23-a
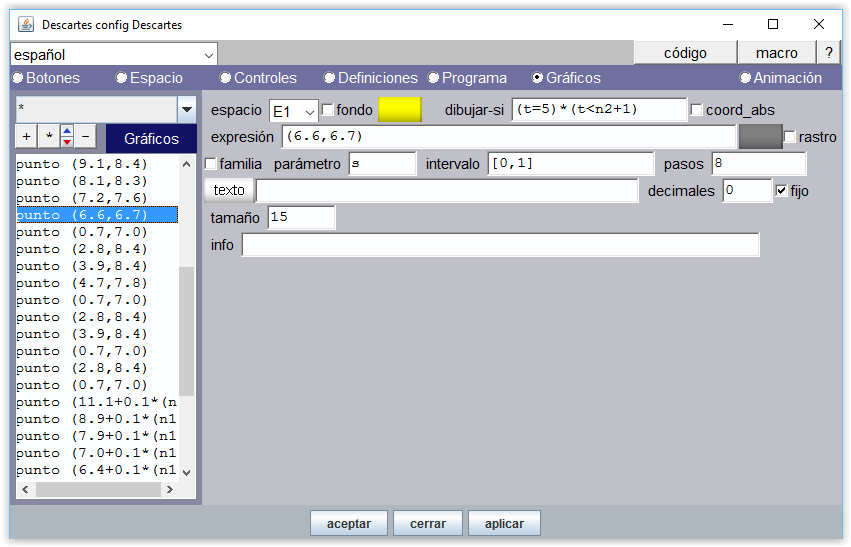
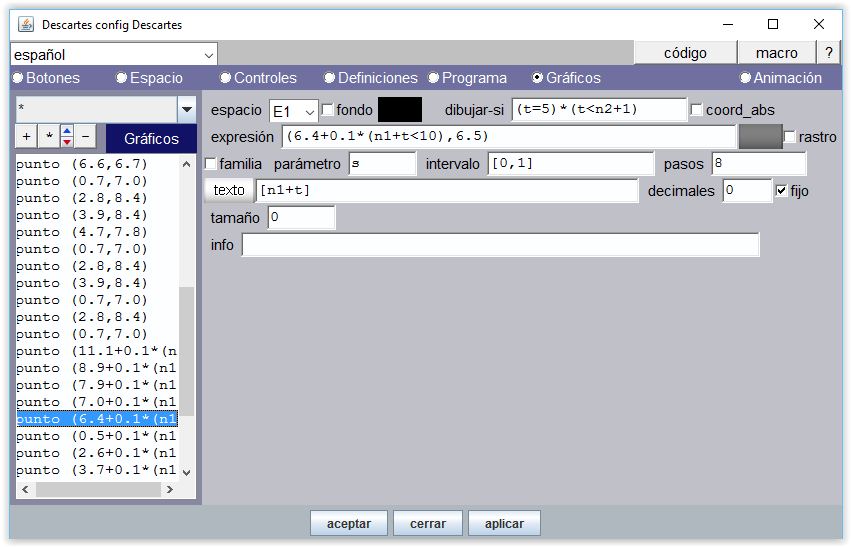
Para asignar posiciones de los controles y los elementos gráficos (imágenes, puntos, textos,…) en la escena hay que configurar en primer lugar el tamaño que tendrá la escena, asignar un valor de escala y determinar dónde tiene que aparecer el origen de coordenadas cartesianas. Cada punto amarillo, cuya posición es la de su centro, debe ir por encima de la punta del dedo correspondiente y el punto asociado de tamaño 0 cuya misión es la de poner texto [n1+t] sobre aquel, se posiciona teniendo en cuenta que este texto se muestra a cierta distancia del centro del punto correspondiente.
Figura 23-b
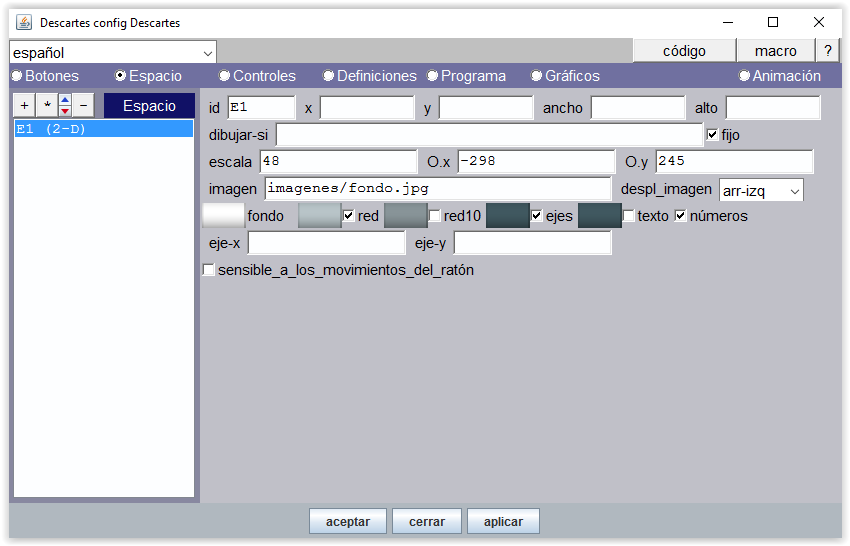
Figura 23-c En la solución que damos a este proyecto, se puede comprobar que la escena tiene dimensión 600x500 píxeles. La imagen siguiente muestra el panel Espacio del Editor de Descartes de dicha escena.
Figura 24 Las marcas red, ejes y números muestran un espacio con cuadrícula y ejes cartesianos numerados. Una vez situados los controles y gráficos se pueden desactivar. Este es el aspecto que presenta el espacio después de programado.
Figura 25 El espacio debe quedar fijo. El origen de coordenadas se ha desplazado hacia abajo 245 px y hacia la izquierda -298 px La unidad cartesiana (escala) es de 48 px. Recuérdese que las posiciones de los controles y los gráficos tipo texto se hace en píxeles tomando como origen [0, 0] el vértice superior izquierdo de la escena mientras que los gráficos tipo punto y tipo imagen se posicionan en coordenadas cartesianas con origen en (O.x, O.y). Como el tamaño de las imágenes de las manos es de 199x199 px y el posicionamiento de las mismas en el espacio es el del vértice superior izquierdo de la imagen podemos verificar en la figura anterior que la mano izquierda está posicionada en (1, 8) y la derecha en (7,8). |
Animamos a que con esta descripción y las herramientas de DescartesJS facilitadas en la serie de artículos publicados hasta este momento, el lector interesado sea capaz de programar la escena de este proyecto.
Facilitamos en los enlaces siguientes las descargas de las carpetas de contenidos de los materiales para que se pueda hacer uso de los archivos de sonido e imágenes y servir de ayuda al comprobar la estructura de carpetas y revisar o estudiar el código de las escenas con el Editor de Descartes.
|
Autoría:
Eduardo Barbero Corral
- Propuesta del proyecto.
- Técnicas de programación contenidas en las unidades didácticas inspiradoras “La suma 1” y “La resta 1” para 2º de Primaria
Ángel Cabezudo Bueno
- Interpretación, ilustraciones y redacción.
- Programación y edición de las escenas contenidas en la carpeta del proyecto “escena_M06”
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Escenas con DescartesJS: Técnicas y trucos (M05)
Escrito por Ángel Cabezudo Bueno
Una cualidad muy importante de la herramienta Descartes es que nos permite elaborar nuevas escenas, modificando otra que ya es funcional, con el objeto de conseguir diferentes resultados: cambiando, añadiendo o eliminando el correspondiente código mediante los paneles de configuración del Editor de Escenas. No se descarta la intervención directa sobre el código HTML en el archivo que contiene la escena, con un editor de texto externo tipo Bloc de notas o Notepad++. Otras veces el cambio de la escena es producido sin alterar el código, simplemente al cambiar los archivos de contenido multimedia que acompañan. Esta es la forma habitual de proceder de los desarrolladores de escenas de Descartes. En este artículo tratamos precisamente como llevar a cabo todo esto.
Contenidos que se abordan
- Basándonos en la escena M04 del puzle 2x2 de arrastre con efecto imán, que desarrollamos en el artículo precedente vamos a elaborar nuevos puzles de tamaño 3x3.
- Después produciremos un determinado número de puzles 3x3 obtenidos a partir del primero utilizado de modelo: todos ellos tienen en común el mismo código de la escena, pero difieren en el conjunto de piezas para montar un puzle particular.
Proyecto para visualizar de forma selectiva una colección de puzles ![]()
- Reuniremos todos los puzles en un mismo proyecto que será gestionado desde otra escena que llamaremos principal. Esta escena principal facilita que podamos seleccionar a voluntad desde un determinado espacio R2 los diferentes puzles que hemos producido para tal fin. Tendremos ocasión de conocer la opción Librería de proyecto del Gestor de Escenas y el espacio HTMLIframe, que es común, donde se visualizan los puzles.
Autoría
- La adaptación de un puzle 2x2 a puzle 3x3 es una propuesta de Eduardo Barbero Corral. Aparte de hacer los cambios propios para redimensionar el puzle y tener en cuenta ahora las 9 piezas en vez de 4, se dan nuevas instrucciones para la detección de piezas montadas (superpuestas) y para controlar las acciones cuando el puzle ha sido armado correctamente.
- La idea de utilizar un espacio HTMLIframe donde presentar las diferentes escenas de los puzles procede de un documento instructivo redactado por nuestro maestro cartesiano Juan Guillermo Rivera Berrío
- La interpretación de estas fuentes, la selección de las imágenes para cada uno de los puzles, la elaboración de las piezas, la edición de las escenas y finalmente la redacción de este artículo es de Ángel Cabezudo Bueno.
Enlaces a los artículos precedentes de esta serie
Dejamos los enlaces a los artículos anteriores por si alguien necesita repasar algún detalle de procedimiento que en este obviamos:
- Escenas con DescartesJS: Técnicas y trucos (B01) – Situar puntos en el plano cartesiano
- Escenas con DescartesJS: Técnicas y trucos (B02) – Identificar nombres en una imagen
- Escenas con DescartesJS: Técnicas y trucos (B03) – Distribución de nombres en un mapa
- Escenas con DescartesJS: Técnicas y trucos (M04) – Puzle de arrastre con efecto imán
Idea del proyecto
|
Escena_M05: Adaptación de escenas. Librería de proyecto. Espacios HTMLIframe Se trata de modificar esta escena, motivo del artículo anterior (la Figura 1 lleva un enlace) Figura 1 Por esta otra (la Figura 2 lleva enlace a la nueva escena) Figura 2 Cuando se superponen dos piezas y también cuando el puzle ha quedado armado debe de indicarse mediante sendos mensajes de texto. También, este segundo caso tendrá que ir acompañado de una señal acústica.
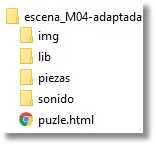
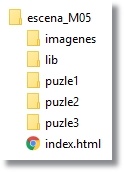
La nueva estructura de carpetas es la que se muestra en la figura 5
Figura 5 La carpeta piezas contiene 9 archivos: 1.jpg, 2.jpg,.. , 9.jpg.
|
|
La figura muestra el caso para el listado del panel Controles que es similar al de los demás.
Figura 6
Figura 7
Figura 8 En esta ventana es posible seleccionar un bloque de elementos, por ejemplo desde g1 a g4 inclusive, copiarlos con ctrl+C, abrir una línea después de g4 y pegarlos con ctrl+V; a continuación se puede modificar uno a uno los elementos de la copia. |
||||||||||
Transformaciones que producen la adaptación del puzle 2x2 al puzle 3x3
Es fundamental repasar las explicaciones que se dieron para elaborar la escena 2x2 del artículo anterior y entender bien el significado de los auxiliares que se utilizaron:
- c1, c2, c3, c4: toman el valor 1 cuando la correspondiente pieza está casi colocada en una casilla, no necesariamente la correcta. Así p.e., c1=(g1.x<0)*(abs(g1.x-ent(g1.x)-0.5)<0.05)*(abs(g1.y-ent(g1.y)-0.5)<0.05)
- s12, s13, s14, s23, s24, s34: toman valor 1 cuando están montadas la pareja de piezas que indican los subíndices. P.e en
s12=c1*c2*(ent(g1.x)=ent(g2.x))*(ent(g1.y)=ent(g2.y)) las piezas 1 y 2 está encajadas en una casilla c1=c2=1 y además sus posiciones coinciden.
- montadas = s12+s13+s14+s23+s24+s34 vale 0 si ninguna pieza está montada. Si al menos un sumando vale 1 hay piezas montadas.
- armado, vale 1 si todas las piezas están encajadas en su corresopondiente casilla. Así p.e. la pieza 1 debe de encajarse en la casilla cuyo vértice superior izquierda es (-2,1) y en consecuencia (ent(g1.x)=-2)*(ent(g1.y)=1) tiene que vale 1. Cada pieza bien encajada se evalúa a través de una expesión similar a la anterior y armado se define como el producto de las cuatro expresiones.
En la adaptación al puzle 3x3 se ha cambiado la lógica y no se utilizan las expresiones s12, s13, ... En su lugar, Eduardo Barbero Corral, propone una definición de los auxiliares p1, p2, p3,.., p9, de tal manera que cada casilla queda identificada por un número diferente y las expresiones para montadas y armado vienen dadas como veremos más adelante en función de estos nuevos auxiliares.
La escena ya adaptada se puede descargar desde aquí y verificar las trasformaciones que se explican a continuación.
| 1. |
Creación de la carpeta escena_M04-adaptada Simplemente se copia la carpeta escena_M04 que puede descargarse desde aquí y se renombra. |
||
| 2. |
Creación de las subcarpetas img y sonido Se incorporan a las mismas los archivos correspondientes. |
||
| 3. |
Sustitición de las imagenes en la carpeta piezas Las nuevas imagenes se denominan segun el lugar (fila, columna) que ocupan en la cuadrícula, 1.jpg para la casilla (1,1), 2.jpg para la (1,2),... , 9.jpg para la (3,3). Se obtienen troceando una imagen de 450x450 píxeles con alguna herramienta específica. En el artículo anterior explicábamos como se hace con PhotoScape 3.7. Las piezas o trozos obtenidos tienen el tamaño 150x150px. Para la elaboración de este artículo hemos elegido el tema de animales y en particular la adaptación del puzle 2x2 a 3x3 que estamos explicando se basa en la imagen de una ardilla. |
||
| 4. |
Actuaciones en el Gestor de Escenas Configuración: Cambiar las dimensiones a 800x510 Espacio: Escala 150 (no cambia), O.x=80, O.y=225, Imagen de fondo img/fondo.jpg, despl_imagen='expand.' Se expande dado que la imagen tiene menor tamaño que el espacio que debe ocupar. Controles: Eliminar el control de Inicio. La adaptación de esta escena está orientada a poder formar parte de una colección de puzles dentro del mismo proyecto. Cada puzle podrá ser seleccionado y por tanto iniciado de otra forma. Añadir g5,…, g9, g5.x, g5.y,… , g9.x, g9.y y mantener separada cada agrupación de controles. Modificar los valores min y máx de los controles numéricos para acomodarlos al nuevo tamaño del espacio. Desplazar finalmente los controles añadidos a la posición correcta en el listado segun el grupo al que pertenezca (Ver figura 9) 'g1.x' expresión='(0,0,0,0)' valor='rnd+0.6' min='-3.3' max='2.3' antes era min=’ -2.3’ y max=’2.3’
Figura 9 Gráficos Imágenes: Añadir las piezas 5.jpg a 9.jpg (para reducir esfuerzos se puede utilizar las herramientas de gestión del listado similar a Controles, copiando una imagen ya existente y modificando nombres). Cambio de las dimensiones del tablero:
Imagen: dibujar-si='armado', expresión='(1.1, 2, 0.5, 0.5)', archivo='img/feliz.png’
Programa
Figura 11
p1=c1*(ent(g1.x)+10*ent(g1.y)) Si cada pieza ocupa su posición correcta se obtiene un valor diferente para cada expresión: p1=17, p2=18, p3=19, p4=7, p5=8, p6=9, p7=-3, p8=-2, p9=-1 montadas=c1*((p1=p2)+(p1=p3)+(p1=p4)+(p1=p5)+(p1=p6)+(p1=p7)+(p1=p8)+(p1=p9))+c2*((p2=p3)+(p2=p4)+(p2=p5)+(p2=p6)+(p2=p7)+(p2=p8)+(p2=p9))+c3*((p3=p4)+(p3=p5)+(p3=p6)+(p3=p7)+(p3=p8)+(p3=p9))+c4*((p4=p5)+(p4=p6)+(p4=p7)+(p4=p8)+(p4=p9))+c5*((p5=p6)+(p5=p7)+(p5=p8)+(p5=p9))+c6*((p6=p7)+(p6=p8)+(p6=p9))+c7*((p7=p8)+(p7=p9))+c8*(p8=p9) armado=(p1=17)*(p2=18)*(p3=19)*(p4=7)*(p5=8)*(p6=9)*(p7=-3)*(p8=-2)*(p9=-1)
evento='sí', condición='armado', acción='reproducir', parámetro='sonido/correcto.mp3', ejecución='alternar'
|
|
Proyecto para visualizar de forma selectiva una colección de puzles Nuestro objetivo ahora es reunir una colección de puzles similares al adaptado en escena_M04-adaptada y utilizar un espacio HTMLIframe de DescartesJS donde poderlos visualizar de una forma selectiva y controlada. Puede resultar interesante para algún propósito educativo reunir una colección de puzles que trate un mismo tema, por ejemplo “animales”. Una vez elaborado un puzle con la imagen de cierto animal, como la ardilla, es muy sencillo transformarlo en otro puzle con diferente imagen, ya que bastaría tomar una imagen del mismo tamaño 450x450 píxeles y trocearla en 9 cuadrados de 150x150px con la misma numeración 1.jpg, 2.jpg,.. 9.jpg que reemplazarían las correspondientes de la ardilla. Los distintos puzles así obtenidos los guardaríamos en carpetas con nombres diferenciados: puzle1, puzle2, puzle3,… Como cada puzle va a ser consultado desde una misma escena, es conveniente que el mismo interprete descartes-min.js se comparta con lo que se ahorra espacio. Tiene sentido hablar de Librería de proyecto y que otorguemos esta categoría a dicho intérprete. Basta sacarlo de cada carpeta en los diferentes puzles, eliminando la carpeta lib y situando esta al mismo nivel que las carpetas de aquellos. La estructura de carpetas del proyecto sería como la mostrada en la figura 15
Actuaciones sobre los archivos puzle.html Tenemos que cambiar la referencia al lugar que ahora ocupa el intérprete descartes-min.js: Donde dice: <script type='text/javascript' src='lib/descartes-min.js'></script> hay que escribir <script type='text/javascript' src='../lib/descartes-min.js'></script> Ya que la carpera lib está situada ahora fuera de la carpeta que contiene el puzle, un nivel por encima. Esto se puede hacer modificando directamente cada archivo con un editor de texto plano o bien abriéndolo a través del Gestor de Escenas de Descartes, seleccionando la opción Librería de proyecto > solo para JS y guardando, sin más que hacer.
La Figura 18 lleva un enlace al proyecto resultante Figura 18 Interaccionar con la escena y observar los resultados facilita la comprensión del objetivo del proyecto. |
Actuaciones en el Gestor de Escenas
Accedemos al Gestor de Escenas, Descartes.jar. Por defecto obtenemos una escena dimensión 970x550 píxeles con la opción Librería Portable solo para JS. Esta opción es la que nos interesa ahora para la escena que debe contener el archivo index.html según la estructura mostrada en la Figura 15. Abramos el Editor de Escenas para proceder a configurarla.
- Redimensionado de la escena
En primer lugar, abrimos la ventana del código, pulsando el botón código desde cualquiera de los paneles de configuración (por defecto al abrir el Editor de escenas está activo el panel de Espacio).
La dimensión de la escena debe de llevar los valores width=970 y height=610
- Panel Botones
Desmarcar los cuatro botones créditos, config, inicio y limpiar
- Panel Espacio
El espacio por defecto E1 (2-D) lo ocupa todo y lleva por fondo la imagen imagenes/fondo2.jpg que debe expandirse pues el tamaño de esta es menor que el del espacio.
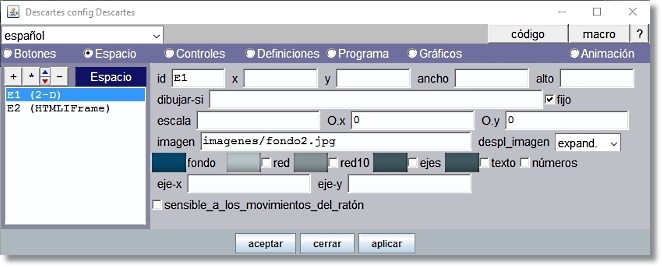
Figura 19
Desmarcar la red, los ejes, el texto y los números.
Se añade el espacio E2 (HTMLIframe) y queda superpuesto a E1.
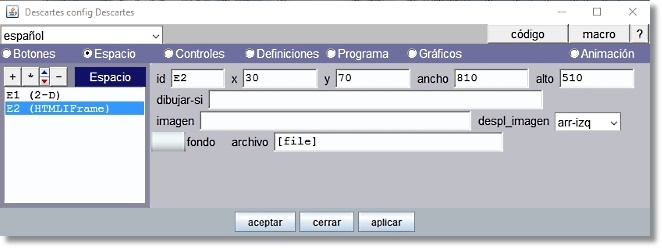
Figura 20
 |
Los espacios HTMLIframe permiten la visualización de todo el contenido incluido en un fichero html. Los parámetros en este tipo de espacio pueden consultarse con más detalle en la documentación técnica sobre Espacios HTMLIframe |
Observar que el ancho 810 píxeles y alto 510 píxeles coincide con la dimensión de la escena de cada puzle que tiene que ser representada en este espacio.
Situamos el comienzo de la representación en x=30 píxeles (distancia al borde izquierdo de E1) y en y=70 píxeles (distancia al borde superior de E1). Es decir hemos dejado un margen lateral de 30 píxeles y un margen en la cabecera donde situar en otro momento el título de la escena “PUZLES DE ANIMALES”
Obsérvese que nos queda a la derecha un margen de representación para E1 de 970 – (810 +30) = 130 píxeles con suficiente holgura para situar los controles de botón rotulados como Puzle1, Puzle2, Puzle3,…
El margen al pie de E1 es 610-(70+510) = 30 píxeles donde se escribirá el nombre del animal cuya imagen representa el puzle seleccionado. (ver Figura 18)
El parámetro archivo lleva la expresión [file], file es una variable que en todo momento contiene la trayectoria al archivo puzle.html que ha sido seleccionado. [file] explicita el contenido actual de la variable file.
La figura 21 muestra la escena tal como se ve en el Editor de escenas hasta este momento de la configuración
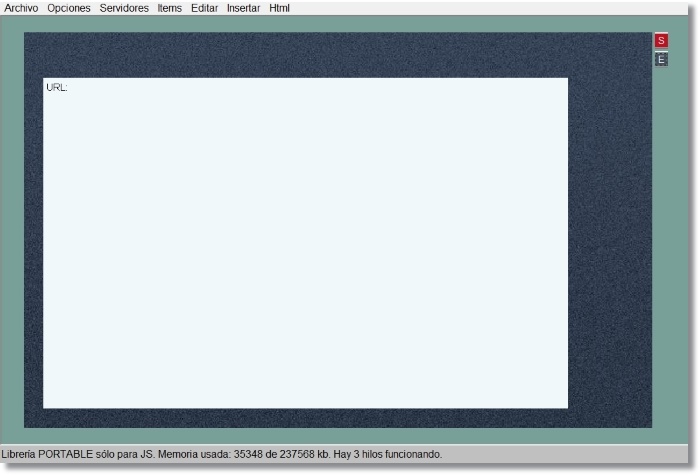
Figura 21
- Panel Controles
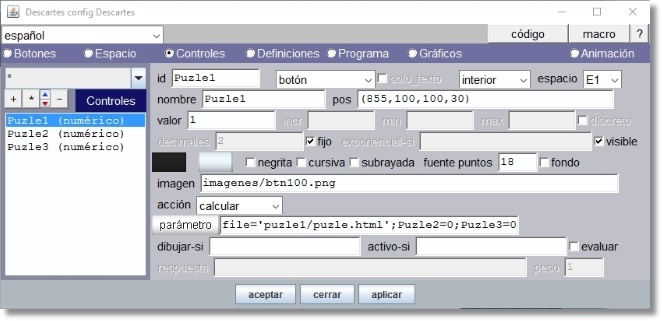
Figura 22
Este panel lleva los controles de botón identificados respectivamente como Puzle1, Puzle2, Puzle3,… tantos como puzles tengamos en la colección, en este caso son tres.
Consultar documentación Imágenes en controles numéricos tipo botón.
El nombre o rótulo que lleva el botón se ha hecho coincidir con el identificador.
La expresión de posición pos=’(855,100,100,30)’ para Puzle1 se ajusta al formato (x,y,w,h) donde x= distancia (píxeles) al borde lateral izquierdo de E1, y= distancia al borde superior de E1, w= ancho del botón, h=alto del botón.
Para Puzle2, y=150 y para Puzle3, y=200. Vamos desplazando 50 píxeles hacia abajo los sucesivos botones.
Valor = 1 es el valor que toma la variable identificada por Puzle1, Puzle2, Puzle3,… cuando se pulsa el botón correspondiente.
El texto del rótulo lleva formato: se escribe con color de relleno y borde y se selecciona un valor (18 puntos) para la fuente.
El archivo imágenes/btn100.png se utiliza en lugar del botón y coincide en tamaño. En la misma carpeta imagenes hay otras dos con el mismo nombre seguido de “_over” y “_down” , en este caso estás imágenes aparecerán en vez de btn100.png cuando el cursor del ratón se encuentra sobre el botón o cuando se pulsa respectivamente.
La acción “calcular” se realiza cuando el botón es pulsado y el parámetro contiene las tres asignaciones separadas por ; que se ejecutan: file='puzle1/puzle.html'; Puzle2=0; Puzle3=0. Las asignaciones para el botón Puzle2 son file='puzle2/puzle.html'; Puzle1=0; Puzle3=0 y para Puzle3, file='puzle3/puzle.html'; Puzle1=0; Puzle2=0.
- Panel Programa
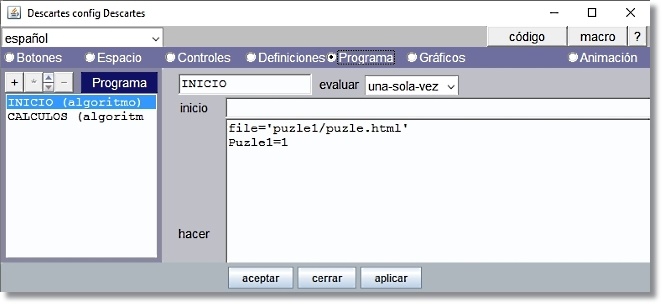
Figura 23
El algoritmo INICIO establece los valores cuando se inicia la escena. Establece que puzle debe de visualizarse al inicio asignando file='puzle1/puzle.html' y Puzle1=1.
El algoritmo CALCULOS (añadido por defecto a Programa) no se utiliza y puede eliminarse.
- Panel Gráficos
Añadimos cuatro elementos gráficos tipo texto. El primero para poner título a la escena “PUZLES DE ANIMALES” en el espacio de cabecera
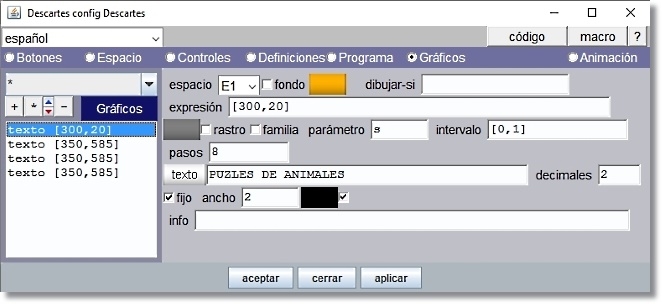
Figura 24
El color de relleno del texto (fondo) es ‘ffa800’ sin trasparencia. Lleva formato Texto simple, tipo de letra SansSerif, negrita, 28 ptos y borde negro.
Los restantes tres textos sirven para informar en el pie de la escena el puzle que se ha seleccionado y el nombre del animal representado en la imagen.
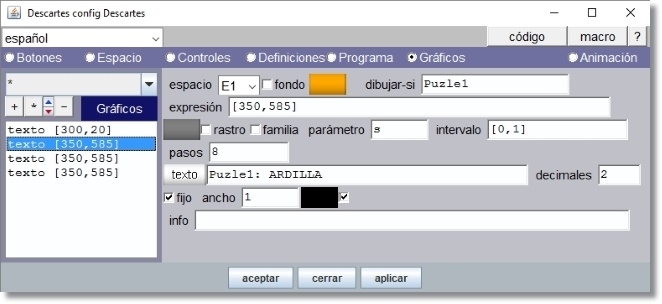
Figura 25
El color de relleno del texto (fondo) es ‘ffa800’ sin trasparencia. Lleva formato Texto simple, tipo de letra SansSerif, negrita, 18 ptos y borde negro.
La diferencia entre estos tres textos está en el identificador que lleva dibujar-si y en el texto que se escribe.
Autoría:
Eduardo Barbero Corral (Programación de la adaptación al puzle 3x3)
Ángel Cabezudo Bueno (Interpretación, elaboración de las escenas, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Escenas con DescartesJS: Técnicas y trucos (M04)
Escrito por Ángel Cabezudo Bueno Los puzles son un excelente material de motivación y está probado que son facilitadores del aprendizaje.
Los puzles son un excelente material de motivación y está probado que son facilitadores del aprendizaje.
La elaboración de un puzle con DescartesJS es una tarea interesante y ahora nos va a permitir seguir avanzando en la presentación de los distintos recursos que se pueden extraer de esta herramienta de programación.
La propuesta que se hace aquí procede, como ya hemos hecho en las escenas precedentes, de una aportación de técnicas con las que nuestro compañero cartesiano Eduardo Barbero Corral realiza sus propios puzles.
Hago repaso de su esquema de trabajo y aporto conceptos complementarios que pueden ayudar a comprender mejor al lector menos experimentado con DescartesJS.
Hemos clasificado este trabajo como de nivel medio debido a que algunas propuestas que se incluyen requieren tener cierta soltura y conocimiento de la herramienta, pero quien esté trabajando a un nivel básico todavía, bien que podrá superar sin dificultad y con estudio una gran parte del contenido.
Un puzle de arrastre parte de una imagen que está troceada en piezas de igual tamaño, generalmente de forma cuadrada y la actividad consiste en armar o componer la imagen original a partir de dichas piezas.
La programación de un puzle, aunque este sea elemental, p.e de cuatro piezas, va a requerir que se aborden estas cuestiones:
- Trocear una imagen en piezas cuadradas utilizando alguna aplicación como PhotoScape o TileMage-Image Splitter ambas gratuitas.
- Diseñar y realizar un tablero virtual donde hay que situar una cuadrícula – que habrá que dibujar con Descartes y las piezas (imágenes).
- Desplazar las imágenes apoyadas en su correspondiente control gráfico.
- Restringir el movimiento de los controles gráficos para que las piezas no puedan desaparecer de la escena cuando se arrastren.
- Procurar un efecto imán para que la imagen sea atraída y encajada en un cuadro cualquiera cuando aquella se sitúe a una distancia muy próxima del mismo.
- Verificar si hay piezas montadas en el mismo cuadro y comunicarlo mediante un mensaje de texto.
- Verificar si todas las piezas están correctamente encajadas en su cuadro correspondiente y comunicarlo mediante un mensaje de texto.
Dejamos los enlaces a los artículos anteriores por si alguien necesita repasar algún detalle de procedimiento que en este obviamos:
Idea del proyecto
|
Escena_M04: Puzle de arrastre con efecto imán La escena va a ser sencilla. Disponemos a un lado, de una cuadrícula de 2x2 (2 filas y dos columnas) y tendremos al otro lado las cuatro piezas mezcladas, situadas de forma aleatoria cada vez que se inicia la escena. Una vez realizado este trabajo se podrá seguir una pauta similar para programar puzles nxn de mayor dimensión: 3x3, 4x4, 5x5, etc. o más general de forma rectangular nxm. La Figura 1 te lleva al puzle ya elaborado para que puedas practicar y entender mejor los resultados que se pretende conseguir en este proyecto. Figura 1La escena debe permitir interaccionar con las piezas, poderlas arrastrar hacia la cuadrícula y situarlas correctamente en su cuadro. Decimos entonces que el puzle ha quedado armado. En dos momentos se requiere que el usuario reciba información a través de sendos mensajes de texto:
En este proyecto se abordarán los siete puntos de la Introducción. Proponemos la siguiente organización para las carpetas y archivos que se van a utilizar en el proyecto. La siguiente Figura 4, indica una estructura similar utilizada para desarrollar las escenas de los anteriores proyectos
La carpeta lib contiene el intérprete descartes-min.js y se puede generar automáticamente sin más que guardar en la carpeta escena_M04, con la opción Librería portable > sólo para JS, el archivo puzle.html que incluye el código de la escena. La carpeta piezas contiene las 4 piezas que se deberán denominar 1.jpg, 2.jpg, 3.jpg y 4.jpg Para realizar este proyecto debes de conseguir una imagen que sea cuadrada para trocear. Si no lo fuera debes recortarla con un programa de edición de imagen y si fuera el caso redimensionarla. Para este artículo se ha seleccionado una imagen cuadrada de 300x300 px. Cada una de las cuatro piezas del troceado resulta ser una imagen cuadrada de 150x150px. |
Troceado de la imagen
|
Existen diferentes programas que permiten trocear una imagen. Si no dispones de ninguno puedes descargarte PhotoScape que es gratuito e incluye una opción de troceado dentro de una interesante gama de posibilidades de edición. Figura 5 |
 |
Paso 1: Añadir la imagen. Seleccionar 2 columnas y 2 filas. Trocear
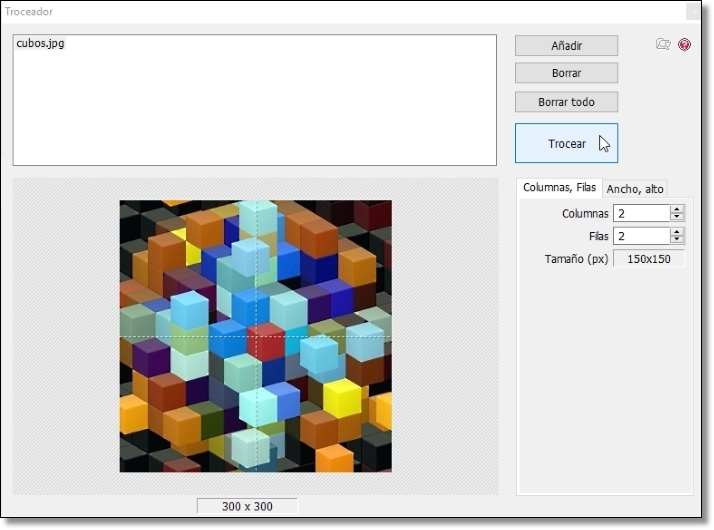
Figura 6
Paso 2: Trocear. Seleccionar carpeta de destino. Trocear.
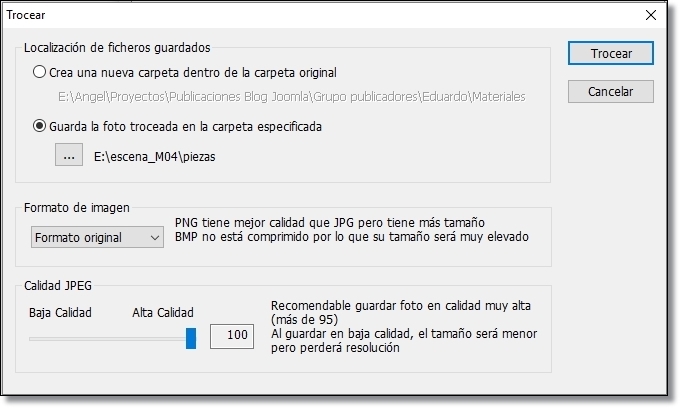
Figura 7
Paso 3: Acceder a la carpeta de destino. Renombrar las imágenes.
PhotoScape nombra cada imagen troceada añadiendo al nombre de la imagen original un número de orden contando de arriba a abajo y de izquierda a derecha es decir sigue un orden por filas y luego por columnas: la pieza 1 es la que corresponde a la casilla (1, 1), la pieza 2 la correspondiente a la casilla (1, 2), la pieza 3 la correspondiente a la casilla (2,1) y la pieza 4 la correspondiente a la casilla (2, 2).
Editor de escenas de Descartes
Abrir el Gestor de escenas y editar la escena, modificando en primer lugar su tamaño a 700x400px.
Escena adecuada para situar una cuadrícula de 300x300px y un espacio separado para situar inicialmente las cuatro imágenes.
Actuaciones en el panel Botones
Desmarcar los cuatro botones.
Actuaciones en el panel Espacio
Ponerlo fijo, para que no se pueda desplazar por arrastre. La escala será de 150 y debe coincidir con la longitud del lado de la pieza para simplificar los cálculos de situación.
Cuida que el tablero esté colocado adecuadamente, debe de estar a la izquierda y verse entero, para ello modificas los valores O.x, O.y según convenga.
 La posición por defecto del origen de coordenadas (O.x, O.y) es el centro de la escena a 350px del borde izquierdo y a 200px del borde superior. La posición por defecto del origen de coordenadas (O.x, O.y) es el centro de la escena a 350px del borde izquierdo y a 200px del borde superior.
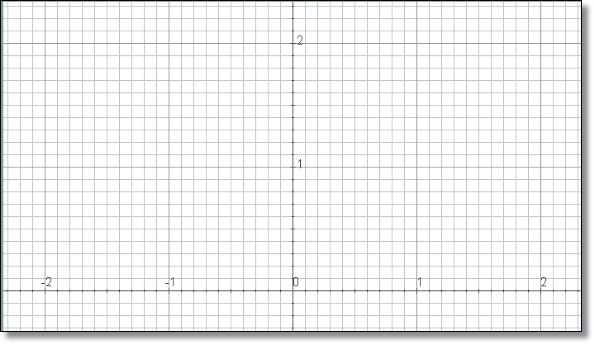
La Figura 8, muestra la red, los ejes y los números en el espacio. Esto nos permite ver mejor cómo organizar los elementos que van a aparecer en la escena. Después hay que quitarlos y poner un color de fondo para la escena al gusto del programador (ver Figura 1)
Para dibujar más adelante la cuadrícula 2x2 en el lado izquierdo de la escena, debemos posicionar el origen de coordenadas de tal manera que las coordenadas de los vértices del marco sean valores enteros sencillos. Hemos preferido que estos vértices sean (0,0), (0,2), (-2,2), (-2,0) así que para que la cuadrícula 2x2 quede dentro de la escena hay que situar O.y 150 píxeles más abajo, tal como se aprecia en la Figura 9.
|
Actuaciones en el panel Controles
Las piezas, que son gráficos de imagen, se mueven con controles gráficos que hay que definir previamente.
Agrega el primer control gráfico g1. Ponle un tamaño en número de píxeles que sea la mitad del de la escala, eso significa los pixeles que tiene de radio, para que coincida con el tamaño de una pieza de puzle. Posición (rnd+0.6, rnd*2) para que inicialmente aparezca a la derecha en lugar aleatorio.
Después pon dibujar-si=0 para que sea invisible el disco del control gráfico y no tape la pieza.
Los restantes controles g2, g3 y g4 se definen idénticamente como g1. Para añadir más rápidamente estos controles se pueden copiar g1 tres veces con la herramienta * situada en la ventana de agregar.
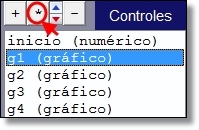 Figura 10
Figura 10
|
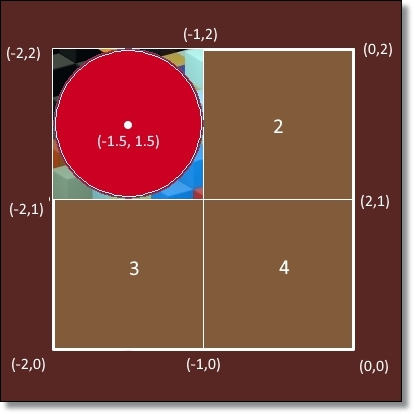
La Figura 11 nos muestra cómo se va a apoyar la pieza del puzle 1.jpg al control gráfico g1. El número de cada celda que aparece en la figura indica el lugar de destino para la correspondiente pieza, ¡no debe de verse en el puzle! La posición de destino correcta de la imagen 1.jpg es (-2, 2) ya que si se da únicamente la expresión de las coordenadas de una imagen, estas se refieren a la posición del vértice superior izquierdo.
Al definir el control g1 con la condición dibujar-si = 0, el control no se verá en la escena y dejará completamente descubierta la imagen que va apoyada. |
Actuaciones en el panel Gráficos
Lo primero es dibujar la cuadrícula 2x2. Esto se consigue, para este caso tan simple, dibujando un polígono de vértices (0,0)(0,2)(-2,2)(-2,0)(0,0) y ancho 6 (ancho en píxeles de la línea) para resolver el borde y dos segmentos perpendiculares para hacer la división en cuatro cuadrados: (-1,0)(-1,2) y (-2,1)(2,1), ancho 1. Poner el mismo color a las líneas (p.e. blanco) y color de relleno al polígono (Ver Figura 10).
Luego se van agregando una a una las imágenes de las piezas.
Para la pieza 1, el archivo es piezas/1.jpg, pones de coordenadas la expresión (g1.x-0.5, g1.y+0.5) para que se pueda mover con el control gráfico y esté centrada. Observar la expresión que ponemos para que la imagen encaje correctamente con el control sobre el que va apoyado, según la Figura 11. Por lo que explicaremos seguidamente escribimos la condición dibujar-si = (c1=0).
 |
dibujar-si es un campo de texto donde puede escribirse una expresión booleana u otra expresión que se interpreta como tal dependiendo del valor que tenga. |
La particularidad de este puzle es el efecto imán. Es decir, que cuando una pieza está muy cerca de ser colocada en una casilla parece como si una fuerza obliga a adaptarse perfectamente en ella. Para conseguir este efecto imán, para cada pieza incluiremos dos entradas de la misma imagen, una se dibuja cuando c1=0 y otra se dibuja cuando c1=1.
Veamos la circunstancia que se da para cada uno de estos valores posibles de la variable auxiliar c1.
Después de leer las actuaciones en el panel Programa para el caso c1=1 hay que añadir una nueva entrada en el panel Gráficos para dibujar la pieza 1.jpg en la posición (ent(g1.x), 1+ent(g1.y)) y dibujar-si = (c1=1).
En resumen, en el panel Gráficos tenemos para cada pieza 1.jpg, 2.jpg, 3.jpg y 4.jpg dos definiciones, una con la condición dibujar-si = (c1=1) y otra con la condición dibujar-si = (c1=0) y en este mismo orden para que las piezas cuando sean arrastradas sobre el tablero lo hagan por encima de las que ya están encajadas.
Es conveniente añadir también un control numérico de botón con la acción de iniciar la escena.
Actuaciones en el panel Programa
En el algoritmo Cálculos y evaluar siempre, en relación con la variable auxiliar c1 asociada a la imagen 1.jpg, escribimos la entrada
c1=(g1.x<0)*(abs(g1.x-ent(g1.x)-0.5)<0.05)*(abs(g1.y-ent(g1.y)-0.5)<0.05)
abs y ent son las funciones valor absoluto y la parte entera respectivamente con la definición matemática habitual.
La parte (g1.x<0) de la expresión es para que el efecto imán solo se produzca cuando la imagen está en el lado izquierdo de la escena, donde está el tablero para situar las piezas.
Observar que c1 tendrá valor 1 cuando la pieza esté colocada a una distancia muy próxima para encajar en una casilla. Esta distancia se ha fijado en menos de 0.05 tanto para la abscisa como para la ordenada de la pieza (0.05 unidades cartesianas de 150 píxeles equivale aproximadamente a 8 píxeles.).
Cuando c1 tome el valor 1, entonces la imagen en las coordenadas (g1.x, g1.y) se sustituye por la misma imagen en las coordenadas (ent(g1.x), 1+ent(g1.y)), es decir en las coordenadas del vértice superior izquierdo de la casilla que tiene tan cerca.
Añadimos después las restantes auxiliares c2, c3 y c4 asociadas a las imágenes respectivas 2.jpg, 3.jpg y 4.jpg.
Para que el proceso sea menos tedioso podemos obtener estas auxiliares copiando cada vez c1 y cambiando las referencias al subíndice 1 por 2, 3 y 4 en su correspondiente caso.
Propuesta final
Son tres las cuestiones que hasta este momento han quedado sin resolver y aunque el puzle, con lo dicho, es funcional conviene no desatenderlas:
- Notificar mediante un mensaje de texto cuando el puzle ha quedado armado. P.e: ¡Enhorabuena!.
Dependiendo del tema tratado en la imagen original, no siempre resulta fácil saber si la imagen ha sido bien recompuesta. - Notificar mediante un mensaje de texto cuando dos piezas se han superpuesto en la misma casilla.
P.e: “Hay piezas montadas! o, mejor, “Hay piezas superpuestas”. - Restringir el movimiento de los controles gráficos para que no puedan desaparecer de la escena cuando se arrastren, pues se corre el riesgo de hacer desaparecer alguna pieza si se arrastra más allá de los bordes del tablero.
El programador de DescartesJS con más recursos podrá resolver estas cuestiones cuando el número de piezas del puzle supere con mucho a cuatro. Pero queremos que también participen de esta actividad cualquier lector con nivel básico y teniendo en cuenta que manejamos pocas piezas, damos las siguientes pautas para ello.
Notificar mediante un mensaje de texto cuando el puzle ha quedado armado
Para verificar que la pieza 1 ha quedado encajada en la casilla 1 basta preguntar si la expresión c1*(ent(g1.x)=-2)*(ent(g1.y)=1) toma el valor 1.
Análogamente haremos para verificar si las restantes piezas 2, 3 y 4 están encajadas en sus respectivas casillas.
La condición para que las cuatro piezas estén encajadas en sus respectivas casillas y el puzle, por tanto, haya quedado armado es que el producto de las cuatro expresiones correspondientes valga 1.
Recomiendo crear un auxiliar, p.e. llamado armado, en el algoritmo CALCULOS del panel Programa y asignarle el valor del producto anterior.
Luego en el panel Gráficos poner la condición dibujar-si = armado, al Texto "¡Enhorabuena!" (ver Figura 3).
Notificar mediante un mensaje de texto cuando dos piezas estén superpuestas en la misma casilla
Supongamos que dos piezas, la 1 y la 2, están superpuestas y encajadas en cierta casilla, no necesariamente la casilla 1 o la casilla 2. Es obvio que se verifica c1*c2=1 pero también ent(g1.x)=ent(g2.x) y ent(g1.y)=ent(g2.y). En consecuencia c1*c2*(ent(g1.x)=ent(g2.x))*(ent(g1.y)=ent(g2.y)) tomará el valor 1.
Análogamente podemos suponer para las parejas de piezas 1 y 3, 1 y 4, 2 y 3, 2 y 4, 3 y 4. ¡En total hay 6 combinaciones posibles!.
Asignemos cada expresión a su correspondiente auxiliar, por ejemplo, s12, s13, s14, s23, s24, s34 y añadámoslos como entradas en el algoritmo CALCULOS.
Añadamos una entrada más, definiendo p.e el auxiliar montadas = s12+s13+s14+s23+s24+s34
Es obvio que montadas tomará el valor 1 cuando alguna pareja de piezas está superpuesta en una determinada casilla. Para notificar al usuario del puzle de esta circunstancia, bastará añadir, en el panel Gráficos, una entrada con el texto “Hay piezas montadas” y dibujar-si=montadas (ver Figura 2).
Restringir el movimiento de los controles gráficos
Es importante limitar el desplazamiento de los controles gráficos y en consecuencia la correspondiente pieza que va apoyada. Con esto evitaremos que por descuido al arrastrar el control más allá de los bordes del tablero la pieza pueda desaparecer y no podamos terminar de montar el puzle.
Sabemos que (g1.x, g1.y) son las coordenadas del control gráfico g1. Estas coordenadas se pueden definir convenientemente como controles numéricos y podemos conseguir esa limitación de movimientos.
En estas condiciones definimos el control gráfico g1 en la posición por defecto (0, 0) y definimos g1.x y g1.y según se indica en las figuras
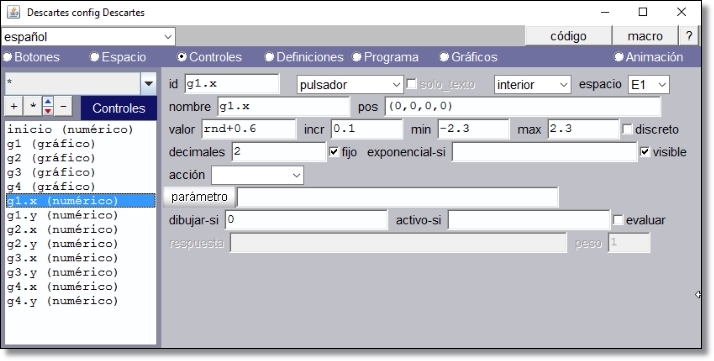
Figura 12
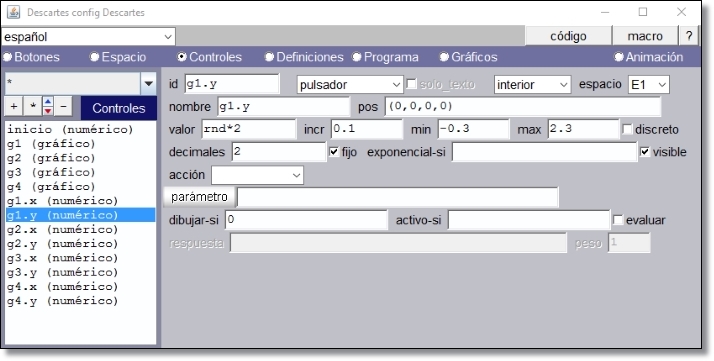
Figura 13
Estos controles quedan ocultos en la escena con la condición dibujar-si=0. El valor se g1.x y g1.y cambia al arrastrar el control gráfico g1 pero el desplazamiento queda restringido al espacio entre los valores mínimo y máximo.
Completamos copiando las mismas definiciones de g1.x y g1.y para g2.x y g2.y, g3.x yg3.y, g4.x yg4.y
Tablero con cuadrícula o sin cuadrícula
El programador del puzle podrá optar por facilitar un tablero con cuadrícula para situar las piezas o prescindir de la misma. El puzle que hemos instrumentado en este artículo podría seguir siendo funcional si prescindimos de los dos segmentos perpendiculares que acompañan al polígono de 4 vértices que delimitan el tablero.
Ahora bien si nos interesa dejar la cuadrícula y pensamos en puzles de mayor dimensión, por ejemplo de 4x5 es más práctico dibujarla utilizando dos familias de segmentos. Solo con el fin de diferenciar aquí las dos familias utilizamos en el ejemplo siguiente un color diferente para dibujar cada una, en el puzle todos los segmentos tendrán el mismo color.

Figura 14
Configuración de la familia de 5 segmentos horizontales:
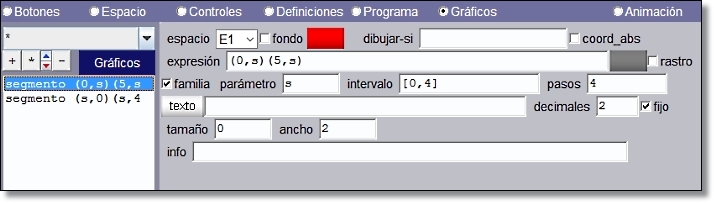
Figura 15
 |
|
Configuración de la familia de 6 segmentos verticales:
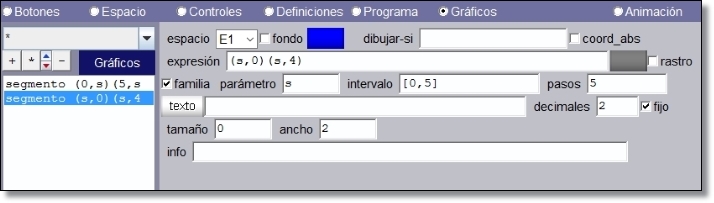
Figura 16
Esperamos haber facilitado con esta nueva edición de Técnicas y Trucos el aprendizaje a los que siguen el nivel básico y estimulado a todos los demás cartesianos para enfocar, con su propia técnica, la solución de los problemas abordados aquí.
Autoría:
Eduardo Barbero Corral (Proyecto y técnicas de programación)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Más...
Incorporando construcciones Geogebra en escenas Descartes. Ejemplo 1: Ejecutando comandos Geogebra.
Escrito por Elena Álvarez SáizLa posibilidad de comunicar escenas Descartes con páginas html facilita incorporar resultados obtenidos de la ejecución de comandos Geogebra e incluso construcciones completas que pueden ser manipuladas desde la propia escena.
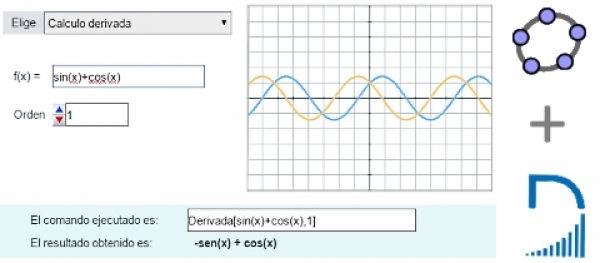
En este artículo se presenta una primera escena de ejemplo que utiliza los resultados de tres comandos Geogebra: Derivada, Integral y Circunferencia. Estos tres comandos tienen en común que su ejecución devuelve un único valor que puede enviarse a la escena Descartes como una cadena de caracteres. En próximos artículos se verá cómo incorporar los resultados de comandos que devuelven una lista de datos o una lista de listas.
Para poder comprender el código con el que se establece la comunicación desde Descartes, se recuerda la sintáxis de los comandos Geogebra que se utilizan en este ejemplo:
- Derivada[función,orden].
Por ejemplo: Derivada[cos(x),2] calcula la segunda derivada de la función cos(x)
- Integral[función,extremo_Inf,extremo_Sup].
Por ejemplo: Integral[cos(x),1,2] calcula la integral definida de la función cos(x) en el intervalo [1,2]
- Circunferencia[Punto1,Punto2,Punto3].
Por ejemplo: Circunferencia[(0,0),(1,1),(2,2)] calcula la ecuación de la circunferencia que pasa por los puntos A=(0,0), B=(1,1) y C=(2,2).
La escena Descartes que se presenta en este artículo incluye cuatro espacios.
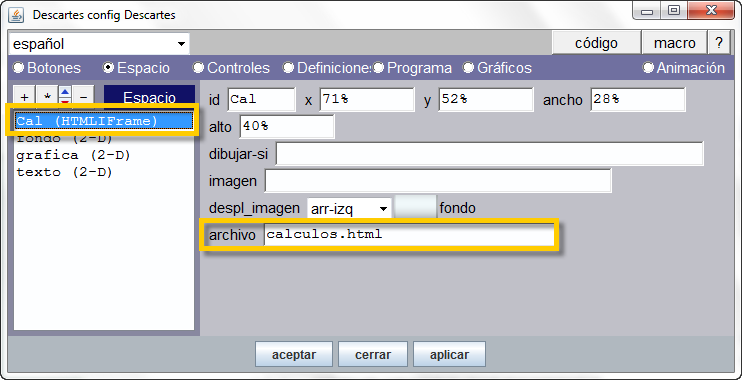
Uno de ellos es un espacio HTMLFrame que tiene como identificador el nombre Cal y será el que permitirá la comunicación con la página calculos.html que está vinculada a este espacio a través del parámetro 'archivo'.
La página calculos.html incluye el código javascript necesario para poder enviar y recibir datos de la construcción Geogebra que está embebida en ella. Esta página no necesita ser modificada y debe incorporarse en el mismo directorio que la página que contenga la escena Descartes (de no ser así se tendrá que modificar la ruta de acceso a ella en el parámetro 'archivo' del espacio HTMLFrame).
El funcionamiento de la escena Descartes que se presenta como ejemplo es sencilla. Elegida una de las tres opciones del menú, se inicia la comunicación con Geogebra. Si la opción elegida del menú es 'Calculo de la Derivada' se ejecuta la función Calculo1(), si se elige la opción 'Circunferencia por tres puntos' la función a ejecutar será Calculo2() y en el caso de que la opción sea 'Cálculo de la integral de un intervalo' la función asociada es Calculo3().
Las tres funciones tienen un código similar, en primer lugar construyen una cadena de caracteres con la sintásis del código Geogebra a ejecutar y después inician la comunicación enviando a la página incluida en el espacio Cal el evento 'evalua' pasándole como parámetro esta cadena de caracteres. Por ejemplo, el código incluido en la función Calculo1() es el siguiente:
n1='Derivada['+f+','+orden+']'
Cal.set('evalua',n1)
A la hora de generar la cadena de caracteres n1 se ha utilizado los valores de f y orden que están vinculados a los dos controles que se muestran en la escena para modificar, respectivametne, la expresión de la función y el orden de la derivada.
La página calculos.html, que está asociada al espacio Cal, recibe entonces el mensaje y ejecuta el código asociado al evento 'evalua' tras lo cual devuelve a la escena Descartes el resultado en una cadena de caracteres que siempre tiene por nombre vCalculado.
Todo este proceso es totalmente transparente al autor de la escena que puede utilizar el valor de la variable vCalculado de la misma forma que cualquier otra variable creada en la propia escena. Así, si por ejemplo se quiere representar la función derivada obtenida tras ejecutar Calculo1(), bastaría con:
- Evaluar la cadena de caracteres que se ha devuelto con el valor de la derivada: f1=_Eval_(vCalculado)
- Definir una función fun1(x)=f1 para poder crear un objeto gráfico de tipo ecuación cuya expresión sea: y=fun1(x)
Se puede practicar con la escena descargándola del siguiente enlace: Ejemplo1_CAS-JS.zip
¿Cómo observar lo que no podemos ver? Taller y laboratorio de curvatura
Escrito por José R. Galo SánchezLos fenómenos físicos son dependientes de las características intrínsecas del medio en el que se desarrollan. Por tanto, pueden estar influidos o condicionados por la forma del espacio en el que acontecen o en el que se manifiestan. Por ejemplo, en un espacio euclídeo, dos rayos de luz emitidos en direcciones paralelas continuarán su viaje indefinidamente sin intersecarse. Sin embargo, si el espacio de propagación es curvo, geometrías no euclídeas, convergerán o divergirán según su curvatura sea positiva o negativa.
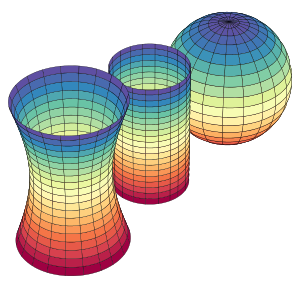
Hiperboloide, cilindro y esfera con curvatura de Gauss negativa, nula y positiva respectivamente
Fuente de la Imagen wikipedia
¿Cómo un habitante de un determinado mundo puede investigar y conocer la forma del espacio en el que habita? Nosotros, como habitantes tridimensionales, observamos diferencias evidentes en la forma que tienen los mundos bidimensionales, las superficies, representadas en la imagen anterior. Pero un habitante bidimensional de alguno de esos lugares ¿cómo puede saber la forma que tiene la superficie que habita? La respuesta puede encontrarse en una relectura del párrafo inicial realizada desde otra perspectiva, es decir, si ese habitante emite dos rayos de luz y comprueba que divergen, entonces su mundo tiene curvatura negativa; si no se intersecan tiene curvatura nula y se cortan su curvatura es positiva. Así pues, un experimento físico realizado en el mundo que habita le permite determinar y confirmar la forma de su hábitat, lo puede ver matemáticamente, aunque no pueda verlo nunca de una perspectiva exterior. La clave la encontramos en la curvatura, ésta es la herramienta matemática que nos permite saber, observar, lo que nunca podremos ver.
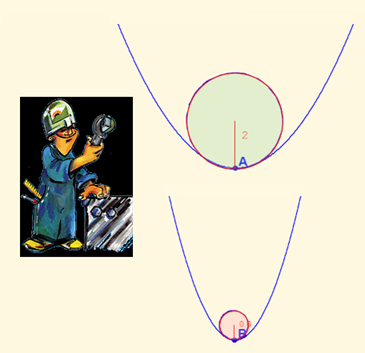
De manera análoga un habitante unidimensional, el de una línea, podrá conocer la forma de su espacio vital si es capaz de determinar la curvatura de la misma y para ello, al igual que antes, puede basarse en algún experimento físico que permita discriminarla. Por tanto, el concepto de curvatura en una línea es un conocimiento previo que ha de comprender y adquirir como base de su investigación. Y al aprendizaje de este concepto le ayuda, nos ayuda, nuestra compañera Consolación Ruiz Gil (Solín) con su unidad didáctica titulada “Curvatura” en la que nos lleva al taller, al laboratorio matemático, y nos introduce progresivamente en ese concepto y en su medida. Para ello:
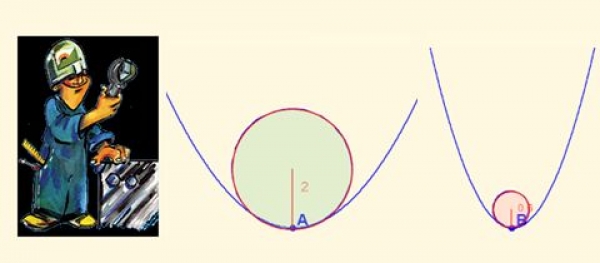
- Tomando como referencia a la circunferencia, curva básica en el estudio geométrico, introduce la medida de su curvatura deduciendo cómo depende de su radio y por tanto es siempre una cantidad positiva. Ésta, disminuye a medida que es mayor el radio e incluso como situación límite puede asignarse a una línea recta una curvatura nula.
- Se plantea un segundo acceso al taller al tratar de dar respuesta a la medición de la curvatura a cualquier otra curva en un determinado punto y, para ello, se marca la estrategia de aproximarla en él por un arco de circunferencia, aquel que más se le asemeja, y consecuentemente asignarle como curvatura la de esa arco. A partir de lo experimentado en este taller, Solín procede a plantear analíticamente cómo determinar ese arco y ello requiere adentrarse en un nivel microscópico. Ello obliga a acudir al laboratorio y utilizar el cálculo infinitesimal. Surge la circunferencia osculatriz y se formaliza el concepto de curvatura en cualquier curva que sea derivable.
- La unidad didáctica finaliza referenciando artículos de difusión y periodísticos en los que la curvatura es la base para la determinación de la forma de nuestro mundo. ¿Cómo es éste? ¿“Es plano” –entendido este término aquí como “Euclídeo” o con curvatura nula--? ¿Tiene curvatura no nula? Las ondas gravitatorias, sobre las que el pasado 11 de febrero de 2016 se publicó su existencia, ayudan a establecer esa curvatura del espacio-tiempo.
Así pues, un experimento físico (LIGO) como es la determinación de la existencia de las ondas gravitatorias nos permite adentrarnos en el conocimiento de la forma del mundo que habitamos estos seres físicamente tridimensionales (largo, ancho, alto), anexos o inmersos en una cuarta componente dimensional tiranizada por ése que siempre pasa (“Tempus fugit”). Y todo ello gracias a la curvatura, la curvatura espacio-tiempo.
LIGO ha sido posible gracias a la posibilidad de medir longitudes del orden de 10^-19 m, pero la Teoría de cuerdas plantea que nuestro universo tiene once dimensiones: una temporal, tres espaciales ordinarias y siete compactas inobservables en la práctica y que solamente son relevantes a escalas pequeñas del orden de la longitud de Planck: 10^-35 m. ¡Quedan curvaturas que estudiar!
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)










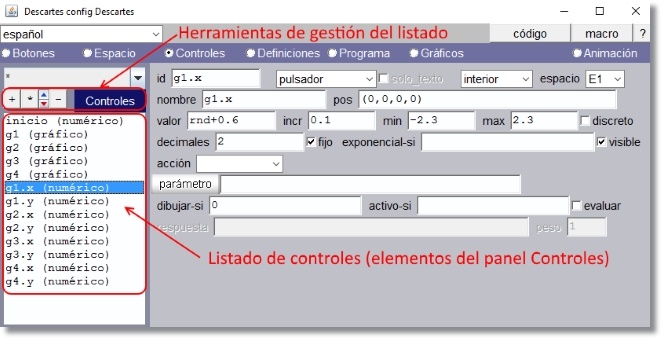




 a ventana con la lista de controles hasta ese momento añadidos con sus definiciones que pueden ser editadas como en un editor de texto (ver Figura 7)
a ventana con la lista de controles hasta ese momento añadidos con sus definiciones que pueden ser editadas como en un editor de texto (ver Figura 7)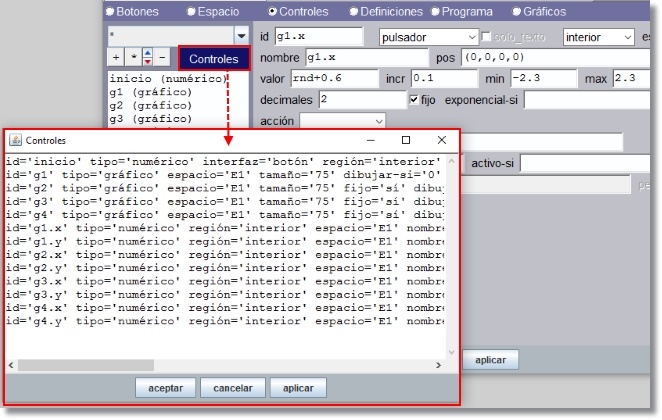
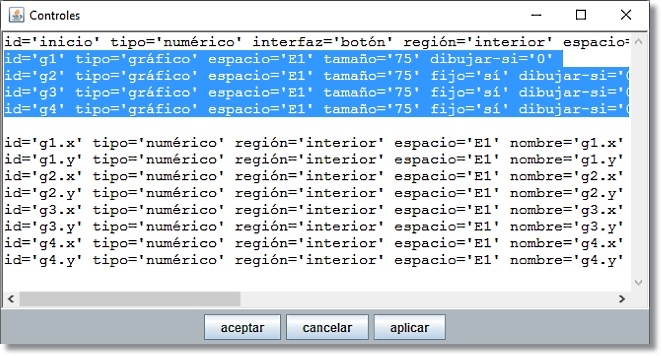
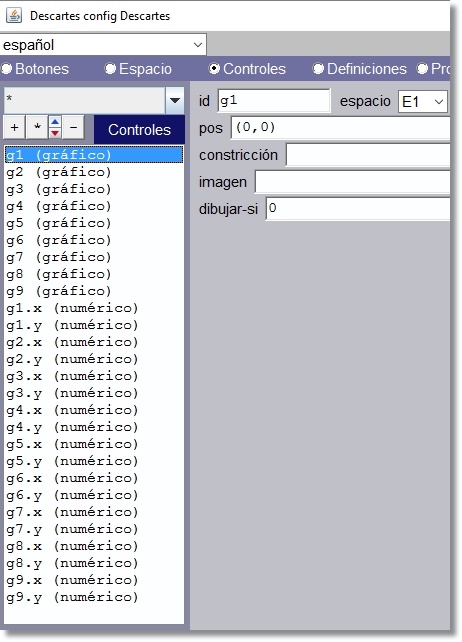

 Figura 10
Figura 10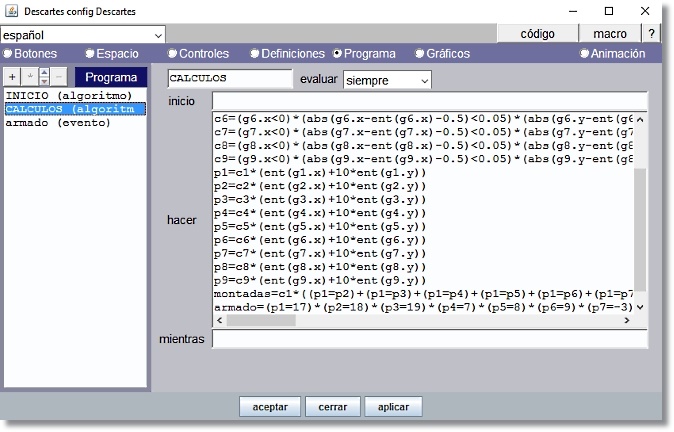
 El archivo index.html lleva la escena que controla la visualización de cada uno de los puzles en un único espacio HTMLIfame que enseguida pasaremos a explicar.
El archivo index.html lleva la escena que controla la visualización de cada uno de los puzles en un único espacio HTMLIfame que enseguida pasaremos a explicar.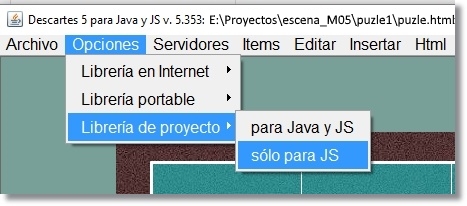





 CONTACTO
CONTACTO
