Cuando confluyen ideas simples con necesidades o requerimientos técnicos mínimos, se logra elaborar magníficos recursos educativos de gran interés y vistosidad. Esto es lo que acontece en la utilidad cartesiana desarrollada por nuestro amigo cartesiano Juan Gmo. Rivera Berrío, presidente de la Red Educativa Digital Descartes de Colombia. Una utilidad que ha denominado "Lupa cartesiana" y que puede observarse en la siguiente escena (pulsa sobre la imagen):
La escena utiliza la posibilidad de la herramienta Descartes que permite integrar varios espacios y el escalado de imágenes.
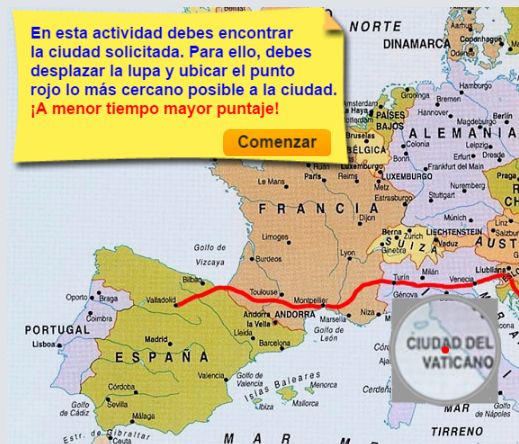
En la siguiente escena podemos ver una entretenida aplicación que permite poner a prueba nuestro conocimiento geográfico. Este recurso se está empleando en el desarrollo de nuevos materiales educativos que pronto se integrarán en el subproyecto GEOgráfica de la RED Descartes.
La creatividad de los cartesianos y del profesorado en general podrá dar una amplia aplicación de esta herramienta en su contexto educativo y en el ámbito cognitivo que sea de su interés particular. Una utilidad que permite introducir al usuario en una visión microcóspica --al nivel que se desee-- en base a una imagen inicial sobre la que se puede profundizar gracias a la visión virtual de la lupa cartesiana.
La fuente de estos recursos y de este artículo se encuentra en la documentación de Descartes.
Descartes en la Universidad. Miscelánea: Desarrollo en serie de Fourier
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Desarrollo en Serie de Fourier
Con esta escena se puede calcular el desarrollo en Serie de Fourier de una función periódica y representar la suma de sus primeros términos. Su objetivo es mostrar que una función periódica puede descomponerse como suma de funciones trigonométricas, senos y cosenos, cuyas frecuencias son múltiplos enteros de la frecuencia fundamental.
A modo de ejemplo se incluye el desarrollo de varias funciones y se representa, en una misma gráfica, la función y la suma de los primeros términos de su desarrollo. Esta representación permite visualizar la aproximación que proporcionan las Series de Fourier.
La miscelánea facilita también introducir una función cualquiera y obtener su desarrollo utilizando cálculo simbólico para mostrar la expresión de los coeficientes de la serie. Cuando la función no es periódica y está definida en un intervalo de la forma [0, p], se puede obtener el desarrollo en Serie de Fourier de su extensión par o impar.
En el siguiente video se muestra cómo utilizar esta miscelánea.
Acceso a la miscelánea: Desarrollo en Serie de Fourier
Descartes en la Universidad. Miscelánea: Derivada de una función en forma explícita, paramétrica e implícita
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Derivada de funciones explícitas, paramétricas e implícitas
En esta miscelánea se muestra cómo calcular la derivada de una función en un punto cuando viene definida en forma explícita, en forma paramétrica o en forma implícita. Para ello se debe introducir la función y el punto y pulsar sobre el botón ¿Cómo se hace? para obtener una descripción del proceso de cálculo.
Las miscelánea permite introducir un valor y comprobar si es la derivada en el punto seleccionado para la función que se esté considerando. Se puede también calcular la recta tangente y normal a la función en el punto.
En el siguiente video se muestra cómo utilizar esta sencilla miscelánea.
Acceso a la miscelánea: Derivada de funciones explícitas, paramétricas e implícitas
Audios y Vídeos Interactivos con Descartes
Continuación de la práctica (1)
En el artículo anterior creamos los espacios: E2 y E3, semitransparente el primero y transparente el segundo, para mostrar mensajes y enmascarar los controles del vídeo, estas especificaciones están ampliamente detalladas en la documentación enlazada en el título del artículo.
En el espacio E2 se mostrarán dos tipos de mensajes: los de información al comenzar la actividad (t=0), y las preguntas con el cuadro de texto, menú desplegable o botón, para introducir, elegir o pulsar la respuesta correcta, y el mensaje de acierto o fallo, una vez se ha respondido y a continuación, pulsado sobre el botón verificar que aparece, en los tiempos de reproducción t1 y t2 (t=t1) y (t=t2).
Pasamos a desarrollar el paso 4. Siguiendo las instrucciones de la documentación activamos la opción de menú Animación y tecleamos los valores indicados. Recordamos que el "id" del control de vídeo es "v1" esto signifíca que para su manejo debemos usar las instrucciones: v1.play() para reproducirlo, y v1.pause() para que se detenga. La animación hace que el valor de t se actualice cada segundo (1000 milisegundos) y únicamente se incrementará si el vídeo se está reproduciendo (a = 1).
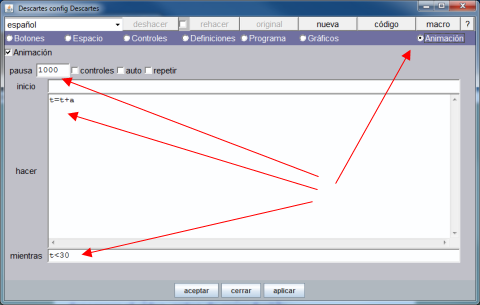
El paso 5 consite en activar la opción de menú Programa y dentro del algoritmo INICIO, que se ejecuta una única vez al iniciar la actividad, definimos tres constantes: Titulo (texto para el encabezado de la escena), t1 (valor en segundos para detener el vídeo por primera vez y efectuar la primera pregunta) y t2 (idem para la segunda pregunta). En el siguiente gráfico observamos lo expuesto.
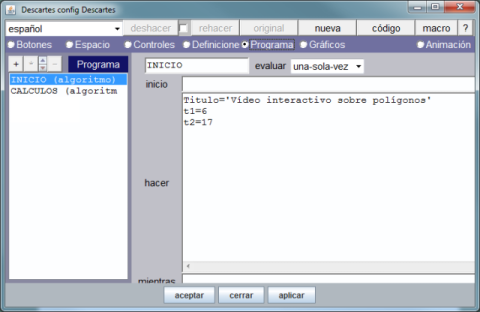
A continuación, siguiendo las indicaciones del paso 6, seleccionamos la opción de menú Gráficos para definir en qué espacio va a ir cada texto, imagen, gráfico etc. cuál va a ser su situación dentro de la escena, y si es texto, qué formato (tamaño, color, tipo de letra, estilo, etc.) va a tener y, en general, cuando el objeto va a estar visible y cuando oculto.
El siguiente vídeo muestra, paso a paso, como insertar texto en la escena. En primer lugar se inserta, en el espacio E1, dentro de una fórmula, la expresión que contiene el valor de la variable Titulo que hemos creado. Luego en E2 y E3 se van creando los textos necesarios para dirigir y documentar la acción de la actividad.
A continuación se crean en E3 los textos "¡EXCELENTE!" de tamaño 48 y color verde que será visible si: (t>t1)&(t<t1+4)&(pregunta_1='4') y "¡No es cierto! Tiene cuatro lados" de igual tamaño y color rojo que será visible si: (t>t1)&(t<t1+4)&(pregunta_1!='4')
En E2, en la posición (110,70) se introduce la segunda pregunta, que será visible si: t=t2, y en E3 se definen los textos a mostrar según sea la respuesta de forma análoga a como lo hemos hecho para la primera pregunta.
El aspecto que debe tener el submenú Gráficos y la escena en este momento del desarrollo es el que muestran estas imágenes.
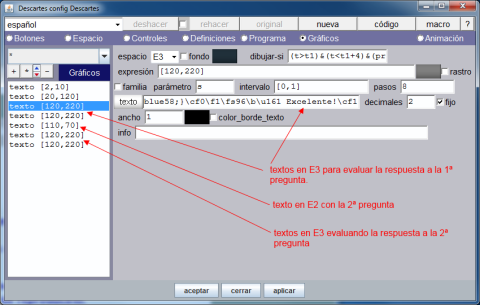
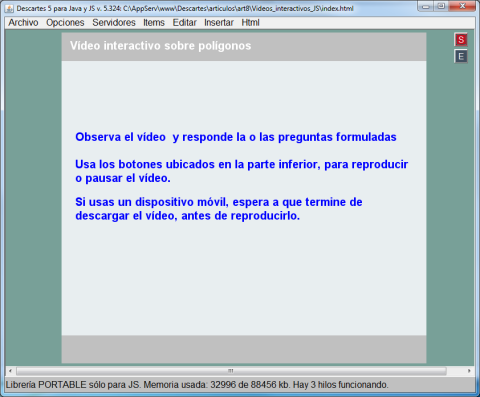
En próximas entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
El logo del subproyecto GEOgráfica hace de enlace a una recreación de la actividad de colorear las provincias de las distintas Comunidades Españolas realizada por Juan Guillermo Rivera Berrío y que en este primer ensayo se centra en la Comunidad Andaluza. Tras un vídeo, alojado en YouTube y que se reproduce dentro de una escena Descartes, donde se hace una presentación cartográfica de la Comunidad, se ejecuta la utilidad de colorear que solicita un clic en una de las provincias, según sea la respuesta, el programa advierte del error o reproduce un vídeo relativo a lo más significativo de dicha provincia. Aunque aún está en fase de pruebas, damos a conocer este subproyecto de GEOgráfica por su gran potencial educativo y cultural ya que pueden incluirse tantos vídeos como se precisen sin que esto influya en el peso de la unidad. Esto ha sido posible gracias a la colaboración de la Red Descartes de Colombia (Juan Gmo. Rivera y Ramiro Lopera) y de España (José R. Galo).
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Más...
Audios y Vídeos Interactivos con Descartes
En artículos anteriores mencionamos la posibilidad de insertar contenido multimedia en las utilidades didácticas que tengamos proyectado realizar. Ahora veremos cómo proceder, utilizando el Editor de Escenas, para crear una utilidad con un vídeo interactivo. Esto es, el vídeo se reproduce y plantea una cuestión, deteniéndose en ese punto hasta que se introduce una respuesta y según sea esta, continúa su reproducción en un punto u otro de su contenido o salta a otro vídeo en una posición predefinida.
Antes de continuar debe analizarse detenidamente la documentación enlazada en el título. En ella, José R. Galo Sánchez incluye un documento elaborado por Juan Guillermo Rivera Berrío donde se describe, paso a paso, la creación de una escena que tiene un vídeo interactivo.
Supuesto que se ha estudiado la documentación técnica y si se ha considerado necesario, descargado el documento, vamos a proceder a elaborar el proyecto propuesto, para lo cual, lo primero que hacemos es crear una nueva carpeta, a la que nombramos VideoInteractivo, que es donde vamos a guardar dicho proyecto.
Dentro de la carpeta anterior debemos crear una carpeta para alojar el vídeo que vamos a utilizar, en nuestro caso creamos la carpeta llamada vídeos y también creamos las carpetas: imagenes, donde guardaremos las imágenes que utilizaremos y css, donde irá el archivo de estilo. El editor, al guardar el archivo index.html crea la carpeta lib con el intérprete descartes-min.js según se muestra en el siguiente vídeo.
Abrimos, por lo tanto, el Editor de Escenas y damos las dimensiones que aconseja el paso 1, 640x580, guardando el resultado en la carpeta VideoInteractivo con el nombre index.html tal como hemos visto en el vídeo.
Por defecto, el Editor de Escenas Descartes, crea una escena mínima que iremos modificando para adaptarla a nuestro proyecto.
Tal y como hemos visto en artículos anteriores, la escena está contenida en un archivo de extensión html si ahora abrimos el archivo index.html con un editor de texto plano o un editor de código html, observamos lo siguiente.
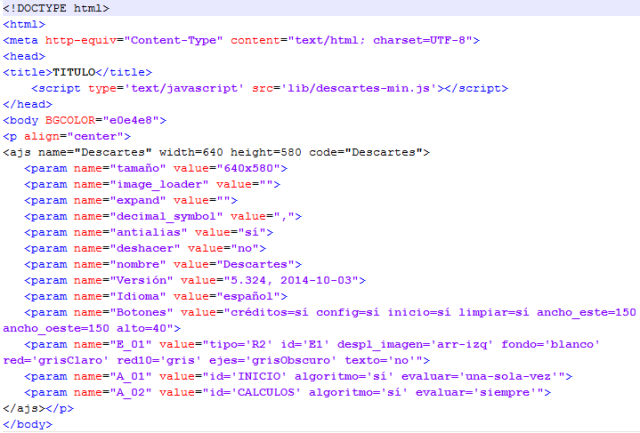
Podemos modificar el título del documento y algunos otros parámetros html directamente con el propio editor de textos, aunque las modificaciones relativas al código JS es conveniente realizarlas con el Editor de Escenas, también pueden hacerse directamente con el de textos. Con cualquiera de los métodos quitamos los botones: créditos, config, inicio y limpiar. (donde pone botón=si ponemos botón=no o desmarcamos la casilla correspondiente en el menú botones del Editor de Escenas). También, de manera similar, suprimimos los ejes y las redes.
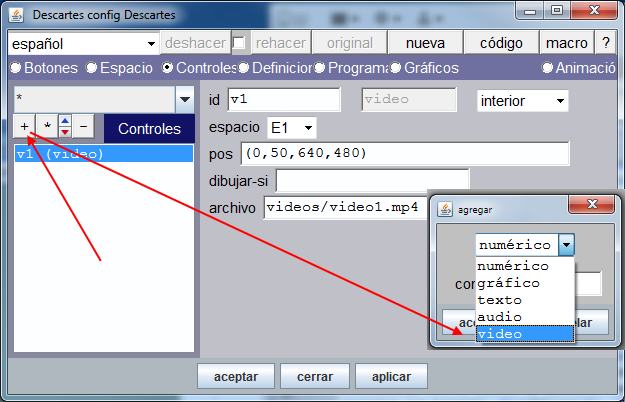
Suponemos que en la carpeta vídeos hemos guardado un vídeo con el nombre video1.mp4. Ahora, realizamos el paso 2 de las instrucciones. Con el Editor de Escenas abierto, seleccionamos el menú controles y pulsamos el signo +, en el cuadro agrega que se abre desplegamos las opciones y elegimos vídeo. Asignamos los valores que se muestran a continuación.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
En siguientes entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Ildefonso Fernández Trujillo
Descartes en la Universidad. Miscelánea: Proyección sobre planos coordenados
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Proyección sobre planos coordenados
En esta miscelánea se muestra cómo proyectar puntos y superficies sobre planos coordenados.
Por defecto, en la escena aparece la proyección de un punto sobre el plano z=0. Sin embargo, también es posible proyectar triángulos y ciertas superficies sobre los tres planos coordenados XY, YZ y XZ.
La proyección de un punto P sobre cualquier plano es aquel punto del plano que se encuentra a distancia mínima de P.
Para proyectar un triángulo T bastará considerar el formado por la proyección de los vértices de T y en el caso de una superfice, su proyección se obtendrá proyectando todos sus puntos. Elegida la opción superficies, la escena permite practicar con porciones de paraboloides o cilindros intersecados por un plano vertical que se encuentran en el primer octante.
En la propia escena se ha incluido un botón con instrucciones que aclaran cómo utilizar esta miscelánea.
Acceso a la miscelánea: Proyección sobre planos coordenados
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



 CONTACTO
CONTACTO
