Los fenómenos físicos son dependientes de las características intrínsecas del medio en el que se desarrollan. Por tanto, pueden estar influidos o condicionados por la forma del espacio en el que acontecen o en el que se manifiestan. Por ejemplo, en un espacio euclídeo, dos rayos de luz emitidos en direcciones paralelas continuarán su viaje indefinidamente sin intersecarse. Sin embargo, si el espacio de propagación es curvo, geometrías no euclídeas, convergerán o divergirán según su curvatura sea positiva o negativa.

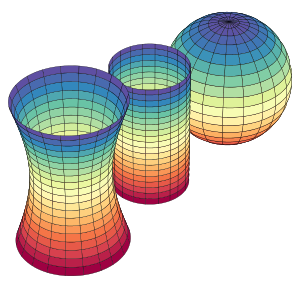
Hiperboloide, cilindro y esfera con curvatura de Gauss negativa, nula y positiva respectivamente
Fuente de la Imagen wikipedia

¿Cómo un habitante de un determinado mundo puede investigar y conocer la forma del espacio en el que habita? Nosotros, como habitantes tridimensionales, observamos diferencias evidentes en la forma que tienen los mundos bidimensionales, las superficies, representadas en la imagen anterior. Pero un habitante bidimensional de alguno de esos lugares ¿cómo puede saber la forma que tiene la superficie que habita? La respuesta puede encontrarse en una relectura del párrafo inicial realizada desde otra perspectiva, es decir, si ese habitante emite dos rayos de luz y comprueba que divergen, entonces su mundo tiene curvatura negativa; si no se intersecan tiene curvatura nula y se cortan su curvatura es positiva. Así pues, un experimento físico realizado en el mundo que habita le permite determinar y confirmar la forma de su hábitat, lo puede ver matemáticamente, aunque no pueda verlo nunca de una perspectiva exterior. La clave la encontramos en la curvatura, ésta es la herramienta matemática que nos permite saber, observar, lo que nunca podremos ver.

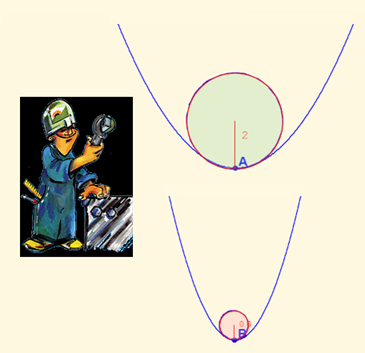
De manera análoga un habitante unidimensional, el de una línea, podrá conocer la forma de su espacio vital si es capaz de determinar la curvatura de la misma y para ello, al igual que antes, puede basarse en  algún experimento físico que permita discriminarla. Por tanto, el concepto de curvatura en una línea es un conocimiento previo que ha de comprender y adquirir como base de su investigación. Y al aprendizaje de este concepto le ayuda, nos ayuda, nuestra compañera Consolación Ruiz Gil (Solín) con su unidad didáctica titulada “Curvatura” en la que nos lleva al taller, al laboratorio matemático, y nos introduce progresivamente en ese concepto y en su medida. Para ello:

• Tomando como referencia a la circunferencia, curva básica en el estudio geométrico, introduce la medida de su curvatura deduciendo cómo depende de su radio y por tanto es siempre una cantidad positiva. Ésta, disminuye a medida que es mayor el radio e incluso como situación límite puede asignarse a una línea recta una curvatura nula.
• Se plantea un segundo acceso al taller al tratar de dar respuesta a la medición de la curvatura a cualquier otra curva en un determinado punto y, para ello, se marca la estrategia de aproximarla en él por un arco de circunferencia, aquel que más se le asemeja, y consecuentemente asignarle como curvatura la de esa arco. A partir de lo experimentado en este taller, Solín procede a plantear analíticamente cómo determinar ese arco y ello requiere adentrarse en un nivel microscópico. Ello obliga a acudir al laboratorio y utilizar el cálculo infinitesimal. Surge la circunferencia osculatriz y se formaliza el concepto de curvatura en cualquier curva que sea derivable.
• La unidad didáctica finaliza referenciando artículos de difusión y periodísticos en los que la curvatura es la base para la determinación de la forma de nuestro mundo. ¿Cómo es éste? ¿“Es plano” –entendido este término aquí como “Euclídeo” o con curvatura nula--? ¿Tiene curvatura no nula? Las ondas gravitatorias, sobre las que el pasado 11 de febrero de 2016 se publicó su existencia, ayudan a establecer esa curvatura del espacio-tiempo.

Así pues, un experimento físico  (LIGO) como es la determinación de la existencia de las ondas gravitatorias nos permite adentrarnos en el conocimiento de la forma del mundo que habitamos estos seres físicamente tridimensionales (largo, ancho, alto), anexos o inmersos en una cuarta componente dimensional tiranizada por ése que siempre pasa (“Tempus fugit”). Y todo ello gracias a la curvatura, la curvatura espacio-tiempo.

LIGO ha sido posible gracias a la posibilidad de medir longitudes del orden de 10^-19 m, pero la Teoría de cuerdas plantea que nuestro universo tiene once dimensiones: una temporal, tres espaciales ordinarias y siete compactas inobservables en la práctica y que solamente son relevantes a escalas pequeñas del orden de la longitud de Planck: 10^-35 m. ¡Quedan curvaturas que estudiar!