| Agudo | Su medida es menor de 90°. |
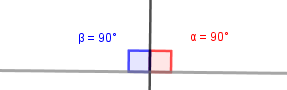
| Recto | Su medida es de 90°. |
| Obtuso | Su medida es mayor de 90° y menor de 180°. |
| llano | Su medida es de 180°. |
Carlos Alberto Rojas Hincapié
Geometría Plana
fundamentos para Secundaria & Media
INTERACTIVO
Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
1ª edición – 2024
Fondo Editorial
2024
Título de la obra
Autor
Geometría Plana
fundamentos para Secundaria & Media
Carlos Alberto Rojas Hincapié
Primera edición: 2024
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Diseño de personajes:
Orlando Antonio Martinez Hoyos
Red Educativa Digital Descartes,
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-94-3
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Puedes descargar el libro en formato pdf:
Tabla de contenido
De la colección iCartesiLibri surge este libro digital interactivo, diseñado de tal forma que permita el aprendizaje significativo a través de la intervención directa y personal del usuario, el cual se convierte en el protagonista del libro, en tanto que podrá interactuar con algunos objetos de aprendizaje. Estos objetos de aprendizaje interactivos fueron diseñados con el editor DescartesJS.
La herramienta Descartes se caracteriza por una innata interactividad, por permitir realizar representaciones de objetos bi y tridimensionales, por gestionar expresiones de texto y de fórmulas, por integrar objetos multimedia como imágenes, audios y vídeos, por tener la posibilidad de reflejar casos concretos y también potenciar la conceptualización de tareas y procedimientos mediante la utilización de semillas aleatorias y controles numéricos, gráficos y de texto, y con ellos poder abordar la evaluación de manera automática, tanto la correctiva como la formativa.
Con Descartes es posible el diseño y desarrollo de objetos educativos que promueven el aprendizaje significativo, posibilitando esa deseada construcción del conocimiento.
Retomando la introducción a la documentación de DescartesJS de Radillo, Abreu y Espinosa, podríamos coincidir en que este libro está destinado tanto a personas que no han usado DescartesJS como a personas que tienen cierta experiencia y desean mejorarla. En cada apartado del libro se proponen ejercicios y se incluyen ejemplos para que el lector pueda comprender paso a paso la funcionalidad de DescartesJS y su enorme potencial para crear objetos interactivos de aprendizaje.
Este libro, que, acompañado del diseño y elaboración de diferentes objetos interactivos de aprendizaje con todas las ventajas de las tic
Todos los recursos incluidos en este libro se basan en el estándar HTML y consecuentemente son plenamente accesibles y operativos en cualquier ordenador, tableta o smartphone sin más que utilizar un navegador compatible con dicho estándar. Diseñar en HTML, significa que usaremos:
"La enseñanza de la geometría en la educación, ha perdido interés por parte de muchos docentes, por lo tanto, se hace necesario recuperar la motivación y el
interés del docente por esta área del conocimiento, y darle el lugar que le corresponde en cualquier plan de estudios. Esta situación ha influido positivamente en la presentación de esta propuesta pedagógica, que además de pretender impulsar la enseñanza de tan importante asignatura, vincula la interacción de medios computacionales de gran vigencia en los sistemas educativos actuales y con ello contribuir a mejorar la didáctica tradicional en el
proceso de enseñanza – aprendizaje".
Este material interactivo contiene cinco capítulos temáticos, actividades de exploración, actividades de construcción, talleres, juegos, el editor de GeoGebra y actividades evaluativas, los cuales se presentan de modo agradable y que garantizan el aprendizaje al aumentar la motivación cuando se utiliza en ordenadores o diferentes dispositivos móviles.
El Estado colombiano, decidido a elevar la calidad de la educación, introdujo el enfoque basado en el desarrollo de competencias en los estudiantes, lo cual supone el tránsito desde el aprendizaje que centra la atención en el dominio de contenidos, a una educación basada en competencias que no se agota en el sistema educativo, sino que se desarrolla de manera permanente en interacción con el mundo.
De esta manera, consolidar una política de calidad enmarcada en el desarrollo de competencias implica, entonces, una transformación de fondo de las prácticas pedagógicas, del funcionamiento de la institución educativa y del papel de los actores educativos, teniendo como protagonista al estudiante. Buscando desarrollar este modelo se han realizado esfuerzos por elevar la calidad de la educación en el país; en este sentido, el Ministerio de Educación Nacional (MEN) ha puesto a disposición de docentes, directivos docentes, padres de familia y público en general herramientas pedagógicas como:
Herramientas que constituyen el punto de partida y sustento de todas las estrategias de mejoramiento, además son un importante insumo para el diseño curricular
y el cambio en las prácticas pedagógicas
ESTRATEGIAS DE MEJORAMIENTO
Elementos que contribuyen a mejorar los procesos de evaluación por competencias y las prácticas en el aula de clase por parte de los docentes para alcanzar cada vez mejores resultados y hacer que la educación en Colombia mejore su calidad. Ampliar imagen
Componentes / Pensamientos
Específicos del área de matemáticas.
5 categorías conceptuales que conforman esta asignatura según los Lineamientos y los Estándares Básicos de Competencia diseñados por el Ministerio de Educación Nacional, los cuales son:
1. Pensamiento numérico y sistemas numéricos.
Se asocia con "la organización de actividades centradas en la comprensión del uso y de los significados de los números y de la numeración; el desarrollo de diferentes técnicas de cálculo y estimación".
2. Pensamiento espacial y sistemas geométricos.
Contempla las actuaciones del sujeto en todas sus dimensiones y relaciones espaciales para interactuar de diversas maneras con los objetos situados en el espacio, hacer acercamientos conceptuales que favorezcan la creación y manipulación de nuevas representaciones mentales.
3. Pensamiento métrico y sistemas de medidas.
Hace referencia a la comprensión general que tiene una persona sobre las magnitudes y las cantidades, su medición y el uso flexible de los sistemas métricos o de medidas en diferentes situaciones.
4. El pensamiento variacional y sistemas algebraicos y analíticos.
Comprensión y uso de los conceptos y procedimientos de las funciones y sus sistemas analíticos, para el aprendizaje con sentido del cálculo numérico y algebraico.
5. Pensamiento aleatorio y sistemas de datos.
El pensamiento aleatorio se apoya directamente en conceptos y procesos de la teoría de probabilidades y de la estadística inferencial, e indirectamente, en la estadística descriptiva y en la combinatoria.
¿Qué son los Estándares Básicos de Competencias?
"Un estándar es un criterio claro y público que permite juzgar si un estudiante, una institución o el sistema educativo en su conjunto cumplen con unas expectativas comunes de calidad; expresa una situación deseada en cuanto a lo que se espera que todos los estudiantes aprendan en cada una de las áreas a lo largo de su paso por la Educación Básica y Media, especificando por grupos de grados (1 a 3, 4 a 5, 6 a 7, 8 a 9, y 10 a 11) el nivel de calidad que se aspira alcanzar.
(Ministerio de Educación Nacional, 2006, p. 11)".
Estándares Básicos de Competencias en Matemáticas.
Competencias específicas del área de matemáticas.
Son las encargadas de desarrollar la capacidad de formular, resolver y modelar fenómenos de la realidad; comunicar, razonar, comparar y ejercitar procedimientos para fortalecer la adquisición de conocimientos, habilidades, actitudes y comprensiones del pensamiento matemático, relacionándolos entre sí para facilitar el desempeño flexible, eficaz y con sentido. Las competencias específicas en el área de matemáticas que evalúa la prueba Saber desde los grados 1° a 9° se reagrupan en las siguientes:
La capacidad del estudiante para expresar ideas, interpretar, usar diferentes tipos de representación, describir relaciones matemáticas, describir situaciones o problemas usando el lenguaje escrito, concreto, pictórico, gráfico y algebraico, manipular expresiones que contengan símbolos y fórmulas, utilizar variables y describir cadenas de argumentos orales y escritas, traducir, interpretar y distinguir entre diferentes tipos de representaciones, interpretar lenguaje formal y simbólico así como traducir de lenguaje natural al simbólico formal y viceversa, que se resume en decodificar de manera entendible aquello expresado matemáticamente en palabras sencillas y manejables.
Es la capacidad para formular problemas a partir de situaciones dentro y fuera de las matemáticas, desarrollar, aplicar diferentes estrategias y justificar la elección de métodos e instrumentos para la solución de problemas, justificar la pertinencia de un cálculo exacto o aproximado
en la solución de un problema y lo razonable o no de una respuesta obtenida, verificar e interpretar resultados a la luz del problema original y generalizar soluciones y estrategias para dar solución a nuevas situaciones problema.
Está relacionada con la capacidad para dar cuenta del cómo y del porqué de los caminos que se siguen para llegar a conclusiones, justificar estrategias y procedimientos puestos en acción en el tratamiento de situaciones problema, formular hipótesis, proponer opiniones e ideas, explorar ejemplos y contraejemplos, probar y estructurar argumentos, generalizar propiedades y relaciones, identificar patrones y expresarlos matemáticamente y plantear preguntas, reconocer distintos tipos de razonamiento y distinguir y evaluar cadenas de argumentos.
Tomado Saber 3° Guía de orientación (2017).
¿Qué son los Derechos Básicos de Aprendizajes (DBA)?
Los DBA, en su conjunto, explicitan los aprendizajes estructurantes para un grado y un área particular. Se entienden los aprendizajes como la conjunción de unos conocimientos, habilidades y actitudes que otorgan un contexto cultural e histórico a quien aprende.
Los DBA se organizan guardando coherencia con los Lineamientos Curriculares y los Estándares Básicos de Competencias (EBC). Su importancia radica en que plantean elementos para construir rutas de enseñanza que promueven la consecución de aprendizajes año a año para que, como resultado de un proceso, los estudiantes alcancen los EBC propuestos por cada grupo de grados.
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
$\space$ Asociados a la Geometría del grado 6° a 11°
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
"La geometría es la base de toda ciencia exacta.".
Euclides
Geometría (del griego geo, 'tierra'; metrein, 'medir').
Rama de las matemáticas que se ocupa de las propiedades del espacio. En su forma más elemental, la geometría se preocupa de problemas métricos como el cálculo del área y diámetro de figuras planas y de la superficie y volumen de cuerpos sólidos. Otros campos de la geometría son la geometría analítica, geometría descriptiva, topología, geometría de espacios con cuatro o más dimensiones, geometría fractal, y geometría no euclídea.
En la antigüedad, la geometría era una disciplina empírica utilizada para la medición de terrenos, la construcción, observaciones astronómicas, la navegación, entre otros. En un principio era un conjunto de reglas prácticas, los problemas geométricos se resolvían mediante construcciones gráficas, dando origen al dibujo geométrico.
Evolucionó pasando por diferentes culturas tales como la de los babilonios, egipcios, caldeos, hasta llegar a los griegos, quienes ordenaron los conocimientos empíricos y les dieron un tratamiento más racional elevando la geometría a un nivel científico. Sabios como Euclides, Tales de Mileto, Pitágoras, Platón, Arquímedes y otros, contribuyeron grandemente a este proceso científico.
Cuando se habla de historia de la geometría, nos tenemos que remitir al gran matemático y geómetra griego, considerado uno de los grandes matemáticos y llamado "el Padre de la Geometría", Euclides de Alejandría. Nació alrededor de 300 A.C. y murió alrededor de 275 A.C. en Alejandría, Egipto.
Capitulo I. Conceptos preliminares $\qquad$
Euclides, mejor conocido por su tratado sobre matemáticas llamado "Los Elementos", la vigencia de este tratado hace de Euclides el principal maestro de matemáticas de todos los tiempos.
De los trece libros que componen "Los Elementos", los seis primeros corresponden a lo que se entiende todavía como geometría plana o elemental, en estos presentan un conjunto de axiomas, que Euclides llamó postulados.
Postulados de Euclides.
Los cinco postulados de Euclides son cinco proposiciones no demostrables a partir de los cuales se fundamenta toda la geometría clásica.
Así mismo, la geometría de Euclides fue un punto fundamental en otros campos del conocimiento tales como la física, la química o la astronomía entre otros.
Capitulo I. Conceptos preliminares $\qquad$
Otros precursores que contribuyeron con el estudio de la geometría, para hacer más fácil el desarrollo de ciertos procedimientos y obtener mejores resultados; algunos de ellos fueron (Pasa el mouse sobre la imagen del personaje):
Geómetras precursores.
$\space$ Descargar para imprimir
Algunos conceptos para iniciar.
El punto en la geometría es uno de los entes fundamentales, junto con la recta y el plano, son considerados primarios.
Comencemos hablando del punto, se define como una ubicación en cualquier espacio y se representa como ( . ), no tiene dimensión, longitud, área, volumen, ni otro ángulo dimensional.
Los puntos lo denotamos mediante letras, que pueden ser mayúsculas o minúsculas. Hablamos así, de los puntos $A, B, C, d, e,....$
Podemos describir una recta como cierto conjunto de puntos que cumplen determinadas propiedades, llamadas Postulados.
A partir de dos puntos distintos se determina una línea recta.
Una línea recta $\overleftrightarrow{AB}$ puede ser, además, una semirrecta $\overrightarrow{AB}$ o un segmento de recta $\overline{AB}$, lo cual definimos más adelante.
Capitulo I. Conceptos preliminares $\qquad$
Hablemos de la recta.
¿Qué significa la recta en geometría?
Una recta $\overleftrightarrow{AB}$ es una sucesión infinita de puntos, situados en una misma dirección. La línea recta no tiene principio ni fin. Cuando dibujamos una línea recta, en realidad, representamos una parte de ella.
¡Geonota!
Por dos puntos distintos pasa una recta.
"2° Postulado de Euclides"
Las rectas suelen denotarse con dos puntos y letras mayúsculas, o en ocasiones, con una letra minúscula.
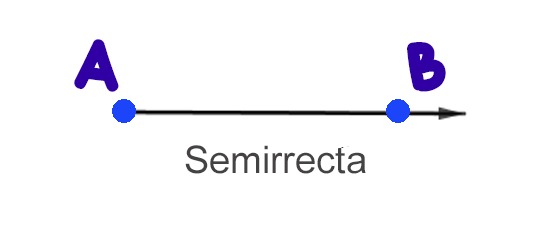Una parte de una recta que tiene un extremo definido, pero se extiende el otro extremo hasta el infinito, corresponde a una semirrecta ($\overrightarrow{AB}$).
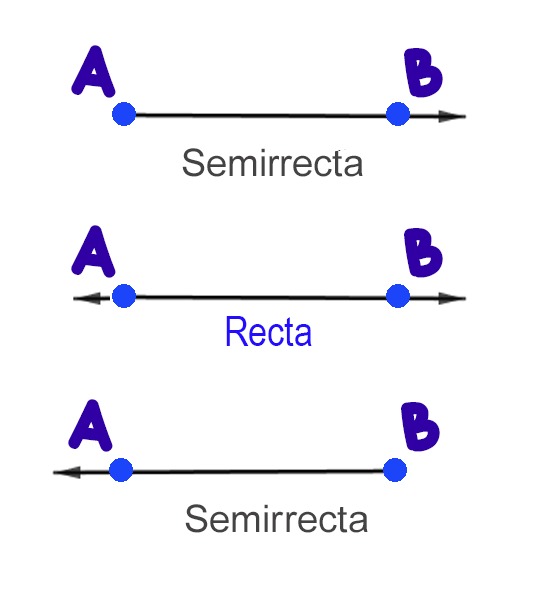Las dos semirrectas de una misma recta siempre son opuestas y además tienen el mismo origen. Las flechas nos indican que van en sentidos opuestos o contrarios ($\overleftarrow{BA}$ , $\overrightarrow{AB}$).
La semirrecta $\overrightarrow{AB}$, también es conocida con el nombre de Rayo $\overrightarrow{AB}$.
Si se conoce otro punto de la semirrecta o rayo, además del origen, también se representa escribiendo primero el origen, luego el otro punto conocido y sobre ellos una flecha así: $\overrightarrow{AB}$
Ahora, si sobre una recta se señalan dos puntos, el trozo de esa recta se llamará Segmento $\overline{AB}$.
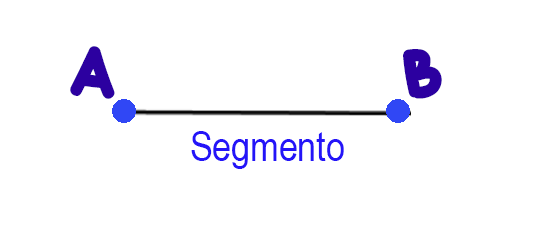Un segmento $\overline{AB}$ tiene un punto de inicio y un punto de fin.
Rectas notables.
Algunos tipos de rectas que son de gran valor para el estudio de geometría; según la relación posicional entre dos o más de ellas:
Capitulo I. Conceptos preliminares $\qquad$
¡Geonota!
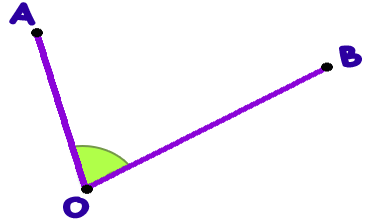Recibe el nombre de ángulo, la abertura entre dos segmentos o semirrectas, se nombra $\angle AOB$.
Para nombrar los ángulos se utilizan letras griegas o se emplean las letras que identifican los lados del ángulo, cuidando que el vértice quede en la mitad, precedidas del símbolo ∠AOB.
| Agudo | Su medida es menor de 90°. |
| Recto | Su medida es de 90°. |
| Obtuso | Su medida es mayor de 90° y menor de 180°. |
| llano | Su medida es de 180°. |
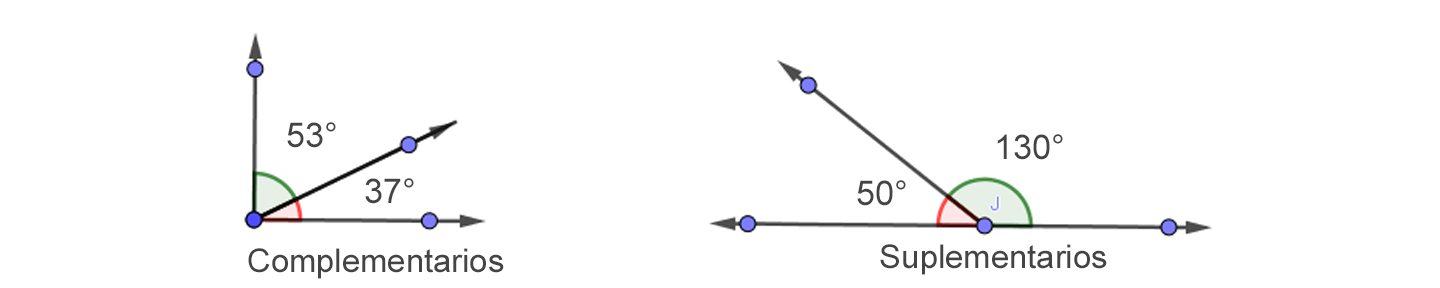
| Complementarios | Cuando la suma de los ángulos es igual a 90º |
| Suplementarios | Cuando la suma de los ángulos es igual a 180º |
Capitulo I. Conceptos preliminares $\qquad$
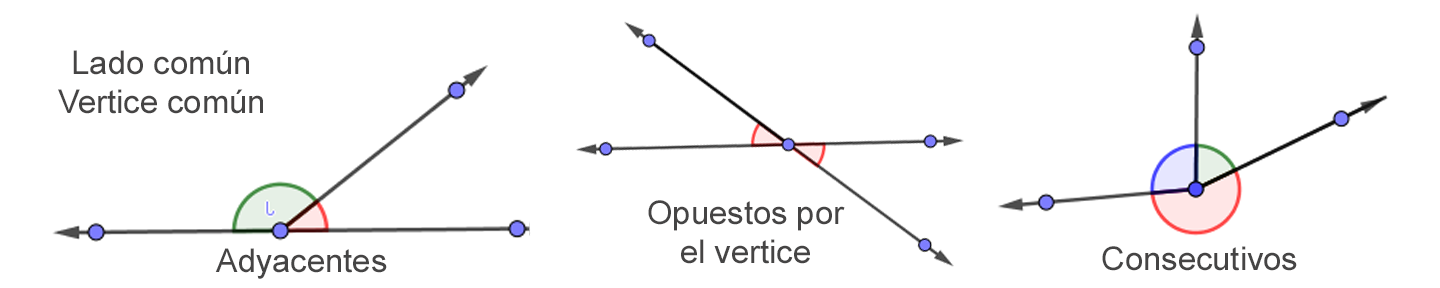
| Adyacentes | Los ángulos con un lado común miden 180º. |
| Opuestos por el vértice | Sus medidas son iguales con igual vértice. |
| Consecutivos | Tienen el vértice y un lado común. |
¡Geonota!
El sistema sexagesimal, tiene como unidad de medida el grado sexagesimal, y una vuelta completa es equivalente a $360 \space grados (360°)$.
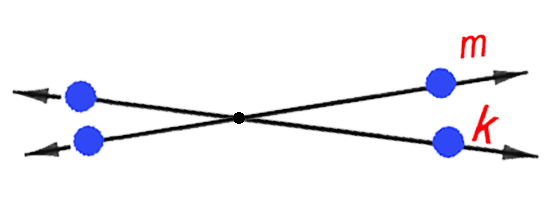
Una situación geométrica es el caso de los ángulos que se forman con el corte de diferentes rectas, por ejemplo, con dos rectas oblicuas o secantes que forman ángulos opuestos por el vértice.
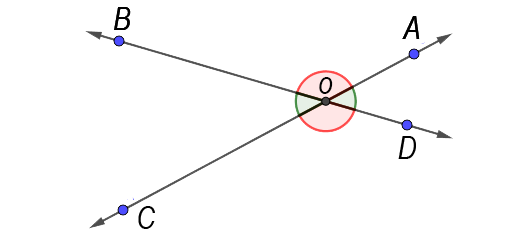
$\angle {AOB} = \angle {COD}$
$\angle {BOC} = \angle {DOA}$
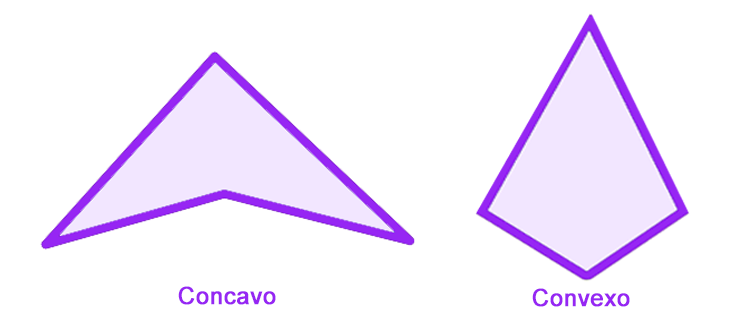
Ángulos cóncavos y convexos.
Los ángulos cóncavos y los convexos son dos clasificaciones de ángulos más generales con respecto a los que ya hemos visto.
Los ángulos convexos son aquellos que miden menos de $180°$, mientras que los ángulos cóncavos o no convexos tienen una amplitud entre $180°$ y $360°$.
xploremos.
Ángulos Cóncavos y convexos.
GeoGebra.
Mueve el punto C y observa cómo cambia el ángulo según sus características.
Capitulo I. Conceptos preliminares $\qquad$
¿Cómo se mide un ángulo?
Para trazar o medir ángulos se utiliza como instrumento de medición el transportador, generalmente, tiene forma de semicírculo $(180°)$, pero también se puede encontrar como un círculo completo $(360°)$.
El ángulo de $360°$ es equivalente a un ángulo de $0°$. Si se siguiera dando la vuelta, se completarían ángulos por ejemplo de $450°$, $600°$ o más grados. Sin embargo, los grados se suelen representar solamente hasta $360°$.
xploremos.
Ángulos opuestos por el vértice.
Mueve el punto de color verde y observa la medida de los ángulos.
¡Piensa! ¿A cuántos grados equivale un ángulo de $510°$?
Respuesta.
Es importante mencionar que los ángulos se miden en sentido contrario a las manecillas del reloj, es decir, hacia la izquierda. Cuando se miden en la dirección contraria, hacia la derecha, se dice que son negativos.
xploremos.
Medir ángulos con el transportador.
Capitulo I. Conceptos preliminares $\qquad$
Arrastra el transportador, mide el ángulo e ingresa su medida, oprime la tecla "enter <┘", verifica la solución. Repite el proceso.
Comprueba lo aprendido respondiendo a la pregunta.
¡Piensa! Si dos rectas se cortan y forman un ángulo de $63.5°$,¿Cuál será el valor de los demás ángulos?
Respuesta.
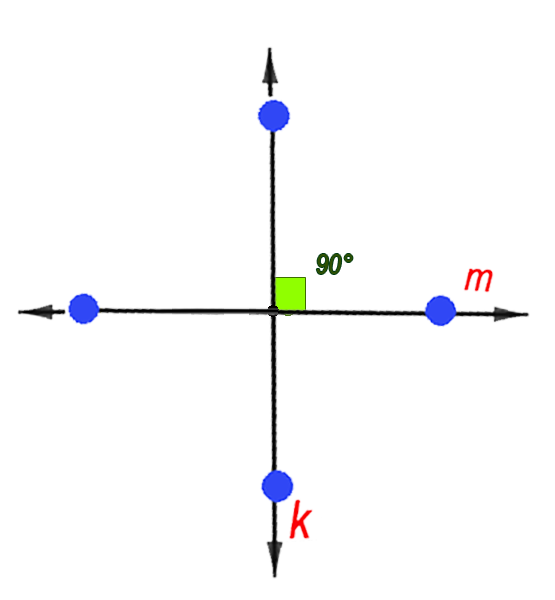
Ángulos formados por rectas paralelas y una recta secante.
Observa la figura, se tiene dos rectas paralelas $m$ y $n$, que son cortadas por una recta secante $p$, estas generan un sistema de ocho ángulos con ciertas características según su posición.
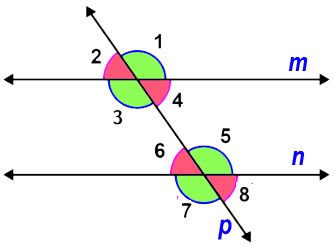
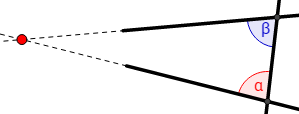
Ángulos opuestos por el vértice, son pares de ángulos de igual medida.
$$\widehat{1} = \widehat{3}, \quad \widehat{2} = \widehat{4}, \quad \widehat{5} = \widehat{7}, \quad \widehat{6} = \widehat{8}$$Ángulos alternos internos, estos están en lados distintos de la recta secante (alternos) y entre las rectas paralelas (externos), son ángulos de igual medida.
$$\widehat{3} = \widehat{5}, \quad \widehat{4} = \widehat{6}$$Capitulo I. Conceptos preliminares $\qquad$
Ángulos alternos externos, estos están en lados distintos de la recta secante (alternos) y fuera de las rectas paralelas (externos), son ángulos de igual medida.
$$\widehat{1} = \widehat{7}, \quad \widehat{2} = \widehat{8}$$Ángulos correspondientes, son los que se encuentran del mismo lado de la recta secante que corta las rectas paralelas y están en el mismo nivel respecto a la recta paralela, son ángulos de igual medida.
$$\widehat{1} = \widehat{5}, \quad \widehat{2} = \widehat{6}, \quad \widehat{3} = \widehat{7}, \quad \widehat{4} = \widehat{8}$$xploremos.
Ángulos formados por rectas paralelas y una recta secante.
Mueve el punto $o$ de color verde y observa los ángulos que se forman por el corte de la recta (roja) oblicua o secante $p$.
En conclusión, en la figura 1.15, según la posición de los ángulos, los de color verde todos son de igual medida y los de color rojo todos son de igual medida.
Observa el ángulo formado por las rectas $m \Vert k$ y la recta secante. Responde la pregunta seleccionando el valor del ángulo que consideres correcto. Oprime el botón Otro ángulo para generar otro ejercicio.
¡Piensa! ¿Cuándo todos los ángulos formados entre dos rectas paralelas y una recta secante, son de igual medida?
Respuesta.
Capitulo I. Conceptos preliminares $\qquad$
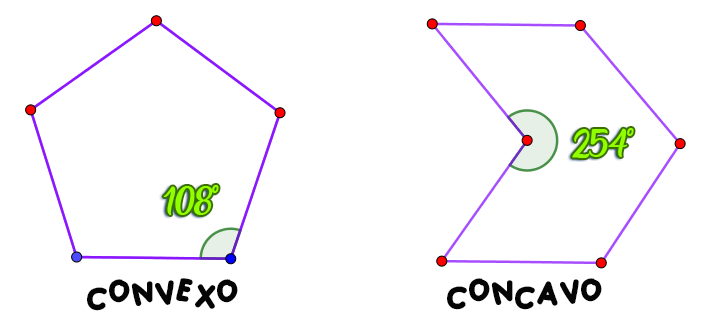
Un polígono es una figura geométrica plana cerrada, formada por segmentos de línea que se cortan en sus extremos, a estos segmentos de línea se les llama lados del polígono, y se cortan formando puntos llamados vértices.
Los polígonos pueden tener cualquier cantidad de lados y ángulos, pero sus lados nunca pueden ser curvos. Si existe alguna curvatura en la figura, no puede ser un polígono.
¡Geonota!
Los polígonos los podemos divide en dos grupos:
Los polígonos se pueden clasificar de muchas formas, pero la más utilizada es según el número de lados, además, de esta forma, también se nombran según la cantidad de lados que este posea.
¡Piensa! Sabes... ¿Cuál es el polígono más pequeño o el más grande que existe según su número de lados?
Respuesta.
Elementos que componen un polígono.
Un polígono está formado por unos elementos básicos:
Capitulo I. Conceptos preliminares $\qquad$
Los polígonos, usualmente, se clasifican en:
Características de los polígonos regulares.
Todos los polígonos regulares tienen las siguientes características:
Otra clasificación que se puede hacer de los polígonos es según el tipo de ángulos que los componen:
Capitulo I. Conceptos preliminares $\qquad$
Existen polígonos regulares con cualquier número de lados, desde un mínimo de tres lados (triángulo equilátero) hasta infinitos lados. De hecho, cuando el número de lados de un polígono regular es infinito, tiende a convertirse en un círculo, pues sus lados, teóricamente, pasarían a convertirse en un solo punto en el espacio, que estarían a la misma distancia de su centro. Esa es la misma definición de circunferencia y círculo.
xploremos.
Clasificación de los polígonos según el número de lados.
GeoGebra.
Escena interactiva, modifica los controles y las casillas de verificación, observa los polígonos y comprueba algunas de sus características.
Algunas precisiones de los polígonos regulares convexos.
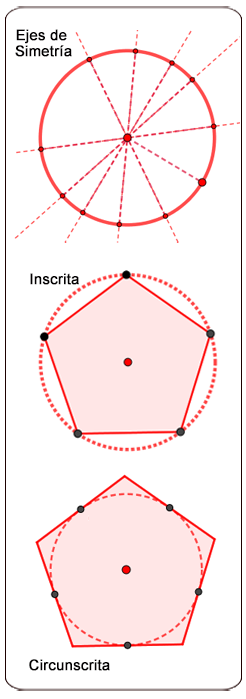
La circunferencia circunscrita a un polígono es la que pasa por todos los vértices del polígono. Si es polígono es regular, el centro de la circunferencia circunscrita y el centro del polígono coinciden.
En todo polígono regular, la medida de cada ángulo interno, donde $n$ es el número de lados del polígono, está dada por cualquiera de las dos expresiones equivalentes:
$$Ángulo \space interno = 180° - \frac{360°}{n} \tag{1}$$ $$Ángulo \space interno = \frac{(n-2)\cdot 180°}{n} \tag{2}$$La suma de los ángulos interiores de un polígono convexo de $n$ lados está dada por la expresión:
$$Suma \space \angle internos = (n-2)\cdot 180° \tag{3}$$
¡Geonota!
El triángulo central de un polígono regular, es el triángulo formado por el centro del polígono y dos vértices consecutivos del mismo polígono.
¡Piensa! Sabes... en un Dodecágono, ¿Cuál es la medida de los ángulos internos, externos y central, además, cuantas diagonales tiene?
Respuesta.
Capitulo I. Conceptos preliminares $\qquad$
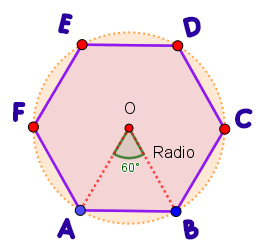
Cada lado del polígono determina un ángulo central, el cual está formado por dos radios, además, la medida del ángulo central es equivalente a un ángulo exterior, se determina mediante la expresión:
$$Ángulo \space central = \frac{360°}{n} \tag{4}$$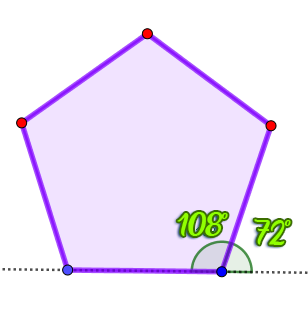 
La suma de todos los ángulos exteriores de cualquier polígono siempre es $360°$, por ejemplo, para un pentágono regular, la medida del ángulo externo es $72°$, por tanto,
El ángulo interno y externo, son un par de ángulos adyacentes, entonces la suma siempre es igual a $180°$.
Número de diagonales de un polígono.
Para encontrar la cantidad de diagonales de cualquier polígono convexo (sea o no regular) viene determinado por el número de lados $n$ que tiene el polígono, para ello, se utiliza la expresión:
$$Número \space diagonales = \frac{n \cdot (n-3)}{2} \tag{5}$$ $$Número \space diagonales \space por\space vértice = (n-3) \tag{6}$$
Emparejamiento. Arrastra el punto de color de la columna izquierda a la columna derecha según corresponda el ángulo con el polígono regular dado, para finalizar oprime el botón verificar.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo I. Conceptos preliminares $\qquad$
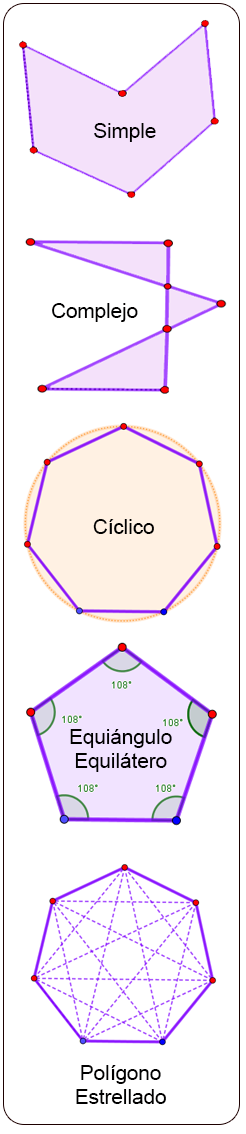
Otros términos de los polígonos.
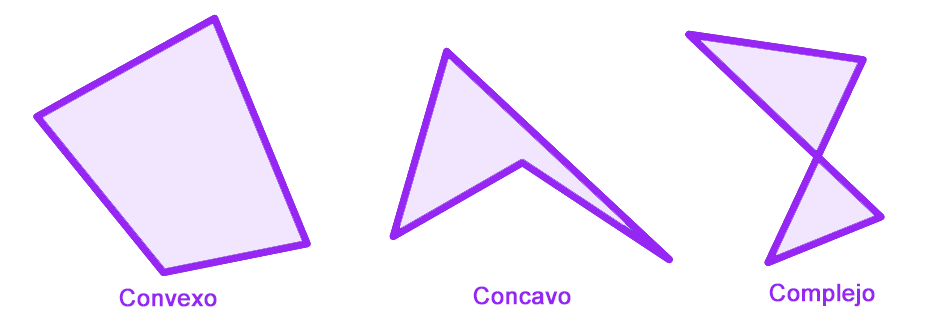
Los Polígonos Simples son un tipo de Polígonos en los que ninguno de sus lados se corta con otro lado.
Los Polígonos Complejos son aquellos en los que alguno de sus lados se corta con otro.
Los Polígonos Cíclicos son aquellos en los que todos sus vértices pasarían por una circunferencia. Si son polígonos regulares, son equiángulos y equiláteros
Los Polígonos Estrellados es todo aquel que tiene una forma semejante a una estrella, así que pueden ser regulares o irregulares.
Un polígono regular estrellado puede construirse a partir del regular convexo uniendo vértices no consecutivos de forma continua. Los irregulares son aquellos que no son regulares
Ejercicio práctico.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo I. Conceptos preliminares $\qquad$
Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Tomada de la Red Educativa Digital Descartes.
"Donde hay materia hay geometría".
Johannes Kepler
La Geometría es la rama de las matemáticas que estudia las figuras geométricas y sus propiedades.
¡Geonota!
¿Qué son las figuras geométricas?
Son figuras que limitan superficies planas a través de una serie de líneas que unen puntos. El orden y el número de dichas líneas es la que define una figura u otra.
Formas geométricas según su forma y número de lados.
Las formas geométricas más comunes y conocidas de las figuras planas, en dos dimensiones, son aquellas figuras que tienen un largo y ancho, por ejemplo, los polígonos.
Es posible clasificar las figuras geométricas de diferente manera, en este caso se clasificarán según en la dimensión que se encuentra, según su forma y número de lados.
Ahora veremos los polígonos principales y sus características un poco más a fondo, las cuales identificamos en el capítulo I.
Capitulo II. Formas geométricas $\qquad$
El triángulo es el polígono con menos lados que puede existir.
¡Geonota!
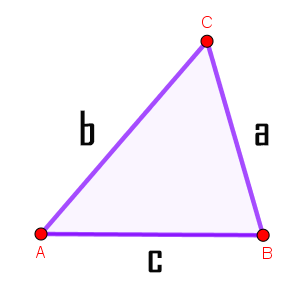
Los polígonos son las figuras geométricas planas que están delimitadas por tres o más lados (rectas) y tienen tres o más ángulos y vértices.Los triángulos tienen: 3 lados ( a, b y c ), 3 vértices ( A, B y C ) y 3 ángulos interiores ($\widehat{A}$, $\widehat{B}$ y $\widehat{C}$). En el triángulo, el lado opuesto a un ángulo, se nombra con la misma letra, pero en letra minúscula.
xploremos.
Las medidas de los lados y ángulos del triángulo.
Mueve los puntos (vértices) y observa las medidas en el triángulo.
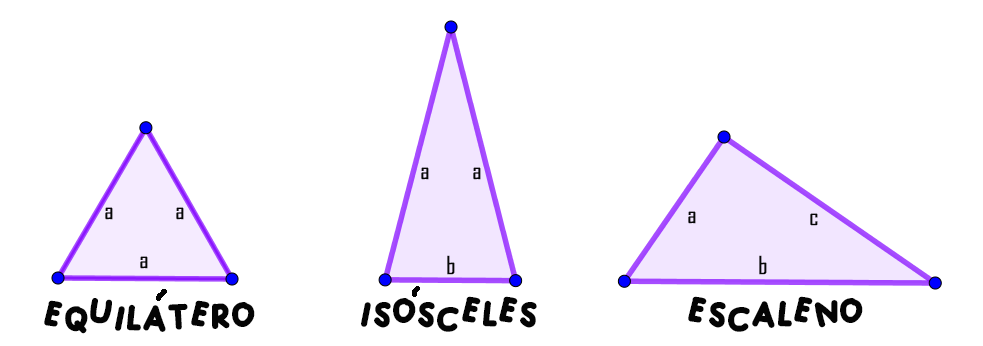
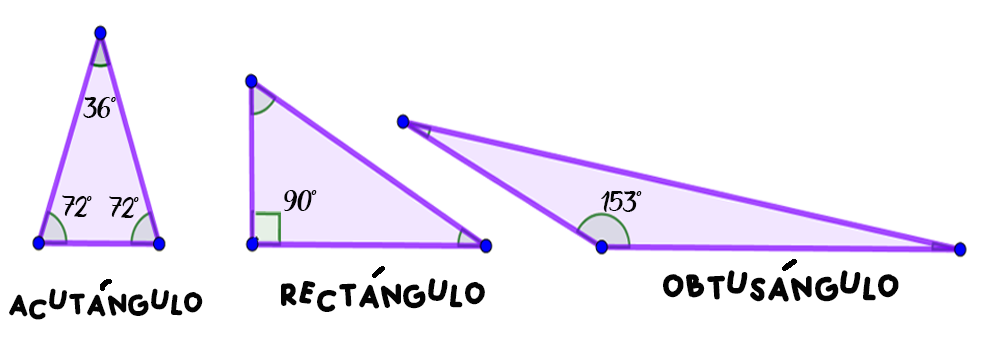
Clasificación de los triángulos.
Los triángulos se clasifican según cómo sean sus ángulos y cómo sean sus lados entre sí, de esta forma, se clasifican en:
¡Geonota!
Es relativamente fácil hallar cuánto mide un ángulo o un lado desconocido en un triángulo, incluso, se pueden hallar dos de sus lados o ángulos teniendo ciertos datos.
Cualquier polígono se puede subdividir en varios triángulos. Existen varias formas, una forma fácil es trazando sus diagonales.
Capitulo II. Formas geométricas $\qquad$
¡Geonota!
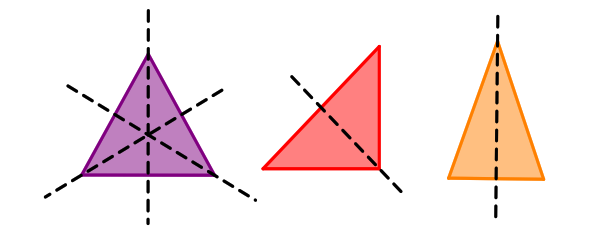
Llamamos “Eje de simetría” a la línea imaginaria que divide la figura y forma dos mitades iguales…, son iguales, pero diferentes, porque tienen orientaciones diferentes,
como si una fuera el reflejo de la otra.
Un polígono regular tiene tantos ejes de simetrías como lados tenga.
Propiedades de los triángulos.
>>
>>
Capitulo II. Formas geométricas $\qquad$
xploremos.
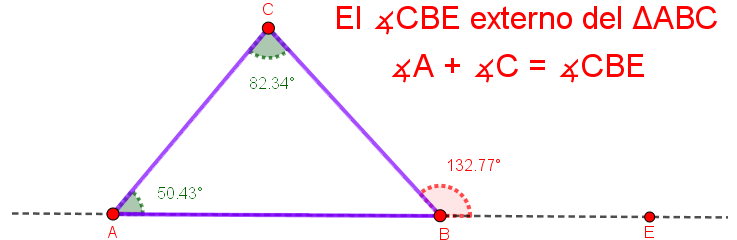
Suma de los ángulos interiores del triángulo.
Mueve los vértices y observa las medidas de los tres ángulos interiores ($\widehat{A}$, $\widehat{B}$ y $\widehat{C}$) del triángulo.
¡Geonota!
Un triángulo no puede tener dos ángulos rectos ( $90°$), ya que el tercero ángulo mediría $0°$, tampoco, puede tener dos ángulos obtusos, ya que se sobrepasa la suma de los ángulos internos, como indica la propiedad.¡Piensa! Si un $ΔABC$ tiene un ángulo de $76°$ y otro de $28°$ ¿Cuál es la medida del tercer ángulo?
Respuesta.
Algunas precisiones de los triángulos.
Según cómo sean sus ángulos y sus lados entre sí, se puede tener:
¡Geonota!
Combinando los tres tipos de triángulos según sus lados y según sus ángulos, se presentan siete posibles tipos de triángulos.
¡Piensa! Sabes... Capitulo II. Formas geométricas $\qquad$
xploremos.
Posibles triángulos según sus lados y ángulos.
Mueve los vértices y observa los tipos de triángulos posibles.
Comprueba lo aprendido respondiendo a la pregunta.
La desigualdad triangular, "La suma de dos de los lados del triángulo, siempre es mayor al tercer lado", veamos a continuación.
La desigualdad triangular.
Para cualquier triángulo tenemos que la suma de las longitudes de dos de sus lados es mayor que la longitud del tercer lado. Es decir, si llamamos a, b y c a las longitudes de los lados del triángulo, tenemos
que las siguientes tres desigualdades se cumplen:
$a + b > c$
$a + c > b$
$b + c > a$
xploremos.
Posibles triángulos según la medida de sus lados.
Mueve los vértices y observa que las desigualdades se cumplen.
En otras palabras, "Un lado cualquiera de un triángulo es menor que la suma de los otros dos".
Capitulo II. Formas geométricas $\qquad$
Rectas y puntos notables del triángulo.
Las líneas notables del triángulo, tienen varias características que forman parte de un estudio amplio de la geometría, uno de los hechos notables es que por cada línea notable hay tres en el triángulo, y que estas se cortan en un solo punto.
En todo triángulo se puede trazar tres alturas, tres mediatrices, tres medianas y tres bisectrices, que se conocen como las líneas notables.
xploremos.
Rectas y puntos notables del triángulo.
GeoGebra.
Active una o más casillas de verificación para analizar el comportamiento de las líneas notables, teniendo en cuenta el tipo de triángulo.
Escena en GeoGebra, Autor Profe Domingo Hely Perez con licencia CC by-nc-sa
Definamos cada línea notable y sus puntos de corte:
¡Geonota!
Existe una recta, llamada la Recta de EULER, esta recta pasa por el ortocentro, el circuncentro y el baricentro. Por el incentro sólo se alinea la recta en los triángulos isósceles.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo II. Formas geométricas $\qquad$
Un caso particular es el triángulo equilátero, por tener todos sus lados y ángulos iguales, esto permite clasificar al triángulo equilátero dentro de los polígonos regulares.
Las líneas notables, coinciden sobre una misma recta trazada, esto quiere decir, que, si se traza una línea notable cualquiera, esta es a su vez, altura, mediatriz, bisectriz y mediana.
Además, los puntos notables, ortocentro, baricentro,
circuncentro e incentro, coinciden en un mismo punto.
Arrastra el punto de color de la columna izquierda a la columna derecha, para finalizar oprime el botón verificar.
Construcción con regla y compás.
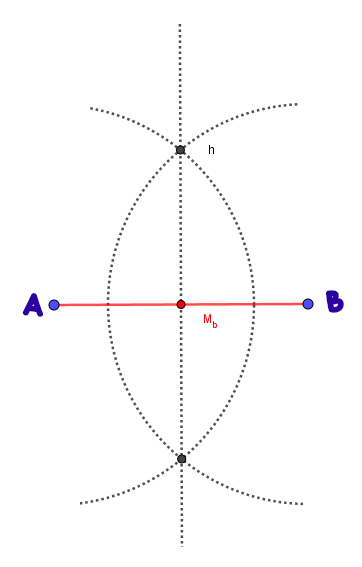
Veamos cómo encontrar el punto medio del lado de un ΔABC cualquiera:
Sea el lado $\overline{AB}$ del triángulo, con el compás haciendo centro en el vértice $A$ y con una abertura mayor que la mitad del lado $\overline{AB}$, trazamos un arco, ahora, haciendo centro en el vértice $B$ y con la misma abertura, cortamos en arco anterior en dos puntos. Trazamos la recta entre los dos puntos obtenidos, y el punto de corte entre la recta y el lado $\overline{AB}$, es el punto medio del lado $\overline{AB}$.
Video. Construir triángulos utilizando regla y compás
Capitulo II. Formas geométricas $\qquad$
xploremos.
Construcción. Medianas de un triángulo.
GeoGebra. Para ver la animación oprime el botón 
.
Mueve el control para ver paso a paso la construcción.
¡Geonota!
Por “construcciones geométricas” se suele entender la geometría que se puede construir con regla y compás.
Construcciones geométricas.
$\space$ Descargar para imprimir
Capitulo II. Formas geométricas $\qquad$
Siguiendo el orden de los polígonos, deberíamos decir Tetrágonos, pero siguiendo el mismo razonamiento, y sabiendo que todos los polígonos simples tienen el mismo número de lados que de vértices o de ángulos interiores, los llamaremos Cuadriláteros.
¡Geonota!
Según la geometría planteada por Euclides, los cuadriláteros son polígonos que tienen cuatro vértices y cuatro lados.
Si definimos los cuadriláteros, podemos decir, que es un polígono de cuatro lados, dependiendo de sus ángulos interiores puede ser convexo o no convexo (posee un ángulo interior mayor de $180°$).
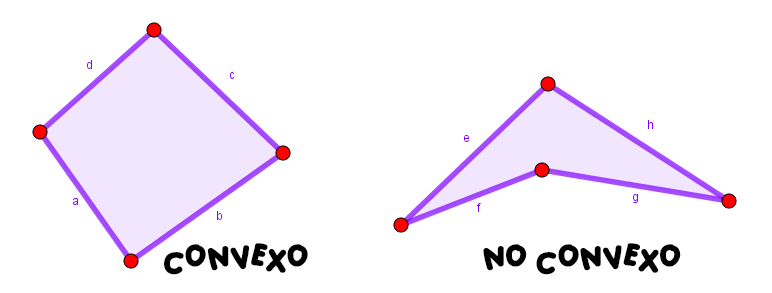
Todos los cuadriláteros tienen cuatro lados, cuatro ángulos interiores, cuatro ángulos exteriores, cuatro vértices y dos diagonales (segmentos que unen los vértices opuestos).
Capitulo II. Formas geométricas $\qquad$
Propiedades y características de los cuadriláteros.
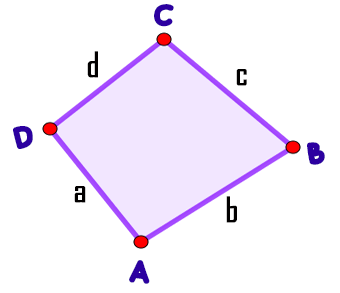
La suma de los ángulos internos de un cuadrilátero convexo es 360º:
$$\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360º$$Si un cuadrilátero está circunscrito, la suma de sus lados opuestos son iguales:
$$\overline{AB} + \overline{CD} = \overline{BC} + \overline{DA}$$
¡Geonota!
Las siguientes propiedades se mencionan cuadriláteros especiales como el cuadrado, el rectángulo, entre otros, estos serán más detallados y trabajados en la sección siguiente.
¡Piensa! Si dos ángulos internos de un cuadrilátero son rectos y un tercero es de $76°$, ¿Cuál es la medida del cuarto ángulo del cuadrilátero?
Respuesta.
Capitulo II. Formas geométricas $\qquad$
xploremos.
Cuadrilátero convexo o no convexo.
GeoGebra.
Escena interactiva, active una o más casillas de verificación para analizar los elementos del cuadrilátero, mueve el vértice E y observa los cambios.
Los cuadriláteros varían en su forma diferenciándose varios tipos y figuras que se pueden clasificar según:
La forma más representativa de clasificar los diferentes tipos de cuadriláteros en general, y teniendo en particular los cuadriláteros convexos, es de acuerdo al paralelismo de sus lados.
Los cuadriláteros se clasifican en tres grupos, Paralelogramos, Trapecios y Trapezoides, según las medidas de lados y su paralelismo, además, de sus ángulos, al igual que en los triángulos. Veamos características representativas de cada grupo:
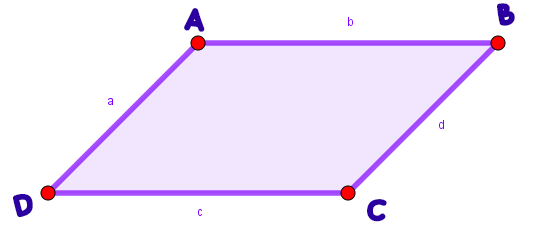
Son los cuadriláteros que tienen los lados opuestos paralelos e iguales. Además, todos los paralelogramos cumplen las siguientes propiedades:
¡Geonota!
En los paralelogramos, dos lados consecutivos siempre miden lo mismo que los otros dos, y dos ángulos consecutivos son suplementarios, miden $180°$.
Capitulo II. Formas geométricas $\qquad$
Los paralelogramos se dividen en cuatro tipos:
Cuadrados, Rectángulos, Rombos y Romboides.
xploremos.
El cuadrado y sus características.
GeoGebra.
Active una o más casillas de verificación para analizar las características del cuadrado.
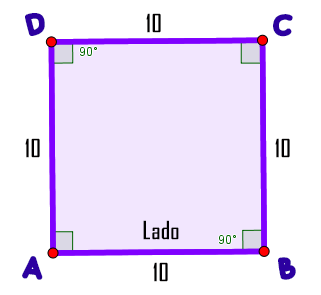
Sus 4 lados son iguales:
$$\overline{AB}=\overline{BC}=\overline{CD}=\overline{DA}$$Sus ángulos son iguales:
$$\widehat{A} = \widehat{B} = \widehat{C} = \widehat{D} = 90º$$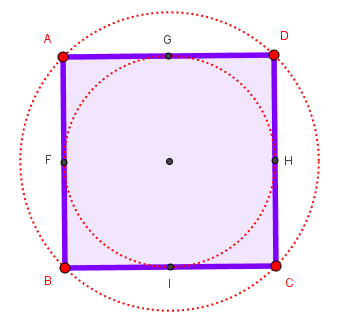
Por tener lados y ángulos iguales corresponde a un polígono regular, por lo tanto, tiene circunferencia circunscrita e inscrita, siendo su centro el centro del cuadrado.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo II. Formas geométricas $\qquad$
xploremos.
El rectángulo y sus características.
GeoGebra.
Active una o más casillas de verificación para analizar las características del cuadrado.
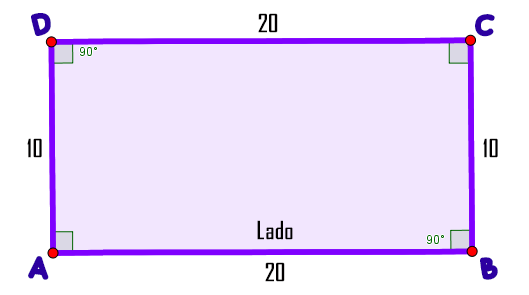
Sus lados opuestos son paralelos e iguales:
$$\overline{AB}=\overline{DC} \space \Vert \space \overline{CB}=\overline{DA}$$Sus ángulos son iguales:
$\widehat{A} = \widehat{B} = \widehat{C} = \widehat{D} = 90º$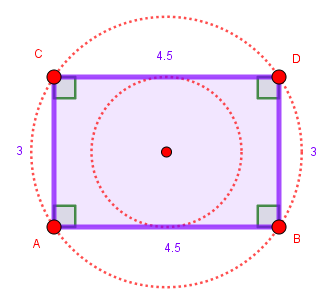
¡Piensa! ¿El cuadrado será un rectángulo? o ¿El rectángulo será un cuadrado?
Respuesta.
Capitulo II. Formas geométricas $\qquad$
El Rombo.
Paralelogramo que tiene sus lados iguales y sus ángulos diferentes de $90°$.
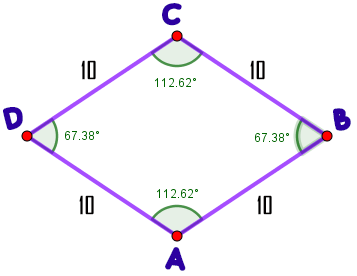
Sus ángulos opuestos son iguales dos a dos, posee dos ángulos obtusos y dos ángulos agudos:
$\widehat{A} = \widehat{C} \qquad$ y $\qquad \widehat{B} = \widehat{D}$
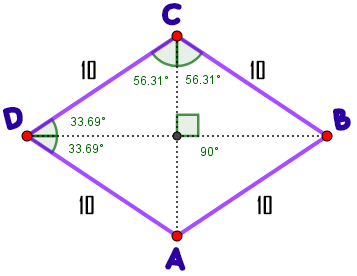
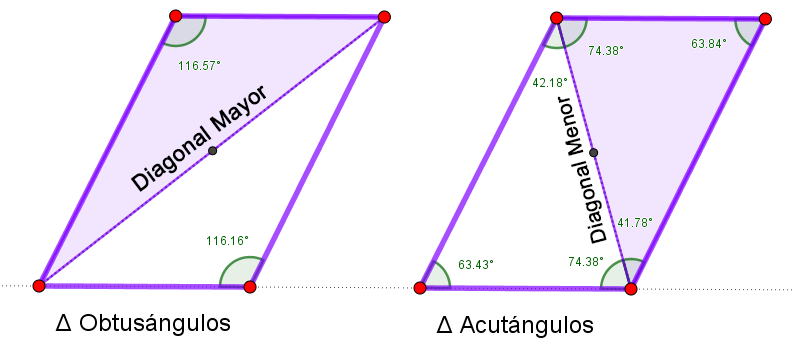
Una de las diagonales divide al cuadrado en 2 triángulos isósceles acutángulos u obtusángulos.
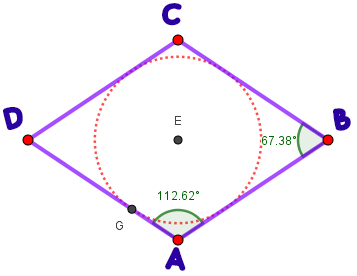
Tiene circunferencia inscrita y su centro es el centro del rombo, pero no tiene circunferencia circunscrita ya que no pasa por los vértices del rombo.
Tiene dos ejes de simetría y estos, corresponden a las mismas diagonales.
¡Geonota!
No se debe confundir las figuras geométricas por su ubicación o forma en la que estén, ya que a la figura la definen sus características, no cómo se encuentre situada.
¡Piensa! ¿El cuadrado será un rombo? o ¿El rombo será un cuadrado?
Respuesta.
Capitulo II. Formas geométricas $\qquad$
El Romboide.
Es el paralelogramo que tiene sus lados iguales dos a dos y sus ángulos distintos de 90º.
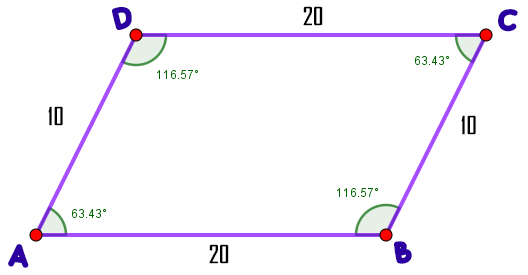
Sus ángulos opuestos son iguales:
$$\widehat{A} = \widehat{C} \qquad \widehat{B} = \widehat{D}$$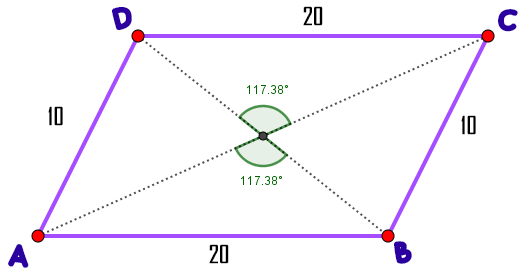
Las diagonales son de diferente longitud y pueden formar cualquier ángulo excepto $90º$, ya que entonces sería un rombo.
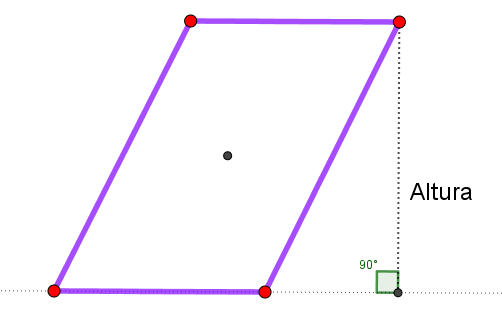La altura es la distancia entre lados opuestos, según su posición puede tomarse como base un lado u otro, como en el rectángulo. No se debe confundir la altura con el lado, como sucede en el rectángulo.
Capitulo II. Formas geométricas $\qquad$
Desplaza las afirmaciones a la derecha si las considera ciertas o a la izquierda si no lo son, para finalizar oprime el botón verificar.
Comprueba lo aprendido respondiendo a la pregunta.
Los trapecios son cuadriláteros que tienen dos lados paralelos no consecutivos y de diferente longitud, o sea, dos lados, uno frente al otro, paralelos, y los otros dos no paralelos.
¡Geonota!
La suma entre un ángulo interno y el ángulo externo adyacente a él es siempre igual a $180°$. Esta propiedad se mantiene para cualquier polígono, por lo que
Capitulo II. Formas geométricas $\qquad$
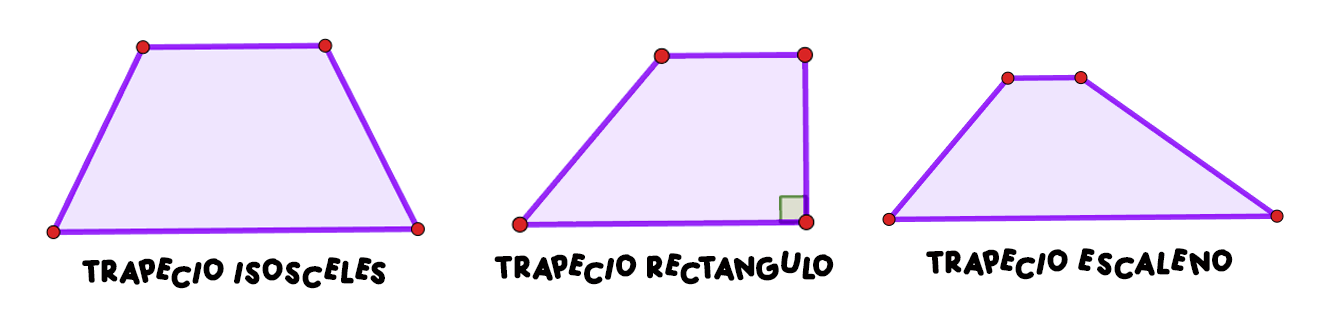
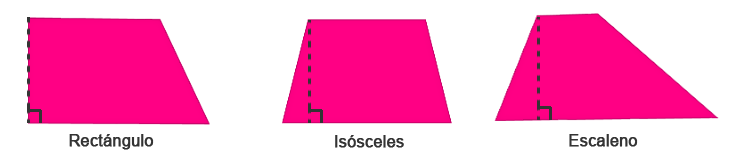
Un trapecio puede clasificarse como trapecio rectángulo, trapecio isósceles y trapecio escaleno, características que dependerán de sus ángulos.
El Trapecio Isósceles.
Es el trapecio que tiene los ángulos de la base iguales dos a dos, además, los lados no paralelos son de igual longitud. Se puede relacionar con el triángulo isósceles, cortándolo con una paralela a la base.
xploremos.
El trapecio isósceles y sus características.
GeoGebra.
Active una o más casillas de verificación para analizar las características del trapecio isósceles.
El Trapecio Rectángulo.
Es el trapecio que tiene dos ángulos de 90º. Se puede relacionar con el triángulo rectángulo, cortándolo con una paralela a la base.
xploremos.
El trapecio rectángulo y sus características.
GeoGebra.
Active una o más casillas de verificación para analizar las características del trapecio rectángulo.
Capitulo II. Formas geométricas $\qquad$
El Trapecio Escaleno.
Es el trapecio sin ninguna característica especial de ángulos. Se puede relacionar con el triángulo escaleno, cortándolo con una paralela a la base. Tiene todos los lados distintos
xploremos.
El trapecio rectángulo y sus características.
GeoGebra.
Active una o más casillas de verificación para analizar las características del trapecio rectángulo.
El trapezoide, también conocido como un cuadrilátero general, es un polígono irregular de cuatro lados, es decir, un cuadrilátero, cuyos lados no son paralelos. Por lo tanto, un trapezoide se define por lo que no tiene de los otros, aunque puede tener alguna característica aislada.
Se pueden distinguir dos tipos de trapezoides:
Trapezoides Simétricos.
Los trapezoides simétricos, son llamados también Deltoides o Cometas, tienen un eje de simetría y sus lados consecutivos son iguales dos a dos.
Capitulo II. Formas geométricas $\qquad$
Trapezoides Asimétricos.
Los trapezoides asimétricos son escalenos, o sea, todos sus lados son distintos.
No tienen lados paralelos y ninguna regularidad geométrica.
Cabe destacar también que existen los trapezoides cruzados, que son los trapezoides asimétricos (complejos) en los que dos de sus lados se cruzan. Estos tienen sus dos diagonales exteriores.
En general, los trapezoides:
¡Geonota!
Los trapezoides se pueden mezclar entre sí, es decir, un trapezoide puede ser cóncavo y simétrico, por ejemplo, pero no puede ser cóncavo y convexo a la vez, ni simétrico y asimétrico al mismo tiempo.
Actividad. Arrastra al recuadro violeta los cuadriláteros que cumplen la condición indicada.
Capitulo II. Formas geométricas $\qquad$
Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
La Circunferencia, es una de las figuras geométricas básicas y una pieza fundamental en el mundo que nos rodea, y es a partir de ella que se construyen o generan otras figuras. Es la única figura que no tiene ninguna línea recta, ¡las circunferencias se encuentran en todos lados!
¡Geonota!
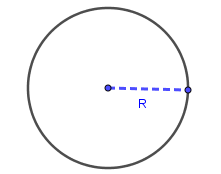
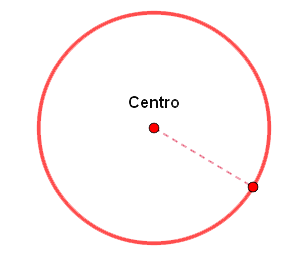Una circunferencia es una línea curva cerrada en la que todos sus puntos están a la misma distancia de otro llamado centro. En otras palabras, cualquier punto de la circunferencia es equidistante de su centro.
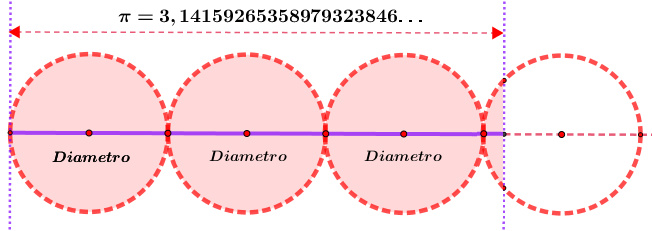
Al ser la circunferencia una línea, esta tiene una sola dimensión, su longitud. La línea curva cerrada que forma su contorno, mide algo más del triple que su
diámetro. A esta relación se estableció con el nombre de número pi $(\pi)$
Capitulo II. Formas geométricas $\qquad$
No debemos confundir el concepto de círculo con el concepto de circunferencia, que en realidad una circunferencia es la curva que encierra a un círculo (la circunferencia es una curva, el círculo una superficie).
Propiedades de la circunferencia.
La circunferencia tiene unas propiedades geométricas muy especiales, además, está muy relacionada con otros tipos de líneas curvas como: elipses, óvalos, parábolas, hipérbolas, entre otras.
Elementos de la circunferencia.
En toda circunferencia encontramos los siguientes elementos:
xploremos.
La circunferencia y sus elementos.
GeoGebra.
Active una o más casillas de verificación para analizar los elementos de la circunferencia.
Capitulo II. Formas geométricas $\qquad$
¡Geonota!
El círculo es una figura geométrica delimitada por una circunferencia, por lo tanto, el círculo es el área que contiene la circunferencia.
Comprueba lo aprendido respondiendo a la pregunta.
Ejercicio práctico.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo II. Formas geométricas $\qquad$
Evaluación. 10 preguntas con límite de tiempo (Máx. 5 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Tomada de la Red Educativa Digital Descartes.
“Sentir no es otra cosa que pensar”.
R. Descartes
Para iniciar, reconozcamos cuáles son algunos atributos medibles de diferentes figuras, objetos y comprender que la medición conlleva a un proceso de comparación con una unidad establecida.
Usemos algún objeto que se pueda utilizar para tomar medidas, tales como: palos de diferentes longitudes, cuerdas, lápices, cartones, entre otros.
xploremos.
Medir objetos con diferente material.
Utilice diferente material para registrar medidas, complete la tabla.
¡Piensa! ¿Con qué y cómo medimos? ¿Qué obtuvimos?
Capitulo III. Área y perímetro $\qquad$
¡Geonota!
Cuando se comparan diferentes mediciones con objetos diferentes, surge la necesidad de establecer o fijar una unidad de medida.
¡Piensa! A partir de las siguientes figuras geométricas, responda:
¿Existen atributos medibles y no medibles?
Cuando hablamos de atributos medibles nos referimos a las características de los objetos que pueden ser medidos, esto incluye longitud, altura, peso, masa, área o volumen.
Cuando comparamos dos objetos con atributos medibles tenemos que detectar qué objetos tienes más o menos del atributo que se compara.
¡Piensa! ¿Todos los atributos son comparables entre sí?, ¿Todos los atributos se pueden medir con el mismo instrumento?En conclusión, podemos decir que:
Existen muchos atributos medibles en un mismo objeto, cada uno de estos atributos tiene sus respectivas unidades e instrumentos de medición.
Esto nos conlleva a conocer e identificar las unidades de medida, entre ellas estudiaremos: las unidades que miden longitudes y áreas, las cuales se analizaran en la sección siguiente.
Capitulo III. Área y perímetro $\qquad$
¡Geonota!
El primer paso que nos lleva al concepto de la medición:
"Los atributos medibles nos permiten comparar objetos o situaciones entre sí."
Es muy común que ocurra una confusión entre algunos conceptos, entonces, para no cometer este error, veamos las definiciones.
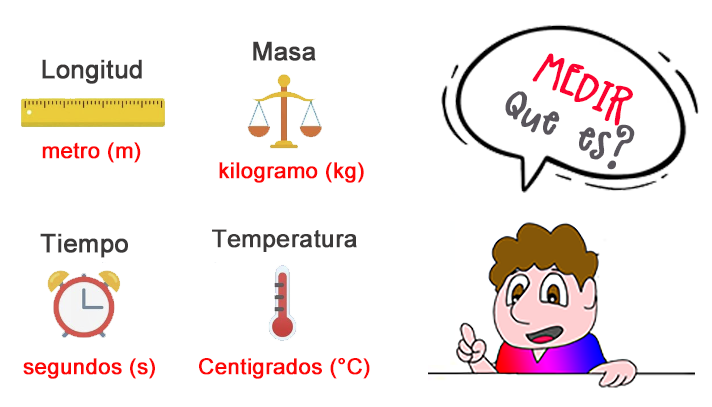
¿Qué se entiende por magnitud?
Magnitud es toda aquella propiedad o cualidad que se puede medir, por ejemplo, magnitudes como peso, masa, longitud, velocidad, tiempo, temperatura, presión, fuerza, área. Sin embargo, cada magnitud puede medirse en distintas unidades de medición que resultan comparables entre sí.
¿Que se entiende por medir?
Medir es comparar dos magnitudes de la misma especie, donde una se toma como patrón. Se trata de determinar la cantidad de una magnitud comparada con otra que se toma como unidad.
¿Que se entiende por unidad?
Es el patrón que escogemos para realizar las medidas que deseamos, un metro, por ejemplo.
El Sistema Internacional de Unidades (SI).
Surgió de la necesidad de unificar y dar coherencia a una gran variedad de subsistemas de unidades que dificultaban la transferencia de resultado de mediciones en la comunidad internacional. Este se convirtió en un sistema que pudiera ser adoptado por todos los países en diferentes campos como: la ciencia, la tecnología, la producción, la investigación, entre otros.
El Sistema Internacional consta de 7 unidades básicas, definidas como magnitudes fundamentales, a partir de las cuales se definen las demás.
En este sistema, se identifican las magnitudes fundamentales o básicas, como aquellas magnitudes que no se pueden definir en función de ninguna otra magnitud, que servirán de base para deducir las demás magnitudes, algunas de ellas son: longitud, masa, tiempo, temperatura, entre otras.
Capitulo III. Área y perímetro $\qquad$
Se identifican también otros tipos de unidades, que se conocen como unidades derivadas, son magnitudes que pueden ser expresar en función de las magnitudes fundamentales.
Unidades de longitud.
La unidad fundamental para medir longitudes es el metro y se simboliza con la letra minúscula $m$. Algunos instrumentos para medir longitudes son: la cinta métrica, el flexómetro, la regla, entre otros.
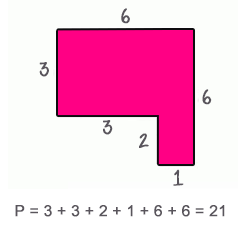
Definición de perímetro.
El perímetro de una figura geométrica es la distancia total alrededor de la figura geométrica, se calcula al sumar las longitudes de todos los lados de la figura. Dado que el perímetro es una longitud, usamos unidades de una dimensión (unidimensionales) como metros ($m$), centímetro ($cm$), entre otras, para obtener la medida.
Debido a la naturaleza del perímetro, es posible que dos figuras que tienen diferentes formas puedan tener el mismo perímetro dependiendo de las dimensiones de sus lados. Por ejemplo, es posible formar a un círculo usando una cuerda y luego, usar la misma cuerda para formar un cuadrado.
La fórmula del perímetro es diferente para diferentes figuras geométricas dependiendo en el número de lados y de su forma.
xploremos.
Tomemos medidas con la regla.
Mueve la regla desde sus extremos, primero uno y después el otro.
Escena de Eduardo Barbero Corral adaptada por el autor, con licencia CC by-nc-sa
¡Geonota!
La longitud de un objeto es lo que mide el segmento de recta que va desde uno de sus extremos hasta el otro extremo.
Capitulo III. Área y perímetro $\qquad$
Equivalencias entre las unidades de longitud.
El metro es la unidad principal de la cual se derivan otras unidades más grandes, los múltiplos o más pequeñas, los submúltiplos.
Cada unidad de longitud es 10 veces mayor que la unidad inmediata inferior y 10 veces menor que la unidad inmediata superior.
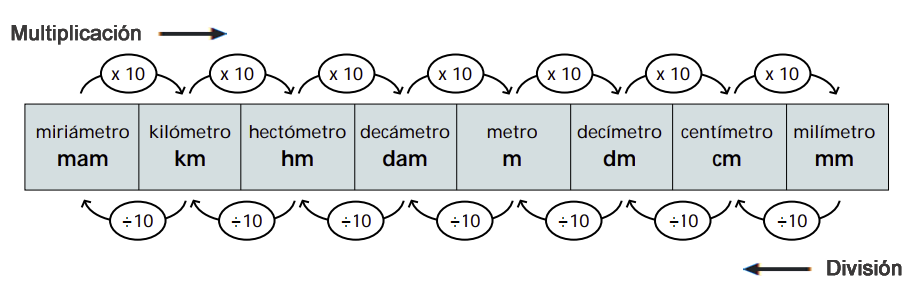
Ejemplo. ¿A cuántos centímetros equivalen $12$ Kilómetros?
Comprueba lo aprendido respondiendo a la pregunta.
En la actualidad se conoce otro sistema de medidas que se utiliza en algunos campos, es el Sistema Inglés de unidades basado en unidades no-métricas, utilizado actualmente en los Estados Unidos y en otros territorios de habla inglesa.
xploremos.
Unidades de longitud (Sistema Internacional y Sistema Ingles).
Oprime cualquier botón con el nombre de la unidad de medida y observa su equivalencia en las demás unidades.
Hoy en día, estas unidades están siendo lentamente reemplazadas por el Sistema Internacional de Unidades, aunque en Estados Unidos la inercia del antiguo sistema y el alto costo de migración ha impedido en gran medida el cambio.
Capitulo III. Área y perímetro $\qquad$
Unidades de superficie o área.
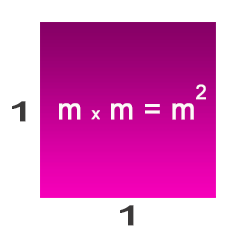La unidad principal para medir áreas es el metro cuadrado y se simboliza como $m^2$, es una unidad derivada del metro.
La unidad de superficie corresponde a un cuadrado que tiene de lado un metro lineal por un metro lineal.
Definición de área o superficie.
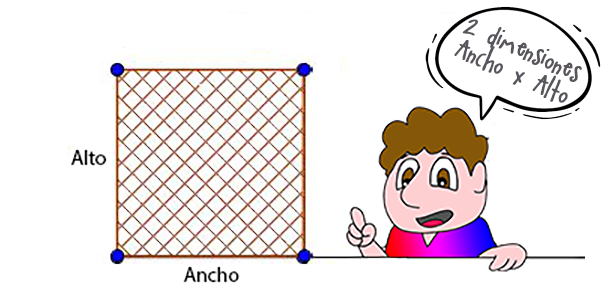
El área de una figura geométrica está definida como la región cubierta por la figura, esta es una medida en 2 dimensiones (bidimensional), por lo que se usan unidades cuadradas como $m^2$ o $cm^2$ para medirla.
La fórmula para encontrar el área depende de la forma de la figura geométrica.
¡Piensa! Si dos figuras geométricas tienen la misma área, ¿Tendrán la misma forma y las mismas dimensiones?
Respuesta.
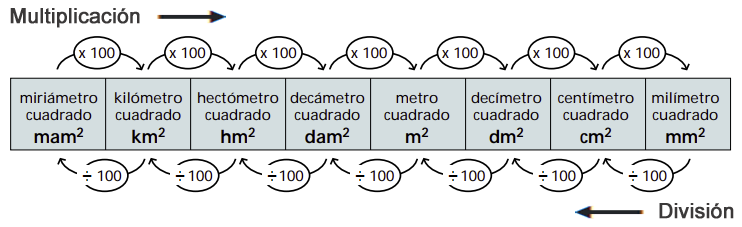
Equivalencias entre las unidades de superficie.
Estas medidas aumentan y disminuyen de 100 en 100, cada unidad de superficie es 100 veces mayor que la unidad inmediata inferior y 100 veces menor que la unidad inmediata superior.
¡Geonota!
Medir una superficie es hallar el área, es comparar con otra superficie elegida como unidad, calculando el número de unidades que contiene.
Capitulo III. Área y perímetro $\qquad$
Ejemplo. ¿$\space 12 \space km^2$ son equivalentes a cuantos $cm^2 \space$?
xploremos.
Conversión de unidades de superficie.
Dada una medida expresada en una unidad, convertirla a la unidad de la derecha. Ingresa el valor de la conversión, oprime "enter <┘" y verifica tu respuesta. Si deseas una ayuda, oprime en ayuda.
Escena de Eduardo Barbero Corral adaptada por el autor, con licencia CC by-nc-sa
El área y el perímetro se estudian para las líneas cerradas o figuras planas cerradas.
¡Geonota!
Las líneas poligonales son aquellas que tienen segmentos de línea recta. Si una línea es poligonal cerrada da origen a lo que conocemos como polígonos.
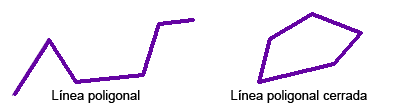
El cálculo de un área o superficie de una figura plana está basado en dos conceptos básicos: la multiplicación y el concepto de cuadrado o rectángulo.
¿Cuántos cuadrados tiene la imagen?
Se puede contar y sumar los 4 cuadros de cada fila ( $4+4+4+4$ ), o multiplicar las filas por las columnas ( $4 \times 4$ ). En todos los casos, obtenemos que en la figura hay 16 cuadrados.
Capitulo III. Área y perímetro $\qquad$
Si tomamos como 1 unidad de superficie a cada cuadrado, obtenemos que este mide 16 unidades de superficie o unidades cuadradas, que expresamos como: $16 \space u^2$.
Ahora, consideremos un cuadrado de $1 \space cm$ de lado cuya área es $1 \space cm \times 1 \space cm = 1 \space cm^2$, como referencia para encontrar el área de las figuras planas, para este caso, toda la imagen tiene 16 cuadrados, su superficie o área es de $16 \space cm^2$.
xploremos.
Superficie de una figura plana.
Arrastra la unidad de medida, cuantas veces se necesite y cubra completamente la superficie a medir.
Se debe comprender que la medición directa de una superficie implica un proceso de recubrimiento con una unidad de medida dada.
xploremos.
Superficie de una figura plana.
Arrastra la unidad de medida, cuantas veces se necesite y cubra completamente la superficie a medir. Responde a la pregunta.
Fórmulas para determinar área y perímetro.
Los conceptos de perímetro y área se refieren a medidas de las figuras geométricas, el área a la superficie interna y el perímetro al borde que rodea dicha superficie de la figura.
Hay una gran variedad de figuras geométricas, por lo que necesitamos varias fórmulas para calcular su área y perímetro. Sin embargo, podemos familiarizarnos con las fórmulas de las figuras geométricas más comunes, las cuales son el cuadrado, el triángulo, el rectángulo y las ya mencionadas en secciones anteriores.
Capitulo III. Área y perímetro $\qquad$
¿Como calcular área y perímetro en un cuadrado o rectángulo?
Hemos visto que en el concepto de multiplicación va implícito en el del cuadrado, y con igual procedimiento se tendría para un rectángulo, dado que, la superficie de un rectángulo se calcula de la misma forma, aplicando multiplicación:
$$Ancho \times Largo$$
Las unidades de medida que tiene el área, como el área representa el espacio que ocupa una figura en dos dimensiones; es decir, largo y ancho, por esto, las unidades de longitud van al cuadrado.
| Cuadrado | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
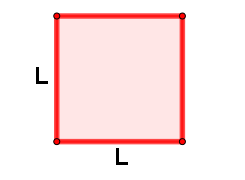Lado (L) $$A = L \times L$$ |
$$P = L + L + L + L$$ $$P = 4L$$ |
| Rectángulo | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
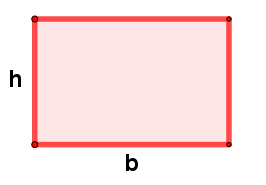Base (b) |
$$P = b + h + b + h$$ $$P = 2b + 2h = 2(b + h)$$ |
¡Geonota!
En el cuadrado, la base $(b)$ y la altura $(h)$ son de igual medida y corresponden a dos de los lados del cuadrado.
xploremos.
¿Cuantás unidades de área contiene?
GeoGebra.
Mueve los deslizadores (base o altura) y activa la casilla de verificación. Consideremos un cuadrado con unidad de área $1 \space cm^2$. Observa el área de la figura dada.
¿Que sucede cuando se traza la diagonal en el cuadrado?, ¿Ǫué figura o figuras se forman? ¿puedes calcular el área de estas figuras? Estas preguntas nos van a llevar a deducir el área de los triángulos, que veremos más adelante.
Capitulo III. Área y perímetro $\qquad$
xploremos.
Calcular área de un cuadrado o rectángulo.
Mueve la regla desde sus extremos, primero uno y después el otro. Ingresa el valor obtenido para el área, oprime "enter <┘" y desplaza las unidades de medida al círculo rosa.
Escena de Eduardo Barbero Corral adaptada por el autor, con licencia CC by-nc-sa
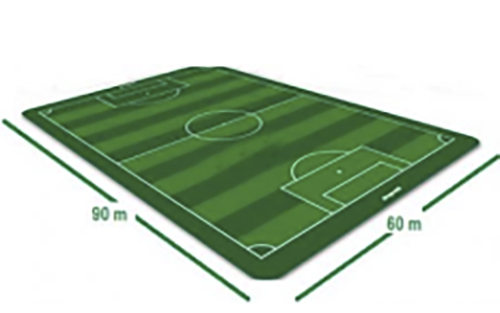
¡Piensa!... Se desea construir una cancha de futbol que tenga las dimensiones como se muestra en la figura. ¿Cuál es el perímetro que debe ocupar la cancha? ¿Cuál es el área del terreno que se debe adquirir para su construcción?
Respuesta.
¿Como calcular área y perímetro en el paralelogramo?
¡Geonota!
El cuadrado y el rectángulo son cuadriláteros que tienen los lados opuestos paralelos e iguales, características o propiedades que los incluye como paralelogramos, por lo cual, la superfice o área del paralelogramo o romboide esta dada por:
$$Área = Ancho \times Largo$$
xploremos.
Transformación de romboide a rectángulo.
GeoGebra.
Mueve el deslizador y observa cómo se transforma un paralelogramo en un rectángulo, Puedes dar respuesta a la pregunta: ¿Serán de igual área?
Capitulo III. Área y perímetro $\qquad$
| Paralelogramo (Romboide) | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
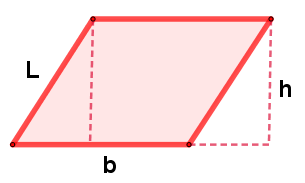Lado(L) |
$$P = b + L + b + L$$ $$P = 2b + 2L =2(b + L)$$ |
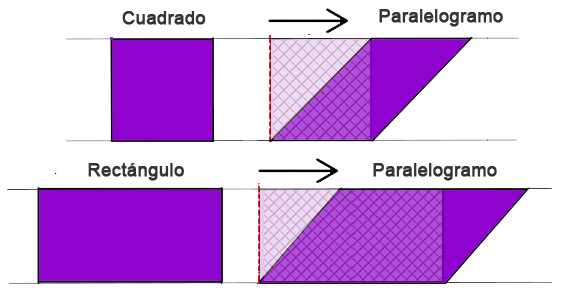
Según la forma del paralelogramo, el trazado de la altura puede quedar completa o parcialmente fuera de este, y seguimos utilizando "base x altura" para el hallar el área de paralelogramo.
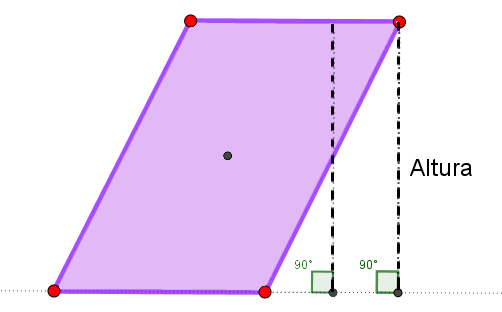Recordemos, la relación que existe entre la base y la altura es de perpendicularidad (forman ángulos de $90°$). Para facilitar el trazo de la altura, se toma como base el lado horizontal inferior de las figuras.
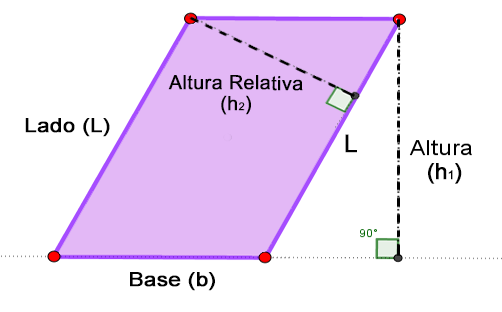Otra forma que se tiene para hallar el área del romboide es si se conoce su altura relativa y la medida del lado correspondiente a esta altura.
¡Geonota!
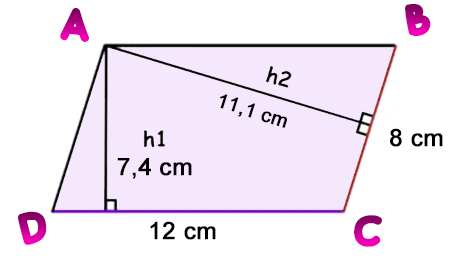
Se debe cumplir que el área o superficie es igual a:
$$Área = Base \space \times \space Altura = Lado \space \times \space Altura_{relativa} $$Compruebemos con la siguiente figura los resultados del área:
¡Piensa!... Calcular el área de un paralelogramo que tiene forma de romboide cuya altura mide $12 \space cm$ y su base mide $3$ veces su altura.
Respuesta.
Capitulo III. Área y perímetro $\qquad$
¿Como calcular área y perímetro del triángulo?
Partiendo de la siguiente pregunta:
¿Qué relación se presenta entre el área del paralelogramo y el área del triángulo?
Se tiene un paralelogramo, del cual ya conocemos como calcular su área. Para la deducción del área del triángulo trazamos una de las diagonales del paralelogramo.
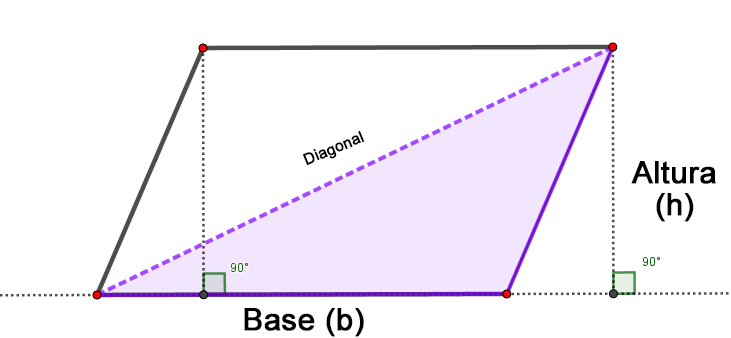
Entre el triángulo y el paralelogramo se tiene como relaciones:
Igual base, igual altura y el área del triángulo ocupa la mitad del área del paralelogramo construido.
| Triángulo | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
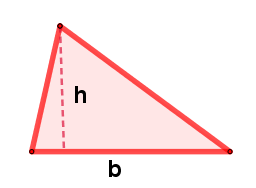Base (b) |
Lado (L) $$P = L_1 + L_2 + L_3 $$ |
¡Geonota!
El triángulo equilátero, es aquel que tiene los tres lados de igual longitud, único triángulo que es polígono regular.
El triángulo equilátero es un triángulo especial, para el cual, si se conoce la medida de la base (lado) y altura, se calcula el área con la misma expresión de cualquier triángulo.
Pero si no se conoce la medida de la altura sino solo su lado, se puede expresar en función de la medida de su lado (la deducción de esta expresión, se verá un capítulo más adelante):
| Triángulo Equilátero | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
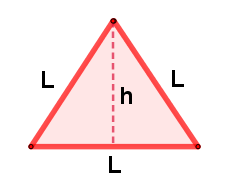Lado (L) $$A = \frac{\sqrt{3} \times L^2}{4}$$ |
Lado (L) $$P = L + L + L= 3L $$ |
Capitulo III. Área y perímetro $\qquad$
Recordemos que la altura en el triángulo, es la recta que pasa por un vértice y es perpendicular al lado opuesto, es por lo que a cada vértice le corresponde una altura. También utilizamos el nombre de altura para referirnos a la menor distancia entre un vértice y el lado opuesto (o su prolongación), pues es sobre esta recta en la que medimos esa distancia.
Algunas veces las alturas de un triángulo coinciden con uno de sus lados, en otras ocasiones incluso está por fuera del triángulo.
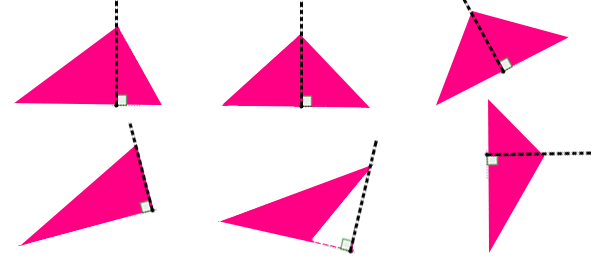
La altura correspondiente a un lado no cambia, aunque cambie la posición del lado, puede ser vertical, horizontal u oblicua, según la disposición del lado sobre el que se traza.
<<
>>
Comprueba lo aprendido respondiendo a la pregunta.
xploremos.
El triángulo mitad de grande al paralelogramo que lo rodea.
GeoGebra.
Mueve el deslizador y observa el paralelogramo que rodea al triángulo como ayuda para calcular el área.
Arrastra el punto $P_1$ o $P_2$ para modificar los triángulos. Responde a la pregunta: ¿Cuál es el área para cada triángulo?
Capitulo III. Área y perímetro $\qquad$
¿Como calcular área y perímetro de un rombo?
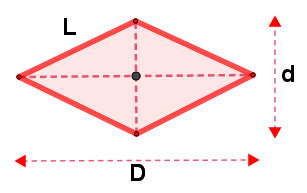
Veamos como deducir la fórmula para el rombo, en esencia se siguen los mismos procedimientos, por tanto, vamos a deducir su fórmula en términos de las diagonales, para ello vamos a transformar en este caso el rombo en un rectángulo, del cual ya conocemos como calcular su área.
Observe que se presenta las siguientes características:
La diagonal mayor $(D)$ del rombo coincide con el largo del rectángulo, la altura del rectángulo es la mitad de la diagonal mayor $(d)$ y el área del rombo es igual al área del rectángulo formado.
| Rombo | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
Diagonal mayor (D) |
Lados ($L$) |
¿Como calcular área y perímetro de un trapecio?
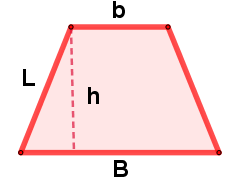
Siguiendo la misma deducción de la fórmula del área del triángulo, veamos como deducir la del trapecio, en esencia se sigue el mismo procedimiento, duplicamos el trapecio para construir un paralelogramo.
El paralelogramo que se forma tiene las siguientes características con respecto al trapecio:
Igual altura, la base del paralelogramo es igual a la suma de la base mayor $(B)$ y la base menor $(b)$ del trapecio, por tanto, el área del trapecio es la mitad del área del paralelogramo construido.
| Trapecio | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
Base mayor (B) |
Lados ($L_1, L_2$) |
Capitulo III. Área y perímetro $\qquad$
El trapecio no es un paralelogramo, es un cuadrilátero que tiene un par de lados paralelos llamados bases.
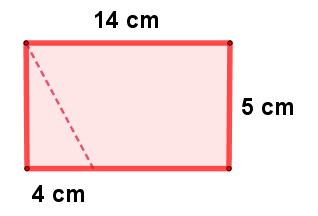
¡Piensa!... Se tiene la siguiente figura, ¿Cuántas veces es mayor el área del trapecio que el área del triángulo?
Respuesta.
¡Geonota!
Recordemos que el trapecio puede ser rectángulo, isósceles o escaleno y para calcular su perímetro es la suma de todos sus lados, para el caso del trapecio isósceles, los lados no paralelos son iguales.
Comprueba lo aprendido respondiendo a la pregunta.
¿Como calcular área y perímetro de un polígono regular?
Analizaremos el área y perímetro de los polígonos regulares de cinco o más lados, teniendo presente que el menor polígono regular es el triángulo equilátero (
¡Geonota!
Recordemos que un polígono es regular cuando todos sus lados son iguales y todos sus ángulos también y es irregular si no cumple con estas condiciones.
<<
>>
Elementos principales del polígono (
¡Piensa!... ¿Cómo se puede deducir la fórmula para calcular el área de un polígono regular?
Respuesta.
Capitulo III. Área y perímetro $\qquad$
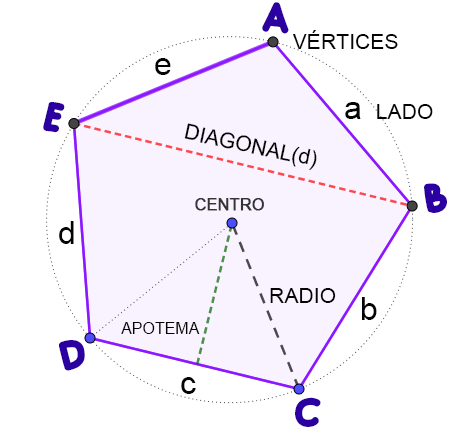Representación gráfica de los elementos que componen el polígono regular en una circunferencia circunscrita, donde $A, B, C, D, E$ vértices del polígono y $a, b, c, d, e$ lados iguales.
| Polígono regular | ||
|---|---|---|
| Gráfico | Área (A) | Perímetro (P) |
 |
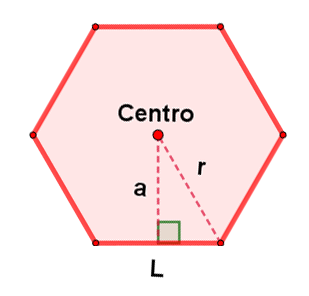Radio $(r)$ |
Lados ($L$) |
¡Piensa!... Un panadero, desea hacer galletas para vender en su panadería, y quiere
usar el molde que tenga una mayor superficie para incrementar sus ganancias:
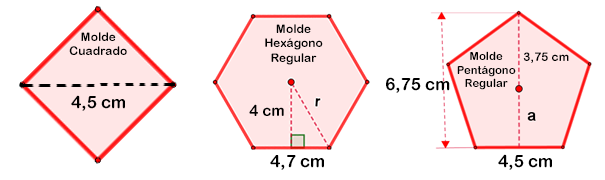
¿Qué molde le conviene usar?, ¿Por qué?, ¿Cuál es el perímetro de cada molde?, ¿Cuál es el área de cada molde?, ¿Qué procedimiento utilizaste para realizar los cálculos?
¿Como calcular área del círculo y longitud de la circunferencia?
Al igual que en los polígonos regulares, podemos medir el perímetro o el área de la circunferencia a través de una fórmula matemática. Para ello, necesitamos conocer el radio o diámetro de la misma.
Recordemos, la línea curva que forma el contorno de la circunferencia, mide algo más del triple de su diámetro, que equivale a pi$(\pi)$ $$(\pi = 3,14159265358979323846… )$$
¡Geonota!
Si divides lo que mide la longitud de una circunferencia, medida de su línea curva, entre lo que mide su diámetro, se obtiene el número de pi:
$$\frac{Longitud \space circunferencia}{Diámetro} = 3,141592653589…\approx 3.1416 $$De aquí se obtiene longitud de la circunferencia conociendo su diámetro:
$$Longitud \space de \space la \space circunferencia = Diámetro \times \pi \tag{7}$$Además, sabemos que el diámetro es dos veces el radio ( $ d =2r$ ), donde, podemos calcular de nuevo la longitud de la circunferencia a partir del valor del radio:
$$Longitud \space de \space la \space circunferencia = 2 \cdot r \cdot \pi \tag{8}$$Capitulo III. Área y perímetro $\qquad$
Llamaremos longitud de la circunferencia al perímetro de la circunferencia, y se denota a la longitud con la letra $L$.
El área de un círculo se puede hallar considerándola como un polígono regular de muchos lados, en el cual la apotema coincide con el radio.
| Circunferencia - Círculo | ||
|---|---|---|
| Gráfico | Área del Círculo(A) | Longitud (Perímetro) de la Circunferencia (L) |
 |
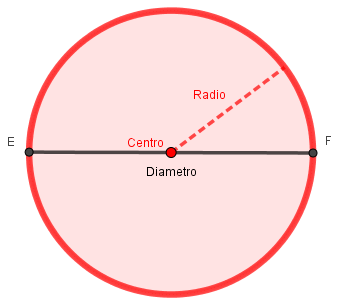Radio $(r)$ |
Longitud ($L$) |
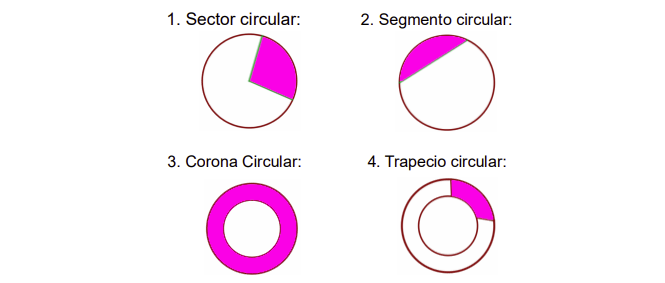
Algunas regiones importantes que se presentan en el circulo:
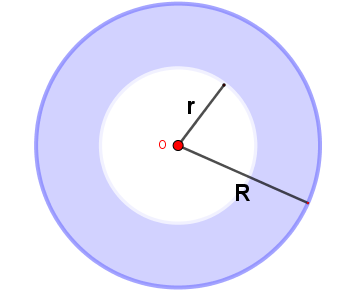
¡Piensa!... Una piscina tiene una forma de corona circular (anillo de color azul en la figura), delimitada por dos circunferencias de
radio interior $r = 2 \space m$ y radio exterior $R = 4 \space m$, ver figura:
¿Cuál es el perímetro y área de la piscina? (la corona circular es el área que corresponde a la región sombreada) Respuesta.
xploremos.
Calcular área y longitud de la circunferencia.
Mueve la regla desde sus extremos, primero uno y después el otro, verifica el valor del radio, oprime el botón y observa los cálculos.
Capitulo III. Área y perímetro $\qquad$
Comprueba lo aprendido respondiendo a la pregunta.
La geometría tiene numerosas aplicaciones prácticas en la vida diaria. Desde la construcción de edificios y la planificación urbana hasta la fabricación de objetos y la resolución de problemas cotidianos, es allí donde encontramos gran combinación de figuras planas, formando las figuras compuestas, que pueden incluir: cuadrados, círculos, triángulos, rectángulos, trapecios, entre otras.
El área de figuras compuestas se puede calcular determinando el área de las figuras que la componen, sumándolas o restándolas según sea el caso. Es de gran ayuda descomponer la figura o transponer partes de un lado a otro para completar figuras planas conocidas.
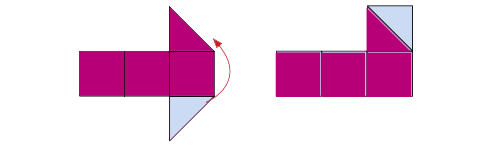
Lea detenidamente el problema, realice los cálculos y verifica tu respuesta, oprime el botón solución y un nuevo ejercicio.
Formulas. Áreas y perímetros
$\space$ Descargar para imprimir
Capitulo III. Área y perímetro $\qquad$
Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Ejercicio práctico.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo III. Área y perímetro $\qquad$
Evaluación. 10 preguntas con límite de tiempo (Máx. 15 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Tomada de la Red Educativa Digital Descartes.
“No sabe hablar quien no sabe callar”.
Pitágoras
El Teorema de Pitágoras es uno de los teoremas que más ha maravillado a todas las civilizaciones a lo largo de la historia. Algunos historiadores sugieren que en Babilonia por el año 1600 a.C., se calculaban las diagonales de ciertas figuras utilizando este teorema, sin embargo, la primera demostración formal conocida se le otorga usualmente al filósofo matemático griego Pitágoras de Samos, considerado el primer matemático puro.
Este teorema cuenta con una gran cantidad de demostraciones realizadas por personajes importantes de la ciencia y la matemática a lo largo de toda la historia.
En la antigüedad se utilizaba el teorema de Pitágoras para medir terrenos en agricultura, la altura de ciertos objetos, obtener el volumen de sólidos como pirámides y conos.
En la matemática, el teorema permitió el fortalecimiento de algunas áreas como la geometría y el cálculo, además del descubrimiento de los números irracionales
En la actualidad, el teorema sigue siendo indispensable en toda área donde es necesario el cálculo de longitudes, como en ingeniería, agricultura, física, astronomía y hasta en las artes.
Capitulo IV. Aplicaciones de la geometría $\qquad$
El Teorema de Pitágoras solo se cumple en los triángulos rectángulos, los lados menores son los que forman el ángulo recto y se llaman catetos, el lado mayor se llama hipotenusa.
En general, llamaremos la hipotenusa $h$ y los catetos $a$, $b$.
¡Geonota!
En otras palabras, el área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
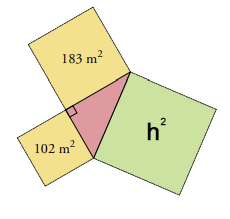
En el triángulo, como es triángulo rectángulo, se debe cumplir que:
El área del cuadrado mayor es igual a la suma de las áreas de los cuadrados menores.
¿Como calcular un lado del triángulo conocidos los otros dos?
Si sabemos que un triángulo es rectángulo, el teorema de Pitágoras nos permite calcular la longitud del tercero lado si conocemos la longitud de dos de sus lados.
| Teorema de Pitágoras | ||
|---|---|---|
| Triángulo Rectángulo Hipotenusa $(h)$ | Cálculo de la hipotenusa conociendo los dos catetos | Cálculo de un cateto conociendo el otro y la hipotenusa |
 |
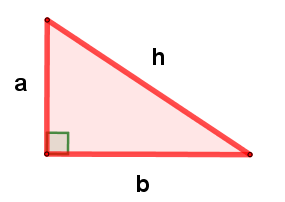Conocidos $a, b$ $$h^2 = a^2 +b^2 $$ $$h = \sqrt{a^2 + b^2}$$ | Conocidos $h, b$ $$a^2 = h^2 - b^2 \\ a = \sqrt{h^2 - b^2}$$ Conocidos $h, a$ $$b^2 = h^2 - a^2 \\ b = \sqrt{h^2 - a^2}$$ |
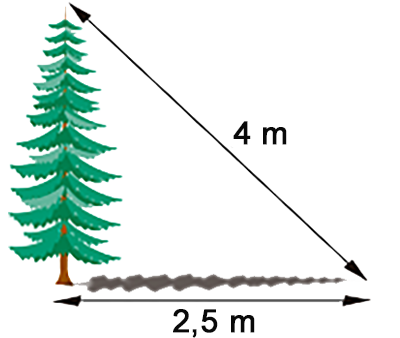
¡Piensa!... En un atardecer, un árbol proyecta una sombra de $2,5$ metros de longitud.
Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de $4$ metros. ¿Cuál es la altura del árbol?
Respuesta.
Capitulo IV. Aplicaciones de la geometría $\qquad$
Tener presente que, en el triángulo rectángulo, la hipotenusa siempre es el lado de mayor longitud y corresponde al lado opuesto del ángulo recto ($90°$).
¡Geonota!
Si tres números naturales, $a, b, c$, cumplen que $c^2 = a^2 + b^2$, es decir, si pueden ser las medidas de los lados de un triángulo rectángulo, entonces decimos que forman una terna pitagórica, por ejemplo:
$$ 3^2 + 4^2 = 5^2, \quad 9^2 + 40^2 = 41^2, \quad 12^2 + 35^2 = 37^2$$Si tomamos una terna pitagórica $a, b, c$ y la multiplicamos por un número natural $k$, obtenemos otra terna pitagórica, por tanto, se cumple que:
$ka, kb, kc$ es una terna pitagórica.
$$3, 4, 5 \to 2(3), 2(4), 2(5) \to 6, 8, 10$$
Comprueba lo aprendido respondiendo a la pregunta.
Observa la figura dada, utiliza la regla para medir sus lados, y selecciona la casilla de verificación para realizar los cálculos, aplica el teorema de Pitágoras para hallar la diagonal.
Oprime el botón verificar y comprueba tus resultados. Oprime el botón otra figura para otro ejercicio. (El resultado verifícalo midiendo la diagonal con la regla).
Mueve la regla desde sus extremos, primero uno y después el otro.
Escena de Eduardo Barbero Corral adaptada por el autor, con licencia CC by-nc-sa
Capitulo IV. Aplicaciones de la geometría $\qquad$
xploremos.
Puzzle Pitagórico - Demostración de Perigal.
Se utilizan para comprobar el Teorema de Pitágoras. Son construcciones de piezas en los cuadrados sobre los catetos y luego con todas las piezas se forma el cuadrado sobre la hipotenusa, esto comprueba que ambas áreas son iguales.
GeoGebra.
Arrastra las piezas y rotarlas desde el punto si es necesario.
Ver construcción
Puzzles Pitagóricos.
$\space$ Descargar para imprimir
Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Capitulo IV. Aplicaciones de la geometría $\qquad$
¡Geonota!
"Si dos rectas cualesquiera son cortadas por rectas paralelas, los segmentos que determina en una de las rectas son proporcionales a los segmentos correspondientes de la otra recta." Thales
Observa que, hay tres rectas paralelas, las rectas A, B y C. Las rectas paralelas son aquellas que guardan la misma distancia entre sí, es decir, por más que se prolonguen nunca se van a intersecar, juntar o tocar.
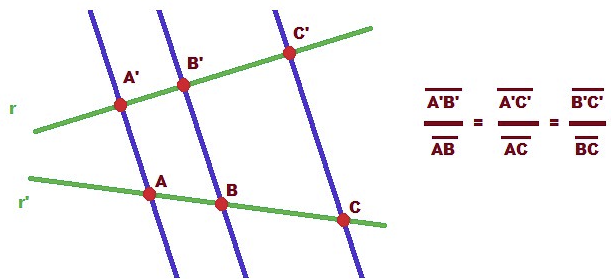
Ahora, llevemos el teorema a los triángulos, para esto, hablaremos de semejanza, como definición previa, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales.
¡Geonota!
Si en un triángulo dado se traza un segmento paralelo a uno de sus tres lados, el nuevo triángulo generado será semejante al primero.
Dado un Δ $ABC$ , si se traza un segmento paralelo, $\overline{DE}$ , a uno de los lados del triángulo, se obtiene otro triángulo Δ $ADE$ , cuyos lados son proporcionales a los del triángulo Δ $ABC$.
De acuerdo con el teorema, se verifica que:
$$\frac{\overline{AB}}{\overline{AE}} = \frac{\overline{AC}}{\overline{AB}} = \frac{\overline{BC}}{\overline{DE}}$$
Capitulo IV. Aplicaciones de la geometría $\qquad$
El Teorema de Thales recoge uno de los postulados más básicos de la geometría: Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
¡Geonota!
"En una circunferencia de centro en $O$ y diámetro $AC$, cualquier punto $B$ de esa circunferencia no perteneciente a $AC$ determina un triángulo rectángulo Δ $ABC$ con el ángulo de $90°$ en $B$." Thales
Video. Construcción utilizando el software de GeoGebra.
Teorema de Pitágoras aplicando el teorema de Thales en la construcción de triángulo rectángulo.
xploremos.
Demostremos el teorema de Pitágoras.
Observa el video y responde a las preguntas que se muestran, algunas se responden escribiendo verdadero o falso.
Escena de Juan Guillermo Rivera adaptada por el autor, con licencia CC by-nc-sa
GeoGebra. Utiliza el software y realiza la construcción como ayuda para verificar la demostración del teorema de Pitágoras. Clic aquí.
Capitulo IV. Aplicaciones de la geometría $\qquad$
¡Geonota!
"En un triángulo rectángulo, cuando se traza la altura que corresponde al vértice del ángulo recto con respecto a la hipotenusa, se forman dos triángulos rectángulos." Euclides
Ilustración de los principales elementos del triángulo rectángulo:
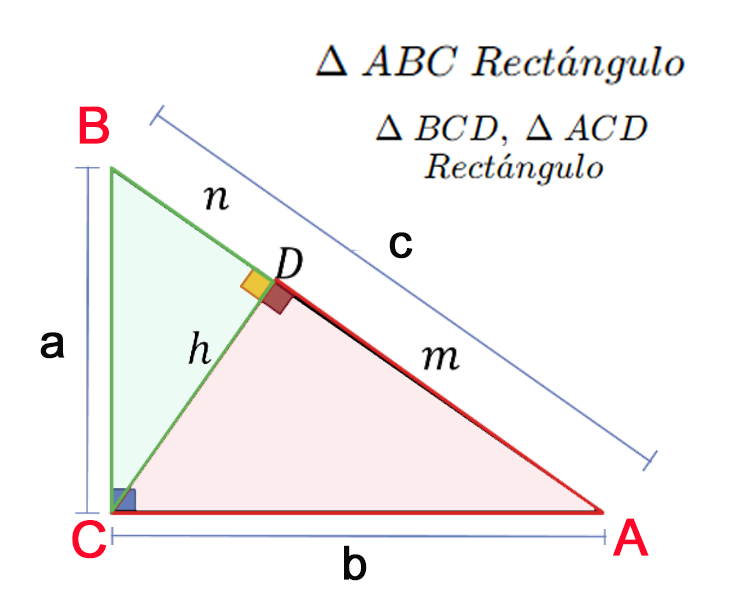
Las relaciones métricas del triángulo rectángulo son cuatro. Los tres triángulos formados al trazar la altura relativa a la hipotenusa son rectángulos y semejantes.
La hipotenusa es igual a la suma de las proyecciones.
$$ c = n + m \tag{10}$$Por semejanza de triángulos, tenemos que:
Teorema de la Altura. El cuadrado de la altura relativa es igual al producto de los catetos.
$$ \frac{h}{m} = \frac{n}{h} \to h^2 = nm \tag{11}$$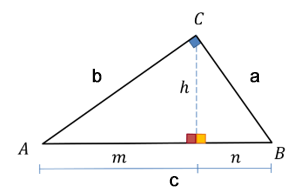
Teorema del Cateto. El cuadrado de un cateto, es igual al producto entre su proyección (que se encuentra de su lado) y la hipotenusa.
$$ \frac{b}{c} = \frac{m}{b} \to b^2 = mc \tag{12}$$ $$ \frac{a}{c} = \frac{n}{a} \to a^2 = nc \tag{13}$$El producto entre la hipotenusa y la altura relativa a ella, es igual al producto de los catetos.
$$ \frac{c}{a} = \frac{b}{h} \to hc = ab \tag{14}$$Capitulo IV. Aplicaciones de la geometría $\qquad$
¡Piensa!... Situación-Problema.
La casa de Charlie, su amigo, su tío Nando y el estadio de futbol se encuentran ubicados de la siguiente forma:
La distancia donde se encuentra el tío Nando al estadio es de $10,76 \space km$, y del tío Nando a la casa de Charlie es $3,38 \space km$, como se muestra en la siguiente imagen:
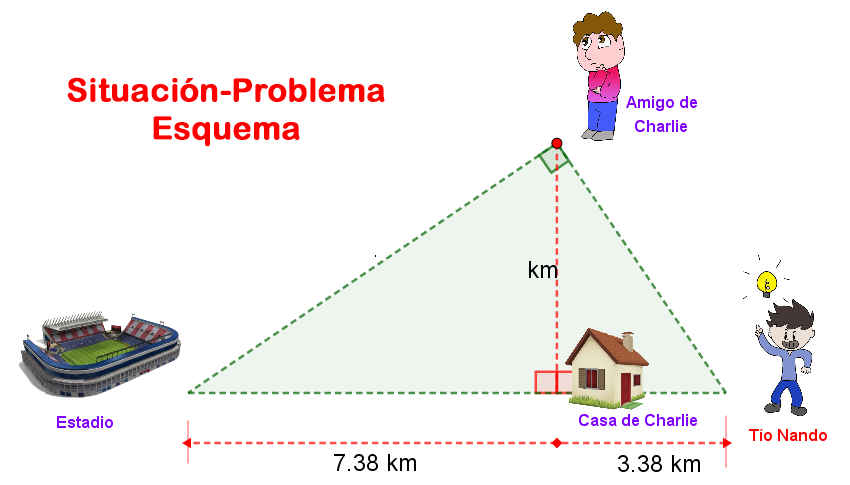
Además, su amigo afirma que la distancia donde se encuentra ubicado a la casa de Charlie es mayor que la de casa de Charlie a donde se encuentra el tío Nando, pero menor que la distancia de la casa de Charlie al estadio de futbol.
De este modo, se debe identificar que la figura es un triángulo rectángulo, y que la distancia entre la casa de Charlie a donde se encuentra su amigo corresponde a la altura que está trazada en el triángulo rectángulo mayor.
Con estos datos, se puede aplicar el teorema de la altura, encuentra las distancias de todos los puntos.
Respuesta.
Ejercicio práctico.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo IV. Aplicaciones de la geometría $\qquad$
Evaluación. 10 preguntas con límite de tiempo (Máx. 15 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Tomada de la Red Educativa Digital Descartes.
“El juego es condición fundamental para ser serio”.
Arquímedes
¿Por qué jugar con la geometría?
Para enseñar geometría se puede partir de la experiencia propia del estudiante, en primer lugar, investigando todo a su alrededor, para identificar y reconocer, las características y propiedades de las diferentes formas geométricas, además, invitarlo a la observación de todo lo que lo rodea en su entorno, para ir adquiriendo una serie de habilidades lógico-matemáticas que son fundamentales.
Desde la cotidianidad se puede entender poco a poco el estudio de la geometría, esto se puede hacer también a partir de diferentes juegos que involucren las figuras geométricas.
Hay que tener en cuenta la importancia de las geometrías en la vida diaria y presentar estas desde un enfoque globalizado cuyo objetivo es relacionar los distintos campos de las matemáticas con conocimientos de otras materias, así como utilizar las habilidades para resolver problemas de la vida cotidiana. Por ello, es esencial ver que la geometría está presente en multitud de situaciones del entorno más cercano.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
En síntesis, para mejorar la enseñanza-aprendizaje de la Geometría, se deben poner en práctica recursos educativos y motivadores para el estudiante, pues serán oportunos para crear ambientes favorables para comprender conceptos y desarrollar actitudes positivas hacia esta materia.
En este aspecto, presenta una especial relevancia el juego como recurso didáctico, ya que además de ofrecer un carácter divertido a su aprendizaje, permite partir del propio error y el de los demás.
Esto implica para el estudiante afrontar nuevos conocimientos sin tener miedo; promueve la socialización y la autonomía, y también, se pueden desarrollar la atención, la concentración, la memoria y la resolución de problemas. "Alsina, 2004"
Por lo tanto, es fundamental conocer la principal finalidad de la enseñanza-aprendizaje de la geometría, para después saber cómo aplicar sus contenidos mediante el uso de recursos educativos y actividades innovadoras, a partir de diferentes juegos.
¿Que es el Tangram Chino?
El Tangram es un puzle o rompecabezas formado por un conjunto de piezas de formas poligonales que se obtienen al fraccionar una figura plana y que pueden acoplarse de diferentes maneras para construir distintas figuras geométricas.
Las figuras que se obtienen con este puzle llamado Tangram estarán formadas siempre por todas las piezas en las que se disecciona la figura plana que lo origina, por tanto, las formas geométricas que se obtienen podrán ser distintas, pero siempre tendrán la misma área.
El Tangram es de origen chino y su gran popularidad en Europa y en los Estados Unidos surgió a principios del siglo XIX; ésta fue creciendo con el tiempo debido a su carácter lúdico y educativo, de forma que en la
actualidad existen numerosos juegos y juguetes infantiles basados en el tangram.
El Tangram es un juego chino muy antiguo llamado "Chi Chiao Pan" que significa "juego de los siete elementos" o "tabla de la sabiduría".
Existen varias versiones sobre el origen de la palabra Tangram, una de la más aceptada cuenta, que la palabra la inventó un inglés uniendo el vocablo cantones "tang" que significa chino con el vocablo
latino "gram" que significa escrito o gráfico.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Construcción del Tangram Chino utilizando la regla.
Tomemos una hoja de papel, cartulina o cualquier material fácil de recortar:
Construyamos un cuadrado $ABCD$ de cualquier tamaño. (Sugerencia: de $12 \times 12 \space cm$)
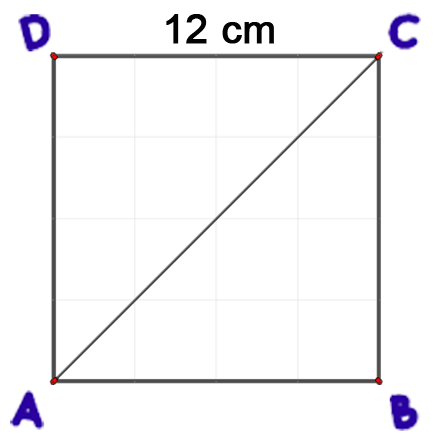Tracemos una diagonal del cuadrado $ABCD$ (en este caso, la diagonal $AC$) y, de esta manera, éste se descompone en dos triángulos isósceles rectángulos: $ΔADC$ y $ΔABC$.
Con ayuda de la cuadrícula puedes conseguir un patrón para realizar los trazos.
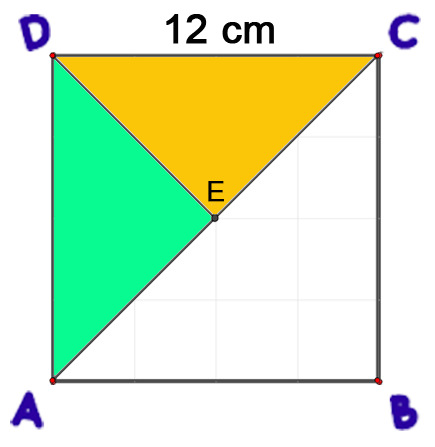Trazamos el segmento $\overline{DE}$, siendo $E$ punto medio de la diagonal $AC$. El triángulo Δ$ACD$ se descompone en dos triángulos isósceles rectángulos: Δ$ADE$ y Δ$DCE$
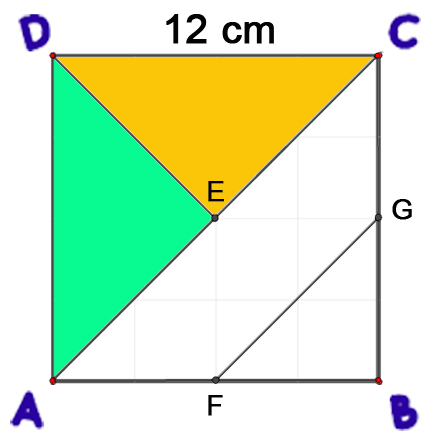Se traza el segmento $\overline{FG}$, siendo $F$ y $G$ puntos medios de los lados $AB$ y $BC$ respectivamente en el triángulo
isósceles rectángulo $ΔABC$, el cual se descompone en un triángulo isósceles rectángulo $ΔFGB$ y un trapecio isósceles $AFGC$.
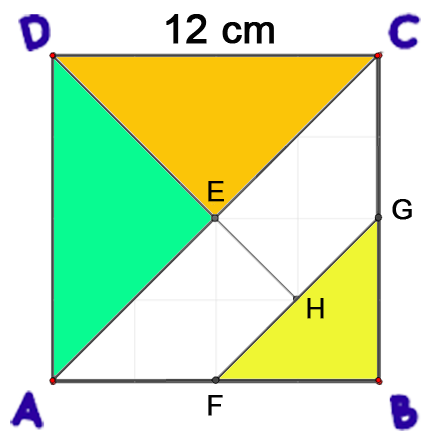Se traza el segmento $\overline{EH}$, siendo $H$ el punto medio del segmento $FG$ en el trapecio isósceles $AFGC$, el cual se descompone en dos trapecios
rectángulos $BFHE$ y $EHGC$
Se trazan los segmentos $\overline{FI}$ y $\overline{HJ}$, siendo $I$ y $J$ los puntos medios de los segmentos $\overline{AE}$ y $\overline{EC}$ respectivamente en el trapecio isósceles $AFGC$.
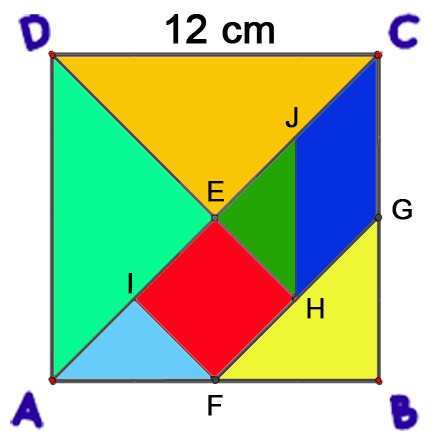El trapecio isósceles $AFGC$ se descompone en dos triángulos isósceles rectángulos, un cuadrado y un paralelogramo. De esta forma, se obtiene la construcción del Tangram Chino.
¡Piensa!...
¿Cuáles definiciones o propiedades geométricas están involucradas en esta construcción?
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Lea detenidamente cada actividad y responda las preguntas.
xploremos.
Las siete piezas del Tangram.
GeoGebra.
Activa la casilla de verificación para obtener la silueta de una figura. Arrastrar cada pieza y rotar desde el punto según la posición deseada para formar la figura.
Si deseas obtener una ayuda, activa la casilla de verificación correspondiente a la ayuda. Activa una figura a la vez
¡Piensa!...
Según cada silueta, ¿Será posible arrastrar solo algunas piezas para formar la figura sin rotarlas?, si es posible, ¿Cuantas piezas serían necesarias en cada silueta para formar la figura?
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
El Tangram y las fracciones.
¿Te has dado cuenta cómo de grandes son cada una de las piezas del Tangram? ¿qué fracción del total del cuadrado ocupa cada una de ellas? ¿Podrías decir cuántos triángulos grandes se necesitan para rellenar todo el cuadrado? ¿Y triángulos medianos? Pensemos las mismas preguntas para los triángulos pequeños, el cuadrado y el paralelogramo.
Si no has tenido problema para esto, te va a resultar muy fácil saber ¿qué fracción del total del cuadrado ocupa un triángulo grande? ¿Y el triángulo mediano? ¿Y los demás?
(Si no identificas la fracción, haz clic en cada pieza y observa).
¡Piensa!...
Observa el Tangram, y responde: ¿Ǫué parte del cuadrado que forma el Tangram corresponde en fracción cada una de las siete piezas?
¡Piensa!... Para hacer este ejercicio no puedes utilizar regla, pero si puedes manipular las fichas del Tangram Chino.
Responde las preguntas a continuación:
Descarga a continuación los dos ejercicios y forma un pequeño cuadernillo de trabajo:
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Área y perímetros utilizando el Tangram.
¿Qué relación existe entre el área de cada una de las piezas del Tangram Chino con respecto al área del cuadrado original?
xploremos.
Área de las siete piezas del Tangram.
Ingresa el valor de la longitud del lado del cuadrado y oprime "enter <┘". ¿Identificas el área?, haz clic en cada pieza y observa.
Recordemos, que unidades de área son unidades cuadradas ($u^2$).
¡Piensa!...
¿Cuál es el área de un cuadrado cuyos lados miden $12 \space cm$? ¿Cuál es el área de cada una de las piezas que componen el Tangram construido a partir de dicho cuadrado? ¿Qué relación encontramos entre el Tangram Chino (cuadrado original) y las construcciones de diferentes figuras geométricas?
¡Geonota!
Con el Tangram Chino pueden identificarse: figuras congruentes, figuras semejantes y figuras equivalentes.
Si se tienen dos figuras geométricas cualesquiera, se puede tener:
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
En conclusión, el Tangram Chino en primer lugar se puede utilizar para jugar libremente con él, familiarizarse y conocer las distintas piezas. Luego se puede convertir en un gran aliado para la enseñanza y aprendizaje de la Geometría.
El tangram, a través de la percepción visual, nos ayuda a despertar el desarrollo del sentido espacial, así como su imaginación y fantasía, además, desde lo didáctico podemos trabajar:
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Un poco sobre los pentominós y los geniales rompecabezas que pueden armarse con ellos.
Video. Los pentominós.
Canal,/ everst88 . Este video está bajo una licencia Creative Commons Reconocimiento 3.0
Los pentominós o pentaminós son figuras geométricas compuestas por cinco cuadrados del mismo tamaño unidos por sus lados. Son por tanto unas curiosas formas de polígonos que recubren, por ejemplo, cinco cuadros de un tablero de ajedrez. Así al menos fueron presentados por Solomon Wolf Golomb en 1954 al mundo matemático, como subformas de un concepto más general llamado poliominó. Debido a sus propiedades y características, tienen diversas aplicaciones en matemáticas, geometría, diseño, y juegos, entre otras áreas.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Con esas condiciones, estos son los 12 pentominós posibles:
¡Geonota!
Los pentominós obtenidos a partir de otros por reflexión o volteado (simetría axial) o por rotación no cuentan como un pentominó diferente.
Plantillas para recortar.
$\space$ Descargar para imprimir
xploremos.
Las doce piezas del pentominó.
GeoGebra.
Arrastra, invierte o gira cada pieza desde el punto según las instrucciones dadas. Con estas 12 piezas se pueden armar diferentes figuras de distintas formas.
Escena de Cristina Masotta, TheMadMathematician_1, con licencia CC by-nc-sa
¡Piensa!...
¿Los Pentominós, tienen todos la misma superficie(área)? ¿Tienen el mismo perímetro?
Respuesta.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Para responder a las preguntas, tomemos como una unidad cuadrada un cuadrado de un pentominó y observemos los siguientes pentominós.
¡Geonota!
"Unidad cuadrada, es un cuadrado, donde todos sus lados miden una unidad lineal".
Si cada lado de un cuadrado es una unidad lineal, entonces el perímetro de los pentominós $P$ y $T$ serán diferentes:
$$P = 10 u \neq T = 12 u$$Pasa el mouse sobre la siguiente imagen y observa:
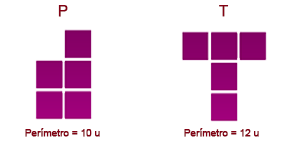
GeoGebra. Utilizando el interactivo con los 12 pentominós, construir los posibles rectángulos que tienen igual área, donde sus lados se representan en unidades.
¿Cuál debería ser el área de cualquiera de los rectángulos formados por todos los pentominós?
Escena de Cristina Masotta, TheMadMathematician_1, modificada por el autor
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Con la 12 fichas del pentominó o algunas de ellas, se pueden construir diferentes figuras geométricas, por lo cual, se puede afianzar el concepto de área y perímetro, además, de estimular la imaginación y las habilidades del pensamiento creativo.
Observa la construcción de todos los posibles rectángulos con todas las 12 fichas del Pentominó.
¡Piensa!...
¿Estas construcciones de los rectángulos serán únicas o se tienen otras posibilidades diferentes para construir cada rectángulo?
Son muchos los beneficios que en la educación puede aportar el Pentominó, tales como el desarrollo de la creatividad, la atención, memorización, planificación, el desempeño intelectual, la implementación de la lógica matemática, la eficiencia, el autocontrol y las múltiples habilidades que se pueden desarrollar, además de trabajar temas como:
Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Beneficios de jugar con las figuras geométricas.
El juego y la manipulación de las figuras geométricas ayuda a desarrollar habilidades cognitivas como el razonamiento lógico y la resolución de problemas, esto, ayuda a reconocer patrones y simetrías, lo que estimula el pensamiento.
Al manipular figuras geométricas, se desarrollan habilidades motoras finas, mejorando la coordinación motriz entre los sentidos visuales y corporales.
Las figuras geométricas son la base de las matemáticas. Comprenderlas desde temprana edad facilita el aprendizaje de conceptos más avanzados, como la geometría y la trigonometría, repasemos las figuras geométricas con algunos juegos.
Tetris es el rompecabezas más famoso del mundo, diseñado por el matemático Ruso Alexei Pajitno en el año de 1984, como buen aficionado a los rompecabezas, recreo en un ordenador un juego similar a un pentominó.
Tetris está centrado en elegir la forma idónea de las piezas que van apareciendo en la pantalla con el fin de conseguir que todas encajen, y todo ello en tan solo unos pocos segundos. Es por este motivo que uno de los beneficios es la capacidad que esta actividad tiene para poner el cerebro en funcionamiento y mejorar el pensamiento crítico, vital para escoger la forma correcta en todo momento.
Además, estimula la memoria, ya que, se deben colocar las piezas que van apareciendo mientras se observa cuál será la siguiente forma y retenerla en la memoria para saber cómo se colocará está.
xploremos.
Rompecabezas Tetris.
Para iniciar, oprime el botón jugar y utiliza las flechas del teclado para desplazar o cambiar de posición las piezas del Tetris.
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Las Torres de Hanói es un rompecabezas o juego matemático inventado en 1883 por el matemático francés Édouard Lucas. El juego, en su forma más tradicional, consiste en tres varillas verticales. En una de las varillas se apila un número indeterminado de discos (elaborados de madera) que determinará la complejidad de la solución, por regla general se consideran ocho discos.
Los discos se apilan sobre una varilla en tamaño decreciente. No hay dos discos iguales, y todos ellos están apilados de mayor a menor radio en una de las varillas, quedando las otras dos varillas vacías.
El juego consiste en pasar todos los discos de la varilla ocupada (es decir la que posee la torre) a una de las otras varillas vacantes. Para realizar este objetivo, es necesario seguir tres simples reglas:
Este juego desarrolla habilidades tales como: la agilidad mental pasando rápidamente una pieza de un lugar al otro, pensamiento lógico matemático contando y contando, la autonomía por el juego, estimula la concentración, desarrollando la paciencia, la coordinación visual espacial, potencia la imaginación y creatividad: creando muchas historias diferentes alrededor de este juego.
xploremos.
La Torre de Hanoi.
GeoGebra. Author: Matematicaula, 侯杰材
Haz clic en los discos para moverlos, y de una varilla a otra, clic en la varilla a mover.
Escena de Matematicaula, 侯杰材, 河內塔 (Tower of Hanoi), con licencia CC by-nc-sa
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Comprueba lo aprendido resolviendo la sopa de letras.
Sopa de letras.
Descargar para imprimir
Ejercicio práctico.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo V. Exploremos, juguemos y aprendamos $\qquad$
Evaluación. 10 preguntas con límite de tiempo (Máx. 15 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Tomada de la Red Educativa Digital Descartes.
Referencias bibliográficas $\qquad$
Otras Ciberweb
https://www.diferenciador.com/ciencias/
https://edu.gcfglobal.org/es/geometria-basica/#
https://www.matematicas10.net/2015/12/ejemplos-de-polígonos-simples.html
https://calculo.cc/temas/temas_geometria/fig_geometrica/teoria/triangulos1.html
