FUNCIÓN LINEAL Y CUADRÁTICA

Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
Córdoba (España)
2021
Título de la obra:
FUNCIÓN LINEAL Y CUADRÁTICA
Autor:
Carlos Alberto Rojas Hincapié.
Diseño plantilla del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-16-5

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Conociendo la estructura del libro interactivo
Para el inicio de cada capítulo nos centramos en:
Sabemos o queremos aprender
 Competencias o logros que se aprenderas y que se enfocan a distinguir, formular y representar a través de los conceptos situaciones mediante una función.
Competencias o logros que se aprenderas y que se enfocan a distinguir, formular y representar a través de los conceptos situaciones mediante una función.
Para complementar los momentos de aprendizaje, encontraremos:

Exploración.
Escenas de exploración que proporciona ayuda a la comprensión de los contenidos que se trataran en la sección a estudiar.

Escena interactiva.
Escena interactiva que proporciona ayuda a la comprensión de los contenidos y a la solución de las actividades propuestas.

Son preguntas de análisis que se plantean de los conceptos presentados en cada sección.

Preguntas que permiten evaluar los aprendizajes, de acuardo a las competencias estudiadas en cada sección.
 Recuerda, este icono que se encuentra en la parte superior izquierda del libro, te lleva en cualquier instante a la tabla de contenido, desde de aqui puedes ir a cualquier sección.
Recuerda, este icono que se encuentra en la parte superior izquierda del libro, te lleva en cualquier instante a la tabla de contenido, desde de aqui puedes ir a cualquier sección.
 Click en el icono, utiliza la calculadora donde la encuentres, si es necesario.
Click en el icono, utiliza la calculadora donde la encuentres, si es necesario.
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto DescartesJS: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
Véase https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
El contenido de este libro se basa en la función lineal y cuadrática para docentes y estudiantes que, por la dificultad de concertar un horario presencial, permite una opción autodidacta acompañada de material interactivo para una mayor comprensión de los temas tratados.
Retomando la introducción a la documentación de DescartesJS de Radillo, Abreu y Espinosa, podríamos coincidir en que este libro está destinado tanto a personas que no han usado DescartesJS como a personas que tienen cierta experiencia y desean mejorarla. En cada apartado del libro se proponen ejercicios y se incluyen ejemplos para que el lector pueda comprender paso a paso la funcionalidad de DescartesJS y su enorme potencial para crear objetos interactivos de aprendizaje.
Algunos objetos interactivos fueron diseñados por las siguientes personas: Alexandra Guzmán Velásquez, Carlos Alberto Jaime Vergara, Carlos Alberto Rojas Hincapié, Carlos Alberto Serrato Hernández, Carlos Mario Restrepo Restrepo, Claudio Francisco Nebbia Rubio, Erika Paulina Tovilla Rubio, José Luis Abreu León, José R. Galo Sánchez, Juan Guillermo Rivera Berrio, Julio Arnoldo Pardo Saavedra, Julio Cesar Domínguez Tovar, Héctor Javier Herrera Mejía, María Lourdes Velasco Arregui, Marta Olivero Serrat, Miguel Ángel Cabezón Ochoa, Oscar Escamilla González, Valentina Muñoz Porras, entre otros.
Estos objetos interactivos se adaptaron y modificaron al Plugin de DescartesJS para las presentes plataformas y puedan ser utilizados en el libro por docentes y estudiantes según las actividades requeridas en cada sección. Todas las modificaciones de los objetos interactivos fueron realizadas por el presente autor del libro interactivo, además de la elaboración de otros objetos interactivos.
 Exploración.
Observa las siguientes escenas interactivas como introducción a los conceptos de la función lineal.
Exploración.
Observa las siguientes escenas interactivas como introducción a los conceptos de la función lineal.
 Escena interactiva.
Escena interactiva.
Exploremos el plano cartesiano.
Mueve el punto rojo y observa que cada punto tiene un valor en el plano de coordenadas.
 Escena interactiva.
Escena interactiva.
Exploremos las partes del plano cartesiano.
Escribe, en cada uno de los recuadros, los nombres correspondientes, inicia siempre con letra mayúscula. (Escribir en palabras).
Comprueba tus respuestas

 Escena interactiva.
Escena interactiva.
Gráfica de un movimiento.
Modifica los valores de la función, oprime el botón arranque y observa el movimiento de los atletas y la gráfica de sus trayectorias.
Escena interactiva adaptada por el autorVéase. Proyecto Descartes.org, Telesecundaria.
 Identificar, con ayuda de objetos interactivos de aprendizaje, las características y los elementos de la función lineal y afín, su dominio, recorrido, si es creciente o decreciente, intersección con los ejes y aplicaciones en la solución
de situaciones de la realidad que modelan dichos conceptos matemáticos.
Identificar, con ayuda de objetos interactivos de aprendizaje, las características y los elementos de la función lineal y afín, su dominio, recorrido, si es creciente o decreciente, intersección con los ejes y aplicaciones en la solución
de situaciones de la realidad que modelan dichos conceptos matemáticos.
Aprenderás a:
Lograrás:
Introducción
Ya debes estar familiarizado con las coordenadas cartesianas y saber representar puntos. Esta unidad didáctica está pensada para introducir el concepto de función y tener nociones básicas de cara a cursos posteriores.
Mediante ejemplos y ejercicios se llega a la consolidación de los conceptos marcados como objetivos para este capítulo.
¿Que es una función?
Una función es una relación entre dos magnitudes que pueden variar, de manera que a cada valor de la primera le corresponde un único valor de la segunda llamado imagen.
La variable que consideramos en primer lugar, $ x $, se denomina variable independiente, la otra variable, $y$, se denomina variable dependiente pues su valor depende del que haya tomado la primera.
Una función $f(x)$ con variables $x$ e $y$ se expresa de la forma:$$\color{Red}y = f(x)$$
En este caso, $f ( x )$ es la imagen de $x $, es decir, el valor que corresponde a $y$ por la función o relación.
 Escena interactiva.
Escena interactiva.
Representación de una función por medio de diagrama.
Dominio de una función. Es el conjunto $X$ de todos los números reales para los cuales la función $f$ existe o esta definida.
Rango de una función También conocido como imagen o recorrido, es el conjunto de todos los valores que cumplen $y=f(x)$, o sea el valor de la función $f$ en $x$.
Gráfica de una función
Es la representación en el plano cartesiano de todos los pares $(x,y)$; donde $x$ es un valor de la variable independiente, mientras que $y$ es la imagen de la función del punto $x$.
Ejemplo. Representación gráfica la función con fórmula $\color{red} p(a) = 4a$ teniendo en cuenta que $p$ es el perímetro de un cuadrado de lado $a$.
Se dan valores a la variable $a = 1, 2, 3, 4$ (valores positivos pues se trata de longitudes).
Calculamos la imagen de cada valor de $ a$ para obtener $p$:
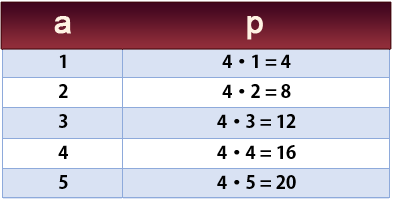
Ahora representamos los pares de puntos $(a, p)$ en el plano de coordenadas, perímetro vs. lado del cuadrado.
 Escena interactiva.
Escena interactiva.
Observa la gráfica obtenida, con clic izquierdo sostenido puedes mover la imagen o el control para zoom.
Gráfica: Perímetro vs. lado del cuadrado, $\quad \color{Red} p(a) = 4a$
La representación gráfica de una función lineal es una función de proporcionalidad directa, recta que pasa por el origen de coordenadas, su expresión algebraica es de la forma: $$\color{Red}y = mx $$ donde $m$ es la pendiente de la recta ($m$ sería la constante de proporcionalidad).
 Escena interactiva.
Escena interactiva.
Mueve el control m y observa el cambio en la pendiente.
Con ayuda de la escena interactiva, responde las preguntas de la siguiente página.

 Escena interactiva.
Escena interactiva.
Observa y analíza esta otra forma de la función $\color{Red}y = mx + b$
Mueve los controles m, x, b y observa el cambio en la función.

Las gráficas de la ecuación $y = mx + b$ son rectas paralelas a la función $y = mx$, que atraviesan al eje de ordenadas $y$ a una altura $b$.
Estas funciones se denominan funciones afines.
En consecuencia, solo se precisan un par de valores para obtener su respectiva gráfica, siempre y cuando el dominio de la función que se puede abreviar Dom f = Df y su imagen que se puede escribir imagen de f = imf o recorrido de la función sean los números reales.
La representación gráfica de una función afín es una recta que no pasa por el origen de coordenadas, donde $b$ es la ordenada de $x = 0$ (su gráfica es una línea recta).

Con la escena interactiva que se muestra a continuación, responde:
 Escena interactiva.
Escena interactiva.
Observa y analiza esta otra forma de la función.
Mueve el control m y b, observa la función afin $\color{Red}y = mx + b$.

Elementos de la función afín, y = mx + b
La función lineal $f(x) = mx + b$ es una función de primer grado (es decir, un polinomio en $x$ de grado menor o igual a 1), donde $m$ se conoce como la pendiente, grado de inclinación de la linea recta y $b$ es la intersección con el eje $y$ u ordenada, que tiene como corte en el eje $y$ el punto $(0, b)$
Una de las formas de hallar la pendiente m de una recta es tomar dos puntos sobre dicha recta, sean los puntos $\begin{aligned} P_1 (x_1, y_1) \end{aligned}$ y $\begin{aligned} P_2 (x_2, y_2) \end{aligned}$, entonces la pendiente está dada por la expresión: $$\color{Red} m = \frac{y_2 - y_1}{x_2 - x_1} $$
 Escena interactiva.
Escena interactiva.
Observa la pendiente $m$ de la línea recta.
 Desplaza el punto rojo o azul, o ingresa los valores de cada uno y oprime "enter <┘", observa el resultado de la pendiente.
Desplaza el punto rojo o azul, o ingresa los valores de cada uno y oprime "enter <┘", observa el resultado de la pendiente.
¿Qué se puede concluir si $m > 0$, si $m < 0$, o si $m = 0$?
Si se tienen dos puntos que pertenecen a una recta se puede hallar la función lineal (ecuación de la recta) que pasa por estos puntos aplicando el método conocido como punto- pendiente
Primero se halla la pendiente y luego aplicamos la expresión: $$\color{Red} y - y_1 = m (x - x_1)$$
 Escena interactiva.
Escena interactiva.
Observa y analiza otro procedimiento para encontrar la ecuación de la función lineal.
 Escribe los valores y oprime "enter <┘". Puedes comprobar las respuestas utilizando la calculadora.
Escribe los valores y oprime "enter <┘". Puedes comprobar las respuestas utilizando la calculadora.
La representación gráfica de una función constante es una recta paralela al $eje\space x$, cuya expresión algebraica es de la forma: $$y = k$$ donde $k$ es una constante, y su valor es un número real.
 Escena interactiva.
Escena interactiva.
Observa y analiza la gráfica de la función constante.
Modifica el valor de $k$, observa la función $\space\space y = k$
Responde a las preguntas que encontrarás en la página siguiente.

| a) $y = -2x + 1\space\space$ | b) $y = 0.5x - 1\space\space$ | c) $y = -x\space\space$ | d) $y = -1.5$ |
| a) $y = -2x + 3\space\space$ | b) $y = 3x\space\space$ | c) $y = 3x + 5$ |
Verifica las respuestas en la siguiente escena.
Iniciemos recordando la ecuación general de la recta, la función lineal.Véase Libro electrónico: Función lineal, cuadrática y volúmenes
La ecuación $Ax + By + C = 0$ donde $A,B$ y $C$ son números reales y $A,B$ no son simultáneamente nulos, se conoce como la ecuación general de primer grado en las variables $x$ e $y$.
La ecuación explícita de la recta cuando se conocen dos puntos excluye las rectas paralelas al eje y, cuyas ecuaciones son de la forma $x = constante$, pero todas las rectas del plano, sin excepción, quedan incluidas en la ecuación $Ax + By + C = 0$ que se conoce como la ecuación general de la línea recta.
Teniendo presente la expresión anterior, se tiene que:
El coeficiente de la $x$ es la pendiente $ m = \frac{-A}{B}$ y la ordenada o intersección con el $eje\space y$ es $b = \frac{-C}{B} $
El término independiente b, se llama ordenada en el origen de una recta, siendo (0, b) el punto de corte con el eje de ordenadas.
 Escena interactiva.
Escena interactiva.
Se tiene la función lineal en forma general, encuentra el valor de la pendiente.
Escribe en los recuadros el valor que corresponde a la pendiente de la función dada y oprime "enter <┘"


Posiciones relativas entre rectas planas
Rectas paralelas. Sean $ m_1$ y $m_2 $ pendientes de dos rectas respectivamente, entonces las rectas son paralelas si sus pendientes son iguales, $ m_1 = m_2 $. Observa un ejemplo en la gráfica siguiente.
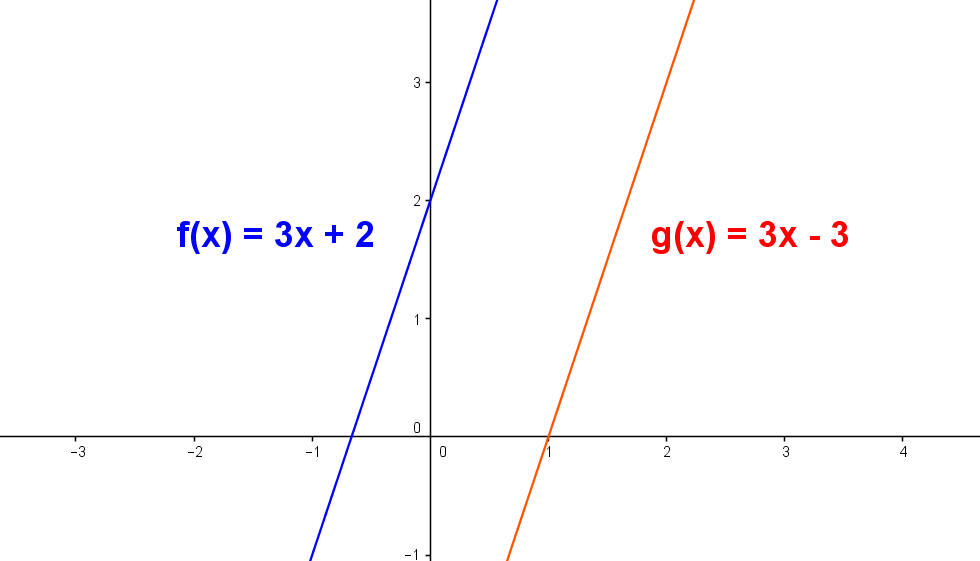
Rectas perpendiculares. Dos rectas en el plano son perpendiculares si el producto de sus pendientes $ m_1 $ y $ m_2 $ son tales que cumplen que: $ m_1 . m_2 = -1 $.
Por ejemplo, la pendiente de una recta es $ m_1 = 3 $. y la pendiente de la otra recta es $ m_2= \frac{-1}{3} $. por tanto $ m_1 . m_2 = \frac{-1}{3} . 3 = \frac{-3}{3} = -1 $, con lo cual se verifica la perpendicularidad, observa en la gráfica siguiente.
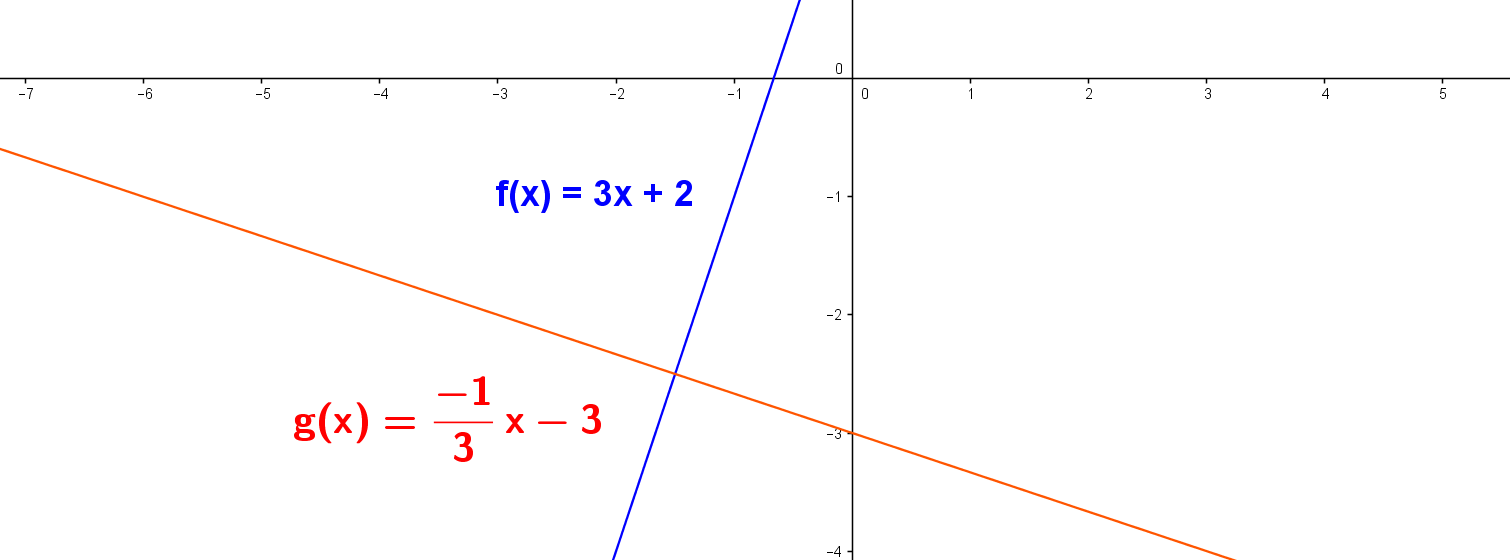
Rectas secantes: Se cortan en un punto en común, por tanto sus pendientes son distintas.
Rectas coincidentes: Tienen los mismos coeficientes. Las rectas coincidentes son dos líneas rectas que se ubican en un mismo plano, tienen todos sus puntos en común, es decir, se ubican una sobre la otra.
Ahora, verifica como son las rectas entre si con la escena interactiva.
 Escena interactiva.
Escena interactiva.
Ingresa los coeficientes de cada recta y oprime "enter <┘". Para ver la gráfica de las rectas, oprime el botón solución.
Una ecuación lineal es una igualdad matemática entre dos expresiones algebraicas, denominadas miembros, en las que aparecen elementos conocidos y desconocidos.
 Escena interactiva.
Escena interactiva.
Soluciona ecuaciones de primer grado (lineales).

 Escena interactiva.
Escena interactiva.
Planteamiento de problemas con ecuaciones lineales.
Indicaciones
Observa el planteamiento de los siguientes problemas.
 Oprime el botón más ejemplos para ver otros problemas o el botón datos diferentes para cambiar los datos del problema.
Oprime el botón más ejemplos para ver otros problemas o el botón datos diferentes para cambiar los datos del problema.
Un sistema de ecuaciones está formado por dos o más ecuaciones con dos incógnitas en la que deseamos encontrar una solución común, que corresponde a un punto $(x,y)$ que verifica todas las ecuaciones a la vez.
Se tomará la ecuación lineal, expresada en la forma: $$\color{red} ax + by = c$$
donde $a, b$ y $c$ son números reales y las variables $x$, $y$ las incógnitas.
Los sistemas de solución de ecuaciones, también conocidos como:
Métodos de solución.
1. Método de Reducción.
El método consiste en multiplicar una o las dos ecuaciones por algún número de modo que obtengamos un sistema en que los coeficientes de $x$ o de $y$ sean iguales y de signo contrario, para eliminar dicha incógnita al sumar las dos ecuaciones.
2. Método de Sustitución.
El Método consiste en despejar una de las incógnitas de una de las ecuaciones y reemplazar este valor en la otra ecuación, de esta forma se llega a una ecuación de primer grado con una incógnita.
3. Método de Igualación.
El método consiste en una pequeña variante del de sustitución. Para resolver un sistema de ecuaciones hay que despejar una incógnita, la misma, en las dos ecuaciones e igualar el resultado de ambos despejes, con lo que se obtiene una ecuación de primer grado con una incógnita.
4. Método Gráfico.
Nos vamos a centrar en esta ocasión en el método gráfico, para resolver un sistema de dos ecuaciones lineales con dos incógnitas.
Las variables $x$ y $y$ son las incógnitas, que nos darán como solución el punto común $(x, y)$ entre las rectas graficadas. Tener presente:
Observa ejemplos de la solución gráfica de un sistema de ecuaciones 2 x 2 en la siguiente escena interactiva.
 Escena interactiva.
Escena interactiva.
Solución método gráfico de un sistema de ecuaciones lineales.
Se pueden presentar los posibles casos:
 Observa ejemplos de los métodos de reducción, sustitución e igualación. Escenas interactivas adaptada por el autor.
Véase. Proyecto Descartes.org, ed@d, matemáticas.
Observa ejemplos de los métodos de reducción, sustitución e igualación. Escenas interactivas adaptada por el autor.
Véase. Proyecto Descartes.org, ed@d, matemáticas.

Resuelve el siguiente sistema de ecuaciones lineales.
 Verifica la solución utilizando el método gráfico. Ingresa los coeficientes $a, b, c, e, d$ y $f$ respectivamente del sistema
Verifica la solución utilizando el método gráfico. Ingresa los coeficientes $a, b, c, e, d$ y $f$ respectivamente del sistema
y oprime el botón solución para ver la solución gráfica.
 Identificar y resolver problemas que se ajustan a funciones cuadráticas mediante soluciones gráficas y analíticas
que establecer relaciones entre variables.
Identificar y resolver problemas que se ajustan a funciones cuadráticas mediante soluciones gráficas y analíticas
que establecer relaciones entre variables.
Aprenderás a:
 Escena interactiva.
Escena interactiva.
Analiza la siguiente escena interactiva de la función $y = x^2$.
Analiza las dos escenas interactivas que se muestran a continuación, y responde a las preguntas que encontraras en la página siguiente.
 Escena interactiva.
Escena interactiva.
Mueve el punto azul y aumenta o disminuye el número de decimales con ayuda del control de la escena.

 Escena interactiva.
Escena interactiva.
Mueve el punto azul y aumenta o disminuye el número de decimales con ayuda del control de la escena.

1. ¿Cuál de las dos gráficas corresponde a una función? ¿Por qué?
2. ¿Cuál es la imagen de $x=2$ en cada una de las dos gráficas?
La parábola es la gráfica de la función cuadrática o polinomio de segundo grado, cuya ecuación general es: $$\color{red} y = ax^2 + bx + c $$
donde a, b y c son números reales.
Aparece en numerosos fenómenos naturales o, cuando menos frecuentes, en nuestras ciudades: el caño de una fuente, la trayectoria que describe un balón de fútbol en un golpe franco, el movimiento de un proyectil disparado por un cañón,...
Las parábolas se conocen comúnmente como las gráficas de funciones cuadráticas. Definición geométrica de la parábola:
La parábola es el conjunto de los puntos del plano que se encuentran a la misma distancia de un punto fijo llamado Foco (F) y la directriz (d)
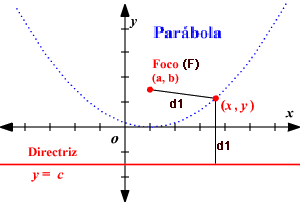
El eje focal es el eje perpendicular a la directriz(d) que pasa por el foco(F). El punto de la parábola que pertenece al eje focal se llama vértice.
La directriz (d), es la línea recta perpendicular al eje focal que se ubica a una distancia $c$ del vértice y fuera de la parábola (Figura 1.3).
 Escena interactiva.
Escena interactiva.
Representación gráfica de la parábola $\color{red} y = x^2$.
Con el mouse, puedes desplazar el punto P a lo largo de la parábola y comprobar que la distancia de P al foco F y a la recta d es siempre la misma.
En el gráfico tienes representada la parábola cuya directriz es la recta $y = -\frac14$ y cuyo foco es el punto $F(0,\frac14)$.
Decimos que la ecuación de esta parábola es incompleta, esto se debe a que no aparecen los términos $bx$ y $c$, es decir $b = c = 0$.
 Escena interactiva.
Escena interactiva.
Observemos el gráfico de la parábola $\quad \color{red}y = ax^2$
Mueve el control a, observa que sucede con la gráfica de la parábola.
Responde las preguntas a continuación con ayuda de la escena interactiva.

Observa que si $x = 0$ entonces $y = 0$. Comprueba que todas estas parábolas cortan siempre, y en un único punto, al eje $x$; ese punto es el origen de coordenadas.

A la recta por la que, doblando el papel, permitiría superponer las dos mitades o ramas de la parábola, se le llama eje de simetría.
La parábola $y=ax^2$ es una curva simétrica respecto de $x=0$, de modo que dibujando una mitad hasta el vértice, podemos obtener la otra rama como si de un espejo se tratara. Puedes comprobarlo también de forma analítica.
 Escena interactiva.
Escena interactiva.
Observemos el gráfico de la parábola $\quad \color{red}y = ax^2$.
 Mueve el control a, observa y responde las preguntas de la página siguiente.
Mueve el control a, observa y responde las preguntas de la página siguiente.
Observa que hemos tomado valores de x que son simétricos respecto al origen que es el vértice, es decir: $$x = 1,\quad x = -1 $$ $$x = 2,\quad x = -2$$

Además, desplaza el punto $P$ y comprueba que los puntos de la tabla se encuentran sobre la gráfica y que, efectivamente, son simétricos.
 Escribe un valor para $a$ y completa la siguiente tabla, puedes comprobar con la escena interactiva anterior:
Escribe un valor para $a$ y completa la siguiente tabla, puedes comprobar con la escena interactiva anterior:
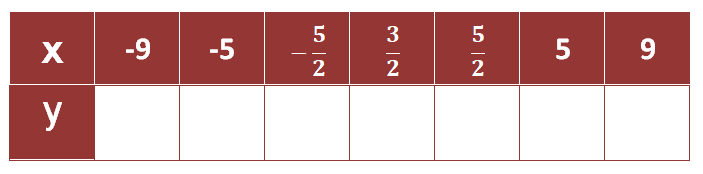

La ecuación de esta parábola también es incompleta con $a=\not 0$, pero ahora solo falta el término $bx$, es decir, $b = 0$.
 Escena interactiva.
Escena interactiva.
Observemos el gráfico de la parábola $\quad \color{red}y = ax^2 + c$.
Mueve los controles a y c, observa y responde las preguntas.
Igual que antes se han considerado valores de $x$ simétricos respecto al vértice. Con el puntero del ratón, puedes comprobar la simetría, y también se puede ver en la tabla de valores.
En la escena interactiva, cambia los valores de $a$ y $c$ para ver las simetrías.
Igual que en el caso anterior, analiza y a partir de las preguntas y la experimentación propuesta responde.

 Escribe un valor para $a$, $c$ y completa la siguiente tabla, puedes comprobar con la escena interactiva anterior:
Escribe un valor para $a$, $c$ y completa la siguiente tabla, puedes comprobar con la escena interactiva anterior:

De nuevo, la ecuación de esta parábola también es incompleta con $a=\not 0$. Ahora falta el término $c$; tenemos entonces $c = 0$.
 Escena interactiva.
Escena interactiva.
Observemos el gráfico de la parábola $\quad \color{red}y = ax^2 + bx$.
Mueve los controles a y b, observa y responde las preguntas.
Igual que en el caso anterior, analiza y a partir de las preguntas y la experimentación propuesta responde.

 Ahora observa el siguiente análisis:
Ahora observa el siguiente análisis:
Si los puntos de corte con el eje $x$, al estar sobre dicho eje, deben tener su coordenada $y = 0$; es decir, se verificará que:
$$a x^2 + b x = 0 $$entonces, si resolvemos esta ecuación, obtendremos los valores de $x$ a los cuales corresponde $y = 0$.
Procedamos así, sacamos factor común $x$ y tendremos que:
$$( a x + b ) x = 0$$ $$entonces,\space ( a x + b ) = 0 \quad y \quad x = 0$$por tanto, una de las soluciones es $x = 0$, con lo cual, uno de los puntos de corte es el origen de coordenadas $(0,0)$.
La otra solución se obtendrá a partir de, $$a x + b = 0$$ $$a x = -b$$ $$x = \frac {-b}{a}$$ por lo tanto, el otro punto de corte tendrá coordenadas $( -\frac {b}{a}, 0 )$.

 Escribe un valor para $a$, $b$ y completa la siguiente tabla, puedes comprobar con la escena interactiva anterior:
Escribe un valor para $a$, $b$ y completa la siguiente tabla, puedes comprobar con la escena interactiva anterior:
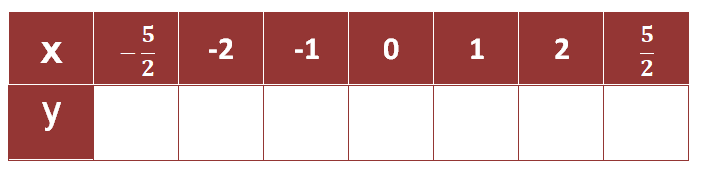

¡Recuerda!
Primero realizar los cálculos y luego verifica los resultados con ayuda de las escenas interactivas.
 Escena interactiva.
Escena interactiva.
Observemos el gráfico de la parábola $\quad \color{red}y = ax^2 + bx$.
Mueve los controles a y b, observa y responde las preguntas.
¿Identificas el eje de simetría?
Línea imaginaria que divide la parábola en dos partes iguales.
Vamos a ver, por fin, la función cuadrática completa, es decir, la función donde los coeficientes $a, b$ y $c$ son números reales distintos de cero.
 Escena interactiva.
Escena interactiva.
Observemos el gráfico de la parábola $\quad \color{red}y = ax^2 + bx + c$.
Mueve los controles a, b y c, observa los cambios en la gráfica.
Responde las preguntas a continuación con ayuda de la escena interactiva.

 Sugerencia.
Sugerencia.
Utilizando la escena interactiva de la página anterior.
 Para los numerales 5, 6 y 7, resuelve las ecuaciones de las parábolas obtenidas y encuentra la cantidad de soluciones.
Para los numerales 5, 6 y 7, resuelve las ecuaciones de las parábolas obtenidas y encuentra la cantidad de soluciones.
¿Cuántas soluciones obtienes en cada numeral?
El vértice de la parábola
Ya se debe saber que el vértice de la parábola está situado siempre sobre el eje de simetría de la misma y, además después de responder al numeral 8, se tiene que dicho vértice tiene por abscisa $x=-\frac {b}{2a}$, por tanto la ordenada del vértice se obtiene sustituyendo el valor $x$ en la ecuación de la parábola.
El vértice $(x,y)$ de la parábola se identificará como el punto $v(h,k)$.

 Escena interactiva.
Escena interactiva.
Observemos los principales datos de una parábola de la forma: $\color{red}y = ax^2 + bx + c$.
Mueve los controles a, b y c, observa y responde las preguntas.

Se pueden aprovechar todos los conceptos ya vistos (simetría, vértice, corte con los ejes,...) para representar de forma sencilla y eficaz cualquier parábola.

En efecto, podemos seguir los siguientes pasos:
Ya sea ha estudiado la parábola de la forma $y = a x^2 + b x + c $ en detalle paso a paso, de modo que debemos conocer bastante bien y como encontrar todos sus datos.
Ahora vamos a practicar lo aprendido en esta sección con la actividad siguiente.

 Elige una ecuación de una función cuadrática, grafícala y encuentra todos los elementos de esta.
Elige una ecuación de una función cuadrática, grafícala y encuentra todos los elementos de esta.
 Escena interactiva.
Escena interactiva.
Comprueba tu respuesta con la escena interactiva que aparece al pulsar el botón Respuesta.

¡Recuerda!
Puedes hacer el ejercicio cuantas veces desees, primero realizar los cálculos y luego verifica los resultados con ayuda de la escena interactiva.
Se han trabajado los principales conceptos, relaciones y gráficas de $$\color{red}y = ax^2 + bx + c$$
Ahora, centrémonos en el vértice y observemos otra expresión que relaciona el vértice en la ecuación de la parábola, esta expresión es: $$\color{red}y = a(x - h)^2 + k$$ donde $h$ y $k$ corresponden respectivamente al punto en el eje $x$ y al punto en el eje $y$ del vértice, es decir, el vértice tiene de coordenadas $(h, k)$. El punto $a$ indica la abertura hacia arriba o hacia abajo de la parábola y cuanto más se aleje su valor del cero, la curva tendrá una abertura más pequeña.
 Pero veamos de donde sale esta expresión, sea:
$$\color{red}ax^2 + bx + c = 0$$
Agrupando los términos con variable $x$ y sacando factor común,
Pero veamos de donde sale esta expresión, sea:
$$\color{red}ax^2 + bx + c = 0$$
Agrupando los términos con variable $x$ y sacando factor común,
En la fórmula $\quad \displaystyle (ax^2 + bx) + c = a(x^2 + \frac{b}{a}x) + c = 0 $
completamos el cuadrado perfecto, ¿recuerdas cómo?, es decir, sumamos y restamos la misma expresión para no alterar la ecuación, en este caso es $(\frac{b}{2a})^2$, recuerda que se tiene que multiplicar por $a$, el término fuera del trinomio. $$ a \bigg(x^2 + \frac{b}{a}x + (\frac{b}{2a})^2 \bigg) + c - a \bigg(\frac{b}{2a}\bigg)^2 = 0 $$
Ahora, factorizamos el trinomio cuadrado $(x^2 + \frac{b}{a}x + (\frac{b}{2a})^2)$, el cuál corresponde a un trinomio cuadrado perfecto: $$ a \bigg(x + \frac{b}{2a} \bigg)^2 + c - a \bigg(\frac{b}{2a} \bigg)^2 = 0 $$ por lo tanto, se tiene que $\quad h = -\frac{b}{2a} \quad y \quad k = c - a (\frac{b}{2a} )^2$
Entonces, se obtiene la expresión en términos del vértice $(h,k)$ $$\color{red}y = a(x - h)^2 + k$$

 Escena interactiva.
Escena interactiva.
Comprueba tu respuesta con la escena interactiva que aparece al pulsar el botón Respuesta.

Secciones cónicas
Una sección cónica es la curva resultante de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice,
Se clasifican en cuatro tipos de cónicas: elipse, parábola, hipérbola y circunferencia, ver el gráfico a continuación:
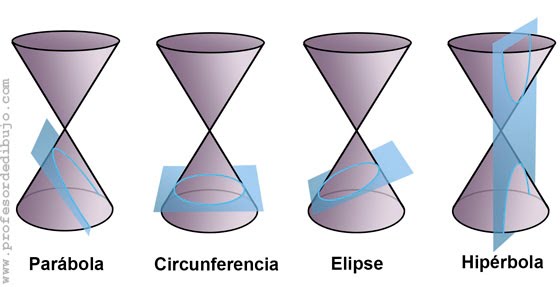
Las cónicas se representan mediante ecuaciones de segundo grado con dos incógnitas.
La ecuación general que representa una sección cónica, es una ecuación cuadrática con variables $x$ y $y$ de la forma: $$\color{red}Ax^2 + By^2 + Cx + Dy + E + Fxy= 0$$ en la que $A$ y $B$ no pueden ser cero al mismo tiempo, se va a trabajar con el coeficiente de $xy=0$ por simplicidad.
Ahora nos vamos a centrar en la expresión que genera una parábola, y que nos representa una función, en este caso se hará el análisis para cuando se tiene que $A =\not 0$, $D =\not 0$ y $B = 0$. ¿Qué sucede cuando pasa lo contrario, $A = 0$ y $B =\not 0$.
Para nuestro caso cuando $B = 0$, se tiene que la expresión es: $$\color{red}Ax^2 + Cx + Dy + E = 0$$ la cual corresponde a una parábola vertical con abertura hacia arriba o hacia abajo, que determina una función ( Ver 3D).
Cuando en la ecuación $Ax^2 + Cx + Dy + E = 0$ se completa el trinomio cuadrado perfecto para la variable $x$, se obtiene la ecuación llamada canónica de una parábola vertical, de la forma: $$\color{red}(x - h)^2 = 4p(y - k)$$ donde el punto v(h,k) corresponde al vértice de la parábola y p la distancia del vértice al foco o del vértice a la directriz.
Analiza el proceso que se realizó para obtener la ecuación canónica.
 ¡Recordemos!
¡Recordemos!
Una parábola consta de lo siguientes elementos:
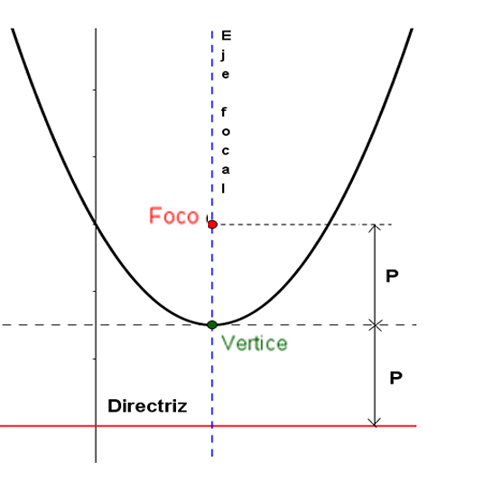
Ejemplo.
Observa el procedimiento para pasar a la ecuación canónica:

 Dada la ecuación general $\color{red}Ax^2 + Cx + Dy + E = 0$, encuentra su ecuación canónica, gráfica y los elementos de la parábola.
Dada la ecuación general $\color{red}Ax^2 + Cx + Dy + E = 0$, encuentra su ecuación canónica, gráfica y los elementos de la parábola.
 Escena interactiva.
Escena interactiva.
Realiza todos los cálculos antes y comprueba tu respuesta con la escena interactiva.
¿Si conozco el vértice $v(-2,-4)$ y el foco $F(-2,-7)$, puedo encontrar la ecuación general?
La función cuadrática o también conocida como ecuación de segundo grado, donde $\color{red}y = f(x)$, se puede expresar de la forma: $$\color{red}f(x) = a x^2 + bx + c$$
 La ecuación cuadrática es la ecuación: $f(x)=0$ que puede tener una solución real doble, o dos números reales o dos números complejos.
La ecuación cuadrática es la ecuación: $f(x)=0$ que puede tener una solución real doble, o dos números reales o dos números complejos.
Para resolver o encontrar las soluciones de la ecuación cuadrática $$\color{red}a x^2 + bx + c = 0$$ se puede:
Entonces, se puede presentar uno de los siguientes casos, si:
 ¡Recuerda!
¡Recuerda!
La ecuación cuadrática presentar las posibles soluciones:
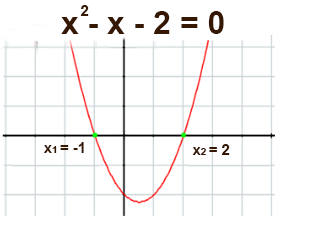
En la figura se ve la solución gráfica de la ecuación $f(x) = x^2 - x - 2$, donde tiene dos soluciones reales diferentes
$x_1 = -1$ y $x_2 = 2$, que corresponden a los cortes con el eje $x$.
 Escena interactiva.
Escena interactiva.
Observemos la solución de la ecuación $\quad \color{red}ax^2 + bx + c = 0$.


Escena interactiva.
 Con las indicaciones dadas, encuentra la solución de la ecuación cuadrática aplicando uno de los métodos.
Con las indicaciones dadas, encuentra la solución de la ecuación cuadrática aplicando uno de los métodos.
Verifica la solución en la escena interactiva.
Piensa. ¿Cómo se debe lanzar verticalmente una pelota, para que alcance la máxima distancia horizontal?, ¿cómo se llama esta trayectoria? ¿Desde las matemáticas, cómo se puede interpretar este movimiento?
Veamos las siguientes situaciones aplicadas a la física.

Situación Problema 1.
Observa en la siguiente escena la curva que se describe, cuando se lanzada verticalmente con una determinada velocidad una pelota.
 Escena interactiva.
Escena interactiva.
Modifica el control de la velocidad y oprime el botón animar

Situación Problema 2.
 Modifica el control de la velocidad y oprime animar para ver la trayectoria de la pelota.
Modifica el control de la velocidad y oprime animar para ver la trayectoria de la pelota.
 Escena interactiva.
Escena interactiva.
Ingresa los valores de Y max y t vertice, oprime "enter <┘" para ver los resultados y verifica en la escena interactiva.


Situación Problema 3.
 Se va a realizar un cercado para un área rectangular, expresada mediante una función cuadrática.
Se va a realizar un cercado para un área rectangular, expresada mediante una función cuadrática.
Oprime en botón animar, realiza los cálculos y verifica en la escena interactiva las respuestas.
 Escena interactiva.
Escena interactiva.
Ingresa los resultados de la medida de los lados y el total del Área encontrada, oprime "enter <┘" para ver los resultados.
Rojas, C., Restrepo, C., Herrera, H., Córdoba, F., Cardeño, J. (2013).Objetos virtuales de aprendizaje –OVA–. 1° Versión. Fondo Editorial ITM. Medellín
Rojas, C., Restrepo, C., Correa, D., Castrillón, E., Ortiz, H., Herrera, H., Córdoba, F., Cardeño, J. (2012). Función lineal, cuadrática y volúmenes. Guía para docentes. Fondo Editorial ITM. Medellín
Ruiz, C. (2014). Proyectodescartes.org-EDAD. Obtenido de: http://proyectodescartes.org/EDAD/materiales_didacticos
Abreu L., José y Muñoz P., (2004). Proyectodescartes.org-Telesecundaria. Obtenido de: http://proyectodescartes.org/Telesecundaria/materiales_didacticos
Barbero, E. (2004). ProyectoDescartes.org. Obtenido de: http://proyectodescartes.org/uudd/materiales_didacticos
Ramírez, M. (2011). Álgebra y Trigonometría. Caldas(Ant.) Corporación Universitaria Lasallista. 315 pag.