Matemáticas Básicas
Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
Título de la obra:
Matemáticas Básicas
Autor:
Carlos Alberto Rojas Hincapié
Actualización: Joel Espinosa Longi
Imagen portada: Education cartoon vector created by pch.vector - www.freepik.com
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Nunito y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Actualización: Joel Espinosa Longi
Núcleo del libro interactivo: julio 2022
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56476-1-9
De la colección iCartesiLibri surge este libro digital interactivo, diseñado de tal forma que permita el aprendizaje significativo a través de la intervención directa y personal del usuario, el cual se convierte en el protagonista del libro, en tanto que podrá interactuar con algunos objetos de aprendizaje. Estos objetos de aprendizaje interactivos fueron diseñados con el editor DescartesJS.
La herramienta Descartes se caracteriza por una innata interactividad, por permitir realizar representaciones de objetos bi y tridimensionales, por gestionar expresiones de texto y de fórmulas, por integrar objetos multimedia como imágenes, audios y vídeos, por tener la posibilidad de reflejar casos concretos y también potenciar la conceptualización de tareas y procedimientos mediante la utilización de semillas aleatorias y controles numéricos, gráficos y de texto, y con ellos poder abordar la evaluación de manera automática, tanto la correctiva como la formativa. Con Descartes es posible el diseño y desarrollo de objetos educativos que promueven el aprendizaje significativo, posibilitando esa deseada construcción del conocimiento.Véase http://proyectodescartes.org/iCartesiLibri/descripcion.htm.
Todos los recursos incluidos en este libro se basan en el estándar HTML y consecuentemente son plenamente accesibles y operativos en cualquier ordenador, tableta o smartphone sin más que utilizar un navegador compatible con dicho estándar. Diseñar en HTML, significa que usaremos:
El sistema de los Números Reales lo conforman los siguientes conjuntos numéricos:

Se denomina el conjunto de los Números Naturales o enteros positivos. Están definidas las siguientes operaciones básicas: adición y multiplicación. El conjunto de los Números Naturales surgió de la necesidad de contar, lo cual se manifiesta en el ser humano desde sus inicios. Este conjunto se caracteriza porque tiene un número ilimitado de elementos
El Conjunto de los Números Enteros surge de la necesidad de dar solución general a la sustracción, pues cuando el sustraendo es mayor que el minuendo, esta sustracción no tiene solución en los Números Naturales (por ejemplo: $5 - 20 = ¿?$). Debido a esto, la recta numérica se extiende hacia la izquierda, de modo que a cada punto que representa un número natural le corresponda un punto simétrico, situado a la izquierda del cero. Punto simétrico es aquel que está ubicado a igual distancia del cero (uno a la derecha y el otro a la izquierda de él). Se dividen en:
Enteros Negativos: $\mathbb{Z}^-$, Enteros Positivos: $\mathbb{Z}^+$ y el Cero: $\{0\}$
Por lo tanto, el conjunto de los Números Enteros es la unión de los tres subconjuntos mencionados: $\mathbb{Z} = \mathbb{Z}^- \cup \{ 0 \} \cup \mathbb{Z}^+$
El conjunto de los Números Racionales se creó debido a las limitaciones de cálculo que se presentaban en el conjunto de los Números Naturales y Números Enteros. Para solucionar esta dificultad, se creó este conjunto, el cual está formado por todos los números de la forma $\frac{a}{b}$. Esta fracción en la cual el numerador es $a$ y el denominador $b$ donde $a$, $b$ son números enteros con $b$ distinto de cero.
Este conjunto se representa gráficamente, dividiendo cada intervalo de una recta numérica en espacios iguales, que representen números enteros.
Observa la representación en la recta de fracciones propias e impropias.
Cada una de estas subdivisiones representa una fracción con denominador igual al número de partes de la subdivisión. Cada fracción es un número racional y cada número racional consta de infinitas fracciones equivalentes.
Conjunto de Números Decimales Infinitos no Periódicos. Este conjunto surgió de la necesidad de reunir a ciertos números que no pertenecen a los conjuntos anteriores; entre ellos se pueden citar a las raíces inexactas, el número Pi ($\pi$), etc. A él pertenecen todos los números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción.
No deben confundirse con los números racionales, porque éstos son números decimales finitos, infinitos periódicos e infinitos semi periódicos que sí pueden transformarse en una fracción.
El sistema de los números reales esta conformado por la unión del conjunto de los números racionales y el conjunto de los números irracionales: $\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}^*$.
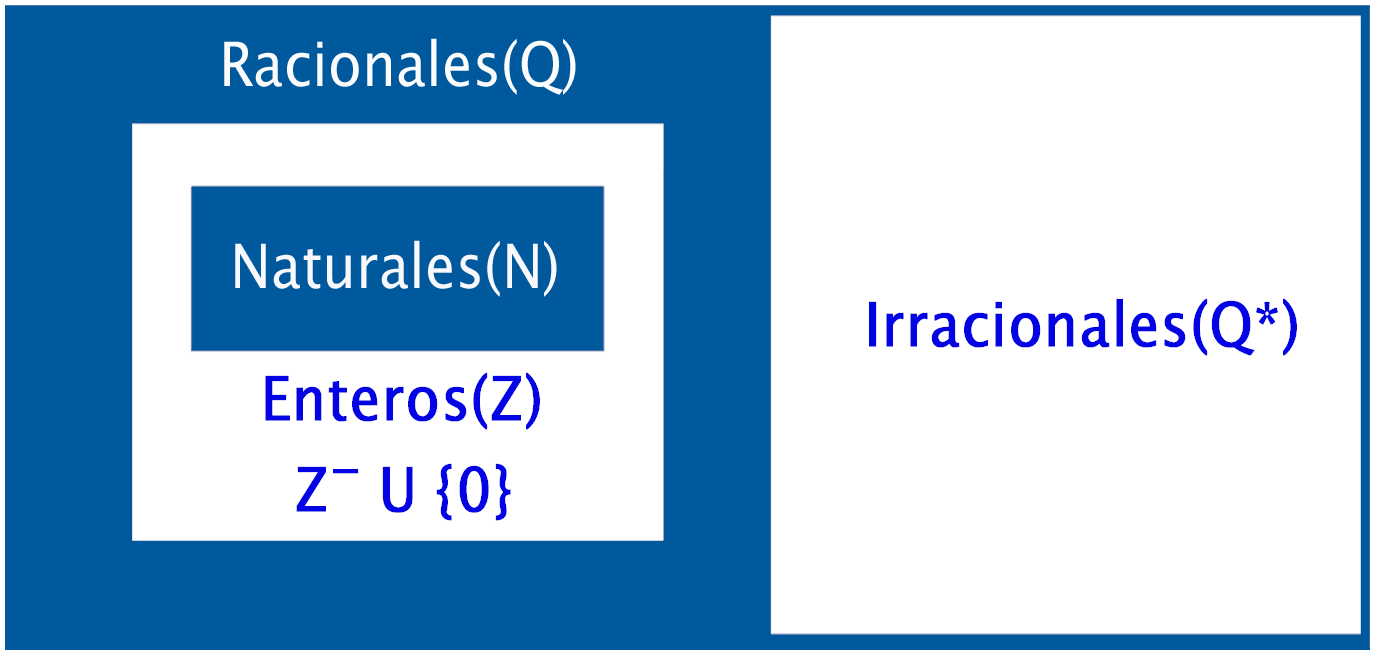
Representación gráfica del conjunto de los números reales.
Todos los conjuntos numéricos pueden ser representados en la recta numérica.
 jercicio 1: Identifica a que conjunto numérico pertenece el número dado. Oprime el botón correspondiente al conjunto numérico al cual pertenece el numero dado, $\mathbb{N}$ (Naturales), $\mathbb{Z}$ (Enteros), $\mathbb{Q}$ (Racional), $\mathbb{Q}^*$ (Irracional) o $\mathbb{R}$ (Real) y verifica tu respuesta.
jercicio 1: Identifica a que conjunto numérico pertenece el número dado. Oprime el botón correspondiente al conjunto numérico al cual pertenece el numero dado, $\mathbb{N}$ (Naturales), $\mathbb{Z}$ (Enteros), $\mathbb{Q}$ (Racional), $\mathbb{Q}^*$ (Irracional) o $\mathbb{R}$ (Real) y verifica tu respuesta.
 jercicio 2: Clasifica cada uno de los siguientes números en el recuadro correspondiente al conjunto numérico, ubicándolos en el conjunto más pequeño al que pertenezcan:
jercicio 2: Clasifica cada uno de los siguientes números en el recuadro correspondiente al conjunto numérico, ubicándolos en el conjunto más pequeño al que pertenezcan:
 jercicio 3: Resuelve los siguientes ejercicios con su debido procedimiento.
jercicio 3: Resuelve los siguientes ejercicios con su debido procedimiento.
En la nomenclatura de la potenciación se diferencian tres partes, la base, el exponente y la potencia.
Una potencia es el resultado de multiplicar un número por sí mismo varias veces. El número que multiplicamos se llama base, el número de veces que multiplicamos la base se llama exponente.

El exponente determina la cantidad de veces que la base se multiplica por sí misma:
Ejemplos:
 xploremos
xploremos
1. Ingresa la base y el exponente indicado, oprime la tecla “intro” y verifica.
2. Verifica ingresando la base y el exponente del ejercicio propuesto y escribe la potencia, (recuerda $(B)^E = P$), oprime la tecla “intro” para verificar.
Las propiedades de la potenciación son válidas para todos los conjuntos numéricos.
Todo número diferente de cero, elevado al exponente cero, es igual a uno:
$$a^0 = 1$$Todo número diferente de cero, elevado al exponente uno, es igual a el mismo:
$$a^1 = a$$ xploremos
xploremos
Verifica lo aprendido en esta sección por medio de un paso a paso.
Recuerda, una potencia que tiene de base una potencia, se coloca la misma base y se multiplican los exponentes.
 jercicio 1: Da clic en el botón “Ejercicio”, soluciona en tu cuaderno, escribe el exponente, la base y pulsa la tecla “intro” y verifica tu respuesta.
jercicio 1: Da clic en el botón “Ejercicio”, soluciona en tu cuaderno, escribe el exponente, la base y pulsa la tecla “intro” y verifica tu respuesta.
 jercicio 2: Mide tus conocimientos de lo aprendido en esta sección y responde las siguientes preguntas seleccionando la respuesta correcta.
jercicio 2: Mide tus conocimientos de lo aprendido en esta sección y responde las siguientes preguntas seleccionando la respuesta correcta.
Las expresiones radicales son expresiones que incluyen un radical, el cual es el símbolo de calcular una raíz.
En la nomenclatura de la radicación se tienen las siguientes partes:
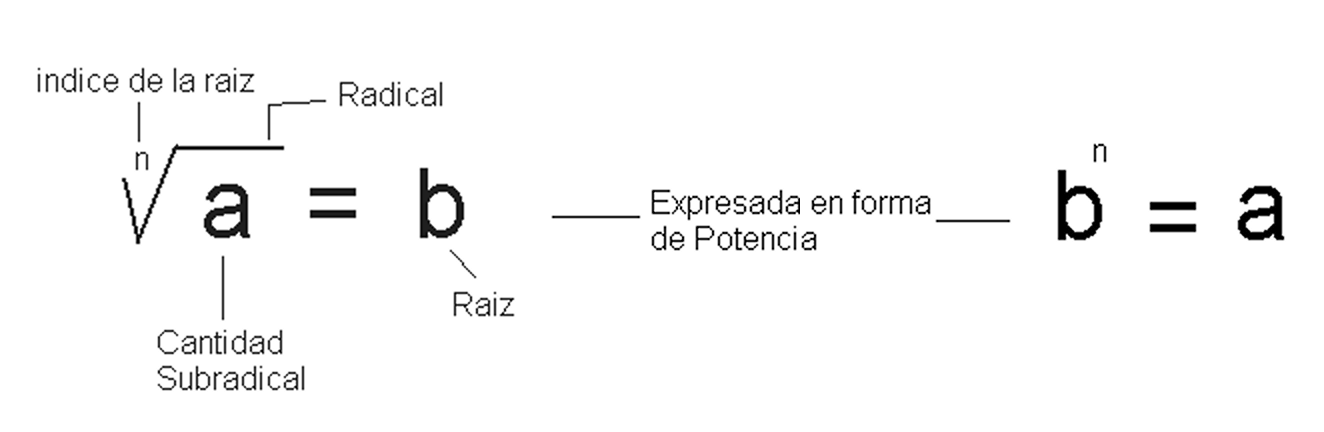
Para operar sumas o restas de expresiones radicales, deben tener el mismo índice y el mismo radicando, o sea radicandos semejantes.
Resuelva expresiones radicales de suma y resta. ingresa el coeficiente numérico y el valor del radical, pulsa la tecla “intro” y observa la solución.
Para simplificar expresiones radicales, buscamos términos exponenciales dentro del radical, donde usamos la factorización o descomposición en factores primos y aplicamos las reglas de los exponentes.
Se debe llevar a un índice común (m.c.m.) y se expresa en una sola raíz, simplificando la expresión si es posible, por ejemplo:
$$\large \dfrac{\sqrt[3]{4}}{\sqrt{2}} = \dfrac{\sqrt[3 \times 2]{4^2}}{\sqrt[2 \times 3]{2^3}} = \dfrac{\sqrt[6]{4^2}}{\sqrt[6]{2^3}} = \dfrac{\sqrt[6]{2^4}}{\sqrt[6]{2^3}} = \sqrt[6]{\dfrac{2^4}{2^3}} = \sqrt[6]{2}$$ jercicios
jercicios
1. Resuelve y simplifica en tu cuaderno aplicando las propiedades vistas en el capítulo.
2. Resuelve y simplifica en tu cuaderno aplicando las propiedades vistas en el capítulo.
3. Mide tus conocimientos de lo aprendido en esta sección y responde las siguientes preguntas tipo ICFES:
Combinación de números, letras, signos de agrupación, con operaciones indicadas. Por ejemplo:
$$\dfrac{3a-5}{a+4}, \quad x^2-5x+2, \quad 2b+3, \quad 8y-3xy+2x$$Se llama término en una expresión algebraica, a cada parte de ella que viene a ser separada por el signo mas ($+$) ó el signo menos ($-$), los términos están formados por números y letras o expresiones combinadas multiplicadas entre sí (llamados factores). Por ejemplo:
$x^2-5x+2 \longrightarrow$ Expresión de tres términos
$2b+3 \longrightarrow$ Expresión de dos términos
$8y-3xy+2x-5 \longrightarrow$ Expresión de cuatro términos
El término puede tener factor literal y factor numérico o coeficiente numérico o coeficiente del término.
 xploremos
xploremos
Observa y explora las diferentes expresiones algebraicas.
Cuando un término en apariencia no presenta coeficiente numérico, como en la expresión algebraica $b - 4c$ en donde $b$ es el término que en apariencia no presenta el coeficiente numérico, se asume a la unidad $(1)$ como su coeficiente numérico. Luego el término $1b = b$.
Para conocer el valor numérico de una expresión algebraica, se sustituyen las letras por números reales y se efectúan operaciones.
Por ejemplo:
Aquéllas expresiones que poseen una misma parte, bien sea literal (letras) o radical (raíces). Por ejemplo:
$ab - 2ab \longrightarrow$ Términos semejantes, poseen la misma parte literal: $ab$
$\sqrt[3]{x}, 5 \sqrt[3]{x} \longrightarrow$ Términos semejantes, poseen la misma parte radical: $\sqrt[3]{x}$
Los términos semejantes pueden sumarse o restarse. Por ejemplo:
 jercicio: Simplificar términos semejantes en expresiones algebraicas cuando sea posible.
jercicio: Simplificar términos semejantes en expresiones algebraicas cuando sea posible.
 xploremos
xploremos
Verifica los conocimientos de lo visto en esta sección:
Son expresiones algebraicas con características especiales, así por ejemplo un polinomio en la variable $x$, es una expresión algebraica de la forma:
Algunos polinomios reciben nombres especiales de acuerdo con el número de términos que posean:
$5x^2 \longrightarrow$ Monomio (un término)
$2b+3 \longrightarrow$ Binomio (dos términos)
$8x^2 + 2x - 5 \longrightarrow$ Trinomio (tres términos)
Sean los polinomios: $P1 = x^3 + 2x^2 - 5x + 7$ y $P2 = 4x^3 - 5x^2 + 3$
Si a un signo de agrupación (paréntesis, llaves, corchetes) lo antecede un signo mas ($+$), al eliminar el signo de agrupación, todos los términos que haya dentro de él quedarán con los mismos signos, para el caso, que el signo de agrupación lo antecede un signo menos ($-$), o sea una resta, al eliminar el signo de agrupación todos los términos dentro de éste cambian de signo.
Nota: Al sumar o restar dos o más polinomios, se suman los términos semejantes de cada polinomio.
Modifica los coeficientes de cada polinomio y observa los resultados.
 xploremos
xploremos
Verifica los conocimientos de lo visto en esta sección:
Signos iguales: ($+$)
$$( + ) \cdot ( + ) = ( + )$$ $$( - ) \cdot ( - ) = ( + )$$Signos diferentes: ($-$)
$$( + ) \cdot ( - ) = ( - )$$ $$( - ) \cdot ( + ) = ( - )$$Para multiplicar polinomios entre sí, se aplica la propiedad distributiva, multiplicando cada término del primer polinomio por todo el segundo polinomio, ejemplo:
$$(3x + 4) \cdot (5x - 7) = 3x \cdot (5x - 7) + 4 \cdot (5x - 7)$$Se aplica a la parte literal, el producto de potencias de igual base:
$$b^m \cdot b^n = b^{m+n}$$Se aplica la propiedad distributiva.
$$( (3x) \cdot (5x) - (3x) \cdot 7 ) + ( 4 \cdot (5x) - 4 \cdot 7 )$$Suma de términos semejantes.
$$15x^2 - 21x + 20x - 28$$por lo tanto, tenemos que:
$$(3x + 4) \cdot (5x - 7) = 15x^2 - 1x - 28$$Se debe tener en cuenta la ley de los signos entre los términos a multiplicar, donde los positivos son aquéllos términos que los antecede un signo mas ($+$) ó aquéllos términos que en apariencia no poseen signo que los anteceda; y los negativos son aquéllos términos que los antecede un signo menos ($-$).
 xploremos
xploremos
Verifica los conocimientos de lo visto en esta sección:
Corresponden a productos especiales, destacables en operaciones matemáticas y que tienen su base en la potenciación de polinomios.
Corresponde al cuadrado del primer término, mas el doble producto del primer término por el segundo término, mas el cuadrado del segundo término, veamos como se genera:
$(a + b)^2 = (a + b) \cdot (a + b)$ ———————— Definición de potencia
$(a + b)^2 = a^2 + 2ab + b^2$
Ejemplo:
$$(2m + 3)^2 = (2m)^2 + 2 \cdot (2m) \cdot (3) + (3)^2 = 4m^2 + 12m + 9$$Corresponde al cuadrado del primer término, menos el doble producto del primer término por el segundo término, mas el cuadrado del segundo término, veamos como se genera:
$(a - b)^2 = (a - b) \cdot (a - b)$ ———————— Definición de potencia
$(a - b)^2 = a^2 - 2ab + b^2$
Ejemplo:
$$\begin{align*} (y - 5x)^2 &= (y)^2 - 2 \cdot (y) \cdot (5x) + (5x)^2 \\ &= y^2 - 10xy + 25x^2 \end{align*}$$Si se tienen tres o más términos, se agrupan y se aplica la misma definición:
$(a + b + c)^2 = [( a + b ) + c]^2 = a^2+b^2+c^2+2ab+2ac+2b$
Escribe los valores de los coeficientes y exponente, pulsa la tecla “intro” y observa el resultado cuando tienen diferentes exponentes dentro de los términos del binomio.
 xploremos
xploremos
Verifica los conocimientos de lo visto en esta sección:
Véase http://proyectodescartes.org/Telesecundaria/materiales_didacticos/3m_b01_t01_s01-JS/index.html.
Los binomios se desarrollan de la siguiente forma:
$(a + b)^0 = 1$
$(a + b)^1 = a + b$
$(a + b)^2 = a^2 + 2ab + b^2$
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$
$(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4$
Detallando el desarrollo de los binomios se tiene que:
Los términos simétricos tienen los mismos coeficientes, la simetría de los términos permite disponer los coeficientes de cada binomio en forma de un triángulo conocido como:
Triángulo de Pascal
$(a+b)^0$ = —————————————————————— 1 $(a+b)^1$ = ——————————————————— 1 1 $(a+b)^2$ = ———————————————— 1 2 1 $(a+b)^3$ = —————————————— 1 3 3 1 $(a+b)^4$ = ———————————— 1 4 6 4 1 $(a+b)^5$ = —————————— 1 5 10 10 5 1 $(a+b)^6$ = ———————— 1 6 15 20 15 6 1
Con este triángulo se puede deducir que:
Ejemplo:
$(m - 2n)^5 = (m)^5 - 5(m)^4(2n) + 10(m)^3(2n)^2 - 10(m)^2(2n)^3 + 5(m)(2n)^4 - (2n)^5$
$(m - 2n)^5 = m^5 - 10m^4n + 40m^3n^2 - 80m^2n^3 + 80mn^4 - 32n^5$
Para dividir dos monomios:
Siendo $m > n$
$\dfrac{a^m}{a^n} = a^{m-n}$;
Siendo $m < n$
$\dfrac{a^m}{a^n} = \dfrac{1}{a^{n-m}}$;
Siendo $m = n$
$\dfrac{a^m}{a^n} = 1$;
Para dividir un polinomio por un monomio, se divide cada término del polinomio por el monomio, teniendo en cuenta la ley de signos y las propiedades de la potencia de bases iguales, ejemplo:
$$\begin{align*} \dfrac{18x^5-9x^3+24x^4}{-3x^2} &= \dfrac{18x^5}{-3x^2} - \dfrac{9x^3}{-3x^2} + \dfrac{24x^4}{-3x^2} \\\\ &= -6x^{5-2} + 3x^{3-2} - 8x^{4-2} \\\\ &= -6x^3 + 3x - 8x^2 \end{align*}$$ xploremos
xploremos
Observa varios ejercicios, verás que para hacer la división siempre se dividen los monomios de mayor grado, se multiplica y se cambia de signo, y se suma. Este proceso se repite hasta obtener un resto de grado menor que el del divisor. La división de polinomios debe cumplir dos condiciones. La primera, que el Dividendo = divisor · cociente + resto y, la segunda, que gr(resto) < gr(divisor)
El grado del cociente es la diferencia de los grados del dividendo y del divisor. Cuando el resto es cero, se dice que el dividendo es divisible entre el divisor.
En la siguiente escena se ven divisiones de polinomios con la expresión en coeficientes, cuyo procedimiento es el mismo: División de coeficientes, Multiplicación del último coeficiente por el divisor cambiando de signo el resultado y, Suma de este resultado con lo que resta en el dividendo.
Observa varios ejercicios en cada uno de los tres niveles de la escena.
 jercicio 1: Simplifique la siguiente expresión algebraica de (sumas, restas, productos, cocientes, potencias), resuelve primero en tu cuaderno y luego verifica la solución.
jercicio 1: Simplifique la siguiente expresión algebraica de (sumas, restas, productos, cocientes, potencias), resuelve primero en tu cuaderno y luego verifica la solución.
 jercicio 2: Mide tus conocimientos de lo aprendido en esta sección y resuelve la actividad:
jercicio 2: Mide tus conocimientos de lo aprendido en esta sección y resuelve la actividad:
Factorizar un polinomio es expresarlo como el producto de otros polinomios que tengan menor grado que éste. Casos de factorización:
Hace referencia al término común de un polinomio, pueden ser factores numéricos o factores literales. Para encontrar el factor común, se realiza lo siguiente:
Ejemplo: Encontrar el factor común para el polinomio: $3m^3 - 6m^2n$
Factor común numérico de $3$ y $6$ es $3$
Factor común literal de $m^3$ y $m^2n$ es $m^2$
Por lo tanto, el factor común del polinomio $= 3m^3 - 6m^2n = 3m^2$
Ahora, veamos por medio de un paso a paso como hallar el factor común de un polinomio, pulsa en botón “Paso1” y sigue las instrucciones.
Una vez encontrado el factor común para un determinado polinomio, se procede a encontrar el otro factor que multiplica al factor común, dividiendo cada término del polinomio dado por el factor común. Quedando en ésta forma factorizado completamente el polinomio dado.
Ejemplo:
$5p^2q^3 + 10p^2q^2 + 20p^3q^4$
el factor común del polinomio es $5p^2q^2$ ahora dividimos cada termino por el factor común:
$$\begin{align*} \dfrac{5p^2q^3}{5p^2q^2} + \dfrac{10p^2q^2}{5p^2q^2} + \dfrac{20p^3q^4}{5p^2q^2} &= p^{2-2}q^{3 - 2} + 2p^{2-2}q^{2-2} + 4p^{3 - 2}q^{4 - 2} \\ &= q + 2 + 4pq^2 \end{align*}$$division de coeficientes numéricos, propiedad de división de potencias de igual base, por lo tanto,
${5p^2q^3 + 10p^2q^2 + 20p^3q^4 = 5p^2q^2 \cdot ( q + 2 + 4pq^2)}$
Se caracteriza por ser una diferencia (resta) entre dos términos que poseen raíz cuadrada exacta.
Ejemplo: $9a^2 - b^2$
raíz cuadrada del primer término $\longrightarrow 3a$
raíz cuadrada del segundo término $\longrightarrow b$
Una diferencia de cuadrados se factoriza como la suma de las raíces cuadradas, multiplicada por la diferencia de las mismas, simbólicamente se tiene:
$a^2 - b^2 = ( a + b )( a - b )$
Ejemplo 1:
$25p^2$
$\darr$
$\sqrt{25p^2}$
$\darr$
$5p$
$-$
$4p^2$
$\darr$
$\sqrt{4p^2}$
$\darr$
$2p$
$= (5p + 2p) \cdot (5p - 2p)$
Ejemplo 2:
$$\begin{align*} k^2 - (1+v)^2 &= (k + (1+v)) \cdot (k - (1+v)) \\ &= (k + v + 1) \cdot (k - v - 1) \end{align*}$$ jercicio: Factorizar los siguientes polinomios si es posible.
jercicio: Factorizar los siguientes polinomios si es posible.
 xploremos
xploremos
Verifica los conocimientos de lo visto en esta sección:
Véase http://proyectodescartes.org/Telesecundaria/materiales_didacticos/3m_b01_t01_s01-JS/index.html.
Estos trinomios se factorizan de la siguiente forma:
Todo trinomio de la forma $x^2 + bx + c$, siempre que $x^2 + bx + c = 0$ tenga solución, equivale al producto de dos binomios o factores.
$x^2 + bx + c = ( x + p )( x + q )$
Donde el primer término de cada binomio, es la raíz cuadrada del primer término del trinomio $x$ y los segundos términos de cada binomio son los números $p$ y $q$, cuya suma $p + q = b$ y el producto $p \cdot q = c$.
Simbólicamente se tiene:
$x^2$
$\darr$
$\sqrt{x^2}$
$\darr$
$x$
$+$
$bx$
$\darr$
$b=p+q$
$+$
$c$
$\darr$
$c = p \cdot q$
$= (x + p) \cdot (x + q)$
Ejemplo:
$x^2$
$\darr$
$\sqrt{x^2}$
$\darr$
$x$
$+$
$8x$
$\darr$
$b=3+5$
$+$
$15$
$\darr$
$c = 3 \cdot 5$
$= (x + 3) \cdot (x + 5)$
Se puede presentar que el trinomio tenga la forma $x^{2n} + bx^n + c$, el cual se factoriza de igual forma.
Ejemplo:
$x^4 - x^2 - 6 = (x^2 - 3)(x^2 + 2)$
donde,
$b = (-3 + 2) = -1$
$c = (-3)(2) = -6$
 jercicio: Practiquemos factorizando algunos trinomios, si es posible.
jercicio: Practiquemos factorizando algunos trinomios, si es posible.
Estos trinomios se factorizan de la siguiente forma:
Se caracterizan por ser muy parecidas a la forma $x^{2n} + bx^n + c$, con la diferencia de que la variable $x^{2n}$ ya tiene un coeficiente $a$ diferente de cero y uno. Por ejemplo:
$$2x^2 + 7x - 15 \\ 3x^2 + 17x + 10 \\ 5x^2 - 17x + 6$$Para factorizar trinomios de la forma $ax^{2n} + bx^n + c$, lo que se hace es llevarlo a la forma $y^{2n} + by^n + c$, y luego se resuelve como en el caso anterior.
Simbólicamente se tiene: $ax^{2n} + bx^n + c \; \rightarrow$ Trinomio dado
$= \dfrac{a (ax^{2n} + bx^n + c)}{a}\; \rightarrow$ Multiplico y divido por $a$
$= \dfrac{a^2 x^{2n} + abx^n + ac}{a}\; \rightarrow$ Aplico distributiva
El primer término de cada binomio será: $(ax^n + p) \cdot (ax^n + q)$
por lo tanto, $(ax^n)^2 + b(ax^n) + ac = (ax^n + p) \cdot (ax^n + q)$
donde: $p + q = b$ y $p \cdot q = a \cdot c$
Ejemplo: $3x^2 + 17x + 10 \; \rightarrow$ Trinomio dado
$= \dfrac{3 (3x^2 + 17x + 10)}{3}\; \rightarrow$ Multiplico y divido por $3$
$= \dfrac{(3x)^2 + 17(3x) + 30}{3}\; \rightarrow$ Aplico distributiva
donde: $15 + 2 = 17$ y $15 \cdot 2 = 30$
entonces: $= \dfrac{(3x + 15)(3x + 2)}{3}\; \rightarrow$ Factor común $3(x + 5)$
$= x^2 + 17x + 10 = (x + 5)(3x + 2) \; \rightarrow$ Simplificando el $3$
 jercicio: Practiquemos factorizando algunos trinomios, si es posible.
jercicio: Practiquemos factorizando algunos trinomios, si es posible.
 xploremos
xploremos
Verifica los conocimientos de lo visto en esta sección:
Véase http://proyectodescartes.org/Telesecundaria/materiales_didacticos/3m_b01_t01_s01-JS/index.html.
Se trata de la suma entre dos términos cuya característica es que pueden expresarse como cantidades que se pueden elevar al cubo, por lo tanto cada término posee raíz cúbica exacta.
Ejemplo: $x^3 + 27 = x^3 + 3^3$
raíz cúbica del primer término $\longrightarrow x$
raíz cúbica del segundo término $\longrightarrow 3$
Para factorizar una suma de cubos, se tiene en cuenta lo siguiente:
$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
Ejemplo:
$y^3 + 64x^3 = (y + 4x)(y^2 - 4xy + 16y^2)$
Se trata de la resta entre dos términos cuya característica es que pueden expresarse como cantidades que se pueden elevar al cubo, por lo tanto cada término posee raíz cúbica exacta.
Ejemplo: $p^3 - 8k^3 = p^3 - (2k)^3$
Raíz cúbica del primer término $\longrightarrow p$
Raíz cúbica del segundo término $\longrightarrow 2k$
Para factorizar una diferencia de cubos, se tiene en cuenta lo siguiente:
$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$
Ejemplo:
$y^3 - 64x^3 = (y -4x)(y^2 + 4xy + 16x^2)$
Ahora, veamos algunos ejemplos de la factorización de suma y diferencia de cubos.
Algunos polinomios no se pueden factorizar directamente, mediante la aplicación de los casos vistos hasta ahora, sino que es necesario agrupar adecuadamente los términos antes de factorizar.
Ejemplo, factorizar el siguiente polinomio: $x^3 - 6x^2 - x + 6$
$x^3 - 6x^2 - x + 6 \longrightarrow$ agrupamos $\longrightarrow$
factor común $\longrightarrow$
factor común $\longrightarrow$
diferencia de cuadrados $\longrightarrow$
$(x^3-6x^2)-(x-6)$
$x^2(x-6)-(x-6)$
$(x-6)(x^2-1)$
$(x-6)(x-1)(x+1)$
 jercicio
jercicio
Mide tus conocimientos de lo aprendido en esta sección y resuelve la actividad:
Recordemos:
Para simplificar fracciones, escribimos el numerador y el denominador como un producto de factores y cancelamos los FACTORES COMUNES a ambos.
¡CUIDADO! No podemos simplificar términos. Sólo factores.
Una fracción aritmética está simplificada cuando el único factor común al numerador y al denominador es el número UNO.
Ejemplos:
$\dfrac{4}{8} = \dfrac{1 \cdot \cancel{2} \cdot \cancel{2}}{1 \cdot \cancel{2} \cdot \cancel{2} \cdot 2}$
$\dfrac{48}{270} = \dfrac{1 \cdot \cancel{2} \cdot 2 \cdot 2 \cdot 2 \cdot \cancel{3}}{1 \cdot \cancel{2} \cdot 3 \cdot 3 \cdot \cancel{3} \cdot 5} = \dfrac{8}{45}$
$\dfrac{4 + \cancel{3}}{\cancel{3}} = 4$ $\longrightarrow$ ¡Error! $\dfrac{4 + 3}{3} = \dfrac{7}{3}$ $\longrightarrow$ ¡Correcto!
Para simplificar, cancelamos los FACTORES COMUNES al numerador y al denominador.
Cuando el denominador de una fracción es cero ($0$) se dice que la fracción no existe o no está definida.
Al igual que las fracciones aritméticas, decimos que una fracción algebraica está simplificada, cuando el único factor común al numerador y al denominador es el número UNO, es decir, cuando el numerador y el denominador sean primos entre sí. Para simplificar fracciones algebraicas procedemos de la siguiente forma:
Ejemplos:
$= \dfrac{(x-2)}{(x+2)} \longrightarrow$ Suprimiendo factores comunes
$= \dfrac{-(x+1)}{(x+6)} = -\dfrac{x+1}{x+6}$
En algunos casos, se requiere cambiar el orden de los términos de uno o varios factores, para el segundo ejemplo, se requiere cambiar el orden del factor $(x - 6)$, por eso se le antecedió con un signo menos ($-$) al signo de agrupación y se cambió el orden de los términos dentro del signo de agrupación, quedando $-(6 - x)$.
 jercicio 1: En la siguiente escena simplifica en tu cuaderno la expresión racional dada, luego verifica haciendo clic en el botón “Solución”.
jercicio 1: En la siguiente escena simplifica en tu cuaderno la expresión racional dada, luego verifica haciendo clic en el botón “Solución”.
Para sumar o restar fracciones racionales hacemos lo siguiente:
 jercicio 2: Simplifiquemos expresiones racionales de suma y diferencia.
jercicio 2: Simplifiquemos expresiones racionales de suma y diferencia.
 jercicio 3: Resuelve en tu cuaderno y practica simplificando expresiones racionales.
jercicio 3: Resuelve en tu cuaderno y practica simplificando expresiones racionales.
Para multiplicar fracciones racionales hacemos lo siguiente:
Recordemos, cuando multiplicamos fracciones se tiene que:
$$\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{a \cdot c}{b \cdot d} \longrightarrow \dfrac{\textsf{numeradores}}{\textsf{denominadores}}$$Ejemplo:
$$\dfrac{4}{5} \cdot \dfrac{-3}{7} = \dfrac{4 \cdot (-3)}{5 \cdot 7} = \dfrac{-12}{35}$$Multipliquemos y simplifiquemos la siguiente fracción racional:
$\dfrac{x^2-25}{3x^2+11x+10} \cdot \dfrac{4x+8}{x^2-2x-15}$
$= \dfrac{(x+5)\cdot(x-5)}{(3x+5)\cdot(x+2)} \cdot \dfrac{4\cdot(x+2)}{(x+3)\cdot(x-5)}$ Factorizamos las expresiones
$= \dfrac{(x+5)\cdot\cancel{(x-5)}\cdot 4\cdot\cancel{(x+2)}}{(3x+5)\cdot\cancel{(x+2)}\cdot(x+3)\cdot\cancel{(x-5)}}$ Simplificamos
por lo tanto $\dfrac{x^2-25}{3x^2+11x+10} \cdot \dfrac{4x+8}{x^2-2x-15} = \dfrac{4\cdot(x+5)}{(3x+5)\cdot(x+3)}$
 jercicio 4: Simplifiquemos productos de expresiones racionales.
jercicio 4: Simplifiquemos productos de expresiones racionales.
 jercicio 5: Resuelve en tu cuaderno y practica simplificando expresiones racionales.
jercicio 5: Resuelve en tu cuaderno y practica simplificando expresiones racionales.
Para dividir fracciones racionales hacemos lo siguiente:
Recordemos, cuando dividimos fracciones se tiene que:
$\dfrac{a}{b} ÷ \dfrac{c}{d} = \dfrac{a}{b} \times $ $\dfrac{d}{c}$
$\darr$
inverso multiplicactivo $= \dfrac{a \cdot d}{c \cdot b} \longrightarrow \dfrac{\mathsf{numeradores \; entre \; sí}}{\mathsf{denominadores \; entre \; sí}}$
Ejemplo:
$\dfrac{4}{5} ÷ \dfrac{-3}{7} = \dfrac{4}{5} \times \dfrac{7}{-3} = \dfrac{4 \cdot 7}{5 \cdot (-3)} = \dfrac{28}{-15}$
Dividamos y simplifiquemos la siguiente fracción racional:
$\dfrac{3x-15}{x+3} ÷ \dfrac{12x+18}{4x+12} = \dfrac{3x-15}{x+3} \cdot \dfrac{4x+12}{12x+18}$
$= \dfrac{3 \cdot (x-5)}{(x+3)} \cdot \dfrac{4 \cdot (x+3)}{6 \cdot (2x+3)} = \dfrac{12 \cdot (x-5) \cdot (x+3)}{6 \cdot (x+3) \cdot (2x+3)} = \dfrac{2 \cdot (x-5)}{2x+3}$
 jercicio 6: Simplifiquemos divisiones de expresiones racionales.
jercicio 6: Simplifiquemos divisiones de expresiones racionales.
 jercicio 7: Resuelve en tu cuaderno y practica simplificando expresiones racionales.
jercicio 7: Resuelve en tu cuaderno y practica simplificando expresiones racionales.
 jercicio 8: Simplifica las siguiente expresión racional (sumas, restas, productos, cocientes, potencias), resuelve primero en tu cuaderno y luego verifica la solución.
jercicio 8: Simplifica las siguiente expresión racional (sumas, restas, productos, cocientes, potencias), resuelve primero en tu cuaderno y luego verifica la solución.