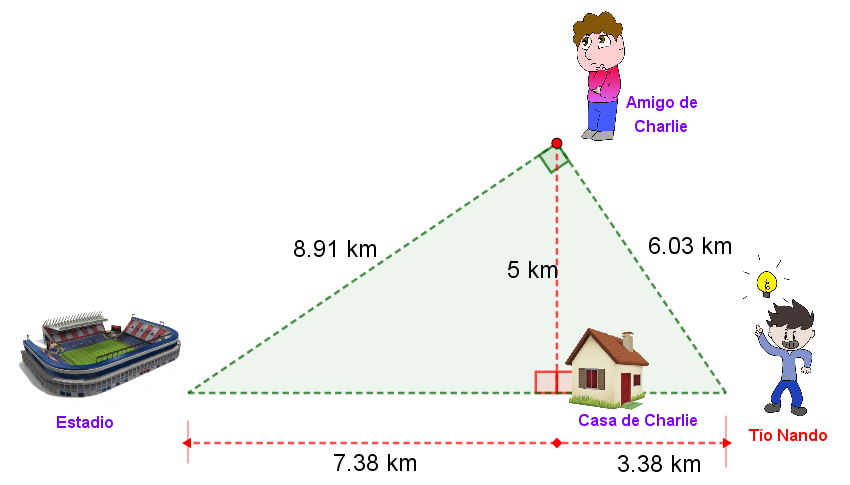
Situación-ProblemaSituación-ProblemaSe Sabe que la distancia del tío Nando al estadio de futbol es de $10,76 \space km$, pero entre la casa de Charlie y el tío es de $3,38 \space Km$, por tanto, entre la casa de charlie y el estadio es de $7,78 \space Km$ ¿Cuáles son las distancias para saber qué camino es el más corto para recorrer?.
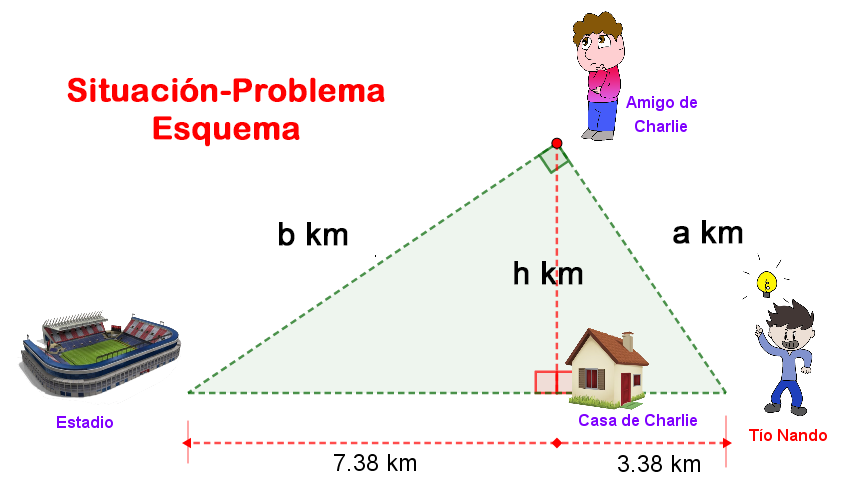
Lo que hay que observar primero de la figura es que es un triángulo rectángulo, y se puede aplicar el teorema de la altura y el teorema de los catetos.
Aplicando el teorema de la altura, se tienes que la distancia de la casa de Charlie a donde el amigo, es la raíz cuadrada de multiplicar las distancias de la casa a donde el tío y de la casa al estadio, por lo tanto, $$ \frac{h}{m} = \frac{n}{h} \to h^2 = nm \to h = \sqrt{mn} = \sqrt{(7.78)(3.38)} \approx 5 km$$
Ahora, aplicando el teorema de los catetos para hallar las distancias del amigo de charlie al estadio, y del amigo de charlie a donde se encuentra el tío. $$ \frac{b}{c} = \frac{m}{b} \to b^2 = mc \to b = \sqrt{mc} = \sqrt{(7.78)(10.78)} \approx 8,91 km$$ $$ \frac{a}{c} = \frac{n}{a} \to a^2 = nc \to a = \sqrt{nc} = \sqrt{(3.38)(10.78)} \approx 6,03 km$$
