 Solución
Solución Solución
Solución¿Se puede hallar el área del polígono a partir de su descomposición triangular?
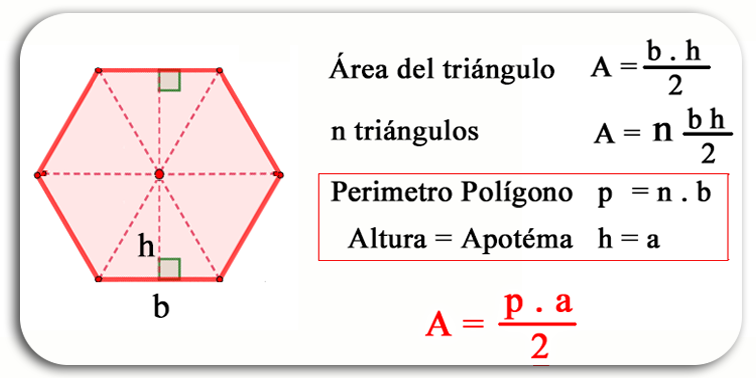
Si del centro se trazan radios a todos sus vértices, el polígono queda dividido en tantos triángulos iguales como lados tiene el polígono.
El área del polígono será igual al área de un triángulo multiplicada por el número de triángulos ($n$). Si el lado del polígono se nombra $L$ y la altura de cada triángulo es el apotema del polígono identificada como $a$, el área de cada uno de los triángulos será: $A = \frac{a\times L}{2}$
Si el polígono tiene $n$ lados, el número de triángulos que se formarán será igual a $n,$ pero $n \times L$ significa el número de lados ($n$) por el valor de un lado ($L$) del polígono; que si recuerdas, es la fórmula para obtener el perímetro del polígono regular. Por eso la fórmula que se utiliza para obtener el área de un polígono regular es igual a la mitad del producto del perímetro por el apotema.
Observe la siguiente demostración creada en geogebra, autor, Juan Pablo Serrano, denominada: "Polígono regular que se desenrolla y enrolla".