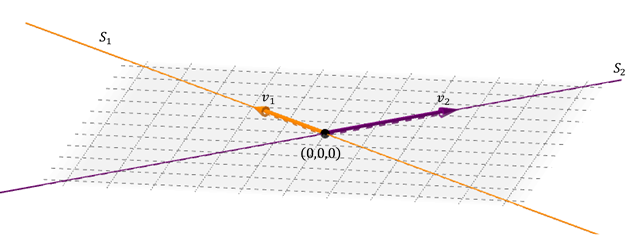
A continuación consideraremos diferentes casos de suma de subespacios en \({\mathbb{R}^3}\).
Un caso posible de suma de dos subespacios en \({\mathbb{R}^3}\) es el de dos rectas que se cortan:
Los dos vectores LI de las rectas generan un plano: aquél que contiene a ambas rectas. La suma es directa porque la intersección entre las rectas es el vector nulo.
\[{S_1} \cap {S_2} = \left\{ {\left( {0,0,0} \right)} \right\}\;\;\;y\;\;\;{S_1} + {S_2} = gen\left\{ {{v_1},{v_2}} \right\}\;\]
\({S_1} \oplus {S_2} = S\) donde \(S\) es el plano que contiene a las dos rectas
Otro caso posible de suma de dos subespacios en \({\mathbb{R}^3}\) es el de dos planos que se cortan en una recta:
\[{S_1} \cap {S_2} \ne \left\{ {{0_V}} \right\}\;\;\;y\;\;\;{S_1} + {S_2} = gen{\rm{\{ }}{v_1},{v_2},{v_3},{v_4}{\rm{]}} = gen\left\{ {\;{v_1},{v_2},{v_3}} \right\}\]
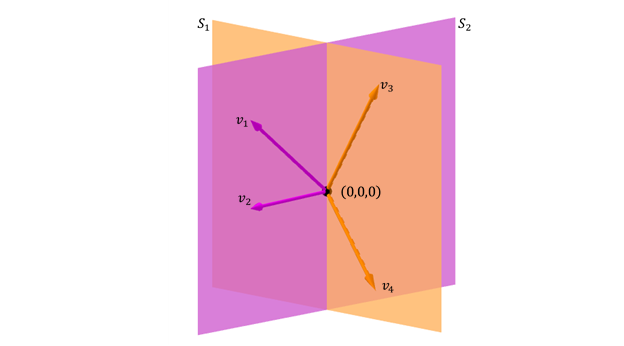
La suma de los subespacios es \({\mathbb{R}^3}\) pero no es suma directa porque la intersección no es el vector nulo:
\[{S_1} + {S_2} = {\mathbb{R}^3}\;\]
Otro caso posible de suma de dos subespacios en 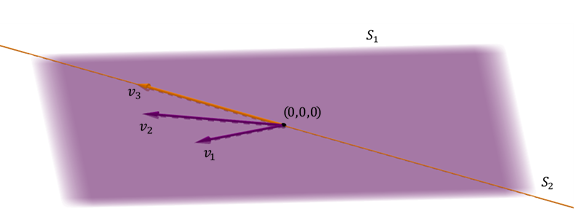\({\mathbb{R}^3}\) es el de un plano y una recta incluida en el plano. 
\[{S_1} + {S_2} = {S_1}\;\;\;\;\;\;\;pues\;\;\;{S_2} \subset {S_1}\]
Se obtiene el mismo plano, y la suma no es directa porque la intersección no es igual al vector nulo.
Otro caso posible de suma de dos subespacios en 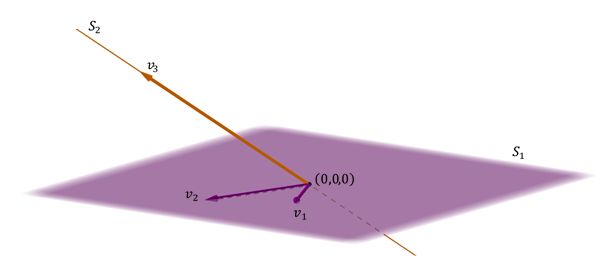\({\mathbb{R}^3}\) es el de un plano y una recta no incluida en el plano. 
\[{S_1} \cap {S_2} = \left\{ {\left( {0,0,0} \right)} \right\}\;\;\;\;\;y\;\;\;\;\;{S_1} + {S_2} = gen\left\{ {{v_1},{v_{2,}}{v_3}} \right\} = {\mathbb{R}^3}\;\;\]
Se genera \({\mathbb{R}^3}\) porque el vector director de la recta no es coplanar con los vectores del plano, y además es directa porque la intersección es el vector nulo:
\[{S_1} \oplus {S_2} = {\mathbb{R}^3}\]
Observación: En el último caso, la unión de las bases de los dos subespacios forma una base de todo el espacio. En este caso, cada vector de \({\mathbb{R}^3}\) puede expresarse de forma única como suma de un vector de \({S_1}\) y otro de \({S_2}\).
Dados \({S_1} = gen\left\{ {\left( {1,2,1} \right),\;\left( {0,2,0} \right)} \right\}\) y \({S_2} = \left\{ {\left( {x,y,z} \right):\;\;\;x + y = y – kz = 0} \right\}\),
a) Hallar los valores de \(k\) para los cuales \({S_1} \oplus {S_1} = {\mathbb{R}^3}\).
b) Para \(k = 0\) , comprobar que \(v = \left( {3,2,1} \right)\) puede expresarse de forma única como suma de un vector \({v_1} \in {S_1}\) y otro de \({v_2} \in {S_2}\).
Sean los subespacios de \({\mathbb{R}^4}\):
\(S = gen\left\{ {\left( {1,1,1,1} \right),\;\left( {0,1,0,1} \right)} \right\}\) y \(T = \left\{ {\left( {x,y,z,t} \right):\;\;\;x – z = 0\;\;\;,\;\;x – z + t = 0} \right\}\)
¿Cuál de las siguientes afirmaciones es correcta? Justificar.