
Hallar la ecuación del plano perpendicular al vector \(\vec n = \left( {3,2,1} \right)\) que pasa por el punto \({P_0}\left( {1,1, -1} \right)\).
Las componentes de \(\vec n\) nos indican los coeficientes \(a\), \(b\) y \(c\) de la ecuación del plano:
\[\pi :\;\;3x + 2y + z + d = 0\]
¿Cómo hallamos \(d\)?
El punto debe verificar la ecuación, entonces reemplazamos \({P_0}\) y obtenemos el coeficiente que faltaba:
\[3.1 + 2.1 - 1 + d = 0\; \Rightarrow d = - 4\]
Así obtenemos la ecuación del plano:
\[\pi :\;\;3x + 2y + z - 4 = 0\]
Éste es el único plano que pasa por el punto \({P_0}\;\;\)y es perpendicular al vector \(\vec n\).
Para efectuar un gráfico aproximado del plano que obtuvimos, podemos buscar sus intersecciones con los ejes coordenados:
Para hallar la intersección con el eje \(x\), debemos plantear \(y = z = 0\) y despejar el valor de \(x\). Análogamente para las otras intersecciones, tal como se muestra en el siguiente cuadro:

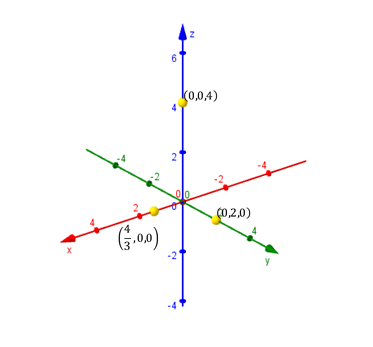
Tres puntos no alineados determinan un único plano que los contiene.
Trazamos los segmentos que unen los puntos hallados y obtenemos la representación gráfica de una porción del plano:
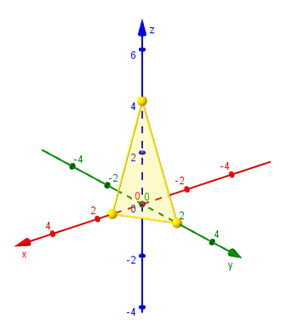
Mostramos una gráfica del plano realizada con GeoGebra:
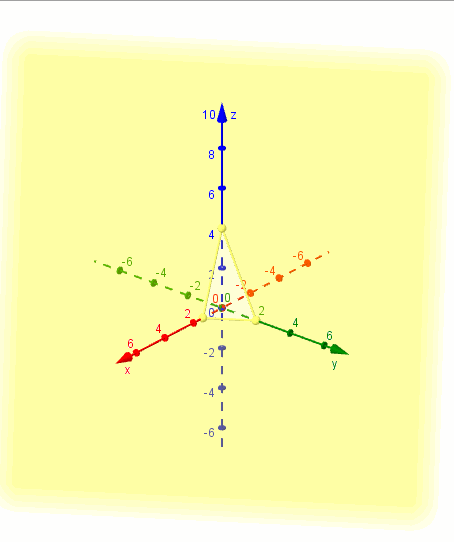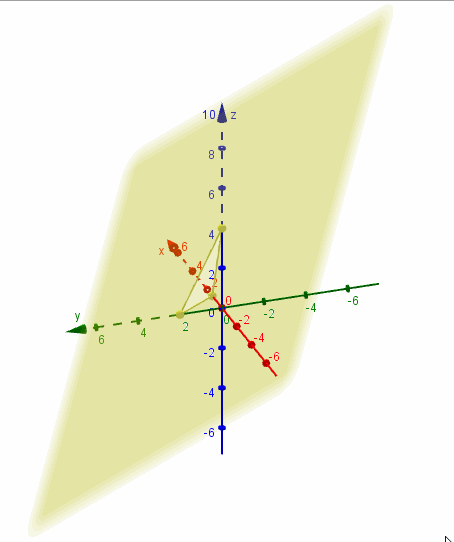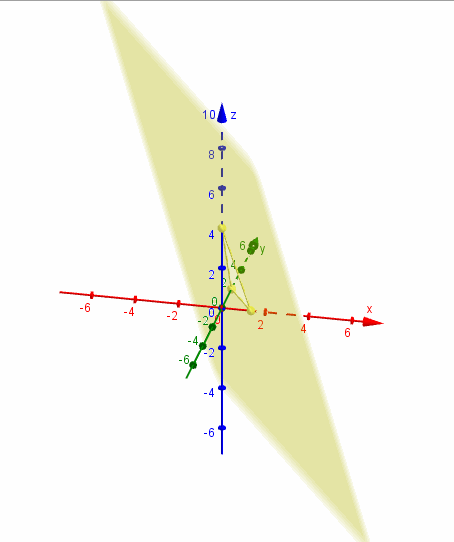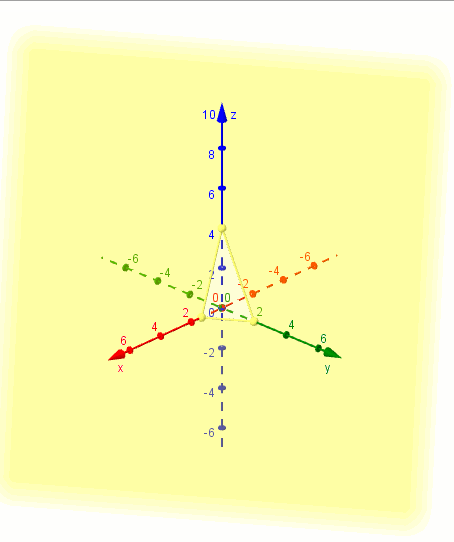
Dados los puntos \(R\left( {1,2,3} \right)\) y \(S\left( {3, - 1,2} \right)\), encontrar la ecuación del plano que corta perpendicularmente al segmento \(RS\) en su punto medio.
Busquemos las coordenadas del punto medio:
\[M = \left( {\frac{{1 + 3}}{2},\frac{{2 + \left( { - 1} \right)}}{2},\frac{{3 + 2}}{2}} \right) = \left( {2,\frac{1}{2},\frac{5}{2}} \right)\]
Como el plano corta perpendicularmente al segmento \(RS\), podemos tomar \(\overrightarrow {RS} \;\;\)como vector normal del plano:
\[\overrightarrow {RS} = \left( {2, - 3, - 1} \right)\]
Escribimos la ecuación del plano al que llamaremos \(\beta \):
\[\beta :\;\;\;2x - 3y - 1z + d = 0\]
Para hallar \(d\) reemplazamos el punto \(M\):
\[2.2 - 3.\frac{1}{2} - \frac{5}{2} + d = 0\; \Rightarrow d = 0\]
Y así obtenemos la ecuación buscada:
\[\beta :\;\;\;2x - 3y - z = 0\]
Este plano pasa por el origen, o sea que interseca a los tres ejes en \(\left( {0,0,0} \right)\). Necesitamos al menos dos puntos más para graficarlo.
Para facilitar el gráfico podemos elegir puntos que estén sobre los planos coordenados. Por ejemplo \(y = 0\;\):
\[\; \Rightarrow 2x - z = 0 \Rightarrow z = 2x\]
Entonces haciendo \(x = 1\) debe ser \(z = 2\), y obtenemos el punto \({P_1}\left( {1,0,2} \right)\)
Para tomar otro punto del plano podemos hacer que \(z = 0\)
\[\; \Rightarrow \;2x - 3y = 0 \Rightarrow y = \frac{2}{3}x\]
Y si \(x = 3\) entonces \(y = 2\). Obtenemos el punto \({P_2}\left( {3,2,0} \right)\)
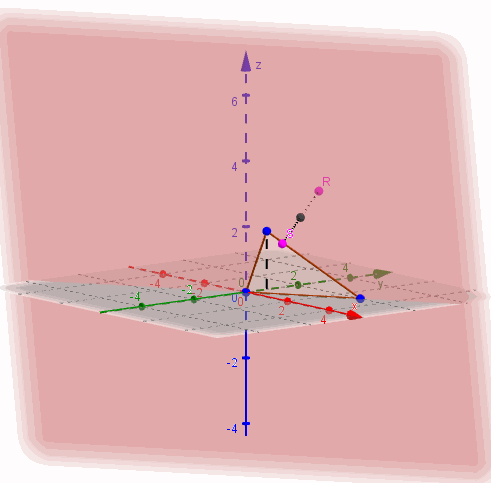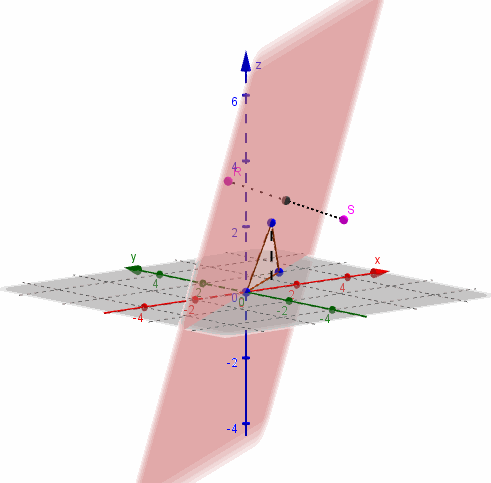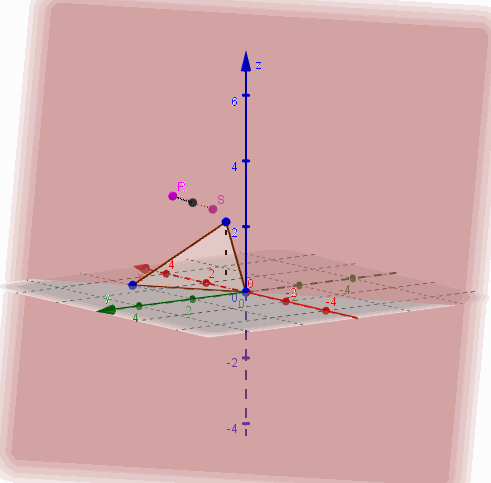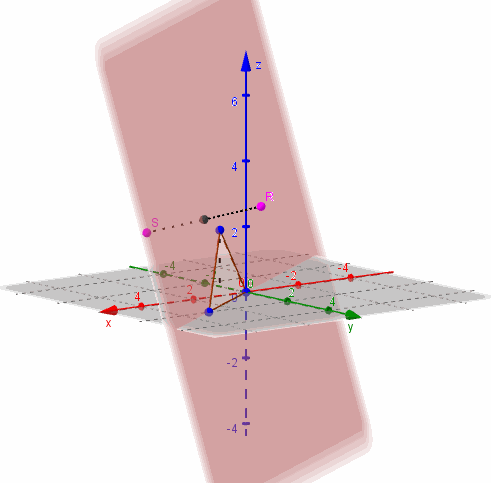
Entonces \(\beta \) contiene a los puntos \(\left( {0,0,0} \right),\;\left( {1,0,2} \right)\,\) y \(\left( {3,2,0} \right)\):
Dados \( A\left( {4,5,2} \right),\;B\left( {1,3,4} \right), \; C\left( {2,2,5} \right)\) hallar, si es posible, el plano que contiene a los tres puntos.
Habíamos dicho que tres puntos no alineados determinan un único plano que los contiene.
Hagamos una figura de análisis:
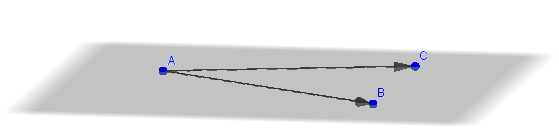
Con los tres puntos, podemos armar dos vectores, por ejemplo:
\[\overrightarrow {AB} = \left( { - 3, - 2,2} \right)\]
\[\overrightarrow {AC} = \left( { - 2, - 3,3} \right)\]
El vector normal debe ser perpendicular a ambos vectores cómo muestra la siguiente figura:
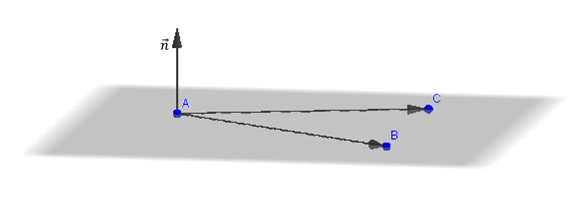
¿Qué operación nos permite hallar un vector perpendicular a otros dos?
\[\overrightarrow {AB} \times \overrightarrow {AC} = \left( {0,5,5} \right)\]
¿Qué resultado habríamos obtenido si \(A\), \(B\) y \(C\) estuvieran alineados?
El vector \(\left( {0,5,5} \right)\) es perpendicular al plano que buscamos, entonces podemos tomar \(\vec n \; = \;\left( {0,5,5} \right)\) y escribir la ecuación del plano:
\[\alpha :\;\;\;5y + 5z + d = 0\]
Para hallar \(d\) podemos reemplazar cualquiera de los tres puntos. Reemplacemos \(A\):
\[5.5 + 5.2 + d = 0 \Rightarrow d = - 35\]
Luego:
\[5y + 5z - 35 = 0\]
Podemos dividir por 5 ambos miembros:
\[\alpha :\;\;\;y + z - 7 = 0\]
El lector puede comprobar que los puntos \(B\) y \(C\) verifican esta ecuación.
Busquemos las intersecciones con los ejes para graficar el plano:
\[y = z = 0 \Rightarrow - 7 = 0\;\;\;Absurdo\]
Entonces \(\alpha \) no corta al eje \(x\).
¿En qué punto corta al eje \(y\)? \(\;\left( {0,7,0} \right)\)
¿Y al eje \(z\)? \(\left( {0,0,7} \right)\)
Observemos que el plano contiene a todos los puntos de la forma \(\left( {x,7,0} \right)\) con \(x \in \mathbb{R}.\)
Lo mismo ocurre con los puntos del tipo \(\left( {x,0,7} \right)\) con \(x \in \mathbb{R}.\)
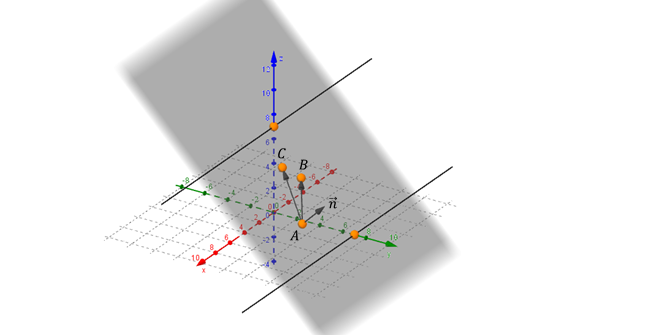
Podemos observar entonces que:
\[\;a = 0 \Rightarrow el\;plano\;es\parallel \;\;al\;eje\;x\]