Ejemplo 1

Sea $S=\left\{\left(x,y,z\right)\in {\mathbb{R}}^3|2x+3y-z=0\right\}$. Hallar $S^{\mathrm{\perp }}$.

Resolución

Tenemos que buscar los vectores de ${\mathbb{R}}^3$ que sean perpendiculares a todos los vectores de ese plano.

Primero buscamos una base de $S$, por ejemplo:

$$B_S=\left\{\left(-1,1,1\right),\left(0,1,3\right)\right\}$$

Para hallar el complemento ortogonal, buscamos todos los vectores $\left(x,y,z\right)$ que sean ortogonales a $\left(-1,,1,1\right)$ y a $\left(0,1,3\right)$.

Se obtiene así un sistema de ecuaciones que define el complemento ortogonal:

$$\{\begin{array}{c}\left(x,y,z\right).\left(-1,1,1\right)=0\\ \left(x,y,z\right).\left(0,1,3\right)=0\end{array}\Rightarrow \{\begin{array}{c}-x+y+z=0\Rightarrow -x-3z+z=0\\ y+3z=0\end{array}$$

$$\{\begin{array}{c}x=-2z\\ y=-3z\end{array}Ecuacionesde{S}^{\mathrm{\perp }}$$

¿Cuál es una base del subespacio $S^{\mathrm{\perp }}$?

$$B_{S^{\mathrm{\perp }}}=\left\{\left(-2,-3,1\right)\right\}$$

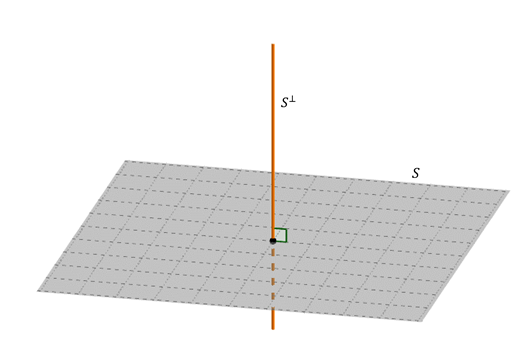
La base es un vector perpendicular al plano $S$. Por lo tanto, el complemento ortogonal de un plano que pasa por el origen es la recta perpendicular que pasa por el origen.

Si $S$ es una recta que pasa por el origen: ¿cuál es su complemento ortogonal?

Ejercicio para el lector

Para justificar el procedimiento que utilizamos para encontrar las ecuaciones de $S^{\mathrm{\perp }},$ les pedimos que demuestren la siguiente propiedad:

Sean $u,v,w$ vectores de ${\mathbb{R}}^n$.

Si $w$ es ortogonal a $u$ y a $v$, entonces es ortogonal a cualquier combinación lineal de $u$ y $v$.

Ejemplo 2

Dado siguiente subespacio de ${\mathbb{R}}^4$:

$$S=\left\{\left(x_1,x_2,x_3,x_4\right)\in {\mathbb{R}}^4|x_1+x_2-3x_3=0\wedge x_2-x_4=0\right\}$$

Halle base y dimensión del complemento ortogonal.

Resolución

Tenemos que buscar los vectores de ${\mathbb{R}}^4$ que son ortogonales a los vectores de $S$.

Hallemos una base de $S$:

$$\left(-x_2+3x_3,x_2,x_3,x_2\right)=x_2\left(-1,1,0,1\right)+x_3\left(3,0,1,0\right)$$

$$\Rightarrow B_S=\left\{\left(-1,1,0,1\right),\left(3,0,1,0\right)\right\}$$

Ahora buscamos los $\left(x_1,x_2,x_3,x_4\right)$ tales que:

$$\{\begin{array}{c}\left(x_1,x_2,x_3,x_4\right)\left(3,0,1,0\right)=0\\ \left(x_1,x_2,x_3,x_4\right)\left(-1,1,0,1\right)=0\end{array}\Rightarrow \{\begin{array}{c}3x_1+x_3=0\\ -x_1+x_2+x_4=0\end{array}$$

Hallamos las ecuaciones que definen a $S^{\mathrm{\perp }}$:

$$S^{\mathrm{\perp }}=\left\{\left(x_1,x_2,x_3,x_4\right)\in {\mathbb{R}}^4|3x_1+x_3=0\wedge -x_1+x_2+x_4=0\right\}$$

Busquemos una base de $S^{\mathrm{\perp }}$:

$$\left(x_1,x_2,-3x_1,x_1-x_2\right)=x_1\left(1,0,-3,1\right)+x_2\left(0,1,0,-1\right)$$

$$\Rightarrow B_{S^{\mathrm{\perp }}}=\left\{\left(1,0,-3,1\right),\left(0,1,0,-1\right)\right\}\Rightarrow \dim \left(S^{\mathrm{\perp }}\right)=2$$