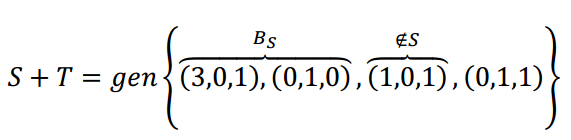
Dados los siguientes subespacios de
Nos interesa hallar
Busquemos una base de
Ahora armamos un vector genérico:
Busquemos una base de
Ahora armamos un vector genérico:
Entonces
Sabemos que todo conjunto de más de 3 vectores en
Podríamos armar una matriz con estos 4 vectores y llevarla a la forma escalonada. O si no, como el espacio es
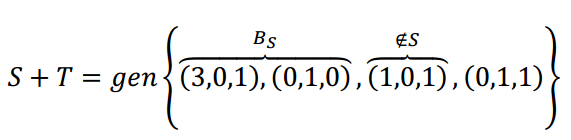
Por lo tanto:
En este caso, como
Generalizando:
Dados los siguientes subespacios de
Hallar base y dimensión de
Cómo hemos visto, un método para analizar si son LI o LD, consiste en armar una matriz con los vectores como filas y llevarla a su forma escalonada. Por conveniencia colocaremos los vectores en el siguiente orden:
La matriz escalonada tiene 3 filas LI (su rango es 3), entonces podemos afirmar que la dimensión de
Como se anuló la última fila, el vector
Recordemos que las filas de la matriz escalonada componen otra base de la suma: