Matrices y sistemas de ecuaciones lineales
Un conjunto de ecuaciones que deben cumplirse simultáneamente forma un sistema de ecuaciones.
Interesa buscar las soluciones comunes a todas ellas. En nuestro caso trataremos con sistemas de ecuaciones lineales, donde cada ecuación es lineal.
Entonces un sistema de m ecuaciones lineales con n incógnitas será de la forma:
Encontrar una solución del sistema es encontrar n números reales ordenados, x1, x2, ... , xn, que satisfagan todas las ecuaciones.
Un sistema en el que todos los términos independientes son cero se llama homogéneo.
Estos sistemas siempre tienen la solución x1 = x2 = ... = xn = 0, llamada solución trivial o impropia.
Atendiendo al número de soluciones los sistemas de ecuaciones pueden ser:
- Compatibles: Con solución.
- Compatible determinado: Solución única.
- Compatible indeterminado: Más de una solución (lo que equivale a que habría infinitas soluciones).
- Incompatibles: Sin solución.
Expresión matricial de un sistema
Las matrices nos dan la posibilidad de expresar un sistema en forma matricial:o bien A · X = B, donde A es la matriz de los coeficientes, X es la matriz de las incógnitas y B la de los términos independientes.
Sistemas equivalentes
- Cambiar el orden de las ecuaciones del sistema.
- Multiplicar o dividir los dos miembros de una ecuación por un número distinto de 0.
- Suprimir una ecuación que sea combinación lineal de las otras.
- Sustituir una ecuación por una combinación lineal de ella y de las otras.
Método de eliminación de Gauss
- La/s fila/s nulas están en la parte inferior de la matriz.
- Un elemento principal (o pivot) de una fila es el primer número distinto de cero (comenzando desde la izquierda). El pivot de una fila debe estar en una columna más a la derecha que los pivots de las filas superiores.
- Si aparece alguna ecuación de la forma 0 = k, el sistema es incompatible.
- No aparecen ecuaciones de la forma 0 = k, el sistema es compatible
- Determinado si el número de ecuaciones y de incógnitas es igual.
- Indeterminado si el número de ecuaciones es menor que el de incógnitas
Resolución de sistemas por inversión de la matriz de los coeficientes
A · X = B ⇒ A-1· A · X = A-1· B ⇒ In· X = A-1· B ⇒ X = A-1· B
Observa que cuando A es cuadrada e inversible, el sistema es compatible determinado.
Teorema de Rouché-Frobenius
El sistema es compatible ⇔ r(A) = r(A')
Escribimos el sistema como se indica a continuación:- Si el sistema es compatible, existe un conjunto de valores x1, x2, ... , xn, solución del sistema, se cumple A1x1 + A2x2 + ... + Anxn = B, donde las Ai son las columnas de A. Luego B es combinación lineal de las columnas de A y por lo tanto r(A') = r(A).
- Si r(A) = r(A'), la columna formada por los términos independientes que las diferencia, será combinación lineal de las anteriores, A1x1 + A2x2 + ... + Anxn = B, luego (x1, x2, ... , xn) es solución del sistema, que por tanto, es compatible.
- Si r(A) = n ⇒ el sistema es determinado.
- Si r(A) < n ⇒ el sistema es indeterminado.
Resumen: Clasificación de un sistema nxn por determinantes
Dado un sistema de ecuaciones lineales AX=B , con A∈Rn×n:
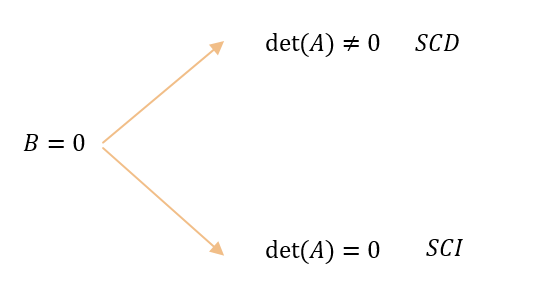
Si el sistema de ecuaciones lineales es homogéneo: