Resultados de aprendizaje de la 2ª edición del curso "Edición de libros interactivos"
Escrito por José R. Galo SánchezClausura del curso (5 de noviembre de 2021)
Resultados de aprendizaje
|
La clausura del curso se realizó el día 5 de Noviembre de 2021. Un resumen, no exhaustivo, de los resultados de aprendizaje alcanzados se puede observar en el siguiente vídeo: ¡Enhorabuena a todos los participantes! y gracias por compartir su saber con los discentes y docentes de la aldea global. Y ¡enhorabuena! y agradecimiento a la Institución Universitaria Pascual Bravo por la gestión de este curso y su ofrecimiento altruista para que cualquier interesado de cualquier lugar lo haya podido cursar o que pueda cursarlo en diferido mediante los vídeos grabados en las sesiones en línea realizadas. En nuestro subproyecto iCartesiLibri iremos publicando estos magníficos libros interactivos. |
Curso de diseño de objetos interactivos con DescartesJS
Escrito por Juan Guillermo Rivera BerríoCurso DescartesJS cohorte 2021-2
Diseñar recursos educativos abiertos en formato de escenas interactivas con la herramienta de autor Descartes JS, que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente.
Encuentros semanales
Primera etapa: 19 de nov 2021 hasta 8 dic 2021 (4 sesiones)
Segunda etapa: 14 ene 2022 hasta 6 feb 2022 (4 sesiones)
Agenda
1. Introducción (herramientas de autor, plantillas)
2. Editor y espacios (espacios 2D, 3D yHTMLIframe)
3. Imágenes
4. Algunos elementos mínimos de Programación
5. Controles (pulsador, barra, audio, vídeo, texto, botón, radio botón, etc.)
6. Vídeos interactivos
7. Gráficos
8. Variables y funciones
Segundo número de la "Revista Digital RED Descartes"
Escrito por José R. Galo SánchezEl segundo número de nuestra publicación periódica: "Revista Digital de la RED Descartes" —panhispánica, educativa e interactiva— ha llegado rápido. Hemos querido satisfacer a nuestros lectores y que este primer año contara con los dos números que han de corresponderse con la periodicidad semestral que hemos elegido. Si bien el primer número lo publicamos en agosto, hace tres meses, nuestras ganas de compartir y divulgar han actuado cual filtro relativista y han logrado estirar el tiempo —en tres meses hacer lo correspondiente a seis—, o según se mire quizás sea contraer —convertir un semestre en un trimestre—. Y nosotros, o mejor dicho nuestros dispuestos articulistas han volcado su saber y buen hacer en unos contenidos diversos y atractivos... ¡Puedes comprobrarlo fácilmente! Basta que cliques con el ratón o pulses con tu dedo sobre la imagen que tienes un poquito más abajo y seguro que más de un autor conectará su saber con algunos de tus focos de interés. Y, para poder satisfacerte lo máximo posible, necesitamos tus comentarios y observaciones. ¡Conecta con RED Descartes! Y si deseas compartir, tus artículos serán muy bienvenidos.
| Para acceder al segundo número pulse sobre la imagen |
Como se indica en el editorial de este segundo número, se constata cómo la crisis pandémica del COVID y las crisis colaterales laborales, económicas y energéticas han producido un acercamiento al tercer entorno —según lo denomina el filósofo y matemático Javier Echevarría— y, en particular, el desarrollo de contenidos educativos digitales se ha incrementado sustancialmente. El modelo educativo se ha visto forzado a cambiar o al menos a asomarse un poquito a ese tercer entorno. En nuestra RED Descartes hemos experimentado ese crecimiento productivo y también en nuestro servidor de contenidos, cuya puerta no tiene llave alguna, se ha constatado ese acercamiento a través de un incremento sustancial en las estadísticas de accesos. Consecuentemente, no es de extrañar que algunos de los contenidos de este número de nuestra revista evidencien esa prolífica producción y, a su vez, ellos le abrirán o acercarán a otros mundos virtuales alternativos mediante los hiperenlaces que incluyen.
Pero no sólo de recursos tecnológicos viven los docentes/discentes del tercer entorno y, por ello, también podremos o tendremos que abrir bien los ojos y a su vez destaponar concienzudamante nuestros oídos para poder constatar la percepción virtual de nuestra mente o el sinsentido de nuestros sentidos que es ocasionado por las denominadas ilusiones ópticas y también en las menos tratadas ilusiones acústicas. Impresionantes ilusiones que aquí se catalizan mediante la utilización de escenas interactivas, las cuales colaboran a su mejor percepción o, si lo miramos desde otra perspectiva, a magnificar su equívoco. ¡Bueno! este mundo de la ilusión se convierte en un mundo engañoso o liante, de ahí su atractivo, puesto que nos descoloca.
Y podremos también aprender de herramientas tecnológicas que nos permiten construir el pensamiento computacional, como la Micro:bit, o a construir mundos virtuales a través de DescartesJS.
Pero un exceso de tercer entorno embriaga y, a veces, nos adentra en mundos difusos. Por ello, siempre es necesario ¡a la fuerza, al menos por mera necesidad biologica! regresar al primer y al segundo entorno. Y estos no pueden ser ajenos a nuestra práctica educativa y, consecuentemente, experiencias constructivas con elementos tangibles, con recursos manipulativos, y fomentando la relación y cooperación directa entre personas, trabajando codo con codo, podremos planificar la construcción de un domo o cúpula geodésica. ¿Algo fácil, verdad?... Pues, por favor, ¡descienda de su tercer entorno! y experimentará cómo las ideas, los conceptos, necesitan de una concreción plástica para verse matizados y realmente comprendidos en base a la evidencia y lo que nuestra mente ve trivial o fácil cambia cuando ha de plasmarse en la realidad.
¡Quedáis invitados a publicar vuestros artículos en nuestra revista! Como referencia para la composición de su contenido podéis consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Octava y última sesión de la 2ª edición del curso "Edición de libros interactivos"
Escrito por José R. Galo SánchezOctava sesión (22 de octubre de 2021)
|
8A.
|
Más...
Proyecto de investigación en AJDA (III)
Escrito por Jesús Manuel Muñoz CalleEn Julio de 2021 se ha defendido y publicado un nuevo Trabajo Final de Grado dentro del Proyecto de Investigación que llevan conjuntamente el departamento de Ingeniería Telemática de la ETSI de la Universidad de Sevilla y el Proyecto AJDA.
Su autor ha sido Guillermo Mejías Climent y se titula "Aplicación web para la educación mediante gamificación sobre el Proyecto AJDA (Aplicación de Juegos Didácticos en el Aula) con funcionalidades de gestión de ficheros de preguntas". Este trabajo profundiza y amplía el realizado por Carlos Ramos León, 2019 y se centra en la gestión de ficheros de preguntas de la juegos didácticos de AJDA.
A continuación citamos las principales aportaciones y mejoras del mismo:
- Se desarrolla y mejora el generador de ficheros de preguntas para los distintos tipos de juegos de AJDA.
- Se implementa la posibilidad de importar y exportar estos ficheros de preguntas a diferentes formatos: pdf, doc, csv, xml, txt.
- Se mejora e introducen nuevas funcionalidades en el buscador de ficheros y de preguntas.
¿Estás buscando actividades con ejercicios para practicar las medidas horarias?
En este artículo te proponemos dos objetos de aprendizaje interactivos para el aprendizaje de las diferentes maneras de expresar el tiempo. Son actividades dirigidas, principalmente, al alumnado de Ciclo medio y superior de primaria.
Los dos objetos pertenecen al proyecto Canals, un subproyecto de la RED que está formado por unidades desarrolladas con la herramienta DescartesJS. Se basan en materiales elaborados por la reconocida profesora Maria Antònia Canals.
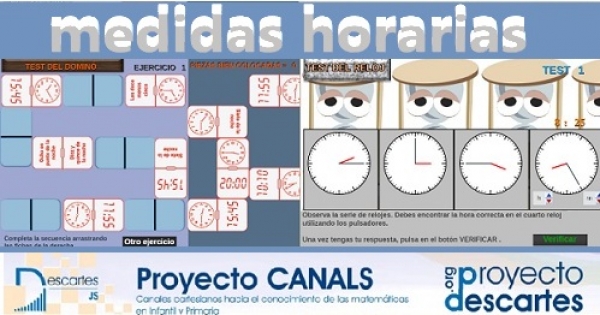
Dominó de medidas horarias: Dominó formado por 28 rectángulos, en el que se combinan diferentes maneras de expresar la hora por escrito: lenguaje verbal, lenguaje numérico, notación típica del reloj digital, y esquema de un reloj de esfera dibujado.
El test del reloj: Escena que presenta un test para determinar la serie formada por diferentes medidas horarias.
Para trabajar en el aula te proponemos insertar estos objetos en un blog.
En el siguiente vídeo puedes ver una pequeña muestra de las actividades y los pasos a seguir para su inserción en el blog.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
