Día Internacional de la Mujer y la Niña en la Ciencia con RED Descartes - 2022
Escrito por José Antonio Salgueiro GonzálezUn año más, desde RED Descartes queremos aportar nuestros recursos y colaboración para celebrar la efemérides del "Día Internacional de la Mujer y la Niña en la Ciencia", a la vez que animamos a programar y desarrollar actividades en el aula con nuestro alumnado para cumplir con los objetivos establecidos:
- Visibilizar el trabajo de las mujeres que se dedican a las áreas STEM (Science, Technology, Engineering and Mathematics), creando así referentes femeninos para la infancia que puedan contribuir a la elección de estas áreas como carreras profesionales.
- Conocer los diferentes factores que afectan a la situación actual de la mujer en las áreas STEM para fomentar prácticas que conduzcan a su eliminación y alcanzar la igualdad de género en el ámbito científico.

| JUEGO DIDÁCTICO SOBRE GRANDES CIENTÍFICAS |
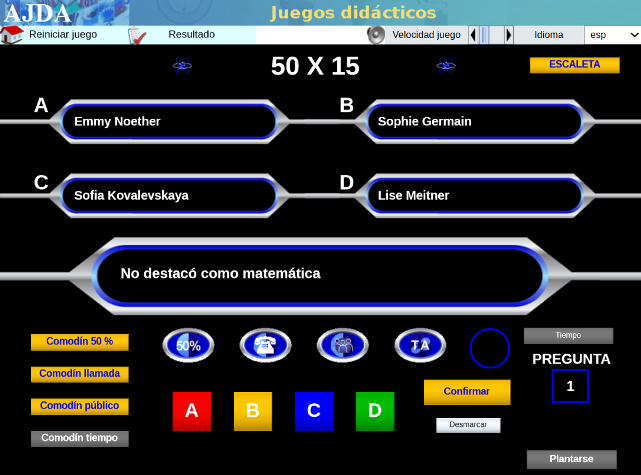
El juego es una de las estrategias didácticas de gran valor que motiva a nuestro alumnado y que se potencia con las tecnologías de la información y la comunicación. Así que os dejamos el que ha creado nuestro compañero Jesús M. Muñoz Calle, del proyecto Aplicación de Juegos Didácticos en el Aula, para difundir algunos de los decubrimientos y avances científicos gracias a la mujer, con algunas capturas de pantalla por si fueran necesarias. Es idóneo para organizar una pequeña competición en el aula proyectado desde la pizarra digital interactiva.
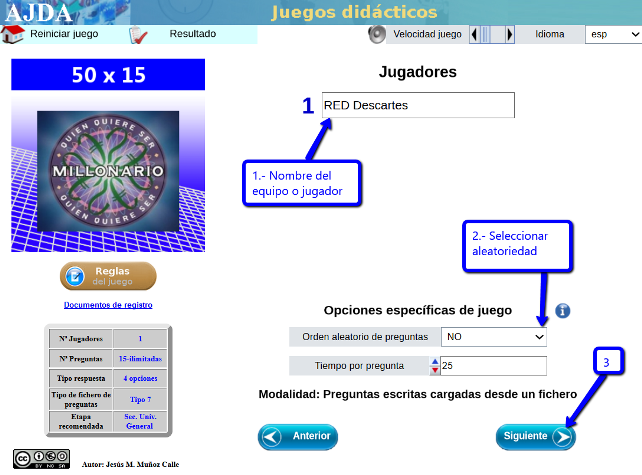
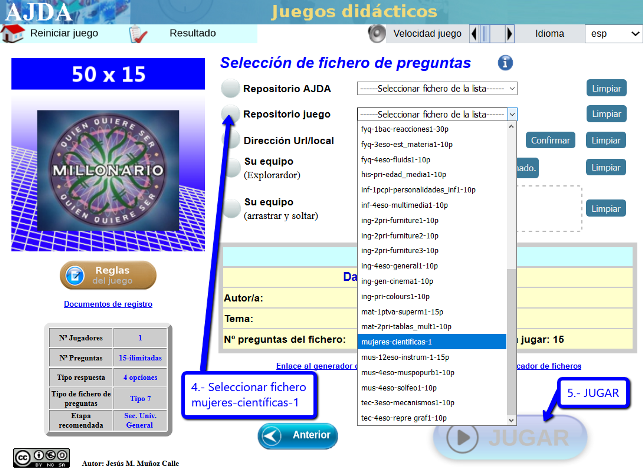
| LA MUJER EN LA CIENCIA |
"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. Pues bien, de este proyecto hemos seleccionado las siguientes entrevistas a grandes matemáticas de la historia, cuyas voces son interpretadas por científicas del ámbito educativo. Así, aportamos los siguientes recursos:
- Entrevista a Hipatia de Alejandría, interpretada por Eva Mª. Perdiguero Garzo, profesora de matemáticas.
- Entrevista a Sofía Kovalévskaya, interpretada por Marta Macho Stadler, matemática y divulgadora científica.
- Entrevista a Emmy Noether, interpretada por Elena Vázquez Abal, matemática y divulgadora científica.
- Entrevista a Ada Lovelace, interpretada por Montse Gelis Bosch, profesora de matemáticas.
- Entrevista a María Gaetana Agnesi, interpretada por Elena Ramírez Ezquerro, profesora de matemáticas.
Para descubrir al personaje misterioso, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje:
- Puzle dedicado a Hipatia de Alejandría
- Puzle dedicado a Sofía Kovalévskaya
- Puzle dedicado a Emmy Noether
- Puzle dedicado a Ada Lovelace
- Puzle dedicado a María Gaetana Agnesi
| CONTRIBUCIONES DE ALUMNAS A LA CIENCIA |
Son varios los proyectos difundidos desde el portal de RED Descartes donde las alumnas son protagonistas y divulgadoras de la ciencia, especialmente de la matemática. Así, hemos seleccionado con motivo del día 11 de febrero las siguientes contribuciones y aportaciones de alumnas a la ciencia, clasificadas por etapa educativa, con objeto de que puedan usarse en las pizarras digitales de las aulas, en los espacios virtuales de aprendizaje, abrir debates y plantear la actividad que cada docente determine.
| CIENTÍFICAS EN INFANTIL Y PRIMARIA |
- Color y cantidad. Pensamos juntos para resolver una situación
- Significado de perímetro
- Experiencia de pensamiento autónomo en resolver un problema. Alumna de 3 años
- Ángulo recto para construir un metro cuadrado en papel
- Alumnas de cuarto de primaria en la investigación y aprendizaje de capacidades y su expresión en lenguaje matemático
| CIENTÍFICAS EN SECUNDARIA |
- Antonia y Maite nos enseñan la aplicación de la maqueta en la semejanza de figuras
- Ángela y Cristina nos muestran la utilidad de la maqueta en el aprendizaje de la semejanza
- Alba y Ángela nos enseñan a discutir y resolver sistemas de ecuaciones con Descartes y herramientas tecnológicas
- Natalia y Celeste comunican y comparten ideas matemáticas con Descartes
- Carmen, divulga la simplificación de fracciones algebraicas y la suma de las mismas
- Rocío, divulga la resolución de una unidad liberada de PISA
- Virginia, María y Laura, divulgan una técnica de resolución de problemas
- María del Castillo e Irene, divulgan las operaciones con fracciones algebraicas
- María y Claudia entrevistan a Sofía Kovalévskaya, con su matrimonio de conveniencia para poder estudiar matemáticas.
- Mireia y María entrevistan y divulgan la obra de Sophie Germain, la primera mujer en acceder a la Academia de Ciencias de París.
- Antonia y Maite entrevistan y divulgan la vida y obra de Ada Lovelace, con su reflexión sobre la mujer en la ciencia y el techo de cristal.
- Clara, Ángela y Cristina, entrevistan y divulgan la vida y obra de Mary Cartwright, a quien conocí gracias a mis alumnas.
- María y Julia, entrevistan y divulgan la vida y obra de Mary Somerville, conocida como "La Reina de las ciencias del siglo XIX".
- Ángela y Alejandro, entrevistan y divulgan la vida y obra de Euclides
| CIENTÍFICAS EN BACHILLERATO |
- María, divulga la resolución de triángulos rectángulos
- Claudia y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Margarita y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Ángela y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Laura y Ángela, ponen a prueba tus conocimientos de Matemáticas-1
- Zuleima y Raquel, ponen a prueba tus conocimientos de Matemáticas-1
- Ana y Virginia, ponen a prueba tus conocimientos de Matemáticas-1
- María y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Lucía e Ismael, ponen a prueba tus conocimientos de Matemáticas-1
- Ángela y Laura y ponen a prueba tus conocimientos de Matemáticas-2
- Joana y Ana ponen a prueba tus conocimientos de Matemáticas-2
- Aurora, Alba, Ángela y Teresa recrean la importancia de la seguridad al desarrollar experiencias en el laboratorio
- Carmen, Joana, Beatriz y Ángela muestran, de forma desenfada, las normas en el laboratorio de Química.
| CIENTÍFICAS EN LA UNIVERSIDAD |
- Sofía, Marcos y Juan Luis nos enseñan a calcular el volumen de un cono por integrales triples.
- Daniela, Beatriz y Jonathan nos muestran algunas aplicaciones de las coordenadas esféricas.
- Tania y Samuel nos enseñan a cambiar de coordenadas cartesianas a polares y cilíndricas.
- Lucía y Alicia nos presentan el cálculo de áreas de figuras planas utilizando integrales dobles.
- Daniela, Beatriz y Jonathan calculan el aforo de un recinto para conciertos.
- Lucía y Alicia nos explican cómo calcular el volumen del Atomium de Bruselas.
- Almudena y Clara nos enseñan a calcular el gradiente de un campo escalar y el uso correcto del operador nabla.
- Clara y Almudena nos muestran el rotacional y la divergencia de un campo vectorial.
- Tania y Samuel nos presentan la resolución de ecuaciones diferenciales con variables separables.
- Andrea y Andrés nos enseñan la función delta de Dirac, sus propiedades y algunas aplicaciones.
Octava sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezOctava sesión (4 de febrero de 2022)
|
1A.
|
Séptima sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezSéptima sesión (28 de enero de 2022)
|
1A.
|
Volumen VII de la publicación periódica "Recursos educativos interactivos de RED Descartes"
Escrito por José R. Galo SánchezNuestra organización no gubernamental "Red Educativa Digital Descartes" (RED Descartes) ha publicado el séptimo volumen de su publicación periódica anual
Recursos educativos interactivos de RED Descartes
ISSN: 2444-9180 Dep. Legal: CO-2079-2015
Este volumen consta de cuatro números y recogen todos los materiales que se han desarrollado a lo largo del año 2021 y aquellos que han sido modificados durante dicho periodo. Los contenidos de cada número son los siguientes:
- Vol. VII-Núm. 1:
- AprendeMX.
- ASIPISA.
- Canals.
- Competencias.
- ED@D 1º a 3º de ESO.
- Geográfica.
- Ingeniería.
- Miscelánea.
- Problemas.
- Pizarra Interactiva.
- Plantillas.
- Prometeo.
- Telesecundaria.
- Un_100.
- Unidades didácticas.
- Vol. VII-Núm. 2:
- ED@D 4º de ESO.
- Vol. VII-Núm. 3:
- iCartesiLibri.
- Vol. VII-Núm. 4:
- AJDA, Aplicación De Juegos Didácticosa en el Aula.
Estos DVD se pueden descargar desde la zona de descargas de nuestro espacio web.
Enhorabuena a todas y todos los socios de RED Descartes por la publicación de este nuevo volumen, el cual ayudará a la difusión del trabajo altruista que realizan en pro de la Educación en la aldea global gracias a las TIC.
Más...
Sexta sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezSexta sesión (21 de enero de 2022)
|
1A.
|
En 2022 se cumple el noveno año del nacimiento del Proyecto Aplicación de Juegos Didácticos en el Aula AJDA, integrado dentro la Red Educativa Digital Descartes. Llegado a este punto, en este artículo se pretende realizar un pequeño balance en cifras de los recursos y actividades desarrolladas en este proyecto educativo abierto, gratuito y universal, las cuales se distribuyen en su Web, Blog, Canal de Youtube y DVD.
Actualmente hay publicados 510 juegos didácticos, los cuales se pueden agrupar o clasificar atendiendo a diferentes criterios. Uno de ellos es por el tipo de cuestiones que se plantean y que se resume en la siguiente tabla:
- "Integración de herramientas de gamificación en plataformas de Enseñanza Virtual", Pedro García Frutos, 2018.
- "Aplicación web para la creación y modificación de ficheros de juegos para la Aplicación de Juegos Didácticos en el Aula (AJDA)", Carlos Ramos León, 2019.
- "Aplicación Web multiusuario para gamificación educativa en el aula basada en Websocket", Alberto Jiménez Vázquez, 2019.
- "Aplicación de gestión de juegos para la educación con framework Spring y Primefaces",Ana María Lobón Roldán, 2020.
- "Aplicación web para la educación mediantegamificación sobre el Proyecto AJDA (Aplicaciónde Juegos Didácticos en el Aula) confuncionalidades de gestión de ficheros de preguntas", Guillermo Mejías Climent, 2021.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)














 CONTACTO
CONTACTO
