Mostrando artículos por etiqueta: universidad
Título: Sitios singulares del Nautilus en el primer verticilo
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
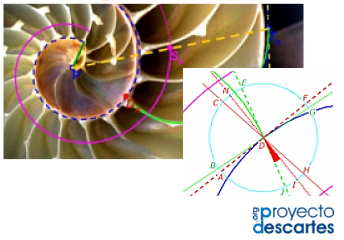
En el primer verticilo del Nautilus encontramos algunos sitios que podemos catalogar como singulares, pues se muestran como específicos respecto a su entorno o que aparentemente se salen de la uniformidad cordobesa que hemos ido detectando y desgranando en los artículos publicados anteriormente sobre la "Ontogenia matemática del Nautilus". Pero, hasta en estas situaciones, la proporción cordobesa y la espiral cordobesa aparece sin más que rascar matemáticamente en la concha del Nautilus, por supuesto con gran mimo.
Esos sitios singulares son:
- La concha embrionaria.
- El sifúnculo en la segunda cámara septal y su relación con la ampliación del fragmacono en el primer septo.
- La confluencia de la pared dorsal con la concha embrionaria en la fase de transición entre el primer y segundo verticilo (cámaras octava, novena y décima).
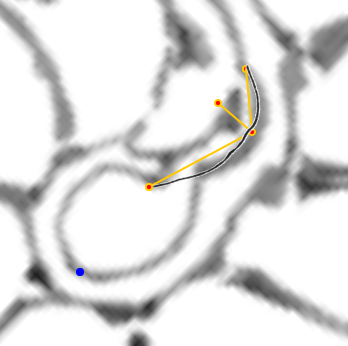 |
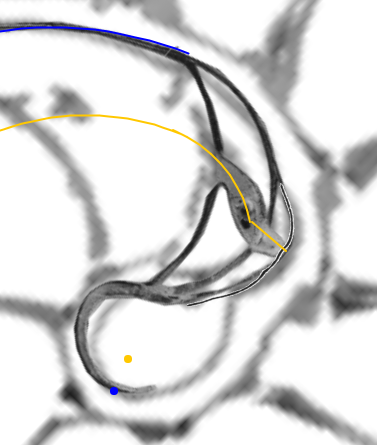 |
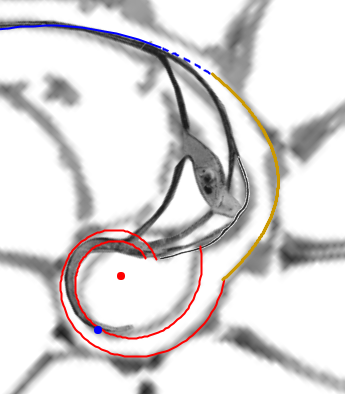 |
| La concha embrionaria | El sifúnculo en la segunda cámara septal y la ampliación del fragmacono |
La pared dorsal en la transición entre el primer y segundo verticilo |
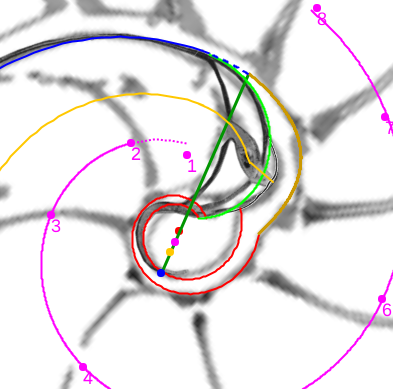
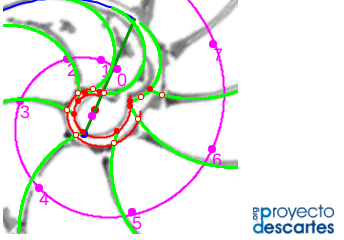
En este artículo analizamos estas singularidades y encuadramos su modelado en el contexto cordobés del Nautilus. Para ello, acudimos y aplicamos la invariante enunciada desde el inicio y que reiteradamente hemos ido aplicando en toda la modelación: "Todo punto interior a la concha o sobre ella se obtiene como la intersección de dos espirales cordobesas, una longitudinal similar a la ventral y otra transversal similar a la septal". La siguiente escena interactiva ha servido de base para el análisis de estos sitios singulares.
Modelando los sitios singulares del Nautilus en el primer verticilo
Pulsad sobre la imagen para acceder a la escena
En el siguiente pdf (o desde este enlace) tienen desarrollados los contenidos de este artículo
Ontogenia matemática del Nautilus VII
Aquí, hemos dado continuidad a los artículos anteriores (I, II, III, IV, V y VI) y por fin, creo, he cumplido mis deberes, si bien no seré yo quien excluya la posibilidad de que puedan surgir nuevas cuestiones, pues eso es lo que ha ido aconteciendo a lo largo de estos meses en los que les he ido relatando mi investigación a través de este blog de RED Descartes. Pero, independientemente de que afloren nuevas cuestiones o no, sí les indico que éste no será este el último artículo de esta serie, tengo que tratar de completarla adecuadamente y, por tanto, estimo necesario recopilar todo lo expuesto en una escena interactiva de Descartes o en una animación o en un gif animado o en un recurso similar o... y así mostrar la ontogenia matemática del Nautilus en un hilo temporal que recoja su crecimiento, si bien real y paradójicamente éste ha de ser atemporal porque en la literatura existente los datos relativos a los tiempos en el crecimiento de la concha son muy genéricos o yo no he logrado localizarlos. En la siguiente animación reflejamos el modelo uniforme del Nautilus y próximamente podremos aportar el modelo ontogénico (de nuevo les pido un poquito más de paciencia, no nos demos un atracón que pueda conducir a una indigestión).

Modelo uniforme del Nautilus
Y también tendremos que desarrollar alguna cosita en 3D ¿no les parece?... Hasta pronto...

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: La fórmula más bella
Sección: iCartesiLibri
Bloque: Análisis matemático
Unidad: Historia del Ánalisis matemático y del Cálculo
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autores: Pedro Roses Amat
ISBN: 978-84-18834-41-7
 versión en pdf con enlace a los interactivos
versión en pdf con enlace a los interactivos
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Física. Volumen 1
Sección: iCartesiLibri
Bloque: Física
Unidad: Mecánica
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autor: Juan Gmo. Rivera Berrío
Diseño del libro: Juan Gmo. Rivera Berrío
Obra derivada: OpenStax University Physics, University Physics Volume 1
ISBN del volumen: 978-84-18834-40-0
ISBN de la obra completa: 978-84-18834-39-4
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Compostaje y lombricultivo
Sección: iCartesiLibri
Bloque: Ciencias
Unidad: Ciencias agroindustriales
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autor: Yezid Gallego Oviedo
Revisión y edición: Juan Gmo. Rivera Berrío
ISBN: 978-84-18834-38-7
 versión en pdf con enlace a los interactivos
versión en pdf con enlace a los interactivos
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Química en al vida cotidiana: el jabón
Sección: iCartesiLibri
Bloque: Química
Unidad: Reacciones químicas
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autor: Margarita Patiño-Jaramillo, John Jairo García-Mora, Sonia Jaquelliny Moreno-Jiménez
Diseño del libro: Juan Gmo. Rivera Berrío
ISBN: 978-84-18834-37-0
 versión en pdf con enlace a los interactivos
versión en pdf con enlace a los interactivos
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Septos del Nautilus en el primer verticilo. Puntos notables.
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Modelo tangencial de los septos y de la pared ventral en el segundo y tercer verticilo del Nautilus
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
En este nuevo artículo sobre la ontogenia matemática del Nautilus, después de haber modelizado los septos en el segundo y tercer verticilio bajo el invariante de tangencialidad, nos adentramos en la modelización de los septos en el primer verticilo. Esta primera fase de crecimiento vimos que se muestra diversa y con apariencia poco regular, cambiante (menor número de cámaras septales, ocho frente a las dieciséis de la etapa juvenil y adulta, con secciones y amplitudes que cambian como necesidad biológica para alcanzar la flotabilidad) y, ahora, ha llegado el momento de mostrar el modelo matemático que da explicación a esta etapa e introduce la regularidad esperada que parecía no acaecer, pero que queda al descubierto bajo la perspectiva matemática. De nuevo, el hecho de que intervengan dos espirales con diferente polo, en este caso la espiral de la pared ventral y la espiral de los polos de los septos, conduce a proporciones variables entre los radios vectores y consecuentemente a que se formen septos con factores de escala variables. Ello nos conduce y permite determinar las ecuaciones de los septos, los puntos de tangencia con la pared ventral y los de intersección con la pared dorsal (para ello necesitaremos introducir un grosor en el modelo matemático de esa pared, que es lo que físicamente acontece).
Completaremos el contenido de este documento agrupando y relacionando entre sí diferentes puntos que se han ido detectando en este análisis. Unos que denominamos notables, porque matemáticamente son los que establecen el modelo matemático y dan explicación causal al mismo, y que son polos de diferentes espirales. Y otros que catalogaremos como destacables, posible fuente de inspiración matemática futura, y que son centros desde los que algunos objetos se observan con perspectiva angular constante.
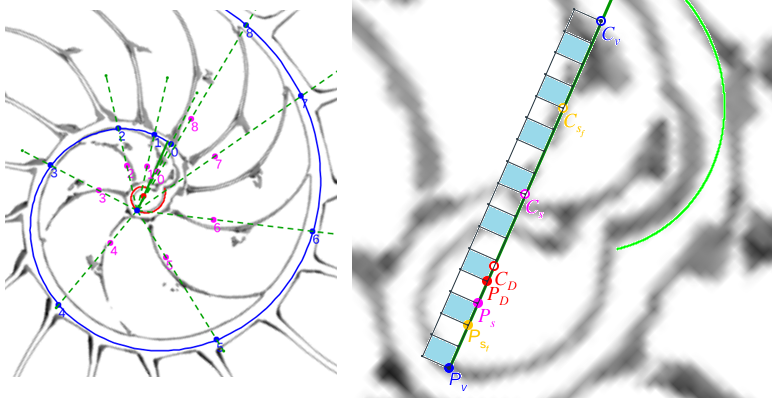 |
|
| Propociones entre los radios vectores de la espiral ventral y los de la espiral de los polos de los septos | Puntos notables y destacables |
Así pues, doy continuidad a los artículos anteriores (I, II, III, IV y V), con un contenido adicional que espero sea de su interés —¡para mí es siempre una satisfacción! ir pudiendo relatarles progresivamente lo que, poco a poco, me cuenta la concha de este animalito—, y he de adelantarles que serán necesarios algunos artículos adicionales porque aún nos quedan secretos que dilucidar en esta ontogenia, en particular lo que acontece en la transición de la fase embrionaria (primera y segunda cámara septal) donde el sifúnculo cambia abruptamente de posición, y en la fase de transición entre el primer y segundo verticilo (cámaras octava, novena y décima) donde al finalizar la primera vuelta se produce el encuentro del fragmacono con la concha embrionaria. Y también habrá que abordar la síntesis o resumen final, es decir, plasmar y reproducir ese modelo ontogénico de la concha del Nautilus.
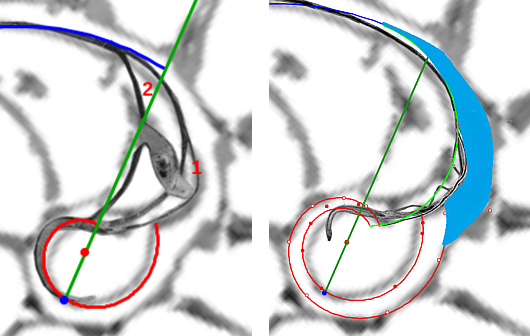 |
|
| El sifúnculo en la segunda cámara septal | Transición entre el pimer y segundo verticilo |
Como observamos, una mirada atenta y un continuo deseo de comprensión nos hace ir visualizando cada vez más detalles que inicialmente pueden parecer nimios, pero que finalmente se han ido mostrando como retos cuya resolución es de interés. Todo ello, a costa de que a ustedes a lo mejor les ocurra como a mi sobrina nieta (Aurora, cerca de los cuatro años) que ayer, al verme una vez más delante de la pantalla de mi ordenador, indagando la imagen de la sección del Nautilus con diversos objetos matemáticos superpuestos, la cual ya ha observado en multitud de ocasiones y quizás hayan sido demasiadas para ella, dijera: "¡Tita!, ¡el tito todavía no ha hecho sus deberes!". Por tanto, espero poder ir finalizando mis deberes, que realmente no son más que satisfacciones aunque requieran esfuerzo y dedicación, y que en el trancurso hacia su final les pueda tener como lectores y juntos podamos desarrollar nuestra vocación como μαθηματικός (mathēmatikós) o amantes del conocimiento.
En el siguiente pdf (o desde este enlace) tienen desarrollados los contenidos de este artículo
Ontogenia matemática del Nautilus VI

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Curvas y superficies paramétricas (segunda edición)
Sección: iCartesiLibri
Bloque: Geometría
Unidad: Geometría plana y tridimensional
Nivel/Edad: Bachillerato y Universidad (16 años o más)
Idioma: Castellano
Autores: Juan Guillermo Rivera Berrío y Josep Maria Navarro Canut
ISBN: 978-84-18834-35-6
 versión en pdf con enlace a los interactivos
versión en pdf con enlace a los interactivos
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional






.png)