DESCUBRIMOS al Personaje Misterioso (V)
Escrito por Ángel Cabezudo BuenoLa semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a un matemático, astrónomo y físico alemán que vivió desde 1777 a 1855. Contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la geodesia, el magnetismo y la óptica. Denominado como "el príncipe de los matemáticos" es considerado uno de los científicos que más influencia ha tenido en la historia.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través de una escena de DescartesJS que presenta tres imágenes que se pueden ir seleccionando sucesivamente a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen representa una composición alegórica que incluye la efigie de nuestro personaje inmerso en el espacio astronómico que tanto estudió y en donde se observan diferentes elementos matemáticos vinculados a su obra científica. También podemos reconocer su firma autógrafa.
La segunda imagen es un dibujo que recrea la historia de nuestro personaje a los 10 años, en el aula donde es instruido en aritmética, sentado en su pupitre con sus compañeros y donde su profesor les plantea en la pizarra el problema de sumar todos los números del 1 al 100.
La tercera imagen representa la parte ilustrada en el anverso de un billete de 10 marcos emitido por el Deutsche Bundesbank (Banco Federal Alemán) y que utiliza como motivo la figura de nuestro personaje y su famosa gráfica de Distribución Normal de probabilidad.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0.
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este quinto personaje matemático y no os perdáis el sexto podcast que emitiremos el próximo día 20 de octubre en este blog de difusión.
Vamos a introducir otra unidad EDAD de 2ºESO, la correspondiente a Proporcionalidad. En el vídeo hemos intentado explicar a grosso modo las caracteriíticas de la misma:
La unidad es muy extensa y trata los siguientes contenidos:
1.Proporción numérica
Razón y proporción
2.Proporcionalidad directa
Razón de proporcionalidad
Regla de tres directa
Reducción a la unidad
3.Proporcionalidad inversa
Constante de proporcionalidad
Regla de tres inversa
Reducción a la unidad
4.Proporcionalidad compuesta
Proporcionalidad compuesta
5.Repartos proporcionales
Directamente proporcionales
Inversamente proporcionales
6.Tanto por ciento
Tanto por ciento de una cantidad
Tanto por ciento correspondiente a una proporción
7.Variaciones porcentuales
Aumentos porcentuales
Disminuciones porcentuales
Encadenamiento de aumentos y disminuciones porcentuales
Para leer recomendamos... Mes de octubre.
Escrito por Eva M. Perdiguero GarzoEsta semana volvemos a disfrutar de las posibilidades de los Juegos didácticos. La aparición del concurso televisivo Boom ha espoleado la capacidad de Jesús de crear juegos interactivos y el resultado han sido cinco versiones.
Para esta ocasión hemos seleccionado Artificieros, publicado hace un par de días.
Se trata de desactivar una bomba cortando el cable correcto de los seis que encontramos conectados a ella.
Con cada pregunta correcta podremos cortar uno y, si acertamos, desactivaremos el explosivo.
Aquí tenéis el acceso directo al juego.
Ofrece un marcador en el se van acumulando las puntuaciones de los jugadores para conocer al ganador.
Como es habitual, dispone de tres versiones: juego oral, sin preguntas y el normal con la carga de las baterías de preguntas.
Tenemos las opciones de descargar las fichas de seguimiento, generar nuestras propias preguntas, modificar el idioma de la interface o cargar preguntas disponibles en los repositorios.
En el siguiente vídeo utilizamos el juego con la interface en inglés y cargamos una batería de preguntas de las disponibles en el listado también en inglés.
Como veis las posibilidades de los juegos se abren a todas las materias.
Utilízalos.
Más...
Entrevista al personaje misterioso (V)
Escrito por Eva M. Perdiguero Garzo
Y con éste van cinco. Seguimos conociendo poco a poco a nuestros matemáticos ilustres en la historia. En nuestra entrevista anterior ¿lograste descubrir al personaje? Para nosotros era un personaje clave y muy querido. Por si aún no descubriste quién era puedes hacer en el puzle publicado.
Continuamos esta semana con el curso ya empezado con otro personaje que desde niño le encantaban las sumas y jugar con los números. A lo largo de la entrevista seguro que descubres quién es, si es así deja tu comentario en esta entrada.
La entrevista y el guión, así como el montaje ha sido realizado por Eva M Perdiguero, Ángel Cabezudo y Antonio Pérez. Y la interpretación del personaje ha sido realizada por Antonio Pérez Sanz, compañero y profesor de matemáticas del IES Salvador Dalí, Madrid. Antonio es uno de los mayores divulgadores de las matemáticas, no dejéis de visitar su blog: http://aperez4.blogspot.com.es/ y su web: http://platea.pntic.mec.es/aperez4/
El trabajo lleva licencia CC BY-NC-SA 4.0. Los efectos de sonido pertenecen al Banco de imágenes y sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
Estrategia
Estrategia
Hacer cualquier cosa que se esté haciendo de la mejor manera posible es inherente a la acción, parte de ella y muchas veces la manera de hacer eclipsa al hecho.
Conseguir hacer algo, o conseguir algo, que a priori no es evidente ni inmediato por propia iniciativa y esfuerzo produce satisfacción intelectual y muchas veces placer, particularmente cuando en el desarrollo del proceso intervienen el mundo de las formas, el mundo de las ideas, las metafísicas de ambos mundos, y las realidades paralelas con sus respectivas metafísicas.
Crear es seguir el método adecuado. Por eso la estrategia es arte.
Arte de planear y dirigir las operaciones bélicas o militares.
Arte de dirigir las operaciones militares.
Técnica y conjunto de actividades destinadas a conseguir un objetivo.
Arte, traza para dirigir un asunto.
En un proceso regulable, conjunto de las reglas que aseguran una decisión óptima en cada momento.
Camuflaje - estratega - estratégico - táctica - maniobra - habilidad - pericia
Construir - Dibujar - Pintar - Esculpir - Resolver
Tocar - Hablar - Componer - Escribir
Pensar.
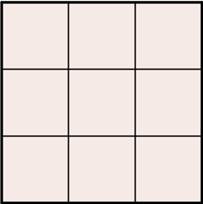 En la situación concreta que nos ocupa, en la que tenemos un cuadrado con nueve celdas iguales, las cuales debemos rellenar con los números del 1 al 9, sin repetirlos y de manera que la suma de los números de cada fila, cada columna, la diagonal principal y la diagonal secundaria sea la misma, la intuición nos indica que los números de mayor peso: 7, 8 y 9 no pueden estar en la misma fila, columna o diagonal por razones obvias. También se llega rápidamente, por los mismos motivos anteriores, a que dos de ellos no pueden estar alineados.
En la situación concreta que nos ocupa, en la que tenemos un cuadrado con nueve celdas iguales, las cuales debemos rellenar con los números del 1 al 9, sin repetirlos y de manera que la suma de los números de cada fila, cada columna, la diagonal principal y la diagonal secundaria sea la misma, la intuición nos indica que los números de mayor peso: 7, 8 y 9 no pueden estar en la misma fila, columna o diagonal por razones obvias. También se llega rápidamente, por los mismos motivos anteriores, a que dos de ellos no pueden estar alineados.
Entonces esas tres cifras deben ocupar las posiciones siguientes.
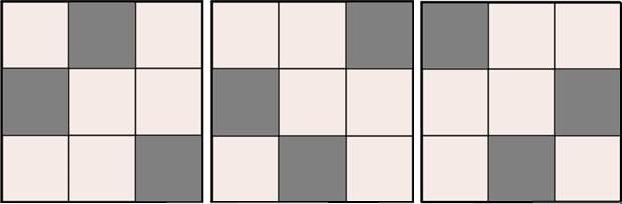
Por señalar algunas de ellas.
Con un número mínimo de pruebas observamos que el 9 no puede ir en los vértices de las diagonales ni tampoco el siete pues de inmediato se produce sobresuma o necesidad de duplicidad, así que la disposición de las tres cifras mayores está perfectamente delimitada.
Ahora podríamos seguir nuestra conjetura con la cifra que va en el centro, que a poco que ensayemos resulta que únicamente puede ser el... y claro, encontrar la posición de las demás cifras es trivial.
Siguiendo esta estrategia preguntarse cuanto debe sumar cada línea es redundante pues los propios ensayos van delimitando lo que es; o no, posible para cumplir el objetivo.
Si se quiere proponer esta situación en clase y a la par desarrollar otras competencias del currículo puede usarse la intuitiva miscelánea de Salvador Calvo-Fernández Pérez "cuadrado mágico" para efectuar los ensayos hasta dar con la solución usando el siguiente enlace, o bien puede descargarse la miscelánea desde este enlace, donde también puede usarse directamente.
Para comprobar la bondad de la estrategia encontrada podemos intentar extenderla a cuadrados de 4x4, 5x5 ect. en este vídeo. Puede observarse como se crea una estrategia para cuadrados de 4x4 y a partir de dicha observación podemos extender la solución a cuadrados más complejos.
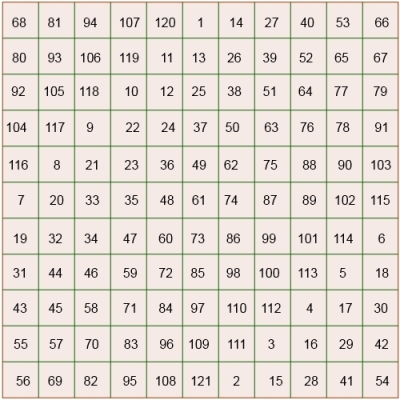
En el enlace vinculado a la siguiente imagen nos lleva a una hoja de Excel donde puede observarse el método para obtener cuadrados mágicos de hasta 11x11 pudiendose ampliar facilmente la dimensión del cuadrado y, si se desea, analizar la estrategia de construcción de los mismos.
Las misceláneas
Como hemos comprobado en este artículo para casi cualquier situación que planteemos en clase existe una miscelánea que puede ayudarnos en el desarrollo de la práctica. En el siguiente video se muestra como acceder a las misceláneas del Proyecto Descartes, como usarlas en línea o como descargarlas para su uso en local.
Desde aquí os animamos a participar en el proyecto aportando misceláneas o sugiriendo utilidades que no existan y considereis que sería conveniente disponer de ellas.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
