DESCUBRIMOS al Personaje Misterioso (VI)
Escrito por Ángel Cabezudo BuenoLa semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?”, entrevistamos a una matemática excepcional que vivió desde 1850 a 1891. Considerada como la más grande anterior al siglo XX, destacó por dos ideas fundamentalmente, como nos dijo la profesora de la universidad de Estrasburgo Michèle Audin (nacida en 1954): Su famoso teorema, asociado al nombre de Cauchy, que asombró a su maestro Weierstrass, prueba que no siempre una ecuación en derivadas parciales con coeficientes analíticos y condiciones iniciales analíticas tiene solución analítica y el estudio dificilísimo del movimiento de rotación de un cuerpo sólido alrededor de un punto fijo, cuya modelización matemática conduce a un sistema de ecuaciones diferenciales y por el que le concedieron en 1888 el Premio Bordin de la Academia de las Ciencias de París.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través de una escena de DescartesJS que presenta tres imágenes que se pueden ir seleccionando sucesivamente a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen representa el DOODLE que GOOGLE-RUSSIA dedicó el día 15 de enero de 2014 a nuestra matemática rusa en el 164 aniversario de su nacimiento.
La segunda imagen es una composición de una fotografía de nuestra matemática muy joven, quizá recién casada, poco antes de salir de su Rusia natal en 1869 para estudiar en Heidelberg y un retrato de su maestro Carl Weierstrass con quien estudió posteriormente en Berlín.
La tercera imagen representa las portadas de tres libros que tratan de nuestra matemática. Uno de ellos se menciona al final de la entrevista que la hicimos, el titulado “Demasiada felicidad” de Alice Munro, Premio Nobel de Literatura en 2013. Los otros libros son “Recordando a…” de Michèle Audin, a la que ya hemos mencionado anteriormente y “Love and Mathematics” de Pelageya Polubarinova-Kochina (1899-1999), jefa del departamento de mecánica teórica de la Universidad de Novosibirsk.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0.
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este sexto personaje matemático y no os perdáis el septimo podcast que emitiremos el próximo día 3 de noviembre en este blog de difusión.
Misceláneas. I
Las distintas utilidades de cada uno de los subproyectos de la Red Descartes están formadas por una, dos, tres o más escenas. Lo que todas las escenas tienen en común es que dependen de la librería "descartes-min.js".
Una escena es el conjunto de instrucciones contenidas entre la etiqueta 'ajs' y su cierre.
El siguiente gráfico muestra parte de una escena que Juan Guillermo Rivera Berrío incluye en el artículo digital 'Ficheros y Vectores' para la documentación técnica del editor de escenas "Descartes". También se observa la manera de insertar la escena en un documento HTML5 y de enlazar la librería que interpreta, en primera instancia, el código. Así, cualquier navegador compatible con este tipo de documentos mostrará la escena.
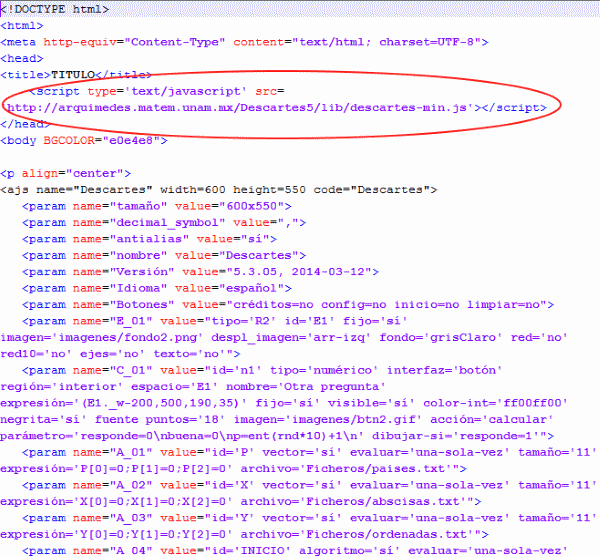
Por lo tanto las Misceláneas son utilidades digitales formadas por una o más escenas.
Para crear una escena podemos seguir, básicamente, dos métodos. Uno es utilizar un editor de texto plano como el Bloc de Notas, Gedit, TextEdit o cualquier otro, lo que exige un conocimiento de JavaScript y de la librería descartes-min.js excepcional; otro, usar el editor gráfico de escenas Descartes que supone una gran ayuda para este cometido.
En cualquiera de las dos opciones anteriores nos encontraremos con un dilema inicial: comenzar la escena desde cero; o bien, usar una escena ya elaborada como plantilla, a partir de la cual desarrollar la nuestra.
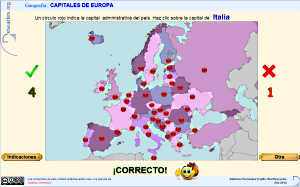
Leyendo el artículo mencionado anteriormente observé que la escena del ejemplo era, en síntesis, la aplicación "Capitales administrativas de los paises del mundo" que en otra plataforma había desarrollado y que estaba tratando de adaptar a DescartesJS. Después de analizar el código del ejemplo, decidí usarlo como plantilla para mi adaptación y este ha sido el resultado para la situación, en un mapa mudo, de las capitales administrativas de los paises de Europa.
Usar una plantilla, propia o ajena, facilita y agiliza sobremanera la creación de Misceláneas. En el vídeo siguiente se muestran algunos pormenores del inicio del proceso de creación de una utilidad. En siguientes artículos se explicará como desarrollar, terminar, probar y publicar uno de estos pequeños recursos digitales.
Siguiendo con la utlización de luegos didácticos llega el turno de Duelo de magos. Podemos acceder a la web del juego completo o directamente al juego propiamente dicho. También os dejamos el enlace para descargarlo.
Se trata de un juego en el que dos oponentes se enfrentan entre sí en un duelo a muerte a partir de las preguntas que propongamos.
Al acertar una pregunta recuperamos un poco de vida y no recibimos daño del ataque del contrario. Si por el contrario fallas, perderás parte de tu vida.Como estáis adivinando, solo puede quedar uno. Aprovechamos esa motivación innata de los alumnos por vencer a otros para que trabajen sobre la materia que elijamos.
En este juego tenemos la posibilidad de modificar el daño que recibe el jugador que falla la pregunta con lo que ajustamos la duración de la partida.
Como en todos los juegos, podemos crear nuestras baterías de preguntas o utilizar las que ya hay creadas, también variar el idioma de la interfaz.
Además encontraréis las versiones sin preguntas, solo para jugar, y para preguntas orales, así como las fichas para realizar una evaluación de la actividad.
Aquí tenéis un vídeo que comenta las posibilidades del juego y su funcionamiento, en el ejemplo hemos cargado unas preguntas Tecnología de 3º de ESO sobre electricidad con la interfaz en gallego:
Ya solo falta que se lo propongas a tus alumnos.
Y recuerda que dispones de muchos más juegos
Entrevista al personaje misterioso (VI)
Escrito por Ángel Cabezudo Bueno Por Ángel Cabezudo Bueno, 20-10-2014
Por Ángel Cabezudo Bueno, 20-10-2014
Sexta entrevista de este espacio donde vamos conociendo mejor la parte humana de los matemáticos ilustres en la Historia.
Hoy vamos a entrevistar a la mujer matemática más grande anterior al siglo XX.
Tuvo una vida muy corta, en la segunda mitad del siglo XIX, murió a los 41 años, pero vivió intensamente enfrentada a una sociedad cargada de prejuicios sobre lo que le era permitido hacer a la mujer y particularmente si ésta quería dedicarse a la investigación y la docencia de las matemáticas. Sin derecho a ocupar un asiento en un aula universitaria tuvo que aprender matemáticas de una forma privada, eso sí, de la mano de grandes maestros y gracias al atractivo de sus grandes aptitudes para esta ciencia. Consiguió finalmente una plaza vitalicia como profesora en la universidad de Estocolmo aunque la pudo disfrutar por poco tiempo.
A través de la entrevista, el personaje femenino de hoy, nos irá aportando una serie de datos importantes acerca de su vida y su obra que permitirán al oyente averiguar su identidad. Te invitamos a que dejes un comentario reflejando el nombre de esta matemática y tras una semana, el lunes 27 de octubre, publicaremos la solución a través de un puzle en este mismo blog de difusión.
Los autores del guion son Marta Macho-Stadler, profesora de Matemáticas en la Facultad de Ciencia y Tecnología de la Universidad del País Vasco-Euskal Herriko Unibertsitatea y Ángel Cabezudo Bueno, profesor de matemáticas y socio colaborador de Red Educativa Digital Descartes. El trabajo lleva licencia CC BY-NC-SA 4.0.
Marta Macho-Stadler interpreta a nuestro personaje matemático femenino.
Ángel Cabezudo Bueno es el conductor de la entrevista e interpreta las voces masculinas que intervienen.
Los efectos especiales pertenecen al Banco de sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
El montaje del audio ha corrido a cargo de Ángel Cabezudo Bueno y se ha realizado con la aplicación Audacity 2.0.5.
Más...
El ángulo de depresión y la comunicación audiovisual con Descartes
Escrito por José Antonio Salgueiro GonzálezPublicamos hoy el quinto artículo dedicado a compartir y difundir algunas propuestas didácticas para el desarrollo de la comunicación audiovisual en nuestro alumnado a través de las Matemáticas con Descartes, fomentando su creatividad e imaginación y las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales. Así, el equipo protagonista de hoy nos ilustra este concepto matemático con un ejemplo de creación propia basado en el monumento más conocido de Sevilla.
Recordamos y enlazamos a las publicaciones relacionadas con este proyecto: Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes, Comunicación audiovisual con iCartesiLibri,Resolución de problemas y comunicación audiovisual y mutimedia con Descartes y ¡Diviértete! aprendiendo con Descartes.
Esta producción audiovisual está inspirada en la página "Aplicación sobre triángulos rectángulos: cálculo del ángulo de depresión", del libro interactivo dedicado a la Trigonometría en el Proyecto iCartesiLibri, que cuenta además con Cálculo diferencial y Cálculo integral: integrando con Paco.
Proyecto Un_100. Estadística: Población y muestra
Escrito por Xosé Eixo BrancoEl proyecto Un_100 comprende 101 unidades didácticas del nivel universitario en las áreas de Matemáticas y de Física. Es un proyecto que ha contado con el patrocinio de varias instituciones mejicanas y la participación en su desarrollo de otras de Chile, Colombia, España y México. Todas las unidades tienen un mismo esquema o plantilla común, con un diseño gráfico genérico, y sobre él cada desarrollador ha incorporado los contenidos y ha elaborado su secuencia didáctica personal. Se distinguen cuatro fases o momentos: Motivación, Inicio, Desarrollo y Cierre, y se complementa con un acceso a la documentación de la unidad en la que además se incluyen los créditos.
El tema de esta unidad es la representación de la muestra de una población.
Se trata de que el usuario adquiera experiencia en el uso del concepto de muestreo.
Se parte de una pregunta de investigación, cuál es la altura de los niños o de las niñas de una cierta edad o nivel educativo en una determinada comunidad y se pasa después a su desarrollo en dos partes, en la primera se indaga cuál debe ser el tamaño de la muestra para que sea representativa y en la segunda parte la relación entre el tamaño de la muestra y la dispersión de la población. En ambos casos el usuario puede configurar la población y la muestra y observar los resultados que se muestran con los datos estadísticos y las gráficas correspondientes para un mejor análisis
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
