En esta ocasión, para adentrarnos en la estructura interna de una miscelánea, haremos una síntesis de la documentación técnica y de usuario de Descartes v5, analizando simultáneamente el editor de escenas y el código que genera.

Si navegamos por la página Capitales de Europa y observamos el código fuente de la misma vemos que las primeras líneas de este es lo que muestra la imagen siguiente.

Los parámetros de la etiqueta <ajs> de apertura de la escena y los valores de la configuración base se establecen seleccionando la opción de menú: "Botones" en el Editor de Escenas y marcando/desmarcando o eligiendo las características que queremos para nuestra utilidad según se muestra a continuación.

En el vídeo del artículo anterior mostramos como crear los espacios de dos dimensiones: R2 y HTMLIFrame que van a contener a los diversos protagonistas de la escena. En el gráfico inicial se observa el código generado con aquellas acciones. Conviene señalar que se han creado seis espacios, que el principal es el primero, con id = E1, y que en el código todos los espacios comienzan con: <param name=E...

Ahora pasamos a la opción de menú: Controles, aquí definimos los botones, campos de texto, pulsadores etc... que vayamos a necesitar. En nuestro caso particular hemos definido controles para los botones: Otra, Indicaciones,Finalizar y Continuar. También hemos definido dos controles que su única función es contener un gráfico y hemos introducido un cambio respecto al código publicado anteriormente, hemos definido un control tipo menú según muestra esta imagen,

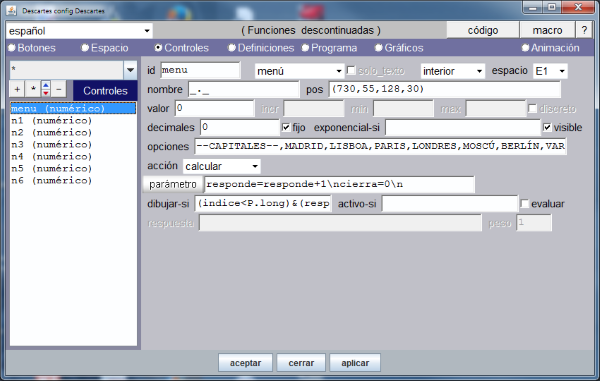
La introducción del control tipo menú ha sido debida a que vamos a elaborar una nueva versión de la utilidad basada en la selección del nombre de la capital en un menú desplegable que muestra todas las capitales administrativas del continente; en lugar de en el evento click sobre un punto en un gráfico como sucedía en la primera versión. Así conocemos si la persona que usa la utilidad ha memorizado el nombre de la capital del país y puede identificar en un mapa mudo el lugar donde está esa capital. Los resultados obtenidos con este cambio son los que pueden observarse siguiendo el siguiente enlace

El código producido por la opción Controles de esta nueva versión es:

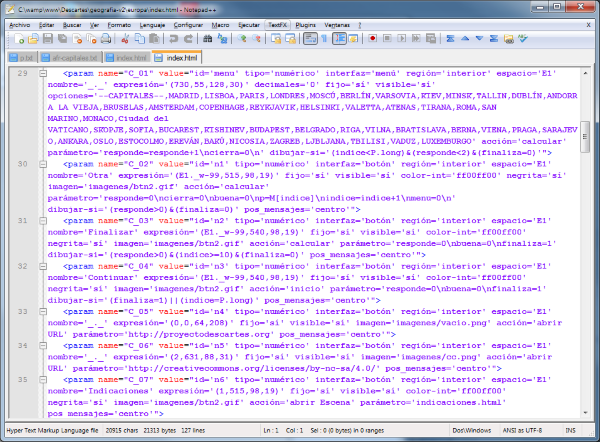
Que debe analizarse y comparar con el código de la versión anterior para apreciar las diferencias. También es conveniente observar el funcionamiento de esta versión de la utilidad para posteriormente poder comprender el significado de cada línea de código contrastandolo con el de la primera versión.

Llegados a este punto se muestra la necesidad de tener una idea clara de como deseamos que reaccione la utilidad que estamos creando a las acciones procedentes de la interactividad, esto se traduce en que debemos tener perfectamente definido cuando queremos que un control se muestre o se oculte, como y cuando debe reaccionar el control ante un evento etc, etc es decir debemos tener un buen guión para la utilidad.
En la práctica lo anterior se traduce, entre otras acciones, en que debemos tener definidas las variables necesarias para controlar las situaciones que puedan producirse. Por ejemplo en el gráfico donde se muestra el control menú puede observarse que el campo de texto parámetro tiene el contenido: responde=responde+1\ncierra=0\n el significado de esto es que cuando hagamos una selección entre las opciones del menú, el valor de la variable responde se incrementa en uno y la variable cierra toma el valor 0. Más adelante veremos como y donde se definen las variables pero todo el que tenga interés en la creación de utilidades debe acudir a la documentación que se enlaza al comienzo del artículo donde hay explicaciones más explícitas y documentadas sobre el tema.

En siguientes artículos se continuará con la explicación del código generado por las opciones: Definiciones, Programa y Gráficos del menú principal del Editor de Escenas para la elaboración de la utilidad.

En el subproyecto Un_100, del Proyecto Descartes, nos encontramos un apartado en el que podemos ver tres unidades didácticas que se resumen en el siguiente vídeo:

El Sistema planetario: Modelos geocéntrico y heliocéntrico

En esta unidad se estudian con detenimiento las trayectorias planetarias según Johannes Kepler. Se ve detalladamente la diferencia entre el sistema geocéntrico y el heliocéntrico.

El Sistema planetario: Trayectorias elípticas. Primera Ley de Kepler

Se exponen los parámetros keplerianos que se utilizan para definir una trayectoria elíptica en el espacio y se explica la Primera ley de Kepler que consiste en que todos los planetas siguen trayectorias de tipo elíptico pero cada una con sus valores característicos. Se observan las diferencias entre ellos.

El Sistema planetario: Áreas iguales en tiempos iguales. La segunda Ley de Kepler

Se presenta la Segunda Ley de Kepler que dice que los radios vectores que unen el Sol con cada planeta, barren áreas iguales en tiempos iguales. Se muestra que utilizando esta ley se puede predecir la posición de todos los planetas en todo momento a partir de las de un momento dado.