El menú del Editor de Escenas Descartes tiene las opciones principales: Botones, Espacio, Controles, Definiciones, Programa, Gráficos y Animación. En la pantalla inicial
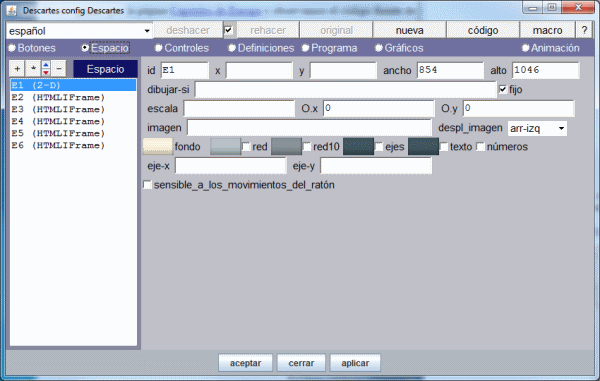
también observamos, en la parte superior, un menú desplegable para seleccionar el idioma y una serie de botones: deshacer, rehacer, original, nueva, código, macro y ayuda cuyo significado y uso se explica en documentación técnica y de usuario de Descartes v5.
Seguiremos estudiando la utilidad que hemos desarrollado en artículos anteriores, aunque vamos a introducir algunas variaciones para disponer de más código para analizar y así poder apreciar cómo, utilizando propiedades genéricas de los objetos que usamos puede escribirse un código adaptable, de forma automática, a diferentes situaciones. En síntesis el cambio principal es que en lugar de estudiar el continente europeo vamos a aplicar la utilidad al continente americano, esto conlleva una serie de cambios evidentes que pueden observarse analizando el código fuente de las nuevas páginas comparándolo con los códigos de las páginas anteriores. Continuaremos observando simultáneamente las acciones sobre el Editor de Escenas y el código que se genera, recordando que ahora toca usar la opción de menú Programa, para crear las variables, algoritmos y funciones que aún no se han implementado dándoles funcionalidad y disponer, con la opción Gráficos, los textos, imágenes y gráficos en la escena para que doten de dinamismo y sentido a la utilidad.
Antes de ver como se usan las opciones de menú: Programa y Gráficos, quizá convenga observar el aspecto y funcionamiento de la utilidad aplicada al continente americano, a continuación están los enlaces que nos lo muestran: Capitales de América (menú), Capitales de América (evento click)
El código que genera la opción de menú Programa en esta ocasión es, para la versión de la utilidad basada en la selección de la capital

Y el código generado por la versión basada en el evento click del ratón:

Las acciones que se han realizado, en el primero de los casos, con la opción de menú Programa, son las que muestra el vídeo siguiente
Ahora pasamos a la opción de menú Gráficos, aquí situamos con precisión los textos, imágenes y gráficos que vayamos a necesitar programando cuando van a estar visibles y cuando ocultos y la manera en que se van a mostrar. Debido a la extensión del artículo dejamos para más adelante el estudio de esta opción del menú.
En siguientes entradas se continuará con la explicación de la opción Gráficos del menú principal del Editor de Escenas, el análisis del código generado y otras consideraciones relativas a las Misceláneas.
Descartes en la Universidad. Miscelánea: Extremos. Multiplicadores de Lagrange
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Extremos. Multiplicadores de Lagrange
Se presenta una escena con la que se quiere mostrar la interpretación geométrica del Teorema de los multiplicadores de Lagrange en el caso particular de una función de dos variables que se encuentra sometida a una condición o restricción definida por una ecuación implícita.
Este teorema afirma que en los puntos en los que la función alcanza un extremo condicionado, el gradiente de la función es proporcional al gradiente de la función que define la condición.
Para comprobar este resultado gráficamente, la miscelánea representa, una vez introducida la expresión de la función y la definición de la curva restricción, estos dos vectores en puntos que están sobre esta curva. De esta manera, se puede comprobar fácilmente cuando un punto puede ser extremo condicionado.
El vídeo siguiente explica el funcionamiento de esta escena.
Acceso a la miscelánea: Extremos. Multiplicadores de Lagrange
Entrevista a Ángel Requena, autor de Turismo Matemático.
Escrito por Eva M. Perdiguero Garzo
Hoy en radio Descartes entrevistamos a Ángel Requena, profesor jubilado en el año 2012. Ángel es el autor de un blog llamado "Turismo matemático" donde podemos encontrar la relación que hay entre Arte y Matemáticas. En dicho blog y en forma de breves entradas encontramos una foto del objeto que a continuación y maestramente, Ángel nos relaciona con las matemáticas. La dirección del blog es: https://mateturismo.wordpress.com/
Según las propias palabra de Ángel Requena sobre su blog: ... Desde la Capilla Sixtina al Quijote, desde Guerra y Paz a la Catedral de Chartres, podemos encontrar huellas matemáticas de gran calado. Ignorarlas quizá no resten nada a la satisfacción estética pero tenerlas presente puede aumentar el placer que producen....
En la entrevista que podéis escuchar a continuación, Ángel nos detalla todo su trabajo y nos hace disfrutar con su gran entusiasmo. Aquí tenéis la entrevista minuto a minuto.
1.- ¿Cómo surge la idea de unir matemáticas y turismo? 2:30
2.- ¿Por qué utilizar un blog? 4:35
3.- ¿Cómo clasificas las entradas de tu blog? ¿Hay algún orden? 6:42
4.- ¿En qué parte del arte encontramos más fácilmente matemáticas? 9:25
5.- ¿Qué parte del arte te gusta más? ¿Por qué? 12:10
6.- ¿Cuántos años llevas recopilando información de turismo matemático? 14:14
7.- ¿Cómo podríamos utilizar el estupendo material que tienes en el blog en nuestras aulas de matemáticas? 16:05
8.- ¿Podríamos utilizar el mismo material para planificar alguna excursión o visita a un lugar? 18:35
9.- ¿Crees que es bueno relacionar las matemáticas con otros campos como el arte, la moda, los viajes,… ? ¿En qué nos ayuda hacerlo? 20:00
Seguro que la vais a disfrutar.
Una lección de geometría con ED@D en Moodle
Escrito por Montserrat Gelis BoschHoy veremos cómo crear una serie de actividades con contenidos interactivos enlazados de forma flexible, que permitirán al estudiante acceder a la información y a las actividades siguiendo diferentes ramificaciones o caminos según sea su proceso de aprendizaje.
Con el módulo lección de Moodle y los materiales interactivos de la Red Educativa Digital Descartes podemos crear una serie de páginas para trabajar un determinado tema. En cada página del libro podemos embeber o insertar materiales de la Red y también añadir tablas de ramificación para que el alumnado decida qué actividades realizar y en qué orden, atendiendo a las necesidades de su aprendizaje.
En el siguiente vídeo podemos ver un ejemplo de lección con actividades de geometría. Seleccionaremos actividades para el cálculo de áreas de cuadriláteros y triángulos de la unidad Polígonos, perímetros y áreas para 1º de la ESO del Proyecto ED@D.
Crearemos tres tipos diferentes de actividades. En primer lugar, actividades para introducir las fórmulas con escenas interactivas del Proyecto ED@D para que el estudiante pueda manipular las escenas y deducir las fórmulas de la áreas.
En la siguiente página embeberemos actividades autocorrectivas para practicar problemas sencillos de cálculo de áreas. Crearemos, también, varias páginas con ejercicios para consolidar los conceptos estudiados.
A continuación diseñaremos una tabla de ramifiicación con distintas opciones para que el estudiante seleccione, según necesite, volver a repasar las fórmulas, realizar más ejercicios de cálculo o pasar a la página siguiente para realizar ejercicios de aplicación.
Finalmente crearemos una página en la cual embeberemos una escena de la unidad del Proyecto ED@D con ejercicios de aplicación.
Más...
DESCUBRIMOS al Personaje Misterioso (IX)
Escrito por Ángel Cabezudo BuenoLa semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a una genial matemática nacida en Londres en 1815. Fue una adelantada a su tiempo en más de 100 años al ser capaz de describir con acierto las posibilidades de la máquina analítica que diseñara en aquel tiempo Charles Babbage y para la cual desarrolló un sistema simbólico de representación de instrucciones y concibió un “plan” o secuencia de instrucciones, basadas en tarjetas perforadas, para calcular la serie de números de Bernoulli utilizando los conceptos de bucle y subrutina.
Si a Charles Babbage se le considera el padre del hardware de un ordenador que podría funcionar de forma muy similar a como lo hacen los actuales, nuestra matemática, colaboradora en el proyecto de Babbage, se convirtió en la primera programadora de la historia y por tanto considerada madre de la programación de ordenadores.
Muestra genial matemática, cuya identidad se puede desvelar al montar el puzle realizado con DescartesJS que se acompaña a este artículo, en 1843 pudo asegurar que la máquina analítica no sólo podría servir para hacer cálculos matemáticos sino otras operaciones con informaciones de cualquier naturaleza como música o imágenes.
La imagen del puzle tipo jigsaw (piezas irregulares), es una composición donde aparece la elegante figura de nuestro personaje femenino y de fondo diferentes alusiones a la máquina analítica y a su “plan” de instrucciones.
Las 16 piezas barajadas, obtenidas al cortar la imagen, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula 4x4 a la izquierda de la escena arrastrándolas con clic mantenido y soltarlas sobre el cuadro donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la composición en escala de grises. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece el nombre del personaje, una caricatura y se puede visionar un vídeo: se trata de un cuento audio descrito extraído del libro "La Liga de las Mujeres Extraordinarias" y que por su formato y contenido puede resultar interesante y muy motivador para los alumnos de Primaria y Educación Secundaria Obligatoria aunque a mí que ya peino canas también me ha gustado mucho.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana cuyo tamaño se adapta automáticamente al dispositivo de visualización y se acomoda manualmente al gusto personal pues emplea un Diseño Web Adaptativo (RWD).
El autor de este artículo, la edición de las imágenes y la programación del puzle es de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido la entrevista de este noveno personaje matemático y quedáis invitados para la siguiente.
 Bienvenidos a Radio Descartes y a la serie de entrevistas al personaje misterioso donde pretendemos mostrar la parte humana de los matemáticos célebres aparte de dar a conocer su contribución a la ciencia.
Bienvenidos a Radio Descartes y a la serie de entrevistas al personaje misterioso donde pretendemos mostrar la parte humana de los matemáticos célebres aparte de dar a conocer su contribución a la ciencia.
Hoy entrevistamos a una imaginativa y genial mujer nacida en Londres en 1815: en la actualidad es considerada madre de la programación de ordenadores y por tanto una adelantada en más de 100 años a su tiempo pues entonces la electricidad, verdadera energía que ha permitido el desarrollo de la informática, estaba aún siendo ensayada y estudiada científicamente y su uso no formaba parte de los planes de la tecnología de la época.
No desvelaremos su nombre hasta una semana más tarde en este mismo blog a través de la imagen de un puzle, como hemos venido haciendo con los personajes precedentes. Los escuchantes del podcast que se acompaña sois los que tenéis que descubrirla a través de datos que iremos aportando a lo largo de la entrevista.
Autor del guion, conductor de la entrevista y realizador del podcast: Ángel Cabezudo Bueno
Interpreta al personaje matemático femenino: Montse Gelis Bosch (profesora de matemáticas en el INS Montsacopa de Olot en Girona y colaboradora semanal en este blog donde a través de sus artículos y sus videos nos explica cómo se pueden utilizar con los alumnos los distintos materiales de Descartes integrándolos en cursos Moodle)
Los efectos especiales pertenecen al Banco de sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
El trabajo lleva licencia CC BY-NC-SA 4.0.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)




 CONTACTO
CONTACTO
