La opción Gráficos del menú del Editor de Escenas Descartes nos ayuda a situar cada forma, imagen y texto en el lugar que le corresponde en el escenario y a programar el aspecto que estos elementos van a presentar y cuando van a estar visibles y cuando ocultos. En nuestro caso, y ya con la utilidad en funcionamiento, al desplegar la opción, esta presenta el siguiente aspecto:
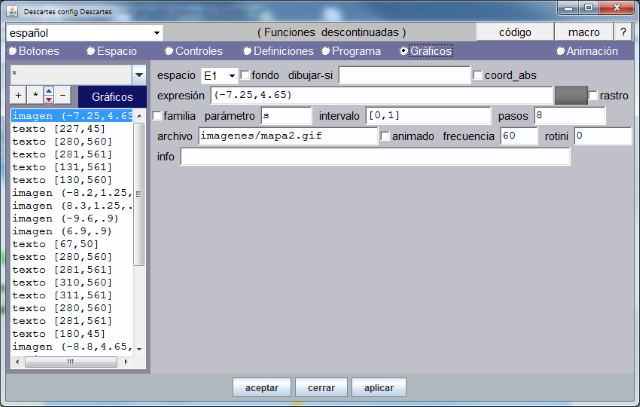
Es conveniente analizar el gráfico anterior detenidamente. Corresponde a la definición de la imagen principal de la utilidad que es el mapa base. Se observan dos regiones: a la izquierda, la zona de inserción, copia, posicionamiento y borrado de los objetos y a la derecha, las características de cada uno de ellos. Vemos que a la "imagen" del mapa se le han asignado unas coordenadas, que corresponden a la esquina superior izquierda del objeto, y otra serie de valores. El significado y uso de cada uno de ellos se explica en los artículos: editor básico, palabras reservadas y en otras entradas de la documentación técnica y de usuario de Descartes v5.
En realidad con la opción de menú Gráficos pueden crearse muchos más objetos como observamos en el siguiente vídeo.
A cada uno de los objetos que podemos agregar le corresponde las opciones de menú adecuadas para su configuración, posicionamiento y visibilidad. La ayuda para conocer todas las opciones y su uso está, como ya hemos indicado, en la documentación técnica.
El material de ejemplo que hemos desarrollado en los artículos anteriores, ha posibilitado la creación de un nuevo subproyecto didáctico de la red Descartes para el área de Geografía. El resultado puede observarse siguiendo el enlace gráfico siguiente.
En el apartado materiales de la página anterior hay un enlace para descargar los contenidos y así poder usarlos localmente o examinar su estructura. Este subproyecto está abierto a todas aquellas personas que quieran participar y colaborar en él.
El código que facilita la creación de estos objetos educativos y el mantenimiento de la infraestructura necesaria para la elaboración y distribución de los mismos se debe a:

La red Descartes ha desarrollado una colección de subproyectos educativos que abarcan cada vez más áreas del curriculum y más niveles
En siguientes entradas continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que la libreria ofrece.
Ildefonso Fernández Trujillo
Utilizando los Juegos didácticos para trabajar la competencia lectora
Escrito por Santos Mondéjar LópezEn todas las materias tenemos que trabajar la competencia lectora. Ese trabajo se compone de la lectura propiamente dicha y la evaluación de la compresión. Esta evaluación se suele realizar de forma oral o escrita. Una tiene la ventaja de que no te llevas el trabajo a casa pero las desventaja de que es lenta, no es algo que dinamice una clase. La otra es más rápida y ordenada, incluso puedes mandar la redacción para casa, pero luego te toca corregir.
Ambas son muy interesantes pero pueden llegar a aburrir tanto al alumno como al profesor. Para esta ocasión os propongo añadir algo de diversión al trabajo de lectura comprensiva. Vamos a leer y evaluaremos con un juego didáctico de nuestro proyecto.
Vamos a utilizar un ejemplo en el que descargaremos un juego. Colocaremos el fichero de las preguntas y modificaremos el juego para que aparezca nuestro fichero precargado. Ya lo habíamos hecho en otro artículo pero dentro de la explicación de un juego, aquí pretendemos centrarnos en eso. De paso abrimos una serie de vídeos más específicos y posibles actividades a realizar. Si os interesa algún tema solo tenéis que proponerlo.
El texto seleccionado puede ser de cualquier tema por lo que lo podremos aplicar a cualquier materia. Yo me he decidido por uno sobre los celíacos. Aprender sobre enfermedades nunca está de más. Además hace poco cumplió cuatro años el blog de un gran divulgador científico que escribió sobre el tema y ya aprovechamos, felicidades Scientia.
Por si os sirve os dejamos los archivos utilizados:
Texto para los alumnos, es el artículo un poco modificado para adaptarlo al nivel de los alumnos, 2º ciclo de ESO. Enlace al artículo original: La enfermedad celiaca, los nuevos alimentos y la demagogia pseudocientífica
Juego Antes y depués para jugar o descargar. Juego modificado del ejemplo.
Presentada la actividad solo queda dejaros un vídeo de cómo preparar el juego. Recordad que hay una forma más sencilla, con solo mandar el fichero a través del formulario de la web de los juegos se publicará y podréis compartirlo y utilizarlo on line.
Os dejamos un vídeo como ejemplo del proceso
En la Red Descartes tienes muchos recursos, utilízalos
Descartes en la Universidad. Miscelánea: Curvas planas y no planas
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Curvas planas y no planas
En esta ocasión se presenta una miscelánea que permite representar curvas paramétricas en el plano y en el espacio. En este último caso la gráfica de la curva aparece sobre una superficie a partir de las ecuaciones de una curva plana.
La escena permite la elección entre varias curvas y también introducir las ecuaciones paramétricas de la curva que se desee representar.
En la representación gráfica aparece sobre la curva un punto que puede modificarse variando el valor del parámetro. De esta manera, se puede observar cómo se recorre la curva cuando el parámetro toma valores en un cierto intervalo.
En el siguiente vídeo se describe el funcionamiento de la miscelánea.
Acceso a la miscelánea: Curvas planas y no planas
Un día en el parque de atracciones. Formación competencial con Descartes
Escrito por Montserrat Gelis BoschEsta semana presentamos la actividad Un día en el parque de atracciones, unidad para 3º de primaria perteneciente al Proyecto Formación Competencial de la Red Educativa Digital Descartes. Este proyecto está formado por materiales dinámicos interactivos basados en unidades liberadas PISA y pruebas de evaluación diagnóstica de diferentes Comunidades Autónomas.
La actividad: En el contexto de un parque de atracciones se plantean una serie de situaciones y problemas geométricos y aritméticos que el estudiante deberá resolver. Se trata de actividades formativas y de autoevaluación, con una barra de seguimiento con los aciertos y errores y una nota numérica al finalizar todas las actividades.
Cada vez que el estudiante actualiza o reinicia la actividad, aparecen distintas preguntas y se modifican los datos numéricos.
Nuestra aula virtual moodle: Todos los objetos digitales interactivos de la Red Educativa Digital Descartes se pueden embeber o insertar en un espacio web. En el caso de moodle, se pueden seleccionar diferentes recursos o actividades en los cuales embeber o insertar nuestro objeto: página, etiqueta, cuestionario, lección, libro...
Unidad liberada original: Modelo de pruebas para la evaluación de tercer curso de Educación Primaria. INEE del Ministerio de Educación, Ciencia y Deporte de España.
En el siguiente vídeo se analizan con detalle las situaciones que se plantean en dicha actividad y se muestran los pasos a seguir para embeber utilizando el recurso página de moodle.
Más...
De nuevo me salgo un poco de mis temas habituales para presentar otra de los proyectos que está desarrollando le Red Descartes, GEOgráfica.
En esta ocasión Ildefonso Fernández Trujillo ha desarrollado una serie de objetos de aprendizaje para primaria y secundaria que facilitarán la tarea de aprender los nombre y localización de los países y sus capitales.
Vemos en la presentación del proyecto que se trata de:
"...una colección de recursos educativos interactivos que ayuden al aprendizaje de la Geografía mundial con diferentes niveles de detalle.
Estos objetos educativos se plantean siguiendo esquemas habitualmente utilizados en materiales y juegos educativos clásicos, pero se introduce aleatoriedad en el planteamiento de las preguntas, es decir, el usuario cada vez que usa el recurso observa diferentes situaciones o perspectivas; y corrección automática, es decir, se le aporta una retroalimentación en la que automáticamente se indica la certeza o incorrección de la respuesta dada. Esa corrección puede ser meramente sumativa o también puede plantearse de manera formativa."
Disponemos de un objeto educativo para cada continente y en dos versiones.
En la primera el objeto preguntará sobre la capital de un determinado país y el usuario podrá bien seleccionar su nombre en una relación completa de las capitales de ese continentecomo ayuda se destaca en color rojo o verde el país sobre el que se está preguntando y también su bandera, por ello también puede utilizarse para aprender el nombre de cada país y su ubicación.
La segunda versión nos pide señalar con el ratón en el mapa la capital del país propuesto.
En ambos casos, si fallamos nos muestra la respuesta correcta y tenemso una marcador de aciertos y errores para realizar un seguimiento del aprendizaje.
Como siempre podemos trabajar "on line" o realizar la descarga de los materiales.
Os dejamos un vídeo con unos comentarios de los materiales:
Finalmente queremos destacar que este proyecto está abierto a todas aquellas personas que quieran participar y colaborar en él. Independientemente de que su interés sea profesional, académico o lúdico. La participación puede efectuarse a cualquier nivel, desde comunicar posibles erratas o incidencias que se detecten, sugerir la adaptación de algún objeto, plantear la elaboración de otros recursos para cubrir determinados contenidos no contemplados o en los que se necesite un nivel de detalle diferente, y/o participar directamente en el equipo de desarrollo de RED Descartes.
Esperamos que sea útil
DESCUBRIMOS al Personaje Misterioso (X)
Escrito por Ángel Cabezudo BuenoPor Ángel Cabezudo Bueno – 9 de febrero de 2015
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos al autor del texto más influyente de la ciencia moderna: “Philosophiae naturalis principia mathematica” – en castellano, “Principios matemáticos de la filosofía natural” donde presenta los fundamentos de la física y de la astronomía formulados en el lenguaje de la geometría pura. Se trata de una obra deductiva donde, a partir de unas proposiciones muy generales, se pueden demostrar propiedades mecánicas a modo de teoremas. La primera edición en latín de 1687, marcó un punto de inflexión en la historia de la ciencia y es considerada, por muchos, como la obra científica más importante jamás publicada.
Muestro genial científico, cuya identidad se puede desvelar al montar el puzle realizado con DescartesJS que se acompaña a este artículo, creía en la universalidad del pensamiento y nos dijo que buscó la verdad en todas las áreas del conocimiento incluyendo las Sagradas Escrituras y la alquimia.
Recibió en vida los mayores honores y reconocimientos. En el momento de su muerte, acaecida en Londres en 1727, fue tratado como un héroe y sepultado con la élite en la Abadía de Westminster.
La imagen del puzle tipo jigsaw (piezas irregulares), es un grabado a color de nuestro personaje, de joven, observando la descomposición de la luz solar cuando atraviesa un prisma de cristal. Las 16 piezas barajadas, obtenidas al cortar la imagen, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula 4x4 a la izquierda de la escena arrastrándolas con clic mantenido y soltándolas sobre el cuadro donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la composición en escala de grises. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece el nombre del personaje, una caricatura y se puede visionar un vídeo: El número 7 de la serie “Universo Matemático” emitido por La 2 de TVE, titulada “A hombros de gigantes…” de la que es guionista y presentador Antonio Pérez Sanz.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana cuyo tamaño se adapta automáticamente al dispositivo de visualización pues emplea un Diseño Web Adaptativo (RWD Responsive Web Desing).
La edición de las imágenes y la programación del puzle es de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0.
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este décimo personaje matemático y no os perdáis el siguiente.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)




 CONTACTO
CONTACTO
