Hoy nos vamos en centrar en contar algunas de las cosas que aprendemos cuando somos tutores de un curso.
En principio tu rol es el de corrector pero eso no impide que no pares de aprender, todos los que nos dedicamos a la educación lo sabemos.
En la segunda edición del curso Aplicaciones de juegos didácticos en el aula, dentro de los ofertados por la CEJA, he encontrado bastantes participantes que han realizado muy buenos trabajos. Como no puedo extenderme demasiado os voy a mostrar cuatro ejemplos. Os ponemos los enlaces a los juegos con sus trabajos precargados, solo tenéis que empezar a jugar.
El primero es un fichero para Cruzar la línea realizado por Raquel Crespo Gutiérrez. Tiene varias cosas que lo hacen destacable. Se ha realizado para alumnos de la EOI en la modalidad a distancia. Solo disponen de unas pocas horas presenciales en las que se resuleven dudas y Raquel ha aprovechado para ponerlos a jugar. Esto ya me parece suficiente para mostrarlo. Otra cosa llamativa es el uso de las contracciones. En los juegos no podemos utilizar el símbolo ' pero es el que debemos escribir en las contracciones. Hemos tenido que cambiarlo por nuestra tilde ´ asumiendo que es un error pero no había otra forma de utilizarlas. Si advertimos a los alumnos no habrá problema. por cierto, no olvidéis poner la interface en inglés, solo hay que cambiar "esp" por "eng" en la casilla del idioma.
El segundo es de Manuel Fernández Labrada que ha creado un fichero muy completo para El primero de la clase. El tema es la música, una materia que no había imaginado que pudiese sacarle tanto partido a los juegos. Para comenzar a jugar debemos elegir la introducción direccta del nombre de los jugadores. Al poder introducir hasta 30 podemos usar un fichero que nos facilite el trabajo. Veréis que el trabajo de Manuel permite realizar un evaluación completa de lo que han aprendido. Es una muy buena muestra de las grandes posibilidades de los juegos.

El tercero es el más sorprendente para mí. Nuria Estébanez Campos ha creado una batería de preguntas para Danza contemporánea. En este caso el juego elegido es Parejas ocultas en el que debemos unir el nombre de la figura con su explicación. Realmente todas las materias tienen su opción de aprovechar estos recursos pero nunca hubiese pensado en la aplicación para danza. El resultado fue muy bueno, imaginad a los alumnos/as cuando Nuria les pidiese que cogiesen los ordenadores, su sorpresa y lo que disfrutarían. Aquí aparece un pequeño problema con la extensión de la explicación ya que el juego no permite todos los caracteres que queramos. Debemos adaptarnos o buscar entre la multitud de juegos disponibles otro que se adpate a lo que necesitemos en cada momento.
Termino con un ejemplo de programación del uso de los juegos en el aula en el caso de La calculadora. Ya estamos empezando a aplicar la nueva ley de educación y Francisca Gallardo Salas nos enseña cómo hacerlo. Las competencias clave, comentando en cada una qué esperamos conseguir, unos criterios de evaluación muy claros y unas observaciones perfectas son lo mínimo que debes revisar en este documento que no tiene desperdicio alguno.
Como hemos dicho al principio, no paramos de aprender.
Terminamos con los enlaces que os permitirán acceder a los juegos en la web o descargarlos:
Esperamos que os sean de utilidad y os animen a utilizar los juegos en el aula
Este mes vamos a retomar el bloque de álgebra con una unidad de 2ºESO. Es una unidad muy corta porque deja las ecuaciones para la unidad siguiente:
En el video hemos tratado los siguientes contenidos:
1.Expresiones algebraicas
¿Qué son?
¿Cómo las obtenemos?
Valor numérico
2.Monomios
¿Qué son?
Sumar y restar
Multiplicar
3.Polinomios
¿Qué son?
Sumar y restar
Multiplicar por un monomio
Audios y Vídeos Interactivos con Descartes
En artículos anteriores mencionamos la posibilidad de insertar contenido multimedia en las utilidades didácticas que tengamos proyectado realizar. Ahora veremos cómo proceder, utilizando el Editor de Escenas, para crear una utilidad con un vídeo interactivo. Esto es, el vídeo se reproduce y plantea una cuestión, deteniéndose en ese punto hasta que se introduce una respuesta y según sea esta, continúa su reproducción en un punto u otro de su contenido o salta a otro vídeo en una posición predefinida.
Antes de continuar debe analizarse detenidamente la documentación enlazada en el título. En ella, José R. Galo Sánchez incluye un documento elaborado por Juan Guillermo Rivera Berrío donde se describe, paso a paso, la creación de una escena que tiene un vídeo interactivo.
Supuesto que se ha estudiado la documentación técnica y si se ha considerado necesario, descargado el documento, vamos a proceder a elaborar el proyecto propuesto, para lo cual, lo primero que hacemos es crear una nueva carpeta, a la que nombramos VideoInteractivo, que es donde vamos a guardar dicho proyecto.
Dentro de la carpeta anterior debemos crear una carpeta para alojar el vídeo que vamos a utilizar, en nuestro caso creamos la carpeta llamada vídeos y también creamos las carpetas: imagenes, donde guardaremos las imágenes que utilizaremos y css, donde irá el archivo de estilo. El editor, al guardar el archivo index.html crea la carpeta lib con el intérprete descartes-min.js según se muestra en el siguiente vídeo.
Abrimos, por lo tanto, el Editor de Escenas y damos las dimensiones que aconseja el paso 1, 640x580, guardando el resultado en la carpeta VideoInteractivo con el nombre index.html tal como hemos visto en el vídeo.
Por defecto, el Editor de Escenas Descartes, crea una escena mínima que iremos modificando para adaptarla a nuestro proyecto.
Tal y como hemos visto en artículos anteriores, la escena está contenida en un archivo de extensión html si ahora abrimos el archivo index.html con un editor de texto plano o un editor de código html, observamos lo siguiente.
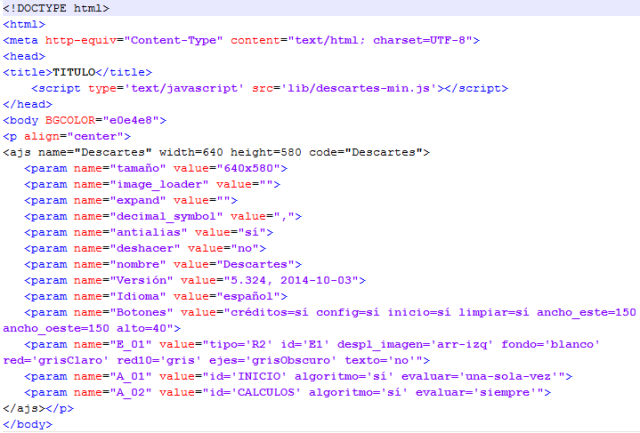
Podemos modificar el título del documento y algunos otros parámetros html directamente con el propio editor de textos, aunque las modificaciones relativas al código JS es conveniente realizarlas con el Editor de Escenas, también pueden hacerse directamente con el de textos. Con cualquiera de los métodos quitamos los botones: créditos, config, inicio y limpiar. (donde pone botón=si ponemos botón=no o desmarcamos la casilla correspondiente en el menú botones del Editor de Escenas). También, de manera similar, suprimimos los ejes y las redes.
Suponemos que en la carpeta vídeos hemos guardado un vídeo con el nombre video1.mp4. Ahora, realizamos el paso 2 de las instrucciones. Con el Editor de Escenas abierto, seleccionamos el menú controles y pulsamos el signo +, en el cuadro agrega que se abre desplegamos las opciones y elegimos vídeo. Asignamos los valores que se muestran a continuación.
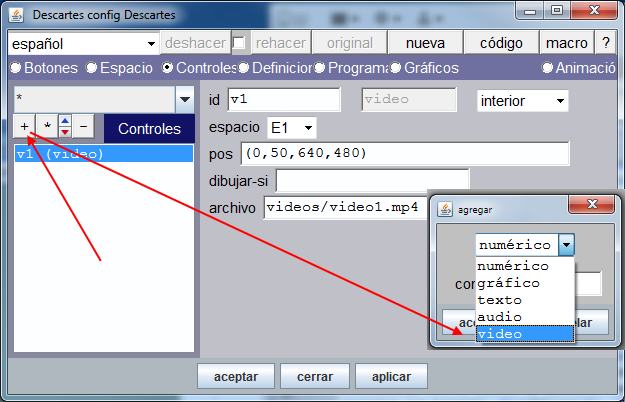
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
En siguientes entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Ildefonso Fernández Trujillo
Volvemos a visitar la zona de problemas del Proyecto Newton para revisar Energía electrica: central hidroeléctrica de Mª Josefa Grima Rojas y Javier Soriano

Es un problema que se centra en la producción de energía a partir del agua que acumulamos en un embalse.
Se trabajan los conceptos de tipos de energía, transformaciones, rendimiento, ventajas y problemas de esta generación y también ejercicios numéricos.
Cada apartado del problema propuesto viene completado con una pregunta que aporta posibles soluciones, todas comentadas explicando el error cometido o ampliando el acierto.
Las preguntas son muy variadas, van desde razonamientos o explicaciones a deducción de fórmulas o cálculos.
Se trata de un problema muy completo que mejora todavía más con las animaciones y la escena interactiva.
Como en todos los problemas disponemos de una autoevaluación y del problema resuelto en PDF.
Os dejamos el vídeo que comenta el problema:
Seguro que os resulta muy útil
Dispones de muchos más recursos en la web del Protecto Descartes
Más...
Proyecto Canals I. Objetos de aprendizaje para Educación Infantil
Escrito por Xosé Eixo BrancoEn este y en sucesivos vídeos presentaremos el Proyecto Canals.
Este subproyecto del proyecto Descartes, recoge 375 objetos de aprendizaje interactivo basados en los materiales que diseñó y elaboró la profesora Mª Antonia Canals durante su extensa vida docente.
Desde el Ministerio de Educación, Cultura y Deporte de España se abordó la producción de recursos TIC que buscaban contribuir a la difusión y conocimiento de dichos materiales, introduciendo una perspectiva enmarcada en el uso educativo de las Tecnologías de la Información y de la Comunicación.
En el año 2013 la asociación no gubernamental Red Educativa Digital Descartes (http://ProyectoDescartes.org) ha convertido estos materiales a DescartesJS pudiéndose, desde este momento, trabajar con ellos en dispositivos tipo tabletas y smartphones, además de los ordenadores personales.
En este primer vídeo nos centraremos en los materiales correspondientes a Educación Infantil.
DESCUBRIMOS al Personaje Misterioso (XII)
Escrito por Ángel Cabezudo BuenoPor Ángel Cabezudo Bueno – 13 de abril de 2015
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos uno de los más grandes científicos de la antigüedad y de la historia: físico, ingeniero, inventor, astrónomo y matemático griego. Nació en Siracusa, Sicilia, en el 287 a.C.
Entre sus avances en física se encuentra sus fundamentos sobre estática, hidrostática y explicación de la palanca.
Estuvo muy interesado por las matemáticas a las que dio un gran impulso al estudiar las áreas y los volúmenes de cuerpos limitados por curvas. Era muy habilidoso y trataba de forma diferente la geometría al hacer demostraciones apoyándose en la mecánica. Dedicó su libro “El Método” a Eratóstenes al que conoció en su paso por la biblioteca de Alejandría.
Desvelamos en el presente artículo la identidad de este matemático mediante el montaje de una imagen dividida en 16 piezas de un puzle tipo jigsaw (piezas irregulares). Se trata de un grabado en colores sepia de nuestro personaje y representa el momento en que es sorprendido por un soldado romano en el asedio de Siracusa. Dibujaba figuras geométricas en la arena y le recriminó al ser molestado. Airado, el soldado le dio muerte con su espada.
Cuando el puzle se completa aparece el nombre del personaje… y algún detalle más.
También se puede visionar un interesante vídeo titulado “La sorprendente historia de…”, cuyo autor es Felipe Bonilla Aguilar ; el coordinador general de este proyecto es José Luis Abreu León.
La siguiente imagen lleva un enlace al puzle que utiliza Diseño Web Adaptativo (RWD Responsive Web Desing).
La edición de las imágenes y la programación del puzle son de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Con este personaje, que hace el número doce de la serie, cerramos este ciclo dedicado a los matemáticos célebres en la historia donde hemos pretendido también dar a conocer su faceta humana y no sólo científica. Esperamos haber acertado en el intento y damos las gracias por la atención recibida.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
