EDAD 4º ESO Opc. A Funciones y gráficas
Escrito por Alfonso Saura EspínEste mes vamos a tratar una unidad sobre funciones y gráficas correspondiente a 4º de la ESO:
En el video hemos tratado los siguientes apartados:
1. Funciones
Concepto
Tablas y gráficas
Dominio y recorrido
2. Propiedades
Continuidad
Simetrías
Periodicidad
Tendencia
3. Monotonía
Tasa de variación media
Crecimiento y decrecimiento
Máximos y mínimos
Audios y Vídeos Interactivos con Descartes
Continuación de la práctica (2)
Los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS son dinámicos debido a la permanente labor de mantenimiento y actualización del código fuente de la librería descartes-min.js por parte de los responsables de la Red Digital Descartes de México, España y Colombia. Hay épocas en las que este dinamismo es vertiginoso tal y como ocurre actualmente. Por eso comenzamos esta nueva entrada del Blog recomendando la visita a dicha documentación mediante el enlace del título y también de este otro que llevan, respectivamente, a la información sobre el uso de vídeos interactivos, tanto en local como en línea y a la información sobre cómo comunicar las escenas con el HTML y viceversa.
Continuando con la práctica, recordamos que ya hemos definido en los espacios: E1, E2 y E3, los gráficos (textos) necesarios para dirigir y complementar el flujo de la actividad. Ahora, siguiendo el paso 7 crearemos los dos controles, tipo botón, para manipular el vídeo ya que los propios del mismo están enmascarados.
Abrimos la opción de menú Controles y procedemos como muestra el vídeo siguiente.
Recordamos que la expresión '\n' que aparece en el vídeo puede interpretarse como un salto de línea y permite introducir una nueva instrucción.
El paso 8 consite en definir, en la opción de menú Programa, dos eventos para controlar la reproducción del vídeo mediante el manejo de la animación tal y como se explica detalladamente en la documentación.
Después de seguir las instrucciones, la opción de menú Programa debe tener el aspecto que muestra el gráfico siguiente.
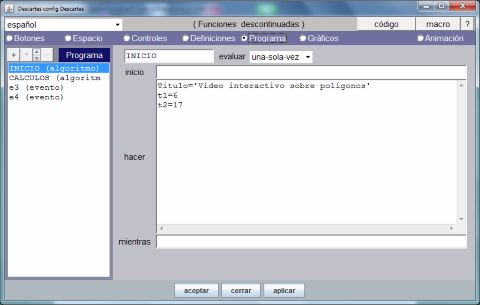
A continuación, siguiendo las indicaciones del paso 9, volvemos a seleccionar la opción de menú Controles para definir en los espacios E1 y E3 los botones, cuadros de texto y controles de tipo menú que son el soporte de la interactividad de la escena tal y como se muestra en el documento videos_interactivos.pdf enlazado al principio del artículo.
El gráfico siguiente muestra cómo debe quedar la opción de menú Controles después de completar el paso anterior.
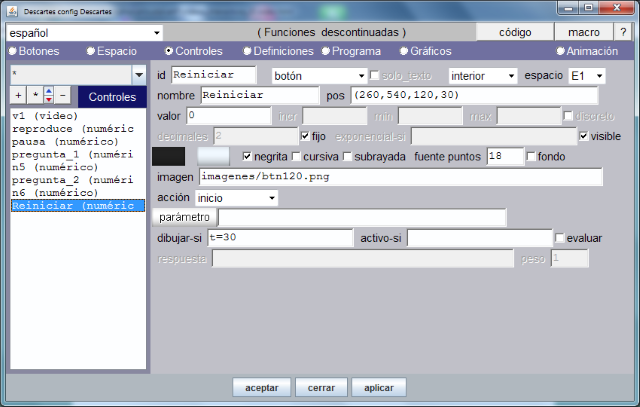
En próximas entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
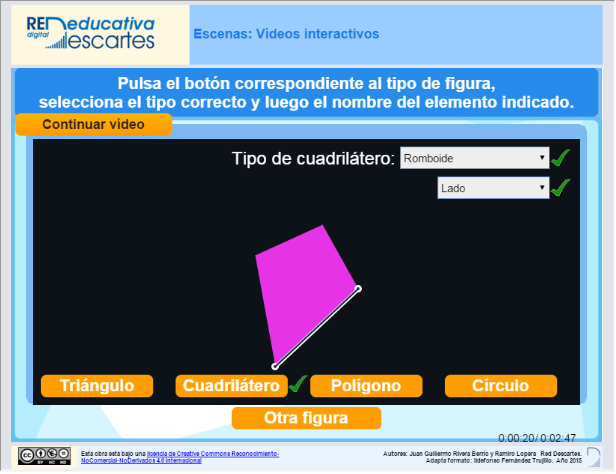
El siguiente gráfico es un enlace a un ejemplo de la implementación de vídeos interactivos dentro de una escena DescartesJS. Este ejemplo, realizado por Juan Guillermo Rivera Berrío y que es una propuesta para evaluación de la viabilidad del proyecto y su potencial formativo y que aún está en fase de prueba, ha sido posible gracias a la colaboración de la Red Descartes de Colombia (Juan Gmo. Rivera y Ramiro Lopera) y de España (José R. Galo).
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Olimpiada de juegos didácticos en el IES Joaquín Turina
Escrito por Santos Mondéjar LópezDentro de las experiencias que se van realizando con el uso de los Juegos didácticos en el aula, hoy os mostramos una q ue expone la experiencia del profesorado además de la de los alumnos.
ue expone la experiencia del profesorado además de la de los alumnos.
Durante el curso 2014-2015 y en el marco de un grupo de trabajo de profesores del IES Joaquín Turina de Sevilla, se ha celebrado una "Olimpiada con el juego didáctico Encuentro". La posibilidad de realizar una actividad interdisciplinar ya es por sí misma motivo para destacar este proyecto. Si además los alumnos se divierten con un concurso y aumenta su motivación tenemos una actividad casi perfecta.
Mediante la realización de estas actividades educativas utilizaremos las nuevas tecnologías de la información y la comunicación al servicio del aprendizaje de nuestro alumnado mediante el empleo de una nueva metodología, dinámica, motivadora, activa, inclusiva y participativa, que además integra un nuevo sistema de desarrollo de los contenidos, búsqueda y selección de la información y de evaluación que permite avanzar en el desarrollo de las Competencias Básicas y la mejora de la convivencia en el aula y del trabajo colaborativo, haciendo que el alumno sea el principal protagonista de todo el proceso.
En el siguiente vídeo se resumen los principales aspectos de esta actividad.
Podemos enumerar algunos aspectos más que se han destacado en las valoraciones de la actividad por parte de profesores y alumnos:
• Plantea una nueva dinámica de actividades lúdico-educativas.
• Fomenta el trabajo en equipo de profesorado y alumnado.
• Aplica una metodología activa y participativa que hace del alumnado el auténtico protagonista de las actividades propuestas en esta actividad.
• Adapta y aplica los materiales elaborados a la práctica totalidad de las materias y áreas del currículum pudiendo versar sobre cualquier tipo contenido, siendo fácilmente adaptable por el profesor a las características específicas de los alumnos a los que va dirigido, permitiendo una atención a la diversidad y desarrollo de las Competencias Básicas.
• Utiliza los materiales elaborados y aplicados, como instrumentos de evaluación. Estos juegos, por su naturaleza, pueden ser excelentes instrumentos de evaluación. Los criterios de evaluación pueden ser muy variados: participación activa y positiva en las actividades, trabajo previo de preparación, grado de consecución de los objetivos de las diferentes actividades, etc.
Para terminar os dejamos unos enlaces:
Una actividad de funciones en nuestro blog. Código de la escena
Escrito por Montserrat Gelis BoschHoy presentamos un vídeo en el cual se indican los pasos a realizar para embeber una actividad interactiva de la Red Educativa Digital Descartes en nuestro blog, a partir del código de la escena.
En vídeos anteriores hemos visto cómo embeber actividades de la Red Descartes en nuestro blog utilizando el código iframe:
<iframe style='width: ..px; height: ..px;' src='dirección web de la página'></iframe>
En el cual deberemos escribir las dimensiones y la dirección web de la página de la actividad.
Pero en algunos casos es posible que deseemos embeber solamente la escena con la actividad y no toda la página. En este caso deberemos utilizar el código que genera la escena.
Para copiar dicho código procederemos de la siguiente forma:
- Elegimos la actividad que queremos embeber, en este caso hemos seleccionado una escena del tema 1 de la unidad Funciones y Gráficas para 4º de la ESO del Proyecto ED@D. para 4º de la ESO del Proyecto ED@D.
- Situamos el ratón sobre la escena y pulsamos el botón derecho.
- Se abre una ventana auxiliar, activamos el botón config que nos da acceso al código y lo copiamos.
Una vez copiado el código, activaremos la edición en html de la página de nuestro blog y lo pegaremos. Deberemos comprobar que contiene el parámetro docBase (para las imágenes y recursos auxiliares) y la línea de código del script de llamada al intérprete.
Una opción interesante que nos permite Blogger es la posibilidad de alojar el script en la plantilla de nuestro blog, lo cual nos ahorra tener que estar pendientes de su inclusión en los códigos y además agilizará la activación de las escenas.
Activaremos la edición de la plantilla de nuestro blog y situaremos, en la cabecera, entre <head> y </head>, la línea de código:
<script type='text/javascript' src='http://arquimedes.matem.unam.mx/Descartes5/lib/descartes-min.js'></script>
Veamos ahora el siguiente vídeo en el cual se muestra el proceso a seguir, paso a paso:
Más...
Retomamos el Proyecto Competencias para fijarnos en una actividad clasificada como competencia lectora pero basada en el método científico:
Seguridad en los teléfonos móviles

Consiste en una serie de datos que los alumnos deben leer y demostrar que han comprendido.
Se aportan unos puntos claves que muestran afirmaciones sobre la peligrosidad del uso de los teléfonos móviles y cada una se matiza con otra afirmación que la contextualiza.
El alumno aprende a tener cuidado con las afirmaciones ya que se necesita bastante información para poder estar seguro de algo.
Fomentamos el pensamiento crítico a partir de afirmaciones que parecen indicar una peligrosidad grande de los teléfonos con otras que explican los estudios realizados.
La base del método científico es la investigación, la comprobación de las hipótesis en un contexto concreto. En esta ocasión aprendemos que hay que completar la información y llegamos a unas conclusiones basadas en hechos.
Como en todo el proyecto competencias siempre tenemos a la vista el progreso y se nos muestra inmediatamente si hemos acertado o no indicando la respuesta correcta para entender el error cometido.
Encontramos preguntas para elegir la opción correcta y en cada una se vuelve a mostrar el texto relacionado con ella.
También hay una pregunta para clasificar cuatro posibles factores entre que tengan influencia o no
Tenemos la opción de recargar la actividad para poder hacerla de nuevo. Aparecerá igual excepto las cuatro opciones que van variando de entre doce.
Disponemos de las preguntas comentadas que podemos imprimir y los créditos para saber a quién agradecer este trabajo.
Aquí tenéis un vídeo que muestra todo lo comentado
En la Red Descartes puedes encontrar muchos más recursos. Utilízalos
La RED Descartes ha desarrollado recursos interactivos que tienen como objetivo principal la Ingeniería y Tecnología.
Todos estos recursos han sido específicamente desarrollados para este ámbito cognitivo o bien forman parte de diferentes subproyectos que han surgido en diferentes etapas de nuestra asociación y con estructuras y diseños acordes con los fines particulares perseguidos en cada uno de ellos.
Los recursos de este subproyecto están agrupados en esta web 1.0 y también puede acceder a ellos realizando una búsqueda en este servidor de recursos.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
