Crear actividad SCORM con Reload a partir de una actividad Descartes
Escrito por Elena Álvarez SáizEn el siguiente vídeo se muestra cómo incorporar una actividad evaluable realizada con Descartes dentro de Moodle como un paquete SCORM. De esta manera se puede almacenar, en el cuaderno de calificaciones, la puntuación obtenida por el alumno cuando realice la tarea.
Un SCORM (Sharable Content Object Reference Model), es un conjunto de especificaciones técnicas en el ámbito de aprendizaje a través de Internet (e-Learning) que definen la estructura de los contenidos, su comportamiento y el comportamiento de los LMS a la hora de alojar y ejecutar dichos contenidos.
Para realizar el paquete SCORM se ha utilizado, por un lado, la posibilidad de comunicación de las escenas Descartes con páginas html (http://descartesjs.org/documentacion/?p=2729) y, por otro, el editor gratuito de SCORM Reload (http://www.reload.ac.uk/editor.html).
En el video se describen tres etapas con los pasos a realizar:
- Etapa 1. Crear la actividad y preparar los ficheros para generar el SCORM.
- Etapa 2. Construir el SCORM que incluya la actividad.
- Etapa 3. Incorporar la actividad SCORM dentro de Moodle.
Se pueden descargar los ficheros a los que se hace referencia en el vídeo haciendo clic en los siguientes enlaces:
El horario. Formación y evaluación competencial
Escrito por Montserrat Gelis BoschHoy presentamos el recurso Horario, que pertenece al Proyecto Formación Competencial de la Red Educativa Digital Descartes. Este recurso se ha realizado a partir de las pruebas de evaluación diagnóstico de la Junta de Extremadura para 4º de Primaria.
Como en todas las actividades del proyecto competencias, se presenta un estímulo al que siguen una serie de preguntas relacionadas. El objetivo es la aplicación de los contenidos académicos y su conexión con la realidad del estudiante.
En este caso el alumno deberá realizar ejercicios de medida del tiempo partiendo de un hecho tan cotidiano como puede ser su horario de clase.
También mostramos cómo añadir este recurso en nuestra aula virtual moodle, utilizando el código para abrir en una ventana emergente.
Este mes vamos a ver una unidad de 4ºESO sobre los números reales:
En el vídeo hemos tratado los siguientes temas:
1.Números racionales e irracionales
Decimales periódicos
Fracción generatriz
Números racionales
Números irracionales
Números reales
2.Calculando con números reales
Aproximaciones
Medida de errores
Notación científica
3.La recta real
Ordenación de los números reales
Valor absoluto
Intervalos
Dentro del curso "Aplicación de juegos didácticos en el aula" que se desarrolló en la 2ª convocatoria de formación de profesorado a nivel regional de la CEJA propusimos a los participantes que compartiesen sus impresiones como forma de mostrar las posibilidades que se abren con el uso de los juegos.
Mª Josefa Chaves Ruiz profesora de 1º de primaria en el CEIP Los Ángeles de Málaga se ha prestado a que publiquemos la experiencia de utilizar los juegos por primera vez con sus alumnos.
El que sean pequeños varía la forma de enfocar la actividad dando más peso al trabajo del docente en el desarrollo de la actividad pero compensa con creces.

Vamos con lo importante, lo que más les gustó a los alumnos:
Ver su nombre en el juego
La puntuación
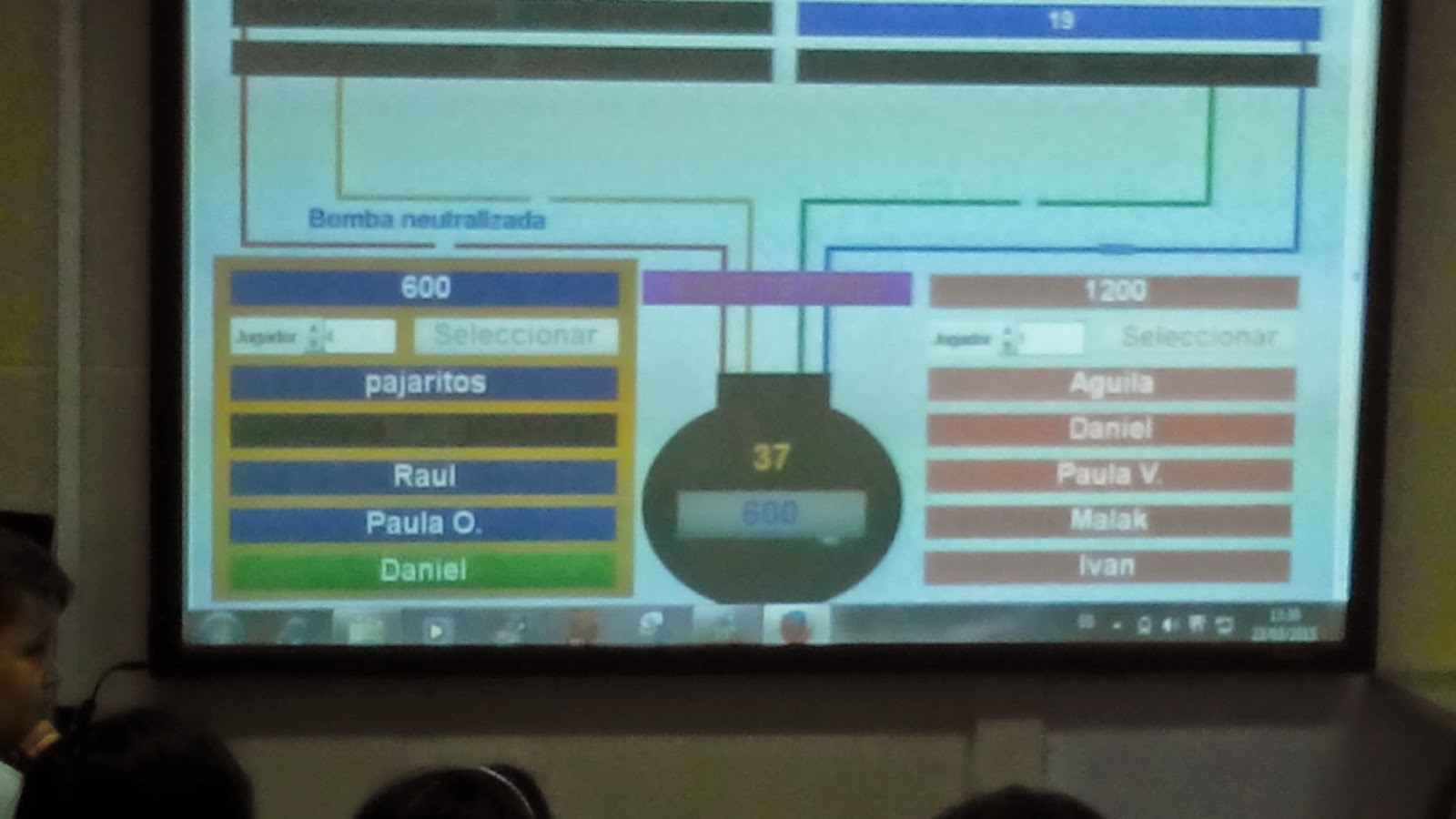
En el juego de duelo de bombas, cómo estallan las bombas cuando fallan
Actuar de público
Vemos que aunque sean cosas muy simples resultan muy motivadoras

La valoración de Mª Josefa también ha sido muy positiva:
Los objetivos planteados se han conseguido de forma adecuada. El aprendizaje de los contenidos y las competencias básicas ha sido satisfactoria,
La participación ha sido la adecuada, si bien todos querían participar. La convivencia ha sido buena, han respetado el turno del equipo que actuaba, mientras los que no actuaban hacían de público.
También puede parecer un problema trabajar con toda una clase sin tener una sala de ordenadores a tu disposición, siempre podemos encontrar la forma de desarrollar la tarea:
La actividad se ha llevado a cabo durante una hora con 18 alumnos divididos en dos grupos, se han hecho dos equipos de 4 o 5 alumnos que competían entre sí y el resto hacía de público respetando a los que jugaban, después los que hicieron de público fueron los concursantes.
También se han utilizado los juegos con otro pequeño grupo utilizando un portátil, menos medios pero más participación por parte de los alumnos.
Los resultados han sido muy positivos, se han quedado con ganas de volver a jugar, lo que les sirve de incentivo y motivación.
Además, un consejo:
La puesta en práctica hay que prepararla con tiempo para que cuando los alumnos vayan a jugar esté todo preparado y no falle nada.
No podemos terminar de mejor forma que con un último comentario de Mª Josefa:
"A mis alumnos desde luego les ha gustado bastante y siempre que vamos a la pizarra digital quieren jugar con estos juegos, por lo que me veo en la obligación de preparar más preguntas para juegos diferentes. Los encuentro muy motivadores, todos quieren participar."
Solo nos queda agradecer a Mª Josefa su participación en el curso y su colaboración en la difusión de los juegos.
Os animamos a seguir compartiendo vuestras experiencias.
Más...
Galardón de la RSME para Marta Macho Stadler
Escrito por José Antonio Salgueiro González La Real Sociedad Matemática Española ha otorgado una de las primeras Medallas de la RSME a Marta Macho Stadler, profesora de Geometría y Topología en el Departamento de Matemáticas de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco.
La Real Sociedad Matemática Española ha otorgado una de las primeras Medallas de la RSME a Marta Macho Stadler, profesora de Geometría y Topología en el Departamento de Matemáticas de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco.
La ponencia encargada de seleccionar a los premiados destaca de Marta "su labor de divulgación de las matemáticas, su compromiso con la igualdad y tender puentes entre los profesores de matemáticas de diferentes niveles educativos".
Pues bien, parte de esa actividad divulgadora para acercar las matemáticas a la ciudadanía, en general, podemos encontrarla en el blog de la Facultad de Ciencia y Tecnología de la UPV/EHU, en la revista digital Matematicalia, en Matemáticas Experimentales, en el Cuaderno de Cultura Científica o en DivulgaMAT.
En relación con su compromiso con la igualdad, Marta conduce Mujeres con Ciencia y recientemente ha recibido el Premio Igualdad 2015 de la Universidad de Alicante.
Del tercer aspecto que la ponencia destaca sobre Marta aprovechamos para recordar su genial interpretación en nuestro programa Radio Descartes, con la entrevista al VI Personaje Misterioso, en esta ocasión correspondía a la mujer matemática más grande anterior al siglo XX.
Mis disculpas a Marta por la sucinta y escueta muestra de su prolífica producción y, en nombre de la RED Descartes, nuestra más sincera felicitación por este merecido premio, a la vez que manifestamos nuestra fortuna por contar con una colaboradora de excepción.
Obviamente, extendemos nuestra felicitación a los compañeros igualmente premiados con las Medallas de la RSME, a saber, José Luis Fernández Pérez y Antonio Martínez Naveira, a la vez que a la Real Sociedad Matemática Española por esta inicitaiva que, como se recoge en su web, "expresan público reconocimiento de la comunidad a personas destacadas por sus aportaciones en cualquiera de los ámbitos de la actividad matemática".
Os recomendamos seguir en las redes sociales a:
- Marta Macho en Twitter
- Marta Macho en Facebook
- Marta Macho en G+
- Mujeres con Ciencia en Twitter
- Real Sociedad Matemática Española en Twitter
- DivulgaMAT en Twitter
- DivulgaMAT en Facebook
Si reconoces al personaje misterioso interpretado por Marta, puedes compartirlo en un comentario de este post.
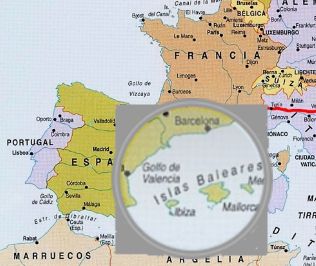
Cuando confluyen ideas simples con necesidades o requerimientos técnicos mínimos, se logra elaborar magníficos recursos educativos de gran interés y vistosidad. Esto es lo que acontece en la utilidad cartesiana desarrollada por nuestro amigo cartesiano Juan Gmo. Rivera Berrío, presidente de la Red Educativa Digital Descartes de Colombia. Una utilidad que ha denominado "Lupa cartesiana" y que puede observarse en la siguiente escena (pulsa sobre la imagen):
La escena utiliza la posibilidad de la herramienta Descartes que permite integrar varios espacios y el escalado de imágenes.
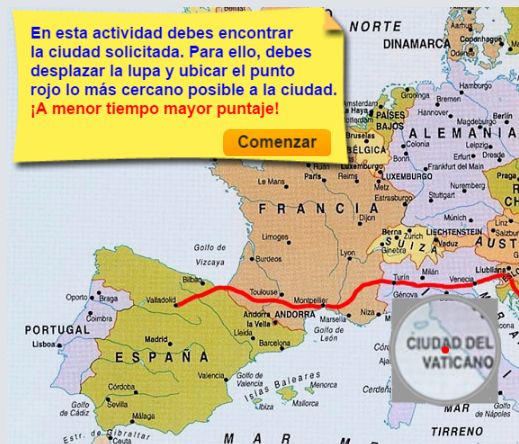
En la siguiente escena podemos ver una entretenida aplicación que permite poner a prueba nuestro conocimiento geográfico. Este recurso se está empleando en el desarrollo de nuevos materiales educativos que pronto se integrarán en el subproyecto GEOgráfica de la RED Descartes.
La creatividad de los cartesianos y del profesorado en general podrá dar una amplia aplicación de esta herramienta en su contexto educativo y en el ámbito cognitivo que sea de su interés particular. Una utilidad que permite introducir al usuario en una visión microcóspica --al nivel que se desee-- en base a una imagen inicial sobre la que se puede profundizar gracias a la visión virtual de la lupa cartesiana.
La fuente de estos recursos y de este artículo se encuentra en la documentación de Descartes.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
