En el siguiente vídeo vamos a ver cómo crear un libro digital de moodle con unidades de la Red Educativa Digital Descartes, utilizando el código para embeber.
<iframe style="width: …px; height: …px;" src="/descartescms/dirección web de la escena"></iframe>
Se han seleccionado las unidades de estadística del Proyecto Pizarra Interactiva (PI).
- En la primera unidad, azar, se introduce la idea de suceso seguro, probable e imposible.
- En la unidad frecuencia, a partir de la simulación del lanzamiento de un dado se introduce el cálculo de la frecuencia absoluta y relativa así como la organización y clasificación de datos en tablas.
- En la tercera unidad, de forma visual y amena, nos acercamos al concepto de media y moda.
- Finalmente, para el estudio de las probabilidades, se proponen diferentes experimentos aleatorios observando los casos posibles y los casos favorables de un suceso y su relación para el cálculo de la probabilidad.
EDAD 3ºESO Ecuaciones de segundo grado
Escrito por Alfonso Saura EspínEsta semana vamos a ver el contenido de 3ºESO de ecuaciones de segundo grado
el índice seguido ha sido el siguiente:
1.Expresiones algebraicas
Identidad y ecuación
Solución de una ecuación
2.Ecuaciones de primer grado
Definición
Método de resolución
Resolución de problemas
3.Ecuaciones de segundo grado
Definición. Tipos
Resolución de ax²+bx=0
Resolución de ax²+c=0
Resolución de ax²+bx+c=0
Suma y producto de las raíces
Discriminante de una ecuación
Ecuación (x-a)·(x-b)=0
Resolución de problemas
Misceláneas. Las Espirales III
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales III
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes caben destacar, entre otras, la creación del subproyecto Pisa con ordenador por parte de Mª José García Cebrian y José R. Galo Sánchez, documentado en este Blog por Santos Mondéjar López y la herramienta creada por el profesor Ángel Cabezudo Bueno que nos ha dotado de la posibilidad de analizar un crecimiento espiral y hallar la expresión matemática que mejor lo ajusta. La siguiente imagen enlaza con la miscelánea que explica el proceso de creación de dicha herramienta y el uso de la misma.
En el proceso de recuperación y adaptación de materiales de la Red Descartes que habían quedado obsoletos y en el de creación de nuevos recursos son varios los trabajos que merecen mención especial que ya está reflejada en el Blog, no obstante animamos a los socios y visitantes de nuestra web a usar y estudiar dichos trabajos y emprender tareas de adaptación-creación de: Unidades, Misceláneas, Discursos... para recuperar todo el esfuerzo e ilusión que en su día se invirtió y dotar a la aldea global de herramientas útiles para la enseñanza y el aprendizaje.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información de las funciones matemáticas disponibles para la construcción de escenas.
Antes de comenzar con el análisis de los gráficos incluidos en la escena en estudio vamos a mostrar un vídeo que relaciona los fractales y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
- Espirales de Antonio Pérez Sanz
- Real Sociedad Matemática Española
- Espirales, fractales, Fibonacci,...
- Visión más espiritual
- Espirales y Laberintos
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior nos quedamos estudiando los gráficos introducidos en la escena: puntos, segmentos, líneas, polígonos, textos... etc. Para lo cual abrimos la opción de menú Gráficos y observamos los 26 objetos creados y que muestra la siguiente imagen.
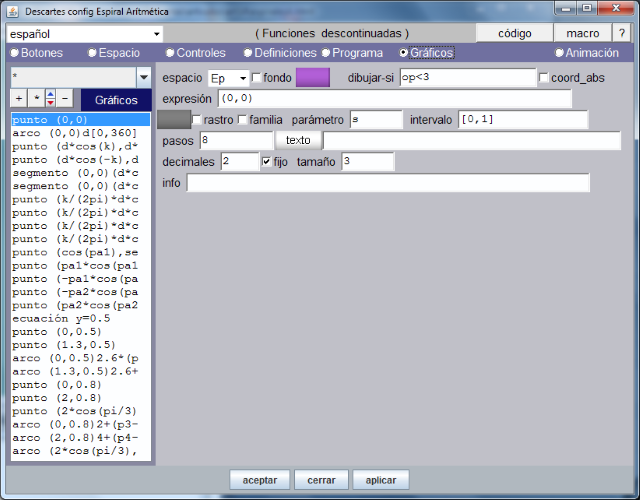
Insistimos en la conveniencia de descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada gráfico. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los gráficos se puede examinar y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos gráficos son las que comienzan por: <param name="G_x" que en nuestro caso llegan hasta <param name="G_26". Recordamos que se debe tener mucha precaución al editar directamente el código.
Observando la imagen vemos que, en primer lugar, se ha definido un punto en el origen de coordenadas (0,0) que, en esta ocasión, está centrado en la escena. Conviene, si no se tiene práctica, estudiar y probar las diferentes maneras de situar el origen de coordenadas de un espacio y el espacio en si mismo, dentro de la escena. También vemos el espacio donde se representará el punto, su color, tamaño y otra serie de parámetros autoexplicativos y de facil uso.
De los parámetros que ayudan a manejar un punto en la escena uno muy interesante es el de 'familia' que mediante un parámetro (variable) que se introduce en la/s coordenada/s y que se declara en el cuadro de texto "parámetro" (o se acepta el ofrecido por el editor 's') permite introducir simultáneamente tantos puntos como se precise en los lugares definidos por las coordenadas.
La siguiente imagen muestra como se han definido la colección de puntos azules que dibujan la espiral de Aquímedes según la definió el geómetra griego, donde se usa el parámetro global 'familia' con el parámetro o variable 'k '. Recordamos que en su momento definimos el control 'k ' y le asignamos un valor inicial y un valor final. Esta manera de proceder hace que la escena sea interactiva ya que el conrol k puede manipularse al estar presente en la escena en forma de pulsador.
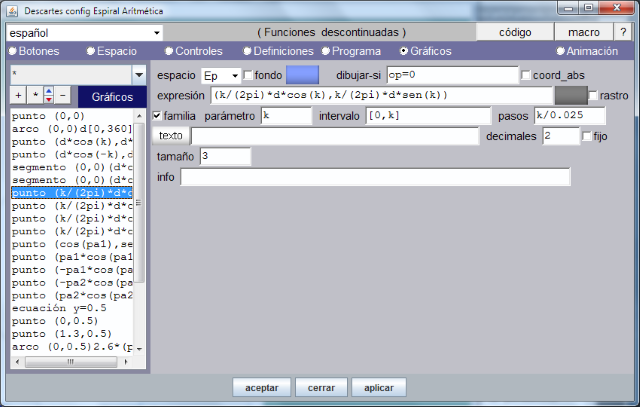
Puesto que disponemos de la escena podemos analizar cada uno de los gráficos cambiando los valores de sus parámetros y observando el efecto de las modificaciones para así aprender a configurar escenas con el editor de código.
Con objeto de practicar con los condicionales hemos elaborado la siguiente escena para su análisis. Es una pequeña aplicación donde se hace una breve introducción al estudio de la distribución de la proporción humana en superficies lisas mediante triángulos, rectángulos, rombos y otras figuras derivadas.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como obtener dos triángulos cordobeses a partir de un folio DIN A4.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral de Teodoro entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Hoy os vamos a presentar un pequeño subproyecto dentro del proyecto Competencias, se trata de PISA con ordenador.
Se emplea la interacción para evaluar en base a la recreación de una situación que permite al alumno contextualizar el problema.
Estos objetos de aprendizaje san desarrollado con Descartes por lo que son ejecutables desde cualquier sistema operativo y dispositivo móvil.
Centrándonos ya en los recursos, disponemos de 19 objetos que podemos descargar de forma individual o todos en un fichero comprimido. Por supuesto también disponemos de enlaces a los objetos publicados en la web de la Red Descartes.
Las actividades propuestas provienen de preguntas aparecidas en las pruebas de evaluación PISA y cada recurso consta de varias preguntas sobre el mismo tema. También tienes disponibles los recursos antes de la adaptación.
Encontramos una serie de datos en forma de textos, tablas de datos o gráficos de los que los alumnos deben extraer la información para responder las preguntas. Éstas cuestiones son de varios tipos, elegir la respuesta correcta, redactarla, seleccionar enunciados para completar la frase correcta, seleccionar varias respuestas válidas…Esta variedad en la forma de responder permite detectar mejor las capacidades del alumnado.
Una vez se han contestado las preguntas se ofrece la opción de revisarlas para que puedan asegurarse de hacerlo bien.
Al terminar encontramos cuatro posibilidades:
- Ver las respuestas correctas, una corrección automática instantánea de las contestaciones exceptuando las preguntas de redacción que deben ser evaluadas por el profesor
- Descargarlas respuestas, esta opción permite al profesor recogerlas y poder calificarlas después
corregidas
- Enviarlas por correo al profesor, los alumnos deben poner su nombre y el correo del profesor para poder indentificarlos y que sea posible el envío
- Imprimirlas, también permite la corrección con la ventaja de mostrar con facilidad al alumnado las pruebas
En todos los casos el alumno verá las respuestas correctas después de realizar la acción elegida
Os dejamos un vídeo en el que repasamos la web y comentamos uno de los recursos: Síndrome de despoblamiento de colmenas
Dispones de muchos más recursos en la web de la Red Descartes
Más...
Operando con enteros. Una lección interactiva
Escrito por Montserrat Gelis BoschEn el vídeo de esta semana se presenta una selección de actividades para introducir en 1º de ESO las operaciones con enteros.
Se trata de actividades pertenecientes a la unidad los números enteros, del Proyecto ED@D y para su aplicación en el aula se propone embeber las escenas en un curso de moodle mediante el recurso Lección.
El recurso Lección de moodle, ofrece muchas posibilidades, desde la edición de páginas de contenido con diferentes ramificaciones hasta las páginas de preguntas. En este caso se han creado una serie de páginas de contenido, pero se puede ampliar la lección con otras actividades en función de las preferencias de cada uno.
Las escenas Descartes se insertan en páginas de contenido utilizando la siguiente línea de código:
<iframe style="width: 600px; height: 400px;" src="https://proyectodescartes.org/EDAD/materiales_didacticos/EDAD_1eso_numeros_enteros-JS/1q3_ejercicios_resueltos_2a.htm"></iframe>
Si se trata de una actividad de la cual no se dispone de la dirección web, se puede copiar todo el código de la escena y pegar en la página de la lección.
EDAD 4º ESO Opc. A Números enteros y racionales
Escrito por Alfonso Saura EspínEste mes vamos a ver el siguiente vídeo sobre la unidad correspondiente a enteros y racionales:
Los temas tratados han sido:
1.Números enteros
Representación y orden
Operaciones
Problemas
2.Fracciones y decimales.
Fracciones equivalentes.
Expresión decimal. Clasificación
3.Números racionales
Representación y orden
Suma y resta
Multiplicación y división
Potencias de exponente entero.
Operaciones con potencias.
Problemas.
4.Notación científica
Definición
Operaciones
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



 CONTACTO
CONTACTO
