Un paquete SCORM (Sharable Content Object Reference Model) consiste en una lista de requisitos técnicos, que contiene una descripción detallada de la estructura de un objeto de aprendizaje y un conjunto de archivos y datos que hacen posible que sea interpretado por diferentes plataformas e-learning, como por ejemplo Moodle.

Si se dispone de un curso en una plataforma Moodle, se pueden crear paquetes SCORM con actividades de evaluación, de forma que las calificaciones obtenidas por el alumnado queden registradas en Moodle.

En los diferentes proyectos de la RED se dispone de muchas actividades con ejercicios de autoevaluación. En este artículo se propone la creación de un paquete SCORM a partir de la autoevaluación de una unidad del proyecto ed@d.

Para crear un paquete SCORM deberemos cumplir con una serie de requisitos previos:

En primer lugar será preciso crear una nueva carpeta, con el material necesario para el funcionamiento de la actividad. Para que la escena se comunique con Moodle, se deberán añadir también dos ficheros JavaScript y un archivo html llamado comunica.html. Este archivo contiene el código para enviar a Moodle la calificación (nota) obtenida en la actividad.

También se deberá modificar la escena del objeto interactivo con el editor DescartesJS, añadiendo un nuevo espacio html (cal), que carga la página comunica.html para la interacción con Moodle y un botón enviar, que al pulsar notificará la calificación de la actividad. También será preciso definir la variable nota, la suma de todas las respuestas correctas que quedará registrada en Moodle.

Finalmente, una vez modificada la escena, nos dispondremos a crear el contenedor SCORM usando un editor que permita crear estos paquetes. Hay varias herramientas para crear contenidos SCORM, en este caso se utiliza el programa RELOAD (Reusable eLearning Object Authoring & Delivery). Con RELOAD crearemos el paquete con los contenidos, los datos, la organización y la estructura de la actividad. El paquete con los archivos y carpetas necesarios se guardará en un fichero ZIP. Este es el fichero que se subirá a Moodle al crear una actividad del tipo SCORM.

Enlaces a los materiales:

Editor RELOAD

Paquete SCORM (autoevaluación de la unidad de proporcionalidad)

En el siguiente vídeo, se muestra con detalle la creación y aplicación en Moodle de un paquete SCORM a partir de una autoevaluación del proyecto ed@d:

>

En este artículo presentamos dos unidades del proyecto Misceláneas con ejercicios de porcentajes e intereses.

Misceláneas es un subproyecto de la Red Educativa Digital Descartes que contiene unidades independientes que tratan diferentes aspectos del currículo de matemáticas y que se pueden utilizar como complemento al estudio de distintos conceptos matemáticos. En este caso hemos seleccionado las unidades: Descuentos y recargos simples y porcentajes encadenados y BANCOS. Interés simple y compuesto.

Estas dos escenas interactivas son un recurso útil para el profesorado ya que en ellas se proponen múltiples ejercicios con autocorrección para practicar porcentajes y, por sus características, adecuados a todos los niveles de secundaria, ya sea de ampliación en los primeros cursos o bien de consolidación y refuerzo en cursos superiores.

En el siguiente vídeo se muestra con detalle la tipología de los ejercicios propuestos en estas escenas. También se propone un ejemplo de aplicación en un curso Moodle sobre el tema de proporcionalidad para segundo de la ESO. En primer lugar se ha insertado la unidad temática proporcionalidad del proyecto ed@d y como complemento se han añadido las dos unidades de porcentajes e intereses. De la misma forma, para completar el tema, se podrían incorporar en el aula virtual otras actividades y tareas sobre proporcionalidad.

Título: Primeros problemas de magnitudes proporcionales
Sección: Unidades didácticas
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: 1º ESO (12 o más años)
Idioma: Castellano
Autoría: Rita Jiménez Igea

Haz clic en la imagen para abrir el recurso

Descargar recurso

Código para embeber como iframe

Código para abrir en ventana emergente

<iframe style="width: 1200px; height: 800px;" src="https://proyectodescartes.org/uudd/materiales_didacticos/Primeros_problemas_magnitudes_proporcionales-JS/index.htm"></iframe>

<a href="https://proyectodescartes.org/uudd/materiales_didacticos/Primeros_problemas_magnitudes_proporcionales-JS/index.htm" target="_blank" onclick="window.open(this.href, this.target, 'width=1200,height=800,top=30,left=100,toolbar=0,menubar=0,scrollbars=1,resizable=1,location=0,status=0'); return false;"><img src="https://proyectodescartes.org/descartescms/images/materiales/uudd/Primeros_problemas_magnitudes_proporcionales-JS.png" alt="Primeros problemas de magnitudes proporcionales" style="display: block; margin-left: auto; margin-right: auto;"></a>

Puedes encontrar todos los materiales de las Unidades Didácticas en
https://proyectodescartes.org/uudd/index.htm - Ver Créditos

Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional

Título: Problemas de proporcionalidad 
Sección: @prende.mx
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: 5º y 6º de Primaria (10 a 11 años)
Idioma: Castellano
Autoría: Varios autores
Promotor: Secretaría de Educación Pública del gobierno de México

Haz clic en la imagen para abrir el recurso

Descargar recurso

Código para embeber como iframe

Código para abrir en ventana emergente

<iframe style="width: 1024px; height: 650px;" src="https://proyectodescartes.org/AprendeMX/materiales_didacticos/M05_030_ProblemasDeProporcionalidad/index.html"></iframe>

<a href="https://proyectodescartes.org/AprendeMX/materiales_didacticos/M05_030_ProblemasDeProporcionalidad/index.html" target="_blank" onclick="window.open(this.href, this.target, 'width=1024,height=650,top=30,left=100,toolbar=0,menubar=0,scrollbars=1,resizable=1,location=0,status=0'); return false;"><img src="https://proyectodescartes.org/descartescms/images/materiales/AprendeMX/M05_030_ProblemasDeProporcionalidad.png" alt="Problemas de proporcionalidad " style="display: block; margin-left: auto; margin-right: auto;"></a>

Puedes encontrar todos los materiales de @prende.mx en
https://proyectodescartes.org/AprendeMX/index.htm - Ver Créditos

Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional

Proporcionalidad. Las Espirales XII

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.

Como muestra enlazamos la unidad sobre Crecimiento Exponencial, del subproyecto TELESECUNDARIA,

la GEOevaluación de los estados y ciudades de México.

y el ejemplo de: Asocia parejas de imágenes y textos (2).

Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y las adaptaciones de los trabajos de Javier de la Escosura Caballero: "Geometría dinámica del trángulo" que enlazamos a continuación

y el de Cuadrilateralia, donde se fomenta el estudio y conocimiento de las características matemáticas de los objetos mediante la manipulación virtual de los mismos y que enlazamos con la imagen siguiente.

Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para trisecar un ángulo con la Concoide de Nicomedes. El ángulo a trisecar es el formado por el eje polar y la recta que une el polo con el punto que se desplaza por la directriz.
El análisis de la escena y su modificación, fundamentalmente en la situación del tercio del ángulo mencionado anteriormente, nos lleva a descubrir interesantes características de la Concoide. También son interesantes las modificaciones funcionales que mejoren las prestaciones de la utilidad.
Mencionar, por último, que la escena es copia de la que en su día publicó el profesor Pedro González Enríquez en su trabajo sobre las trisectrices.

Entradas anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por uno y dos puntos y algunas de las utilidades de los l.g. generados por un punto, en la actual comenzamos a mostrar algunos de los usos de la Concoide.

En esta ocasión, en la sección de vídeo, hemos elegido, debido a su calidad e interés, el mismo que en la entrada anterior, que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografías y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Lituus" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

• Hemos creado la siguiente escena: Espiral de Lituus

• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Lituus incluida.

También, relacionado con el tema de los lugares geométricos (l.g.) y la trisección del ángulo, hemos incluido los trabajos realizados con el programa GeoGebra donde se muestran dos metodos para trisecar un ángulo con la Concoide de Nicomedes.

Método 1.

Método 2.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo

Proporcionalidad. Las Espirales X

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades al subproyecto TELESECUNDARIA.

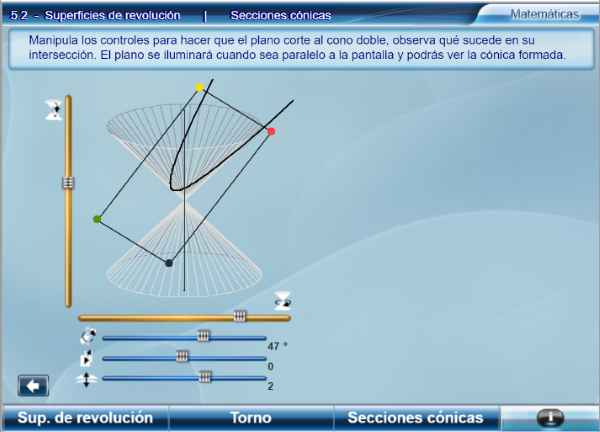
Como muestra, enlazamos la unidad sobre superficies de revolución

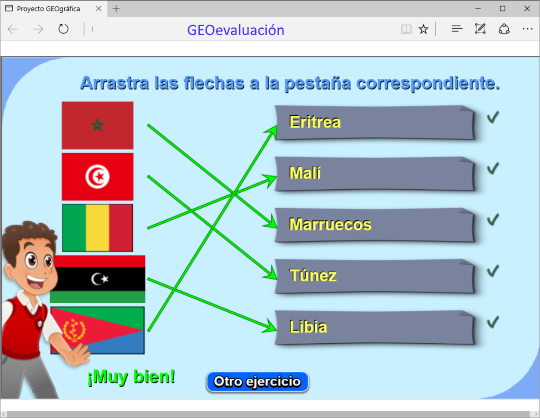
También es continuo el flujo de aportación de unidades al apartado GEOevaluación del subproyecto GEOgráfica

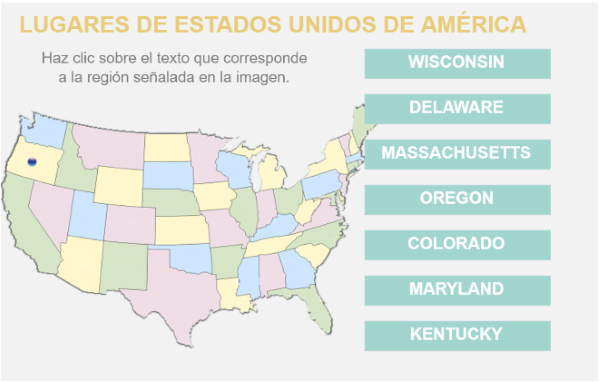
En esta ocasión enlazamos la Evaluación de los Estados Unidos de América

Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos lugares geométricos aunque, en particular, es de especial interés la creada por Ángel Cabezudo Bueno ya que, además de ser la primera de la serie actual, entronca directamente con la fuente origen de dicha serie, el trabajo de José R. Galo Sanchez sobre las proporciones, la belleza en las Matemáticas y la espiral Cordobesa y es consecuencia de la acertada propuesta de espiral gnomónica Cordobesa, ambas: propuesta y miscelánea se muestran y/o enlazan a continuación.

El artículo anterior mostraba, paso a paso y exhaustivamente escenas interactivas con la creación de un lugar geométrico (l.g.) por un punto común a dos segmentos y por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos, el actual vuelve a construir la espiral de Arquímedes y también paso a paso e interactivamente muestra como trisecar un ángulo cualquiera y como hallar la cuadratura de cualquier círculo.

A continuación se exponen las escenas interactivas.

• Generación del lugar geométrico conocido como espiral de Arquímedes.
  

  
  
  

• Trisección de un ángulo mediante la espiral de Arquímedes.

  
  
  

• La cuadratura del círculo mediante la espiral de Arquímedes.

  
  
  

En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la relación de la espiral con la orografía y la interpretación de las señales cosmológicas por las diferentes culturas con objeto de apreciar distintas formas de enfocar el tema que nos ocupa.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Hiperbólica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

• Hemos creado la siguiente escena: Espiral Hiperbólica

  
  
  

• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto. Dejamos para los lectores interesados la inclusión total y/o personalizada de esta opción. 

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Hiperbólica incluida.

También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido los siguientes trabajos realizados con el programa GeoGebra: en el primero se muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el segundo para la cuadratura del círculo.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo

 Proporcionalidad. Las Espirales VIII

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destacan las aportadas por la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes España que, coordinadas por el profesor Juan Guillermo Rivera Berrío, han añadido al subproyecto GEOgráfica una importante cantidad de contenidos, lo que ha hecho necesario dividir el subproyecto inicial en varios subproyectos: GEOcapital, GEOdiver, GEOcolor y GEOevaluación (en estado muy avanzado), estando en fase de desarrollo los de: GEOmontañas y GEOrios, los tres primeros pueden verse y descargarse siguiendo el enlace gráfico siguiente.

GEOevaluación. Bandera - País

El carácter evaluativo - formativo de estas unidades es extraordinario según se manifiesta en la escena anterior y en las que enlazamos a continuación.

También cabe señalar el desarrollo de todo un nuevo subproyecto "PLANTILLAS CON DESCARTES-JS que proporciona herramientas para la creación de contenidos lúdico-didácticos."

Dentro de nuestro ámbito local destacan, entre otras muchas, las siguientes aportaciones:

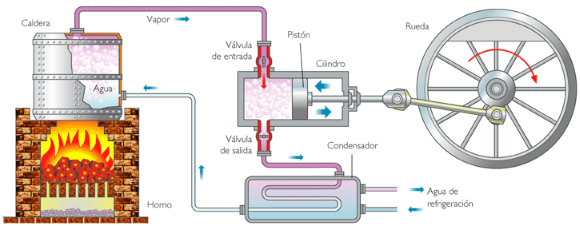
• Dos libros digitales e interactivos en el apartado de Física y Química del subproyecto iCartesiLibri: Teoría de la relatividad y Máquinas térmicas.

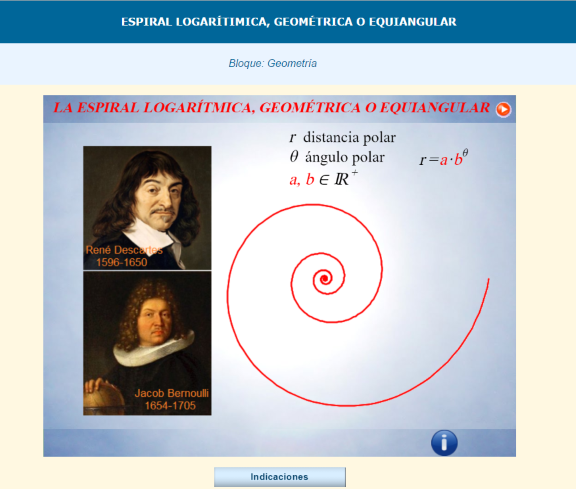
• La sorprendente y hermosa Miscelánea La espiral Logarítmica

• Dentro del subproyecto "Unidades Didácticas" la extensa e instructiva unidad Puzles Descartes que dota a la creación de escenas con el editor DescartesJS de una herramienta versátil y potente para la elaboración de objetos educativos lúdicos e interactivos.

• La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente.

En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la manera de dibujar la espiral áurea con regla y compás con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fibonacci" tal y como anunciamos en el artículo del mes pasado.
En esta ocasión hemos procedido de la siguiente manera:

• Hemos creado la siguiente escena: Espiral de Fibonacci

  
  

• Inclusión del código de la escena anterior en el de la miscelánea en proyecto.

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Fibonacci incluida.

También, relacionando, mediante el programa GeoGebra, la espiral con el Fenaquistiscopio, quisiera enlazar el siguiente trabajo de Nicolas Erdrich.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo

Este mes vamos a ver un vídeo de 4ºESO Opción A, correspondiente a proporcionalidad:

En este vídeop hemos tratado los siguientes apartados:

1.Proporcionalidad directa e inversa
   Proporcionalidad directa
   Proporcionalidad inversa
   Repartos proporcionales
   Proporcionalidad compuesta
   
2.Porcentajes
   Porcentajes
   Aumentos y disminuciones
   Porcentajes sucesivos

3.Interés simple y compuesto
   Interés simple
   Interés compuesto
   Tasa anual equivalente (T.A.E.)
   Capitalización

Proporcionalidad. Las Espirales VII

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destacan las aportadas por la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes España que, coordinadas por el profesor Juan Guillermo Rivera Berrío, han añadido al subproyecto GEOgráfica una importante cantidad de contenidos, lo que ha hecho necesario dividir el subproyecto inicial en varios subproyectos: GEOcapital, GEOdiver y GEOcolor, estando en fase de desarrollo los de: GEOevaluación y GEOrios, los tres primeros se pueden ver y descargar siguiendo el enlace gráfico siguiente.

El potencial formativo de estas unidades queda de manifiesto en la escena anterior y en la que enlazamos a continuación.

En la creación efectiva de las unidades han intervenido:

• Juan G. Rivera Berrío
• Diego Feria Gómez
• Ramiro A. Lopera Sánchez
• José R. Galo Sánchez
• Ángel Cabezudo Bueno
• Ildefonso Fernández Trujillo

Acceso a los contenidos.

Dentro de nuestro ámbito local destacan, entre otras muchas, las siguientes aportaciones:

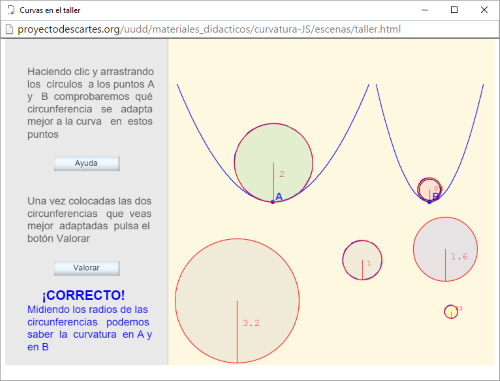
• La actualización de la profesora Consolación Ruiz Gil de su unidad didáctica titulada "Curvatura", este trabajo ha sido recibido por el presidente de la Red Descartes con un artículo magistral en el blog de la web con el título "¿Cómo observar lo que no podemos ver? Taller y laboratorio de curvatura" en el que ejemplariza algunas acepciones del concepto de curvatura, quizás motivado por la extraordinaria y sutil belleza de la unidad actualizada.
  La siguiente imagen enlaza con dicha unidad.

• Las aportaciones del profesor Eduardo Barbero Corral al proyecto iCartesiLibri, consistentes en varios cuadernos en formato de libro digital interactivo para la práctica con las operaciones de números Enteros.
  El uso de estos materiales en el aula o como referencia para la consolidación de conceptos fuera de ella es altamente recomendable. A continuación observamos una escena de uno de dichos cuadernos que es un enlace al cuaderno completo.

En esta ocasión, en la sección de vídeo, hemos elegido uno donde se muestra la presencia de la espiral en las técnicas de sanación relacionadas con el equilibrado de los hemisferios con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Durero" tal y como anunciamos en el artículo del mes pasado.
En esta ocasión hemos procedido igual que en el caso de la espiral Cordobesa:

• De la Miscelánea Espirales generalizadas de Durero hemos extraido la siguiente escena.
• Desarrollo de la gráfica de la espiral de Durero

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Durero incluida.

En próximas entradas continuaremos con el paso a paso del proyecto incluyendo la espiral de Fibonacci y otras más entre sus funcionalidades, reseñando las novedades y analizando el subproyecto Misceláneas. Animamos a los lectores a colaborar en el proyecto con contenidos o aportando ideas y sugerencias. Ildefonso Fernández Trujillo

Proporcionalidad. Las Espirales VI

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destacan las aportadas por la Red Educativa Digital Descartes Colombia (colDescartes), que gracias a la integración de los mapas de Google en las escenas DescartesJS, realizada por Diego Feria Gómez, ha abierto un amplio abanico de posibilidades al proyecto GEOGráfica según muestran las escenas que, creadas por el profesor Juan Guillermo Rivera Berrío, se han añadido al mismo y que se pueden ver y descargar siguiendo el enlace gráfico siguiente.

También es de reseñar la creación, de forma colaborativa, de una Biblioteca virtual formada por libros interactivos y dinámicos con contenido lúdico-formativo adaptado a cada continente y país y que pasan a formar parte del contenido del subproyecto GEODiver dentro de GEOgráfica. El responsable e impulsor de la idea es Juan G. Rivera y han colaborado, además de él mismo:

• Diego Feria Gómez (Oceanía)
• Ramiro A. Lopera Sánchez (Estados de USA y países de Suramérica)
• José R. Galo Sánchez (Países de Europa y Provincias de España)
• Ángel Cabezudo Bueno (Asia)
• Ildefonso Fernández Trujillo (África)

Acceso a los contenidos.

Dentro de nuestro ámbito local destacan las creaciones y adaptaciones de unidades del proyecto ed@d. En esta ocasión enlazamos la creada por: Jesús Muñoz Calle, Joaquín Recio Miñarro y Luis Ramírez Vicente y adaptada por Luis Ramírez Vicente para la asignatura de Física con el título de "Las Ondas".

De la colección de unidades interactivas del subproyecto COMPETENCIA SOCIAL Y CIUDADANA que el profesor Luis Barrios Calmaestra ha creado sobre algunos de los temas curriculares enlazamos el referente a los impuestos.

En esta ocasión en la sección de vídeo aprovechamos el impulso de desarrollo de vídeos lúdico-educativos de la Red Educativa Digital Descartes Colombia para presentar un video-puzle. Consiste, como en un puzle tradicional, en colocar cada pieza en su sitio, pero de fondo, en lugar de una imagen estática se usa un vídeo en reproducción. Se ha simplificado sobremanera el vídeo presentación con objeto de facilitar la toma de contacto, aunque siguiendo los enlaces de la ayuda se puede acceder al código fuente y a la aplicación original. Para acceder, pulsad sobre la siguiente imagen. Nota editores RED Descartes 19 de agosto de 2023: Este vídeo-puzle ya sólo funciona en el navegador Firefox, debe de usar éste si desea ver cómo funcionaba en su momento.
Cuando las adaptaciones educativas estén publicadas dedicaremos nuestra atención a tan interesante innovación.

Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.  

En el artículo anterior se añadieron al proyecto: la escena de la espiral de Teodoro y la escena sobre como dibujar las espirales de 3, 4, 5 ... 20 centros y se quedó en incluir la espiral Cordobesa, cosa que hemos realizado de la siguiente manera:

• De la Miscelánea Espirales generalizadas de Durero hemos extraido la siguiente escena.
• Desarrollo de la gráfica de la aproximación gnomónica de la espiral Cordobesa

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Cordobesa incluida.

En próximas entradas continuaremos con el paso a paso del proyecto incluyendo la espiral de Durero, la de Fibonacci y otras más entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo