
Título de la obra:
Deltoides con proporciones áureas
Autor:
Luis Barrios Calmaestra
Red Educativa digital Descartes
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-99-8

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
En este libro se estudia la existencia y construcción de deltoides con proporciones áureas. Se incluyen escenas interactivas del Proyecto Descartes que ayudan a realizar la construcción paso a paso de las figuras estudiadas y a una mejor comprensión de sus propiedades.
El primer capítulo es una introducción sobre el número de oro, su historia, sus propiedades y su representación gráfica. Se calculan también las primeras potencias del números de oro y se observa su relación con la sucesión de Fibonacci.
El segundo capítulo trata sobre el rectángulo de oro, símbolo de armonía y belleza. Se estudia su construcción y sus propiedades. Se representan algunas figuras y curvas que se pueden inscribir en él y, que por este motivo, reciben la denominación de áureas.
En el tercer capítulo se estudian triángulos isósceles con proporciones áureas, se calculan sus elementos y se observa su presencia en el pentágono regular y en el decágono regular. Así mismo se estudian las proporciones áureas en estos dos polígonos regulares.
El cuarto capítulo estudia los cuadrilaterós con proporciones áureas, el rombo de oro, el romboide, trapecios isósceles y escalenos y trapezoides. Se estudian sus elementos y la forma de construirlos.
Y los capítulos quinto y sexto, que le dan título al libro, tratan sobre un tipo particular de trapezoide, el deltoide, un trapezoide con dos parejas de lados consecutivos iguales. Se estudian deltoides convexos y cóncavos inscritos en un rectángulo áureo. Y se estudia también la existencia de deltoides que, aunque no están inscritos en un rectángulo de oro, verifican que sus lados y sus diagonales están en proporción áurea.
Su descubrimiento se remonta al siglo V a. C., en la época de la Grecia Clásica, en la que era utilizado en arquitectura y escultura. Sin embargo, la primera documentación escrita sobre el número de oro data del siglo III a. C. La tercera definición del libro VI de los "Elementos" de Euclides (325-265 a.C.), es la siguiente:
"Se dice que una recta está dividida en media y extrema razón cuando la longitud de la línea total es a la de la parte mayor, como la de esta parte mayor es a la de la menor".
Esta razón o proporción es lo que hoy conocemos como proporción áurea o número de oro.
Euclides también demostró que esta razón no puede expresarse como cociente de dos números enteros, es decir, que no era un número racional, sino irracional.
En el año 1509 Luca Pacioli (1447-1517) publica un tratado sobre el número de oro, titulado "La Divina Proporción", asignándole este calificativo de "divino".
El calificativo "áureo" se debe al matemático alemán Martin Ohm (1792-1872), quién se refiere a este número como "sección dorada" en su obra "Las matemáticas puras elementales" de 1835.
El símbolo, $\bm{\phi}$, vigésima primera letra del alfabeto griego, con el que lo conocemos en la actualidad, fue propuesto por el ingeniero norteaméricano James Mark Barr (1871-1950), como inicial del nombre del escultor griego Fidias (490-431 a.C.), uno de los arquitectos del Partenón de Atenas, una de las obras más importantes en las que se utiliza la proporción áurea.
Vamos a dividir un segmento de longitud una unidad en dos partes, de forma que la razón entre la parte mayor y la parte menor sea igual a la razón entre el total y la parte mayor. A esta forma de dividir un segmento se le conoce como proporción o sección áurea.
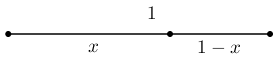
De la condición impuesta para la división del segmento, se obtiene:
$\displaystyle\frac{x}{1-x}=\frac{1}{x} \quad \rightarrow \quad x^{2}=1-x \quad \rightarrow \quad x^2+x-1=0$
Esta ecuación tiene como soluciones:
$x=\displaystyle\frac{-1+\sqrt{5}}{2}>0 \quad$ y $\quad x=\displaystyle\frac{-1-\sqrt{5}}{2}<0 $
La solución válida es la solución positiva.
Si $\quad x=\displaystyle\frac{-1+\sqrt{5}}{2} \quad \rightarrow \quad 1-x=1-\displaystyle\frac{-1+\sqrt{5}}{2}=\displaystyle\frac{3-\sqrt{5}}{2} $
El número de oro, $\phi$, es la razón entre la parte mayor y la menor:
$\phi=\displaystyle\frac{x}{1-x}=\displaystyle\frac{\displaystyle\frac{-1+\sqrt{5}}{2}}{\displaystyle\frac{3-\sqrt{5}}{2}}=\displaystyle\frac{-1+\sqrt{5}}{3-\sqrt{5}}=\displaystyle\frac{(-1+\sqrt{5})(3+\sqrt{5})}{(3-\sqrt{5})(3+\sqrt{5})}$
$\phi=\displaystyle\frac{-3+2\sqrt{5}+5}{9-5}=\displaystyle\frac{2+2\sqrt{5}}{4}=\displaystyle\frac{1+\sqrt{5}}{2}$
El número de oro es un número irracional, es decir, está formado por infinitas cifras decimales no periódicas.
A continuación, se expresa el número de oro con sus mil primeras cifras decimales, que se han calculado utilizando el programa Mathematica:
$\phi=1.6180339887498948482045868343656381177203091798057$
$628621354486227052604628189024497072072041893911374847$
$540880753868917521266338622235369317931800607667263544$
$333890865959395829056383226613199282902678806752087668$
$925017116962070322210432162695486262963136144381497587$
$012203408058879544547492461856953648644492410443207713$
$449470495658467885098743394422125448770664780915884607$
$499887124007652170575179788341662562494075890697040002$
$812104276217711177780531531714101170466659914669798731$
$761356006708748071013179523689427521948435305678300228$
$785699782977834784587822891109762500302696156170025046$
$433824377648610283831268330372429267526311653392473167$
$111211588186385133162038400522216579128667529465490681$
$131715993432359734949850904094762132229810172610705961$
$164562990981629055520852479035240602017279974717534277$
$759277862561943208275051312181562855122248093947123414$
$517022373580577278616008688382952304592647878017889921$
$990270776903895321968198615143780314997411069260886742$
$962267575605231727775203536139362 . . .$
Como no es un decimal exacto, la mejor forma de utilizarlo para hacer cálculos con la mayor precisión es con su expresión matemática y, cuando haya que expresarlo en forma decimal, escoger el número de decimales apropiado para cada situación.
En la siguiente escena de Descartes puedes seguir paso a paso la división de un segmento, con regla y compás, en la razón áurea.
Se verifica que la razón entre la parte mayor y la parte menor en las que se ha dividido el segmento es igual a la razón entre el segmento completo y la parte mayor. Al dividir el segmento de esta forma, estos cocientes coinciden con el número de oro, según se ha visto anteriormente.
$\displaystyle\frac{\overline{AB}}{\overline{AX}}=\displaystyle\frac{\overline{AX}}{\overline{XB}}=\phi$
Demostración
Aplicando el Teorema de Pitágoras
$\overline{AC}^{2}=\overline{AB}^{2}+\overline{BC}^{2}=\overline{AB}^{2}+\displaystyle\frac{\overline{AB}^{2}}{4}=\frac{5\overline{AB}^{2}}{4}$
Por otra parte:
$\overline{AC}^{2}=\big(\overline{AD}+\overline{DC}\big)^{2}=\big(\overline{AX}+\overline{BC}\big)^{2}=\bigg(\overline{AX}+\displaystyle\frac{\overline{AB}}{2} \bigg)^{2}$
$\overline{AC}^{2}=\overline{AX}^{2}+\overline{AX}·\overline{AB}+\displaystyle\frac{\overline{AB}^{2}}{4}$
Se igualan las dos expresiones de $\overline{AC}^{2}$:
$\displaystyle\frac{5\overline{AB}^{2}}{4}=\overline{AX}^{2}+\overline{AX}·\overline{AB}+\displaystyle\frac{\overline{AB}^{2}}{4}$
Se agrupan los términos semejantes:
$\overline{AB}^{2}=\overline{AX}^{2}+\overline{AX}·\overline{AB}\quad\rightarrow\quad\overline{AB}^{2}-\overline{AX}·\overline{AB}=\overline{AX}^{2}$
Se saca factor común y se sustituye la expresión del paréntesis:
$\overline{AB}·\big(\overline{AB}-\overline{AX}\big)=\overline{AX}^{2}\quad\rightarrow\quad\overline{AB}·\overline{XB}=\overline{AX}·\overline{AX}$
Finalmente se obtiene la relación buscada:
$\displaystyle\frac{\overline{AB}}{\overline{AX}}=\displaystyle\frac{\overline{AX}}{\overline{XB}}$
El número de oro es un número algebraico. Esto significa:
• Es solución de una ecuación algebraica con coeficientes racionales, se obtiene como una de las soluciones de $ \, \, x^{2}-x-1=0:$
$x=\displaystyle\frac{-(-1)\pm \sqrt{(-1)^{2}-4\cdot 1 \cdot (-1)}}{2 \cdot 1}=\displaystyle\frac{1 \pm\sqrt{5}}{2} $
• Se puede representar gráficamente con regla y compás, como se puede comprobar en la siguiente escena del proyecto Descartes:
El número $\bm{\sqrt{2}}$ también es algebraico. Sin embargo, otros números irracionales como $\bm{\pi}$ y $\bm{e}$ se dice que son trascendentes porque no verifican estas condiciones.
Se van a necesitar, en cálculos de capítulos posteriores, potencias de exponente positivo y negativo del número de oro. Vamos a calcularlas en este apartado para, cuando aparezcan, utilizar directamente su expresión.
El número de oro se ha obtenido como solución de la ecuación:
$x^{2}-x-1=0$
Sustituyendo el valor de $\phi$ en la ecuación se obtiene el valor de $\phi^{2}$:
$\phi^{2}-\phi-1=0 \quad \rightarrow \quad \phi^{2}=\phi+1 $
Calculamos algunas potencias más:
$\phi^{3}=\phi\cdot\phi^{2}=\phi\cdot(\phi+1)=\phi^{2}+\phi=(\phi+1)+\phi=2\phi+1$
$\phi^{4}=\phi\cdot\phi^{3}=\phi\cdot(2\phi+1)=2\phi^{2}+\phi=2(\phi+1)+\phi=3\phi+2$
$\phi^{5}=\phi\cdot\phi^{4}=\phi\cdot(3\phi+2)=3\phi^{2}+2\phi=\dotso=5\phi+3$
$\phi^{6}=\phi\cdot \phi^{5}=\phi\cdot(5\phi+3)=5\phi^{2}+3\phi=\dotso=8\phi+5$
Calculando más potencias, se puede observar:
• Tanto los números que multiplican a $\phi$ como los que no, son los términos de la sucesión de Fibonacci.
• Cada potencia se obtiene sumando las dos anteriores.
Como $\,\phi\not=0\,$ se verifica que $\,\phi^{0}=1$.
Veamos las potencias de exponente negativo:
Dividiendo por $\, \phi \,$ en la igualdad $\, \, \, \phi^{2}=\phi+1, \, \, \, $ se obtiene:
$\displaystyle\frac{\phi^{2}}{\phi}=\frac{\phi}{\phi}+\frac{1}{\phi} \quad \rightarrow \quad \phi=1+\frac{1}{\phi} \quad \rightarrow \quad \phi^{-1}=\frac{1}{\phi}=\phi-1 $
A partir de este valor, se pueden calcular el resto de potencias de exponente negativo:
$\phi^{-2}=\phi^{-1}\cdot \phi^{-1}=(\phi-1)\cdot (\phi-1)=\phi^{2}-2\phi+1=2-\phi$
$\phi^{-3}=\phi^{-1}\cdot \phi^{-2}=(\phi-1)\cdot (2-\phi)=-\phi^{2}+3\phi-2=2\phi-3$
$\phi^{-4}=\phi^{-1}\cdot \phi^{-3}=(\phi-1)\cdot (2\phi-3)=2\phi^{2}-5\phi+3=5-3\phi$
$\phi^{-5}=\phi^{-1}\cdot \phi^{-4}=(\phi-1)\cdot(5-3\phi)=\dotso=5\phi-8$
$. \, . \, .$
Calculando más potencias, se puede observar:
• Tanto el valor absoluto de los números que multiplican a $\phi$ como el de los que no, son los términos de la sucesión de Fibonacci.
• Cada potencia se obtiene sumando las dos anteriores, igual que sucede con la sucesión de Fibonacci, en la que cada término se obtiene sumando los dos anteriores.
$\phi^{z}=\phi^{z-1}+\phi^{z-2}\,,\,\,z \in \Z$
| $\phi^{1}=\phi$ | $\phi^{-1}=\phi-1$ |
| $\phi^{2}=\phi+1$ | $\phi^{-2}=-\phi+2$ |
| $\phi^{3}=2\phi+1$ | $\phi^{-3}=2\phi-3$ |
| $\phi^{4}=3\phi+2$ | $\phi^{-4}=-3\phi+5$ |
| $\phi^{5}=5\phi+3$ | $\phi^{-5}=5\phi-8$ |
| $\phi^{6}=8\phi+5$ | $\phi^{-6}=-8\phi+13$ |
| $\phi^{7}=13\phi+8$ | $\phi^{-7}=13\phi-21$ |
| $\phi^{8}=21\phi+13$ | $\phi^{-8}=-21\phi+34$ |
| $\phi^{9}=34\phi+21$ | $\phi^{-9}=34\phi-55$ |
| $\phi^{10}=55\phi+34$ | $\phi^{-10}=-55\phi+89$ |
| $\phi^{11}=89\phi+55$ | $\phi^{-11}=89\phi-144$ |
| $\phi^{12}=144\phi+89$ | $\phi^{-12}=-144\phi+233$ |
| $\phi^{13}=233\phi+144$ | $\phi^{-13}=233\phi-377$ |
| $\phi^{14}=377\phi+233$ | $\phi^{-14}=-377\phi+610$ |
A un rectángulo, cuyos lados están en proporción áurea, se le conoce como rectángulo áureo o rectángulo de oro.
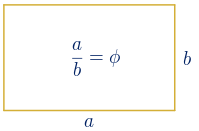
Es un rectángulo muy utilizado desde siempre en arte, buscando el modelo de perfección y belleza, pues es considerado como el rectángulo más armonioso a la vista de todos los que se pueden construir.
El ejemplo más antiguo de construcción en el que aparece el número de oro es la Pirámide de Keops o Pirámide de Guiza, en Egipto, cuya construcción finalizó alrededor del año 2600 a. C. En esta pirámide la altura de una cara entre la mitad de la arista básica coincide con el número de oro, es decir, el rectángulo de lados la altura de una cara y la mitad de la arista básica sería un rectángulo áureo.
Sin embargo, el ejemplo más importante es el Partenón de Atenas, del siglo V a. C., cuya fachada principal se puede inscribir en un rectángulo áureo. Esto supuso que se represente el número de oro con la letra griega $\bm{\phi}$, inicial de uno de los arquitectos que colaboraron en su diseño. Sin embargo, también existen estudios que dudan que ese ajuste sea perfecto.
Aunque se suele decir que tanto el DNI como las tarjetas de crédito son rectángulos áureos, en realidad no lo son. Sus medidas son 85.6 x 53.98 mm y la razón entre los lados es 1.58577.
Se puede construir un rectángulo de oro a partir de un cuadrado cualquiera, utilizando un procedimiento similar al utilizado para la representación gráfica del número $\phi$.
En la siguiente escena de Descartes puedes seguir los pasos para la construcción de un rectángulo de oro.
Demostración
Si se representa por $x$ la longitud del lado del cuadrado, la longitud del segmento $\overline{MB}$ es $x/2$. Aplicando el Teorema de Pitágoras en el triángulo rectángulo $MBC$, se puede calcular la longitud del lado $\overline{MC}$:
$\overline{MC}=\sqrt{x^2+\bigg(\displaystyle\frac{x}{2}\bigg)^{2}}=\sqrt{x^2+\displaystyle\frac{x^{2}}{4}}=\sqrt{\displaystyle\frac{5x^{2}}{4}}={\displaystyle\frac{\sqrt{5}x}{2}}$
De la construcción se deduce que $\overline{MC}=\overline{ME}$.
El lado mayor del rectángulo mide:
$\overline{AE}=\overline{AM}+\overline{ME}=\displaystyle\frac{x}{2}+\displaystyle\frac{\sqrt{5}x}{2}=\displaystyle\frac{x+\sqrt{5}x}{2}=\displaystyle\frac{x(1+\sqrt{5})}{2}$
La razón entre los lados del rectángulo es el número de oro:
$\displaystyle\frac{\overline{AE}}{\overline{AD}}=\displaystyle\frac{\displaystyle\frac{x(1+\sqrt{5})}{2}}{x}=\displaystyle\frac{1+\sqrt{5}}{2}=\phi$
• Si se divide un rectángulo de oro en dos rectángulos iguales, los dos rectángulos obtenidos no son rectángulos áureos.
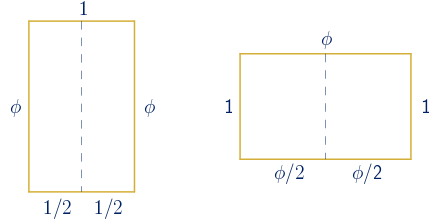
$\displaystyle\frac{\phi}{1/2}=2\phi\not=\phi\quad\quad\quad\quad\displaystyle\frac{1}{\phi/2}=\frac{2}{\phi}=2\phi-2\not=\phi$
• Si a un rectángulo de oro se le añade un cuadrado, cuyo lado mide la longitud del lado mayor, se obtiene otro rectángulo de oro.
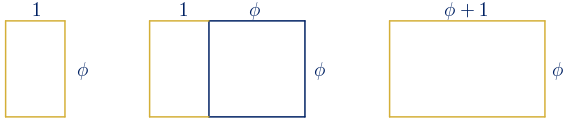
$\displaystyle\frac{\phi+1}{\phi}=1+\displaystyle\frac{1}{\phi}=1+(\phi-1)=\phi$
• Si a un rectángulo de oro se le quita un cuadrado, cuyo lado mide la longitud del lado menor, se obtiene otro rectángulo de oro.
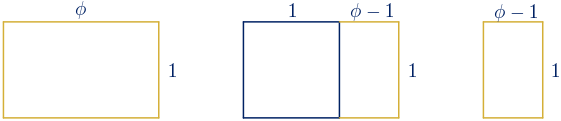
$\displaystyle\frac{1}{\phi-1}=\displaystyle\frac{1}{1/\phi}=\phi$
• Perímetro y superficie. En el rectángulo de oro cuyos lados miden $\phi$ y $1$ unidades, se verifica que:
$P=2\phi+2=2(\phi+1)=2\phi^{2}\approx5.24\,\,u$
$S=\phi\cdot 1=\phi\approx1.618\,\,u^{2}$
En cualquier otro rectángulo semejante, el perímetro se obtiene multiplicando por la razón de semejanza y la superficie por el cuadrado de la razón de semejanza.
Si el rectángulo áureo se considera que es el rectángulo con las mejores proporciones, se puede considerar de igual forma cualquier figura inscrita en un rectángulo de oro. Veamos algunas:
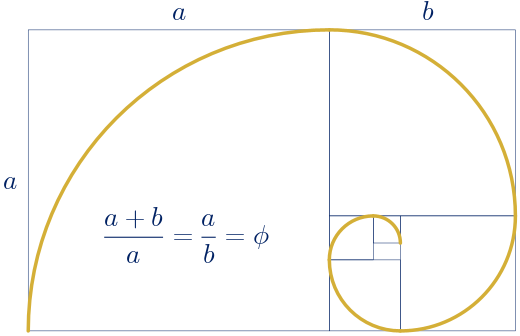
Utilizando la primera de las propiedades de la página anterior, la espiral que se va construyendo de forma indefinida, siempre estará inscrita en un rectángulo áureo.
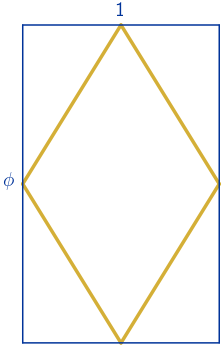
Si en un rectángulo áureo se unen los puntos medios de sus lados, se obtiene un rombo cuyas diagonales guardan la proporción del número de oro. Este rombo se conoce como rombo de oro o rombo áureo.
Se pueden ampliar todas las imágenes de este apartado pulsando con el ratón sobre ellas.
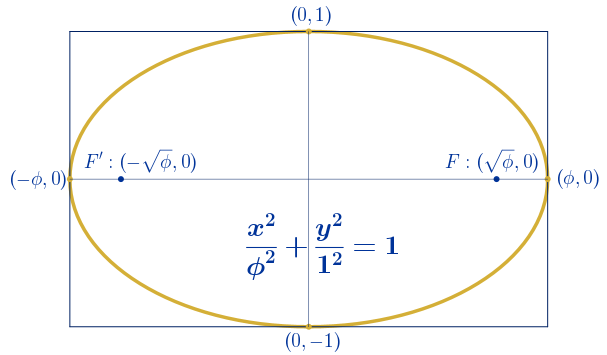
Al inscribir una elipse en un rectángulo áureo, el cociente entre las longitudes del eje mayor y del eje menor coincide con el número de oro. Esta elipse se conoce como elipse de oro o elipse áurea. En la imagen se puede observar la elipse, su ecuación y sus elementos.
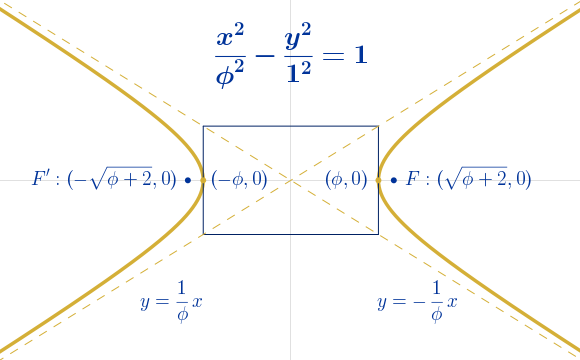
Si construimos una hipérbola con el eje real igual al eje mayor de la elipse y el eje imaginario igual al eje menor de la elipse, sus asíntotas coinciden con las diagonales de un rectángulo áureo.
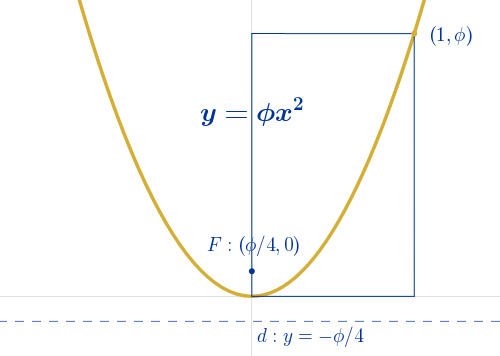
No se puede inscribir una parábola en un rectángulo áureo al no ser una curva cerrada. La parábola $y=\phi·x^{2}$, para $x=0$ y $x=1$ pasa por dos vértices opuestos de un rectángulo áureo. ¿Se le puede llamar parábola áurea?
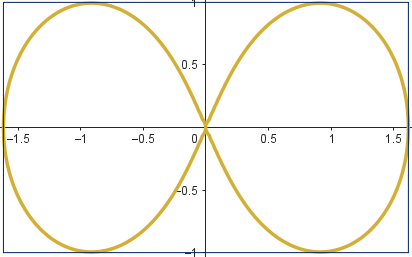
Si inscribimos una lemniscata en un rectángulo de oro, se obtiene una lemniscata de oro o lemnicata áurea. Se podria hablar también del símbolo de oro del infinito.
Aunque no tiene relación con el número de oro, un rectángulo muy interesante por su uso frecuente, es el rectángulo cuyos lados están en proporción $\sqrt{2}$.
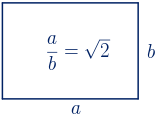
En la siguiente escena de Descartes puedes seguir los pasos para la construcción de un rectángulo de razón $\sqrt{2}$.
Es el formato de los tamaños de papel utilizados y que se conoce como formato DIN, serie A. El más habitual es el A4 que corresponde al folio La hoja completa corresponde al formato A0 de dimensiones 1189 x 841 milímetros y de aproximadamente $1 m^{2}$.
• Si se divide un rectángulo de proporción $\sqrt{2}$ en dos rectángulos iguales, los rectángulos obtenidos tienen también proporción $\sqrt{2}$.
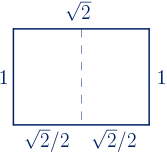
$\displaystyle\frac{1}{\sqrt{2}/2}=\frac{2}{\sqrt{2}}=\frac{2·\sqrt{2}}{\sqrt{2}·\sqrt{2}}=\sqrt{2}$
¿Existe el triángulo de oro? Se puede pensar en un triángulo cuyos lados estén en proporción áurea, es decir cuyos lados midan $1$, $\phi$ y $\phi^{2}$.
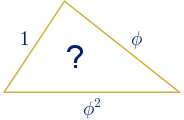
En cualquier triángulo se verifica que la suma de las longitudes de dos lados cualesquiera es mayor que el tercero. En este caso:
$1+\phi=\phi^{2}$
Por tanto, no es posible construir un triángulo con estas medidas.
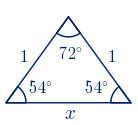
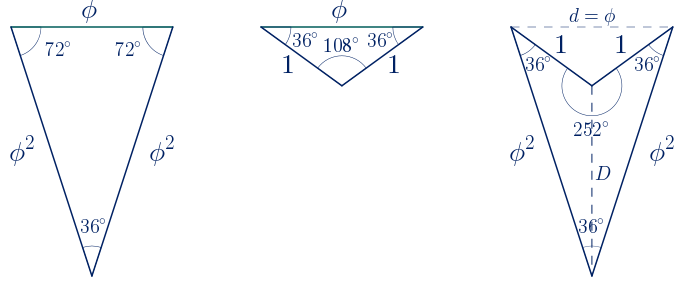
No existe un triángulo escaleno con proporciones áureas, pero sí existe un triángulo isósceles en el que la razón entre las longitudes de los lados iguales y del lado distinto es el número de oro, es decir, un triángulo semejante al triángulo cuyos lados miden $\phi$, $\phi$ y $1$.
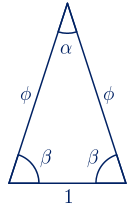
Vamos a calcular los ángulos. Calculamos en primer lugar el ángulo $\alpha$ con el teorema del coseno:
$1^2=\phi^{2}+\phi^{2}-2\phi\cdot\phi\cdot cos(\alpha)=2\phi^{2}-2\phi^{2}cos(\alpha)$
$cos(\alpha)=\displaystyle\frac{2\phi^{2}-1}{2\phi^{2}}=\displaystyle\frac{2(\phi+1)-1}{2(\phi+1)}=\displaystyle\frac{2\phi+1}{2\phi+2}=\displaystyle\frac{2+\sqrt{5}}{3+\sqrt{5}}$
$cos(\alpha)=\displaystyle\frac{2+\sqrt{5}}{3+\sqrt{5}} \cdot \displaystyle\frac{3-\sqrt{5}}{3-\sqrt{5}}=\displaystyle\frac{1+\sqrt{5}}{4}=\displaystyle\frac{\phi}{2}$
$\alpha=arccos \bigg(\displaystyle\frac{1+\sqrt{5}}{4}\bigg)=36º$
Calculamos ahora los ángulos iguales:
$\alpha+2\beta=180º \quad \rightarrow \quad \beta=\displaystyle\frac{180º-\alpha}{2}=\displaystyle\frac{180º-36º}{2}=72º$
El triángulo buscado es cualquier triángulo semejante al de la figura siguiente:
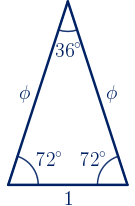
Calculamos el perímetro y superficie:
$P=2\phi+1=\phi^3\approx4.24\,\,u$
$h^{2}=\phi^{2}-\displaystyle\frac{1}{4}=\displaystyle\frac{4\phi+3}{4}$
$h=\displaystyle\frac{\sqrt{4\phi+3}}{2}$
$S=\displaystyle\frac{1}{2}\cdot1\cdot\displaystyle\frac{\sqrt{4\phi+3}}{2}=\displaystyle\frac{\sqrt{4\phi+3}}{4}\approx0.77\,\,u^{2}$
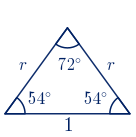
Existe un triángulo isósceles en el que la razón entre las longitudes del lado distinto y de los lados iguales es el número de oro, es decir, un triángulo semejante al triángulo cuyos lados miden $\phi$, $1$ y $1$.
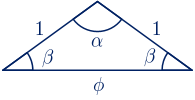
Calculamos en primer lugar el ángulo $\alpha$ con el teorema del coseno:
$\phi^{2}=1^{2}+1^{2}-2\cdot 1\cdot 1\cdot cos(\alpha)=2-2cos(\alpha)$
$cos(\alpha)=\displaystyle\frac{2-\phi^{2}}{2}=\displaystyle\frac{2-(\phi+1)}{2}=\displaystyle\frac{1-\phi}{2}=\displaystyle\frac{1-\sqrt{5}}{4}$
$\alpha=arccos \bigg(\displaystyle\frac{1-\sqrt{5}}{4} \bigg)=108º$
Calculamos ahora los ángulos iguales:
$\alpha+2\beta=180º \quad \rightarrow \quad \beta=\displaystyle\frac{180º-\alpha}{2}=\displaystyle\frac{180º-108º}{2}=36º$
El triángulo buscado es cualquier triángulo semejante al de la figura siguiente:
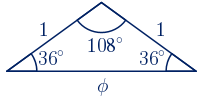
$P=\phi+2\approx3.62\,\,u$
$S=\displaystyle\frac{\phi\cdot\sqrt{3-\phi}}{4}\approx0.48\,\,u^{2}$
• Se ha comprobado anteriormente que no existe un triángulo cuyos lados midan $1$, $\phi$ y $\phi^{2}$. Sin embargo, vamos a estudiar un triángulo rectángulo cuyos catetos miden $1$ y $\phi$.
Calculamos la longitud de la hipotenusa con el Teorema de Pitágoras:

$a^{2}=\phi^{2}+1^{2}=(\phi+1)+1=\phi+2$
$a=\sqrt{\phi+2}\approx1.9\,\,u$
Calculamos ahora los ángulos agudos:
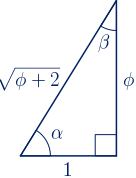
$tg(\alpha)=\displaystyle\frac{\phi}{1}=\phi$
$\alpha=arctg(\phi)=58º\,16'\,57.09''$
$\beta=90º-58º\,16'\,57.09''=31º\,43'\,2.91''$
El triángulo rectángulo es:
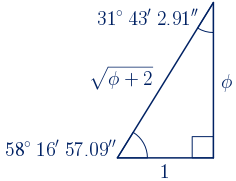
$P=\phi+1+\sqrt{\phi+2}\approx4.52\,\,u$
$S=\displaystyle\frac{1 \cdot \phi}{2}\approx0.81\,\,u^{2}$
• Vamos a estudiar otro triángulo rectángulo de forma que uno de sus catetos mide $1$ y la hipotenusa mide $\phi$ unidades.
Calculamos la longitud del otro cateto con el Teorema de Pitágoras:
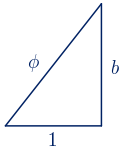
$b^{2}=\phi^{2}-1^{2}=(\phi+1)-1=\phi$
$b=\sqrt{\phi}\approx1.27\,\,u$
Los lados de este triángulo rectángulo están en progresión geométrica de razón $\sqrt{\phi}$. Vamos a calcular los datos que faltan:
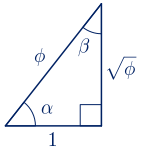
$tg(\alpha)=\displaystyle\frac{\sqrt{\phi}}{1}=\sqrt{\phi}$
$\alpha=arctg(\sqrt{\phi})=51º\,49'\,38.25''$
$\beta=90º-51º\,49'\,38.25''=38º\,10'\,21.75''$
$P=\phi+1+\sqrt{\phi}\approx3.89\,\,u \quad \quad S=\displaystyle\frac{1 \cdot \sqrt{\phi}}{2}\approx0.64\,\,u^{2}$
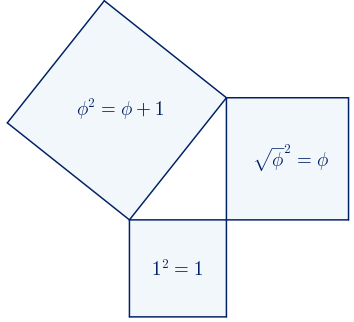
En este triángulo rectángulo, la interpetación geométrica del Teorema de Pitágoras nos proporciona una comprobación geométrica del valor del cuadrado del número de oro.
$\phi^{2}=\phi+1$
Empezamos recordando la construcción de un pentágono regular inscrito en una circunferencia.
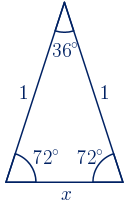
Si la longitud del radio de la circunferencia es 1 unidad, el lado del pentágono regular, utilizando el teorema del coseno, mide:
$x^{2}=1^{2}+1^{2}-2\cdot 1 \cdot 1 \cdot cos(72º)$
$x^{2}=2-2\cdot \displaystyle\frac{\sqrt{5}-1}{4}=\displaystyle\frac{5-\sqrt{5}}{2}$
$x^2=3-\phi\quad \rightarrow \quad x=\sqrt{3-\phi}$
Si necesitamos una longitud determinada del lado del pentágono, se puede construir a partir del procedimiento anterior por semejanza, pero también es posible construir gráficamente, con regla y compás, un pentágono regular conociendo la longitud del lado.
Si la longitud del lado del pentágono regular es 1 unidad, el radio de la circunferencia, utilizando semejanza de triángulos, mide:
$\displaystyle\frac{r}{1}=\displaystyle\frac{1}{x} \quad \rightarrow \quad r=\displaystyle\frac{1}{x}=\displaystyle\frac{1}{\sqrt{3-\phi}}$
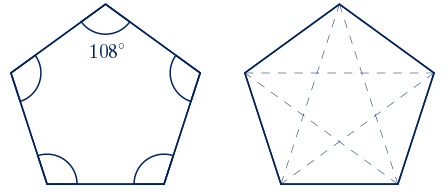
Los ángulos interiores de un pentágono regular miden 108º.
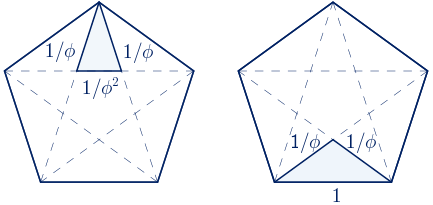
Un pentágono regular tiene 5 diagonales de igual longitud. Cada una de ellas es paralela a uno de los lados.
Si dibujamos un pentágono regular cuyo lado mida una unidad, utilizando lados y diagonales se pueden construir los triángulos con proporciones áureas de los apartados anteriores.
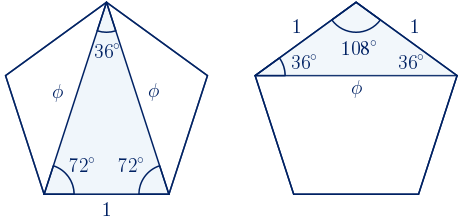
Si la longitud del lado es distinta de 1, el cociente entre la longitud de la diagonal y la longitud del lado coincide con el número de oro.
Además existen otros triángulos semejantes a los dos anteriores.
Empezamos recordando la construcción de un decágono regular inscrito en una circunferencia.
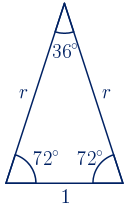
Si la longitud del radio de la circunferencia es 1 unidad, el lado del decágono regular, utilizando el teorema del coseno, mide:
$x^{2}=1^{2}+1^{2}-2\cdot1 \cdot1\cdot cos(36º)$
$x^{2}=2-2cos(36º)=2-\phi=\displaystyle\frac{1}{\phi^2}$
$x=\displaystyle\frac{1}{\phi}=\phi-1$
Si necesitamos una longitud determinada del lado del decágono, se puede construir a partir del procedimiento anterior por semejanza, pero también es posible construir gráficamente, con regla y compás, un decágono regular conociendo la longitud del lado.
Si el lado del decágono regular es 1 unidad, el radio de la circunferencia, utilizando semejanza de triángulos, mide:
$\displaystyle\frac{r}{1}=\displaystyle\frac{1}{x} \quad \rightarrow \quad r=\displaystyle\frac{1}{x}=\displaystyle\frac{1}{1/\phi}=\phi$
Los ángulos interiores de un decágono regular miden 144º.
Un decágono regular tiene 35 diagonales de cuatro longitudes distintas. Cinco de ellas coinciden con diámetros del decágono y hay diez de cada una de las restantes.
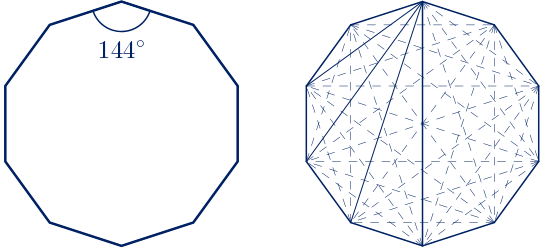
Vamos a calcular la longitud de las cuatro diagonales distintas en un decágono regular cuyo lado mide una unidad.
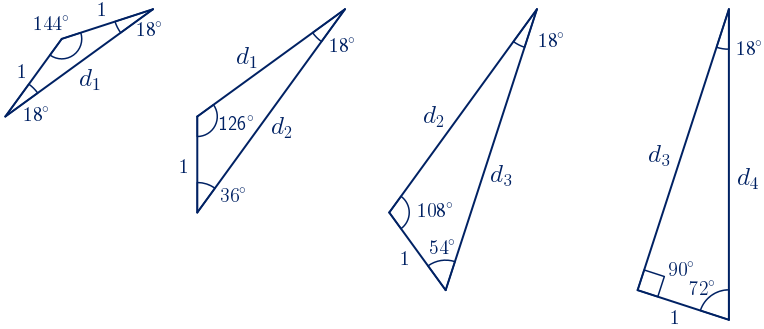
• Se calcula $d_{1}$ aplicando el teorema del coseno:
${d_{1}}^{2}=1^{2}+1^{2}-2\cdot1\cdot 1\cdot cos(144º)=2-2cos(144º)=\phi+2$
${d_{1}}^{2}=\phi+2=\phi^{2}+1 \quad \rightarrow \quad d_{1}=\sqrt{\phi+2}=\sqrt{\phi^{2}+1}$
• Se calcula $d_{2}$ aplicando el teorema del seno:
$\displaystyle\frac{d{2}}{sen(126º)}=\displaystyle\frac{1}{sen(18º)} \quad \rightarrow \quad d_{2}=\displaystyle\frac{sen(126º)}{sen(18º)}=\phi+1=\phi^{2}$
• Se calcula $d_{3}$ aplicando el teorema del seno:
$\displaystyle\frac{d{3}}{sen(108º)}=\displaystyle\frac{1}{sen(18º)} \quad \rightarrow \quad d_{3}=\displaystyle\frac{sen(108º)}{sen(18º)}=\sqrt{4\phi+3}$
• Se calcula $d_{4}$ aplicando la definición de las razones trigonométricas en un triángulo rectángulo:
$cos(72º)=\displaystyle\frac{1}{d_{4}}\quad \rightarrow \quad d_{4}=\displaystyle\frac{1}{cos(72º)}=2\phi$
Anteriormente se demostró que si la longitud del lado de un decágono regular es una unidad, el radio de la circunferencia circunscrita es $\phi$. La diagonal $d_{4}$ es el diámetro de la circunferencia circunscrita, por tanto, su longitud es $2\phi$.
Una vez conocida la longitud de la diagonal $d_{4}$ se puede ver con mayor claridad la longitud de la diagonal $d_{3}$ aplicando el Teorema de Pitágoras en este último triángulo rectángulo:
${d_{4}}^{2}={d_{3}}^{2}+1^{2} \quad \rightarrow \quad {d_{3}}^{2}={d_{4}}^{2}-1$
${d_{3}}^{2}=(2\phi)^{2}-1=4\phi^{2}-1=4(\phi+1)-1=4\phi+3$
${d_{3}}^{2}=4\phi+3=(3\phi+2)+(\phi+1)=\phi^{4}+\phi^{2}=\phi^{2}(\phi^{2}+1)$
$d_{3}=\sqrt{4\phi+3}=\sqrt{\phi^{2}(\phi^{2}+1)}=\phi\sqrt{\phi^{2}+1}=\phi\sqrt{\phi+2}$
Al dibujar las diagonales de un decágono regular, se pueden construir varios triángulos con proporciones áureas.
• Algunos ejemplos semejantes al triángulo del apartado 3.1.1.
• Algunos ejemplos semejantes al triángulo del apartado 3.1.2.
Ya se ha visto en el apartado 2.1.3 como se construye el rombo de oro. Vamos a conocerlo con más detalle.
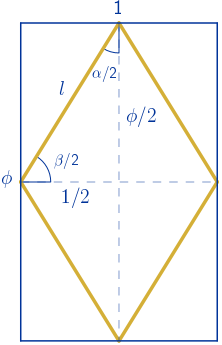
Empezamos calculando el lado aplicando el Teorema de Pitágoras:
$l^{2}=\bigg(\displaystyle\frac{\phi}{2} \bigg)^{2}+\bigg(\displaystyle\frac{1}{2} \bigg)^{2}=\displaystyle\frac{\phi^{2}}{4}+\displaystyle\frac{1}{4}=\displaystyle\frac{\phi^{2}+1}{4}$
$l^{2}=\displaystyle\frac{(\phi+1)+1}{4}=\displaystyle\frac{\phi+2}{4}$
$l=\sqrt{\displaystyle\frac{\phi+2}{4}}=\displaystyle\frac{\sqrt{\phi+2}}{2}\approx0.95\,\,u$
Calculamos ahora los ángulos:
$tg\bigg(\displaystyle\frac{\beta}{2}\bigg)=\displaystyle\frac{\phi/2}{1/2}=\phi \quad \rightarrow \quad \displaystyle\frac{\beta}{2}=arctg(\phi)$
$\beta=2arctg(\phi)=116º\,33'\,54.18''$
$\alpha=180º-116º\,33'\,54.18''=63º\,26'\,5.82''$
Y por último, calculamos el perímetro y la superficie:
$P=4 \cdot\displaystyle\frac{\sqrt{\phi+2}}{2}=2\sqrt{\phi+2}\approx3.8\,\,u$
$S=\displaystyle\frac{\phi\cdot 1}{2}=\displaystyle\frac{\phi}{2}\approx0.81\,\,u^{2}$
Un romboide con proporciones áureas debe ser un romboide cuyos lados midan $\phi$ y $1$, pero se pueden construir infinitos romboides con estas longitudes de sus lados dependiendo de los ángulos interiores. Vamos a buscar un romboide que verifique también que el cociente de sus diagonales sea el número de oro.
En la siguiente escena de Descartes puedes construir romboides cuyos lados tengan estas longitudes, modificando el valor del ángulo agudo en la barra inferior. Encuentra el romboide en el que el cociente entre las longitudes de las diagonales se aproxima más a $\phi$.
En la escena anterior se ha podido encontrar el romboide buscado, vamos a determinarlo ahora realizando cálculos para obtener el valor del ángulo agudo.
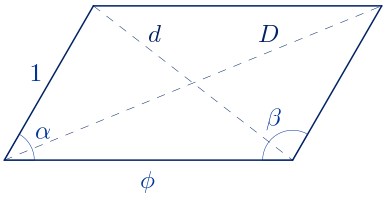
Se verifica que:
$\alpha+\beta=180º \quad \rightarrow \quad \beta=180º-\alpha$
$cos(\beta)=-cos(\alpha)$
Aplicando el teroema del coseno:
$D^{2}=\phi^{2}+1-2\phi cos(\beta)=\phi^{2}+1+2\phi cos(\alpha)$
$d^{2}=\phi^{2}+1-2\phi cos(\alpha)$
El cociente de las diagonales debe ser el número de oro:
$\displaystyle\frac{D}{d}=\phi\quad \rightarrow \quad \displaystyle\frac{D^{2}}{d^{2}}=\displaystyle\frac{\phi^{2}+1+2\phi cos(\alpha)}{\phi^{2}+1-2\phi cos(\alpha)}=\phi^2$
$\phi^{2}+1+2\phi cos(\alpha)=\phi^{4}+\phi^{2}-2\phi^{3} cos(\alpha)$
$1+2\phi cos(\alpha)=\phi^{4}-2\phi^{3} cos(\alpha)$
Se sustituye $\phi^{4}$ por $3\phi+2$ y $\phi^{3}$ por $2\phi+1:$
$1+2\phi cos(\alpha)=(3\phi+2)-2(2\phi+1) cos(\alpha)$
$(6\phi+2) cos(\alpha)=3\phi+1$
$cos(\alpha)=\displaystyle\frac{3\phi+1}{6\phi+2}=\displaystyle\frac{1}{2} \quad \rightarrow \quad \alpha=arccos \bigg( \displaystyle\frac{1}{2} \bigg)=60º$
$\beta=180º-\alpha=180º-60º=120º$
La longitud de las diagonales es:
$D=\sqrt{\phi^{2}+1+2\phi cos(60º)}=\sqrt{\phi^{2}+1+\phi}=\sqrt{2\phi+2}=\sqrt{2} \phi$
$d=\sqrt{\phi^{2}+1-2\phi cos(60º)}=\sqrt{\phi^{2}+1-\phi}=\sqrt{2}$
Cálculo del perímetro:
$P=2\phi+2=2(\phi+1)=2\phi^{2}\approx5.24\,\,u$
Para calcular la superficie se necesita calcular previamente la altura:
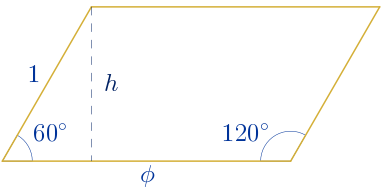
$sen(60º)=\displaystyle\frac{h}{1}=h \quad \rightarrow \quad h=sen(60º)=\displaystyle\frac{\sqrt{3}}{2}$
Cálculo de la superficie.
$S=\phi\cdot h=\phi\cdot \displaystyle\frac{\sqrt{3}}{2}=\displaystyle\frac{\sqrt{3}\phi}{2}\approx1.4\,\,u^{2}$
Existen tres trapecios isósceles con proporciones áureas.
• Empezamos estudiando el trapecio cuyos lados miden $1$, $\phi$, $\phi$ y $\phi^{2}$.
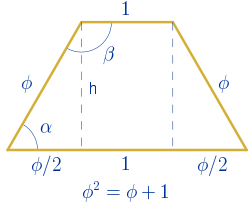
Vamos a calcular los ángulos.
$cos(\alpha)=\displaystyle\frac{\phi/2}{\phi}=\displaystyle\frac{1}{2}$
$\alpha=arccos(1/2)=60º$
$\beta=180º-60º=120º$
Este es el trapecio isósceles aúreo.
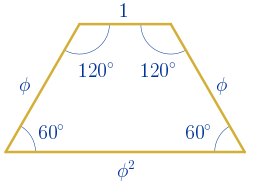
Calculamos ahora la altura con la figura de la página anterior:
$sen(60º)=\displaystyle\frac{h}{\phi}\quad \rightarrow \quad h=\phi\cdot sen(60º)={\displaystyle\frac{\sqrt{3}}{2}}\phi\approx1.4\,\,u$
Y ahora ya se puede calcular el perímetro y la superficie.
$P=1+\phi+\phi+\phi^{2}=3\phi+2=\phi^{4}\approx6.85\,\,u$
$S=\displaystyle\frac{(\phi+1)+1}{2}\cdot \displaystyle\frac{\sqrt{3}}{2}\phi=\displaystyle\frac{(3\phi+1)\sqrt{3}}{4}\approx2.53\,\,u^{2}$
La longitud de la diagonal también tiene relación con $\phi$.
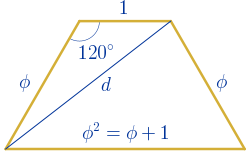
$d^{2}=\phi^{2}+1-2\phi cos(120º)$
$d^{2}=\phi^{2}+1+\phi=2\phi^{2}$
$d=\phi \sqrt{2}\approx2.29\,\,u$
Existen otros dos trapecios isósceles con proporciones áureas:
• Uno cuyos lados miden $\phi$, $1$, $1$ y $\phi^{2}$.
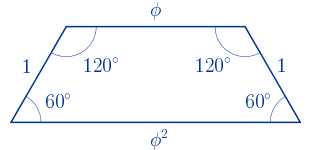
Altura: $h={\displaystyle\frac{\sqrt{3}}{2}}\approx0.87\,\,u$. Diagonal: $d=\phi \sqrt{2}\approx2.29\,\,u$
$P=1+1+\phi+\phi^{2}=2+\phi+(\phi+1)=2\phi+3\approx6.24\,\,u$
$S=\displaystyle\frac{\phi^{2}+\phi}{2}\cdot \displaystyle\frac{\sqrt{3}}{2}=\displaystyle\frac{(2\phi+1)\sqrt{3}}{4}=\displaystyle\frac{\phi^{3}\sqrt{3}}{4}\approx1.83\,\,u^{2}$
• Y otro cuyos lados miden $1$, $\phi^{2}$, $\phi^{2}$ y $\phi$.
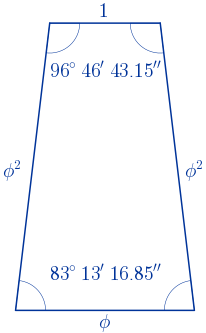
$h\approx2.6\,\,u$
$d\approx2.91\,\,u$
$P=3\phi^{2}\approx7.85\,\,u$
$S\approx3.4\,\,u^{2}$
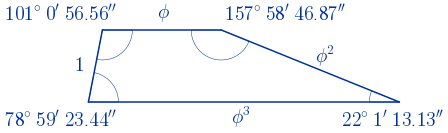
• Un trapecio escaleno con proporciones áureas debe ser un trapecio cuyos lados midan $1$, $\phi$, $\phi^{2}$ y $\phi^{3}$. Empezamos construyendo el que tiene por bases $\phi^{3}$ y $1$.
Vamos a calcular los ángulos. Se traza una paralela al lado $\overline{AD}$ por el vértice $C$ que corta al lado $\overline{AB}$ en el punto $E$. Se calculan los ángulos $\alpha$ y $\beta$ del triángulo $EBC$, que coinciden con los ángulos $\alpha$ y $\beta$ del trapecio $ABCD$. Los ángulos $\delta$ y $\gamma$ son los suplementarios de $\alpha$ y $\beta$.
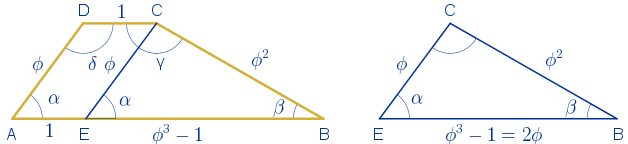
Aplicando el teorema del coseno:
$cos(\alpha)=\displaystyle\frac{\phi^{2}+(2\phi)^{2}-(\phi^{2})^{2}}{2\cdot\phi\cdot2\phi}=\displaystyle\frac{\phi^{2}+4\phi^{2}-\phi^{4}}{4\phi^{2}}=\displaystyle\frac{2\phi+3}{4\phi+4}$
$\alpha=arccos \bigg(\displaystyle\frac{2\phi+3}{4\phi+4} \bigg)=53º\,27'\,8.36''$
$\delta=180º-53º\,27'\,8.36''=126º\,32'\,51.64''$
$cos(\beta)=\displaystyle\frac{(\phi^{2})^{2}+(2\phi)^{2}-\phi^{2}}{2\cdot(\phi^{2})\cdot2\phi}=\displaystyle\frac{\phi^{4}+4\phi^{2}-\phi^{2}}{4\phi^{3}}=\displaystyle\frac{6\phi+5}{8\phi+4}$
$\beta=arccos \bigg(\displaystyle\frac{6\phi+5}{8\phi+4} \bigg)=29º\,46'\,8.49''$
$\gamma=180º-29º\,46'\,8.49''=150º\,13'\,51.51''$
Este es el trapecio escaleno aúreo.
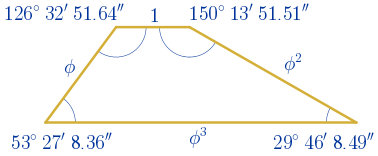
Cálculo del perímetro:
$P=1+\phi+\phi^{2}+\phi^{3}=1+\phi+(\phi+1)+(2\phi+1)=4\phi+3\approx9.47\,\,u$
Cálculo de la superficie. La altura del trapecio es igual a la altura del triángulo $EBC$ que pasa por el vértice $C$.
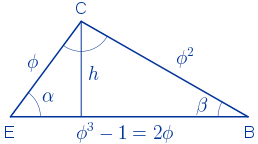
$sen(\alpha)=\displaystyle\frac{h}{\phi}\quad \rightarrow \quad h=\phi\cdot sen(53º\,27'\,8.36'')\approx1.3\,\,u$
$S=\displaystyle\frac{1+\phi^{3}}{2}\cdot 1.3=\displaystyle\frac{1+(2\phi+1)}{2}\cdot 1.3=\phi^{2}\cdot 1.3\approx3.4\,\,u^{2}$
Existen otros dos trapecios escalenos con proporciones áureas:
• Uno cuyas bases miden $\phi^{3}$ y $\phi$.
Altura: $h\approx0.98\,\,u$
$P=1+\phi+\phi^{2}+\phi^{3}=4\phi+3\approx9.47\,\,u$
$S=\displaystyle\frac{\phi^{3}+\phi}{2}\cdot 0.98\approx2.87\,\,u^{2}$
• Y otro cuyas bases miden $\phi^{3}$ y $\phi^{2}$.
Altura: $h=sen(72º)=\displaystyle\frac{\sqrt{\phi+2}}{2}\approx0.95\,\,u$
$P=1+\phi+\phi^{2}+\phi^{3}=4\phi+3\approx9.47\,\,u$
$S=\displaystyle\frac{\phi^{3}+\phi^{2}}{2}\cdot \displaystyle\frac{\sqrt{\phi+2}}{2}=\displaystyle\frac{\phi^{4}\sqrt{\phi+2}}{4}\approx3.26\,\,u^{2}$
Como el trapecio escaleno tiene 4 lados de distinta longitud, existen $C_{4,2}=6$ posibilidades para elegir las bases. En los ejemplos anteriores se han construidos trapecios cuyas bases son:
$\phi^{3}$ y ${1}$ $\phi^{3}$ y ${\phi}$ $\phi^{3}$ y $\phi^{2}$
Faltarían los casos:
$\phi^{2}$ y ${1}$ $\phi^{2}$ y ${\phi}$ $\phi$ y $1$
Pero es imposible construir trapecios escalenos con estos cuatro lados, eligiendo estas parejas para las bases.
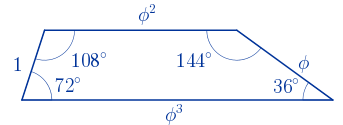
Un trapezoide con proporciones áureas debe ser un trapezoide cuyos lados midan $1$, $\phi$, $\phi^{2}$ y $\phi^{3}$. Se pueden construir infinitos trapezoides, tanto convexos como cóncavos, con estas longitudes de sus lados.
A continuación se indica la forma de construirlos utilizando procedimientos similares en los que cambia la posición de los lados.
En algunos casos se puede observar que existen dos soluciones, obteniéndose un trapezoide convexo y otro cóncavo.
En otros casos se puede comprobar que se obtienen los trapecios escalenos del apartado anterior.
Y en otras situaciones no es posible construirlos como se detalla en el procedimiento.
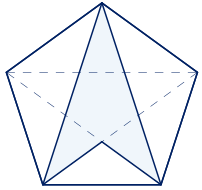
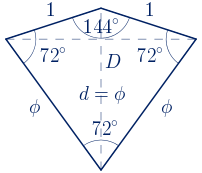
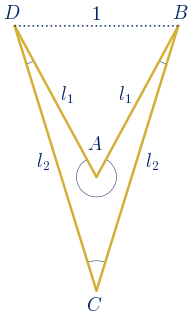
Un deltoide es un trapezoide con dos parejas de lados consecutivos de igual longitud. Puede ser convexo o cóncavo.
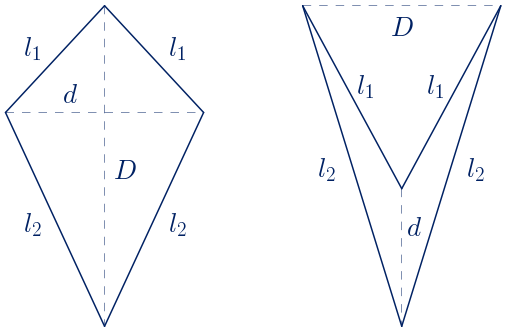
Las diagonales de un deltoide son dos líneas perpendiculares, siendo una de ellas la mediatriz de la otra; en el caso del deltoide cóncavo, prolongando la diagonal interior. Una de las diagonales es el eje de simetría de la figura. Esto supone que el área de un deltoide se puede calcular de forma similar al área de un rombo, como el semiproducto de las dos diagonales.
$S=\displaystyle\frac{D\cdot d}{2}$
Si unimos los puntos medios de los lados de un rectángulo áureo se obtiene un rombo inscrito en un rectángulo de oro, conocido como rombo de oro, que ya se ha estudiado anteriormente. El cociente entre las longitudes de sus diagonales es el número de oro. Pero si intentamos inscribir en un rectángulo de oro una figura no regular, como es un deltoide, nos encontramos con infinitas posibilidades. ¿Existen deltoides cuyos lados y diagonales estén en proporción áurea? ¿Existen deltoides con proporciones áureas que no tengan relación con el rectángulo de oro?
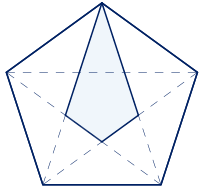
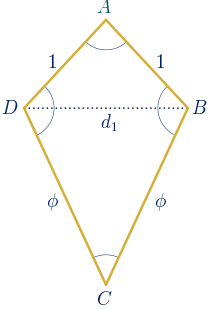
Con triángulos semejantes a los dos triángulos isósceles con proporciones áureas, se pueden construir dos deltoides, uno convexo y otro cóncavo, en los que aparecen proporciones áureas entre sus lados y diagonales. Al ser deltoides que aparecen en el pentágono regular, les llamaremos deltoides pentagonales.
Se escoge un triángulo semejante al primero de los triángulos áureos con razón de semejanza $\phi$. Se construye un deltoide uniendo el nuevo triángulo y el segundo de los triángulos anteriores por el lado común.
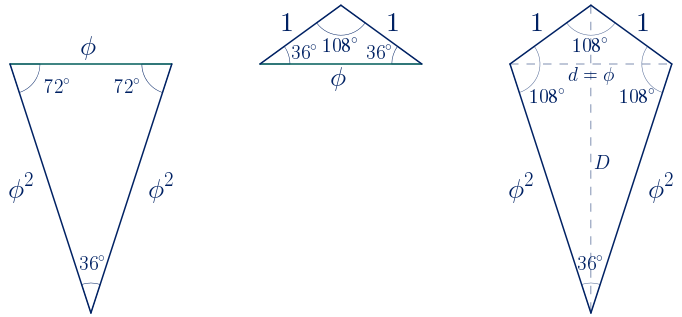
Se obtiene un deltoide convexo en el que la razón entre la longitud de la diagonal menor y la longitud de los lados menores es el número de oro. También es igual al número áureo la razón entre la longitud de los lados mayores y la longitud de la diagonal menor. Los ángulos miden $108º$, $108º$, $108º$ y $36º$.
El perímetro de este deltoide es:
$P=2+2\phi^{2}=2\phi+4\approx7.24\,\,u$
La diagonal menor coincide con el número de oro. La diagonal mayor mide, aplicando el teorema del coseno:
$D^{2}=1+\phi^{4}-2\phi^{2}cos(108º)$
$D^{2}=1+(3\phi+2)-2(\phi+1)\cdot\displaystyle\frac{1-\phi}{2}=4\phi+3$
$D=\sqrt{4\phi+3}\approx3.08\,\,u$
La superficie es igual a:
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\sqrt{4\phi+3}\cdot\phi}{2}=\displaystyle\frac{\sqrt{(4\phi+3)\cdot\phi^{2}}}{2}$
$S=\displaystyle\frac{\sqrt{11\phi+7}}{2}\approx2.49\,\,u^{2}$
Este deltoide aparece al trazar las diagonales de un pentágono regular y de otros polígonos regulares cuyo número de lados es múltiplo de 5.
Se escoge un triángulo semejante al primero de los triángulos áureos con razón de semejanza $\phi$. Se construye un deltoide cóncavo según se observa en la siguiente figura.
La razón entre la longitud de la diagonal menor y la longitud de los lados menores es el número de oro. También es igual al número áureo la razón entre la longitud de los lados mayores y la longitud de la diagonal menor. Los ángulos interiores miden $252º$, $36º$, $36º$ y $36º$.
El perímetro de este deltoide es:
$P=2+2\phi^{2}=2\phi+4\approx7.24\,\,u$
La diagonal menor coincide con el número de oro. La diagonal mayor mide, aplicando el teorema del coseno:
$D^{2}=1+\phi^{4}-2\phi^{2}cos(36º)$
$D^{2}=1+(3\phi+2)-2(\phi+1)\cdot\displaystyle\frac{\phi}{2}=\phi+2$
$D=\sqrt{\phi+2}\approx1.9\,\,u$
La superficie es igual a:
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\sqrt{\phi+2}\cdot\phi}{2}=\displaystyle\frac{\sqrt{4\phi+3}}{2}\approx1.54\,\,u^{2}$
Este deltoide aparece también al trazar las diagonales de un pentágono regular y de otros polígonos regulares cuyo número de lados es múltiplo de 5.
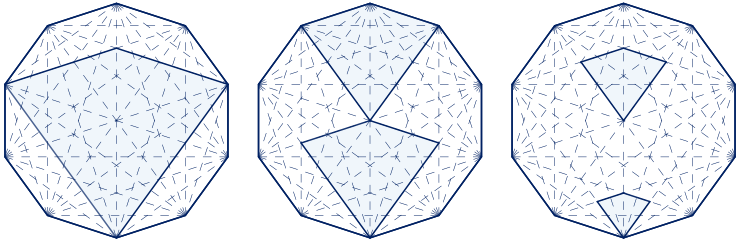
Con dos triángulos iguales de cada uno los triángulos isósceles con proporciones áureas, se pueden construir dos deltoides, uno convexo y otro cóncavo, en los que aparecen proporciones áureas entre sus lados y diagonales. Al ser deltoides que aparecen en el decágono regular, les llamaremos deltoides decagonales.
Se escogen dos triángulos como el primero de los triángulos isósceles con proporciones áureas. Se construye un deltoide uniendo ambos triángulos por uno de los lados mayores como se observa en la figura siguiente.
Se obtiene un deltoide en el que la razón entre la longitud de los lados mayores y la longitud de los lados menores es el número de oro. La longitud de los lados mayores es igual a la longitud de la diagonal menor. Los ángulos miden $144º$, $72º$, $72º$ y $72º$.
El perímetro de este deltoide es:
$P=2+2\phi=2(1+\phi)=2\phi^{2}\approx5.24\,\,u$
La diagonal menor coincide con el número de oro. La diagonal mayor mide, aplicando el teorema del coseno:
$D^{2}=1+1-2cos(144º)=2-2\bigg(-\displaystyle\frac{\phi}{2}\bigg)=2+\phi$
$D=\sqrt{2+\phi}\approx1.9\,\,u$
La superficie es igual a:
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\sqrt{\phi+2}\cdot\phi}{2}=\displaystyle\frac{\sqrt{4\phi+3}}{2}\approx1.54\,\,u^{2}$
Este deltoide aparece al trazar las diagonales de un decágono regular y de polígonos regulares cuyo número de lados es múltiplo de 10.
Se escogen dos triángulos como el segundo de los triángulos isósceles con proporciones áureas. Se construye un deltoide uniendo ambos triángulos por uno de los lados menores como se observa en la figura siguiente.
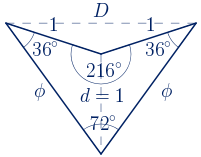
Se obtiene un deltoide en el que la razón entre la longitud de los lados mayores y la longitud de los lados menores es el número de oro. La longitud de los lados menores es igual a la longitud de la diagonal menor. Los ángulos miden $216º$, $72º$, $36º$ y $36º$.
El perímetro de este deltoide es:
$P=2+2\phi=2(1+\phi)=2\phi^{2}\approx5.24\,\,u$
La longitud de la diagonal menor es igual a 1. La diagonal mayor mide, aplicando el teorema del coseno:
$D^{2}=1+1-2cos(144º)=2-2\bigg(-\displaystyle\frac{\phi}{2}\bigg)=2+\phi$
$D=\sqrt{2+\phi}\approx1.9\,\,u$
La superficie es igual a:
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\sqrt{\phi+2}\cdot1}{2}=\displaystyle\frac{\sqrt{\phi+2}}{2}\approx0.95\,\,u^{2}$
Este deltoide aparece también al trazar las diagonales de un decágono regular y de otros polígonos regulares cuyo número de lados es múltiplo de 10.
Una Teselación de Penrose es una teselación construida a partir de un conjunto de figuras de forma que no existe un motivo básico que permita su construcción mediante traslaciones. A este tipo de teselaciones se les llama teselaciones aperiódicas.
Este tipo de teselaciones supuso un reto entre los matemáticos de las décadas de los sesenta y setenta del siglo XX para encontrar un número reducido de figuras que cubrieran el plano con esta propiedad.
El físico y matemático Roger Penrose, (1931- ) encontró en 1974, dos figuras que permitían construir teselaciones aperiódicas. Estas figuras son el deltoide decagonal convexo, cometa y el deltoide decagonal cóncavo, flecha.
Un ejemplo de una teselación aperiódica con estos polígonos se puede observar en la portada del libro. Otro ejemplo es el siguiente:

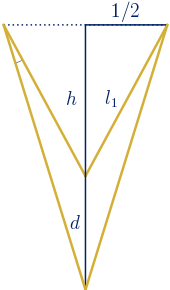
Si intentamos construir un deltoide convexo inscrito en un rectángulo áureo, es decir, cuyas diagonales estén en proporción áurea, tenemos infinitas posibilidades.
Vamos a distinguir dos casos, según el eje de simetría del deltoide coincida con su diagonal menor o su diagonal mayor.
En la siguiente escena de Descartes puedes construir deltoides convexos inscritos en un rectángulo áureo, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul) por el lado derecho del rectángulo. Uniendo los puntos medios de cada lado del rectángulo áureo se obtiene el rombo de oro, que aparece representado. Encuentra el deltoide en el que el cociente de las longitudes de los lados se aproxima más a $\phi$.
Todos tienen en común que el cociente entre sus diagonales es el número de oro. También todos tienen igual área, pero distinto perímetro.
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi\cdot 1}{1}=\displaystyle\frac{\phi}{2}\,\,u^{2}$
En la escena anterior se puede comprobar que no es posible construir un deltoide convexo inscrito en un rectángulo áureo cuyos lados estén también en proporción áurea y que tenga por eje de simetría su diagonal menor; el cociente de las longitudes de sus lados sería siempre menor que el número de oro.
Vamos a comprobarlo analíticamente:
Si existe este deltoide, su lado menor, $l_{1}$, debe ser mayor que $\phi/2$ y su lado mayor, $l_{2}$, debe ser menor que la longitud del segmento $a$.
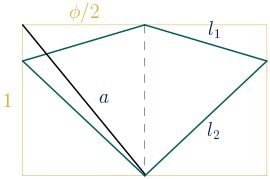
$a^{2}=1^{2}+\bigg(\displaystyle\frac{\phi}{2}\bigg)^{2}=\displaystyle\frac{\phi+5}{4}$
$a={\displaystyle\frac{\sqrt{\phi+5}}{2}}$
Y el cociente entre las longitudes del lado mayor y el lado menor sería menor que el número de oro:
$\displaystyle\frac{l_{2}}{l_{1}}<\displaystyle\frac{a}{\phi/2}=\displaystyle\frac{(\sqrt{\phi+5})/2}{\phi/2}=\displaystyle\frac{\sqrt{\phi+5}}{\phi}\approx1.59<\phi$
Luego no es posible construir el deltoide con las propiedades exigidas.
En la siguiente escena de Descartes puedes construir deltoides convexos inscritos en un rectángulo áureo, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul) por el lado derecho del rectángulo. Uniendo los puntos medios de cada lado del rectángulo áureo se obtiene el rombo de oro, que aparece representado. Encuentra el deltoide en el que el cociente de las longitudes de los lados se aproxima más a $\phi$.
En esta escena se puede comprobar gráficamente que sí es posible construir este deltoide.
Todos tienen en común que el cociente entre sus diagonales es el número de oro. También todos tienen igual área como los anteriores, $S=\phi/2\;\;u^{2}$ y distinto perímetro.
Vamos a determinar este deltoide áureo convexo, calculando la longitud de sus lados y la medida de sus ángulos
Cálculo de la longitud de los lados:
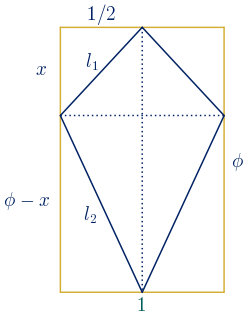
$l_{1}^{2}=x^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}\rightarrow \,\, l_{1}=\sqrt{x^{2}+\displaystyle\frac{1}{4}}$
$l_{2}^{2}=(\phi-x)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{2}=\sqrt{\phi^{2}-2\phi x+x^{2}+\displaystyle\frac{1}{4}}$
Se debe verificar que:
$\displaystyle\frac{l_{2}}{l_{1}}=\phi\quad \rightarrow \quad \displaystyle\frac{l_{2}^{2}}{l_{1}^{2}}=\displaystyle\frac{\phi^{2}-2\phi x+x^{2}+\displaystyle\frac{1}{4}}{x^{2}+\displaystyle\frac{1}{4}}=\phi^2$
$\phi^{2}-2\phi x+x^{2}+\displaystyle\frac{1}{4}=\phi^{2} \bigg(x^{2}+\displaystyle\frac{1}{4} \bigg)=\phi^{2}x^{2}+\displaystyle\frac{\phi^{2}}{4}$
$x^{2}(\phi^{2}-1)+2\phi x+\displaystyle\frac{-3\phi^{2}-1}{4}=0$
Se sustituye $\phi^{2}$ por $\phi+1$:
$\phi x^{2}+2\phi x+\displaystyle\frac{-3\phi-4}{4}=0$
Se resuelve la ecuación de segundo grado:
$x=\displaystyle\frac{-2\phi \pm \sqrt{4\phi^{2}+\phi(3\phi+4)}}{2\phi}=\displaystyle\frac{-2\phi \pm \sqrt{7\phi^{2}+4\phi}}{2\phi}$
$x=\displaystyle\frac{-2\phi}{2\phi} \pm \sqrt {\displaystyle\frac{7\phi^{2}+4\phi}{4\phi^{2}}}=-1 \pm \sqrt {\displaystyle\frac{7}{4}+\displaystyle\frac{1}{\phi}}$
Se sustituye $\displaystyle\frac{1}{\phi}$ por $\phi-1$:
$x=-1 \pm \sqrt {\displaystyle\frac{7}{4}+\phi-1}=-1 \pm \sqrt {\displaystyle\frac{3}{4}+\phi}=-1 \pm \sqrt {\displaystyle\frac{4\phi+3}{4}}$
La soluciones son:
$x_{1}=-1+\displaystyle\frac{\sqrt{4\phi+3}}{2}\approx0.54\,\,$ y $\,\,x_{2}=-1-\displaystyle\frac{\sqrt{4\phi+3}}{2}\approx-2.54$
Con la primera solución se obtiene el deltoide convexo buscado. En la segunda solución el valor de $x_{2}$ es negativo. Gráficamente este valor se debe representar por encima del lado superior del rectángulo áureo obteniéndose un deltoide cóncavo.
La longitud del lado $l_{1}$ es:
$l_{1}^{2}=x^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}=\bigg(-1+\displaystyle\frac{\sqrt{4\phi+3}}{2}\bigg)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{1}^{2}=\bigg(1-\sqrt{4\phi+3}+\displaystyle\frac{4\phi+3}{4}\bigg)+\displaystyle\frac{1}{4}=\phi+2-\sqrt{4\phi+3}$
$l_{1}=\sqrt{\phi+2-\sqrt{4\phi+3}}\approx0.74\,\,u$
La longitud del lado $l_{2}$ es:
$l_{2}^{2}=(\phi-x)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}=\bigg(\phi+1-\displaystyle\frac{\sqrt{4\phi+3}}{2}\bigg)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{2}^{2}=\bigg(\phi^{2}+2\phi+1-(\phi+1)\sqrt{4\phi+3}+\displaystyle\frac{4\phi+3}{4}\bigg)+\displaystyle\frac{1}{4}$
$l_{2}^{2}=4\phi+3-(\phi+1)\sqrt{4\phi+3}$
$l_{2}=\sqrt{4\phi+3-(\phi+1)\sqrt{4\phi+3}}\approx1.19\,\,u$
Cálculo de la medida de los ángulos:
$cos(\^{A})=\displaystyle\frac{l_{1}^{2}+l_{1}^{2}-1^{2}}{2l_{1}^{2}}\approx0.0747$
$\^{A}=85º\,43'\,2.91''$
$cos(\^{C})=\displaystyle\frac{l_{2}^{2}+l_{2}^{2}-1^{2}}{2l_{2}^{2}}\approx0.6466$
$\^{C}=49º\,43'\,2.91''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=112º\,16'\,17.09''$
Perímetro y superficie de este deltoide es:
$P=2l_{1}+2l_{2}\approx3.85\,\,u$
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi\cdot 1}{2}=\displaystyle\frac{\phi}{2}\,\,u^{2}$
Se puede construir gráficamente el deltoide áureo convexo siguiendo los pasos:
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
Si intentamos construir un deltoide cóncavo inscrito en un rectángulo áureo, de forma que dos vértices opuestos del deltoide coincidan con dos vértices consecutivos del rectángulo, y los otros dos vértices estén situados en la mediatriz de los dos vértices anteriores, un sobre el lado del rectángulo y otro en el interior del rectángulo, tenemos infinitas posibilidades.
Vamos a distinguir dos casos, según el eje de simetría del deltoide coincida con su diagonal menor o su diagonal mayor.
En la siguiente escena de Descartes puedes construir deltoides cóncavos inscritos en un rectángulo áureo, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul) por el eje de simetría del rectángulo. Encuentra el deltoide en el que el cociente de las longitudes de los lados se aproxima más a $\phi$.
En la escena anterior se puede comprobar que no es posible construir un deltoide cóncavo inscrito en un rectángulo áureo cuyos lados estén también en proporción áurea y que tenga por eje de simetría su diagonal menor; el cociente de las longitudes de sus lados sería siempre menor que el número de oro.
Vamos a comprobarlo analíticamente:
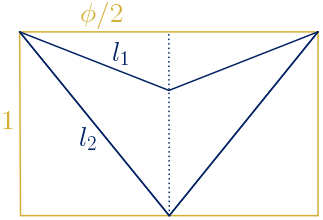
Se calcula la longitud del lado $l_{2}$.
$l_{2}^{2}=1^{2}+\bigg(\displaystyle\frac{\phi}{2}\bigg)^{2}=\displaystyle\frac{\phi+5}{4}$
$l_{2}=\sqrt{1+\displaystyle\frac{\phi^{2}}{4}}={\displaystyle\frac{\sqrt{\phi+5}}{2}}\,\,u$
Para que la razón entre las longitudes de los lados del deltoide sea el número de oro, la longitud del lado menor, $l_{1}$, debe ser:
$\displaystyle\frac{l_{2}}{l_{1}}=\phi \quad \rightarrow \quad l_{1}=\displaystyle\frac{l_{2}}{\phi}$
$l_{1}=\displaystyle\frac{1}{\phi} \sqrt{1+\displaystyle\frac{\phi^{2}}{4}}=\sqrt{\displaystyle\frac{1}{\phi^{2}}+\displaystyle\frac{1}{4}}=\sqrt{2-\phi+\displaystyle\frac{1}{4}}=\sqrt{\displaystyle\frac{9}{4}-\phi}$
$l_{1}=\displaystyle\frac{\sqrt{9-4\phi}}{2} \approx0.79 <\displaystyle\frac{\phi}{2}$
Para poder construir el deltoide la longitud de este lado, $l_{1}$, debe ser mayor que la mitad del lado mayor del rectángulo áureo, $\phi/2$, por tanto, no es posible construir el deltoide con las propiedades exigidas.
En la siguiente escena de Descartes puedes construir deltoides cóncavos inscritos en un rectángulo áureo, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul) por el eje de simetría del rectángulo. Encuentra el deltoide en el que el cociente de las longitudes de los lados se aproxima más a $\phi$.
En esta escena se puede comprobar gráficamente que sí es posible construir este deltoide.
Vamos a determinar este deltoide áureo cóncavo, calculando la longitud de sus lados y la medida de sus ángulos
Cálculo de la longitud de los lados:
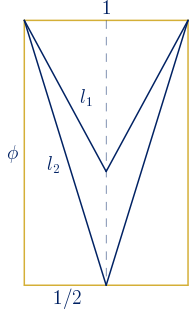
$l_{2}^{2}=\phi^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{2}^{2}=\phi^{2}+\displaystyle\frac{1}{4}=\displaystyle\frac{4\phi^{2}+1}{4}=\displaystyle\frac{4\phi+5}{4}$
$l_{2}=\sqrt{\phi^{2}+\displaystyle\frac{1}{4}}=\displaystyle\frac{\sqrt{4\phi+5}}{2}\approx1.69\,\,u$
Se calcula ahora $l_{1}$:
$\displaystyle\frac{l_{2}}{l_{1}}=\phi \quad \rightarrow \quad l_{1}=\displaystyle\frac{l_{2}}{\phi}=\displaystyle\frac{1}{\phi} \sqrt{\phi^{2}+\displaystyle\frac{1}{4}}=\sqrt{1+\displaystyle\frac{1}{4\phi^{2}}}$
Se sustituye $\displaystyle\frac{1}{\phi^{2}}=\phi^{-2}=2-\phi$
$l_{1}=\sqrt{1+\displaystyle\frac{2-\phi}{4}}=\sqrt{\displaystyle\frac{6-\phi}{4}}={\displaystyle\frac{\sqrt{6-\phi}}{2}}\approx1.05\,\,u$
Cálculo de la medida de los ángulos:
$cos(360º-\^{A})=\displaystyle\frac{l_{1}^{2}+l_{1}^{2}-1^{2}}{2l_{1}^{2}}\approx0.5436$
$\^{A}=302º\,55'\,40.59''$
$cos(\^{C})=\displaystyle\frac{l_{2}^{2}+l_{2}^{2}-1^{2}}{2l_{2}^{2}}\approx0.8257$
$\^{C}=34º\,20'\,38.67''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=11º\,21'\,50.37''$
Perímetro:
$P=2l_{1}+2l_{2}\approx5.48\,\,u$
Superficie:
$l_{1}^{2}=h^{2}+\displaystyle\frac{1}{4}\quad \rightarrow \quad h^{2}=l_{1}^{2}-\displaystyle\frac{1}{4}$
$h^{2}=\displaystyle\frac{6-\phi}{4}-\displaystyle\frac{1}{4}=\displaystyle\frac{5-\phi}{4}$
$h=\displaystyle\frac{\sqrt{5-\phi}}{2}\quad \rightarrow \quad d=\phi-\displaystyle\frac{\sqrt{5-\phi}}{2}$
$S= \displaystyle\frac{1}{2}\bigg(\phi-\displaystyle\frac{\sqrt{5-\phi}}{2} \bigg)\approx0.35\,\,u^{2}$
Se puede construir gráficamente el deltoide áureo cóncavo siguiendo los pasos:
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
En el apartado 5.4.1. se han estudiado deltoides convexos inscritos en un rectángulo áureo, es decir, deltoides convexos de diagonales $1$ y $\phi$. En este apartado vamos a construir deltoides convexos de lados $1$ y $\phi$.
Si intentamos construir un deltoide convexo cuyos lados estén en proporción áurea, por ejemplo, cuyos lados midan $1$ y $\phi$, nos encontramos que existen infinitas posibilidades.
En la siguiente escena de Descartes puedes construir deltoides cuyos lados tengan estas longitudes, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul). En este apartado vamos a estudior deltoides convexos. Encuentra el deltoide en el que el cociente entre las longitudes de las diagonales se aproxima más a $\phi$.
Todos tienen el mismo perímetro, pero distinta superficie.
Vamos a determinar este deltoide áureo convexo, calculando la longitud de sus diagonales y la medida de sus ángulos
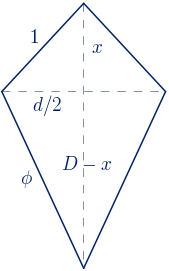
$\displaystyle\frac{D}{d}=\phi \quad \rightarrow \quad D=\phi\cdot d$
$D-x=\phi d-x$
Hay que resolver el sistema de ecuaciones:
$\begin{rcases} x^{2}+\displaystyle\frac{d^{2}}{4}=1\\ (\phi d-x)^{2}+\displaystyle\frac{d^{2}}{4}=\phi^{2}\end{rcases}$
Se desarrolla la segunda ecuación:
$\phi^{2}d^{2}-2\phi dx+x^{2}+\displaystyle\frac{d^{2}}{4}=\phi^{2}=\phi+1$
Se resta a la expresión obtenida la primera ecuación, se simplifica por $\phi$ y se despeja el valor de $x$:
$\phi^{2}d^{2}-2\phi dx=\phi\quad \rightarrow \quad \phi d^{2}-2dx=1\quad \rightarrow \quad x=\displaystyle\frac{\phi d^{2}-1}{2d}$
Se sustituye este valor en la primera ecuación:
$\bigg( \displaystyle\frac{\phi d^{2}-1}{2d} \bigg)^{2}+\displaystyle\frac{d^{2}}{4}=1 \quad \rightarrow \quad \displaystyle\frac{\phi^{2} d^{4}-2\phi d^{2}+1}{4d^{2}}+\displaystyle\frac{d^{2}}{4}=1$
Se quitan denominadores y se agrupan términos:
$\phi^{2} d^{4}-2\phi d^{2}+1+d^{4}=4d^{2}\rightarrow (\phi^{2}+1)d^{4}-(2\phi+4)d^{2}+1=0$
Se sustituye $\phi^{2}$ por $\phi+1$ y se obtiene la ecuación bicuadrada:
$(\phi+2)d^{4}-2(\phi+2)d^{2}+1=0$
Se resuelve la ecuación:
$d^{2}=\displaystyle\frac{2(\phi+2) \pm \sqrt{4(\phi+2)^{2}-4(\phi+2)}}{2(\phi+2)}$
$d^{2}=\displaystyle\frac{2(\phi+2)}{2(\phi+2)} \pm \sqrt {\displaystyle\frac{4(\phi+2)^{2}}{4(\phi+2)^{2}}-\displaystyle\frac{4(\phi+2)}{4(\phi+2)^{2}}}$
$d^{2}=1 \pm \sqrt {1-\displaystyle\frac{1}{\phi+2}}=1 \pm \sqrt {\displaystyle\frac{\phi+1}{\phi+2}}=1 \pm \displaystyle\frac{\phi}{\sqrt{\phi+2}}$
Las soluciones de la ecuación y el valor de $x$ correspondiente son:
$d_{1}=\sqrt{1 + \displaystyle\frac{\phi}{\sqrt{\phi+2}}} \approx1.36\,\,u \quad \rightarrow \quad x_{1}=0.73\,\,u$
$d_{2}=\sqrt{1 - \displaystyle\frac{\phi}{\sqrt{\phi+2}}} \approx0.39\,\,u \quad \rightarrow \quad x_{2}=-0.98\,\,u$
Con la primera solución se obtiene un deltoide convexo.
En la segunda solución el valor de $x_{2}$ es negativo. Gráficamente este valor se debe representar por debajo de la diagonal $d_{2}$ obteniéndose un deltoide cóncavo.
Cálculo de la medida de los ángulos:
$cos(\^{A})=\displaystyle\frac{1^{2}+1^{2}-d_{1}^{2}}{2}\approx0.0747$
$\^{A}=85º\,43'\,2.91''$
$cos(\^{C})=\displaystyle\frac{\phi^{2}+\phi^{2}-d_{1}^{2}}{2\phi^{2}}\approx0.6466$
$\^{C}=49º\,43'\,2.91''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=112º\,16'\,17.09''$
Se obtiene un deltoide convexo semejante al deltoide convexo del apartado 5.4.1. Los ángulos son iguales y los lados son proporcionales con razón de semejanza la longitud del lado menor:
$l_{1}=\sqrt{\phi+2-\sqrt{4\phi+3}}\approx0.74\,\,u$
Perímetro y superficie de este deltoide es:
$P=2+2\phi=2\phi^{2}\approx5.24\,\,u$
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi d_{1}\cdot d_{1}}{2}\approx1.5\,\,u^{2}$
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
Si intentamos construir un deltoide cóncavo cuyos lados estén en proporción áurea, por ejemplo, cuyos lados midan $1$ y $\phi$, nos encontramos que existen infinitas posibilidades.
En la siguiente escena de Descartes puedes construir deltoides cóncavos cuyos lados tengan estas longitudes, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul). En este apartado vamos a estudior deltoides cóncavos. Encuentra tres deltoides en los que el cociente entre las longitudes de las diagonales se aproxima más a $\phi$.
Todos tienen el mismo perímetro, pero distinta superficie.
$P=2+2\phi=2(1+\phi)=2\phi^{2}\approx5.24\,\,u$
Dos de los deltoides tienen como eje de simetría la diagonal menor. Vamos a determinarlos.
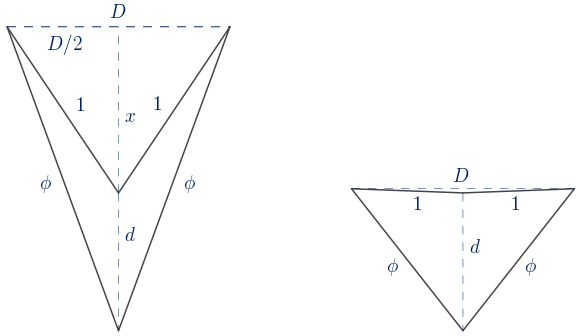
El cociente de sus diagonales debe ser el número de oro:
$\displaystyle\frac{D}{d}=\phi \quad \rightarrow \quad D=\phi\cdot d$
Hay que resolver el sistema de ecuaciones:
$\begin{rcases} x^{2}+\displaystyle\frac{D^{2}}{4}=1\\ (d+x)^{2}+\displaystyle\frac{D^{2}}{4}=\phi^{2}\end{rcases} \quad \rightarrow \quad \begin{rcases} x^{2}+\displaystyle\frac{\phi^{2} d^{2}}{4}=1\\ (d+x)^{2}+\displaystyle\frac{\phi^{2} d^{2}}{4}=\phi^{2}\end{rcases}$
Se desarrolla la segunda ecuación:
$d^{2}+2dx+x^{2}+\displaystyle\frac{\phi^{2}d^{2}}{4}=\phi^{2}=\phi+1$
Se resta a esta ecuación la primera ecuación y se despeja $x$:
$d^{2}+2dx=\phi\quad \rightarrow \quad x=\displaystyle\frac{\phi-d^{2}}{2d}$
Se sustituye este valor en la primera ecuación:
$\bigg( \displaystyle\frac{\phi-d^{2}}{2d} \bigg)^{2}+\displaystyle\frac{\phi^{2}d^{2}}{4}=1 \quad \rightarrow \quad \displaystyle\frac{\phi^{2}-2\phi d^{2}+d^{4}}{4d^{2}}+\displaystyle\frac{\phi^{2}d^{2}}{4}=1$
Se quitan denominadores y se agrupan términos:
$\phi^{2}-2\phi d^{2}+ d^{4}+\phi^{2}d^{4}=4d^{2}$
$(\phi^{2}+1)d^{4}+(-2\phi-4)d^{2}+ \phi^{2}=0$
Se sustituye $\phi^{2}$ por $\phi+1$ y se obtiene la ecuación bicuadrada:
$(\phi+2)d^{4}-(2\phi+4)d^{2}+\phi^{2}=0$
Se resuelve la ecuación:
$d^{2}=\displaystyle\frac{2(\phi+2) \pm \sqrt{4(\phi+2)^{2}-4\phi^{2}(\phi+2)}}{2(\phi+2)}$
$d^{2}=\displaystyle\frac{2(\phi+2)}{2(\phi+2)} \pm \sqrt {\displaystyle\frac{4(\phi+2)^{2}}{4(\phi+2)^{2}}-\displaystyle\frac{4\phi^{2}(\phi+2)}{4(\phi+2)^{2}}}$
$d^{2}=1 \pm \sqrt {1-\displaystyle\frac{\phi^{2}}{\phi+2}}$
$d^{2}=1 \pm \sqrt {1-\displaystyle\frac{\phi+1}{\phi+2}}=1 \pm \sqrt {\displaystyle\frac{1}{\phi+2}}=1 \pm \displaystyle\frac{1}{\sqrt {\phi+2}}$
Las soluciones de la ecuación, el valor de $x$ correspondiente y la longitud de la diagonal mayor son:
$d_{1}=\sqrt{1 +\displaystyle\frac{1}{\sqrt {\phi+2}}} \approx1.24\,\,u \quad \rightarrow \quad x_{1}=0.04\,\,u$
$D_{1}=\phi d_{1}=\phi \cdot \sqrt{1 +\displaystyle\frac{1}{\sqrt {\phi+2}}} \approx1.9986\,\,u$
$d_{2}=\sqrt{1 -\displaystyle\frac{1}{\sqrt {\phi+2}}} \approx0.69\,\,u \quad \rightarrow \quad x_{2}=0.83\,\,u$
$D_{2}=\phi d_{2}=\phi \cdot \sqrt{1 -\displaystyle\frac{1}{\sqrt {\phi+2}}} \approx1.11\,\,u$
Cálculo de la medida de los ángulos de la primera solución:
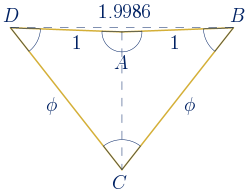
$cos(360º-\^{A})=\displaystyle\frac{1+1-D_{1}^{2}}{2\cdot 1 \cdot 1}\approx-0.9972 \rightarrow \^{A}=184º\,16'\,57.09''$
$cos(\^{C})=\displaystyle\frac{\phi^{2}+\phi^{2}-D_{1}^{2}}{2\phi^{2}}\approx0.2371 \rightarrow \^{C}=76º\,16'\,57.09''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=49º\,43'\,2.91''$
Perímetro y superficie:
$P=2+2\phi=2\phi^{2}\approx5.24\,\,u$
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi d_{1}\cdot d_{1}}{2}\approx1.23\,\,u^{2}$
Cálculo de la medida de los ángulos de la segunda solución:
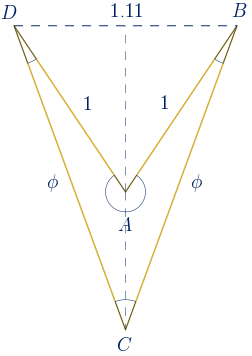
$cos(360º-\^{A})=\displaystyle\frac{1+1-D_{2}^{2}}{2\cdot 1 \cdot 1}\approx0.3792$
$\^{A}=292º\,16'\,57.09''$
$cos(\^{C})=\displaystyle\frac{\phi^{2}+\phi^{2}-D_{2}^{2}}{2\phi^{2}}\approx0.7629$
$\^{C}=40º\,16'\,57.09''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=13º\,43'\,2.91''$
Perímetro y superficie:
$P=2+2\phi=2\phi^{2}\approx5.24\,\,u$
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi d_{2}\cdot d_{2}}{2}\approx0.38\,\,u^{2}$
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
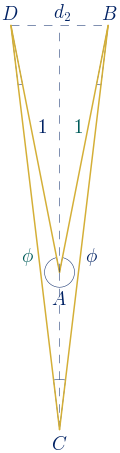
El tercero de los deltoides cóncavos que se obtienen al principio del apartado 6.3 tiene como eje de simetría la diagonal mayor. Vamos a determinarlo.
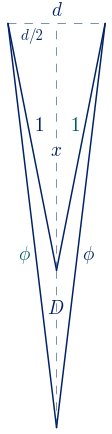
El cociente de sus diagonales debe ser el número de oro:
$\displaystyle\frac{D}{d}=\phi \quad \rightarrow \quad D=\phi\cdot d$
Hay que resolver el sistema de ecuaciones:
$\begin{rcases} x^{2}+\displaystyle\frac{d^{2}}{4}=1\\ (D+x)^{2}+\displaystyle\frac{d^{2}}{4}=\phi^{2}\end{rcases}$
$\begin{rcases} x^{2}+\displaystyle\frac{d^{2}}{4}=1\\ (\phi d+x)^{2}+\displaystyle\frac{d^{2}}{4}=\phi^{2}\end{rcases}$
Se desarrolla la segunda ecuación:
$\phi^{2}d^{2}+2\phi dx+x^{2}+\displaystyle\frac{d^{2}}{4}=\phi^{2}=\phi+1$
Se resta a la expresión obtenida la primera ecuación, se simplifica por $\phi$ y se despeja el valor de $x$:
$\phi^{2} d^{2}+2\phi dx=\phi\quad \rightarrow \quad \phi d^{2}+2dx=1\quad \rightarrow \quad x=\displaystyle\frac{1-\phi d^{2}}{2d}$
Se sustituye este valor en la primera ecuación:
$\bigg( \displaystyle\frac{1-\phi d^{2}}{2d} \bigg)^{2}+\displaystyle\frac{d^{2}}{4}=1 \quad \rightarrow \quad \displaystyle\frac{1-2\phi d^{2} +\phi^{2} d^{4}}{4d^{2}}+\displaystyle\frac{d^{2}}{4}=1$
Se quitan denominadores y se agrupan términos:
$1-2\phi d^{2}+\phi^{2} d^{4}+d^{4}=4d^{2}\rightarrow (\phi^{2}+1)d^{4}-(2\phi+4)d^{2}+1=0$
Se sustituye $\phi^{2}$ por $\phi+1$ y se obtiene la ecuación bicuadrada:
$(\phi+2)d^{4}-2(\phi+2)d^{2}+1=0$
Se resuelve la ecuación:
$d^{2}=\displaystyle\frac{2(\phi+2) \pm \sqrt{4(\phi+2)^{2}-4(\phi+2)}}{2(\phi+2)}$
$d^{2}=\displaystyle\frac{2(\phi+2)}{2(\phi+2)} \pm \sqrt {\displaystyle\frac{4(\phi+2)^{2}}{4(\phi+2)^{2}}-\displaystyle\frac{4(\phi+2)}{4(\phi+2)^{2}}}$
$d^{2}=1 \pm \sqrt {1-\displaystyle\frac{1}{\phi+2}}=1 \pm \sqrt {\displaystyle\frac{\phi+1}{\phi+2}}=1 \pm \displaystyle\frac{\phi}{\sqrt{\phi+2}}$
Las soluciones de la ecuación, el valor de $x$ correspondiente y la longitud de la diagonal mayor son:
$d_{1}=\sqrt{1 + \displaystyle\frac{\phi}{\sqrt{\phi+2}}} \approx1.36\,\,u \quad \rightarrow \quad x_{1}=-0.73\,\,u$
$D_{1}=\phi d_{1}=\phi \cdot\sqrt{1 + \displaystyle\frac{\phi}{\sqrt{\phi+2}}} \approx2.2\,\,u $
$d_{2}=\sqrt{1 - \displaystyle\frac{\phi}{\sqrt{\phi+2}}} \approx0.39\,\,u \quad \rightarrow \quad x_{2}=0.98\,\,u$
$D_{2}=\phi d_{2}=\phi \sqrt{1 - \displaystyle\frac{\phi}{\sqrt{\phi+2}}} \approx0.63\,\,u$
En la primera solución el valor de $x_{1}$ es negativo. Gráficamente este valor se debe representar por encima de la diagonal $d_{1}$ obteniéndose un deltoide convexo. Con la segunda solución se obtiene el deltoide cóncavo buscado.
Cálculo de la medida de los ángulos:
$cos(360º-\^{A})=\displaystyle\frac{1^{2}+1^{2}-d_{2}^{2}}{2}\approx0.9253$
$\^{A}=337º\,43'\,2.91''$
$cos(\^{C})=\displaystyle\frac{\phi^{2}+\phi^{2}-d_{2}^{2}}{2\phi^{2}}\approx0.9715$
$\^{C}=13º\,43'\,2.91''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=4º\,16'\,57.09''$
Perímetro y superficie:
$P=2+2\phi=2\phi^{2}\approx5.24\,\,u$
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi d_{2}\cdot d_{2}}{2}\approx0.12\,\,u^{2}$
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
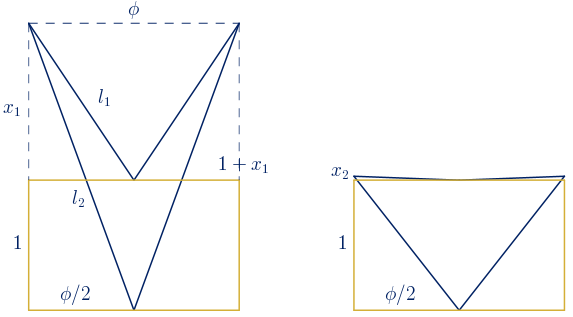
Si intentamos construir un deltoide cóncavo cuyas diagonales estén en proporción áurea, por ejemplo, cuyas diagonales midan $1$ y $\phi$, nos encontramos que existen infinitas posibilidades.
Vamos a distinguir dos casos, según el eje de simetría del deltoide coincida con su diagonal menor o su diagonal mayor.
En la siguiente escena de Descartes puedes construir deltoides cóncavos cuyas diagonales tengan estas longitudes, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul). Encuentra dos deltoides en los que el cociente de las longitudes de los lados se aproxima más a $\phi$.
Vamos a determinar estos dos deltoides cóncavos:
Cálculo de la longitud de los lados:
$l_{1}^{2}=x^{2}+\bigg(\displaystyle\frac{\phi}{2}\bigg)^{2}\quad \rightarrow \quad l_{1}=\sqrt{x^{2}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}^{2}=(1+x)^{2}+\bigg(\displaystyle\frac{\phi}{2}\bigg)^{2}\quad \rightarrow \quad l_{2}=\sqrt{1+2x+x^{2}+\displaystyle\frac{\phi^{2}}{4}}$
Se debe verificar que:
$\displaystyle\frac{l_{2}}{l_{1}}=\phi\quad \rightarrow \quad \displaystyle\frac{l_{2}^{2}}{l_{1}^{2}}=\displaystyle\frac{1+2x+x^{2}+\displaystyle\frac{\phi^{2}}{4}}{x^{2}+\displaystyle\frac{\phi^{2}}{4}}=\phi^2$
$1+2x+x^{2}+\displaystyle\frac{\phi^{2}}{4}=\phi^{2} \bigg(x^{2}+\displaystyle\frac{\phi^{2}}{4} \bigg)=\phi^{2}x^{2}+\displaystyle\frac{\phi^{4}}{4}$
Se sustituye $\phi^{2}$ por $\phi+1$ y $\phi^{4}$ por $3\phi+2$:
$1+2x+x^{2}+\displaystyle\frac{\phi+1}{4}=(\phi+1)x^{2}+\displaystyle\frac{3\phi+2}{4}$
$\phi x^{2}-2x+\displaystyle\frac{2\phi-3}{4}=0$
Se resuelve la ecuación de segundo grado:
$x=\displaystyle\frac{2 \pm \sqrt{4-\phi(2\phi-3)}}{2\phi}=\displaystyle\frac{2 \pm \sqrt{\phi+2}}{2\phi}$
$x=\displaystyle\frac{2}{2\phi} \pm \sqrt {\displaystyle\frac{\phi}{4\phi^{2}}+\displaystyle\frac{2}{4\phi^{2}}}=\displaystyle\frac{1}{\phi} \pm \sqrt {\displaystyle\frac{1}{4\phi}+\displaystyle\frac{1}{2\phi^{2}}}$
Se sustituye $\displaystyle\frac{1}{\phi}$ por $\phi-1$ y $\displaystyle\frac{1}{\phi^{2}}$ por $2-\phi$:
$x=\phi-1 \pm \sqrt {\displaystyle\frac{\phi-1}{4}+\displaystyle\frac{2-\phi}{2}}=\phi-1 \pm \sqrt {\displaystyle\frac{3-\phi}{4}}$
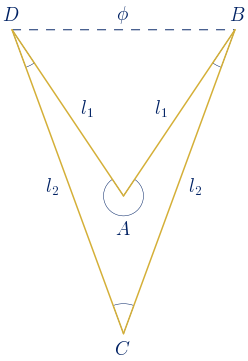
Se obtienen dos soluciones positivas, por tanto, hay dos deltoides con las proporciones buscadas:
$x_{1}=\displaystyle\frac{2 + \sqrt{\phi+2}}{2\phi}=\phi-1+\displaystyle\frac{\sqrt{3-\phi}}{2}\approx 1.21\,\,u$
$x_{2}=\displaystyle\frac{2 - \sqrt{\phi+2}}{2\phi}=\phi-1-\displaystyle\frac{\sqrt{3-\phi}}{2}\approx 0.03\,\,u$
Cálculo de los lados:
$l_{1}=\sqrt{\displaystyle\frac{\phi^{2}}{4}+x_{1}^{2}}$
$l_{1}=\sqrt{\displaystyle\frac{\phi^{2}}{4}+\bigg( \displaystyle\frac{2 + \sqrt{\phi+2}}{2\phi} \bigg)^{2}}$
$l_{1}=\sqrt{\displaystyle\frac{\phi^{2}}{4}+\displaystyle\frac{4 + 4\sqrt{\phi+2}+\phi+2}{4\phi^{2}}}$
$l_{1}=\sqrt{\displaystyle\frac{\phi^{4}+\phi+6 + 4\sqrt{\phi+2}}{4\phi^{2}}}=\displaystyle\frac{\sqrt{\phi+2+\sqrt{\phi+2}}}{\phi} \approx1.45\,\,u$
$l_{2}=\sqrt{1+2x_{1}+x_{1}^{2}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}=\sqrt{1+2\cdot\displaystyle\frac{2 + \sqrt{\phi+2}}{2\phi}+\bigg( \displaystyle\frac{2 + \sqrt{\phi+2}}{2\phi} \bigg)^{2}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}=\sqrt{1+\displaystyle\frac{2 + \sqrt{\phi+2}}{\phi}+\displaystyle\frac{4+4\sqrt{\phi+2}+\phi+2}{4\phi^{2}}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}=\sqrt{\displaystyle\frac{4\phi^{2}+8\phi+4\phi \sqrt{\phi+2}+4+4\sqrt{\phi+2}+\phi+2+\phi^{4}}{4\phi^{2}}}$
Se sustituye $\phi^{2}$ por $\phi+1$ y $\phi^{4}$ por $3\phi+2$:
$l_{2}=\sqrt{\displaystyle\frac{16\phi+12+(4\phi+4)\sqrt{\phi+2}}{4\phi^{2}}}$
$l_{2}=\displaystyle\frac{\sqrt{4\phi+3+(\phi+1)\sqrt{\phi+2}}}{\phi}\approx2.35\,\,u$
Cálculo de los ángulos:
$cos(360º-\^{A})=\displaystyle\frac{l_{1}^{2}+l_{1}^{2}-\phi^{2}}{2l_{1}^{2}}\approx0.3792 \rightarrow \^{A}=292º\,16'\,57.09''$
$cos(\^{C})=\displaystyle\frac{l_{2}^{2}+l_{2}^{2}-\phi^{2}}{2l_{2}^{2}}\approx0.7629 \rightarrow \^{C}=40º\,16'\,57.09''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=13º\,43'\,2.91''$
Perímetro:
$P=2l_{1}+2l_{2}\approx7.6\,\,u$
Superficie:
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi\cdot 1}{2}=\displaystyle\frac{\phi}{2}\,\,u^{2}$
Cálculo de los lados:
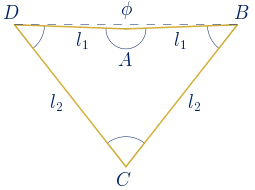
$l_{1}=\sqrt{\displaystyle\frac{\phi^{2}}{4}+x_{2}^{2}}$
$l_{1}=\sqrt{\displaystyle\frac{\phi^{2}}{4}+\bigg( \displaystyle\frac{2 - \sqrt{\phi+2}}{2\phi} \bigg)^{2}}$
$l_{1}=\sqrt{\displaystyle\frac{\phi^{2}}{4}+\displaystyle\frac{4 - 4\sqrt{\phi+2}+\phi+2}{4\phi^{2}}}$
$l_{1}=\sqrt{\displaystyle\frac{\phi^{4}+\phi+6 - 4\sqrt{\phi+2}}{4\phi^{2}}}=\displaystyle\frac{\sqrt{\phi+2-\sqrt{\phi+2}}}{\phi} \approx0.81\,\,u$
$l_{2}=\sqrt{1+2x_{2}+x_{2}^{2}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}=\sqrt{1+2\cdot\displaystyle\frac{2 - \sqrt{\phi+2}}{2\phi}+\bigg( \displaystyle\frac{2 - \sqrt{\phi+2}}{2\phi} \bigg)^{2}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}=\sqrt{1+\displaystyle\frac{2 - \sqrt{\phi+2}}{\phi}+\displaystyle\frac{4-4\sqrt{\phi+2}+\phi+2}{4\phi^{2}}+\displaystyle\frac{\phi^{2}}{4}}$
$l_{2}=\sqrt{\displaystyle\frac{4\phi^{2}+8\phi-4\phi \sqrt{\phi+2}+4-4\sqrt{\phi+2}+\phi+2+\phi^{4}}{4\phi^{2}}}$
Se sustituye $\phi^{2}$ por $\phi+1$ y $\phi^{4}$ por $3\phi+2$:
$l_{2}=\sqrt{\displaystyle\frac{16\phi+12-(4\phi+4)\sqrt{\phi+2}}{4\phi^{2}}}$
$l_{2}=\displaystyle\frac{\sqrt{4\phi+3-(\phi+1)\sqrt{\phi+2}}}{\phi}\approx1.31\,\,u$
Cálculo de los ángulos:
$cos(360º-\^{A})=\displaystyle\frac{l_{1}^{2}+l_{1}^{2}-\phi^{2}}{2l_{1}^{2}}\approx-0.9972 \rightarrow \^{A}=184º\,16'\,57.09''$
$cos(\^{C})=\displaystyle\frac{l_{2}^{2}+l_{2}^{2}-\phi^{2}}{2l_{2}^{2}}\approx0.2371 \rightarrow \^{C}=76º\,16'\,57.09''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=49º\,43'\,2.91''$
Perímetro:
$P=2l_{1}+2l_{2}\approx4.24\,\,u$
Superficie:
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi\cdot 1}{2}=\displaystyle\frac{\phi}{2}\,\,u^{2}$
En ambos casos se obtienen deltoides cóncavos semejantes a los deltoides cónvavos del apartado 6.2.1.
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
En la siguiente escena de Descartes puedes construir deltoides cóncavos cuyas diagonales midan $1$ y $\phi$, modificando el valor del control de la barra inferior o desplazando en la escena el control gráfico (punto azul). Encuentra el deltoide en el que el cociente de las longitudes de los lados se aproxima más a $\phi$.
Vamos a determinar este deltoide áureo cóncavo, calculando la longitud de sus lados y la medida de sus ángulos.
Cálculo de la longitud de los lados:
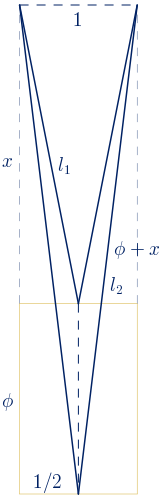
$l_{1}^{2}=x^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}\rightarrow \,\, l_{1}=\sqrt{x^{2}+\displaystyle\frac{1}{4}}$
$l_{2}^{2}=(\phi+x)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{2}=\sqrt{\phi^{2}+2\phi x+x^{2}+\displaystyle\frac{1}{4}}$
Se debe verificar que:
$\displaystyle\frac{l_{2}}{l_{1}}=\phi\quad \rightarrow \quad \displaystyle\frac{l_{2}^{2}}{l_{1}^{2}}=\displaystyle\frac{\phi^{2}+2\phi x+x^{2}+\displaystyle\frac{1}{4}}{x^{2}+\displaystyle\frac{1}{4}}=\phi^2$
$\phi^{2}+2\phi x+x^{2}+\displaystyle\frac{1}{4}=\phi^{2}x^{2}+\displaystyle\frac{\phi^{2}}{4}$
$x^{2}(\phi^{2}-1)-2\phi x+\displaystyle\frac{-3\phi^{2}-1}{4}=0$
Se sustituye $\phi^{2}$ por $\phi+1$:
$\phi x^{2}-2\phi x+\displaystyle\frac{-3\phi-4}{4}=0$
Se obtiene una ecuación parecida a la obtenida para calcular la longitud de los lados del deltoide áureo convexo inscrito en un rectángulo áureo (apartado 5.4.1). La única diferencia es el cambio del signo del coeficiente de x, por tanto, las soluciones de esta ecuación serán las opuestas de la ecuación resuelta en dicho apartado:
En este caso nos interesa la solución positiva, con la que se obtiene un deltoide cóncavo semejante al obtenido en el apartado 6.2.2.
$x_{1}=1+\displaystyle\frac{\sqrt{4\phi+3}}{2}\approx2.54$
La solución negativa:
$x_{2}=1-\displaystyle\frac{\sqrt{4\phi+3}}{2}\approx-0.54$
habría que representarla gráficamente desde el lado superior del rectángulo áureo hacia abajo y se obtendría el deltoide áureo convexo descrito en el apartado 5.4.1.
Cálculo de las longitudes de los lados:
La longitud del lado $l_{1}$ es:
$l_{1}^{2}=x^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}=\bigg(1+\displaystyle\frac{\sqrt{4\phi+3}}{2}\bigg)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{1}^{2}=\bigg(1+\sqrt{4\phi+3}+\displaystyle\frac{4\phi+3}{4}\bigg)+\displaystyle\frac{1}{4}=\phi+2+\sqrt{4\phi+3}$
$l_{1}=\sqrt{\phi+2+\sqrt{4\phi+3}}\approx2.59\,\,u$
La longitud del lado $l_{2}$ es:
$l_{2}^{2}=(\phi+x)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}=\bigg(\phi+1+\displaystyle\frac{\sqrt{4\phi+3}}{2}\bigg)^{2}+\bigg(\displaystyle\frac{1}{2}\bigg)^{2}$
$l_{2}^{2}=\bigg(\phi^{2}+2\phi+1+(\phi+1)\sqrt{4\phi+3}+\displaystyle\frac{4\phi+3}{4}\bigg)+\displaystyle\frac{1}{4}$
$l_{2}^{2}=4\phi+3+(\phi+1)\sqrt{4\phi+3}$
$l_{2}=\sqrt{4\phi+3+(\phi+1)\sqrt{4\phi+3}}\approx4.19\,\,u$
Cálculo de la medida de los ángulos:
$cos(360º-\^{A})=\displaystyle\frac{l_{1}^{2}+l_{1}^{2}-1^{2}}{2l_{1}^{2}}\approx0.9253$
$\^{A}=337º\,43'\,2.91''$
$cos(\^{C})=\displaystyle\frac{l_{2}^{2}+l_{2}^{2}-1^{2}}{2l_{2}^{2}}\approx0.9715$
$\^{C}=13º\,43'\,2.91''$
$\^{B}=\^{D}=\displaystyle\frac{360-\^{A}-\^{C}}{2}=4º\,16'\,57.09''$
Perímetro y superficie:
$P=2l_{1}+2l_{2}\approx13.55\,\,u$
$S=\displaystyle\frac{D\cdot d}{2}=\displaystyle\frac{\phi\cdot 1}{2}=\displaystyle\frac{\phi}{2}\,\,u^{2}$
Para construirlo gráficamente se realizan los cinco primeros pasos de la construcción del deltoide áureo convexo del apartado 5.4.1 y, a partir del sexto, se actúa de forma diferente:
En la siguiente escena de Descartes puedes seguir la construcción paso a paso aplicando el procedimiento descrito:
En el estudio de los deltoides que verifican que tanto el cociente de las longitudes de sus lados como el cociente de las longitudes de sus diagonales es el número de oro, se han obtenido cuatro deltoides, uno de ellos convexo y los otros tres cóncavos.
Se han utilizado dos procedimientos distintos para obtenerlos:
• En el primer procedimiento se ha supuesto que las longitudes de las diagonales son $1$ y $\phi$ y, con esta condición, se han calculado los deltoides que verifican que el cociente de las longitudes de sus lados es igual a $\phi$.
• En el segundo procedimiento se ha supuesto que las longitudes de los lados son $1$ y $\phi$ y, con esta condición, se han calculado los deltoides que verifican que el cociente de las longitudes de sus diagonales es igual a $\phi$.
Por ambos procedimientos se ha llegado a la existencia de cuatro deltoides distintos, siendo semejantes los deltoides obtenidos por cada uno de ellos.
Además, se ha obtenido también, en el apartado 5.4.2, un deltoide cóncavo inscrito en un rectángulo áureo que verifica que el cociente de las longitudes de sus lados es el número de oro, pero no verifica esta condición el cociente de las longitudes de sus diagonales.
En cada caso los deltoides estudiados se han representado gráficamente a distintas escalas para poder observar mejor sus elementos. En la página siguiente aparecen representados los cuatro con la misma escala para poder compararlos.
En la siguiente escena de Descartes puedes representar los deltoides que existen de lados $1$ y $\phi$ y comprobar la existencia de aquellos en los que el cociente de la longitud de sus diagonales es el número de oro.