Subproyecto GEOgráfica.
Cuando en 1970 el futurólogo Alvin Toffler, estudioso de la revolución digital, la revolución de las comunicaciones y la singularidad tecnológica, avanzó en su libro "El shock del futuro" una descripción de la realidad actual acertó en un porcentaje increíblemente alto. Creo recordar que el fenómeno del desplazamiento social masivo y continuo, por motivos lúdicos o de otra índole, no fue previsto en su dimensión real. En aquellos años el término low cost aún no existía; aunque ya empezaba a tomar forma su predecesor, vuelo chárter. Es preciso reconocer que los conceptos anteriores: low cost, revolución digital, revolución de las comunicaciones y la evolución tecnológica han creado una nueva realidad social.
Con objeto de "estar al día" socialmente, varios miembros de la Red Descartes y otros compañeros del ámbito educativo notaron que a raíz de que los términos asociados a los desplazamientos: Latitud, Longitud y Altitud comenzaban a tomar una significación relevante en la vida cotidiana debido a su intervención en todo lo relacionado con la localización de lugares en un mapa, que más adelante, con la aparición de los planos y mapas digitales, incrementó su significación de manera exponencial, decíamos que un grupo de profesores vio que era preciso crear medios para familiarizar al alumnado con dichos términos y con la nueva realidad social. Esto hizo que en el año 2014 varios miembros de la Red Descartes, tanto de España como de Colombia y México, crearan una serie de objetos didácticos, interactivos, lúdicos y con capacidad de evaluar en tiempo real el nivel de conocimientos sobre los países, sus capitales, ríos, monumentos, cultura etc. de la persona que hace uso del objeto didáctico, así nació el subproyecto GEOgráfica.
Recomendamos la lectura completa del Inicio, Introducción y Manual de usuario de la página enlazada con la imagen anterior antes de comenzar a usar los materiales del proyecto.
Desde un principio los miembros de la Red Descartes de Colombia, con su aluvión de excelentes creaciones y extraordinarias ideas tomaron las riendas de la evolución del proyecto al que fueron dando forma. En primer lugar este se desglosó en cuatro apartados:
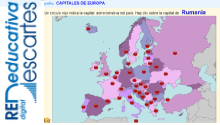
Sin desmerecer el esfuerzo y aciertos de todos y cada uno de los miembros de la Red Descartes que han intervenido en el desarrollo del proyecto GEOgráfica debemos destacar la profunda visión y acierto de la propuesta del profesor Diego Luis Feria Gómez al incluir, en el año 2016, en el apartado GEOcapital, cinco extraordinarios trabajos sobre la geolocalización de las capitales de los cinco continentes mediante el uso, en tiempo real, de mapas de Google.
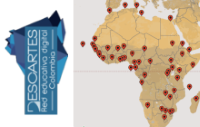
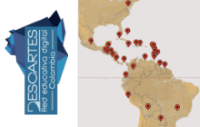
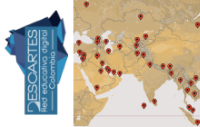
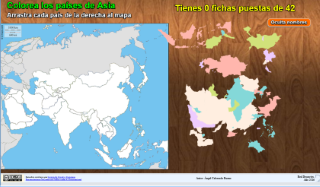
Geolocalización de las capitales de África, América y Asia.
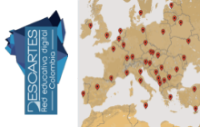
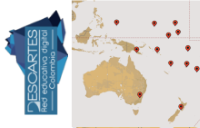
Geolocalización de las capitales de Europa y Oceanía
La propuesta que en boca del autor de este artículo y del profesor Ángel Cabezudo Bueno en su plantilla para la utilidad dicen:"...La Geolocalización de Capitales es una actividad que podemos encontrar en la sección GEOcapital del subproyecto GEOgráfica desarrollado por la "Red Educativa Digital Descartes" proyectodescartes.org En este contexto entendemos por geolocalización de la capital de un determinado país, estado o territorio como la consulta de su ubicación sobre un mapa y cuyo posicionamiento se obtiene a través de sus coordenadas geográficas -latitud y longitud-
La actividad pretende que con la práctica el usuario pueda probar su capacidad de localización en un mapa de Google de las capitales de un determinado territorio del mundo. El objeto interactivo solicita al usuario que señale sobre el mapa el marcador de localización ![]() donde hay que situar la capital de un determinado país, dado aleatoriamente, dentro del conjunto de países registrados. La reiteración de este ejercicio con la ayuda ofrecida y las marcas de latitud y longitud que se dibujan en el mapa facilitan la memorización de estas capitales. No hay que insistir mucho para justificar el interés que hoy en día tiene poder traer enseguida a la memoria este tipo de datos y disponer de una referencia mental de la situación de un determinado país o capital correspondiente frente a las noticias que nos llegan desde diferentes medios de información (prensa, radio, televisión, etc.)..."
donde hay que situar la capital de un determinado país, dado aleatoriamente, dentro del conjunto de países registrados. La reiteración de este ejercicio con la ayuda ofrecida y las marcas de latitud y longitud que se dibujan en el mapa facilitan la memorización de estas capitales. No hay que insistir mucho para justificar el interés que hoy en día tiene poder traer enseguida a la memoria este tipo de datos y disponer de una referencia mental de la situación de un determinado país o capital correspondiente frente a las noticias que nos llegan desde diferentes medios de información (prensa, radio, televisión, etc.)..."
Es inmediata la consecuencia de ampliar la idea de geolocalización a las capitales de las provincias, países o territorios de cualquier nación, fundamentalmente; aunque no de forma exclusiva, de las naciones más grandes, como son: India, Estados Unidos, China y Rusia. De hecho en la actualidad ya existen dos nuevos trabajos, uno sobre la geolocalización de las capitales de los territorios y países de la India y otro sobre las capitales de los estados de los Estados Unidos de América del Norte, que enlazamos a continuación, estando la creación del resto en preparación o a disposición de quien decida implementar algún dearrollo.
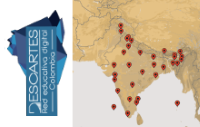
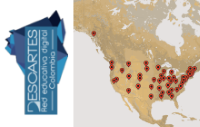
Geolocalización de las capitales de la India y Estados Unidos
También, consecuentemente, sería conveniente la creación de utilidades interactivas de geolocalización de monumentos, museos, edificios emblemáticos, lugares más visitados, restaurantes, cines, teatros etc. de las capitales más grandes y relevantes, o cualquier otra de interés, con objeto de facilitar la movilidad y aprovechar las breves estancias en ellas.
Así mismo existen varias propuestas de ampliación del proyecto GEOgráfica con los apartados de: GEOríos, GEOmontañas, GEOcultura etc. con la intención de convertir el proyecto en un instrumento eficaz para difundir, a un nivel básico, los conocimientos elementales que en la actualidad constituyen, en el área que trata, los requisitos mínimos necesarios para ser considerado como una persona "alfabetizada".
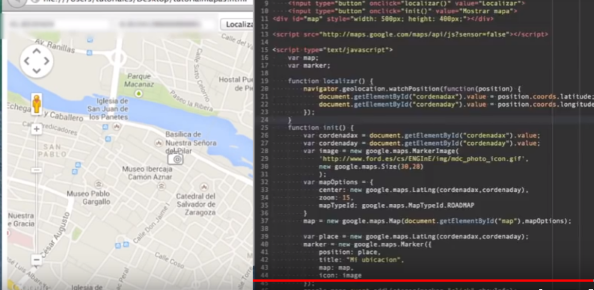
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, de la geolocalización de un lugar.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo. 2018
Particiones del cubo en pirámides (y parte III)
Escrito por José R. Galo SánchezLa partición de un cubo en pirámides triangulares tiene su cardinal mínimo en cinco pirámides, pero hay una única forma de realizar esta partición. La descomposición en seis pirámides triangulares amplía el número de formas de realizarla y da lugar a particiones que podemos encuadrar en dos bloques: no prismáticas o prismáticas. En estas últimas todas las pirámides son equivalentes (igual volumen) o incluso congruentes. En este artículo nos centraremos en la partición prismática de un cubo en pirámides triangulares equivalentes. Análisis previos que nos conducen a esta situación fueron detallados en el artículo "Partición del cubo en pirámides (parte II)".
Particiones de un cubo en pirámides triangulares equivalentes
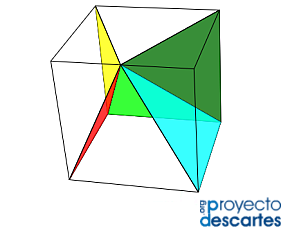
El plano determinado por dos diagonales con igual dirección en dos caras opuestas de un cubo interseca a éste dividiéndolo en dos prismas triangulares cuyas bases son triángulos rectángulos isósceles. Consecuentemente, la descomposición de un cubo en pirámides triangulares puede abordarse analizando la partición de un prisma recto de base un triángulo isósceles rectángulo. Este procedimiento es el que denominaremos partición prismática del cubo. Sin pérdida de generalidad consideraremos que el lado del cubo es la unidad.
Escena 1. División del cubo en dos prismas triangulares
1. Descomposición de un prisma triangular en pirámides triangulares
Consideremos el prisma recto de vértices {A, B, C, E, F, G}, donde la base superior se corresponde con los tres primeros vértices y la inferior con los tres últimos (ver escena 1). Queremos descomponerla en pirámides de base triangular y para ello hemos de tene en cuenta que:
- El menor número de pirámides se obtendrá cuando se consideren sólo los seis vértices del prisma como posibles vértices de las pirámides de la partición.
- Los elementos primarios mínimos para abordar la partición son ocho triángulos (las dos bases del prisma y seis más resultantes de dividir las tres caras laterales en triángulos) y 12 segmentos (las nueve aristas y las tres diagonales de las caras laterales). Y dado que dos pirámides de la partición han de tener tres caras diferentes como mínimo, entonces también son como mínimo tres las pirámides que formarán la partición (ocho caras entre tres nos da un valor mayor que dos).
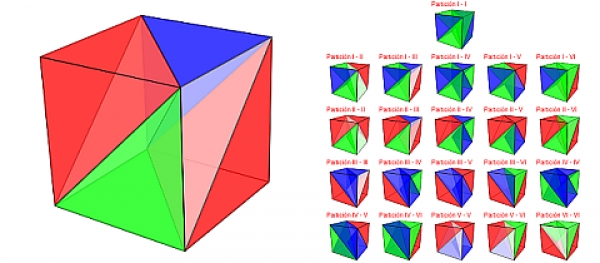
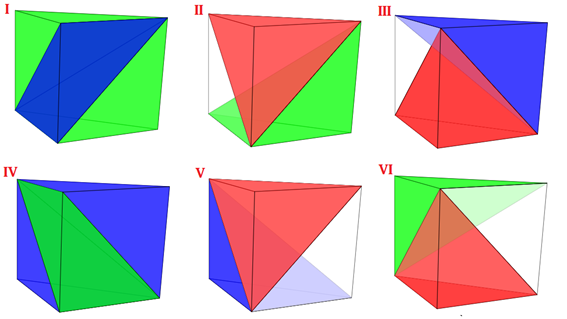
Basándonos en que una pirámide triangular queda determinada sin más que elegir dos segmentos con distinta dirección no coplanarios, una forma de abordar la partición del prisma de vértices {A, B, C, E, F, G} en tres pirámides triangulares se logra considerando dos aristas no coplanarias, una de la base ABC y otra de la EFG (Ver escena 2). Los cuatro vértices de esas dos aristas determinan una pirámide triangular que parte al prisma en tres bloques (se puede simular la situación en dicha escena 2) quedando fijadas, junto a ésta, las otras dos pirámides buscadas. Hay sólo seis posibilidades que vamos a denotar como partición I, II, III, IV, V y VI.
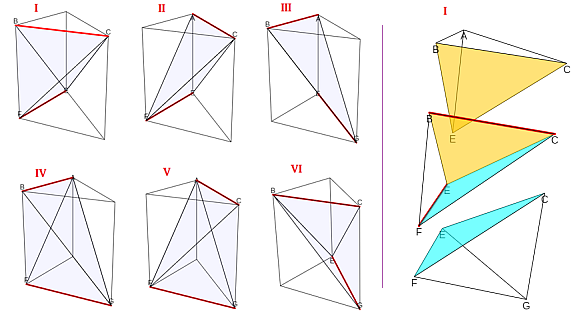
Escena 2. Particiones del prisma en tres pirámides triangulares (I, II, III, IV, V y VI) y detalle de la partición tipo I
- BC con EF que conduce a la pirámide BCEF y determina a ABCE y CEFG
- AC con EF que conduce a ACEF y determina a ABCF y CEFG
- AB con EG que conduce a ABEG y determina a ABCG y BEFG
- AB con FG que conduce a ABFG y determina a ABCG y AEFG
- AC con FG que conduce a ACFG y determina a ABCF y AEFG
- BC con EG que conduce a BCEG y determina a ABCE y BEFG
Distinguiendo los vértices por su nombre, en esas seis particiones aparecen doce pirámides diferentes, lo cual obviamente se corresponde con las combinaciones que se pueden obtener a partir de los seis vértices {A, B, C, E, F, G} agrupándolos de cuatro en cuatro, que son los vértices de una pirámide, y quitando aquellas agrupaciones en las que los cuatro vértices son coplanarios. Así pues, son C6, 4 = 15 combinaciones diferentes {ABCE, ABCF, ABEF, ABEG, ABFG, ACEF, ACEG, ACFG, AEFG, BCEF, BCEG, BCFG, BEFG, CEFG} y se excluyen los tres casos que hemos tachado por ser cuatro vértices coplanarios. Este podría ser también otro procedimiento alternativo al anterior para analizar las diferentes particiones del prisma.
En esas doce pirámides intervienen 15 aristas posibles, pues son combinaciones de seis vértices tomados de dos en dos, C6, 2 = 15. Son las reflejadas en la tabla 1, donde se indica su medida respectiva.
| AB=1 | ||||
| AC=√2 | BC=1 | |||
| AE=1 | BE=√2 | CE=√3 | ||
| AF=√2 | BF=1 | CF=√2 | EF=1 | |
| AG=√3 | BG=√2 | CG=1 | EG=√2 | FG=1 |
Tabla 1. Aristas de las pirámides y longitud de las mismas
En la tabla 2 podemos agrupar toda la información anterior y comparar las pirámides de esas particiones buscando detectar cuales son iguales o del mismo tipo. FIjándonos en la medida de las aristas que las componen se observa que hay tres tipos de pirámides que hemos etiquetado como X, Y, Z y, como detallaremos a continuación, en el tipo X se distinguen dos modalidades que etiquetamos como 1 y 2. También se refleja si la partición está constituida por pirámides congruentes entre sí (y por tanto también equivalentes) o si son sólo equivalentes.
| Partición | Pirámide | Aristas | Tipo | Modalidad | Congruencia y Equivalencia |
| I | ABCE | 1, 1, 1, √2, √2, √3 | X | 2 | Congruencia |
| BCEF | 1, 1, 1, √2, √2, √3 | X | 1 | ||
| CEFG | 1, 1, 1, √2, √2, √3 | X | 2 | ||
| II | ABCF | 1, 1, 1, √2, √2, √2 | Y | Equivalencia | |
| ACEF | 1, 1, √2, √2, √2, √3 | Z | |||
| CEFG | 1, 1, 1, √2, √2, √3 | X | 2 | ||
| III | ABCG | 1, 1, 1, √2, √2, √3 | X | 1 | Equivalencia |
| ABEG | 1, 1, √2, √2, √2, √3 | Z | |||
| BEFG | 1, 1, 1, √2, √2, √2 | Y | |||
| IV | ABCG | 1, 1, 1, √2, √2, √3 | X | 1 | Equivalencia |
| ABFG | 1, 1, 1, √2, √2, √3 | X | 2 | ||
| AEFG | 1, 1, 1, √2, √2, √3 | X | 1 | ||
| V | ABCF | 1, 1, 1, √2, √2, √2 | Y | Equivalencia | |
| ACFG | 1, 1, √2, √2, √2, √3 | Z | |||
| AEFG | 1, 1, 1, √2, √2, √3 | X | 1 | ||
| VI | ABCE | 1, 1, 1, √2, √2, √3 | X | 2 | Equivalencia |
| BCEG | 1, 1, √2, √2, √2, √3 | Z | |||
| BEFG | 1, 1, 1, √2, √2, √3 | Y |
Tabla 2. Desglose de particiones, pirámides que lo conforman, longitud de las aristas que lo componen, tipo de pirámide y modalidad, y congruencia y/o equivalencia
Cada partición del prisma la vamos a distinguir con el número romano que le hemos asignado o sin más que nombrar los tipos de pirámide que la forman para lo que convendremos hacerlo de arriba hacia abajo de acuerdo a la ubicación inicial de la pirámide en la que la base superior tiene de vértices ABC y la inferior EFG. Así la partición II viene dada por {Y, Z, X2}.
Procedamos a analizar cada uno de los tipos de pirámides que aparecen en dichas particiones.
1.1 Pirámide tipo Y
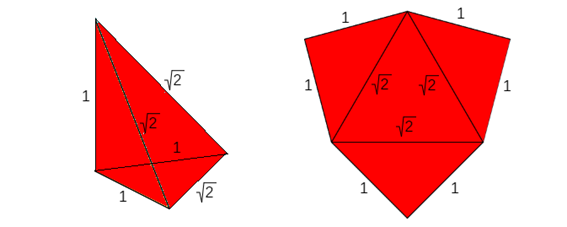
Atendiendo sólo a la forma, es decir, considerando que todas las caras son de igual color y no etiquetando los vértices, sólo es posible una pirámide triangular cuyas aristas midan 1, 1, 1, √2 , √2, √2 (escena 3). Su desarrollo plano está compuesto por un triángulo equilátero de lado 2 y tres triángulos rectángulos isósceles de catetos 1 y de hipotenusa2. El desarrollo, como se ha representado en la figura, tiene simetría axial con eje de simetría cualquiera de las alturas del triángulo equilátero y por tanto, independientemente de la orientación con la que se realiza el plegado (hacia dentro o hacia fuera) se obtiene la misma pirámide. El volumen de esta pirámide es 1/6 u3.
Escena 2. Pirámide triangular tipo Y (trirrectángula)
1.2 Pirámide tipo Z
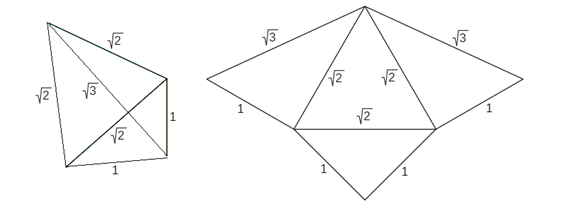
De manera análoga al caso anterior, si atendemos sólo a la forma, sólo es posible una pirámide triangular cuyas aristas midan 1, 1, √2, √2, √2, √3 (escena 3). Su desarrollo plano está compuesto por un triángulo equilátero de lado √2, un rectángulo isósceles de catetos 1 e hipotenusa √2 y dos triángulos rectángulos de catetos 1 y √2 e hipotenusa √3. Este desarrollo, como está representado en la figura, tiene simetría axial con eje de simetría la altura del triángulo equilátero que es altura a la vez del triángulo rectángulo isósceles. Así pues, independientemente de la orientación con la que se realiza el plegado (hacia dentro o hacia fuera) se obtiene la misma pirámide. El volumen de esta pirámide es también 1/6 u3, por tanto, equivalente a la pirámide tipo Y.
Escena 3. Pirámide triangular tipo Z
1.3 Pirámide tipo X
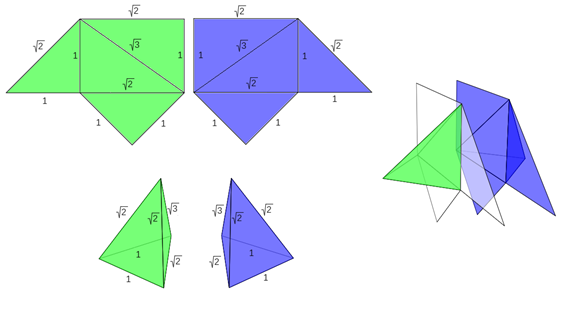
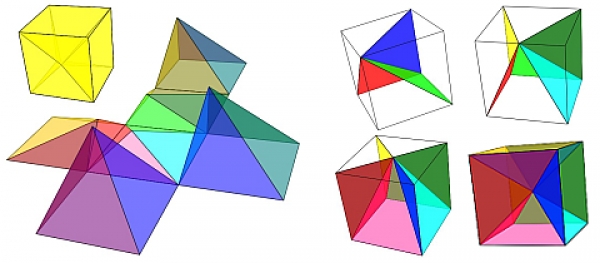
Con las aristas de medidas 1, 1, 1, √2, √2, √3 se pueden construir dos pirámides triangulares siendo una simétrica de la otra (escena 4). Los desarrollos planos son simétricos entre sí. Eligiendo uno de ellos, si se pliega hacia dentro se obtiene una de las pirámides y al plegarlo hacia fuera se obtiene la otra. Ambas tienen volumen 1/6 u3, es decir, son equivalentes entre sí y a las pirámides Y y Z.
También en la parte inferior de dicha figura puede observarse cómo ambas pirámides son simétricas, una respecto a la otra, en el sentido de que si hacen coincidir dos caras que sean iguales el plano que separa a ambas pirámides es un plano de simetría de las mismas. X1 y X2 son, por tanto, congruentes entre sí.
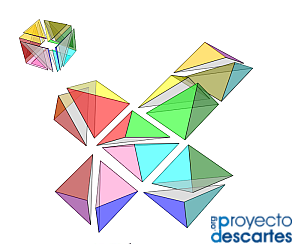
Escena 4. Pirámides triangulares tipo X —X1 en color azul y X2 en color verde—, desarrollo plano de las mismas y simetría de una respecto a la otra
1.4 Particiones del prisma triangular
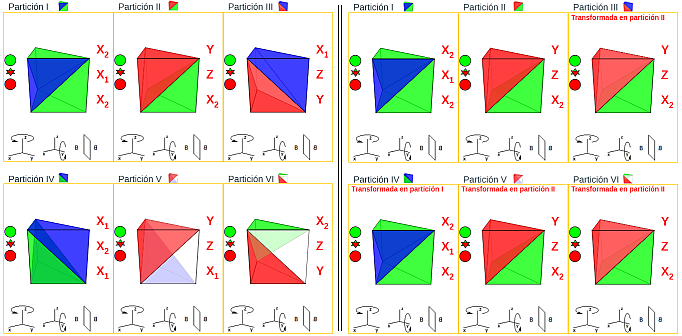
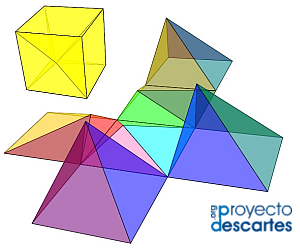
Las seis particiones del prisma reflejadas en la tabla 2 están representadas en la escena 5, donde se han mantenido los colores usados anteriormente en cada tipo de pirámide para así poder distinguir a simple vista cuál es la pirámide utilizada: rojo para tipo Y, blanco para tipo Z, azul para X1 y verde para X2.
Escena 5. Particiones del prisma triangular
No obstante, de esas seis hay solamente dos que no son congruentes entre sí, pues tenemos que se cumplen las siguientes relaciones:
- Las particiones II, III, V y VI son congruentes entre sí:
- La partición tipo V —compuesta por las pirámides Y, Z, X1— es congruente con la III —compuesta por las pirámides X1, Z, Y—, basta realizar un giro de 180⁰.
- La partición VI —compuesta por las pirámides X2, Z, Y— es congruente con la II —compuesta por las pirámides Y, Z, X2— mediante un giro.
- La partición tipo V —compuesta por las pirámides Y, Z, X1— es congruente con la II —compuesta por las pirámides Y, Z, X2— mediante una simetría (según lo indicado con anterioridad Y es simétrica de sí misma, Z también, y X1 es simétrica de X2.
- Las particiones I y IV son congruentes entre sí:
- La partición IV —compuesta por las pirámides X1, X2, X1— es simétrica de la I —compuesta por las pirámides X2, X1, X2—.
Escena 6. Congruencias en las particiones del prisma triangular
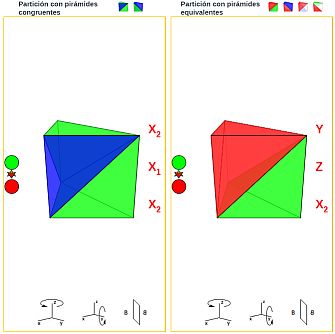
Si nuestro objetivo final es exclusivamente la partición de dicho prisma en pirámides triangulares tendríamos que indicar que, salvo isometrías, sólamente hay dos particiones posibles y, por tanto, bastaría considerar, por ejemplo, la partición I y la II. En ellas, a su vez, en la partición I las pirámides son congruentes entre sí (y consecuentemente equivalentes) y en la II son sólo equivalentes.
Escena 7. Partición del prisma con pirámides congruentes y con pirámides equivalentes
Todo lo analizado en este punto está englobado en el siguiente objeto interactivo: 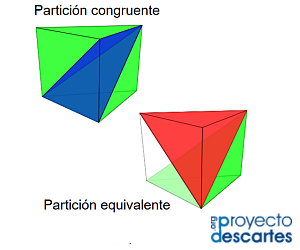
Escena 8. Partición de un prisma triangular en pirámides triangulares equivalentes
2. Partición prismática de un cubo en pirámides triangulares equivalentes
Para abordar la partición prismática del cubo, es decir, su descomposición mediante la unión de dos prismas es necesario tener en cuenta que la orientación de uno de ellos respecto al otro es significativa y consecuentemente hemos de considerar como diferentes las seis particiones del prisma triangular obtenidas en la sección anterior, dado que ellas son el fruto de hacer una distinción entre la cara inferior y la superior del prisma. O bien podemos hacer la lectura de que partiendo de las dos únicas particiones I y II del prisma al aplicarles isometrías tendríamos que son seis las particiones posibles en un prisma al distinguir la cara inferior de la superior.
Seleccionada una de las seis particiones posibles del prisma triangular, al aplicarle isometrías obtendremos otro prisma y los dos juntos conformarán una partición prismática del cubo en seis pirámides triangulares equivalentes. En la tabla 3 se reflejan las posibles transformaciones isométricas a realizar.
 |
 |
 |
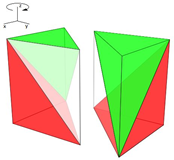 |
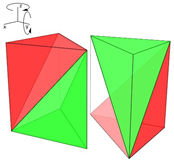 |
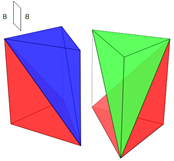 |
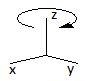
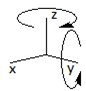
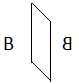
| Giro alrededor del eje Oz | Giro alrededor del eje Oz y del eje Oy | Simetría respecto a un plano |
Tabla 3. Isometrías para obtener un cubo a partir de un prisma triangular
En la tabla 4 se reflejan estas transformaciones aplicadas a cada una de las seis particiones:
| Partición | Giro Oz | Giro Oz, Oy | Simetría |
| I = X2, X1, X2 | X2, X1, X2 = I | X2, X1, X2 = I | X1, X2, X1 = IV |
| II = Y, Z, X2 | Y, Z, X2 = II | X2, Z, Y = VI | Y, Z, X1 = V |
| III = X1, Z, Y | X1, Z, Y = III | Y, Z, X1 = V | X2, Z, Y= VI |
| IV = X1, X2, X1 |
X1, X2, X1 = IV | X1, X2, X1 = IV | X2, X1, X2 = I |
| V = Y, Z, X1 |
Y, Z, X1 = V | X1, Z, Y = III | Y, Z, X2 = II |
| VI = X2, Z, Y | X2, Z, Y = VI | Y, Z, X2 = II | X1, Z, Y = III |
Tabla 4. Isometrías para obtener un cubo a partir de un prisma triangular
Por tanto, las diferentes particiones del cubo en seis pirámides equivalentes se obtienen sin más que hallar las variaciones con repetición de 6 elementos (las seis diferentes particiones del prisma) tomados de dos en dos, es decir, un total de VR6,2=62=36 posibilidades.
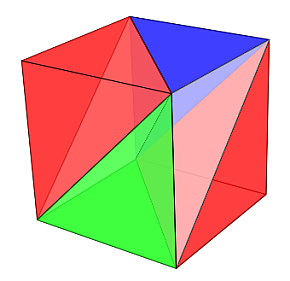
Escena 8. Partición prismática del cubo en pirámides triangulares equivalentes
De partida, al comparar esas 36 posibilidades, se observa que la partición P2-P1 es congruente con la P1-P2 sin más que realizar un giro de 180º alrededor de la vertical (eje Oz) y, por tanto, quedan reducidas a 21 las posibles particiones (combinaciones con repetición CR6,2). Éstan son : {I-I, I-II, I-III, I-IV, I-V, I-VI, II-II, II-III, II-IV, II-V, II-VI, III-III, III-IV, III-V, III-VI, IV-IV, IV-V, IV-VI, V-V, V-VI, VI-VI}. Y en particular, entre ellas, hay tres casos en los que todas las pirámides son congruentes: {I-I, I-IV, IV-IV}.
En la siguiente escena se muestran todas esas particiones:
Escena 9. Partición del cubo con pirámides triangulares equivalentes
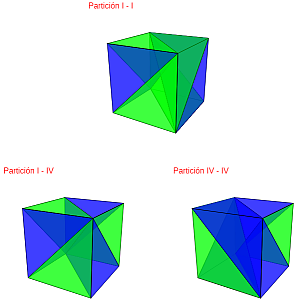
Y en ésta los tres casos en los que hay congruencia entre todas las pirámides.
Escena 10. Partición del cubo con pirámides triangulares congruentes
Pero para finalizar, en lugar de cerrar el tema, quizás sea mejor dejar una pregunta abierta: "Si comparamos las anteriores veintiuna particiones del cubo ¿cuántas son congruentes a su vez entre sí?, es decir, ¿cuántas son diferentes salvo isometrías?"...
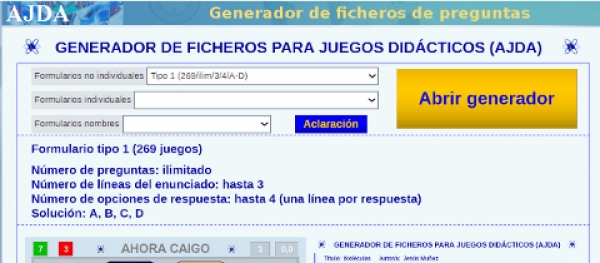
Generador de ficheros de preguntas para juegos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle- Tipo 1: Se trata de preguntas con cuatro opciones de respuesta. Hay 269 juegos que utilizan este tipo de preguntas.
- Tipo 13: Presentan preguntas con seis opciones de respuesta. Hay 7 juegos que utilizan este tipo de preguntas.
- Tipo 19: Las preguntas pueden tener entre 4 y 5 opciones de respuesta. Hay 2 juegos que utilizan este tipo de preguntas.
- Abrir el generador de ficheros de preguntas a través del siguiente enlace de la web del proyecto AJDA.
- Seleccionar el tipo de formulario de preguntas que se quiere generar (tipo 1, 2, 3, individuales....)
- Indicar el nombre del autor, del título de la batería de preguntas y pasar a introducir los contenidos.
- Escribir las preguntas e ir grabando cada una de ellas.
- Generar y guardar el fichero de preguntas con el nombre que queramos.
Particiones del cubo en pirámides (parte II)
Escrito por José R. Galo SánchezLa descomposición de un cubo en pirámides de base triangular surge de manera natural, y fácil, una vez que se han analizado las particiones de un cubo en pirámides de base cuadrada. Basta considerar una de las dos diagonales de dicha base cuadrada para que la pirámide quede partida en dos triangulares. Así pues, toda pirámide cuadrada puede subdividirse de dos formas diferentes en pirámides triangulares, sendas pirámides para sendas diagonales. No obstante, veremos que este procedimiento no conduce a la partición de cardinal mínimo, siendo necesario abordar un planteamiento constructivo independiente para lograrla. Este nuevo esquema nos conducirá a particiones que catalogaremos como no prismáticas o primásticas. Estas últimas serán objeto de un análisis específico en un tercer artículo relativo a este tema.
Particiones de un cubo en pirámides de base triangular
1. Partición mediante descomposición de pirámides de base cuadrada
Si consideramos las diferentes particiones del cubo en pirámides cuadradas obtenidas en el artículo anterior entonces, automáticamente, son conocidas sendas particiones en pirámides triangulares sin más que considerar cada una de las dos diagonales del cuadrado que constituye la base en cada pirámide. Además, las dos subpirámides obtenidas serán equivalentes (con igual volumen), pues la base inicial cuadrada ha quedado dividida en dos partes iguales y la altura es común a ambas y, por tanto, el volumen de cada una de esas pirámides triangulares es la mitad del volumen inicial. En este contexto tendríamos las siguientes situaciones:
- Considerando la partición mínima del cubo en tres pirámides cuadradas obtendríamos una subpartición en seis pirámides triangulares equivalentes. Dado que cada una de esas pirámides cuadradas pueden dividirse de dos formas diferentes, según cual sea la diagonal del cuadrado que se considere, tendríamos a su vez varias posibilidades:
- Si la diagonal que se considera conduce a dividir la pirámides cuadradas por su plano de simetría, entonces las seis pirámides son congruentes ya que hay tres coincidentes entre sí mediante traslación y giro (lo que de manera simplificada se suele indicar como iguales) y las otras tres son simétricas de las primeras ―denotaremos a una de las pirámides como tipo X1 y a su simétrica como X2―. la partición sería {X1, X2, X1, X2, X1, X2} Este caso es el que usualmente puede encontrarse en las fuentes literarias clásicas y en la Web. Veremos que es una situación particular del estudio global, que abordaremos en otro articulo, correspondiente a lo que denominaremos particiones prismáticas porque agrupando esas pirámides de tres en tres el cubo queda descompuesto en dos prismas triangulares.
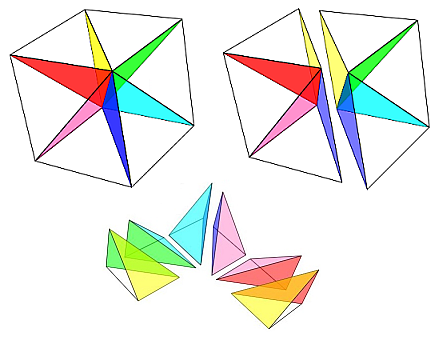
Escena 1. Partición prismática del cubo en seis pirámides triangulares congruentes
(Haz clic en la imagen para acceder al recurso interactivo)
Este proceso de división podría repetirse considerando la mediana de las nuevas bases y así obtendríamos una partición con doce pirámides equivalentes y dos familias de 6 pirámides congruentes entres sí; y con una nueva fracción por la mediana serían 24 pirámides equivalentes y 4 familias congruentes y, en general 3·2n pirámides equivalentes y 2n-1 familias de pirámides congruentes entre sí. Un entretenimiento teórico bonito, pero que físicamente su traslación a un contexto manipulativo rápidamente no es viable.
- Si se considera la diagonal perpendicular al plano de simetría, cada pirámide cuadrada queda divida en dos pirámides equivalentes. La partición cuenta con dos tipos de pirámides que denotaremos como tipo Y (la que cuenta con un triedro trirrectángulo) y la otra que nombraremos tipo Z. La partición es {Y, Z, Y, Z, Y, Z}. Esta partición, a diferencia del caso anterior no es prismática.
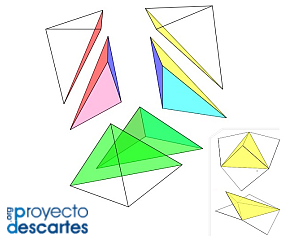
Escena 2. Partición no prismática del cubo en seis pirámides triangulares equivalentes
- Si se combinan las dos posibilidades anteriores se obtienen siempre seis pirámides equivalentes y habría dos posibilidades: {X1, X2, X1, X2, Y, Z} o {X1, Y, Z, X2, Y, Z}, siendo ambas también particiones prismáticas.
- Si la diagonal que se considera conduce a dividir la pirámides cuadradas por su plano de simetría, entonces las seis pirámides son congruentes ya que hay tres coincidentes entre sí mediante traslación y giro (lo que de manera simplificada se suele indicar como iguales) y las otras tres son simétricas de las primeras ―denotaremos a una de las pirámides como tipo X1 y a su simétrica como X2―. la partición sería {X1, X2, X1, X2, X1, X2} Este caso es el que usualmente puede encontrarse en las fuentes literarias clásicas y en la Web. Veremos que es una situación particular del estudio global, que abordaremos en otro articulo, correspondiente a lo que denominaremos particiones prismáticas porque agrupando esas pirámides de tres en tres el cubo queda descompuesto en dos prismas triangulares.
- Análogamente, en el caso de hacer tambien sólo una subdivisión por cada pirámide cuadrada, la partición en cuatro pirámides cuadradas se convertiría en ocho triangulares, la de cinco en diez y la de seis en doce.
En la siguiente escena se aborda de manera general la partición del cubo en pirámides triangulares a partir de las particiones del mismo en pirámides cuadradas:
Escena 3. Partición del cubo en pirámides triangulares por división de pirámides cuadradas. Caso general.
Todas las situaciones anteriores son, o pueden considerarse, interesantes y conducentes a puzles de cierta dificultad tanto en los casos en los que se busca la máxima congruencia o regularidad, como en la posición contraria. Pero ninguna de ellas conduce a la partición con cardinal mínimo, pues el planteamiento realizado viene condicionado por la partición previa en pirámides de base cuadrada. La partición mínima, como veremos en la próxima sección, se corresponde con cinco pirámides y salvo isometrías hay una única posibilidad para su construcción. Por ello, nuestro centro de interés se focalizará en la antes citada descomposición prismática del cubo en seis pirámides triangulares equivalentes, que sin ser el caso único de cardinal mínimo sí que genera una variedad de situaciones que nos proponemos cuantificar y detallar.
2. Partición mediante construcción específica
En esta sección partiendo de un cubo de vértices {A, B, C, D, E, F, G, H}, nos planteamos realizar una partición del mismo en pirámides triangulares buscando, por un lado, que la descomposición tenga cardinal mínimo y, por otro, buscando alternativas en las que sin ser de cardinal minimo se encuentren congruencias o equivalencias.
Dado que las pirámides triangulares son poliedros convexos con cuatro caras triangulares (es decir tetraedros) y cuatro vértices, en la planificación de esta partición han de tenerse en consideración las siguientes observaciones:
- Las caras del cubo han de dividirse en triángulos y, por tanto, se parte de un mínimo de 12 triángulos (2 por cada cara del cubo) y 18 segmentos (las doce aristas del cubo, más seis diagonales necesarias para partir cada una de las seis caras del cubo), que junto a los ocho vértices constituyen los elementos primarios a partir de los cuales se han de construir las pirámides de la partición.
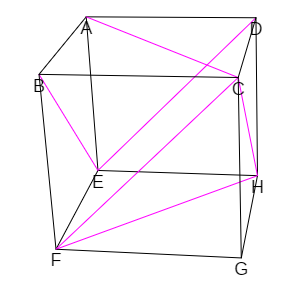
Escena 4. Una posible elección de los elementos primarios para realizar la partición
- El menor número de pirámides se obtiene cuando se consideran exclusivamente los elementos primarios citados. La introducción de cualquier vértice o segmento adicional generará un mayor número de combinaciones posibles, un mayor número de pirámides.
- Dos pirámides de la partición pueden compartir como máximo tres vértices, una cara. O lo que es equivalente han de tener tres caras diferentes.
- Una pirámide triangular de la partición queda determinada sin más que elegir dos segmentos con distinta dirección no coplanarios.
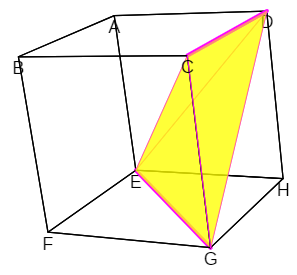
Escena 5. Pirámide triangular determinada por dos segmentos con distinta dirección no coplanarios
- Cuando todas las diagonales correspondientes a las caras opuestas tienen distinta dirección las particiones en pirámides triangulares tienen más de seis pirámides, salvo:
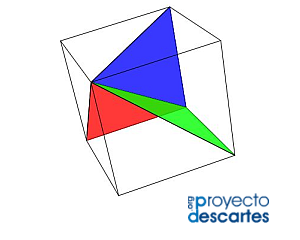
- Una partición con cinco elementos, que es la de cardenal mínimo, formada por cuatro pirámides trirrectángulas y un tetraedro regular.
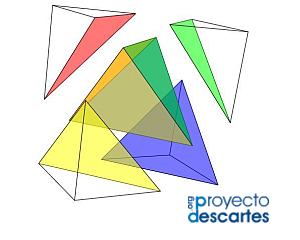
Escena 6. División del cubo en cinco prismas triangulares
- Una partición con seis elementos, que es la partición no prismática indicada antes en la escena 2 y compuesta por las pirámides {Y, Z, Y, Z, Y, Z}.
- Una partición con cinco elementos, que es la de cardenal mínimo, formada por cuatro pirámides trirrectángulas y un tetraedro regular.
- Cuando al menos un par de las diagonales correspondientes a caras opuestas tienen la misma dirección, entonces ese par junto a las dos aristas que son perpendiculares a ellas, forman un rectángulo y la partición en pirámides triangulares es posible sólo si se introduce al menos un segmento que bien subdivida ese rectángulo en dos triángulos o bien que lo corte. Al introducirse en la partición un nuevo elemento primario no puede obtenerse la partición de cardinal mínimo.
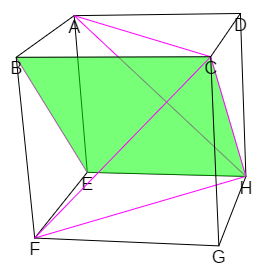
Escena 7. Diagonales coplanarias
Ese segmento adicional puede ser:
- Una diagonal del cubo. Aquí la obtención de una partición obliga a incluir nuevos elementos primarios, puntos y segmentos, y consecuentemente se incrementa el número de pirámides obtenidas.
- La diagonal de ese rectángulo. En este caso el cubo queda dividido en dos prismas triangulares rectos con bases que son triángulos rectángulos isósceles. En esta situación diremos que la partición del cubo es prismática y veremos que conduce a un mínimo de seis pirámides triangulares; y en el caso de ser exactamente seis se cumple que siempre son equivalentes, es decir, que tienen igual volumen.
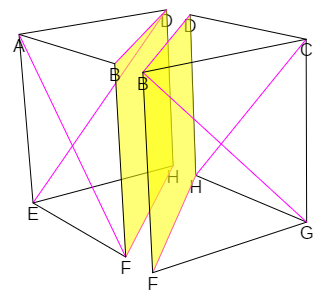
Escena 8. División del cubo en dos prismas triangulares
Así pues, nuestro análisis nos conduce a plantearnos la partición del cubo a través de la descomposición de un prisma triangular en pirámides triangulares. Éste puede ser un buen tema para detallar en un próximo artículo, y ello es mi propósito, confiando en que habrá colegas interesados en seguir comprobando como algo que parece tan simple, la descomposición de un cubo, no lo es tanto y aporta mucho juego, interés, conocimiento y belleza matemática. Por aquí ¡os espero pronto!
Más...
Descripción de los juegos didácticos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle- Carátula del juego. Al pulsar sobre la misma se muestra una captura de pantalla del juego.
- Reglas del juego. Se presenta la descripción, dinámica y objetivo del juego.
- Documentos de registro. Apartado en el que se pueden descargar formularios de registro de respuestas y de resultado de los jugadores.
- Tabla con las principales características del juego.
- Autoría y licencia de uso.
- En la primera ventana se selecciona la modalidad de introducción de preguntas en el juego: mediante fichero, oral, a mano al principio del juego, generadas por el juego y sin preguntas. Esta ventana no aparecerá si el juego dispone de una sola modalidad de introducción de preguntas.
- En la segunda ventana se deben introducir los datos de los jugadores y las opciones de configuración del juego. Estas opciones pueden ser específicas del juego tales como: número de jugadores, orden de aparición de las preguntas, tiempo, sorteo de orden de participación de los jugadores, etc., o opciones generales (se encuentran en un menú superior visible durante todo el trascurso del juego) y son del tipo: reinicio del juego, sonido, idioma, registro de resultados, etc.
- Si se ha elegido la modalidad de introducción de preguntas a través de ficheros, se mostrará una tercera ventana para cargar el fichero de preguntas de distintas formas: arrastrando el fichero, seleccionando el archivo a través del explorador del navegador, escribiendo su nombre o URL o a través de listas desplegables de repositorios.
- A continuación y tras pulsar en el botón Jugar comienza el juego con la dinámica propia del mismo.
Particiones del cubo en pirámides (parte I)
Escrito por José R. Galo SánchezEl estudio y búsqueda de regularidades o propiedades en cualquier objeto puede abordarse desde diferentes perspectivas. Una de ellas es proceder a la disección o descomposición buscando desentrañar el interior o lo particular para comprender el exterior o la globalidad. La máxima aristotélica de que el todo es más que la suma de sus partes no queda contradicha por acudir al hecho de realizar una partición —matemáticamente descomponer un conjunto como unión de subconjuntos cuyas intersecciones tienen medida nula—, sino que metodológica o procedimentalmente es un medio humanamente asequible con el que dar un primer paso a través del cual buscar y tratar de abarcar, en un posterior análisis global, ese todo a partir de sus partes. En esta línea, en este artículo, mostraremos con recursos interactivos algunas particiones usuales de un cubo en pirámides con base cuadrada y comprobaremos como todos esos casos son situaciones particulares de una partición general basada en nueve puntos (los vértices del cubo y un adicional).
El motivo para elegir una determinada partición de la infinidad de particiones posibles y hacerla distinguible del resto puede sustentarse en diversos criterios u objetivos, pero usualmente suelen marcarse pautas como que la partición tenga el menor número de elementos o que sea lo más regular posible, es decir, que las partes sean iguales o congruentes —que coincidan mediante una composición de isometrías (traslaciones, giros o simetrías)— o equivalentes —con igual medida— o cualquier otro parámetro que sea atractivo para quien busque adentrarse en este contexto. Pero la elección también podría estar marcada por criterios opuestos o diferentes a los anteriores. Si pensamos en que la reconstrucción del cubo a partir de las piezas de una partición es un entretenimiento usual, catalogado como rompecabezas o puzle, el diseñador del mismo puede perseguir que todas las piezas sean iguales o plantarse en la situación opuesta de que todas sean diferentes. La dificultad o sencillez, la mayor o menor belleza del modelo obtenido tiene más componente subjetivo que objetivo; pero la belleza matemática siempre estará implícita en todos y cada unos de los planteamientos realizados, al ser medios y soportes conducentes a la extracción y obtención del conocimiento.
En este artículo analizaremos la partición de un cubo en pirámides de base cuadrada y en un artículo posterior nos adentraremos en la partición en pirámides de base triangular (tetraedros aunque no necesariamente regulares).
Particiones de un cubo en pirámides de base cuadrada
Posicionándonos y atendiendo al criterio de que la partición tenga cardinal mínimo o que sea lo menor posible y adicionalmente que sus componentes sean regulares o que sean lo más similares entre sí, podemos encontrar cuatro situaciones, que son las que usualmente se muestran y divulgan, y que reflejaremos en sendos recursos interactivos. En ellos se conjugará la virtualidad digital con la posibilidad de contruir el modelo respectivo de forma tangible, a lo que animamos e invitamos a todos.
1. Tres pirámides cuadradas iguales.
Este caso se corresponde con la partición con cardinal mínimo. Las tres pirámides comparten la misma cúspide y son iguales. Esta partición suele tomarse como base para mostrar que el volumen de una piramide es la tercera parte del área de su base por su altura, pero no nos adentraremos en ese objetivo.
Haz clic en la imagen para acceder al recurso interactivo
2. Cuatro pirámides cuadradas iguales dos a dos.
Esta partición se caracteriza porque las cuatro pirámides también comparten la misma cúspide y son iguales dos a dos.
Haz clic en la imagen para acceder al recurso interactivo
3. Cinco pirámides cuadradas, cuatro iguales y una desigual que es regular.
Aquí las cinco pirámides vuelven a tener la misma cúspide.
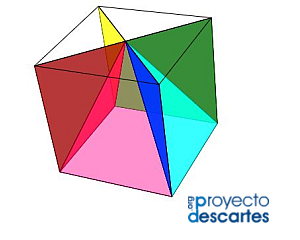 Haz clic en la imagen para acceder al recurso interactivo
Haz clic en la imagen para acceder al recurso interactivo
4. Seis pirámides cuadradas regulares e iguales.
Todas las pirámides comparten la misma cúspide y todas son regulares e iguales (congruentes).
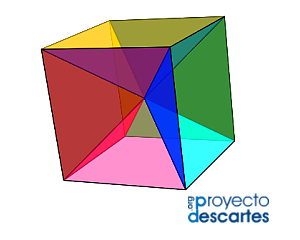 Haz clic en la imagen para acceder al recurso interactivo
Haz clic en la imagen para acceder al recurso interactivo
Todos los casos anteriores son los ejemplos que usualmente se suelen mostrar en múltiples contextos por su simplicidad y belleza. Pero, como hemos indicado, la belleza también puede alcanzarse a través de un análisis global en el que los casos anteriores no sean más que un caso particular de una situación general, y donde la diversidad y la diferencia sean la pauta a lograr. En ese empeño, a continuación, mostraremos de manera razonada y constructiva cómo abordar una partición del cubo en pirámides de base cuadrada, y adicionalmente se podrá observar digital y analógicamente apoyándonos en un nuevo recurso interactivo.
Generalización de la partición del cubo en pirámides cuadradas
Para construir una partición del cubo en pirámides cuadradas es necesario, obligatorio, utilizar los ocho vértices del cubo y las doce aristas del mismo, y adicionalmente hay que seleccionar o marcar cuál o cuáles serán las cúspides de las pirámides a construir. La introducción de puntos adicionales a los vértices hará que aumente el número de combinaciones de cinco puntos que pueden realizarse y consecuentemente podrá incrementarse el número de pirámides de la partición (no todas las combinaciones posibles de vértices son viables para obtener una partición del cubo). Así pues, analicemos diferentes alternativas:
- No incluir ningún punto adicional.
Esta elección obliga a que la cúspide de cada pirámide sea uno de los vértices del cubo y si además imponemos que todas las pirámides compartan la misma cúspide entonces obviamente obtendremos la partición de cardinal mínimo. Este plantemiento es viable pues basta seleccionar un vértice del cubo y desde él trazar segmentos a cada uno de los otros siete vértices, ello conduce a la partición en tres pirámides que ha sido reflejada en el primer caso descrito en este artículo. La partición es única pues, se elija el vértice que se elija, todas las particiones son congruentes mediante giros. - Añadir un punto adicional.
Este punto sería la cúspide común de todas las pirámides a construir para que así el número de éstas sea lo menor posible y constructivamente se procede igual que en el caso anterior trazando segmentos desde la cúspide común a los vértices del cubo. Dicho punto adicional ha de pertenecer al cubo, bien a su interior o a la frontera y por tanto podemos distinguir las siguientes situaciones:- Punto perteneciente a una arista. Aquí obtendremos una partición compuesta por cuatro pirámides. En general las cuatro son distintas, pero entre dos de ellas se da siempre una congruencia (una es simétrica de la otra). Y hay un caso particular en el que las pirámides son iguales dos a dos, que es el segundo caso expuesto en la sección anterior, y que acontece cuando el punto adicional considerado es el punto medio de la arista.
La arista a la que pertenezca el punto no introduce ninguna variación. Todas serán situaciones congruentes. - Punto perteneciente a una cara. Este caso conduce a la partición en cinco pirámides y de las infinitas posibilidades la situación con más regularidad es cuando el punto elegido es el punto donde se intersecan las diagonales de la cara. Es el tercer caso expuesto con anterioridad.
La partición, salvo isometrías, es independiente de la cara seleccionada - Punto perteneciente al interior del cubo. Esta situación hace que sean seis pirámides las que forman la partición. De las infinitas particiones posibles, cuando el punto seleccionado es el punto de intersección de las diagonales del cubo se tiene que las seis pirámides son iguales y regulares, éste es el cuarto caso mostrado antes.
- Punto perteneciente a una arista. Aquí obtendremos una partición compuesta por cuatro pirámides. En general las cuatro son distintas, pero entre dos de ellas se da siempre una congruencia (una es simétrica de la otra). Y hay un caso particular en el que las pirámides son iguales dos a dos, que es el segundo caso expuesto en la sección anterior, y que acontece cuando el punto adicional considerado es el punto medio de la arista.
En el siguiente objeto interactivo puede experimentarse y verse todo lo indicado.
Haz clic en la imagen para acceder al recurso interactivo
En un próximo artículo nos adentraremos en la partición de un cubo en pirámides triangulares.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)









 CONTACTO
CONTACTO
