En el punto anterior hemos definido la velocidad instantánea como un límite de un cociente entre la variación de la concentración de los reactivos en un tiempo determinado cuando este tiempo tiende a cero. Es fácil ver (con conocimientos básicos de matemáticas) que esta relación es justamente la derivada de la concentración respecto del tiempo:![]()
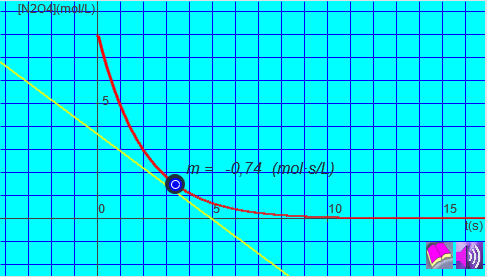
Si recuerdas la interpretación geométrica de la derivada sabrás que la pendiente de la recta tangente a la curva en un punto es igual a la derivada de la función en ese punto.
Supongamos que estudiamos la reacción de formación del amoníaco:
![]()
Si nos fijamos en la variación en la concentración de uno de los reactivos (el nitrógeno), podemos escribir la expresión de la velocidad instantánea del siguiente modo:![]()
El signo negativo significa que el reactivo está desapareciendo.
Pero esta misma velocidad la podemos escribir en función del resto de sustancias intervinientes en la reacción. Si tenemos en cuenta que por cada molécula de nitrógeno desaparecen 3 de hidrógeno, también será cierto que la velocidad de desaparición del hidrógeno es tres veces superior a la del nitrógeno, por tanto:![]()
Y por la misma razón, también podemos escribir la ecuación anterior en función de las variaciones de concentración de los productos:![]()
En el laboratorio, la velocidad de una reacción se calcula midiendo la concentración de alguna de las sustancias intervinientes en diferentes tiempos. Una vez llevados los valores a una gráfica, podemos calcular la pendiente de la tangente en diferentes puntos para conocer la velocidad instantánea en cada momento.