Descubre el Proyecto PI de la RED Descartes
Escrito por Montserrat Gelis BoschEl Proyecto PI, desarrollado por la RED Descartes, ofrece una completa colección de recursos educativos digitales e interactivos para la Educación Primaria, centrados en dos áreas clave: Lengua Castellana y Matemáticas.
Estos materiales están especialmente diseñados para fomentar el aprendizaje autónomo y activo del alumnado, tanto en el aula como en casa. Se pueden utilizar con pizarras digitales, ordenadores o tabletas, y todos ellos se encuentran disponibles de forma gratuita.
Estructura de las unidades:
Cada unidad del Proyecto PI sigue una estructura común, que facilita el trabajo progresivo de los contenidos:
- Introducción: se presentan los conceptos básicos a través de explicaciones claras y ejemplos visuales.
- Exploración: se proponen actividades guiadas para afianzar el aprendizaje paso a paso.
- Ejercicios: serie de actividades interactivas para practicar y comprobar los resultados.
- Evaluación: ejercicios finales con autocorrección que permiten valorar lo aprendido.
Esta estructura coherente favorece la comprensión, el refuerzo y la evaluación de los contenidos trabajados.
En el vídeo que acompaña este artículo, se realiza un breve recorrido por la página web del proyecto y se exploran dos ejemplos concretos, uno por cada área:
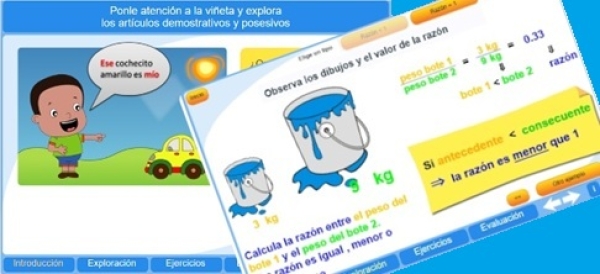
- En el área de Matemáticas, se accede al tema Medidas y se muestra la unidad Razones, donde se aprende a calcular razones y resolver problemas aplicando este concepto.
- En el área de Lengua Castellana, dentro del tema Vocabulario, se presenta la unidad Artículos, demostrativos y posesivos, que trabaja el uso correcto de estas palabras a través de explicaciones, ejemplos y ejercicios interactivos.
El Proyecto PI es una herramienta valiosa para docentes, familias y alumnado. Te invitamos a explorar sus múltiples unidades y a integrar estos recursos en tu práctica educativa diaria.
¡Aprender puede ser interactivo, dinámico y muy motivador!
Puedes ver el vídeo a continuación para conocer mejor este proyecto.
Cómo Buscar Recursos en la RED Descartes Usando Palabras Clave
Escrito por Montserrat Gelis BoschLa RED Descartes es una plataforma educativa que ofrece una gran cantidad de recursos interactivos en áreas como matemáticas, física, química y ciencias sociales. Estos materiales son ideales para estudiantes y docentes que buscan herramientas dinámicas para el aprendizaje.
Para aprovechar al máximo esta plataforma, es fundamental saber cómo encontrar los recursos adecuados de manera rápida y eficiente. Por ello, en este artículo hemos preparado un vídeo tutorial en el que se explica cómo utilizar el buscador de la RED Descartes para localizar materiales específicos a partir de palabras clave.
¿Qué encontrarás en el vídeo?
-
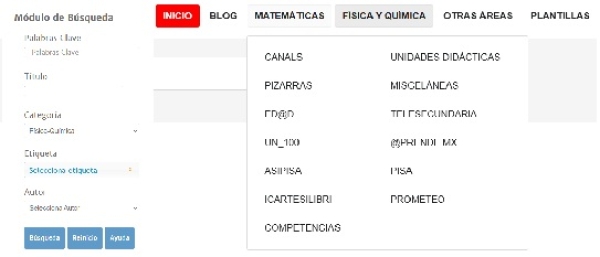
- Explorar el menú principal de la RED Descartes y las diferentes áreas de conocimiento.
- Usar el buscador de palabras clave para encontrar recursos específicos.
- Acceder a materiales interactivos de matemáticas, física, química y otras áreas.
- Descubrir cómo se estructuran estos recursos, incluyendo explicaciones teóricas, ejemplos prácticos y autoevaluaciones.
Ejemplos prácticos que mostramos
-
- Matemáticas: Buscamos el término “álgebra” y accedemos a una unidad sobre productos notables del proyecto Prometeo.
- Física y Química: Escribimos “movimiento” y exploramos un recurso sobre el movimiento de la pelota, donde podemos modificar variables como el peso, la velocidad y el ángulo de lanzamiento.
- Ciencias Sociales: Introducimos la palabra “mapas” y encontramos un libro digital interactivo sobre interpretación de diferentes tipos de mapas.
Mira el vídeo aquí:
Con esta guía, podrás sacar el máximo provecho de la RED Descartes y acceder a una gran variedad de materiales educativos de forma sencilla. Espero que el vídeo te ayude a encontrar fácilmente recursos útiles para tu enseñanza o aprendizaje.
Proyecto Canals: Matemáticas manipulativas e interactivas
Escrito por Montserrat Gelis BoschMaría Antonia Canals fue una destacada profesora y pedagoga que dedicó su vida a la enseñanza de las matemáticas a través de materiales manipulativos y juegos didácticos. Desde la exploración concreta hasta la comprensión abstracta, su legado ha inspirado a generaciones de docentes y alumnos.
La Red Descartes ha desarrollado el Proyecto Canals, una colección de objetos de aprendizaje interactivos basados en sus propuestas, que permite explorar las matemáticas de manera visual y dinámica. Estos materiales están dirigidos a las etapas de infantil, primaria y el primer ciclo de secundaria.
En la página del proyecto, los recursos están clasificados por temas y niveles. En este vídeo, te mostramos una pequeña muestra de ellos, organizada en cinco grandes áreas: cálculo, estadística, geometría, lógica y resolución de problemas. Las unidades seleccionadas son:
 |
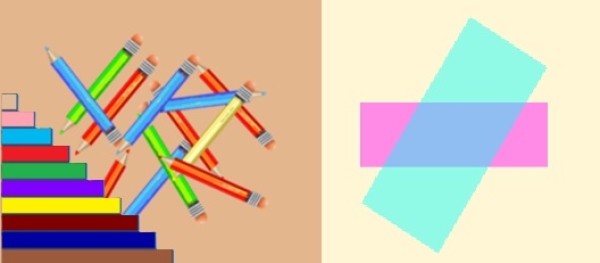
Regletas numéricas (Cálculo): La escena simula unos listones de madera de colores que representan los diez primeros números naturales. A través de una serie de preguntas, se busca que el estudiante se familiarice con estos números, distinga entre pares e impares y realice operaciones básicas.
|
|
|
Interpretación de gráficos (Estadística): Se presentan datos en forma de tabla junto con preguntas que invitan a analizarlos y a elaborar gráficas a partir de ellos. Con esta actividad, se pretende que el estudiante aprenda a leer e interpretar correctamente tablas y gráficos.
|
|
|
Cuadriláteros (Geometría): La escena simula la intersección de dos bandas de colores que generan diferentes cuadriláteros. El estudiante debe identificarlos y reconocer algunas de sus propiedades.
|
|
|
El inicio de la negación (Lógica): Se presentan diferentes objetos en una tabla, y el estudiante debe indicar si cumplen una determinada cualidad, ya sea mediante una afirmación o una negación.
|
|
|
Problemas lógicos para resolver con tablas (Resolución de problemas): En esta actividad, el estudiante debe analizar una serie de pistas para identificar correctamente una serie de datos, desarrollando así su capacidad de razonamiento lógico.
|
A través de estas actividades interactivas, los estudiantes pueden experimentar y comprender conceptos matemáticos de forma intuitiva y divertida. Te invitamos a ver el vídeo y descubrir cómo el Proyecto Canals puede enriquecer la enseñanza y el aprendizaje de las matemáticas. ¡Explora estos recursos y disfrútalos en el aula!
Transformando el Aprendizaje con las Unidades Interactivas de PISA 2017
Escrito por Montserrat Gelis BoschEl presente artículo tiene como objetivo analizar en detalle la unidad interactiva "Tráfico", desarrollada dentro del proyecto Competencias de la RED Descartes y perteneciente al grupo PISA2017.
En este grupo se incluyen unidades adaptadas y enriquecidas a partir de las unidades liberadas del Programa para la Evaluación Internacional de Estudiantes (PISA), abarcando áreas como Ciencias, Comprensión Lectora, Finanzas, Matemáticas y Resolución de Problemas. El objetivo principal de los materiales del grupo PISA2017 es transformar las unidades liberadas originales de PISA en recursos educativos interactivos diseñados para fomentar tanto el aprendizaje autónomo como el guiado.
Estas unidades incorporan correcciones y mejoras, así como funcionalidades adicionales como:
- Interactividad para una mayor participación del estudiante.
- Correcciones automatizadas.
- Opciones para enviar los resultados al tutor.
La versión original de cada unidad se mantiene disponible para comparación y referencia, proporcionando a los usuarios una perspectiva completa del proceso de adaptación y mejora.
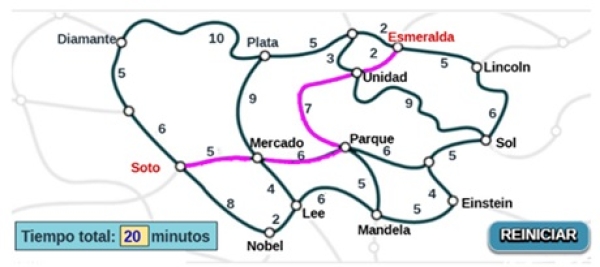
La unidad "Tráfico" pertenece al apartado de Resolución de Problemas y plantea situaciones del mundo real relacionadas con la gestión del tráfico vehicular. En su versión interactiva, esta unidad busca desarrollar habilidades como:
- Análisis y síntesis de información.
- Modelado matemático.
- Toma de decisiones fundamentadas.
La estructura de la unidad incluye:
- Presentación del problema: Introducción de una situación contextualizada, por ejemplo, el diseño de rutas óptimas para minimizar el tiempo de viaje o el consumo de combustible.
- Actividades interactivas: Ejercicios en los que los estudiantes pueden manipular variables, observar resultados en tiempo real y comprobar sus respuestas.
- Retroalimentación inmediata: Corrección automática de las respuestas con explicaciones detalladas.
- Opciones de seguimiento: Posibilidad de enviar los resultados y observaciones al tutor para un análisis posterior.
La unidad "Tráfico" del grupo PISA2017 es un excelente ejemplo de cómo la tecnología puede transformar materiales educativos en recursos interactivos que fomenten el aprendizaje significativo. Este tipo de iniciativas no solo modernizan la enseñanza, sino que también promueven el desarrollo de competencias esenciales en los estudiantes.
En el análisis del impacto de estas unidades, es evidente que la combinación de interactividad, contextualización y retroalimentación inmediata contribuye significativamente a la mejora del proceso de enseñanza-aprendizaje.
Para explorar la unidad "Tráfico" y otras unidades desarrolladas por el grupo PISA2017, te invitamos a visitar la plataforma de la red Descartes. Comparte esta experiencia con tus estudiantes y fomenta en ellos el desarrollo de habilidades que les permitirán enfrentar los retos del mundo real con confianza y competencia.
Más...
Explorando el Análisis de Funciones: Recursos Interactivos para el Último Curso de Bachillerato 2024
Escrito por Montserrat Gelis BoschEn este artículo se presenta Cálculo Diferencial e Integral, una colección de objetos interactivos independientes diseñados para explorar el análisis de funciones, incluyendo conceptos clave como derivadas e integrales, dirigidos al último curso de bachillerato en España y al tercer grado de preparatoria en México.
Los materiales forman parte del grupo de Recursos Educativos Interactivos de Matemáticas para el Bachillerato del Proyecto Prometeo, de la RED Descartes, impulsado por la Dirección General de Evaluación Educativa (DGEE), la Dirección General de Cómputo y Tecnologías de Información y Comunicación (DGTIC), y el Instituto de Matemáticas de la UNAM que abarca los contenidos de Matemáticas del sistema educativo mexicano para tres grados (equivalentes a 4º de ESO y 1º y 2º de Bachillerato).
Estos objetos han sido diseñados de manera autónoma, desde unidades teóricas hasta actividades eminentemente prácticas, permitiendo al profesorado seleccionar aquellos que considere necesarios para incorporarlos como contenido del curso, material de repaso o recursos de ampliación, dirigidos al último curso de bachillerato en España y al tercer grado de preparatoria en México.
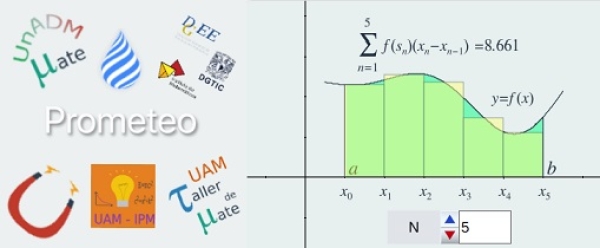
Por ejemplo, la unidad Límite de una sucesión combina definiciones clave con escenas interactivas para reforzar el concepto. Para el cálculo de límites, se ofrecen seis unidades que abordan distintas estrategias y situaciones, con ejercicios variados. También encontramos materiales para el cálculo de derivadas e integrales, con definiciones, ejemplos y ejercicios de cálculo. Además, se exploran aplicaciones prácticas, como el cálculo de máximos y mínimos mediante derivadas, y el cálculo de áreas con integrales, siempre con ejemplos y ejercicios para practicar.
Esta clasificación permite al alumnado y al profesorado abordar el aprendizaje de manera flexible y personalizada, asegurando una comprensión sólida de los conceptos y la práctica de habilidades clave. La incorporación de estos objetos interactivos al estudio del cálculo diferencial e integral fomenta un aprendizaje más dinámico, autónomo y adaptado a las necesidades individuales. Al proporcionar una estructura modular y recursos variados, se promueve tanto la adquisición de competencias básicas como el desarrollo de habilidades avanzadas, logrando que los estudiantes conecten la teoría con su aplicación práctica de forma efectiva y significativa.
En el siguiente vídeo se presenta una pequeña muestra de estos recursos.
Explora el Poder de la Red Descartes: Crea Contenedores Personalizados
Escrito por Montserrat Gelis Bosch¿Quieres trabajar un tema específico en el aula? ¿Tienes varios recursos interactivos y deseas presentarlos como una unidad cohesionada? Te proponemos utilizar el contenedor de actividades del proyecto Plantillas de la RED Descartes.
El proyecto Plantillas ofrece una colección de materiales interactivos que pueden adaptarse fácilmente mediante pequeños ajustes, sin necesidad de tener conocimientos avanzados de programación o edición de código.
En la sección de materiales, se puede acceder a distintos tipos de plantillas:
- Objetos interactivos: Juegos, actividades de selección, asociación, emparejamiento, puzles, identificación de partes, vídeos interactivos y miscelánea.
- Libros interactivos
- Contenedores: Para actividades y plantillas.
En este artículo, te explicaremos cómo modificar la plantilla de contenedor de actividades para crear una unidad con varias actividades de álgebra de la RED Descartes, usando las siguientes unidades:
Para empezar, selecciona “contenedores” en la sección de materiales. Allí verás una imagen de los diferentes tipos de contenedores, para cada plantilla tienes un enlace a un documento PDF con instrucciones para modificarla y un archivo comprimido para descargar la plantilla. En este caso seleccionaremos contenedor de actividades.
Paso a paso para la modificación:
- Descarga el archivo comprimido y extrae el contenido. Verás varias carpetas necesarias para el funcionamiento de la plantilla, pero solo necesitarás modificar el archivo indexb.
- Abre el archivo indexb con un editor de texto, como el Bloc de notas, o un editor de código. Dirígete al final de la página para realizar las siguientes modificaciones:
- Especifica el número de actividades (en este caso, seis).
- Añade el nombre y la dirección de cada actividad, en el mismo orden que aparecen en la lista anterior.
- Guarda los cambios y abre indexb haciendo doble clic para comprobar que las actividades se muestran correctamente.
Esta plantilla también puede subirse a un servidor web, desde el cual se podrá acceder a la actividad.
A continuación, puedes ver un vídeo que muestra en detalle todo el proceso, incluyendo cómo subir esta actividad a un curso en Moodle.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)





 CONTACTO
CONTACTO
