¿Conoces el Proyecto Plantillas?

Se trata de una propuesta de la RED Descartes que contiene múltiples y diversos recursos. La particularidad de este proyecto reside en la facilidad con que se pueden modificar los materiales para adaptarlos a las necesidades del profesorado, generando actividades mediante simples cambios de imágenes o textos, sin necesidad de conocer lenguaje de programación.

En la página del proyecto encontramos toda la información sobre estos recursos e indicaciones para modificarlos, un manual en formato pdf y una serie de vídeos en los cuales se explican los pasos a seguir para modificar cada uno de los tipos de actividades que podemos encontrar.

A modo de ejemplo, en este vídeo vamos a modificar el conocido juego del ahorcado. En la plantilla original se proponen distintas capitales de América, nosotros substituiremos las capitales por conceptos que hagan referencia a triángulos. Una vez modificado el recurso, vamos a ver cómo subir estos materiales en nuestra aula virtual moodle para su aplicación en el aula.

Hoy vamos a reportar la unidad de 2ºESO Fracciones que es válida tanto para la LOMCE como para la LOE:

Hemos tratado los siguientes epígrafes:

1. Fracciones
   Fracciones Equivalentes
   Simplificación de Fracciones
   
2.Fracciones con igual denominador
   Reducción a común denominador
   Comparación de fracciones
   
3.Operaciones con fracciones
   Suma y resta
   Producto
   Cociente
   Potencia
   Raíz cuadrada
   Operaciones combinadas
   
4.Aplicaciones
   Problemas de aplicación

Esta semana presentamos una serie de actividades que forman parte del grupo de objetos PISA con ordenador, incluido en el Proyecto Competencias de la RED Descartes. Estos recursos están estructurados como objetos de aprendizaje y se han creado a partir  del conjunto de preguntas liberadas en la edición PISA 2015, en la cual se introdujo la evaluación por medios informáticos.

Para cada tipo de pregunta se dispone de la versión original y la versión adaptada por la RED Descartes. En la versión adaptada, una vez finalizado el último ejercicio, se presentan diferentes opciones de corrección: corrección en pantalla, descarga en un fichero, envío por correo o impresión.

En el siguiente vídeo se presentan los objetos que forman parte de este proyecto y se muestran las actividades propuestas en el recurso síndrome de despoblamiento de colmenas.

En este video vamos a revisar la unidad correspondiente a "Funciones y gráficas" de 4ª ESO Opción B:

En este vídeo se han tratado los siguientes apartados:

1.Funciones reales
   Funciones, concepto
   Gráfica de una función
   Dominio y recorrido
   Funciones definidas a trozos
   
2.Propiedades de las funciones
   Continuidad y discontinuidades
   Funciones periódicas
   Simetrías

3.Tasa de variación y crecimiento
   Tasa de variación media
   Crecimiento y decrecimiento
   Máximos y mínimos
   Puntos de inflexión

Proporcionalidad. Las Espirales XII

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.

Como muestra enlazamos la unidad sobre Crecimiento Exponencial, del subproyecto TELESECUNDARIA,

la GEOevaluación de los estados y ciudades de México.

y el ejemplo de: Asocia parejas de imágenes y textos (2).

Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y las adaptaciones de los trabajos de Javier de la Escosura Caballero: "Geometría dinámica del trángulo" que enlazamos a continuación

y el de Cuadrilateralia, donde se fomenta el estudio y conocimiento de las características matemáticas de los objetos mediante la manipulación virtual de los mismos y que enlazamos con la imagen siguiente.

Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para trisecar un ángulo con la Concoide de Nicomedes. El ángulo a trisecar es el formado por el eje polar y la recta que une el polo con el punto que se desplaza por la directriz.
El análisis de la escena y su modificación, fundamentalmente en la situación del tercio del ángulo mencionado anteriormente, nos lleva a descubrir interesantes características de la Concoide. También son interesantes las modificaciones funcionales que mejoren las prestaciones de la utilidad.
Mencionar, por último, que la escena es copia de la que en su día publicó el profesor Pedro González Enríquez en su trabajo sobre las trisectrices.

Entradas anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por uno y dos puntos y algunas de las utilidades de los l.g. generados por un punto, en la actual comenzamos a mostrar algunos de los usos de la Concoide.

En esta ocasión, en la sección de vídeo, hemos elegido, debido a su calidad e interés, el mismo que en la entrada anterior, que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografías y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.

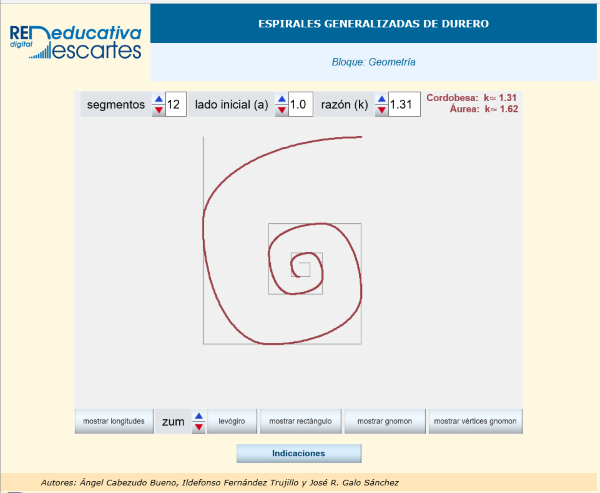
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Lituus" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

• Hemos creado la siguiente escena: Espiral de Lituus

• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Lituus incluida.

También, relacionado con el tema de los lugares geométricos (l.g.) y la trisección del ángulo, hemos incluido los trabajos realizados con el programa GeoGebra donde se muestran dos metodos para trisecar un ángulo con la Concoide de Nicomedes.

Método 1.

Método 2.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo

El subproyecto Miscelánea de la Red está formado por escenas aisladas que se pueden utilizar como complemento a los contenidos que se estén trabajando en el aula, ya sea para reforzar, consolidar o ampliar conocimiento.

En el siguiente vídeo se muestra con detalle una unidad perteneciente a dicho subproyecto y como insertar este objeto en un curso Moodle para su aplicación en el aula.

La unidad PISA. Sistemas de ecuaciones que hoy se presenta ha sido creada en base a las indicaciones para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas. Se plantean temas relacionados con la observación científica de situaciones reales (en este caso mezclas y aleaciones) para su traducción a lenguaje algebraico. En todos los ejercicios se introducen mecanismos para evaluar la respuesta y que sirvan también de guía al alumno, incluso aunque la respuesta sea correcta.

Este mes vamos a ver una unidad de 4ºESo Matemáticas Aplicadas correspondiente a Problemas aritméticos

en este vídeo hemos tratado los siguientes puntos:

1.Proporcionalidad directa e inversa
   Proporcionalidad directa
   Proporcionalidad inversa
   Repartos proporcionales
   Proporcionalidad compuesta
   
2.Porcentajes
   Porcentajes
   Aumentos y disminuciones
   Porcentajes sucesivos

3.Interés simple y compuesto
   Interés simple
   Interés compuesto
   Tasa anual equival

Proporcionalidad. Las Espirales XI

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.

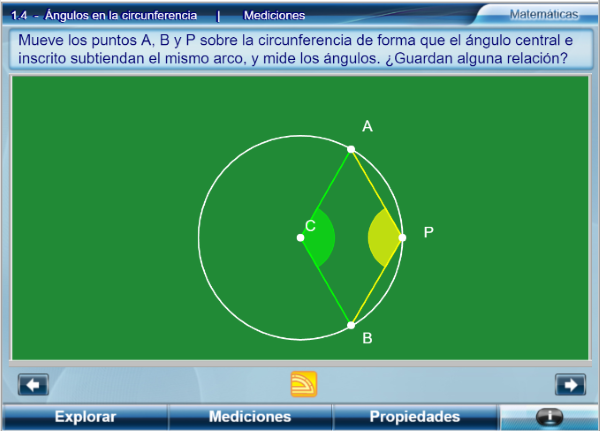
Como muestra enlazamos la unidad sobre Ángulos en la circunferencia, del subproyecto TELESECUNDARIA,

la GEOevaluación de Asia

y los ejemplos de Puzle de intercambio de imágenes tipo 2 donde Descartes realiza directamente el troceado en 4x4 de las imágenes, del subproyecto PLANTILLAS.

Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales y los lugares geométricos, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos objetos matemáticos. Se muestran y/o enlazan a continuación: una escena prolegómeno del estudio del l.g. "Concoide de Nicomedes" para más adelante ver su uso en la trisección de un ángulo, una miscelánea, que es un estudio riguroso y completo sobre las espirales logarítmicas y una segunda que complementa a la anterior. La excelente documentación aportada por ambas es una extraordinaria introducción a estudios más complejos de estos objetos y a la creación de utilidades educativas, dinámicas e interactivas.

Artículos anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por un punto, el actual muestra, según hemos visto, la creación de la Concoide de Nicomedes que es un l.g. definido por dos puntos, cuya posición depende del desplazamiento de un tercer punto por un eje. En próximas entradas se mostrará como trisecar un ángulo agudo con la Concoide.

En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografias y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Logarítmica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

• Hemos creado la siguiente escena: Espiral Logarítmica

• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Logarítmica incluida.

También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido el trabajo realizado con el programa GeoGebra donde se muestra la construcción de la Concoide de Nicomedes para, más tarde, usarla en la trisección de un ángulo.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo

En el vídeo de esta semana se presenta un nuevo objeto digital con actividades interactivas para estudiar la relación entre ángulos y circunferencia y sus propiedades.

Se trata de una unidad que forma parte del subproyecto Telesecundaria, un nuevo subproyecto de la Red que contiene numerosos objetos de aprendizaje desarrollados con la herramienta DescartesJS para Telesecundaria, una modalidad del sistema educativo de México.

La unidad Ángulos y circunferencia pertenece al grupo de unidades de Matemáticas para 3º de Secundaria.

En su desarrollo encontramos tres fases:

Exploración, para observar, modificar y definir las diferentes posiciones de un ángulo respecto de una circunferencia.

Medición, se dispone de herramientas para medir la amplitud de un ángulo central y un ángulo inscrito que comparten un mismo arco de circunferencia y comprobar la relación entre ellos.

Finalmente, en Propiedades, se guía al alumno para la demostración de la relación entre ángulo central y ángulo inscrito a partir de tres situaciones distintas que permiten generalizar todos los casos posibles.

Este mes vamos a ver la siguiende unidad:

Hemos visto los siguientes puntos:

1. Vocabulario estadítico
   Población, muestra, individuo y carácter

2. Carácter. Variable estadística
   Carácter cualitativo. Atributos
   Variables discretas
   Variables continuas

3. Ordenación de datos. Tabulación
   Para variable discreta
   Para variable cualitativa   

4. Gráficos para una variable cualitativa
   Diagrama de barras
   Diagrama de sectores

5. Gráficos para una variable discreta
   Diagrama de barras
   Polígonos de frecuencias
   Diagrama de sectores

6. Medidas de centralización
   Media
   Mediana