Para leer recomendamos... Mes de septiembre.
Escrito por Eva M. Perdiguero GarzoLlega el mes de septiembre, la vuelta al cole se acerca. Los nuevos libros, los colores sin estrenar, los cuadernos en blanco preparados para llenarse de nuevas ideas,... ¡Todo nuevo! Nosotros seguimos con las lecturas. Este es tan buen momento como otro para seguir leyendo. Recomendemos a nuestros alumnos un libro que curiosamente tenga que ver con las matemáticas, seguro que más de uno se sorprende.
En esta ocasión, tenemos un libro para los niños de primaria donde descubrirán un número que se vuelve loco. En el segundo libro descubriremos cómo es posible convivir en una misma ciudad donde confluyeron las tres grandes religiones, ¿tendrán algo que ver las matemáticas en esa convivencia? Un nuevo paseo por la ciudad nos mostrará gran cantidad de números y por último, un libro que nos mostrará la vida de un estudiante de matemáticas inmerso en Alemania durante la segunda guerra mundial.
Todos los detalles los puedes ver en el siguiente vídeo.
Jugamos y aprendemos con Descartes. Sumando naturales.
Escrito por Eva M. Perdiguero GarzoEn el siguiente juego no sólo encontraremos una figura que rellenar haciendo sumas, sino toda una página con diferentes figuras todas ellas con distintas figuras mágicas que rellenaremos con números. Con estos juegos evitarás el aburrimiento y si quieres conseguir solucionarlos tendrás que hacer una suma tras otra. Es muy sencillo en el siguiente vídeo te lo explicamos.
Proyecto Competencias: Apta para beber
Escrito por Santos Mondéjar LópezDen tro del Proyecto Compencias vamos a fijarnos en esta ocasión en un objeto de aprendizaje que evalúa la competencia de Conocimiento e interacción con el medio: Apta para beber
tro del Proyecto Compencias vamos a fijarnos en esta ocasión en un objeto de aprendizaje que evalúa la competencia de Conocimiento e interacción con el medio: Apta para beber
Se trata de comprobar si los alumnos han entendido el proceso de potablización del agua.
Contiene 5 cuestiones, 4 de seleccionar la opción correcta y otra con tres preguntas de "sí o no"
Encontramos una imagen para centrar a los alumnos en el tema, la corrección automática que indíca la respuesta correcta en caso de error, el marcador con los aciertos/errores y una pestaña que nos da información sobre lo que evalúa cada cuestión.
Aquí tenéis un vídeo con el funcionamiento:
Lo mejor es que lo probéis por vosotros mismos, enlace
Recordad que hay muchos más objetos de aprendizaje en el Proyecto Competencias
Radio Descartes. Entrevista a Eva María Perdiguero Garzo
Escrito por Ángel Cabezudo Bueno Por Ángel Cabezudo Bueno - 25 de agosto de 2014
Por Ángel Cabezudo Bueno - 25 de agosto de 2014
Eva María Perdiguero Garzo es Licenciada en Matemáticas en la especialidad de Computación, profesora del IES Ribera del Bullaque en Porzuna (Ciudad Real – España), tiene mucha experiencia en el uso de las TIC, particularmente en el aula de matemáticas; utiliza habitualmente en sus clases escenas de Descartes y nos dice que es fácil encontrar entre éstas algún material útil para el trabajo autónomo de sus alumnos o como refuerzo de sus explicaciones.
Pero el motivo principal de entrevistar en Radio Descartes a Eva María es para que nos hable de su vinculación con RED Descartes y de la actividad que desarrolla con nosotros como coordinadora de este blog que ella misma puso en marcha desde un principio. Con sus respuestas vamos descubriendo paso a paso la razón de ser del blog, sus características principales y los retos que tiene que afrontar en el día a día.
La entrevista minuto a minuto:
- Presentación. 1:00
- ¿De dónde parte tu experiencia en las TIC, cómo llegas con ellas al mundo de la enseñanza y qué pretendes conseguir como docente? 2:40
- ¿Cómo llegaste a Red Educativa Digital Descartes? 4:35
- Háblanos algo acerca de tu trabajo como coordinadora del Blog de RED Descartes. 7:15
- ¿Cuál es la característica que distingue a cada sección de este Blog? 9:55
- Este blog es muy diferente al blog de aula que mantienes como apoyo a tus clases y donde compartes las actividades académicas con tus alumnos. ¿Qué retos son los que tienes que afrontar día a día en cada uno de ellos? 11:32
- El Blog de RED Descartes genera una dinámica que moviliza una buena cantidad de aspectos: técnicos, de comunicación, de conocimiento... ¿Qué nos dices de todo esto? 13:40
- ¿Qué tiene que hacer cualquier persona que quiera colaborar con algún artículo en este blog de RED Descartes o simplemente aportar alguna idea en relación a otros posibles temas que pueden ser tratados aquí? 14:40
- Despedida y cierre. 16:04
Artículo relacionado: ¿Cómo utilizo Descartes en mi aula? Eva María Perdiguero Garzo. Por José Antonio Salgueiro (16-09-2013)
Resolución de problemas y comunicación audiovisual y multimedia con Descartes
Escrito por José Antonio Salgueiro GonzálezPublicamos hoy el tercer artículo dedicado a compartir y difundir algunas propuestas didácticas para el desarrollo de la comunicación audiovisual en nuestro alumnado a través de las Matemáticas con Descartes, que bien podríamos denominar en este caso "el valor añadido de la elegancia en la resolución de problemas", donde podemos observar, si cotejamos con las anteriores, la peculiaridad, creatividad e imaginación de cada equipo para afrontar retos incontrolados: Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes y Comunicación audiovisual con iCartesiLibri.
En esta ocasión abordamos las aplicaciones de la Trigonometría para la resolución de problemas de la vida cotidiana y de la Topografía clásica, habiendo usado un dispositivo móvil tipo tableta para la grabación del vídeo. Sus autores y protagonistas nos contarán los obstáculos encontrados y la forma de solventarlos.
Aprender programando con Scratch
Escrito por José Antonio Salgueiro GonzálezEs el título de la comunicación presentada y defendida por Álvaro Molina Ayuso, miembro de RED Descartes, en el XV CEAM, Congreso de Enseñanza y Aprendizaje de las Matemáticas, organizado por la Sociedad Andaluza de Educación Matemática "Thales" y celebrado en la sede Antonio Machado de la Universidad Internacional de Andalucía en Baeza.
Los estudiantes del Siglo XXI deben saber utilizar las herramientas tecnológicas no solo como elementos para la transmisión de contenidos. Las nuevas tecnologías nos permiten llevar a cabo una transformación en el proceso de aprendizaje ofreciendo al alumno la posibilidad de desarrollar su imaginación y creatividad construyendo, compartiendo, diseñando y experimentado a través de los contenidos. La exploración de nuevas herramientas como el software educativo Scratch es imprescindible para llevar a cabo el proceso de innovación educativa que permita adaptar el proceso de enseñanza-aprendizaje al ritmo que marca la sociedad actual.
Puzles de puntos notables del triángulo: La Recta de EULER
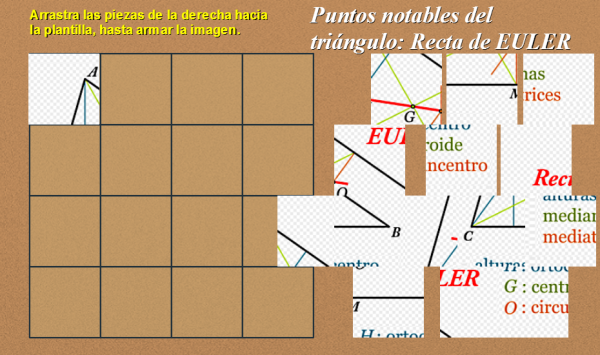
Escrito por Ángel Cabezudo BuenoUna vez publicados los artículos de esta serie de puntos notables del triángulo (Ortocentro, Baricentro, Circuncentro e Incentro) concluimos en éste con una propiedad interesante: Se trata de la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro ó centroide y el circuncentro que es motivo para nuevas reflexiones sobre la geometría del triángulo.
Utilizamos como recurso didáctico, al igual que en los anteriores casos, un puzle de arrastre que cuando se arma se muestran algunas observaciones y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede encontrar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y el visionado de un vídeo.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, todos estos materiales se integrarán en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y formará parte de la Miscelánea en la sección de Materiales de esta Web.
DESCUBRIMOS al Personaje Misterioso (III)
Escrito por Ángel Cabezudo BuenoLa semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” hacíamos una entrevista a un célebre matemático, astrónomo, geógrafo, filósofo, filólogo y poeta de la antigüedad griega y evitábamos dar su nombre con el objetivo de que fueran los escuchantes los que con los datos aportados pudieran averiguarlo.
Hoy, trascurrida una semana tal como anunciábamos, vamos a descubrir al personaje a través de una escena de DescartesJS que presenta tres imágenes seleccionadas a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen es una composición que muestra un grabado con la efigie que se atribuye al personaje y un esquema que refiere los datos que utilizó para medir el radio de la Tierra.
La segunda imagen es un dibujo que representa un mesolabio, ingenio que se atribuye a nuestro personaje, que sirvió para determinar mecánicamente la medida de dos segmentos medios proporcionales entre otros dos y permitía a los constructores de cubos encontrar la arista del cubo de volumen doble a otro dado.
La tercera imagen es una copia del siglo I del mapamundi atribuido a nuestro personaje. Las tierras y océanos quedan situados geográficamente mediante una red de meridianos de longitud y paralelos de latitud tal como se identificaban en aquellos tiempos.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno es y tiene licencia CC BY-NC-SA 3.0
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este tercer personaje y no os perdáis el podcast del próximo que emitiremos el día 8 de septiembre en este blog de difusión.
Puzles de puntos notables del triángulo: El Incentro
Escrito por Ángel Cabezudo BuenoEn los tres artículos publicados anteriormente de esta misma serie hemos tratado y por este orden el Ortocentro, el Baricentro y el Circuncentro.
Con el Incentro, que hoy es el motivo de este artículo, terminamos la serie de puntos notables que estaba prevista.
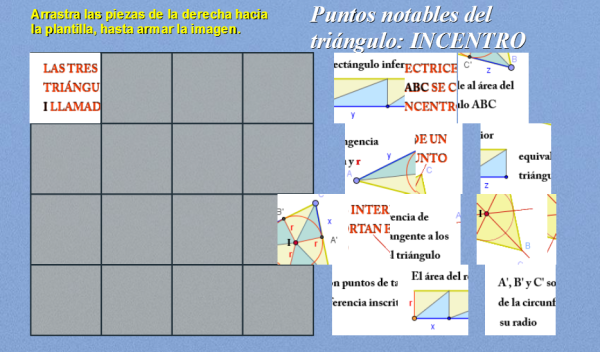
Utilizamos como recurso didáctico, al igual que en los anteriores casos, un puzle de arrastre que una vez armado muestra una imagen donde intervienen como elementos de la composición las bisectrices interiores a un triángulo, el incentro, la circunferencia inscrita y texto. Además cuando se completa el puzle se repasa la definición de bisectriz y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede encontrar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y de Geogebra y con las explicaciones que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, se integrarán todos estos materiales en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y donde además se pondrá como reto armar un nuevo puzle para obtener la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro y el circuncentro que será motivo para nuevas reflexiones sobre la geometría del triángulo.
Entrevista al personaje misterioso (III)
Escrito por Ángel Cabezudo Bueno.png) Tercera entrevista de este espacio donde conoceremos mejor la parte humana de los matemáticos ilustres a lo largo de la historia. Durante la entrevista, el personaje, en este caso un sabio matemático, geógrafo y astrónomo del siglo III a.n.e, irá desvelando datos sobre su vida y obra.
Tercera entrevista de este espacio donde conoceremos mejor la parte humana de los matemáticos ilustres a lo largo de la historia. Durante la entrevista, el personaje, en este caso un sabio matemático, geógrafo y astrónomo del siglo III a.n.e, irá desvelando datos sobre su vida y obra.
Estos datos permitirán al oyente averiguar su identidad. Te invitamos a que dejes un comentario sobre la identidad del personaje. Publicaremos todos los comentarios recibidos pero sin indicar el nombre del matemático, así dejaremos al resto de participantes con la expectativa hasta el final. ¿Te animas?
Tras la semana de reflexión, el lunes 18 de agosto, publicaremos la solución a través de un puzle que nos mostrará la imagen de este tercer personaje misterioso.
El entrevistador y autor del guion es Ángel Cabezudo Bueno y el profesor José Antonio Salgueiro González interpreta al ilustre y culto personaje que viene del más allá. Ambos son socios colaboradores de Red Educativa Digital Descartes. El trabajo lleva licencia CC BY-NC-SA 4.0.
Los efectos de sonido pertenecen al Banco de imágenes y sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
El montaje del audio ha corrido a cargo de Ángel Cabezudo Bueno y se ha realizado con la aplicación Audacity 2.0.4.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



 CONTACTO
CONTACTO
