Mostrando artículos por etiqueta: proporcionalidad
Proporcionalidad. Las Espirales VI
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destacan las aportadas por la Red Educativa Digital Descartes Colombia (colDescartes), que gracias a la integración de los mapas de Google en las escenas DescartesJS, realizada por Diego Feria Gómez, ha abierto un amplio abanico de posibilidades al proyecto GEOGráfica según muestran las escenas que, creadas por el profesor Juan Guillermo Rivera Berrío, se han añadido al mismo y que se pueden ver y descargar siguiendo el enlace gráfico siguiente.
También es de reseñar la creación, de forma colaborativa, de una Biblioteca virtual formada por libros interactivos y dinámicos con contenido lúdico-formativo adaptado a cada continente y país y que pasan a formar parte del contenido del subproyecto GEODiver dentro de GEOgráfica. El responsable e impulsor de la idea es Juan G. Rivera y han colaborado, además de él mismo:
- Diego Feria Gómez (Oceanía)
- Ramiro A. Lopera Sánchez (Estados de USA y países de Suramérica)
- José R. Galo Sánchez (Países de Europa y Provincias de España)
- Ángel Cabezudo Bueno (Asia)
- Ildefonso Fernández Trujillo (África)
Dentro de nuestro ámbito local destacan las creaciones y adaptaciones de unidades del proyecto ed@d. En esta ocasión enlazamos la creada por: Jesús Muñoz Calle, Joaquín Recio Miñarro y Luis Ramírez Vicente y adaptada por Luis Ramírez Vicente para la asignatura de Física con el título de "Las Ondas".
De la colección de unidades interactivas del subproyecto COMPETENCIA SOCIAL Y CIUDADANA que el profesor Luis Barrios Calmaestra ha creado sobre algunos de los temas curriculares enlazamos el referente a los impuestos.
En esta ocasión en la sección de vídeo aprovechamos el impulso de desarrollo de vídeos lúdico-educativos de la Red Educativa Digital Descartes Colombia para presentar un video-puzle. Consiste, como en un puzle tradicional, en colocar cada pieza en su sitio, pero de fondo, en lugar de una imagen estática se usa un vídeo en reproducción. Se ha simplificado sobremanera el vídeo presentación con objeto de facilitar la toma de contacto, aunque siguiendo los enlaces de la ayuda se puede acceder al código fuente y a la aplicación original. Para acceder, pulsad sobre la siguiente imagen. Nota editores RED Descartes 19 de agosto de 2023: Este vídeo-puzle ya sólo funciona en el navegador Firefox, debe de usar éste si desea ver cómo funcionaba en su momento.
Cuando las adaptaciones educativas estén publicadas dedicaremos nuestra atención a tan interesante innovación.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior se añadieron al proyecto: la escena de la espiral de Teodoro y la escena sobre como dibujar las espirales de 3, 4, 5 ... 20 centros y se quedó en incluir la espiral Cordobesa, cosa que hemos realizado de la siguiente manera:
- De la Miscelánea Espirales generalizadas de Durero hemos extraido la siguiente escena.
- Desarrollo de la gráfica de la aproximación gnomónica de la espiral Cordobesa
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Cordobesa incluida.
En próximas entradas continuaremos con el paso a paso del proyecto incluyendo la espiral de Durero, la de Fibonacci y otras más entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales V
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio trilateral entre la Facultad de Ciencia y Tecnología de la Universidad Autónoma de Entre Ríos (FCyT-UADER) en la provincia de Entre Ríos en Argentina, la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes (RED Descartes), están: el libro Opúsculo sobre la función lineal y afín, la recta en el plano creado por las profesoras Irma Manuela Benitez - Alicia Elena Carbonell y María Alicia Gemignani, la siguiente imagen enlaza con dicho libro
y la integración de los mapas de Google en una escena DescartesJS realizada por Diego Feria Gómez, que abre un amplio abanico de posibilidades al proyecto GEOGráfica según muestra la escena que enlazamos a continuación.
También cabe destacar la aportación de la profesora Montserrat Gelis Bosch que ha adaptado al catalán el material sobre planos de simetría en 3D creado por el profesor José R. Galo Sánchez que puede consultarse en los siguientes vínculos,
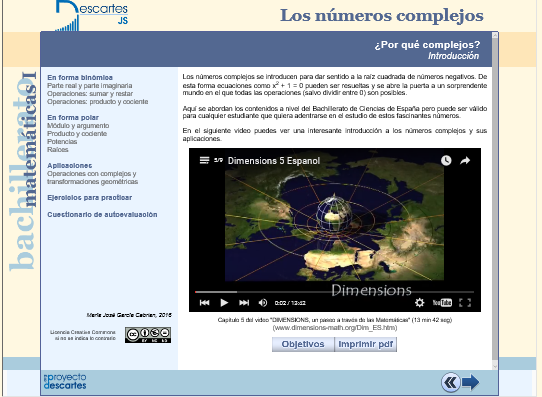
y el Opúsculo sobre los complejos de María José García Cebrian que se enlaza a continuación y que, encarecidamente, aconsejamos visitar y utilizar en el tema de Complejos por su completitud y potencial didáctico.
De la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis enlazamos, por su indudable interés, el libro de estadística.
La extraordinaria acogida a los materiales del proyecto @prende, recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, comentada ampliamente en los foros hace que no sea necesario reiterar los elogios a tan meritotia creación, en la imagen siguiente enlazamos el recurso dedicado a las áreas.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las animaciones y la construcción, paso a paso, de algunas escenas ejemplo, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de como hemos incluido en la miscelánea que estamos creando las escenas de la espiral de Teodoro y las espirales de tres a veinte centros, vamos a mostrar un vídeo de la presencia de la espiral en el organismo con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea, tal y como estaba hasta aquella fecha, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
También hemos añadido al proyecto el contenido de la siguiente escena sobre como dibujar las espirales de 3, 4, 5 ... 20 centros
La escena de la espiral de n centros, que vemos a continuación
está formada por:
- dos controles tipo pulsador
- un control gráfico de color rojo que es la referencia para la construcción de la gráfica.
- un texto.
- dos familias de puntos (los vértices y sus trasladados)
- dos familias de segmentos (los lados y sus prolongaciones).
- una familia de arcos.
Los pulsadores controlan, respectivamente, la cantidad de centros de la espiral y la longitud del lado del polígono regular sobre cuyos vértices se encuentran dichos centros. Inicialmente es visibles la espiral de tres centros.
Con objeto de que puedan verse todas las espirales, la escala del espacio donde se representan tiene un valor de 16 en lugar de 48 que es el valor por defecto. Aunque para ver bien las espirales de más de 9 centros es conveniente poner la longitud del lado a 1. Esto se ha hecho así para que se practique con el cambio de escala. Puede conseguirse el mismo efecto poniendo un control en la escena que modifique la escala; o reduciendo - aumentando el tamaño del lado del polígono base.
Para poder dibujar la colección de centros y los segmentos de los lados y sus prolongaciones, hemos definido:
- Cuatro vectores de tamaño dinámico para albergar las coordenadas de los vértices y sus trasladados que harán posible la gráfica de los segmentos de la escena.
- Un algoritmo que calcula las coordenadas de los vértices y sus trasladados.
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Teodoro y las espirales de n centros incluidas, se puede observar que el nombre del archivo ha cambiado respecto al original, es así para que se puedan comparar los códigos y ver los cambios realizados. Aconsejamos, a quienes comienzan a crear escenas fundamentalmente, y a cualquiera que visite el Blog, leer detenidamente el extraordinario artículo creado por el profesor Ángel Cabezudo Bueno sobre las Escenas con DescartesJS: Técnicas y trucos, donde se detalla con rigor el significado y uso de los componentes que pueden intervenir en una escena aportando una buena colección de atajos y utilidades que agilizan la creación y dotan a las escenas de funcionalidades extraordinarias.
La escena del proyecto puede verse a continuación:
Como aplicación de la proporción Humana hemos elaborado la siguiente escena.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un triángulo cordobés con triángulos cordobeses.
Acceso al recurso en GeoGebraTube
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa, la de Durero, la de Fibonacci y otras más entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales IV
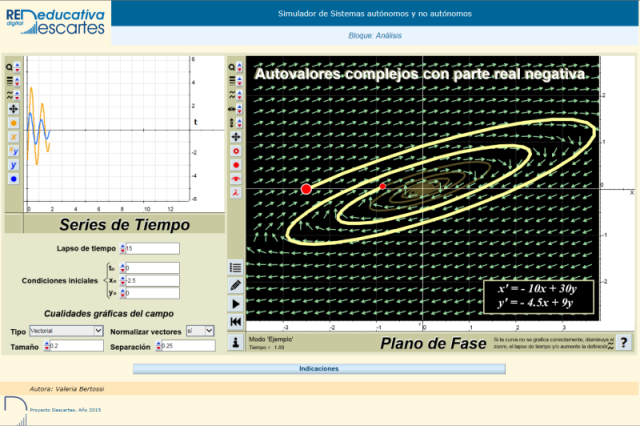
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio de colaboración con la Facultad Regional Santa Fe de la Universidad Tecnológica Nacional de Argentina, está la miscelánea: Simulador de Sistemas diferenciales autónomos y no autónomos creada por la profesora Valeria Bertossi. La siguiente imagen enlaza con la miscelánea.
También cabe destacar la aportación del profesor José R. Galo Sánchez con su trabajo sobre Geometría tridimensional, también disponible en catalán gracias a la profesora Monserrat Gelis Bosch, que enlazamos a continuación.
En próximos artículos comentaremos y/o enlazaremos la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis. Por su indudable interés se aconseja visitar dicho subproyecto al igual que el recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, y que con el nombre @prende proporciona a los alumnos un material lúdico e interactivo que facilitará de forma notable la asimilación de conceptos matemáticos.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las familias 3D, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de la escena de la espiral de Teodoro para incluirla en la miscelánea sobre las espirales en estudio, vamos a mostrar un vídeo que relaciona la música y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea tal como está en la actualidad, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
La escena de la espiral de Teodoro, que vemos a continuación
Está formada por:
- dos controles tipo pulsador
- un texto
- un punto rojo de referencia
- una familia de 139 puntos
- otra de 138 segmentos.
Los pulsadores controlan, respectivamente, la cantidad de puntos y segmentos que están presentes en la escena. Inicialmente son visibles 0 segmentos y 29 puntos.
Con objeto de que puedan verse varias vueltas de la espiral, la escala del espacio donde se representa tiene un valor de 15 en lugar de 48 que es el que viene por defecto.
Para poder dibujar la colección de puntos, y posteriormente los respectivos segmentos, hemos definido:
- Un vector de 140 de tamaño para albergar los arcos que los segmentos que unen los sucesivos puntos con el de referencia forman con la horizontal.
- Una función, x1, para controlar la abscisa de los puntos.
- Otra función, y1, para controlar la ordenada de los puntos.
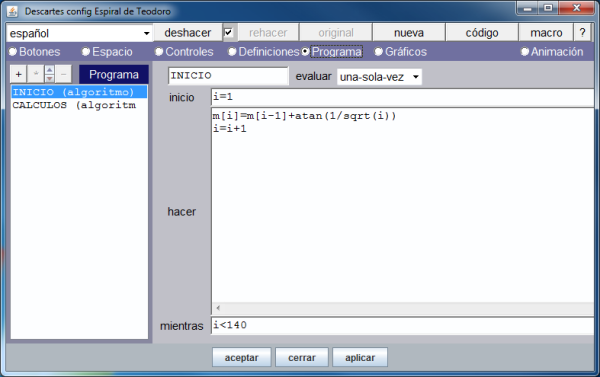
Los gráficos siguientes muestran como se ha hecho lo anterior.
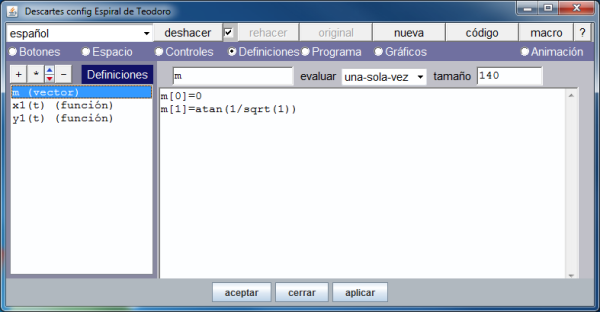
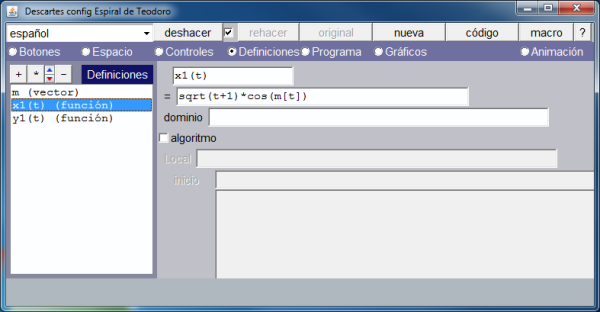
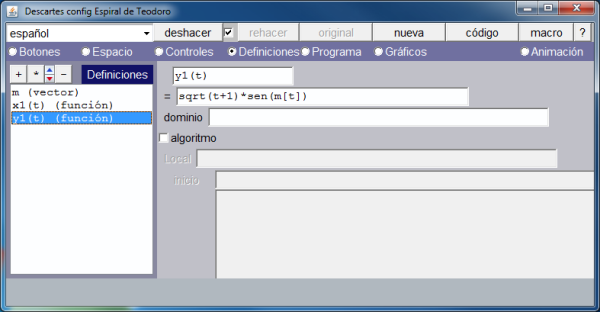
En la imagen que muestra la definición del vector se ve que únicamente se asignan valores a sus dos primeras componentes. Activando la opción de menú: Programa, vemos, en la siguiente imagen, como se han definido el resto de los arcos.
La siguiente imagen muestra los gráficos de la escena, en concreto despliega la forma en que se ha definido la colección de puntos.
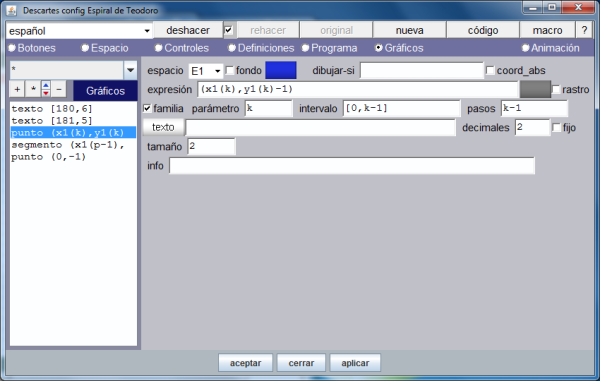
Observamos que los 139 puntos de la espiral se han definido mediante una familia que depende del parámetro k (identificador del pulsador de nombre: puntos presente en la pantalla).
La cantidad de puntos en pantalla depende del valor de este pulsador, el cual podemos manipular a nuestra conveniencia.
Analizada la escena de la espiral de Teodoro podemos pasar a incluirla en la miscelánea que estamos elaborando, acción que dejamos para el siguiente artículo. Aunque, insistimos, es conveniente que, para practicar con el editor de escenas, cada cual lo intente por su cuenta ya que disponiendo de las escenas se puede analizar cada uno de los cambios que se hagan y observar el efecto de cualquier modificación y así aprender a configurar escenas con el editor.
Como aplicación de la proporción Humana hemos elaborado la siguiente escena donde se hace una breve introducción al estudio del Triángulo Cordobés.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un cuadrado con triángulos cordobeses.
Acceso al recurso en GeoGebra
Conviene desplazar el deslizador tesela con las flechas del teclado.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales III
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes caben destacar, entre otras, la creación del subproyecto Pisa con ordenador por parte de Mª José García Cebrian y José R. Galo Sánchez, documentado en este Blog por Santos Mondéjar López y la herramienta creada por el profesor Ángel Cabezudo Bueno que nos ha dotado de la posibilidad de analizar un crecimiento espiral y hallar la expresión matemática que mejor lo ajusta. La siguiente imagen enlaza con la miscelánea que explica el proceso de creación de dicha herramienta y el uso de la misma.
En el proceso de recuperación y adaptación de materiales de la Red Descartes que habían quedado obsoletos y en el de creación de nuevos recursos son varios los trabajos que merecen mención especial que ya está reflejada en el Blog, no obstante animamos a los socios y visitantes de nuestra web a usar y estudiar dichos trabajos y emprender tareas de adaptación-creación de: Unidades, Misceláneas, Discursos... para recuperar todo el esfuerzo e ilusión que en su día se invirtió y dotar a la aldea global de herramientas útiles para la enseñanza y el aprendizaje.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información de las funciones matemáticas disponibles para la construcción de escenas.
Antes de comenzar con el análisis de los gráficos incluidos en la escena en estudio vamos a mostrar un vídeo que relaciona los fractales y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
- Espirales de Antonio Pérez Sanz
- Real Sociedad Matemática Española
- Espirales, fractales, Fibonacci,...
- Visión más espiritual
- Espirales y Laberintos
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior nos quedamos estudiando los gráficos introducidos en la escena: puntos, segmentos, líneas, polígonos, textos... etc. Para lo cual abrimos la opción de menú Gráficos y observamos los 26 objetos creados y que muestra la siguiente imagen.
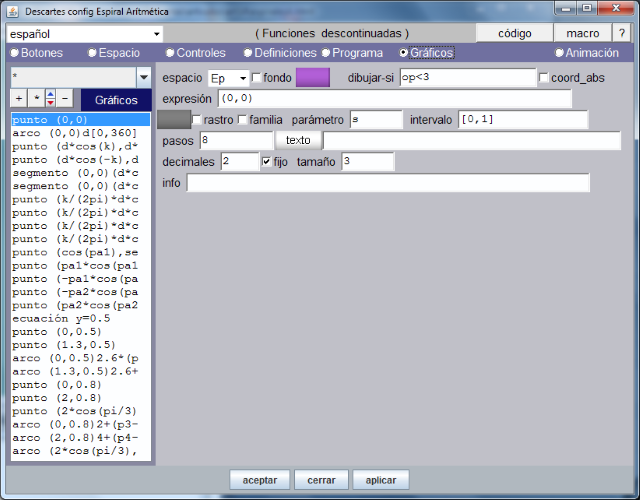
Insistimos en la conveniencia de descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada gráfico. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los gráficos se puede examinar y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos gráficos son las que comienzan por: <param name="G_x" que en nuestro caso llegan hasta <param name="G_26". Recordamos que se debe tener mucha precaución al editar directamente el código.
Observando la imagen vemos que, en primer lugar, se ha definido un punto en el origen de coordenadas (0,0) que, en esta ocasión, está centrado en la escena. Conviene, si no se tiene práctica, estudiar y probar las diferentes maneras de situar el origen de coordenadas de un espacio y el espacio en si mismo, dentro de la escena. También vemos el espacio donde se representará el punto, su color, tamaño y otra serie de parámetros autoexplicativos y de facil uso.
De los parámetros que ayudan a manejar un punto en la escena uno muy interesante es el de 'familia' que mediante un parámetro (variable) que se introduce en la/s coordenada/s y que se declara en el cuadro de texto "parámetro" (o se acepta el ofrecido por el editor 's') permite introducir simultáneamente tantos puntos como se precise en los lugares definidos por las coordenadas.
La siguiente imagen muestra como se han definido la colección de puntos azules que dibujan la espiral de Aquímedes según la definió el geómetra griego, donde se usa el parámetro global 'familia' con el parámetro o variable 'k '. Recordamos que en su momento definimos el control 'k ' y le asignamos un valor inicial y un valor final. Esta manera de proceder hace que la escena sea interactiva ya que el conrol k puede manipularse al estar presente en la escena en forma de pulsador.
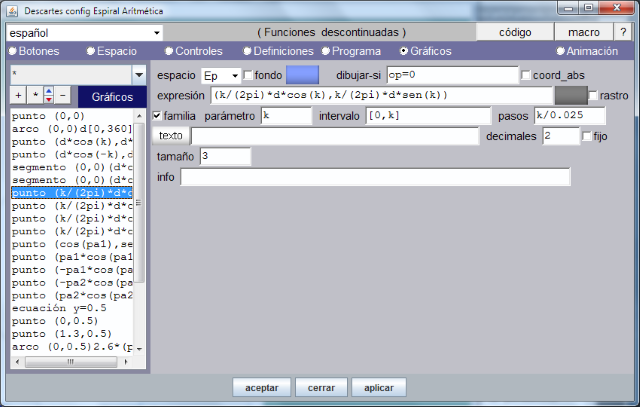
Puesto que disponemos de la escena podemos analizar cada uno de los gráficos cambiando los valores de sus parámetros y observando el efecto de las modificaciones para así aprender a configurar escenas con el editor de código.
Con objeto de practicar con los condicionales hemos elaborado la siguiente escena para su análisis. Es una pequeña aplicación donde se hace una breve introducción al estudio de la distribución de la proporción humana en superficies lisas mediante triángulos, rectángulos, rombos y otras figuras derivadas.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como obtener dos triángulos cordobeses a partir de un folio DIN A4.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral de Teodoro entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales
Debido a que, afortunadamente, continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la ReDescartes aconsejamos acudir a los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre sí, a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas, quedando pendientes los enlaces a algunos de los contenidos de las siguientes novedades:
- Se han publicado nuevos recursos en el subproyecto de Competencias que han sido encargados por el INEE. Son pruebas liberadas del programa PISA para la nueva evaluación de PISA con ordenador.
- Integración de escenas descartes-JS en un paquete Scorm para su uso en Moodle (la profesora Elena Alvarez ha incorporado un ejemplo de integración de Descartes con Moodle mediante un paquete Scorm) y Ficheros de "Juegos Didácticos" para plataformas educativas. de Enric Ripoll Mira
- Experiencia con atención personalizada en matemáticas mediante libro digital en el aula de informática de Juan José López
- ed@d en moodle de Emilio Pazo Núñez.
- Lupa cartesiana de Juan Guillermo Rivera Berrío
este último ya disponible y algunos de los anteriores llevan la documentación incluida o ya están parcialmente disponibles en los foros de la ReDescartes.
En esta ocasión, tal como indica el título, vamos a hacer un recorrido por el concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, enlazaremos algún otro contenido por su indudable interés.
El objetivo de incluir el uso y análisis de Unidades Cartesianas sobre la Proporcionalidad es, además del evidente relacionado con el tema, el de aprender a generar una, o varias Misceláneas a partir de dichas unidades o simplemente, a extraer escenas aisladas para un uso ágil y puntual como ejemplo de apoyo a un aspecto concreto de uso o aplicación del concepto en estudio.
El siguiente vídeo muestra la manera de realizar esta acción y de hacer operativo el objeto derivado de la Unidad o Miscelánra.
Antes de continuar conviene observar la manera en que la profesora Antolina Muñoz Huertas enfoca el tema de la Proporcionalidad en la unidad 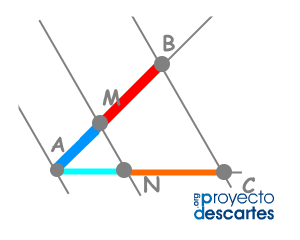 que publicó en el año 2002 y que he adaptado a DescartesJS debido a la importancia del concepto y a la claridad y sencillez con que se expone. Y también porque de esta Unidad, tal y como más tarde haremos con otros trabajos del profesor José R. Galo Sánchez, vamos a extraer escenas para su posible uso de forma individual.
que publicó en el año 2002 y que he adaptado a DescartesJS debido a la importancia del concepto y a la claridad y sencillez con que se expone. Y también porque de esta Unidad, tal y como más tarde haremos con otros trabajos del profesor José R. Galo Sánchez, vamos a extraer escenas para su posible uso de forma individual.
Una escena tratada aisladamente puede cubrir varios objetivos; unos relacionados con un concepto, por ejemplo la proporcionalidad, otros con una aplicación del concepto p.e. el número de oro y otros con el uso del código que hace comportarse a la escena de la forma que lo hace.
En todos los casos al ser un objeto simple es facil abordar su estudio desde cualquier punto de vista.
El número de oro.
La escena sacada tal cual de la Unidad anterior muestra, de forma dinámica e intuitiva, como dividir un segmento en partes que verifiquen la proporción Divina. Cierto que podemos añadir muchos aspectos que la mejoren hasta convertirla en una excelente Miscelánea, pero en esta ocasión queremos que permanezca tal cual está en origen para así comprender las explicaciones que se dan en el vídeo incluido en este artículo.
A continuación se enlaza una Miscelánea que complementa la Unidad anterior, pues introduce la proporción Humana o Cordobesa y que ha sido creada con objetivos fundamentalmente formativos.
Las dos escenas siguientes están sacadas de la excelente Unidad  creada por José R. Galo y la tercera es una escena simple que, en su día, se creó para practicar con el Teorema de Pitágoras y con las funciones Trigonométricas: seno, coseno, tangente, arcotangente...
creada por José R. Galo y la tercera es una escena simple que, en su día, se creó para practicar con el Teorema de Pitágoras y con las funciones Trigonométricas: seno, coseno, tangente, arcotangente...
Rectángulo cordobés I
Rectángulo cordobés II
Espiral por puntos.
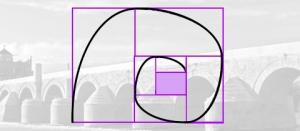
En esta otra escena, de utilidad si nos planteamos el tema de la proporcionalidad de manera algo más avanzada, tenemos una herramienta que puede ayudar a la confección de espirales logarítmicas, arquimedianas, uniformes de doble centro... y con muy pocas modificaciones de cualquier otro tipo.
Espiral logarítmica
Estando a punto de cerrar este artículo nos llega la noticia de que el profesor Ángel Cabezudo Bueno ha culminado un laborioso trabajo colaborativo y ha dado forma a la Espiral Cordobesa. Aunque dedicaré el próximo artículo a este logro a continuación expongo una escena, aún provisional, con la construción, mediante gnomones, de la espiral.
Espiral cordobesa mediante gnomones
En próximas entradas continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Cálculo simbólico en escenas DescartesJS: Introducción.
La siguiente escena es el ejemplo desarrollado de la implementación del cálculo simbólico dentro de escenas DescartesJS. Realizado por Elena E. Álvarez Sáiz, es un completo estudio que la autora ha realizado de la situación, ampliando los comandos utilizados a más de 400 y detallando la manera de proceder en una amplísima documentación parte de la cual se enlaza al principio del artículo.
De este impresionante avance se ha dicho, entre otras cosas, lo siguiente:
¡Felicitaciones Elena!
Antes de despedir este artículo quisiera hacer mención al impresionante trabajo que hace ya algún tiempo presentaron Deyanira Monroy y José Luis Abreu con el nombre de ConGeo para darlo a conocer a aquellos que aún no lo usan y enviarle a sus autores la petición de incluir en descartes-min.js algunos de los comandos como: Punto Medio, Mediatriz, Bisectriz,... cosa que algún creador de escenas agradecería.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
La mayoría de objetos interactivos pertenecientes a los diversos proyectos de la Red Educativa Digital Descartes se pueden embeber en sitios web en los cuales se pueda editar en código html (blog, wiki, google sites, moodle...)
Si disponemos de un aula virtual moodle, también podemos embeber dichas escenas en la mayoría de los recursos que nos ofrece la plataforma: libros, páginas, etiquetas, cuestionarios...
En los cuestionarios, se pueden añadir objetos interactivos en la descripción o en alguna pregunta, independientemente del tipo de pregunta elegido, seleccionando el modo de edición en html.
En la mayoría de los objetos interactivos de la Red, encontramos el código para embeber seleccionando dichos objetos en el apartado materiales del Blog de la Red.
También podemos encontrar el código en la misma escena, situando el ratón sobre ella y pulsando el botón derecho; se abrirá una ventana auxiliar y desde el botón config obtendremos el código que deberemos pegar en la plantilla de edición del cuestionario.
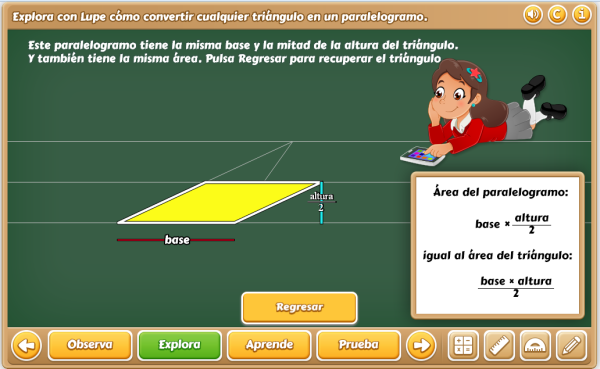
En el siguiente vídeo, se muestran los pasos a seguir para la edición de un pequeño cuestionario. En este caso se han embebido dos escenas de aumentos y disminuciones porcentuales de la Unidad de Proporcionalidad (2º ESO) pertenecientes al Proyecto ED@D.














.png)
.png)