Mostrando artículos por etiqueta: 17 años o más
Título: La involuta de un círculo y la espiral de Arquímedes
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Bachillerato y Universidad/ 17 años o más
Idioma: Castellano
Autores: José R. Galo Sánchez y Ángel Cabezudo Bueno
Haz clic en la imagen para abrir el recurso
Descargar recurso Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Espiral de N centros e involuta del círculo
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Bachillerato y Universidad/ 17 años o más
Idioma: Castellano
Autores: José R. Galo Sánchez y Ángel Cabezudo Bueno
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Voluta en el capitel jónico según Vitruvio y Ortíz y Sanz
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Bachillerato y Universidad/ 17 años o más
Idioma: Castellano
Autoría: José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Espiral de N centros
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Bachillerato y Universidad/ 17 años o más
Idioma: Castellano
Autoría: Ildefonso Fernández Trujillo y José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
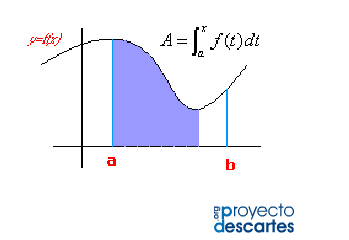
Título: La integral definida y la función área
Sección: Unidades didácticas
Bloque: Análisis
Unidad: Integración de funciones
Nivel/Edad: 2.º Bachillerato (17 años o más)
Idioma: Castellano
Autoría: José Luis Alonso Borrego. Adaptación a Descartes JS: Josep Maria Navarro Canut
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de las Unidades Didácticas en
https://proyectodescartes.org/uudd/indice.html - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Cuadrados mágicos aditivos y multiplicativos
Sección: iCartesiLibri
Bloque: Álgebra
Unidad: Aritmética
Nivel/Edad: Secundaria, Bachillerato y Universidad (12 años o más)
Idioma: Castellano
Autor: Luis barrios Calmaestra
ISBN: 978-84-18834-87-5
Haz clic aquí para ver una versión en pdf
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Álgebra Lineal Interactiva. Ejercicios y problemas.
Sección: iCartesiLibri
Bloque: Álgebra
Unidad: Álgebra lineal
Nivel/Edad: 2º Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autor:Augusto Spela
ISBN: 978-84-18834-86-8
Haz clic aquí para ver una versión en pdf
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
La concha discoidal del Nautilus siempre ha sido un objeto admirado por su gran belleza que es fruto y reflejo armónico de la naturaleza. Capta la atención de cualquier persona curiosa o inquieta, incita a conocer los porqués de su forma e invita a ahondar en ella, más si tiene acceso a ver su interior donde se observan tabiques y cámaras "secretas" que guardan sigilosamente un bello patrón matemático obtenido como consecuencia de la evolución y adaptación al medio del animal que la produce. Un animal denominado "fósil viviente" que lleva haciendo matemáticas desde hace cuatrocientos millones de años, tiempo en el que las posibles ramas evolutivas diferenciadoras no han triunfado por ser menor la perfección alcanzada.
El estudio bidimensional, realizado con anterioridad en otros artículos, de la sección sagital de la concha nautílica permitió determinar su carácter intrínsecamente cordobés (ligado a la proporción cordobesa) y también la obtención del modelo matemático ontogénico de la misma, encontrando respuestas al comportamiento diferenciado del primer verticilo respecto a los dos siguientes. Pero la concha del Nautilus es tridimensional y uno queda insatisfecho si no procede a intentar modelar esa tercera dimensión, siendo precisamente ese salto es el que se sintetiza en este trabajo: "El modelo matemático tridimensional uniforme del Nautilus" y quizás en el futuro contemple plasmar el modelo ontogénico tridimensional. La sección frontal de la concha es la base sobre la que se construye el modelo 3D al aplicarle el crecimiento cordobés, y aquí se reflejan las dificultades, inesperadas, con las que me encontré y cómo se salvaron. La forma elíptica se mostró como base teórica conformadora de ese perfil frontal del Nautilus y ello también aconteció en el callo umbilical. Pero no todo son éxitos dado que los septos se muestran reticientes a mostrar cuál es la superficie matemática que los envuelve y describe... ¡El reto continúa!, pero ahora lo que procede es invitarles a acompañarme en la descripción de lo conseguido.
En un trabajo anterior presenté el modelo ontogénico matemático del Nautilus donde quedó compilado el conocimiento adquirido después de un amplio periodo de tiempo investigando la sección sagital de la concha del Nautilus y buscando dar explicación matemática a esa atractiva y bella bitácora cálcarea que atrapa y engancha, a la vez que engaña, pues se muestra con una simplicidad aparente cuando realmente engloba una complejidad y una diversidad de detalles crípticos que se necesitan descodificar y que requieren de amplia observación, de una paciencia infinita y de un oído atento para captar los sigilosos mensajes que emite en quedos susurros y que no pueden pillarte distraído, en Babia. Cubierto amplia y detalladamente ese objetivo bidimensional, el lance siguiente era obvio ¿verdad? La concha es tridimensional y como tal ha de analizarse y tratar de comprender. Pero el salto desde planilandia suele ser, y es, difícil de lograr y las dificultades previas encontradas generan un gran vértigo y un amplio desasosiego, si bien las alegrías y la adrelalina segregada con ellas —cuando se logra vencer la desesperación que genera el que las musas continuamente te ignoren— genera adicción y ocultando los sinsabores previos dan impulso a continuar, persiguiendo aprender, conocer y saber un poquito más, aunque ello sólo lleve a adentrarse en el socrático conocimiento y en la paradójica conclusión de no saber nada.
Así pues, aceptado el desafío, era necesario tratar de establecer unos límites iniciales, que podían ser ambiciosos, pero que tenían que ser realistas para "no morir en el intento" y no sucumbir en el camino. En analogía a los pasos dados en el estudio bidimensional procedía inicialmente abordar el modelo uniforme, es decir, áquel en el que se considera que la concha crece gnomónicamente siempre de la misma forma en todas las fases vitales del animal que la genera y, por tanto, ignorando su ontogenia, especialmente en su periodo embrionario—. Alcanzado ese objetivo, ya habría posteriormente tiempo personal o ajeno para adentrarse en el modelo ontogénico—. Y este artículo es la síntesis divulgadora del modelo matemático tridimensional uniforme de la concha del Nautilus que he obtenido. Quedan algunos flecos por hilvanar, o quizás puedan interpretarse como jirones que remendar, pero los hilos están urdidos y la tela ha quedado suficientemente tejida para que pueda mostrarse el paño sobre el que otros patronistas y diseñadores pueden aportar su visión y realización.
Modelo teórico tridimensional del Nautilus
En la siguiente presentación se desglosan los diferentes aspectos que he ido progresivamente abordando para lograr el modelo matemático presentado y a continuación procederé a describir resumidamente los pasos dados, las dificultades encontradas y las decisiones tomadas.
Modelo matemático 3D uniforme del Nautilus.
Modelado 3D de las conchas
En la literatura relativa al modelado de las conchas hay forzosamente que remontarse a célebres autores como Moseley (1838) y Thompson (1917), casi doscientos años de conocimiento divulgado al respecto, y a los trabajos de hace medio siglo en el contexto de diseño matemático computacional de Raud (1961 y 1966). Este autor nos indica que toda concha puede modelarse en base a cuatro parámetros esenciales: la curva generatriz o sección transversal, la distancia o posición relativa de la curva generatriz respecto al eje de giro, el factor de crecimiento y la traslación en la dirección del eje de giro (sólo para conchas turbinadas, lo cual no acontece en el Nautilus ya que ésta es discoidal).
Consecuentemente, habiendo determinado previamente que el Nautilus tiene un factor de crecimiento ligado a la espiral cordobesa, lo que era necesario fijar era la sección transversal de la concha y su posición especto al eje de giro, quedando ambos parámetros determinados implícitamente si obtenemos la ecuación de la curva que describe ese perfil tomando como eje de referencia dicho eje de giro.
Un primer paso consistió en la adaptación del modelo de Raud para que una vez fijada la ecuación de la curva generatriz de la concha y el factor de crecimiento se generara automáticamente la superficie de la concha. Ello quedó reflejado en la miscelánea "Modelo 3D de las conchas discoidales" (se recomienda consultar las indicaciones ahí incluidas).
Moddelo 3D de las conchas discoidales
La sección transversal del Nautilus
Para determinar la ecuación de la curva generatriz del Nautilus consideré la sección del Nautilus aportada por Tanabe et al. (1985), pero una vez que trabajé con ella detecté que la imagen incluida en ese artículo debió de sufrir una edición erroneá en el proceso de publicación y se produjo una alteración en sus proporciones ya que esa imagen no cuadraba ni con los datos biométricos aportados por esos mismos autores, ni con el modelo bidimensional ontogénico (Galo, 2023). Ello forzó a la busqueda de otras secciones que aportaran luz y dieran forma adecuada a la necesitada sección, a la vez que sirvieran de constraste y verificación con el citado modelo 2D. En concreto consideré la sección aportada por esos mismos autores en su artículo Tanabe et al. (1990) y los cortes realizados por Gonzalez-Restrepo (2019) obtenidos a partir de la concha digitalizada del Museo de D'Arcy Thompson. Esta tarea ha quedado condensado en las misceláneas:
- "Crecimiento en algunas secciones frontales del Nautilus", donde se verifica que la sección frontal de Tanabe (1985) no sigue el crecimiento cordobés y, sin embargo, los datos numéricos aportados por dichos autores sí siguen esa proporción; que la sección de Tanabe (1990) y datos respectivos sí siguen el crecimiento cordobés e igualmente aontece con la imagen de González-Restrepo (2019).
- "Secciones frontales y modelo ontogénico del Nautilus", donde se constrastan las imágenes de las secciones frontales del Nautilus usadas en la miscelánea anterior con el modelo ontogénico 2D (Galo,2023) comprobando que la de Tanabe (1995) no se corresponde, pero sí las de Tanabe (1995) y González-Restrepo (2019).
Consecuentemente se marcaba como necesario la determinación de un tipo (holotipo) para la sección frontal y eso ha quedado reflejado en la miscelánea "Elección de Tipo para la sección frontal del Nautilus" en la que les aconsejo leer la el documento de instrucciones ya que en él se detalla el estudio realizado y las fuentes consultadas (incluidas también en la bibliografía de este artículo divulgador). El tipo elegido es el reflejado en la siguiente imagen, no obstante por cuestiones meramente personales —por haberlas obtenido González-Restrepo a petición mía y por ser cortes realizados sobre el Nautilus del museo de D'Arcy Thompson— también incluiré en el modelado 3D del Nautilus el citado corte de González-Restrepo (2019).
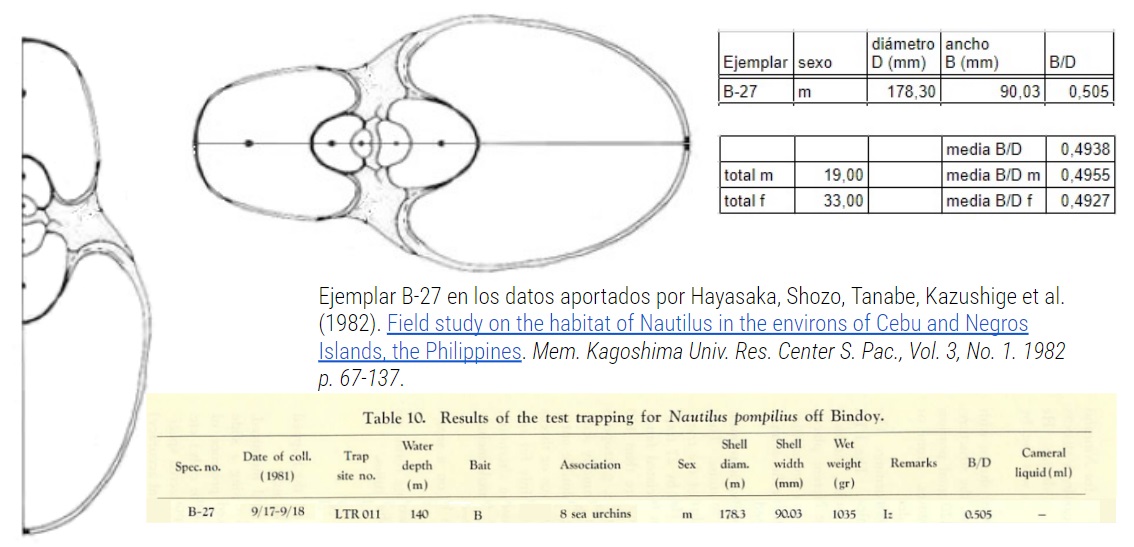
Tipo del Nautilus. Sección frontal Tanabe (1990).
Aproximación de la sección frontal y generación del modelo 3D uniforme asociado
Fijado el tipo para la sección frontal, se plantea la necesidad de obtener la ecuación paramétrica de la curva que la modela y para ello opté por aproximar la imagen de esta sección por una curva de Bézier. A partir de esa curva, según lo antes indicado, se genera el modelo 3D uniforme asociado. Pueden verse las imágenes siguientes y también interactuar con el recurso "Nautilus, modelado de la sección frontal con una curva de Bézier y modelo 3D uniforme asociado".
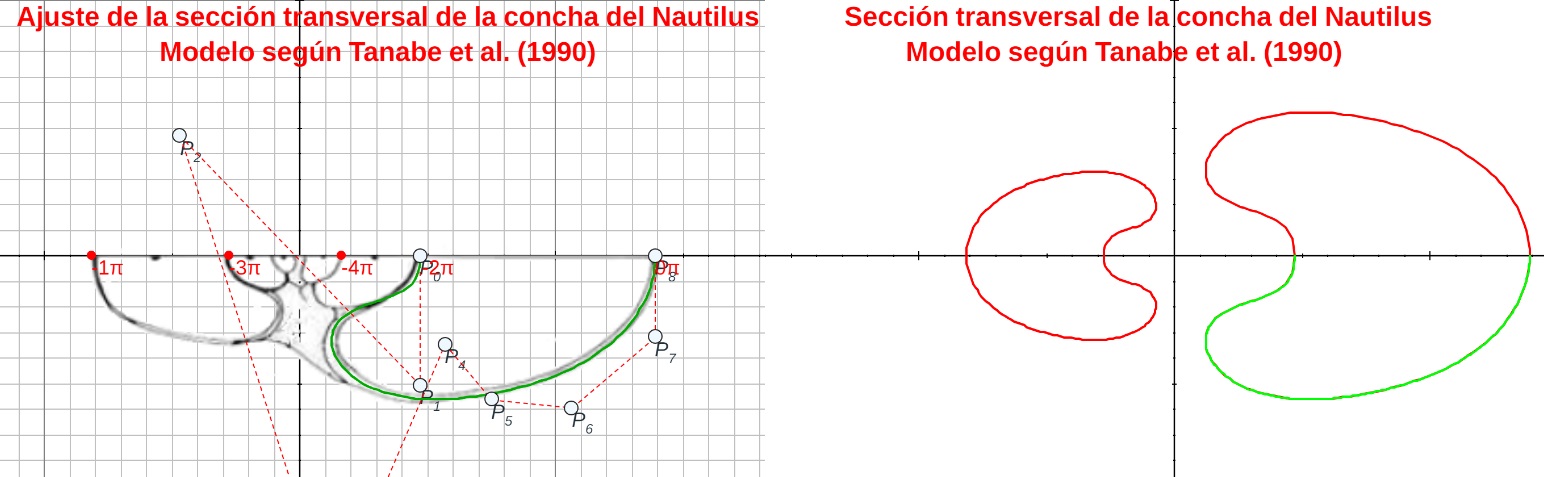
Aproximación de la sección frontal del Nautilus con una curva de Bézier
Modelo 3D asociado a la aproximación de la sección frontal mendiante una curva de Bézier (sin callo umbilical)
Con este recurso, también fue fácil obtener respuesta a la pregunta ¿cuál puede plantearse como el modelo teórico de esa sección frontal? La elipse se mostró como una alternativa evidente y en este punto he de reseñar que esta posibilidad ya la calibramos Ángel Cabezudo Bueno, Ildefonso Fernández Trujillo y yo en los trabajos previos a nuestro artículo "Sobre la forma y crecimiento cordobés del Nautilus Pompilius" (2016). En aquel momento no dispusimos de las fuentes científicas de Tanabe et al. que ahora se han usado aquí y no pudimos constatarlo fehacientemente, pero ahora sí. ¡Gracias Ángel! y ¡gracias Ildefonso! La intuición inicial se ha mostrado cierta en la yocto-yotta realidad en la que Ángel y yo habitamos. Para ti, Ildefonso, que ya habitas en el continuo matemático, todo esto es mera obviedad, pero mediante esta simplicidad matemática sentimos próxima tu satisfacción y compañía.
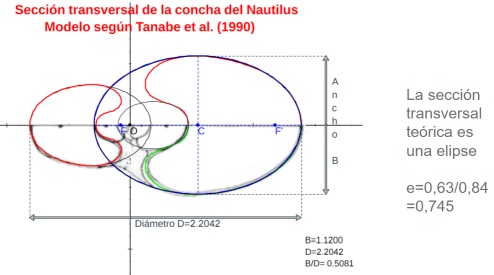
Modelo teórico de la sección frontal del Nautilus
Modelo teórico de la sección frontal y generación del modelo 3D uniforme asociado
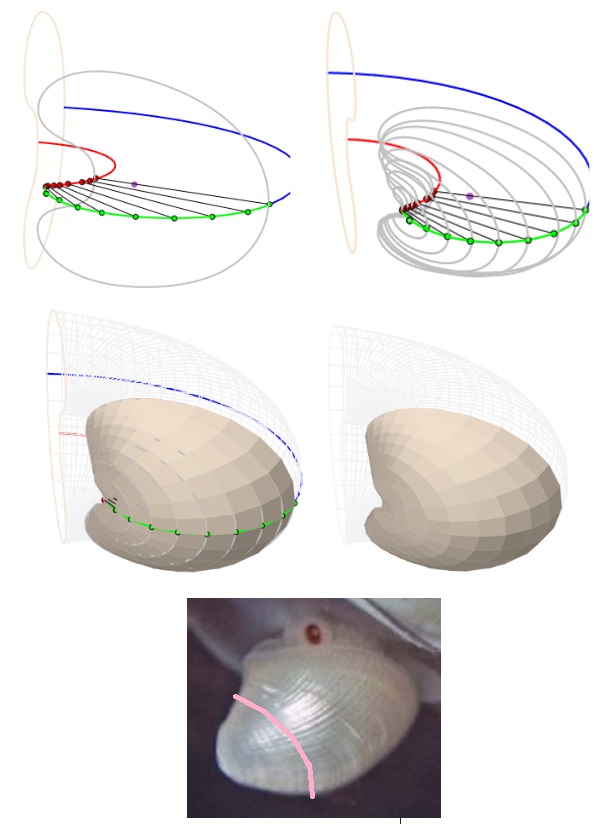
El modelo teórico de la concha ventral surgía de manera natural ligado a la forma elíptica y los salientes dorsales y el callo umbilical se mostraban fieles a ese carácter o impronta. Observad las siguientes imágenes y el recurso interactivo "Nautilus, modelo teórico de la sección frontal, de la sección umbilical y modelo 3D uniforme asociado".
Nota bene: En el primer verticilo puede observarse cierto desajuste entre el modelo teórico y la realidad, pero recordemos que estamos trabajando el modelo uniforme y, en él, obviamos la ontogenia del animal que se manifiesta de manera más evidente justo en ese primer verticilo.
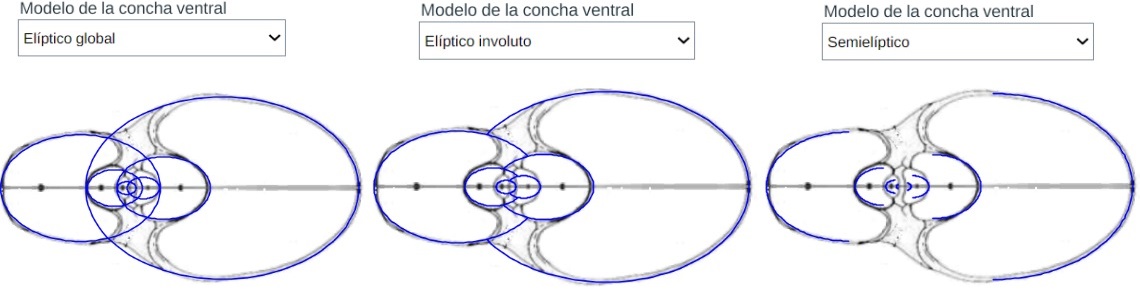
Modelo teórico de la pared ventral y de la dorsal (la pared dorsal es la ventral del verticilo anterior)
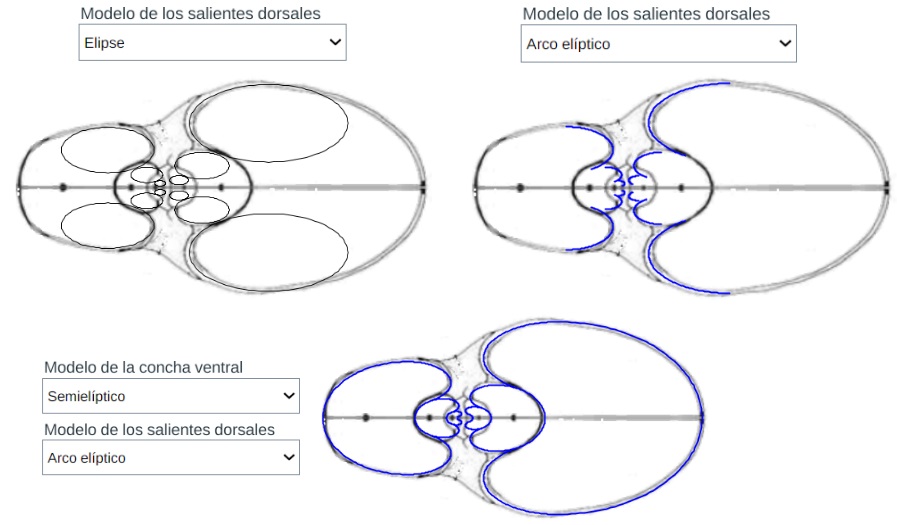
Modelo teórico de los salientes dorsales y de la concha sin el callo umbilical
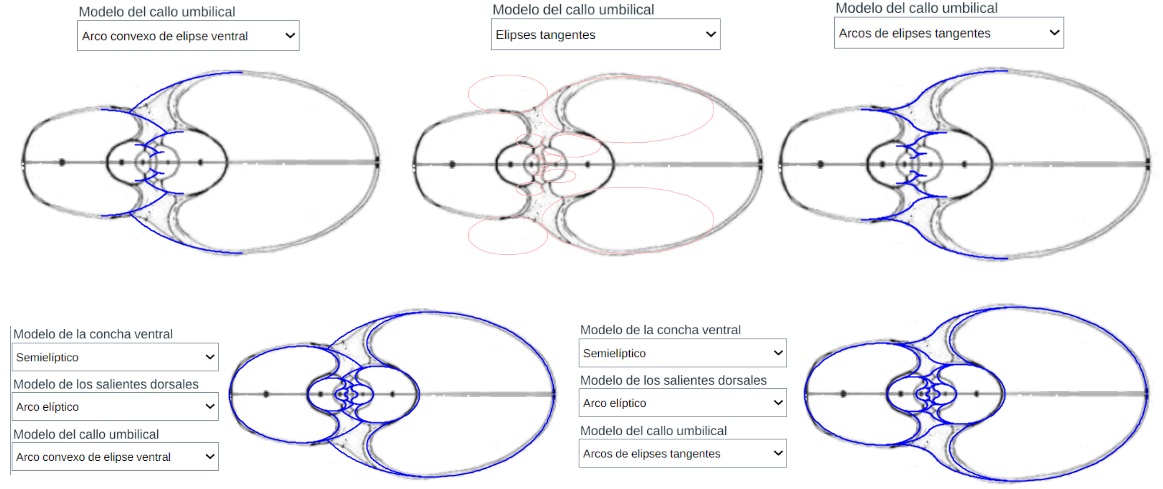
Modelo teórico del callo umbilical y de la concha con el callo
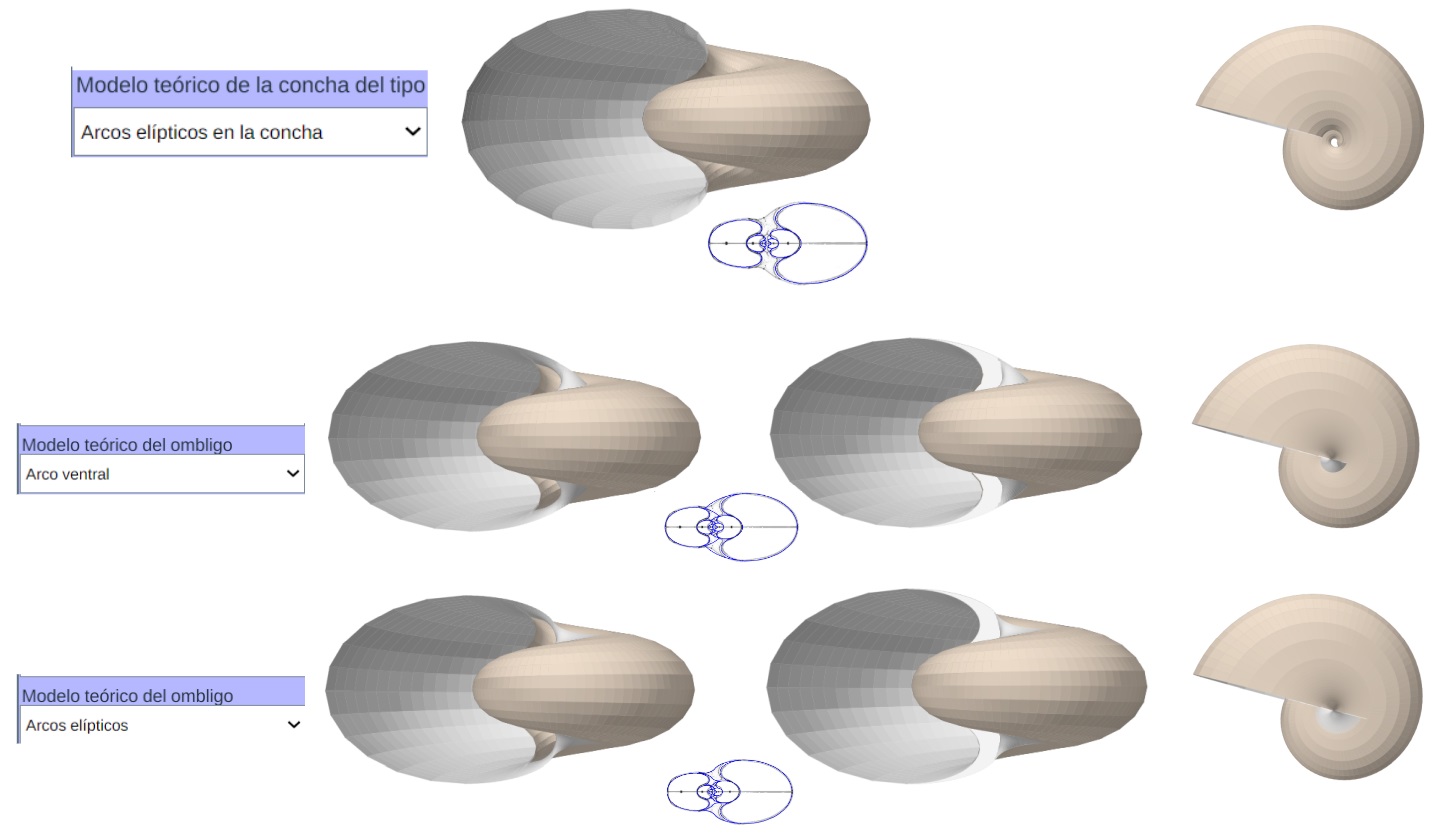
Modelo teórico 3D uniforme sin y con callo umbilical (con perfil ventral elíptico o con arcos elípticos)
La concha embrionaria inicial
En el modelo bidimensional ontogénico (Galo 2023) observamos que el primer septo amplifica el fragmacono embrionario y es el que marca el inicio de la pared ventral. Así pues, el eje que pasa por el punto de inicio de la pared ventral y el polo ventral marca el comienzo del modelo uniforme, en el caso 3D se corresponde con el plano que pasa por esos dos puntos y es perpendicular al plano sagital. Consecuentemente, parte de la cámara septal formada por el primer y segundo septo queda sin modelar y tiene un crecimiento diferenciado (es cuando el primer septo es el que está ampliándose). Para que en el modelo global no quede un vacío irreal he optado por seccionar transversalmente esa parte de la cámara y escalar la sección frontal teórica de la concha ajustándola a cada una de esas secciones (ver imagen siguiente), de esa manera el crecimiento se aborda teniendo siempre el mismo perfil, pero con una escala diferenciada acorde con las secciones que sí se conocen. Es una alternativa personal por la que he optado al no tener información al respecto en las fuentes consultadas y cuya aplicación matemática aporta cierto parecido con el aspecto que puede observarse en fotos de esa concha primigenia. No deja de ser una solución estética de compromiso sobre la que pido sean magnánimos.
La concha embrionaria inicial, una solución de compromiso
Aspectos abiertos
No ha mucho que un entrañable colega y amigo —Josep Maria Navarro Canut— me dijo: "¡Lo que está dando de sí el Nautilus!" y ¡es verdad!, ello está aconteciendo así. Aquí, en particular, y en nuestro contexto vital en general, es evidente que es tan corto nuestro conocer y tan amplio nuestra necesidad de saber que cualquier detalle es un nuevo hito sobre el que investigar y aprender. Así pues, ¿hay algo más que modelar matemáticamente en el Nautilus?, ¿qué opinan? Mi respuesta es afirmativa. Yo trato de escuchar al Nautilus y, la realidad, es que no para de susurrar. Otra cuestión es que yo sepa escuchar e interpretar adecuadamente sus indicaciones, si bien les garantizo que empeño no deja de haber nunca en mí. ¿Qué aspectos quedan abiertos aún, por ahora?, lo que surja después llegará y lo trataremos en su momento. Citemos lo siguiente:
- Si bien para el modelado 3D se ha considerado la sección transversal de la concha, la abertura de ésta no coincide con la sección, sino que presenta un perfil que no es plano, sino cóncavo-convexo, desde las primeras etapas vitales.
-
En la sección sagital los septos están modelados por espirales cordobesas, ¿pero cuál es la superficie que modela tridimensionalmente a estos? A priori, su modelado se presenta complicado y difícil. Se observa, y parece lógico lo que acontece, que la intersección de los septos con la concha se asemeja al perfil de la abertura, pero ¿cómo es en sí el diseño 3D global de los mismos?
El perfil cócavo-convexo de la boca del Nautilus y los septos (¡un gran problema abierto!)
- Finalmente, el modelo ontogénico 3D que incluiría como puntos pendientes a detallar la concha inicial embrioanaria, las particularidades de los septos en el primer verticilo y la confluencia de la pared dorsal con la concha inicial en la transición del primer verticilo .
Modelo matemático tridimensional uniforme
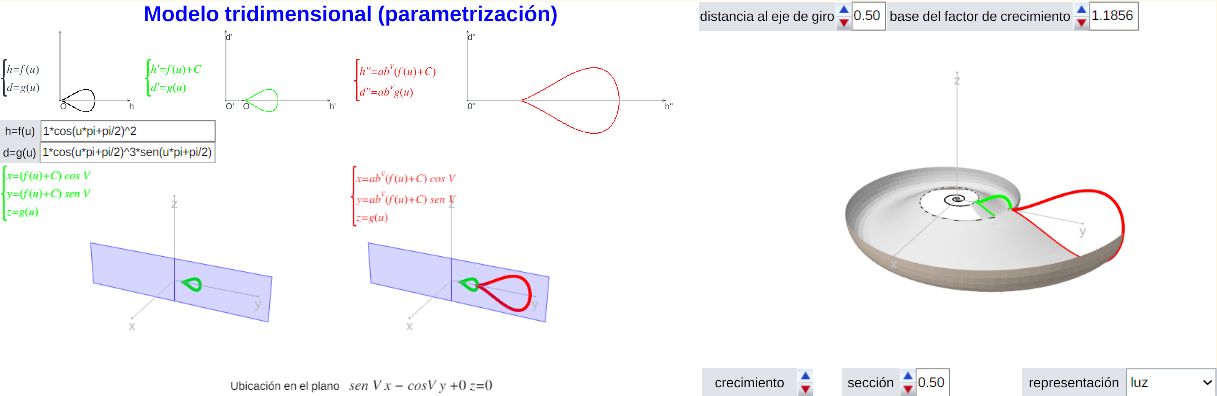
El modelo tridimensional uniforme al que hemos llegado está reflejado en el siguiente recurso interactivo. A través de los parámetros disponibles puede verse su base constructiva y su representación 3D. En estas indicaciones se hace una descripción del modelo y de cada uno de esos parámetros. ¡Le invitamos a interactuar con él!
Recurso interactivo donde se construye el modelo tridimensional uniforme del Nautilus. Acceso a ventana completa y a las indicaciones.
Finalmente en las siguientes imágenes animadas podemos observar ese modelo matemático de la concha y un detalle del callo umbilical:
El modelo matemático 3D uniforme del Nautilus (Arcos elípticos en la concha y arcos elípticos en el callo umbilical)
Detalle del callo umbilical en el modelo matemático 3D uniforme del Nautilus (Arcos elípticos en el callo umbilical)
Espero que les haya parecido interesante y puesto que quedan tareas abiertas no descarto dirigirme a ustedes con nuevos logros si consiguiera alcanzarlos.
¡Hasta pronto! y ¡qué tengan un productivo y feliz año 2024!
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016) .Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
Galo J.R. (2023). Modelo ontogénico matemático del Nautilus. Blog de la Red Educativa Digital Descartes.
González-Restrepo, F. (2019). Cortes del Nautilus a partir de la digitalización 3D del museo Dundee. Red Descartes Colombia.
Hayasaka, Shozo, Tanabe, Kazushige et al. (1982). Field study on the habitat of Nautilus in the environs of Cebu and Negros Islands, the Philippines. Mem. Kagoshima Univ. Res. Center S. Pac., Vol. 3, No. 1. 1982 p. 67-137.
Moseley Henry, (1838). On the geometrical forms of turbinated and discoid shellsPhilPhil. Trans. R. Soc.128: 351–370.
Raup, D. M. (1961). The Geometry of Coiling in Gastropods. Proceedings of the National Academy of Sciences of the United States of America, 47(4), 602–609.
Raup, D. M. (1966). Analysis of Shell Coiling: General Problems. Journal of Paleontology, Vol. 40(5), 1178-1190.
Tanabe, Kazushige(1985). Record of Trapping Experiment. In: Hayasaka, S. (ed.) Marine ecological studies on the habitat of Nautilus pompilius in the environs of Viti Levu, Fiji. Kagoshima University, Research Center for the South Pacific, Occasional Papers, 4, 10-17.
Tanabe, Kazushige(1988). Record of Trapping Experiment. Kagoshima University, Research Center for the South Pacific, Occasional Papers, No. 15, p.5-15.
Tanabe, Kazushige & Hayasaka, Shozo & Tsukahara, Junzo. (1985). Morphological analysis of Nautilus pompilius. In: Hayasaka, S. (ed.) Marine ecological studies on the habitat of Nautilus pompilius in the environs of Viti Levu, Fiji. Kagoshima University, Research Center for the South Pacific, Occasional Papers. 4. 38-49.
Tanabe, Kazushige & Tsukahara, Junzo. (1987). Biometric Analysis of Nautilus pompilius from the Philippines and the Fiji Islands. In book: Nautilus: The Biology and Paleobiology of a Living Fossil. Chapter: 7. Publisher: Plenum Publishing Corporation. Editors: W. Bruce Saunders and Neil H. Landman.
Tanabe, Kazushige & Tsukahara, Jyunzo & Hayasaka, Shozo. (1990). Comparative morphology of living Nautilus (Cephalopoda) from the Philippines, Fiji and Palau. Malacologia 31(2):297-312.
Tanabe, Kazushige & Tsukahara, Jyunzo & Shinomiya, Akihiko & Oki, Kimihiko. (1991). Notes on Nautilus Pompilius captured from Port Moresby area, Papua New Guinea. Kagoshima Univ. Res. Center S. Pac., Occasional Papers, No. 21. p. 33-38.
Tanabe, Kazushige & Tsukahara, Junzo. (1995). Morphological Analysis of Living Nautilus from Palau. Kagoshima Univ. Res. Center S. Pac., Occasional Papers, No. 27. p. 41-55.
Thompson, D’A. W., (1917). On growth and Form. Cam. Univ. Press
Realizado en el año 2023, vigésimo quinto aniversario del Proyecto Descartes
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
La concha del Nautilus, un prototipo de belleza natural ampliamente divulgado, es un icono que habitualmente se utiliza para mostrar cómo la Naturaleza hace matemáticas. Pero el canon aúreo en el que insistente y cansinamente se le encuadra es erróneo. ¡El Nautilus es cordobés!, así lo demostramos en nuestro modelo uniforme (Galo J.R., Cabezudo A. y Fernández I., 2016) —modelo donde se considera que el crecimiento que acontece en todas las etapas vitales es siempre el mismo—. No obstante, como es habitual en todo ser vivo, la ontogenia de este animal presenta alometrías que quedan reflejadas en su concha y que pedían ser matemáticamente desentrañadas. Esto es lo que se detalla en el "Modelo ontogénico matemático del Nautilus" que aquí les presento.
Le invito a conocer este modelo e inicialmente, para situarle, le mostraré el cuaderno de bitácora de la investigación (que sintetiza lo publicado en artículos anteriores en este blog de RED Descartes) y posteriormente le detallaré el modelo matemático ontogénico en sí.
Queda cubierta una etapa ardua, y simultáneamente muy gratificante, en la que el Nautilus ha ido progresivamente activando mis neuronas hasta lograr descodificar y comprender el porqué matemático del rastro vital que va esculpiendo a medida que conforma su concha. Pero todo nuevo conocimiento más que actuar como cierre lo que suele proceder es como catalizador de nuevos objetivos y, por ello, mis siguientes pasos se centrarán en atisbar qué acontece fuera del la sección sagital bidimensional del Nautilus analizada y descrita en este artículo. La concha del Nautilus es tridimensional y, de nuevo, mi oído y el resto de sentidos incluido el sentido matemático, quedan prestos a desentrañar los susurros de mi paisano cordobés. Les emplazo a que más adelante lean mis avances al respecto y a que compartan sus opiniones y observaciones... tengan paciencia. Hasta pronto.
Cuaderno de bitácora
En la siguiente presentación tiene reflejado, sintéticamente, el camino seguido en esta investigación. Se incluyen hiperenlaces a artículos en los que puede profundizar sobre algún aspecto concreto.
Cuaderno de bitácora (puede controlar este recurso con el menú ፧ ubicado en la parte inferior) o verlo en este pdf:
Modelo ontogénico matemático del Nautilus
A partir del análisis previo he llegado al Modelo ontogénico del Nautilus que se desglosa en la siguiente presentación.
Modelo ontogénico matemático del Nautilus.
Todo lo anterior puede observarse en el siguiente recurso interactivo, que por defecto se presenta como una animación, pero puede pasar a modo manual sin más que pulsar el botón inferior izquierda, que está etiquetado con la imagen de una mano, y usar el control "paso".
Recurso interactivo donde se describe el modelo ontogénico matemático del Nautilus. Acceso a ventana completa y a las indicaciones.
Este modelo ontogénico puede observarse en la siguiente imagen animada. Al no tener datos sobre la temporalización real del crecimiento del Nautilus se ha asignado el mismo tiempo a cada septo.
Imagen animada del modelo ontogénico matemático del Nautilus
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016 a) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
Greenwald L., Ward P.D. (2010) Buoyancy in Nautilus. In: Saunders W.B., Landman N.H. (eds) Nautilus. Topics in Geobiology, vol 6. Springer, Dordrecht.
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Tanabe K. & Uchiyama, K. 1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.
Thompson, D’A. W., (1917). On growth and Form. Cam. Univ. Press.
Ward, P. (1979). Cameral liquid in Nautilus and ammonites. Paleobiology, 5(1), pp. 40-49.
Ward, P., Greenwald, L., & Magnier, Y. (1981). The chamber formation cycle in Nautilus macromphalus. Paleobiology, 7(4), 481-493. doi:10.1017/S0094837300025537
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Os números complexos
Seção: iCartesiLibri
Bloco: Números
Unidade: Números e operações
Nível/Idade: Terceiro Ano do Ensino Médio.15 aos 17 anos.
Idioma: Português do Brasil
Autores: María José García Cebrian
Tradução: Lindberg Barbosa Lira de Almeida
Editora: Red Educativa Digital Descartes
ISBN: 978-84-18834-68-4
Haz clic aquí para ver una versión en pdf
Clique na imagem para abrir o recurso
| Código para incorporar como iframe |
Código para abrir na janela pop-up |
Você pode encontrar todos outros livros interativos em
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Esta obra está autorizada com uma Licença
Creative Commons Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
