INTRODUCCIÓN

En esta miscelánea se aborda la modelación tridimensional de las conchas discoidales.

Según Raup, D. M. (1966) en el artículo "Analysis of Shell Coiling: General Problems." toda concha puede modelarse en base a cuatro parámetros esenciales: curva generatriz o sección transversal, la distancia o posición relativa de la curva generatriz respecto al eje de giro, factor de crecimiento y la traslación en la dirección del eje de giro (sólo para conchas turbinadas). Aquí, partiendo de la ecuación parámetrica de la curva generatriz, realizamos una adaptación del modelo de Raud con objeto de obtener la superficie que modela a toda concha discoidal, la cual sigue un crecimiento gnomónico geométrico, es decir si se considera la trayectora que seguiría un punto al crecer la concha ésta sería una espiral logarítmica.

OBJETIVOS

1. Modelar las conchas discoidales a nivel tridimensional.
2. Visualizar cómo influyen los parámetros indicados por Raud en la modelación de conchas.

INSTRUCCIONES

En la escena se distinguen tres espacios:

1. A la izquierda en la parte superior se refleja la curva generatriz que representa la sección frontal o coronal de la concha.
   
   
   
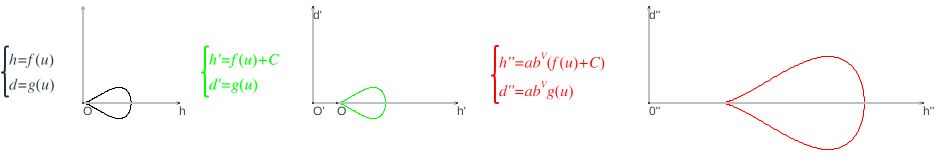
   Puede observarse la gráfica y la ecuación paramétrica de:
   • La sección frontal (en color negro)
   • La sección frontal trasladada según el valor del control numérico etiquetado como "distancia al eje de giro" (en color verde).
   • la sección frontal trasladada y escalada con factor de escala exponencial ab^V (en color rojo).
Se tienen dos controles en los que puede definir la curva generatriz escribiendo la expresión funcional que desee sin más restricción de denominar el parámetro como u.
2. A la izquierda en la parte inferior se ubican las secciones anteriores en el plano de ecuación sen V x - cos V y +0 z =0 que representa al plano coronal y que gira alrededor del eje Oz según el valor del ángulo V.
   
   
   
   
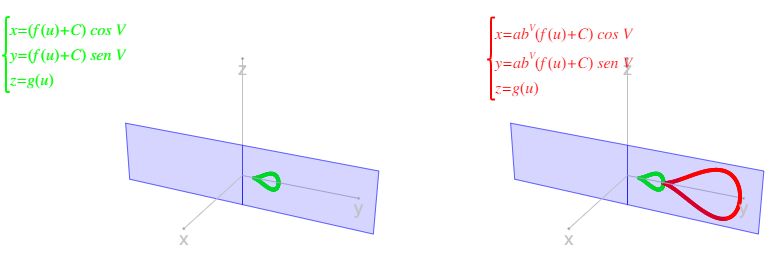
3. En la parte derecha se representa la concha tridimensional generada a partir de la sección frontal considerada dependiendo de los parámetros "distancia al eje de giro" y "base del factor de crecimiento" que pueden modificarse con los controles numéricos ubicados en la parte superior.
   
   
   
   
   
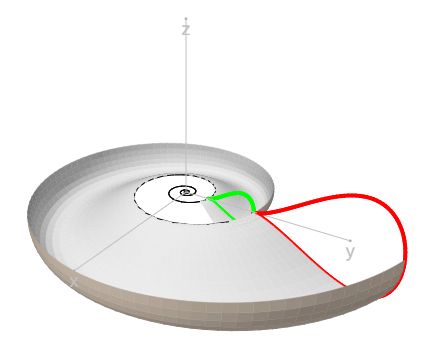
   El factor de crecimiento se corresponde con b^2π, donde b es la base que se modifica en el control "base del factor de crecimiento". El valor por defecto que se muestra es b=1.185580 que se corresponde con el crecimiento cordobés.
   
   Al cambiar la distancia al eje pueden obtenerse conchas involutas (se interseca la concha al crecer con la concha del giro anterior) o evolutas (no se intersecan). Ese efecto también se obtiene según el valor del factor de crecimiento y también depende de la forma de la sección frontal.
   
   También se tienen tres controles ajenos al modelo de la concha y que sólo cambian la presentación visual de la gráfica tridimensional de la concha:
   • crecimiento: que permite simular el crecimiento de la concha.
   • sección: parte de la sección transversal que se representa en 3D (de 0 a 1). El objetivo es poder ver el interior de la concha.
   • representación: que permite dibujar la concha bien como una retícula o malla, o bien como una superficie.

Realizado en el año del vigésimo quinto aniversario del Proyecto Descartes