
Título de la obra:
Cuadrados mágicos aditivos y multiplicativos
Autor:
Luis Barrios Calmaestra
Red Educativa digital Descartes
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-87-5

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Un cuadrado mágico aditivo de orden n está formado por un conjunto de números dispuestos en n filas y n columnas, de forma que la suma de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre la misma. A esta suma se le llama constante mágica.
Un cuadrado mágico multiplicativo de orden n está formado por un conjunto de números dispuestos en n filas y n columnas, de forma que el producto de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre la misma. A este producto se le llama constante mágica.
Sobre el origen y el interés de los cuadrados mágicos a lo largo de la historia hay muchas publicaciones y se pueden encontrar multitud de cuadrados mágicos de cualquier orden, conteniendo a su vez cuadrados mágicos de orden inferior y con muy diversas propiedades que aumentan su complejidad y su admiración por ellos, constituyendo auténticas obras de ingeniería aritmética.
En este libro se exponen algunos de los cuadrados mágicos aditivos más conocidos, la forma de construirlos, sus propiedades y la forma de generar, a partir de ellos, otros cuadrados mágicos con las mismas características. También se explica como construir, a partir de los cuadrados mágicos aditivos, otros cuadrados mágicos multiplicativos con propiedades similares a los primeros.
Dadas las extraordinarias características que tienen estos objetos matemáticos, hacen pensar que puedan existir un número muy reducido de ellos, sin embargo, aunque sean solo unos pocos los conocidos, es sorprenderte comprobar la existencia de infinitos cuadrados mágicos tanto aditivos como multiplicativos.
Antes de empezar el estudio de los cuadrados mágicos de orden 3, vamos a justificar la no existencia de cuadrados mágicos de orden 2.
Un cuadrado mágico aditivo o multiplicativo de orden 2 estaría formado por cuatro números distintos dispuestos en 2 filas y 2 columnas, de forma que la suma o el producto de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre igual. A esta suma o producto se le llama constante mágica.
Si el cuadrado mágico aditivo es de la forma:
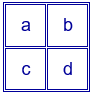
Se tiene que verificar:
$a+b=c+d=a+c=b+d=a+d=b+c$
De lo que se deduce:
$a=b=c=d$
Entonces, no puede existir un cuadrado mágico aditivo de orden 2 con los cuatro números distintos. Un razonamiento similar nos lleva a la misma conclusión para los cuadrados mágicos multiplicativos.
Como no tiene interés el estudio de estos cuadrados con los cuatro números iguales, pasemos al etudio de cuadrados mágicos aditivos y multiplicativos de orden superior a 2.
Un cuadrado mágico aditivo de orden 3 está formado por un conjunto de números dispuestos en 3 filas y 3 columnas, de forma que la suma de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre la misma. A esta suma se le llama constante mágica.
El más conocido, sin duda, es el cuadrado mágico de orden tres con los nueve primeros números naturales, de constante mágica 15, de origen chino y del año 2800 a. C.
La constante mágica se calcula dividiendo la suma de todos los números utilizados entre el orden del cuadrado.
$\displaystyle\frac{1+2+3+4+5+6+7+8+9}{3}=\frac{45}{3}=15$
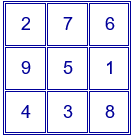
La suma de los números situados en cada una de las filas, en cada una de las columnas y en cada una de las diagonales es igual a 15.
$2+7+6=9+5+1=4+3+8=15$
$2+9+4=7+5+3=6+1+8=15$
$2+5+8=6+5+4=15$
Se colocan los números del 1 al 9 según se observan en la primera figura. Los números situados en el cuadrado de 3x3 conservan su posición en el cuadrado mágico. Los números que quedan fuera del cuadrado se colocan en la casilla opuesta, según se observa en la tercera figura, completando así el cuadrado mágico.
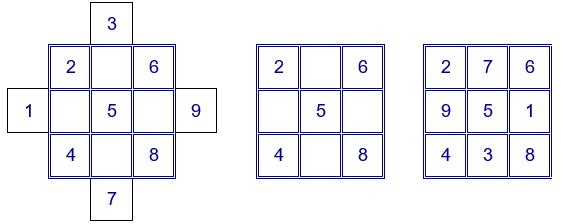
Este método fue publicado por el francés Simon de la Loubère en 1691, pero ya era conocido anteriormente por astrólogos orientales.
• Se empieza colocando el primer número en la casilla central de la fila superior.
• A continuación se colocan el resto de números desplazándonos una casilla hacia arriba y otra hacia la derecha (entendiendo que si estamos en la fila superior hay que continuar por la inferior y si estamos en columna de la derecha hay que continuar por la de la izquierda).
• En caso de que la casilla que corresponda esté ocupada, se coloca el número debajo del número anterior.
Construcción paso a paso de un cuadrado mágico de orden 3 con este procedimiento.
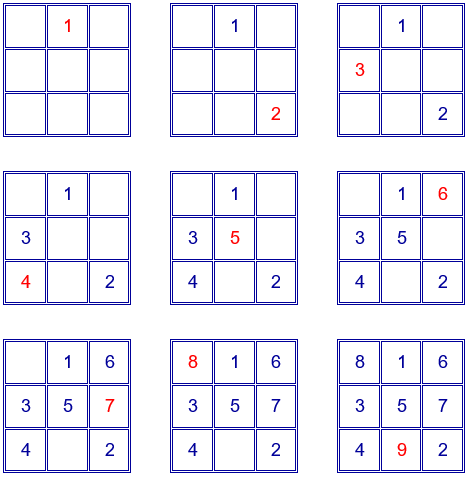
Si a este cuadrado mágico se le realiza una simetría respecto de una de las diagonales, se obtiene el cuadrado mágico anterior.
Un cuadrado latino de orden 3 es un cuadrado de 3 filas y 3 columnas en las que se colocan 3 números, de forma cada número aparece 3 veces y que en cada fila y en cada columna aparecen los 3 números una sola vez. No se exige esta condición para las diagonales.
Utilizando cuadrados latinos, se pueden construir cuadrados mágicos de orden tres.
Se expresan los números del 1 al 9 como las siguientes sumas:
| $1=0+1$ | $2=0+2$ | $3=0+3$ |
| $4=3+1$ | $5=3+2$ | $6=3+3$ |
| $7=6+1$ | $8=6+2$ | $9=6+3$ |
En el primer sumando aparecen los números 0, 3 y 6. En el segundo, los números 1, 2 y 3.
Se construyen ahora dos cuadrados de tres filas y tres columnas con los dos conjuntos de números, de forma que, en cada fila y en cada columna no se repita ningún número. En las dos diagonales principales no es obligatorio que los números sean distintos. De hecho, es imposible construir cuadrados latinos de orden 3 sin repetir números en las diagonales.
Sumando los números de las casillas que ocupan la misma posición en ambos cuadrados se obtiene, en algunos casos, un cuadrado mágico aditivo. Hay que evitar la repetición de números en el cuadrado final.
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos aditivos sumando los números de dos cuadrados latinos. Construye en primer lugar los dos cuadrados latinos moviendo los números al interior de los cuadrados superiores y, posteriormente, pulsa el botón "Comprobar" para comprobar si lo has hecho correctamente.
En esta escena de Descartes puedes elegir los números para construir los cuadrados latinos. Escribe en cada casilla los números escogidos y después pulsa el botón "Comprobar" para ver si se obtiene un cuadrado mágico aditivo.
El cuadrado mágico inicial, construido con los 9 primeros números naturales, se obtiene como suma de los números de los dos cuadrados latinos siguientes:
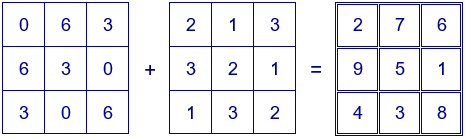
Los números de cada uno de los cuadrados latinos están en progresión aritmética. Para poder construir con ellos un cuadrado mágico se ha repetido el término central en diagonales distintas.
Generalizando el caso anterior, se pueden construir cuadrados mágicos aditivos sumando dos cuadrados latinos formados por los números a-d1, a, a+d1 y b-d2, b, b+d2.
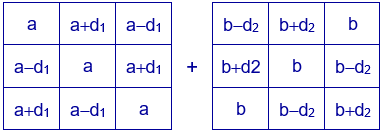
Se obtiene el cuadrado mágico de constante mágica 3a+3b.

En la siguiente escena de Descartes puedes construir cuadrados mágicos aditivos de orden tres, a partir del procedimiento anterior, conociendo solamente 4 números. Modifica los valores de los controles a, d1, b y d2.
También se puede construir un cuadrado mágico aditivo de orden 3 a partir de tres números cualesquiera a, b y c. Este procedimiento es similar al anterior, pero vamos a plantearlo de forma distinta.
• Se empieza colocando uno de los números, por ejemplo a, en la casilla central.
• Una de las diagonales se completa con los números que resultan de las operaciones a-b y a+b. La suma de los números de esta diagonal es 3a.
• La otra diagonal se completa con los resultados de las operaciones a-c y a+c. La suma de los números de esta diagonal también es 3a.
• La constante mágica de este cuadrado es 3a. Ahora ya se puede calcular la casilla central de cada uno de los lados, para que su suma coincida con la constante mágica, obteniendo los números: a+b-c, a+b+c, a-b-c y a-b+c.
Se obtiene el siguiente cuadrado mágico aditivo:
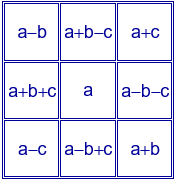
Para los valores a=5, b=3 y c=1 se obtiene el primer cuadrado mágico aditivo de orden 3.
En la siguiente escena de Descartes puedes construir cuadrados mágicos aditivos de orden tres, a partir del procedimiento anterior, modificando los valores de a, b y c.
Si a todos los números del cuadrado mágico se le suma o se le resta un mismo número, se multiplican o dividen por un mismo número, o se realizan ambas transformaciones a la vez, se obtiene otro cuadrado mágico.
Por ejemplo:
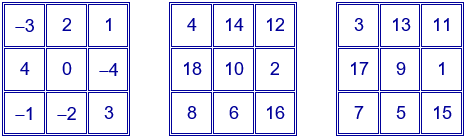
En el primero se ha restado 5 a todos los números del cuadrado mágico inicial, obtienendo un cuadrado mágico con números enteros y de constante mágica 0.
En el segundo se han multiplicado por 2 los números del cuadrado mágico inicial, obteniendo un cuadrado mágico formado por los nueve primeros números pares y de constante mágica 30.
En el tercero se han multiplicado por 2 los números del cuadrado mágico inicial y se le ha restado 1, obteniendo un cuadrado mágico formado por los nueve primeros números impares y de constante mágica 27.
Al realizar giros o simetrías en cualquier cuadrado mágico se obtiene otro cuadrado mágico con las mismas características.
En la siguiente escena de Descartes puedes construir cuadrados mágicos aditivos de orden tres modificando los valores de a (número por el que se multiplican los números del cuadrado inicial) y de b (número que se suma o se resta al resultado anterior).
Un cuadrado mágico multiplicativo de orden 3 está formado por un conjunto de números dispuestos en 3 filas y 3 columnas, de forma que el producto de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre el mismo. A este producto se le llama constante mágica.
Aplicando el producto de potencias con la misma base, a partir de cualquier cuadrado mágico aditivo, se puede construir un cuadrado mágico multiplicativo con potencias de base cualquier número natural distinto de 1 y de exponente cada uno de los números del cuadrado mágico aditivo. Por ejemplo, si n es un número natural mayor que 1, se pueden construir infinitos cuadrados mágicos multiplicativos, de orden 3 y de constante mágica $n^{15}$.
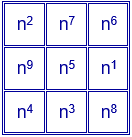
Para $n=2$ se obtiene el cuadrado mágico multiplicativo de constante mágica $2^{15}=32768$.
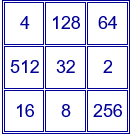
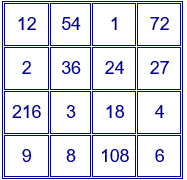
El cuadrado mágico multiplicativo de orden 3 más conocido y con los números más pequeños es el siguiente:
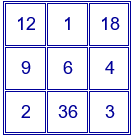
• El producto de los números situados en cada fila, en cada columna y en cada una de las diagonales es igual a 216.
$12\cdot1\cdot18=9\cdot6\cdot4=2\cdot36\cdot3=216$
$12\cdot9\cdot2=1\cdot6\cdot36=18\cdot4\cdot3=216$
$12\cdot6·3=18\cdot6\cdot2=216$
• Está formado por todos los divisores de 36. El número 36 se factoriza como $2^{2}\cdot3^{2}$ y tiene $(2+1)\cdot(2+1)=9$ divisores.
$div(36) = \{1, 2, 3, 2^{2}, 2·3, 3^{2}, 2^{2}·3, 2·3^{2}, 2^{2}·3^{2}\}$
• La constante mágica se obtiene como la raíz cúbica del producto de todos los divisores, $2^{9}\cdot3^{9}=6^{9}=10077696$.
$\displaystyle\sqrt[3]{1\cdot 2\cdot3\cdot4\cdot6\cdot9\cdot12\cdot18\cdot36}=\sqrt[3]{6^9}=6^3=216$
• La casilla central se obtiene como la raíz cúbica de la constante mágica, cuyo resultado es $2\cdot3=6$.
Generalizando el cuadrado mágico multiplicativo anterior, si p y q son dos números primos, el número de divisores de $(pq)^{2}=p^{2}q^{2}$ es igual a $(2+1)(2+1)=9$. Son los siguientes:
$div(p^{2}q^{2}) = \{ 1, p, q, pq, p^{2}, q^{2}, p^{2}q, pq^{2},p^{2}q^{2} \}$
Con los nueve divisores anteriores se puede formar un cuadrado mágico multiplicativo de orden 3, de la siguiente forma:
• La constante mágica se obtiene multiplicando todos los números del cuadrado mágico, es decir, multiplicando todos los divisores y calculando la raíz cúbica del resultado obtenido. El producto de todos los divisores es $p^{9}q^{9}$. Su raíz cúbica es $p^{3}q^{3}$.
• Se empieza colocando en la casilla central el número $pq$, que se obtiene como la raíz cúbica de la constante mágica.
• Se coloca a continuación el número $p^{2}q^{2}$. Solo hay dos grupos de tres números que, junto con $p^{2}q^{2}$, tengan como producto $p^{3}q^{3}$. Son $1, pq, p^{2}q^{2}$ y $p, q, p^{2}q^{2}$. Si el número que queremos colocar se sitúa en una esquina, debería haber tres grupos de tres números con producto la constante mágica. Como solo pertenece a dos grupos, se debe colocar en la casilla central de uno de los lados. Lo colocamos en la casilla inferior central.
• Se completan la columna central y la fila inferior. En la fila inferior da igual el orden de los elementos $p$ y $q$.
• El resto del cuadrado se puede completar añadiendo los elementos que faltan para completar, en primer lugar, las diagonales y, posteriormente, las columnas.
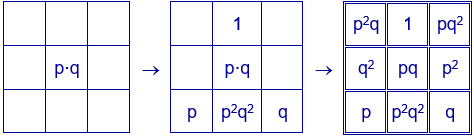
Se pueden construir infinitos cuadrados mágicos mediante este procedimiento, siendo $p$ y $q$ dos números primos cualesquiera. Para $p=2$ y $q=3$ se obtiene el cuadrado mágico multiplicativo anterior con los divisores de $6^{2}=36$ y de constante mágica $6^{3}=216$.
Si $p$, $q$, o ambos no son primos, el procedimiento también es válido, aunque en este caso el cuadrado mágico no contiene todos los divisores de $p^{2}q^{2}$. Para algunos valores no primos, pueden aparecer números repetidos en el cuadrado mágico.
Al realizar giros o simetrías en el cuadrado se obtiene otro cuadrado mágico con las mismas características.
Si a todos los números del cuadrado mágico se multiplica o se dividen por un mismo número, se elevan a un mismo exponente o se extrae una raíz del mismo índice, o se realizan ambas transformaciones a la vez, se obtiene otro cuadrado mágico. Por ejemplo, si vididimos por 6 el cuadrado mágico multiplicativo se obtiene otro cuadrado mágico multiplicativo con números racionales y de constante mágica 1:
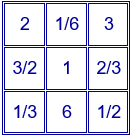
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos multiplicativos de orden tres dando valores a los números p y q. Comprueba lo comentado en la página anterior sobre si p y q son o no primos.
Un procedimiento descrito para la construcción de cuadrado mágicos aditivos ha sido a partir de dos cuadrados latinos. También este método se puede utilizar para la construcción de cuadrados mágicos multiplicativos.
Se construyen ahora dos cuadrados latinos de tres filas y tres columnas con dos conjuntos de números, de forma que, en cada fila y en cada columna no se repita ningún número. En las diagonales no es obligatorio que los números sean distintos. Multiplicando los números de las casillas que ocupan la misma posición en ambos cuadrados se obtienen un cuadrado mágico multiplicativo.
El cuadrado mágico del ejemplo anterior se obtiene multiplicando los dos cuadrados latinos siguientes:
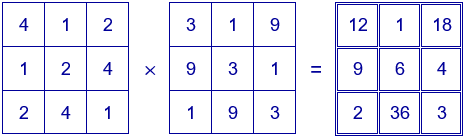
Y el cuadrado mágico con los divisores de $p^{2}q^{2}$ se obtiene multiplicando estos dos cuadrados latinos:
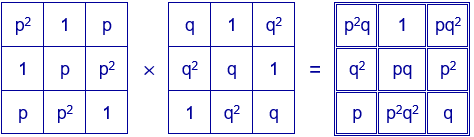
Los números de cada uno de los cuadrados latinos están en progresión geométrica. Para poder construir con ellos un cuadrado mágico se ha repetido el término central en diagonales distintas.
Generalizando el caso anterior, se pueden construir cuadrados mágicos multiplicativos multiplicando dos cuadrados latinos formados por los números $a$, $ar_1$, $ar_1^{2}$ y $b$, $br_2$, $br_2^{2}$.
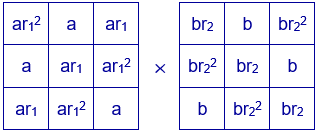
Se obtiene el cuadrado mágico de constante mágica $a^{3}b^{3}r_1^{3}r_2^{3}$.
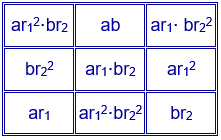
Para $a=1$, $r_1=p$, $b=1$ y $r_2=q$ se obtiene el cuadrado mágico multiplicativo de la página anterior.
En la siguiente escena de Descartes puedes construir cuadrados mágicos multiplicativos de orden tres, a partir del procedimiento anterior, modificando los valores de a, r1, b y r2.
En esta escena de Descartes puedes elegir los números para construir los cuadrados latinos. Escribe en cada casilla los números escogidos y después pulsa el botón "Comprobar" para ver si se obtiene un cuadrado mágico multiplicativo.
Si en un cuadrado mágico aditivo o multiplicativo, la suma o el producto de los números de las dos diagonales no coincide con la constante mágica, el cuadrado recibe el nombre de semimágico.
Existe un cuadrado semimágico multiplicativo de orden 3 muy interesante porque, aunque el producto de los números de cada una de las diagonales no coincide con la constante mágica, sí coincide el producto de los números de las dos diagonales. Se obtiene como producto de dos cuadrados latinos.
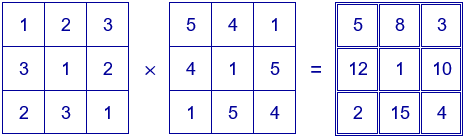
Propiedades:
• El producto de los números situados en cada fila es igual a 120.
$5\cdot8\cdot3=12\cdot1\cdot10=2\cdot15\cdot4=120=5!$
• El producto de los números de cada columna es igual a 120.
$5\cdot12\cdot2=8\cdot1\cdot15=3\cdot10\cdot4=120=5!$
• No verifican esta propiedad las diagonales, pero sí se verifica que el producto de los números de las dos diagonales juntas es igual a 120.
$(5\cdot1\cdot4)\cdot(3\cdot1\cdot2)=120=5!$
Un cuadrado mágico aditivo de orden 4 está formado por un conjunto de números dispuestos en 4 filas y 4 columnas, de forma que la suma de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre la misma. A esta suma se le llama constante mágica.
La constante mágica se calcula dividiendo la suma de todos los números utilizados entre el orden del cuadrado. Si el cuadrado se construye con los 16 primeros números naturales, la constante mágica es:
$\displaystyle\frac{1+2+3+...+14+15+16}{4}=\frac{136}{4}=34$
A partir del cuadrado con los dieciséis primeros números naturales ordenados por filas, se pueden construir distintos cuadrados mágicos aditivos, de orden 4 y de constante mágica 34, intercambiando las posiciones de algunos números.
Por ejemplo, invirtiendo los números de las dos diagonales:
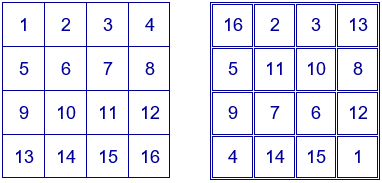
La suma de los números situados en cada una de las filas, en cada una de las columnas y en cada una de las diagonales es igual a 34.

Alberto Durero (1471-1528) es un artista renacentista alemán. Algunas de sus obras se encuentran en el Museo del Prado, como "Adán" y "Eva" o un autorretrato suyo. En la Galería Nacional de Arte de Karlsruhe (Alemania), se encuentra uno de sus grabados más famosos, "Melancolía I", realizado en 1514 y en el que se pueden observar algunos elementos matemáticos. En la parte superior derecha del grabado aparece un cuadrado mágico aditivo de orden cuatro.
Es el cuadrado mágico de orden 4 más conocido. Se obtiene cambiando las dos columnas centrales del cuadrado mágico anterior:

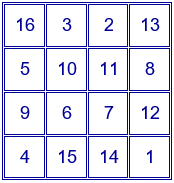
En la fila inferior figura el año de realización, 1514, y los números que indican el orden que ocupan en el abecedario las iniciales de su apellido (4:D) y nombre (1:A).
Otro cuadrado mágico aditivo de orden cuatro, menos conocido que el anterior, pero no menos interesante, es un cuadrado mágico que se conoce como Chautisa Yantra y que se encuentra en la ciudad india de Khajuraho, en la fachada del templo Parsvanatha.

En su puerta hay una inscripción del año 954 d.C. con el siguiente cuadrado mágico aditivo, de constante mágica 34.

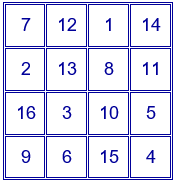
En la siguiente página puedes ver las propiedades de este cuadrado mágico. Como se puede comprobar, este cuadrado mágico aditivo tiene más grupos de cuatro números cuya suma es 34.
Un cuadrado latino de orden 4 es un cuadrado de 4 filas y 4 columnas en las que se colocan 4 números, de forma cada número aparece 4 veces y que en cada fila y en cada columna aparecen los 4 números una sola vez. No se exige esta condición para las diagonales.
Utilizando cuadrados latinos, se pueden construir cuadrados mágicos de orden cuatro.
Se expresan los números del 1 al 16 como las siguientes sumas:
| $1=0+1$ | $2=0+2$ | $3=0+3$ | $4=0+4$ |
| $5=4+1$ | $6=4+2$ | $7=4+3$ | $8=4+4$ |
| $9=8+1$ | $10=8+2$ | $11=8+3$ | $12=8+4$ |
| $13=12+1$ | $14=12+2$ | $15=12+3$ | $16=12+4$ |
En el primer sumando aparecen los números 0, 4, 8 y 12. En el segundo, los números 1, 2, 3 y 4.
Se construyen ahora dos cuadrados de cuatro filas y cuatro columnas con los dos conjuntos de números, de forma que, en cada fila y en cada columna no se repita ningún número. En las dos diagonales principales no es obligatorio que los números sean distintos. Sumando los números de las casillas que ocupan la misma posición en ambos cuadrados se obtienen un cuadrado mágico aditivo. Hay que evitar la repetición de números en el cuadrado final.
El cuadrado mágico conocido como Chautisa Yantra, se obtiene como suma de los números de los dos cuadrados latinos siguientes:
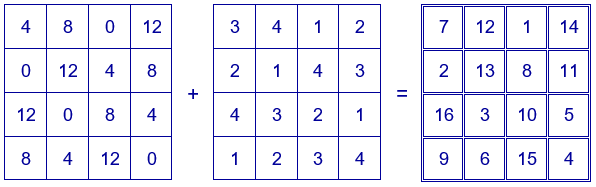
También es posible obtener un cuadrado mágico repitiendo números en filas o columnas en los dos cuadrados que se suman, en este caso no serían cuadrados latinos. Por ejemplo, el cuadrado mágico de Alberto Durero se obtiene de la siguiente forma:
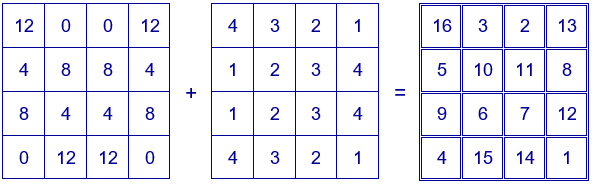
Y construir otros cuadrados mágicos con distintos números:
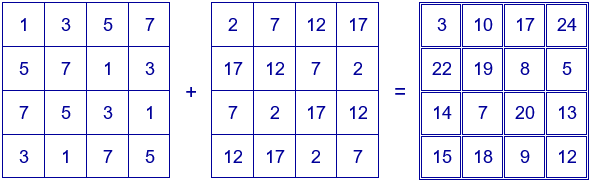
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos aditivos sumando los números de dos cuadrados latinos. Construye en primer lugar los dos cuadrados latinos moviendo los números al interior de los cuadrados superiores y, posteriormente, pulsa el botón "Comprobar" para comprobar si lo has hecho correctamente.
En esta escena de Descartes puedes elegir los números para construir los cuadrados latinos. Escribe en cada casilla los números escogidos y después pulsa el botón "Comprobar" para ver si se obtiene un cuadrado mágico multiplicativo.
Los números de cada uno de los cuadrados latinos están en progresión aritmética.
Generalizando el caso anterior, se pueden construir cuadrados mágicos aditivos sumando dos cuadrados latinos formados por los números a, a+d1, a+2d1, a+3d1 y b, b+d2, b+2d2, b+3d2.
En el siguiente ejemplo se ha escogido la misma distribución de los términos de las progrsiones aritméticas en los cuadrados latinos con la que se obtiene el cuadrado mágico Chautisa Yantra.
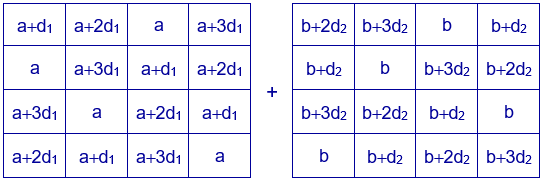
Se obtiene el cuadrado mágico con las mismas propiedades que el modelo escogido y de constante mágica 4a+4b+6d1+6d2.

En la siguiente escena de Descartes puedes construir cuadrados mágicos aditivos de orden cuatro, a partir del procedimiento anterior, conociendo solamente 4 números. Modifica los valores de los controles a, d1, b y d2.
Si en lugar de coger como los elementos iniciales de las dos progresiones aritméticas distintos se cogen iguales, se obtienen los cuadrados latinos:
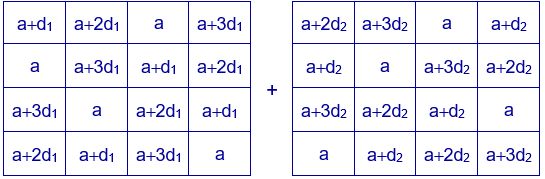
El cuadrado mágico aditivo de orden 4 queda de la forma:

Y para simplificar la expresión, si en lugar de a, se escoge a/2:
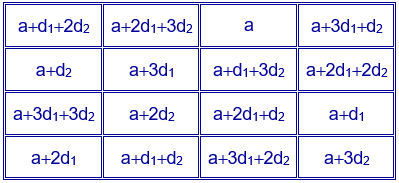
En la siguiente escena de Descartes puedes construir cuadrados mágicos aditivos de orden cuatro, a partir del procedimiento anterior, modificando los valores de a, d1 y d2.
Si a todos los números de un cuadrado mágico se le suma o se le resta un mismo número, se multiplican o dividen por un mismo número, o se realizan ambas transformaciones a la vez, se obtiene otro cuadrado mágico con las mismas propiedades que el inicial.
Por ejemplo, si en el cuadrado Chautisa Yantra, se resta a cada número $34/4=8.5$ se obtiene otro cuadrado mágico con las mismas propiedades que el primero y de constante mágica $0$.
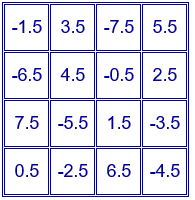
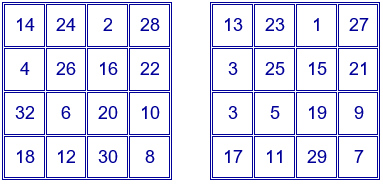
El primero de los dos cuadrados siguientes contiene los 16 primeros números pares, se obtiene multiplicando por 2 los números del cuadrado inicial y tiene constante mágica 68. El segundo contiene los 16 primeros números impares, se obtiene restando 1 a todos los números del cuadrado anterior y tiene constante mágica 64.
En la siguiente escena de Descartes puedes construir, partiendo del cuadrado mágico conocido como Chautisa Yantra, otros cuadrados mágicos aditivos de orden cuatro modificando los valores de a (número por el que se multiplican los números del cuadrado inicial) y de b (número que se suma o se resta al resultado anterior), con las mismas propiedades que el cuadrado inicial.
Un cuadrado mágico multiplicativo de orden 4 está formado por un conjunto de números dispuestos en 4 filas y 4 columnas, de forma que el producto de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre el mismo. A este producto se le llama constante mágica.
Aplicando el producto de potencias con la misma base, a partir de cualquier cuadrado mágico aditivo, se puede construir un cuadrado mágico multiplicativo con potencias de base cualquier número natural distinto de 1 y de exponente cada uno de los números del cuadrado mágico aditivo. Por ejemplo, si n es un número natural mayor que 1, se pueden construir infinitos cuadrados mágicos multiplicativos, de orden 4 y de constante mágica $n^{34}$.
Con este procedimiento se obtienen cuadrados mágicos con números muy grandes. Por ejemplo, para $n=2$ se obtiene el cuadrado de constante mágica $2^{34}\approx1.718·10^{10}$.
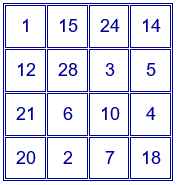
Harry A. Sayles publicó, en 1913, el siguiente cuadrado mágico multiplicativo de orden 4. Tiene la constante mágica más pequeña posible para un cuadrado mágico multiplicativo de orden 4, que es igual a $5040=7!$, y las propiedades del cuadrado mágico de Durero.
Si $p$ y $q$ son dos números primos, el número total de divisores de $(pq)^{3}=p^{3}q^{3}$ es igual a $(3+1)(3+1)=16$. Son los siguientes:
$\{ 1, p, q, pq, p^{2}, q^{2}, p^{2}q, pq^{2},p^{2}q^{2}, p^{3}, q^{3}, p^{3}q, pq^{3},p^{3}q^{2}, p^{2}q^{3}, p^{3}q^{3} \}$
Con estos 16 divisores se pueden construir cuadrados mágicos multiplicativos de orden 4. Vamos a hacerlo de forma lúdica.
Hay un pasatiempo formado por 16 tarjetas, coloreadas con cuatro colores distintos, por ejemplo, amarillo, azul, rojo y verde y, enumeradas de con cuatro números diferentes, por ejemplo 1, 2, 3 y 4, de forma que todas las tarjetas son distintas porque se diferencian en el número, en el color o en ambos.
Consiste en colocar los números formando un cuadrado de cuatro filas y cuatro columnas, de forma que, en cada fila, en cada columna y en las dos diagonales no se pueden repetir números ni colores.
En la siguiente escena de Descartes puedes intentar encontrar una solución. Mueve los números con el ratón al interior del cuadrado.
Para construir cuadrados mágicos multiplicativos de orden 4 se necesita hacer una modificación de este juego utilizando solamente números y sin utilizar colores. Se dispone de 16 tarjetas, cada una tiene una pareja de coordenadas (m,n), siendo m y n números enteros comprendidos entre 0 y 3, ambos incluidos.
Vamos a construir un cuadrado de cuatro filas y cuatro columnas, de forma que, en cada fila, en cada columna y en las dos diagonales no se repitan ni la primera ni la segunda coordenada.
En algunos casos particulares se puede conseguir un cuadrado mágico multiplicativo repitiendo coordenadas en algunas líneas, pero siempre que la suma de cada una de las coordenadas por filas, por columnas y en las dos diagonales sea igual a 6.
Puedes utilizar la siguiente escena de Descartes para resolverlo.
Una vez encontrada una solución, el cuadrado mágico se construye colocando en cada casilla el valor de $p$ elevado a la primera coordenada por el valor de $q$ elevado a la segunda coordenada.
Por ejemplo:
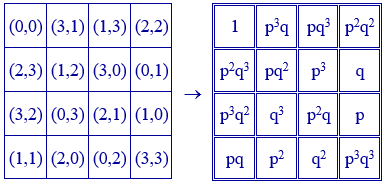
En el cuadrado con las coordenadas, la suma de la primera o segunda coordenada en cada fila, en cada columna y en las dos diagonales es igual a 6. Por tanto, la constante mágica de este cuadrado mágico multiplicativo es $p^{6}q^{6}$.
La siguiente solución del pasatiempo no cumple todas las condiciones, pues repite coordenadas en las diagonales. Sin embargo verifica también que la suma de las dos coordenadas en cada fila, en cada columna y en las dos diagonales es igual a 6.
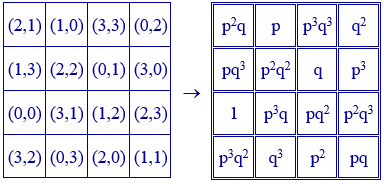
Si $p$, $q$ o ambos no son primos, el procedimiento también es válido, aunque en este caso el cuadrado mágico no contiene todos los divisores de $p^{3}q^{3}$. Para algunos valores no primos, pueden aparecer números repetidos en el cuadrado mágico.
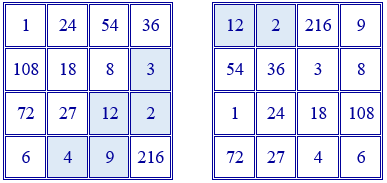
La solución no es única y, una vez encontrada una solución, si se permutan los números de la primera coordenada o de la segunda se vuelve a obtener otra solución distinta.
Las soluciones con los números más pequeños se obtienen con los valores $p=2$ y $q=3$. Los cuadrados mágicos contienen los divisores de $2^{3}·3^{3}=216$, siendo la constante mágica $2^{6}·3^{6}=46656$.
Sustituyendo en el primero de los ejemplos anteriores se obtiene un cuadrado mágico, similar al de Durero, pero multiplicativo. Las casillas coloreadas, desde abajo, indican el día (4) y el mes (9) del cumpleaños del autor y el orden que ocupan en el abecedario las iniciales de su nombre (12:L) y apellidos (2:B,3:C).
Sustituyendo en el segundo ejemplo se obtiene un cuadrado mágico, similar al cuadrado Chautisa Yantra, pero multiplicativo. Las casillas coloreadas indican los números que indican el orden que ocupan en el abecedario las iniciales de su nombre (12:L) y primer apellido (2:B).
Los ejemplos anteriores se han construido con los divisores de números que se descomponen de la forma $N=p^{3}q^{3}$, siendo $p$ y $q$ números primos. Pero existen más números con 16 divisores. Al expresar 16, como producto de números naturales sin incluir el 1, de todas las formas posibles, se tiene:
$16 = 8·2 = 4·4 = 4·2·2 = 2·2·2·2$
Entonces, tienen exactamente 16 divisores los números cuya factorización es de la forma:
• $N=p^{15}$, con $p$ primo. Número de divisores: $15+1=16$.
• $N=p^{7}·q$, con $p$ y $q$ primos. Número de divisores: $8·2=16$.
• $N=p^{3}·q^{3}$, con $p$ y $q$ primos. Número de divisores: $4·4=16$.
• $N=p^{3}·q·r$, con $p$, $q$ y $r$ primos. Número de divisores: $4·2·2=16$.
• $N=p·q·r·s$, con $p$, $q$, $r$ y $s$ primos. Número de divisores: $2·2·2·2=16$.
Los procedimientos que se describen a continuación para la construcción de cuadrados mágicos multiplicativos son válidos también para números que puedan expresarse de estas formas con factores no primos, aunque para estos números los cuadrados construidos solo contienen parte de sus divisores y no todos, como sucede cuando los factores son primos.
Al realizar giros o simetrías en cada uno de los cuadrados se obtiene otro cuadrado mágico con las mismas características.
Si $p$ es un número primo, el número $p^{15}$ tiene $15+1=16$ divisores:
$\{ 1, p, p^{2}, p^{3}, p^{4}, p^{5}, p^{6}, p^{7}, p^{8}, p^{9}, p^{10}, p^{11}, p^{12}, p^{13}, p^{14}, p^{15} \}$
El producto de todos los divisores es $p^{120}$. La constante mágica es la raíz cuarta de este producto, $p^{30}$.
Sustituyendo en cualquier cuadrado mágico aditivo, el número de cada casilla por una potencia de $p$ con exponente dicho número menos una unidad, se obtiene un cuadrado mágico multiplicativo con las mismas características que el cuadrado mágico aditivo utilizado y con constante mágica $p^{30}$.
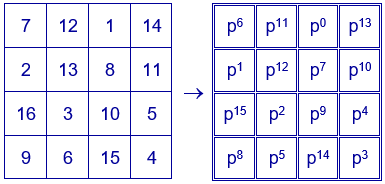
Ejemplo para $p=2$. Constante mágica $2^{30}$.
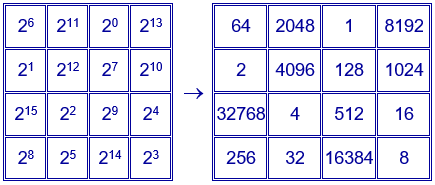
Si $p$ y $q$ son dos números primos, el número $p^{7}q$ tiene $16$ divisores:
$\{ 1, p, p^{2}, p^{3}, p^{4}, p^{5}, p^{6}, p^{7}, q, pq, p^{2}q, p^{3}q, p^{4}q, p^{5}q, p^{6}q, p^{7}q \}$
El producto de todos los divisores es $p^{56}q^{8}$. La constante mágica es la raíz cuarta de este producto, $p^{14}q^{2}$.
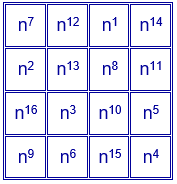
Se pueden distribuir los 16 divisores en el siguiente cuadrado de cuatro filas y cuatro columnas, situando los números de la primera fila y la primera columna y, en las casillas restantes, el producto del primer elemento de la fila por el primer elemento de la columna.
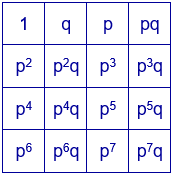
Sustituyendo ahora en cualquier cuadrado mágico aditivo, el número de cada casilla por la expresión que figura en esa casilla en el cuadrado con los divisores, se obtiene un cuadrado mágico multiplicativo con las mismas características que el cuadrado mágico aditivo y con constante mágica $p^{14}q^{2}$.
Por ejemplo, en el siguiente cuadrado mágico aditivo el número que ocupa la primera casilla es 7. Se escoge en el cuadrado superior la expresión que ocupa la casilla número 7, que corresponde a $p^{3}$ y se coloca en la primera asilla del cuadrado mágico multiplicativo. Se repite este procedimiento con cada casilla.
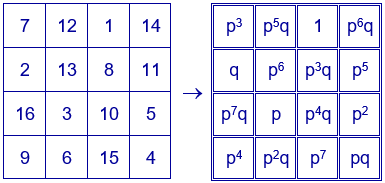
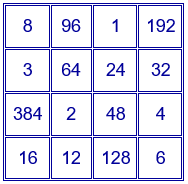
Ejemplo para $p=2$ y $q=3$. El cuadrado mágico está construido con los divisores de $2^{7}·3=384$. Constante mágica $2^{14}·3^{2}=147456$.
Si $p$ y $q$ son dos números primos, el número $p^{3}q^{3}$ tiene $16$ divisores:
$\{ 1, p, q, pq, p^{2}, q^{2}, p^{2}q, pq^{2},p^{2}q^{2}, p^{3}, q^{3}, p^{3}q, pq^{3},p^{3}q^{2}, p^{2}q^{3}, p^{3}q^{3} \}$
El producto de todos los divisores es $p^{24}q^{24}$. La constante mágica es la raíz cuarta de este producto, $p^{6}q^{6}$.
Se pueden distribuir los 16 divisores en un cuadrado de cuatro filas y cuatro columnas, situando los números de la primera fila y la primera columna y, en las casillas restantes, el producto del primer elemento de la fila por el primer elemento de la columna.
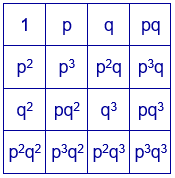
Sustituyendo en cualquier cuadrado mágico aditivo, el número de cada casilla por la expresión que figura en esa casilla en el cuadrado con los divisores, se obtiene un cuadrado mágico multiplicativo con las mismas características que el cuadrado mágico aditivo y con constante mágica $p^{6}q^{6}$.
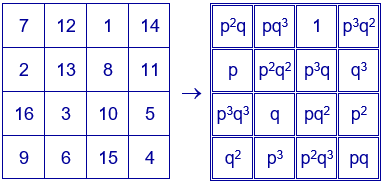
Ejemplo para $p=2$ y $q=3$. El cuadrado mágico está construido con los divisores de $2^{3}·3^{3}=216$. Constante mágica $2^{6}·3^{6}=46656$.
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos multiplicativos de orden cuatro dando valores a los números p y q. Comprueba lo comentado en la página anterior sobre si p y q son o no primos.
Si $p$, $q$ y $r$ son números primos, el número $p^{3}qr$ tiene $16$ divisores:
$\{ 1, p, q, r, pq, pr, qr, pqr, p^{2}, p^{2}q, p^{2}r, p^{2}qr, p^{3}, p^{3}q, p^{3}r, p^{3}qr \}$
El producto de todos los divisores es $p^{24}q^{8}r^{8}$. La constante mágica es la raíz cuarta de este producto, $p^{6}q^{2}r^{2}$.
Se distribuyen los 16 divisores en un cuadrado de cuatro filas y cuatro columnas, según se ha explicado en el caso anterior.
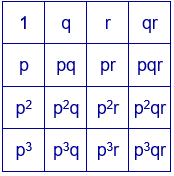
Se construye ahora el cuadrado mágico multiplicativo a partir de un cuadrado mágico aditivo, por el procedimiento explicado anteriormente. La constante mágica es $p^{6}q^{2}r^{2}$.
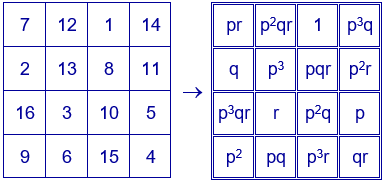
Ejemplo: $p=2$, $q=3$ y $r=5$. El cuadrado mágico contiene los divisores de $2^{3}·3·5=120$. Constante mágica $2^{6}·3^{2}·5^{2}=14400$.
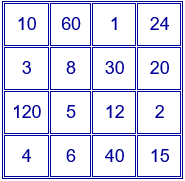
Si $p$, $q$, $r$ y $s$ son números primos, el número $pqrs$ tiene $16$ divisores:
$\{1, p, q, r, s, pq, pr, ps, qr, qs, rs, pqr, pqs, prs, qrs, pqrs \}$
El producto de todos los divisores es $p^{8}q^{8}r^{8}s^{8}$. La constante mágica es la raíz cuarta de este producto, $p^{2}q^{2}r^{2}s^{2}$.
Se distribuyen los 16 divisores en un cuadrado de cuatro filas y cuatro columnas, según ya se ha realizado varias veces con anterioridad.
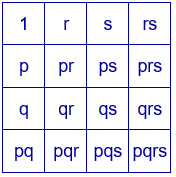
Se construye ahora el cuadrado mágico multiplicativo a partir de un cuadrado mágico aditivo, por el procedimiento explicado anteriormente. La constante mágica es $p^{2}q^{2}r^{2}s^{2}$.
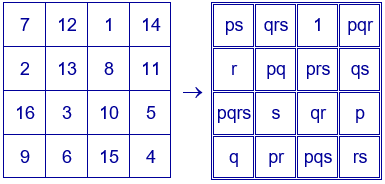
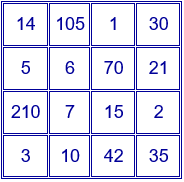
Ejemplo: $p=2$, $q=3$, $r=5$ y $s=7$. El cuadrado mágico contiene los divisores de $2·3·5·7=210$. Constante mágica $2^{2}·3^{2}·5^{2}·7^{2}=44100$.
En las dos páginas siguientes puedes practicar con escenas de Descartes para construir cuadrados mágicos multiplicativos con estos dos últimos procedimientos.
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos multiplicativos dando valores a p, q y r.
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos multiplicativos dando valores a p, q, r y s.
Un procedimiento descrito para la construcción de cuadrado mágicos aditivos ha sido a partir de dos cuadrados latinos. También este método se puede utilizar para la construcción de cuadrados mágicos multiplicativos.
Se construyen ahora dos cuadrados latinos de cuatro filas y cuatro columnas con dos conjuntos de números, de forma que, en cada fila y en cada columna no se repita ningún número. En las dos diagonales principales, no es obligatorio que los números sean distintos. Multiplicando los números de las casillas que ocupan la misma posición en ambos cuadrados se obtienen un cuadrado mágico multiplicativo. Hay que evitar la repetición de números en el cuadrado final.
Ejemplo. Si se construye un cuadrado latino con los números 1, 2, 3 y 4 y otro con los números 1, 5, 6 y 7, se obtiene uno de los cuadrados mágicos multiplicativos de menor constante mágica que se puede construir, $5040=7!$. Se pueden construir varios cuadrados mágicos multiplicativos con estos cuadrados latinos. Los cuadrados mágicos obtenidos con estos números no son pandiagonales. (Un cuadrado mágico multiplicativo es pandiagonal si el producto de los tres elementos de las diagonales secundarias por el elemento del vértice opuesto es igual a la constante mágica).
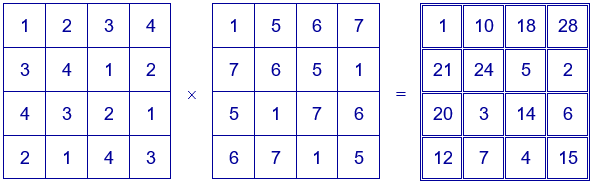
La constante mágica más pequeña para un cuadrado mágico multiplicativo pandiagonal es $14400=2^{6}·3^{2}·5^{2}$. Este cuadrado mágico multiplicativo fue publicado por Harry A. Sayles. Se obtiene con todos los divisores de $N=p^{3}·q·r$, con $p=2$, $q=3$ y $r=5$, $(120=2^{3}·3·5)$.
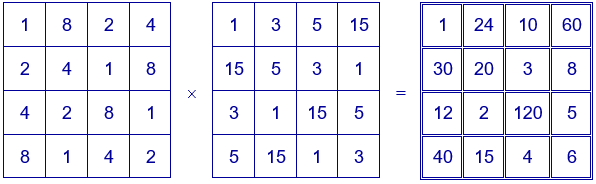
Igual que éste, todos los cuadrados mágicos multiplicativos obtenidos anteriormente con los números que tienen dieciséis divisores, se pueden obtener multiplicando los números de dos cuadrados latinos.
Ejemplo. Uno de los cuadrados mágicos multiplicativos que se pueden obtener con los divisores de $N=p^{3}·q^{3}$, con $p=2$ y $q=3$, se puede obtener también con los dos cuadrados latinos siguientes. En este caso se repiten números en las diagonales de los cuadrados latinos.
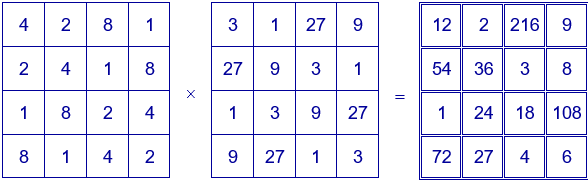
En esta escena de Descartes puedes elegir los números para construir los cuadrados latinos. Escribe en cada casilla los números escogidos y después pulsa el botón "Comprobar" para ver si se obtiene un cuadrado mágico multiplicativo.
Los números de cada uno de los cuadrados latinos del último ejemplo están en progresión geométrica.
Generalizando este caso, se pueden construir cuadrados mágicos multiplicativos multiplicando dos cuadrados latinos formados por los números $a$, $ar_1$, $ar_1^{2}$, $ar_1^{3}$ y $b$, $br_2$, $br_2^{2}$, $br_2^{3}$.
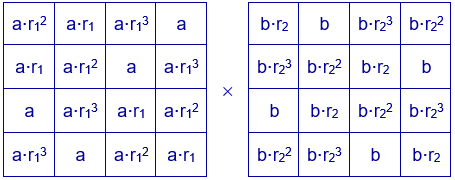
Se obtiene el cuadrado mágico de constante mágica $a^{4}b^{4}r_1^{6}r_2^{6}$.
Se puede sustituir a·b por una constante nada más y representarla por a. Se obtiene el cuadrado mágico:

Para $a=1$, $r_1=p$, $b=1$ y $r_2=q$ se obtiene el cuadrado mágico multiplicativo de la página 54.
En la siguiente escena de Descartes puedes construir cuadrados mágicos multiplicativos de orden cuatro, a partir del procedimiento anterior, modificando los valores de a, r1 y r2.
Un cuadrado mágico aditivo de orden 5 está formado por un conjunto de números dispuestos en 5 filas y 5 columnas, de forma que la suma de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre la misma. A esta suma se le llama constante mágica.
La constante mágica se calcula dividiendo la suma de todos los números utilizados entre el orden del cuadrado. Si el cuadrado se construye con los 25 primeros números naturales, la constante mágica es: $(1+2+3+...+23+24+25)/5=325/5=65$
Para construirlo se colocan los números del 1 al 25 de la forma:
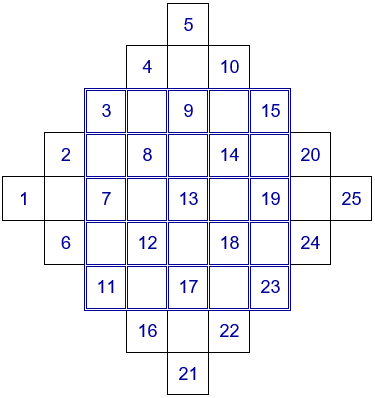
Los números que quedan fuera del cuadrado se colocan en las casillas libres según se observa en la siguiente figura:
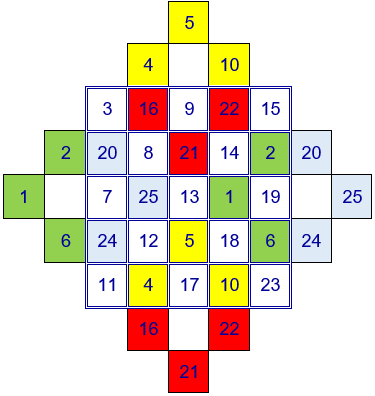
Y se obtiene el cuadrado mágico siguiente. La suma de los números situados en cada una de las filas, en cada una de las columnas y en cada una de las diagonales es igual a 65.
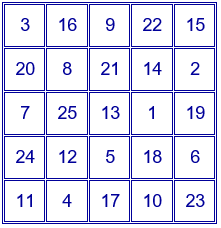
• Se coloca el primer número en la casilla central de la fila superior.
• A continuación se colocan los siguientes números desplazándonos una casilla hacia arriba y otra hacia la derecha (si estamos en la fila superior hay que continuar por la inferior y si estamos en columna de la derecha hay que continuar por la de la izquierda).
• En caso de que la casilla que corresponda esté ocupada, colocamos el número debajo del número anterior.
Construcción paso a paso de un cuadrado mágico de orden 5.
Un cuadrado latino de orden 5 es un cuadrado de 5 filas y 5 columnas en las que se colocan 5 números, de forma cada número aparece 5 veces y que en cada fila y en cada columna aparecen los cinco números una sola vez. No se exige esta condición para las diagonales.
Utilizando cuadrados latinos, se pueden construir cuadrados mágicos de orden tres.
Se expresan los números del 1 al 25 como las siguientes sumas:
| $1=0+1$ | $2=0+2$ | $3=0+3$ | $4=0+4$ | $5=0+5$ |
| $6=5+1$ | $7=5+2$ | $8=5+3$ | $9=5+4$ | $10=5+5$ |
| $11=10+1$ | $12=10+2$ | $13=10+3$ | $14=10+4$ | $15=10+5$ |
| $16=15+1$ | $17=15+2$ | $18=15+3$ | $19=15+4$ | $20=15+5$ |
| $21=20+1$ | $22=20+2$ | $23=20+3$ | $24=20+4$ | $25=20+5$ |
En el primer sumando aparecen los números 0, 5, 10, 15 y 20. En el segundo, los números 1, 2, 3, 4 y 5.
Se construyen ahora dos cuadrados latinos de cinco filas y cinco columnas con los dos conjuntos de números, de forma que, en cada fila y en cada columna no se repita ningún número. En las dos diagonales no es obligatorio que los números sean distintos.
Sumando los números de las casillas que ocupan la misma posición en ambos cuadrados se obtiene, en algunos casos, un cuadrado mágico aditivo. Hay que evitar la repetición de números en el cuadrado final.
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos aditivos sumando los números de dos cuadrados latinos. Construye en primer lugar los dos cuadrados latinos moviendo los números al interior de los cuadrados superiores y, posteriormente, pulsa el botón "Comprobar".
En esta escena de Descartes puedes elegir los números para construir los cuadrados latinos. Escribe en cada casilla los números escogidos y después pulsa el botón "Comprobar" para ver si se obtiene un cuadrado mágico aditivo.
El cuadrado mágico construido con los 25 primeros números naturales, por el primer procedimiento, se obtiene como suma de los números de los dos cuadrados latinos siguientes. Observa la construcción de los cuadrados latinos colocando números repetidos en las diagonales.
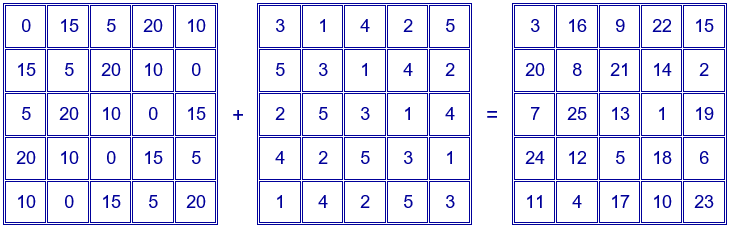
El cuadrado mágico construido con por el segundo procedimiento, se obtiene como suma de los números de los dos cuadrados latinos siguientes:
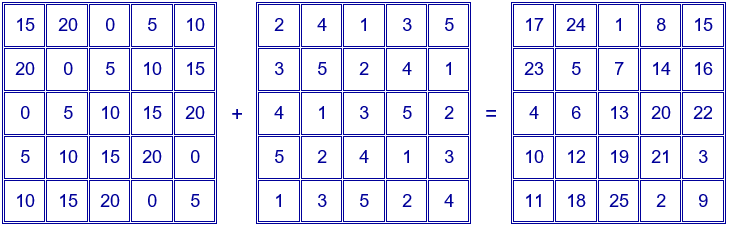
Los números de cada uno de los cuadrados latinos están en progresión aritmética. Para poder construir con ellos un cuadrado mágico se ha repetido el término central en las dos diagonales de los dos cuadrados latinos del primer ejemplo y en uno del segundo.
Generalizando el caso anterior, se pueden construir cuadrados mágicos aditivos sumando dos cuadrados latinos formados por los números a-2d1, a-d1, a, a+d1, a+2d1 y b-2d2, b-d2, b, b+d2, a+2d2. Utilizando el modelo del primer ejemplo:
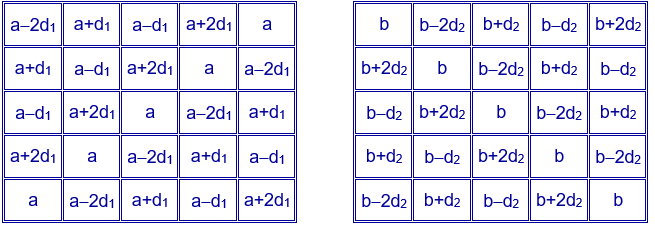
Al sumar los dos cuadrados se obtiene un cuadrado mágico de constante mágica 5a+5b.
Se puede sustituir a+b por un solo número c, pero por comodidad, lo vamos a llamar a. Se obtiene un cuadrado mágico, con constante mágica 5a.

Por tanto, se puede calcular un cuadrado mágico aditivo de orden 5 a partir de tres números nada más.
En la siguiente escena de Descartes puedes construir cuadrados mágicos aditivos de orden cinco, a partir del procedimiento anterior, modificando los valores de a, d1 y d2.
El siguiente cuadrado mágico está formado también por los veinticinco primeros números naturales. Es distinto de los dos anteriores. Su constante mágica también es 65.
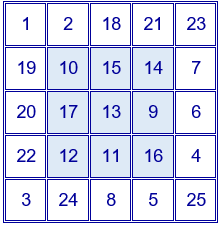
Tiene la particularidad de que el cuadrado coloreado en la parte interior es un cuadrado mágido de orden 3. Está formado por los nueve números que ocupan las posiciones centrales entre los veinticinco primeros números naturales, es decir, los números comprendidos entre el 9 y el 17, ambos incluidos.
Se obtiene sumando 8 a cada uno de los elementos del cuadrado mágico aditivo de orden 3 del capítulo 1. Su constante mágica es 39. El resto de elementos se ajustan para obtener la constante mágica.
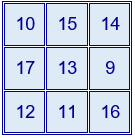
Si a todos los números del cuadrado mágico se le suma o se le resta un mismo número, se multiplican o dividen por un mismo número, o se realizan ambas transformaciones a la vez, se obtiene otro cuadrado mágico.
Ejemplo. Si en el cuadrado mágico anterior se resta 13 a cada uno de los números que lo forman, se obtiene un cuadrado mágico con números enteros, de orden 5 y de constante mágica 0 y en su interior, un cuadrado mágico de orden 3 y de constante mágica 0.
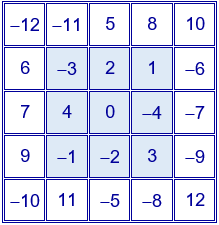
Si se multiplican todos los números del cuadrado mágico por 2, se obtiene un cuadrado mágico formado por los veinticinco primeros números pares y de constante mágica 130.
Si a todos los números del cuadrado anterior se le resta 1, se obtiene un cuadrado mágico formado por los veinticinco primeros números impares y de constante mágica 125.
Al realizar giros o simetrías en cualquier cuadrado mágico se obtiene otro cuadrado mágico con las mismas características.
En la siguiente escena de Descartes puedes construir, partiendo del cuadrado mágico anterior, otros cuadrados mágicos aditivos de orden cinco modificando los valores de a (número por el que se multiplican los números del cuadrado inicial) y de b (número que se suma o se resta al resultado anterior).
Un cuadrado mágico multiplicativo de orden 5 está formado por un conjunto de números dispuestos en 5 filas y 5 columnas, de forma que el producto de los números situados en cada una de las filas, en cada una de las columnas y en las dos diagonales es siempre el mismo. A este producto se le llama constante mágica.
Aplicando el producto de potencias con la misma base, a partir de cualquier cuadrado mágico aditivo, se puede construir un cuadrado mágico multiplicativo con potencias de base cualquier número natural distinto de 1 y de exponente cada uno de los números del cuadrado mágico aditivo. Por ejemplo, si n es un número natural mayor que 1, se pueden construir infinitos cuadrados mágicos multiplicativos, de orden 5 y de constante mágica $n^{65}$.
A partir del cuadrado mágico aditivo de la página anterior, se obtiene el cuadrado mágico multiplicativo siguiente:
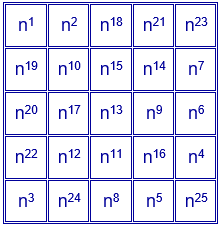
Con este procedimiento se obtienen cuadrados mágicos con números muy grandes. Por ejemplo, para n=2 se obtiene el cuadrado de constante mágica $2^{65}\approx3.69·10^{19}$.
Al expresar 25, como producto de números naturales sin incluir el 1, de todas las formas posibles, se tiene solamente:
$25 = 25·1 = 5·5$
Entonces, tienen exactamente 25 divisores, los números cuya factorización es de la forma:
• $N=p^{24}$, con $p$ primo. Número de divisores: $24+1=25$.
• $N=p^{4}·q^{4}$, con $p$ y $q$ primos. Número de divisores: $5·5=25$.
Los procedimientos que se describen a continuación para la construcción de cuadrados mágicos multiplicativos son válidos también para números que puedan expresarse de estas formas con factores no primos, aunque para estos números los cuadrados construidos solo contienen parte de sus divisores y no todos, como sucede cuando los factores son primos.
Si $p$ es un número primo, el número $p^{24}$ tiene $24+1=25$ divisores:
El producto de todos los divisores es $p^{300}$. La constante mágica es la raíz quinta de este producto, $p^{60}$.
Sustituyendo en cualquier cuadrado mágico aditivo, el número de cada casilla por una potencia de $p$ con exponente dicho número menos una unidad, se obtiene un cuadrado mágico multiplicativo con las mismas características que el cuadrado mágico aditivo utilizado y con constante mágica $p^{60}$.
Si $p$ y $q$ son dos números primos, el número $(p·q)^4=p^{4}·q^{4}$ tiene $(4+1)·(4+1)=5·5=25$ divisores:
$div(pq)^{4}=\{ 1, p, q, pq, p^{2}, q^{2}, p^{2}q, pq^{2},p^{2}q^{2}, p^{3}, q^{3}, p^{3}q, pq^{3},$$ p^{3}q^{2}, p^{2}q^{3}, p^{3}q^{3}, p^{4}, q^{4}, p^{4}q,pq^{4}, p^{4}q^{2}, p^{2}q^{4}, p^{4}q^{3},p^{3}q^{4},p^{4}q^{4}, \}$
El producto de todos los divisores es $p^{50}·q^{50}$. La constante mágica es la raíz quinta de este producto, $p^{10}·q^{10}$.
Con los veinticinco divisores anteriores se puede formar un cuadrado mágico multiplicativo de orden 5, con un cuadrado mágico multiplicativo de orden 3 en su interior.
El número de la casilla central debe ser $p^{2}q^{2}$, que se obtiene calculando la raíz quinta de la constante mágica.
Para construir el cuadrado mágico de orden 3, cuya casilla central sea $p^{2}q^{2}$, se puede multiplicar por $pq$ los números del cuadrado mágico multiplicativo de orden 3.
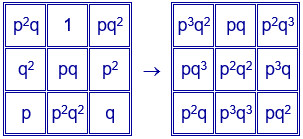
De esta forma se obtiene un cuadrado mágico multiplicativo de constante mágica $p^{6}q^{6}$.
A continuación, se colocan los divisores no utilizados, empezando por las esquinas, después las casillas centrales y, por último, las casillas restantes, procurando que el producto de los números de cada fila, columna y diagonal coincida con la constante mágica.
Una solución es el cuadrado:
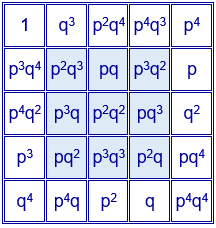
Ejemplo para $p=2$ y $q=3$. El cuadrado mágico contiene los divisores de $2^{4}·3^{4}=1296$. Constante mágica del cuadrado de orden 3: $2^{6}·3^{6}=46656$. Constante mágica del cuadrado de orden 5: $2^{10}·3^{10}=60466176$.
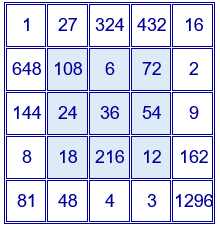
Se pueden distribuir los 25 divisores de $p^{4}·q^{4}$ en un cuadrado de cinco filas y cinco columnas, situando los números de la primera fila y la primera columna y, en las casillas restantes, el producto del primer elemento de la fila por el primer elemento de la columna.
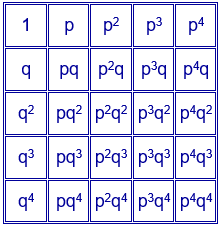
Sustituyendo en el cuadrado mágico aditivo obtenido por el primer procedimiento, el número de cada casilla por la expresión que figura en esa casilla en el cuadrado con los divisores, se obtiene un cuadrado mágico multiplicativo con las mismas características que el cuadrado mágico aditivo y con constante mágica $p^{10}q^{10}$.
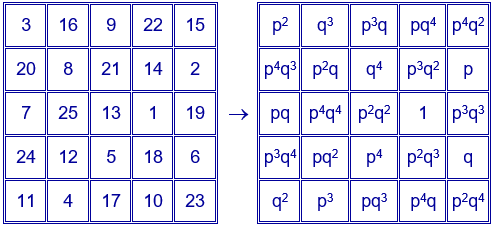
Ejemplo para $p=2$ y $q=3$. El cuadrado mágico contiene los divisores de $2^{4}·3^{4}=1296$. Constante mágica: $2^{10}·3^{10}=60466176$.
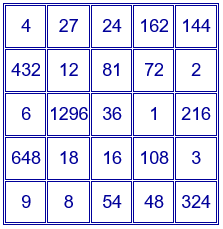
Sustituyendo ahora en el cuadrado obtenido por el segundo procedimiento, el número de cada casilla por la expresión que figura en esa casilla en el cuadrado con los divisores, también se obtiene un cuadrado mágico multiplicativo con las mismas características que el cuadrado mágico aditivo y con constante mágica $p^{10}q^{10}$.
Ejemplo para $p=2$ y $q=3$. El cuadrado mágico contiene los divisores de $2^{4}·3^{4}=1296$. Constante mágica: $2^{10}·3^{10}=60466176$.
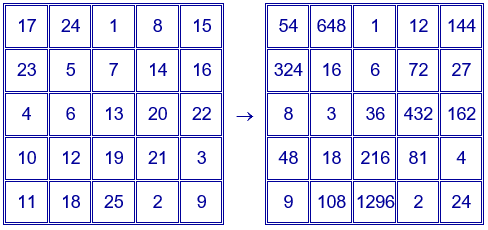
En la siguiente escena de Descartes puedes construir distintos cuadrados mágicos multiplicativos de orden cinco, conteniendo un cuadrado mágico multiplicativo de orden 3, dando valores a los números $p$ y $q$.
De la misma forma que en los cuadrados de orden 3 y 4, también se pueden obtener cuadrados mágicos multiplicativos de orden 5, multiplicando cuadrados latinos.
El cuadrado mágico multiplicativo de orden 5, pandiagonal, con la constante mágica más pequeña que existe fue publicado en 1913 por Harry A. Sayles. Se obtiene multiplicando los dos cuadrados latinos siguientes:
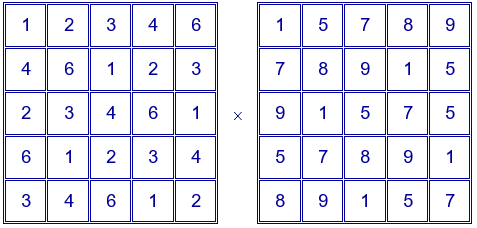
El cuadrado que se obtiene tiene constante mágica $362880=9!$.
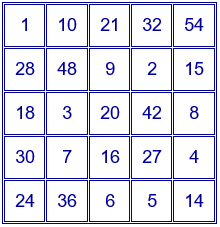
Otro ejemplo de cuadrado mágico multiplicativo con constante mágica mayor, que también puede obtenerse con los divisores de $N=p^{4}·q^{4}$, con $p=2$ y $q=3$.
Al multiplicar los dos cuadrados latinos siguientes:
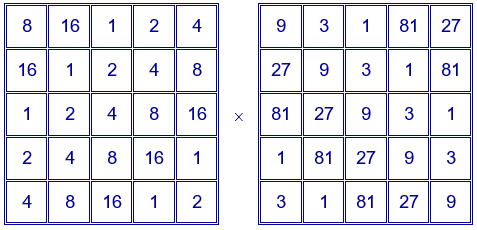
Se obtiene el siguiente cuadrado mágico multiplicativo de orden 5 y de constante mágica $2^{10}·3^{10}=60466176$:
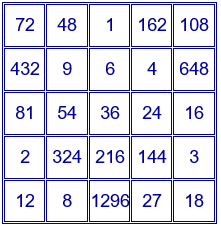
El primer cuadrado se ha construido con los números 1, 2, 4, 8 y 16.
El segundo cuadrado está construido con los números 1, 3, 9, 27 y 81.
Los dos conjuntos de números están en progresión geométrica. Generalizando este caso, se pueden construir cuadrados mágicos multiplicativos, multiplicando dos cuadrados latinos formados por los números $a$, $ar_1$, $ar_1^{2}$, $ar_1^{3}$, $ar_1^{4}$ y $b$, $br_2$, $br_2^{2}$, $br_2^{3}$, $br_2^{4}$.
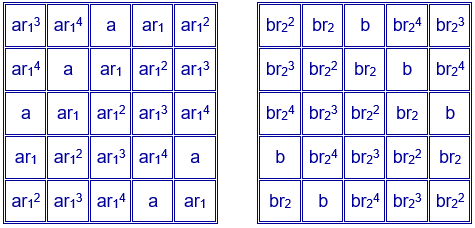
Se obtiene el cuadrado mágico de constante mágica $a^{5}b^{5}r_1^{10}r_2^{10}$.
Se puede sustituir a·b por una constante nada más y representarla por a. Se obtiene el cuadrado mágico:
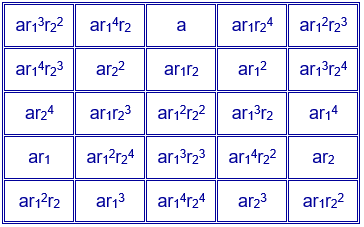
En la siguiente escena de Descartes puedes construir cuadrados mágicos multiplicativos de orden cinco, a partir del procedimiento anterior, modificando los valores de a, r1 y r2.
En esta escena de Descartes puedes elegir los números para construir los cuadrados latinos. Escribe en cada casilla los números escogidos y después pulsa el botón "Comprobar" para ver si se obtiene un cuadrado mágico multiplicativo.
En los capítulos anteriores se han estudiado de forma detallada procedimientos de construcción de cuadrados mágicos aditivos y multiplicativos de orden 3, 4 y 5. Según aumenta el orden de los cuadrados mágicos, va aumentando también la cantidad de números necesarios para su construcción, $n^{2}$, y la constante mágica de los mismos, sobre todo en los cuadrados mágicos multiplicativos.
Para los cuadrados mágicos aditivos, las constantes mágicas son:
$15, 34, 65, 111, 175, 260, . . ., \displaystyle\frac{n^{2}·(n^{2}+1)}{2n}$ con $n\ge3$
Para los cuadrados mágicos multiplicativos, construidos con cuadrados latinos en los que se han utilizado progresiones geométricas con potencias de números primos, las constantes mágicas para $p=2$ y $q=3$, son:
$6^{3}, 6^{6}, 6^{10}, 6^{15}, 6^{21}, 6^{28}, . . ., 6^{\frac{n·(n+1)}{2}}$ con $n\ge3$
Aunque también existen cuadrados mágicos multiplicativos con constante mágica menor que estos pero que también crece a un ritmo mucho mayor que la de los cuadrados mágicos aditivos. Además tienen el inconveniente de que no es fácil su construcción.
En este capítulo se limitará el estudio a cuadrados mágicos de orden 6, 7 y 8 para conocer su existencia.
• Para los cuadrados mágicos aditivos se detalla un procedimiento de construcción en cada caso.
• Para los cuadrados mágicos multipicativos se exponen directamente los de menor constante mágica.
Vamos a construir un cuadrado mágico cualquiera.
La constante mágica se calcula dividiendo la suma de todos los números utilizados entre el orden del cuadrado. Si el cuadrado se construye con los 36 primeros números naturales, la constante mágica es:
$\displaystyle\frac{1+2+3+...+34+35+36}{6}=\frac{666}{6}=111$
En el cuadrado con los 36 primeros números naturales ordenados, figuran en los bordes las sumas de los números de las filas, columnas y diagonales. Se puede comprobar que solamente la suma de los números situados en las diagonales coincide con la constante mágica.
Se empieza invirtiendo las diagonales.
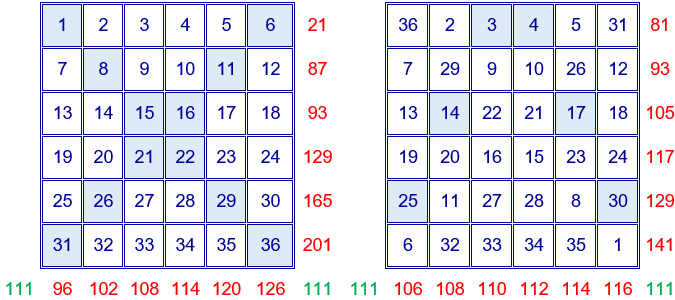
Si observamos la suma de las columnas, para conseguir que coincida con la constante mágica, hay que intercambiar dos números de la primera y sexta columnas, dos números de la segunda y quinta columnas y dos números de la tercera y cuarta columnas.
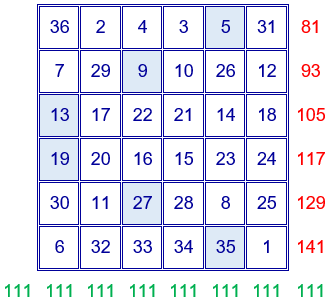
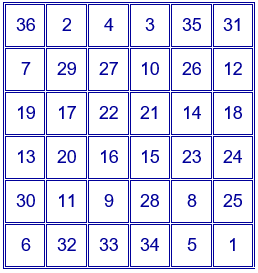
Si observamos ahora la suma de las filas, para conseguir que coincida con la constante mágica, hay que intercambiar dos números de la primera y sexta filas, dos números de la segunda y quinta filaas y dos números de la tercera y cuarta filas.
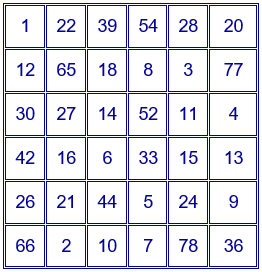
La constante mágica más pequeña para un cuadrado mágico multiplicativo de orden 6 es $25945920$.
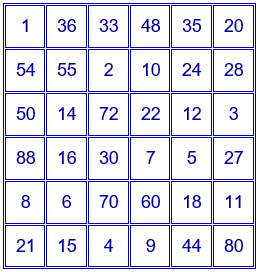
Otro ejemplo con un cuadrado mágico multiplicativo de orden 6 y de constante mágica $39916800=11!$.
La constante mágica se calcula dividiendo la suma de todos los números utilizados entre el orden del cuadrado. Si el cuadrado se construye con los 49 primeros números naturales, la constante mágica es:
$\displaystyle\frac{1+2+3+...+47+48+49}{7}=\frac{1225}{7}=175$
Utilizando el segundo de los procedimientos de construcción para cuadrados mágicos aditivos de orden impar, se obtiene este cuadrado mágico aditivo de orden 7.
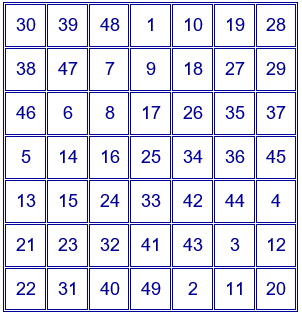
La constante mágica más pequeña para un cuadrado mágico multiplicativo de orden 7 es $3632428800\approx3.63·10^{9}$.
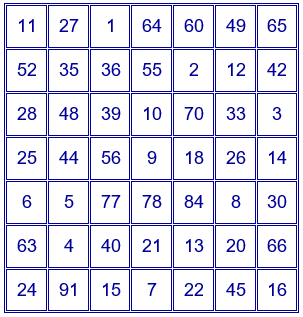
Para comprender mejor la importancia de esta menor constante mágica, si construímos dos cuadrados latinos de orden 7 con las primeras potencias de los números $2$ y $3$:
$1, 2, 4, 8, 16, 32, 64$ y $1, 3, 9, 27, 81, 243, 729$
la constante mágica del cuadrado mágico multiplicativo de orden 7 que se obtiene multiplicando estos cuadrados latinos es:
$2^{21}·3^{21}=6^{21}\approx2.19·10^{16}$
La constante mágica se calcula dividiendo la suma de todos los números utilizados entre el orden del cuadrado. Si el cuadrado se construye con los 64 primeros números naturales, la constante mágica es:
$\displaystyle\frac{1+2+3+...+62+63+64}{8}=\frac{2080}{8}=160$
En el cuadrado con los 64 primeros números naturales ordenados, seleccionamos las casillas coloreadas.
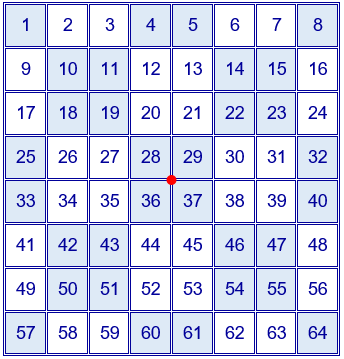
Se intercambian todos los números de las casillas simétricas respecto del punto que representa el centro del cuadrado. Se obtiene el siguiente cuadrado mágico aditivo de orden 8.
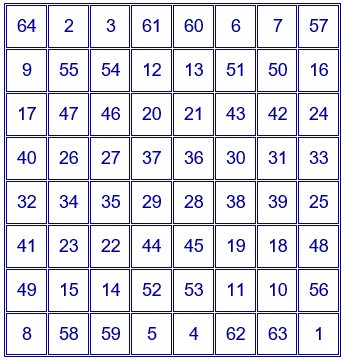
Este cuadrado mágico posse además otras propiedades.
• El cuadrado de orden 4 formado por las 16 casillas centrales es un cuadrado mágico aditivo de constante mágica 130.
• El cuadrado de orden 4 formado uniendo los cuatro cuadrados de orden dos de las esquinas es un cuadrado mágico aditivo de constante mágica 130.
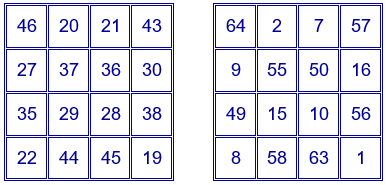
La constante mágica más pequeña para un cuadrado mágico multiplicativo de orden 8 es $670442572800$.
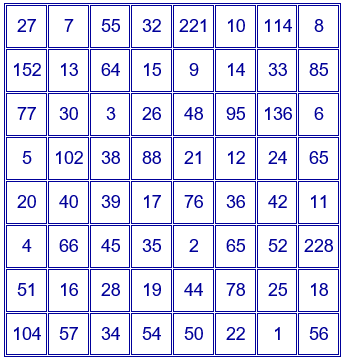
El siguiente cuadrado mágico de orden 8 es a la vez aditivo, de c. m. $760$ y multiplicativo de c. m. $51407948592000$.
