Curso "Libros interactivos con DescartesJS y herramientas de IA"
Escrito por José Antonio Salgueiro GonzálezVídeos del curso "Diseño de libros interactivos con DescartesJs y herramientas de IA"
Presentación
Recursos y tutoriales previos:
En preparación

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:
En preparación...
´
- Vídeo de la 1ª sesión (17 de octubrel 2025). Presentación de la 1ª sesión.
Asamblea general de RED Descartes en Cartagena
Escrito por José Antonio Salgueiro GonzálezUn año más, y como es tradición desde siempre, marcada por el calendario escolar, hemos celebrado nuestra Asamblea General Ordinaria en forma presencial, simultaneada con modalidad virtual para aquellos socios y socias que no han podido asistir físicamente. El acto tuvo lugar en esta ocasión en la bella y milenaria ciudad de Cartagena, situada en la costa del mar Mediterráneo y una de las ciudades más pobladas de la comunidad autónoma de la Región de Murcia. Fue fundada por los cartaginenses cerca del año 220 a.C. y alcanzó su auge durante el período romano. Por este motivo, nos desplazamos hasta Cartagena, Puerto de Culturas, desde diversos lugares y puntos geográficos de la península, como Burgos, Lebrija, Baza, Madrid, Santiago de Compostela, Logroño, Santomera, Zaragoza, Santander, Córdoba y Sangonera la Verde. Particularmente, para quien suscribe este artículo, y después de tantos años colaborando desde entornos virtuales, ha sido un placer conocer personalmente a nuestro compañero Alfonso Saura.
Durante una fructífera jornada hemos tratado, grosso modo, asuntos de relevancia como el ingente repositorio de recursos educativos abiertos e interactivos validados en el aula, para todas las modalidades de enseñanza y etapas educativas, desde infantil a universidad, generados con dos potentes herramientas de software libre: DescartesJS y libro interactivo, que se encuentran alojados en el repositorio de código GitHub, desde donde puede descargarse, gracias al soporte proporcionado por el Instituto de Matemáticas de la Universidad Nacional Autónoma de México. En el ámbito de la formación, y dentro del programa de Educación Abierta de RED Descartes, desde Colombia se desarrolló, entre octubre de 2024 y febrero de 2025, la I Edición del Curso "Diseño de libros interactivos con IA y DescartesJS", mientras que del 11 de abril hasta el 18 de julio se ha impartido la I Edición del Curso "Diseño de objetos interactivos con DescartesJS e IA", cuyas sesiones se graban en vídeo y se difunden para el conocimiento libre. Además, con una periodicidad quincenal tienen lugar las reuniones en línea para compartir los avances en las investigaciones sobre aprovechamiento óptimo de la Inteligencia Artificial en la generación de contenido digital. Si deseas participar en estas reuniones, puedes contactar con nosotros enviando un correo a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Hemos reflexionado sobre la revista digital de la RED Descartes, panhispánica, educativa e interactiva, cuyo noveno número se publicó días antes de esta asamblea, de nuestra publicación electrónica seriada anual y el importante número de descargas que se producen (con objeto de usar en local todos nuestros recursos educativos abiertos), del gran número de libros interactivos publicados en nuestra biblioteca cartesiana y en nuestra librería, de la ampliación de contenidos en el Proyecto Miscelánea, de la incorporación de RED Descartes al Pacto por la Generación D y las líneas de trabajo en el subproyecto “Aplicación de juegos didácticos en el aula”, que ha sido galardonado con el Tercer premio autonómico Antonio Domínguez Ortiz convocado por la Consejería de Desarrollo Educativo y FP de la Junta de Andalucía en su XXXIII edición, por “La Escuela de Alquimia”.
En otro orden de cosas, y como resulta preceptivo en estas asambleas, hemos tratado asuntos de gestión y organización, memoria y propuesta de actividades, cierre económico, propuesta de presupuestos y elección de la junta directiva para el nuevo bienio.
Aprovechando la estancia en Cartagena, una puerta abierta desde la que han penetrado todas y cada una de las civilizaciones que por el mar Mediterráneo han navegado, y con nuestro compañero José Ireno Fernández como anfitrión, la primera jornada, antes de la llegada de todos los socios asistentes, recorrimos el centro de la ciudad y almorzamos sin ningún plan establecido, siendo la cena el primer encuentro debidamente organizado en el restaurante El paso de los elefantes, donde, entre otros, pudimos saborear la famosa tapa conocida como Marinera.
El sábado comenzamos visitando el Ascensor Panorámico, que con sus 45 metros de altura salva el desnivel de la calle y nos permitió otear una amplia zona de la ciudad, para acceder, posteriormente, al Castillo de la Concepción, que nos sorprendió con la colección de diseños e inventos del gran Leonardo da Vinci, además de exponer a su Hombre de Vitrubio y unas descripciones y características de los sólidos platónicos, construidos en la sala en cuestión, para terminar almorzando en el restaurante Mare Nostrum, tras visitar el Museo Nacional de Arqueología Subacuática.
La jornada matinal del domingo la dedicamos a dar un paseo tempranero hasta llegar a los exteriores del Museo Naval y la sala anexa donde se encuentra el prototipo del famoso submarino construido en Cádiz por Isaac Peral, continuando con sendas visitas guiadas al Foro Romano Molinete y al Museo Teatro Romano de Cartagena. Finalmente, como auténticos navegantes, pudimos contemplar la ciudad desde el exterior, desde el mar, disfrutando de los accidentes marítimos cercanos y las fortalezas defensivas de las sucesivas épocas, y todo en el Barco Turístico, para terminar degustando el típico caldero en la Casa del Pescador. Y, después de una merecida siesta, nos desplazamos hasta el extraordinario y bello Cabo de Palos, donde terminamos cenando buen pescado fresco regado con caldos de la denominación Jumilla.
Concluimos este pequeño resumen sobre la asamblea general 2025 con una selección de fotografías gracias a Josep María Navarro, nuestro reportero gráfico, habiendo elegido para ello un presentador de diapositivas en HTML5, que podemos visualizar en dispositivos móviles sin más que utilizar el dedo adelante o atrás para la transición de las mismas. Ahora bien, en un ordenador personal lo conseguiremos con las teclas o flechas de movimiento del cursor, pudiendo pulsar la tecla F (full) para el modo de pantalla completa.
El uso de este tipo de presentadores permite evitar la dependencia con presentadores comerciales como el PowerPoint de Microsofot o el KeyNote de Apple que, además, restringen la incorporación de algunos objetos diseñados en JavaScript, como las escenas interactivas de DescartesJS y GeoGebra, entre otros. Otra ventaja de usar HTML5 es poder compartir nuestras presentaciones vía web.
Si tienes interés en usar alguno de estos presentadores, te recomendamos el libro digital interactivo homónimo "Presentadores de diapositivas HTML5", donde encontrarás toda la información necesaria.
También ponemos a tu disposición el álbum completo de fotos de RED Descartes durante la experiencia cartagenera.
Participantes de tres continentes y trece países
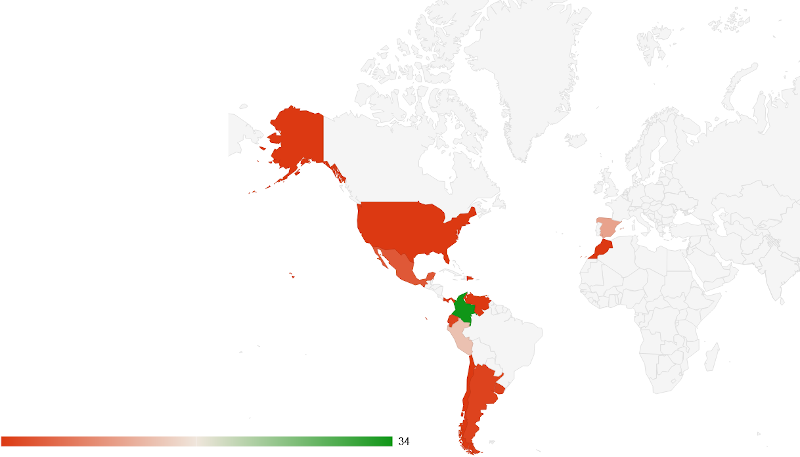
Escrito por José Antonio Salgueiro GonzálezComienza la I Edición del Curso para el Diseño de Objetos interactivos con DescartesJS e IA, que forma parte del programa de Educación Abierta de RED Descartes y cuenta con participantes distribuidos en tres continentes y doce países, todos profesionales de la educación que comprenden diversas etapas educativas y una amplia gama de especialidades. Como viene siendo habitual, compartimos el diagrama de sectores con el porcentaje de personas inscritas según el país de origen:
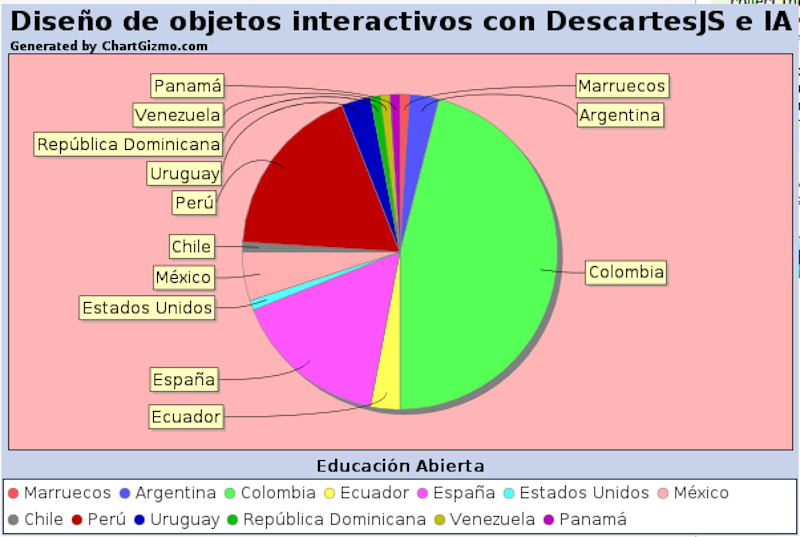
Nuestra gran experiencia y trayectoria en el desarrollo de acciones formativas nos ha encaminado a convocar un curso bastante demandado en el que se aúnan las herramientas de inteligencia artificial para la enseñanza y la potente herramienta de autor DescartesJS, de software libre, promovida y soportada por nuestra asociación en colaboración con instituciones y organizaciones de Colombia y México, fundamentalmente.
Pues bien, una vez han sido atendidas todas las inscripciones de forma personalizada y cada participante ha recibido las debidas instrucciones iniciales y los recursos y materiales para la primera sesión, corresponde, en el marco del programa de Educación Abierta de nuestra red, compartir la información con nuestros seguidores, usuarios y personas interesadas en aprender de forma independiente. Así que, en primer lugar, proporcionamos la
para continuar con el resto de recursos:
- Descarga el software libre DescartesJS para tu sistema operativo
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
- Descripción detallada de cada sesión
Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente en la página denominada
Diseño de objetos interactivos con DescartesJS e IA
Diseño de objetos interactivos con DescartesJS e IA
Escrito por José Antonio Salgueiro GonzálezVídeos del curso "Diseño de objetos interactivos con DescartesJs e IA"
Presentación
Recursos y tutoriales previos:
- Descarga el software libre DescartesJS para tu sistema operativo
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
- Descripción detallada de cada sesión

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:
- Vídeo de la 1ª sesión (11 de abril 2025). Presentación de la 1ª sesión. Resumen sesión 1.ª
- Vídeo de la 2ª sesión (25 abril 2025). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (9 de mayo 2025). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (23 de mayo 2025). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (6 de junio 2025). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (20 de junio de 2025). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (4 de julio de 2025). Presentación de la 7ª sesión .
- Vídeo de la 8ª sesión (18 de julio de 2025).. Presentación de la 8ª sesión .

Herramientas de Inteligencia Artificial
 |
101. Generador de cómics17 de septiembre de 2025 Esta herramienta permite generar tiras cómicas usando inteligencia artificial. El usuario introduce una idea para la historia, selecciona diversos ajustes, y la aplicación produce automáticamente tanto el guion como las imágenes del cómic. Principales características: En este video, puedes observar su funcionamiento Ejemplos: el ocaso del dragón, Newton y Leibnitz, Supermán y el bosque de los secretos. |
|
 |
100. Generador de evaluaciones arrastrar y soltar -V220 de agosto de 2025 Crea Evaluaciones Visuales e Interactivas en Segundos, no en Horas. Ejemplos: científicos famosos, IoT, animales, flores y 4IR (inglés). |
|
 |
99. Generador de evaluaciones arrastrar y soltar -V120 de agosto de 2025 Transforma cualquier tema en un juego interactivo al instante! ¿Cansado de los métodos de estudio aburridos? ¿Necesitas una forma rápida y divertida de crear material didáctico? Ejemplos: científicos famosos, cuarta revolución industrial, estilos artísticos, IoT e insectos. |
|
 |
98. Generador mágico de arte IA19 de agosto de 2025 Esta herramienta es un generador de arte que utiliza inteligencia artificial para crear imágenes en más de 50 estilos. Los usuarios pueden seleccionar, deseleccionar, borrar y descargar las imágenes generadas, tanto de forma individual como en un archivo comprimido (ZIP). Adaptación de la aplicación publicada en WebSim. El cómo se usa se puede ver en este video.
|
|
 |
97. Análisis gramatical interactivo - V218 de agosto de 2025 ¡Aprender gramática nunca fue tan dinámico y personal! ¿Quieres mejorar tu dominio de la gramática de una forma interactiva y moderna? Con esta herramienta solo tienes que escribir un tema y nuestra inteligencia artificial avanzada generará un párrafo único para ti. A continuación, ponte a prueba con un taller interactivo que te retará a identificar verbos, sustantivos, adjetivos y preposiciones. Recibe una puntuación al instante, visualiza las respuestas correctas y descarga tus ejercicios para practicar donde quieras. Algunos ejemplo generados: colibrí, delfín, flores y Roma en español; apple, butterflies y tiger en inglés. Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Gemini 2.5 Pro, las API de Pollinations y videos de Pexels. La herramienta puede cometer errores. Considera verificar antes de descargar y compartir. |
|
 |
96. Análisis gramatical interactivo18 de agosto de 2025 Una herramienta que convierte el aprendizaje en un juego. Elige un tema que te apasione (videojuegos, el universo, tu serie favorita... ¡lo que sea!). Algunos ejemplos gerados: Aves, banano, ciclismo, ciudad, mar y monk (ingles). Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Gemini 2.5 Pro, las API de Pollinations y videos de Pexels. La herramienta puede cometer errores. Considera verificar antes de descargar y compartir. |
|
 |
95. Creador IA17 de agosto de 2025 ¿Cansado de las IAs genéricas? ¡Crea tu propia mente artificial personalizada! ✨ ¿Qué hace especial a Creador IA?
|
|
 |
94. Generador de fragmentos literarios17 de agosto de 2025 ✨ ¡Presentamos el Generador Literario IA! ✍️ Transforma cualquier idea (¡una sola palabra!) en:
¡Descarga tu lección completa en un clic! Ideal para profes, estudiantes y escritores. Idea original de Édgar Herrera Morales Algunos fragmentos generados: Odiseo, Don Quijote de la Mancha, IoT, Cien años de soledad, Machu Picchu y Tom Sawyer (inglés). |
|
 |
93. Generador de cuestionarios con tiempo de respuesta - V215 de agosto de 2025 Crea cuestionarios interactivos en segundos con inteligencia artificial Características destacadas: • Genera hasta 20 preguntas automáticamente sobre cualquier tema • 31 estilos artísticos para imágenes (desde fotográfico hasta cartoon 3D) • Temporizador configurable con barra visual • 24 paletas de colores personalizables • Soporte en 3 idiomas (Español, Inglés, Francés) • Descarga cuestionarios independientes y funcionales ⚡ Perfecto para: Educadores y profesores Algunos cuestionarios generados: biología marina, capitales del mundo y pintores famosos |
|
 |
92. Generador de cuestionarios con tiempo de respuesta - V114 de agosto de 2025 ¡Revoluciona tus trivias con el Generador de Cuestionarios con Inteligencia Artificial! ?✨ |
|
 |
91. Generador de líneas de tiempo con Pollinations13 de agosto de 2025 ¿Líneas de tiempo aburridas? ¡Nunca más! ?➡️✨ Transforma cualquier tema histórico en una obra de arte visual con nuestra nueva herramienta GRATUITA. ✅ IA genera textos e imágenes Algunos ejemplos los hemos creado con el tema "IoT", usando diferentes estilos visuales: Tarjetas flotantes, grid iconográfico y vertical clásico ¡Pruébala ahora! |
|
 |
90. Generador de páginas Retro con Pollinations12 de agosto de 2025 ¿Extrañas el Internet de los 90 y 2000? ¡Viaja en el tiempo con el Generador RetroWeb! Sumérgete en una auténtica interfaz de Internet Explorer y crea sitios web completos de cualquier época, desde la era BBS de 1980 hasta la Web 2.0. Solo elige el año, el tema y deja que nuestra IA haga su magia, generando contenido, imágenes y GIFs de la época. Define el estilo (página personal o corporativa), el tipo de diseño (marcos, tablas, centrado) y los elementos multimedia que quieres incluir. ¡Cada sitio es único! ¡Descarga tu joya nostálgica en un solo clic y comparte el caos glorioso de la web de ayer! Algunos ejemplos los hemos creado con el tema "Computadores", obteniendo: 1980, 1995, 1996, 2005 y 2010 |
|
 |
89. Chatbots personalizados - Parte 212 de agosto de 2025 Esta segunda versión de Chatbots personalizados ofrece 12 chatbots en las siguientes áreas del conocimiento:
Los Chatbots fueron diseñados por varios miembros de las Red Descartes |
|
 |
88. Crea tu cuento infantil con Pollinations - v210 de agosto de 2025 ✨ ¡Crea Cuentos Mágicos en Segundos! ✨ Con el Creador de Cuentos Infantiles, solo tienes que describir a tu personaje ("un conejito valiente"), elegir un estilo visual (¡como Pixar o Disney!), y nuestra IA se encarga del resto. En instantes, tendrás un cuento digital completo, con ilustraciones preciosas y texto único, que puedes descargar y compartir. Esta segunda versión es una mejora de la herramienta 17, publicada el 17 de marzo de 2025. Incluye selectores para el número de actos, modelo de lenguaje y estilo de imagen. Algunos cuentos generados son: La princesa de pelo de fuego y el secreto del bosque y La Princesa Juanita y el Secreto de la Luna. Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Gemini 2.5 Pro y las API de Pollinations |
|
 |
87. Chat IA de Pollinations10 de agosto de 2025 Descubre la nueva frontera de la conversación con nuestro AI Chat Studio. Esta no es una simple ventana de chat; es una potente herramienta creativa que integra la generación de texto e imágenes en una interfaz fluida. Elige entre distintos modelos de IA, personaliza su voz y define su personalidad para adaptarla a tus necesidades, desde un asistente formal hasta un creativo sin filtros. Cuando termines, exporta toda tu conversación, incluidas las imágenes, con un solo clic. Pide una imagen y la verás aparecer en la conversación. Ideal para artistas, diseñadores y para dar vida a tus ideas visualmente. Activa la voz de la IA y escucha respuestas fluidas con pausas naturales entre párrafos ¿Prefieres hablar a escribir? Usa el micrófono para dictar tus preguntas y obtener respuestas de forma rápida y natural. Esta herramienta es una adaptación de https://www.ai-ministries.com/pspeak.html, en la que hemos mejorado el diseño, el estilo de respuesta y la lista de voces. Un ejemplo de una conversación guardada con diferentes personalidades, la puedes ver aquí. |
|
 |
86. PicVaan - Transforma tu visión en arte con IA7 de agosto de 2025 Herramienta diseñada por SugamDeol en Vercel, que convierte textos o imágenes en sorprendentes obras visuales con ayuda de las API de Pollinations. Elige un modelo, describe tu idea o edita una imagen, ¡y deja que la creatividad florezca! Visita el blog IA Generativas, para acceder al instructivo de esta herramienta. Generación de imágenes con IA desde texto o mediante edición de imágenes existentes. Interfaz intuitiva con herramientas para resaltar zonas a modificar. Tres modelos IA disponibles (Kontext, Flux y Turbo) para elegir según calidad o velocidad. Mejora automática de prompts para obtener resultados más impactantes. Configuración personalizada de calidad y tamaño del lienzo. Galería integrada para visualizar y guardar tus creaciones. |
|
 |
85. Generador de código con IA5 de agosto de 2025 Esta herramienta fue generada en WebSim, cuya versión original en inglés puedes verla aquí. Es una plataforma basada en inteligencia artificial que permite crear sitios web, juegos y aplicaciones directamente desde descripciones de texto o una URL. Utiliza modelos avanzados como Claude 3.5 Sonnet y GPT‑4o para generar código HTML, CSS, JavaScript, Python, Java, C++, TypeScript, entre otros. Una vez generado el código se puede ejecutar en la misma plataforma o descargarlo para ejecutarlo en local. También puedes agregar nuevos prompts para ajustar el diseño, cambiar colores, añadir secciones o materiales multimedia, todo en tiempo real. Algunas aplicaciones generadas son: películas animadas, IoT y estilos artísticos (más de 100). Estos ejemplos fueron la base de inspiración de la herramienta 83 (generador de tarjetas didácticas). |
|
 |
84. Generador del juego "Encuentra la imagen"4 de agosto de 2025 Herramienta que permite generar el juego "Encuentra la imagen correcta". Algunos juegos generados son: actores famosos (estilo Pop Art), artistas famosos (estilo cartoon), felinos (dibujo a lápiz), IoT (estilo fotográfico) y 4RI (estilo futurista) La versión en inglés se ha publicado aquí, con estos ejemplos: fruits (pointillism style) and insects (marble sculpture style). |
|
 |
83. Generador de tarjetas didácticas2 de agosto de 2025 Las flashcards, también conocidas como tarjetas tarjetas didácticas, son tarjetas que contienen información dividida generalmente en dos partes: en el anverso (parte frontal) se coloca una pregunta, palabra, concepto o imagen y en el reverso (parte posterior) se coloca la respuesta, explicación o información relacionada (versión en inglés aquí).
Con esta herramienta puedes generar tarjetas didácticas con imágenes (anverso) e información relacionada (reverso). Las imágenes se pueden generar con un estilo artístico seleccionado entre 30 disponibles. Las imágenes y descripciones se pueden regenerar. Una vez aprobadas las tarjetas, puedes descargarlas en un archivo HTML. Ejemplos de tarjetas generadas: actores famosos, artistas famosos, dioses griegos, famous artists y felinos. |
|
 |
82. Generadores de imagen con PollinationsProyecto de aula - Red Educativa Digital Descartes 1 de agosto de 2025 Del curso "Diseño de objetos interactivos con DescartesJS e IA" se presentaron dos proyectos de aula. El primer proyecto era una herramienta que permitiera generar imágenes con la API de Pollinations, incluyendo relación de aspecto y estilos artísticos. Cerca de 20 proyectos fueron entregados, de los cuales seleccionamos cinco, que peresentamos en esta herramienta. Los autores de los generadores de imagen son: Carlos Alberto Rojas Hincapié, Elena Álvarez Saiz, María José García Cebrian, Jhon Jairo García Mora y José M. Fernández (Zhema). |
|
 |
81. Generador de trivia breakout1 de agosto de 2025 Trivia Breakout es una herramienta educativa interactiva con formato de “juego tipo breakout” para aprender mediante cuestionarios, la cual permite:
Algunos ejemplos de trivias creadas son: Cuarta revolución industrial, Álgebra y Sistemas embebidos. Una versión en inglés se puede acceder aquí. La idea de esta aplicación surge del libro Métodos Numéricos de Elena Álvarez, que intervenimos con Gemini 2.5 Pro |
|
 |
80. Generador de Memes CatGPT23 de julio 2025 CatGPT es un generador de memes basado en IA, creado en colaboración entre Pollinations.AI y Tanika Godbole (la autora del concepto original “CatGPT”) . La idea (publicada en Pollinations por @voodoohop) busca transformar las preguntas de los usuarios en cómics de gatos con un toque sarcástico. Características principales: generación instantánea de memes, aprovecha el modelo GPT-Image‑1 de OpenAI a través de la API de Pollinations para crear imágenes en segundos, respuestas con actitud felina, las viñetas muestran al gato respondiendo con humor y desdén, fiel al estilo del cómic original, interfaz amigable y sin límites, no requiere registro ni clave de API, Compartir y descargar. ? ¿Cómo usarlo? Accedes a la web. Escribes tu pregunta (por ejemplo, “¿Qué debería comer hoy?”). Haces clic en “Generate Meme”. El sistema crea tu meme con sabiduría de gato perezoso y sarcástico. Una opción interesante, es subir una imagen de referencia:
|
|
 |
79. Analizador de personalidad con IA20 de julio 2025 ¿Estás dispuesto a que una inteligencia artificial analice tu personalidad? ¿Sí?, entonces tómate una selfie y espera a que la IA haga su evaluación y te de una severa crítica a partir de tu selfie. El analizador de personalidad es una aplicación para el entretenimiento y reir un poco con las ocurrencias de la IA; por ejemplo "En la vasta extensión del universo de las selfies, este espécimen se atreve a desafiar las leyes de la estética. Con una barba que parece haber sido diseñada por un artista del surrealismo..." Además de obtener tu perfil psicológico, fortalezas y debilidades, puedes preguntarle a la IA sobre tu personalidad. Herramienta diseñada por andr3as |
|
 |
78. Detective de alucinaciones IA18 de julio 2025 Esta herramienta es una adaptación de una web interactiva presentada por Claude 4 y denominada "3 verdades y una alucinación": La idea es que primero llamaremos a la API para obtener una lista de ~5 temas aleatorios para que el usuario elija. O pueden elegir lo que quieran (entrada de texto libre). Luego, usando nuevamente la API, generaremos tres frases sobre el tema y una falsa, alucinada. El usuario debe intentar identificar cuál es la alucinación. Una vez que el usuario haya seleccionado una respuesta, mostramos si acertó o no, qué es falso sobre la alucinación y actualizamos la puntuación. Agreguemos algunos componentes divertidos, como rachas y demás (Claude). Hemos intervenido la aplicación, cambiando la API de Claude Sonnet 4 por la de Pollinations, el nombre de la herramienta y mejorando su diseño. Como herramienta es útil para generar cuestionarios, que permitan evaluar la capacidad del usuario de identificar alucinaciones de IA. Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Claude 4 Sonnet y las API de Pollinations |
|
 |
77. Generador de Iceberg personalizado15 de julio 2025 En la herramienta 18, presentamos un modelo de generación de Iceberg que incluía dos controles: ingreso del tema y el número de niveles. 1. Modelo independiente de WebSim (el anterior está alojado en WebSim)- Algunos ejemplos de iceberg generados son: Dibujos animados, Imperio Inca y estilos artísticos. Versión en inglés aquí. Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Gemini 2.5 |
|
 |
76. Diccionario moderno12 de julio 2025 Esta aplicación permite buscar palabras o expresiones contemporáneas, con sus significados, incluyendo:
La herramienta genera, si se desea, una palabra aleatoria. Incluye, además, un historial con definiciones e imágenes generadas en la sección de favoritos. Esta es una versión en español de la original diseñada en inglés en WebSim, en la que hemos incluido la API de Pollinations. |
|
 |
75. Generador de trivias iceberg11 de julio 2025 En educación, la técnica del iceberg es una metáfora visual y metodológica que se utiliza para ayudar a los estudiantes a analizar, comprender y reflexionar sobre fenómenos complejos, problemas o comportamientos, yendo más allá de lo que se ve “en la superficie”. Por otra parte, el término “trivia” proviene del latín trivium, que originalmente hacía referencia a conocimientos considerados básicos o comunes. Hoy, sin embargo, el concepto se asocia con preguntas curiosas, datos interesantes o poco conocidos. El generador de trivias iceberg es una herramienta que permite, a partir de un tema, generar preguntas y respuestas que van desde un nivel superficial (conocimiento básico) a niveles más profundos u oscuros. Estas preguntas y respuestas van acompañadas de imágenes, según el modelo (flux, gptimage o kontext) y estilo seleccionado por el usuario. La trivia generada se puede descargar en formato HTML o PDF. Algunos ejemplos de trivias generadas, son: Esta es una versión mejorada de la original diseñada en WebSim. Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Gemini 2.5 y las API de Pollinations. |
|
 |
74. Estudio de Dibujo10 de julio 2025 Estudio de Dibujo pone a tu alcance un completo conjunto de herramientas: paletas de colores personalizables, pinceles de distintos estilos, frascos de pintura, brochas, aerosoles y mucho más, para que puedas dar vida a tus ideas de la forma más libre y expresiva. Además, puedes cargar tus propias imágenes para editarlas, o aprovechar la potencia de la inteligencia artificial para generar nuevas creaciones que impulsen tu imaginación. Combina técnicas digitales y creatividad asistida por IA para explorar posibilidades infinitas y transformar cada boceto en una obra única. Esta herramienta es una alternativa a las herramientas 52 "Dibujos para colorear" y 63 "Dibujos para colorear V2 con Pollinations". ¡Empieza a crear, mezcla estilos y deja que tu arte cobre vida en Estudio de Dibujo! Herramienta original diseñada por @Red_Bot@Red_Bot en Websim |
|
 |
73. PixPal: Tu Co-piloto Creativo8 de julio 2025 Potente aplicación web de Inteligencia Artificial diseñada para ser un asistente creativo "todo en uno". Herramienta diseñada por andr3as |
|
 |
72. Flux.1 Kontext versus GPT-Image-17 de julio 2025 Esta herramienta, diseñada con el editor DescartesJS, es similar a la herramienta 69, pero incluyendo el modelo GPT-Image-1 para la edición de imagen. El procedimiento, entonces, es similar: 1. Imagen de referencia. La imagen se puede ingresar, preferiblemente, a través de una URL de la imagen (por ejemplo, imágenes de Pixabay, NightCafé, Lexica, Krea, AIGallery, Recraft y Lumenor) . Si se genera ingresando un prompt, solo se podrá editar con Flux.1 Kontext. La herramienta fue creada por Juan Guillermo Rivera Berrío utilizando el editor DescartesJS y las API de Pollinations. |
|
 |
71. Fábrica de chatbots5 de julio 2025 Esta herramienta permite generar chatbots personalizados con solo ingresar el tema del chatbot y activar o no la inclusión de imágenes. Es posible, también, definir la personalidad; por ejemplo, en el tema incluir "Química con tono sarcástico". El chatbot descargado, permite:
Herramienta diseñada por Juan Guillermo Rivera Berrío con tecnología Gemini 2.5 y las API de Pollinations |
|
 |
70. Generador de cuestionarios de falso y verdadero - v22 de julio 2025 Esta herramienta, diseñada con Gemini 2.5 y usando las API de Pollinations, permite generar cuestionarios tipo falso o verdadero a partir de un tema ingresado por el usuario. Se trata de una versión mejorada a la publicada como herramienta 24. Las mejoras son las siguientes: 1. Mayor número de preguntas. La primera versión solo admite un máximo de 10 preguntas, en esta versión no hay límte; sin embargo, se sugiere no usar más de 30 preguntas. La herramienta fue creada por Juan Guillermo Rivera Berrío utilizando el editor DEscartesJS y la API de Pollinations. |
|
 |
69. Imágenes en contexto con Pollinations y DescartesJS1 de julio 2025 Esta herramienta hace uso del nuevo modelo flux.1 kontext de Pollinations, para incluir elementos o estilos nuevos a una imagen de referencia. El procedimiento es el siguiente: 1. Imagen de referencia. La imagen se puede ingresar a través de una URL de la imagen (por ejemplo, imágenes de Pixabay, NightCafé, Lexica, Krea, AIGallery, Recraft y Lumenor) o generarla ingresando un prompt. En ocasiones es conveniente incluir el mensaje "conservando el contexto"; por ejemplo, "Ponle gafas conservando el contexto". En esta presentación, puedes ver algunos ejemplos de indicaciones exitosas La herramienta fue creada por Juan Guillermo Rivera Berrío utilizando el editor DescartesJS y la API de Pollinations. |
|
 |
68. Generador de entradas para blogs24 de junio 2025 Al escribir una entrada de blog con mucho texto, añadir variedad puede hacerla mucho más atractiva para los lectores. Si bien la Inteligencia Artificial (IA) puede ayudar en muchos aspectos, como estructurar el contenido, investigar o incluso crear diagramas directamente dentro de la consigna, hay un área que tradicionalmente ha sido difícil sin herramientas adicionales: las imágenes. Esta herramienta permite crear una publicación de blog rica en imágenes, dividiendo el proceso en los siguientes pasos. En este video: https://youtu.be/4g-DXX9oz5g, puedes ver un ejemplo de cómo crear una entrada. Esta herramienta fue creada por Juan Guillermo Rivera Berrío utilizando la tecnología Gemini 2.5. |
|
 |
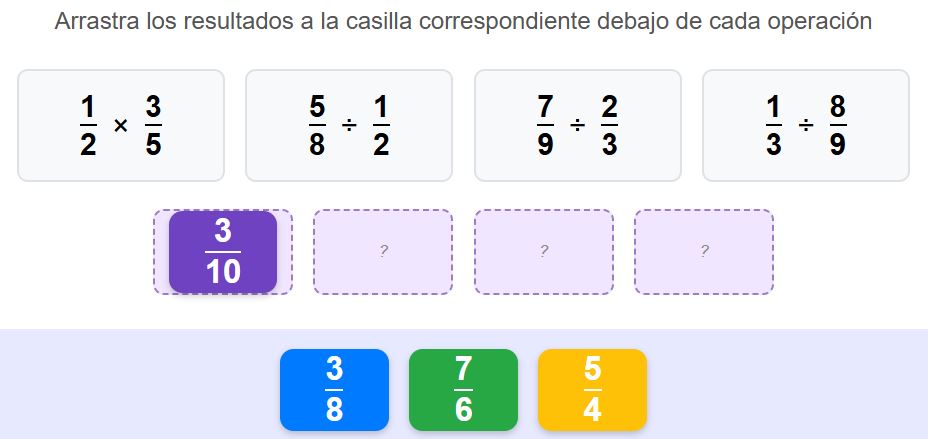
67. Resolviendo operaciones aritméticas9 de junio 2025 Herramienta educativa interactiva diseñada para ayudar a los estudiantes a practicar y reforzar sus habilidades en la solución de operaciones aritméticas con diferentes tipos de números. A través de una interfaz intuitiva, los usuarios pueden seleccionar entre varias categorías numéricas y participar en actividades de arrastrar y soltar para poner las respuestas correctas. Presenta, además, la posibilidad de descargar la evaluación generada para uso en local.
Esta aplicación es especialmente útil para estudiantes de educación básica y media que deseen mejorar su comprensión del orden numérico en diferentes contextos. Además, al ser parte del Proyecto Descartes, se alinea con metodologías educativas activas y participativas. Esta herramienta fue creada por Juan Guillermo Rivera Berrío utilizando la tecnología Gemini 2.5. |
|
 |
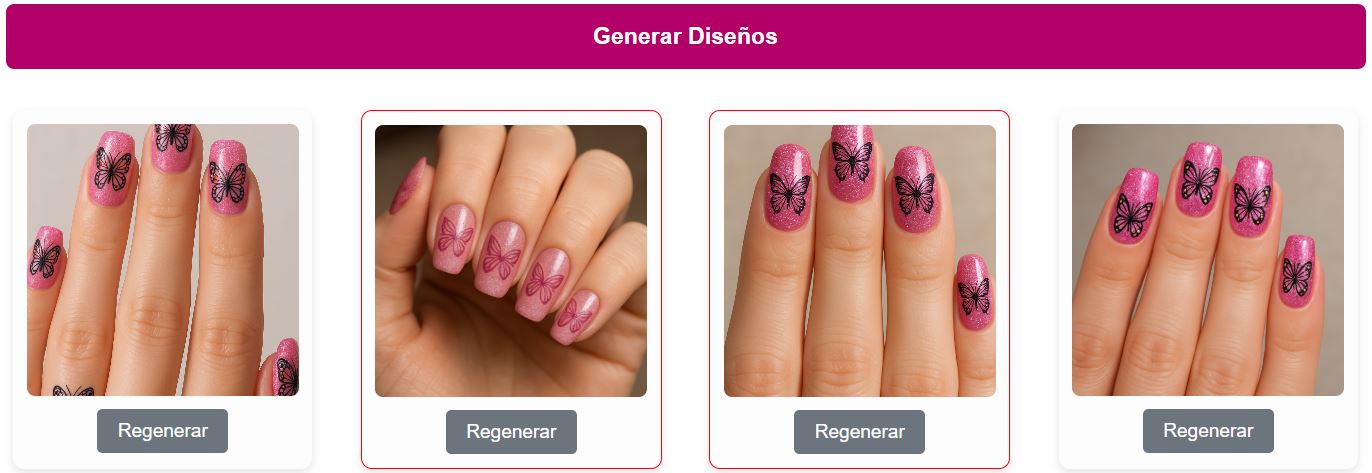
66. Diseñador de uñas con Pollinations7 de junio 2025 La generación de manos y dedos realistas es uno de los desafíos más conocidos para los modelos de IA generativa de imágenes. A veces, incluso con prompts muy específicos, los resultados pueden ser imperfectos. Esta herramienta permite generar diseños de uñas con varios modelos artísticos, usando la API de Pollinations con los modelo Flux y Turbo; sin embargo, para lograr mejores resultados, hemos incluido el modelo Imagen de GPT, con el cual podemos obtener imágenes como:
En cada imagen incluimos botones de regeneración, para obtener otras imágenes. Adicionalmente, al hacer clic sobre una imagen se presenta el botón de descarga. Esta herramienta fue creada por Juan Guillermo Rivera Berrío utilizando la tecnología Gemini 2.5. |
|
 |
65. Galería de Pollinations5 de junio 2025 Galería interactiva de imágenes generadas con la API de Pollinations. En ella, los usuarios pueden explorar una colección de imágenes organizadas en forma de mosaico, lo que permite una visualización atractiva y estructurada del contenido visual generado por Pollinations. La página ofrece opciones para descargar las imágenes o abrirlas en otra pestaña para una mejor experiencia de navegación. Las imágenes corresponden a creaciones de los usuarios de la herramienta de IA Pollinations, incluyendo el prompt que las genera, estilos, tamaños y demás parámetros de creación. Es importante advertir que las imágenes con contenido NSFW han sido filtradas. Esta galería fue creada por Juan Guillermo Rivera Berrío utilizando la tecnología Gemini 2.5. |
|
 |
64. Juego de Ordenar Números con Pollinations4 de junio 2025 Herramienta educativa interactiva diseñada para ayudar a los estudiantes a practicar y reforzar sus habilidades en el ordenamiento de diferentes tipos de números. A través de una interfaz intuitiva, los usuarios pueden seleccionar entre varias categorías numéricas y participar en actividades de arrastrar y soltar para organizar los elementos en el orden correcto. Presenta, además, la posibilidad de descargar el juego actual para uso en local. Esta aplicación es especialmente útil para estudiantes de educación básica y media que deseen mejorar su comprensión del orden numérico en diferentes contextos. Además, al ser parte del Proyecto Descartes, se alinea con metodologías educativas activas y participativas. Herramienta desarrollada por Juan Guillermo Rivera Berrío utilizando tecnologías como Pollinations y Gemini 2.5 |
|
 |
63. Dibujos para colorear V2 con Pollinations3 de junio 2025 Esta herramienta interactiva permite generar y colorear imágenes de manera personalizada, combinando inteligencia artificial y creatividad manual. Características principales
Herramienta desarrollada por Juan Guillermo Rivera Berrío utilizando tecnologías como Pollinations y Gemini 2.5 Pro Preview |
|
 |
62. Generador de presentaciones con imágenes y texto V2 - Con Deepseek y Pollinations1 de junio 2025 Esta versión presenta mejoras con respecto a la herramienta 22, creada con la herramienta de IA Create. Las mejoras son las siguientes:
La presentación descargada contiene las imágenes en formato Base64, para su ejecución en local sin necesidad de estar conectado a Internet. Estos son dos ejemplos de presentaciones generadas: Felinos y Estilos artísticos. |
|
 |
61. Generador de cuestionarios de selección múltiple - V220 de mayo 2025 Este nuevo modelo permite intervenir el diseño, incluyendo MathJax para expresiones matemáticas, regenerar imágenes y límites más amplios del número de preguntas. En este video se muestra el procedimiento para generar el cuestionario. Algunos ejemplos de cuestionarios, que hemos generado, son sobre animales y factorización de polinomios. La herramienta fue diseñada usando las API de Pollinations y tecnología Gemini 2.5 Pro. |
|
 |
60. Generador de juegos tipo scrambled19 de mayo 2025 El juego Scrambled consiste en ordenar letras, palabras o frases que han sido mezcladas para formar una palabra o enunciado correcto. Esta herramienta permite generar juegos de palabras desordenadas; por ejemplo, palabras de animales, palabras sobre comidas y juego de palabras sobre flores. La herramienta fue diseñada usando la API de Pollinations y tecnología Gemini 2.5 Pro |
|
 |
59. Diálogo inteligente de IA con Pollinations18 de mayo 2025 Esta herramienta es un poderoso asistente de chat con inteligencia artificial que puede responder preguntas, brindar sugerencias creativas, escribir textos e incluso ayudarlo a resolver problemas complejos. Uso completamente gratuito e ilimitado, con 16 modelos de lenguaje y 13 personalidades del bot, recuerda conversaciones y las guarda en formato MD. Esta herramienta diseñada por el Laboratorio Azad (China), la cual la hemos traducido al español. La herramienta fue diseñada usando la API de Pollinations |
|
 |
58. Generador de tutoriales interactivos17 de mayo 2025 ¿Quieres diseñar tutoriales llamativos e interactivos para tus estudiantes? Esta herramienta te los diseña con unos cuanto clics, solo tienes que ingresar el tema del tutorial, el número de pasos y ¡listo! a generar el tutorial. Pero, si lo deseas, puedes configurarlo para obtener un mejor resultado, así:
He aquí algunos tutoriales obtenidos: producto de matrices, las leyes de Newton ysistemas embebidos La herramienta fue diseñada usando la API de Pollinations y la IA Gemini 2.5 Pro Preview |
|
 |
57. Crea tu juego Memoriza con Pollinations16 de mayo 2025 Un creador de juegos tipo "Memoriza" o "Encuentra las parejas". El procedimiento es sencillo:
La herramienta fue diseñada usando la API de Pollinations y la IA Gemini 2.5 Pro Preview |
|
 |
56. Generador de secuencias temporales15 de mayo 2025 ¿Quiéres generar secuencias temporales con tres o cuatro momentos? Esta herramienta te ayudará en ello; para ello, sigue estas instrucciones: 1. Elige el número de momentos de la secuencia (3 o 4)
|
|
 |
55. Puzle de arrastre de piezas14 de mayo 2025 Esta herramienta permite generar puzles o rompecabezas tipo arrastre de piezas, así:
La herramienta fue diseñada usando la API de Pollinations y la IA Gemini 2.5 Pro Preview
|
|
 |
54. Puzle de intercambio de piezas13 de mayo 2025 Esta herramienta permite generar puzles o rompecabezas tipo intercambio de piezas, así:
La herramienta fue diseñada usando la API de Pollinations y la IA Gemini 2.5 Pro Preview
|
|
 |
53. Generador de evaluaciones tipo completar la frase12 de mayo 2025 Esta herramienta permite generar evaluaciones tipo "completa la frase" y descargarlas en formato HTML, para compartir. Se tienen las siguientes configuraciones:
La herramienta fue diseñada usando las API de Pollinations y la IA Gemini 2.5 Pro Preview
|
|
 |
52. Dibujos para colorear11 de mayo 2025 Esta herramienta presenta una paleta de colores, para colorear dibujos así:
En 2012 se creó un applet similar, que da cuenta del origen de esta propuesta (ver este video). La herramienta fue diseñada usando las API de Pollinations y la IA Gemini 2.5 Pro Preview
|
|
 |
51. Asocia imágenes y textos con pollinations10 de mayo 2025 Esta herramienta permite, a partir de un prompt ingresado por el usuario, generar un juego de asociación de imágenes y textos, siguiendo este procedimiento:
El juego generado se puede descargar en formato HTML, para compartir. Algunos juegos creados son los siguientes: Juego animales estilo Pixar y Juego pintores famosos estilo cartoon. Una versión modificada, permite generar plabras en inglés, para generar juegos como: fruits y farm animals, la versión se puede abrir aquí, ideal para juegos de aprendizaje del vocabulario en inglés. La herramienta fue diseñada usando las API de Pollinations y la IA Gemini 2.5 Pro Preview
|
|
 |
50. Clasificador de imágenes con pollinations9 de mayo 2025 Herramienta para generar una evaluación tipo clasificación de imágenes. El procedimiento es el siguiente:
La herramienta fue diseñada usando las API de Pollinations y la IA Gemini 2.5 Pro Preview
|
|
 |
49. Emparejamiento de imágenes y palabras8 de mayo 2025 Herramienta para generar una evaluación tipo emparejamiento. Con un tema ingresado por el usuario, la herramienta genera 5 palabras y 5 imágenes para emparejar. Se incluye un botón para generar nuevas palabras si las existentes no son del agrado del usuario. Se incluye, también, un botón de descarga del emparejamiento generado, para compartirlo. Sugerencias:
La herramienta fue diseñada con la aplicación 39 de esta página. con la ayuda de Gemini 2.5 Pro Preview 05-06 |
|
 |
48. Clasificador de palabras con Pollinations7 de mayo 2025 Herramienta para generar una evaluación tipo clasificación de palabras. El procedimiento es el siguiente:
La herramienta fue diseñada usando las API de Pollinations y las herramientas de IA ChatGPT, Gemini 2.5 y DeepSeek |
|
 |
47. Chatbots personalizados con Pollinations6 de mayo 2025 Esta herramienta ofrece 12 chatbots personalizados en las siguientes áreas del conocimiento:
La herramienta fue diseñada usando las herramientas 39 y 46, las imágenes de los botones fueron creadas con Ideogram |
|
 |
46. Creador de páginas web con Pollinations2 de mayo 2025 Esta herramienta es perfecta para diseñar y publicar páginas web profesionales de forma rápida, intuitiva y sin necesidad de saber programar. Ya seas emprendedor, creativo, docente o simplemente alguien con una idea que compartir, esta app te genera las plantillas, bloques visuales y funciones inteligentes que necesitas para que tu sitio esté en línea en cuestión de minutos. ¡Diseña, personaliza y publica con solo unos clics! Algunos ejemplos que puedes probar:
La herramienta original fue diseñada Logise en https://logise.neocities.org/webgeniusai.
|
|
 |
45. Investigación profunda con Pollinations1 de mayo 2025 Usando GPT-4o, a partir de un tema o pregunta de investigación, ingresado por el usuario, esta herramienta presenta buenos resultados obtenidos en su búsqueda en la web. Se ha configurado para que, por defecto, entregue las fuentes consultadas y los enlaces correspondientes. En nuestras pruebas, hemos verificado las fuentes en varias consultas, evidenciando una alta confiablidad de las mismas. La herramienta original fue diseñada en WebSim por Trey6383 en inglés.
|
|
 |
44. Generador de cuestionarios tipo flashcards22 de abril 2025 Esta herramienta permite, a partir de un tema ingresado por el usuario, generar un cuestionario tipo falso o verdadero, presentado a través de 12 tarjetas tipo flashcard. Una vez generado el cuestionario, se puede descargar en formato HTML. Hemos dispuesto 10 modelos de lenguaje, como alternativas en caso de fallar o no estar disponible el modelo seleccionado. La herramienta genera un color de fondo aleatoriamente.
|
|
 |
43. Generador de imágenes de IA de RuangRiung21 de abril 2025 El Generador de Imágenes con IA es ideal para artistas digitales y diseñadores que exploran creatividad con IA. Esta nueva herramienta, en español e indonesio (malayo), combina funcionalidad completa con diseño elegante y una gran diversidad de configuraciones disponibles. La herramienta fue diseñada por Arif Tirtana en inglés y malayo, la cual hemos cambiado uana versión en español; sin embargo, se puede acceder a la versión original aquí.
|
|
 |
42. Sopa de letras con DescartesJS y Pollinations19 de abril 2025 Esta herramienta fue diseñada con la participación de varias inteligencias artificiales y algo de inteligencia humana. El diseño de la sopa se logró con Claude 3.5 Sonnet (ver el libro Plantillas para libros con inteligencia artificialPlantillas para libros con inteligencia artificial), las palabras de las sopas se obtienen con modelos de lenguaje de la API de Pollinations y, finalmente, la comunicación de estas IA se logra con el editor de DescartesJS. Para generar una sopa, el usuario solo tiene que ingresar el tema de la sopa (Frutas, Razas de perros, Ciudades europeas, etc.) y el número de palabras de la sopa. Una vez obtenidas las palabras, se da clic en el botón "Guardar sopa" y... listo, la sopa está lista para degustarla.
|
|
 |
41. Chatbot Arena con DescartesJS y Pollinations17 de abril 2025 Similar al Chatbot Arena gestionada por investigadores de UC Berkeley SkyLab y LMArena, presentamos esta herramienta diseñadas con DescartesJS y usando los modelos LLM de la API de Pollinations. Hemos dejado los tonos del anterior chat multimodal, solo por diversión. Se pueden probar los modelos con indicaciones como: 1. Escribe 10 frases terminadas con la palabra manzana 2. Resuelve la ecuación: 3x+5=2x+12 Entre muchas otras
|
|
 |
40. Hablando con mi asistente virtual16 de abril 2025 Con esta nueva herramienta, puedes hablar (voz) con tu asistente virtual, obteniendo respuesta en texto y audio. Lo hemos configurado para que tenga acento paisa (Antioquia - Colombia), pero si se desea otro acento, basta con modificar las instrucciones dadas al parámetro system del chatbot; por ejemplo, para acento argentino puedes hacer clic aquí. La herramienta fue diseñada por Andreas Papathanasiou, usando la API de openai en Pollinations AI. |
|
  |
39. Generador de código con Pollinations15 de abril 2025 Esta herramienta permite crear páginas y aplicaciones, similar a como lo hace WebSim o v0 de Vercel. En este video presentamos una demostración, en la que se le pide a la herramienta que genere un presentador de diapositivas. La herramienta permite descargar las páginas y aplicaciones creadas, subir archivos para mejorarlos o incluirles más elementos. Si se desea que el archivo HTML incluya los códigos CSS y JS, se puede lograr con este segundo modelo. Algunos ejemplos de aplicaciones obtenidas son: ejemplo 1, ejemplo 2 y ejemplo 3
Herramienta diseñada por Aashir Shaikh usando la API de Pollinations. |
|
  |
38. Generador de libros académicos14 de abril 2025 Esta herramienta permite crear, en una forma muy sencilla, libros académicos. Hemos incluido varios modelos de lenguaje para la generación de las imágenes del libro y estilos artísticos para las imágenes. Es importante descargar el libro ejemplo en este archivo zip y seguir las instrucciones mostradas en la ayuda (icono ?) o en el tutorial para libros de cuentos, cuyo procedimiento es igual. Una vez ingresado el tema de un capítulo del libro, la IA genera un título llamativo y alusivo al capítulo, acompañado de 5 párrafos. Un ejemplo de libro generado es un libro de flores. La herramienta fue diseñada con DescartesJS y Pollinations. |
|
  |
37. Chatbot multimodal DescartesJS - Pollinations12 de abril 2025 Esta herramienta permite obtener respuestas del chatbot en tres formatos: texto, audio e imagen. El audio y la imagen se generan a partir del texto obtenido con GPT-4o. El objetivo final de la herramienta es la generación del contenido digital, necesario para una presentación de diapositivas, como las de este ejemplo, para lo cual se incluye un videotutorial. La voz del audio se puede seleccionar entre 10 voces y el estilo artístico de las imágenes de un menú que incluye 40 estilos. La herramienta fue diseñada usando nuevas funciones, incorporadas al editor DescartesJS, las cuales se explican en un artículo de la "Revista Digital Red Descartes" (Número 9). La herramienta fue diseñada con DescartesJS y Pollinations. |
|
  |
36. Generador de libros de cuentos11 de abril 2025 Esta herramienta permite crear, en una forma muy sencilla, libros de cuentos infantiles. Hemos incluido varios modelos de lenguaje para la generación de las imágenes del libro. Es importante descargar el libro ejemplo en este archivo zip y seguir las instrucciones en este tutorial. Algunos libros de cuentos podrían ser los clásicos como caperucita roja, el patito feo y los tres cerditos, los cuales la IA genera como un cuento resumido de la versión original. Sin embargo, la idea es generar cuentos a partir de un tema particular; por ejemplo, cuentos sobre animales (gatos, grillos, elefantes, etc.) o sobre brujas (la bruja loca, la bruja del bosque, la linda bruja, etc.). La herramienta fue diseñada con DescartesJS y Pollinations. |
|
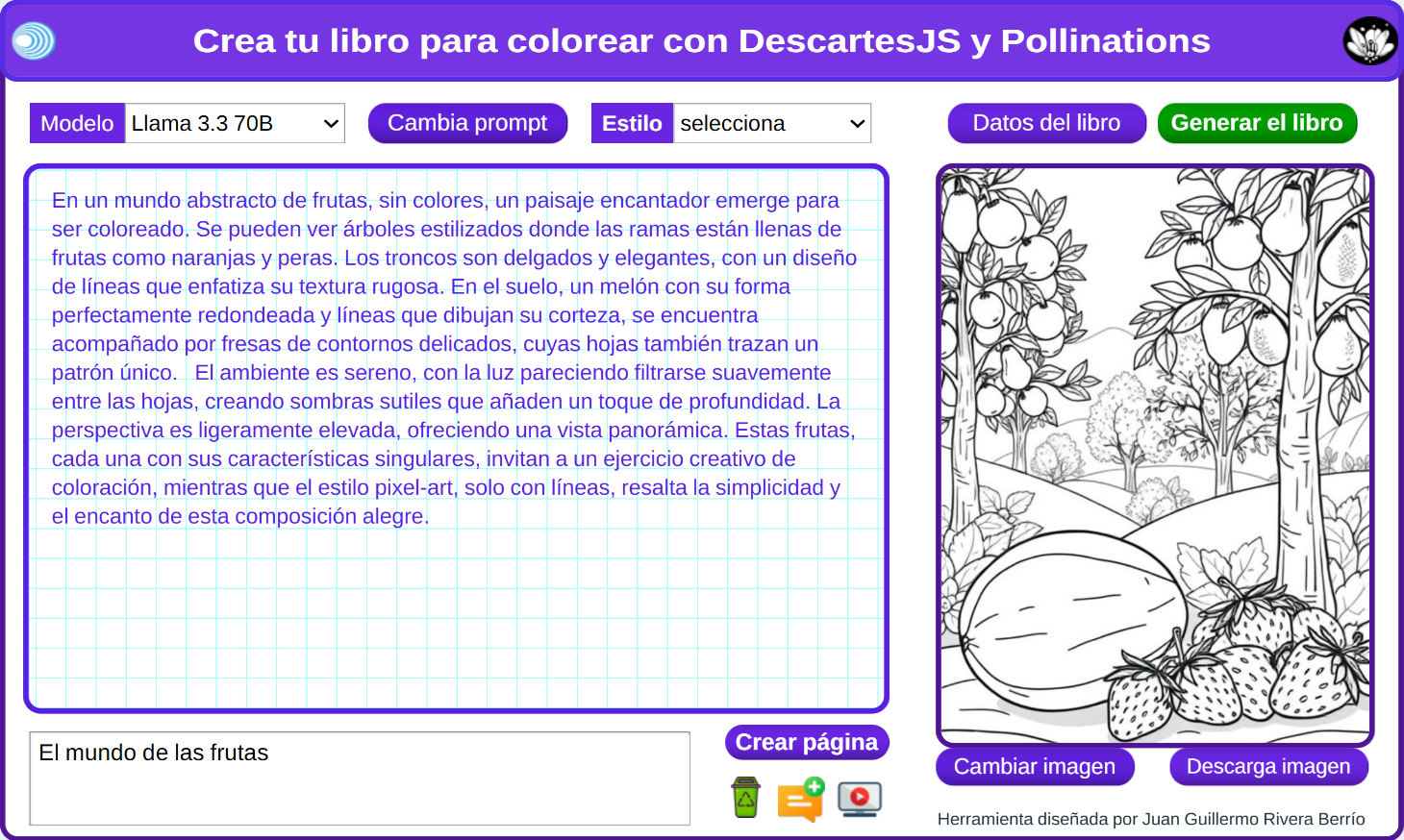  |
35. Creador de libros para colorear9 Esta herramienta permite crear, en una forma muy sencilla, libros para colorear. Hemos incluido varios modelos de lenguaje y estilos artísticos para la generación de las imágenes del libro. Es importante descargar el libro ejemplo en este archivo zip y seguir las instrucciones en este tutorial. Algunos libros que hemos diseñado con la herramienta son: Animales de granja y Princesas y caballeros. La herramienta fue diseñada con DescartesJS y Pollinations. |
|
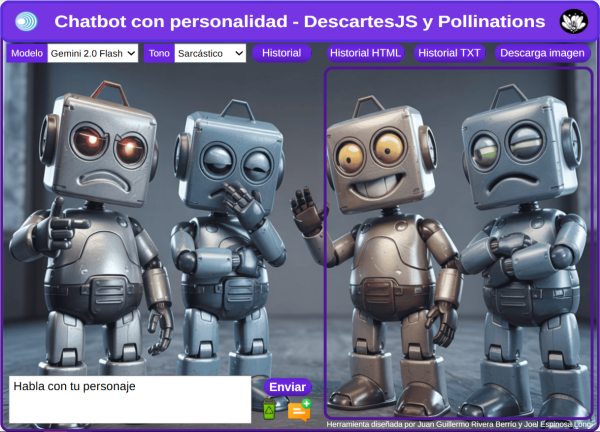  |
34. Chatbot con personalidad - DescartesJS y Pollinations6 de abril 2025 ¿Quieres hablar con un poeta o un filósofo?, con esta herramienta puedes hacerlo. Hemos incluido 10 personajes distintos, solo para que te diviertas. Incluye descarga del historial de cada sesión de chat en HTML y en formato TXT, botones de borrado del prompt actual y de inicio de nuevo chat. Herramienta diseñada con DescartesJS y Pollinations. |
|
  |
33. Investigando con DescartesJS y Pollinations5 de abril 2025 Esta herramienta es una ayuda para investigadores, permitiendo consultar artículos desde seis modelos de lenguaje. La consulta se realiza en fuentes públicas confiables como arXiv, PubMed, Semantic Scholar, CORE, entre otras fuentes. Como valor agregado, se genera una imagen relacionada con la pregunta de investigación, útil para documentos menos rigurosos, como los de tipo ensayo. Es importante verificar la información dada en cada una de las respuestas de la herramienta. |
|
  |
32. Generador de imágenes con enhanced variable4 de abril 2025 Esta herramienta permite generar imágenes ilimitadas, generando un prompt mejorado (enhanced). Ofrece la posibilidad de generar varios prompt a partir del mensaje ingresado por el usuario con su imagen asociada. Las imágenes, correspondientes a un prompt mejorado (enhanced), también se pueden cambiar en forma ilimitada. El prompt se puede copiar si se activa el modo HTML, las imágenes tienen descarga directa en formato png y asociando al nombre de la imagen el número de la semilla que la genera. |
|
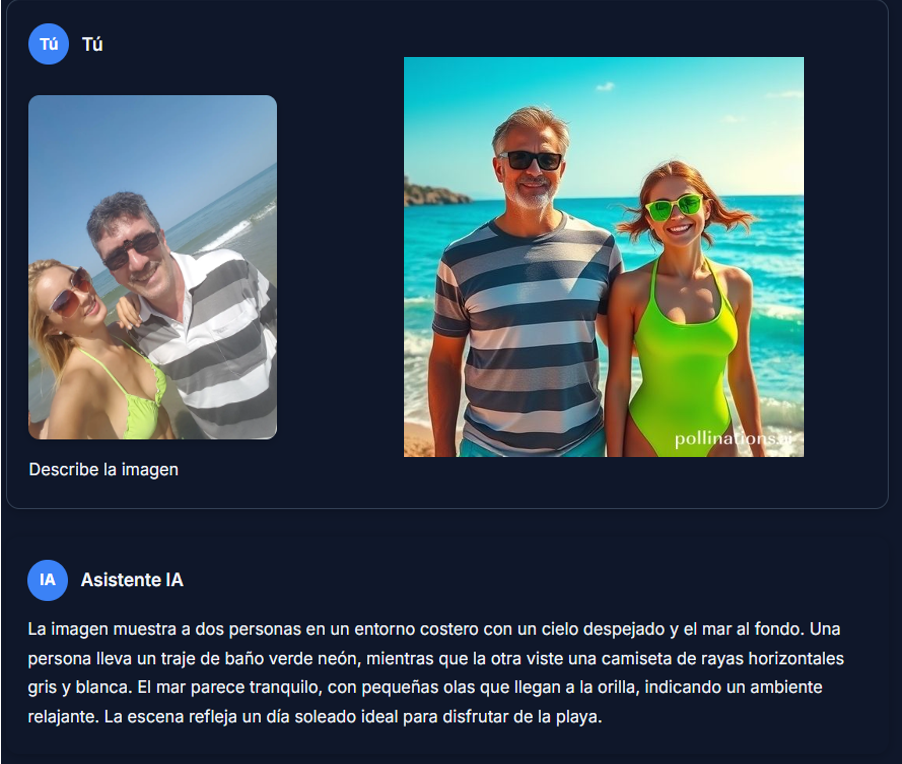  |
31. Asistente con visión computacional29 de marzo 2025 Esta herramienta permite conversar (chatear) con la IA pero, a la cual le podemos subir una imagen para que el asistente la describa (visión computacional). Una vez el asistente describe la imagen, se le puede solicitar que genere una imagen con un estilo artístico determinado, a partir de la descripción obtenida. La aplicación original fue realizada por @youngdawn86034002, a partir de la cual diseñamos una obra derivada en español y poniendo a funcionar los botones de cambio de fondo y nuevo chat, la cual se puede consultar aquí. Tanto el texto como las imágenes se generan con las API de Pollinations, las consultas en la web se realizan con el buscador DuckDuckGo; por ejemplo, la Red Educativa Digital Descartes. |
|
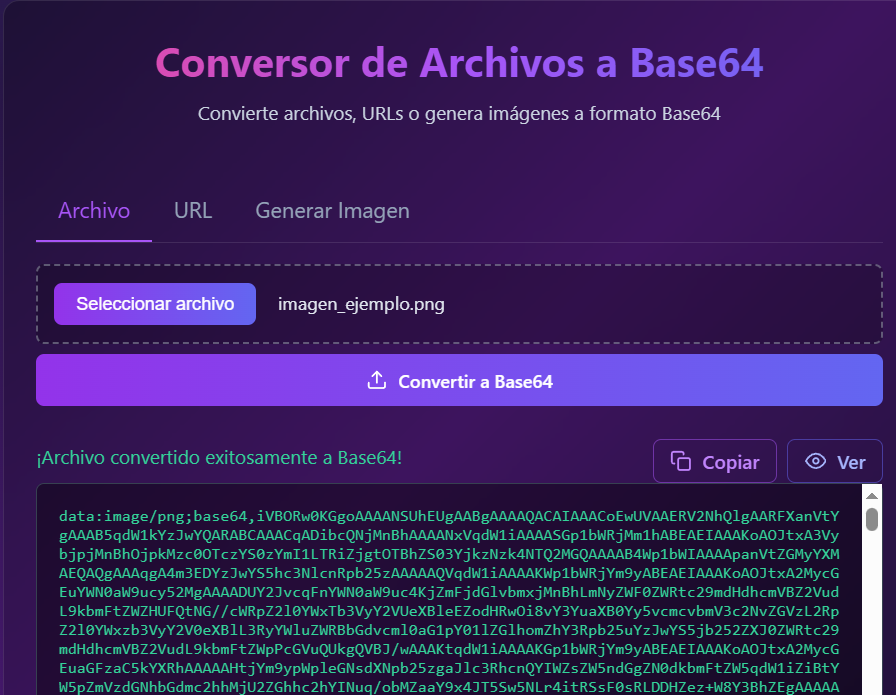  |
30. Conversor de archivos a Base6428 de marzo 2025 Esta herramienta permite convertir archivos de imagen, audio o video a Base64, tal como se observa en este video. Los archivos en Base64 son útiles en múltiples contextos porque permiten representar datos binarios en un formato de texto; por ejemplo, se pueden incluir imágenes, audios o videos directamente en el código HTML o CSS sin necesidad de archivos externos. El archivo a convertir se puede subir desde el computador o de una URL, o generar una imagen con Pollinations y obtenerla de Base64. Una aplicación del Base64 la usamos con una de las herramientas de este sitio, que se puede observar aquí. |
|
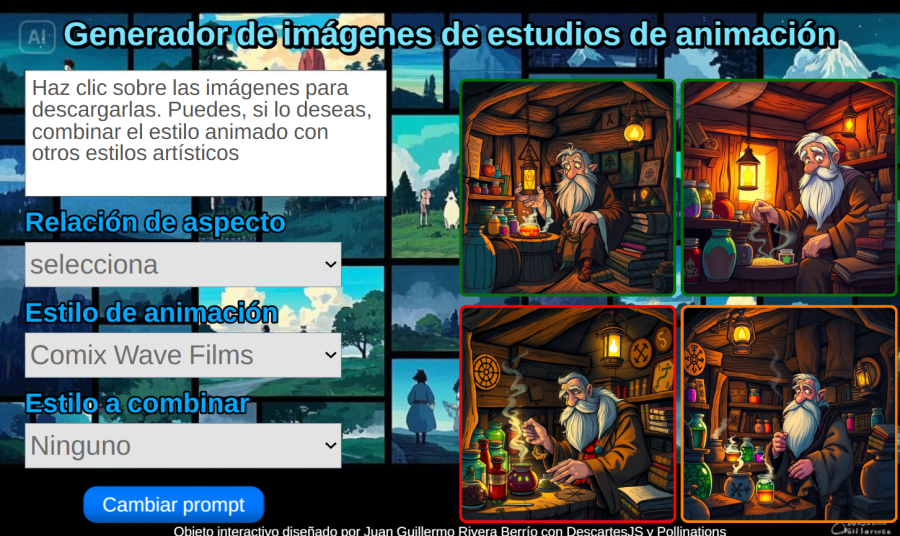  |
29. Crea imágenes estilo estudios de animación con DescartesJS y Pollinations28 de marzo 2025 ¿Recuerdas a Coraline? Esta película animada fue creada con la técnica Stop motion, en la que participaron 35 animadores, cada uno de ellos podía demorarse una semana para una escena de seis segundos. Fue la primera producción de la empresa Laika Entertainment. Sin pretender sustituir el trabajo de los animadores, la herramienta que presentamos permite generar imágenes, usando los estilos del estudio Laika y de otros cinco estudios dedicados a la animación. Se generan cuatro imágenes descargables y la posibilidad de fusionar con otros estilos artísticos. Ofrecemos, además, un botón mágico que genera prompts estilo animación. |
|
  |
28. Estudios bíblicos con Pollinations27 de marzo 2025 El reverendo Dr. Tolerant nos sorprende con esta herramienta, usando la API de Pollinations, para estudiar la bilbia desde diferentes versiones: la versión KJV (King James Version, o Versión del Rey Jacobo), la ASV (American Standard Version), la ERV (English Revised Version) y la AKJV (Authorized King James Version). Hemos traducido la herramienta al español, la versión en inglés se puede consultar aquí. |
|
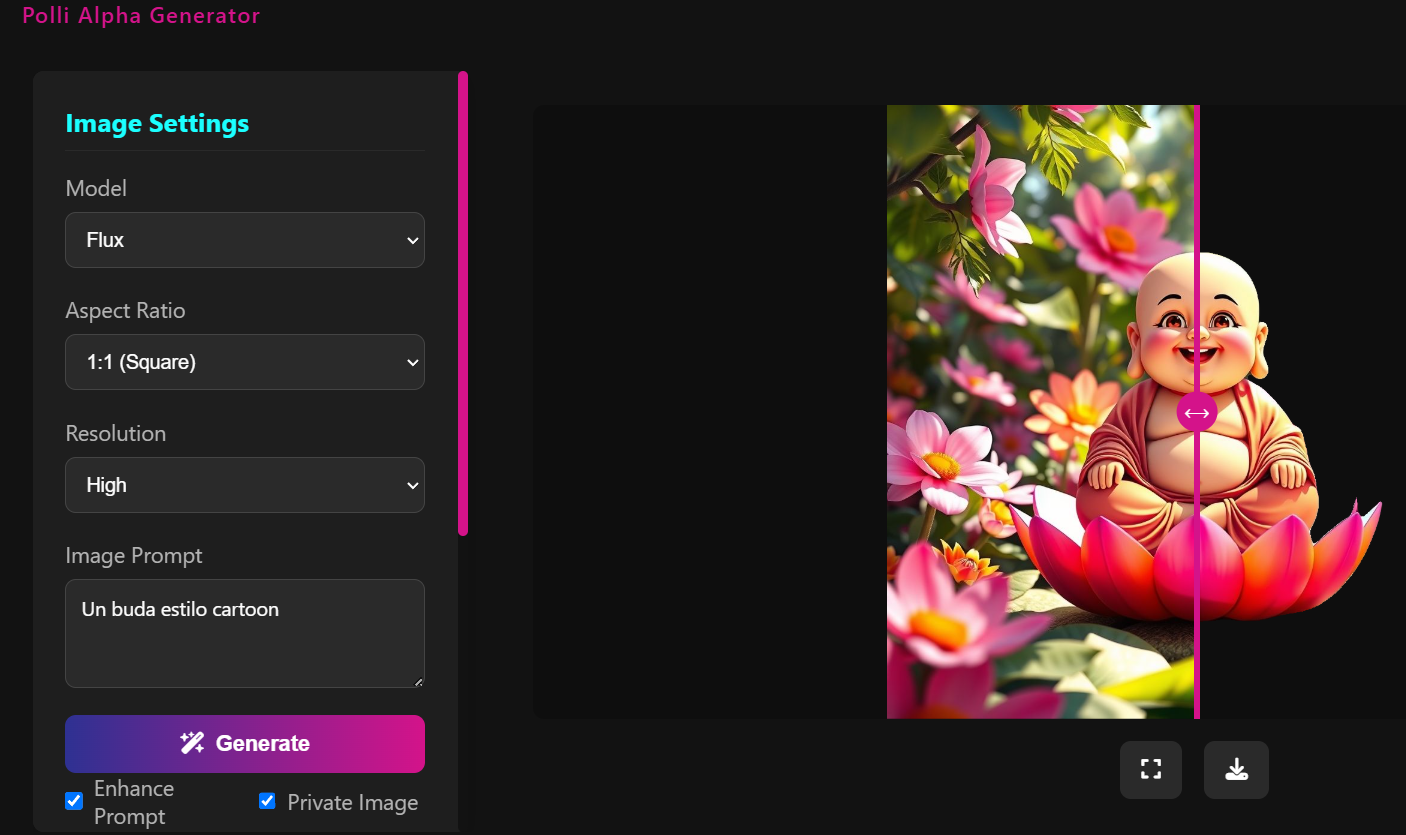  |
27. Generador de imágenes transparentes26 de marzo 2025 Una herramienta basada en la web que utiliza la API de Pollinations para generar imágenes de alta calidad basadas en las indicaciones del usuario. La aplicación cuenta con eliminación automática de fondo, lo que permite a los usuarios crear imágenes con fondos transparentes sin esfuerzo. El título orignal es Polli Alfa Generator, con autoría de Rafael Beznos. |
|
 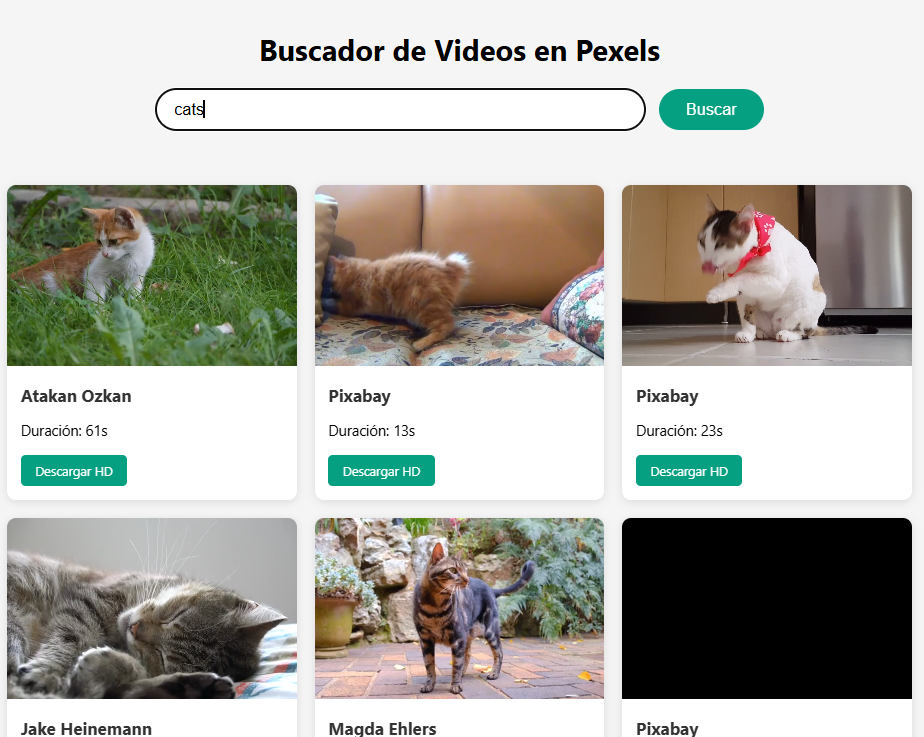 |
26. Buscador de videos en Pexels25 de marzo 2025 ¿Buscas videos para tu página, tu libro o tu presentación? Te presentamos esta herramienta, diseñada por @StoicWarrior en WebSim, nos permite buscar y descargar videos en Pexels. Lo hemos modificado incluyendo el botón "Mas videos", para tener una selección más amplia y descargar el que más nos guste. Sugerimos usar palabras o frases en inglés, pues así se obtienen mayor número de videos. |
|
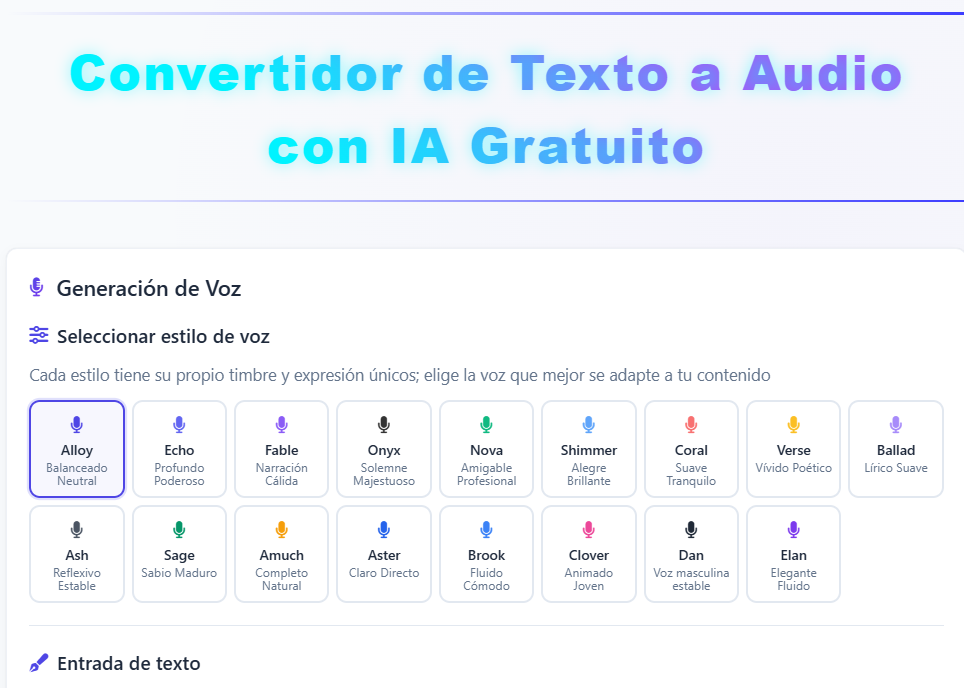 |
25. Convertidor de texto a voz24 de marzo 2025 Esta herramienta, diseñada por el Laboratorio Azad (China), permite convertir texto a voz usando la API OpenAI TTS en Pollinations. |
|
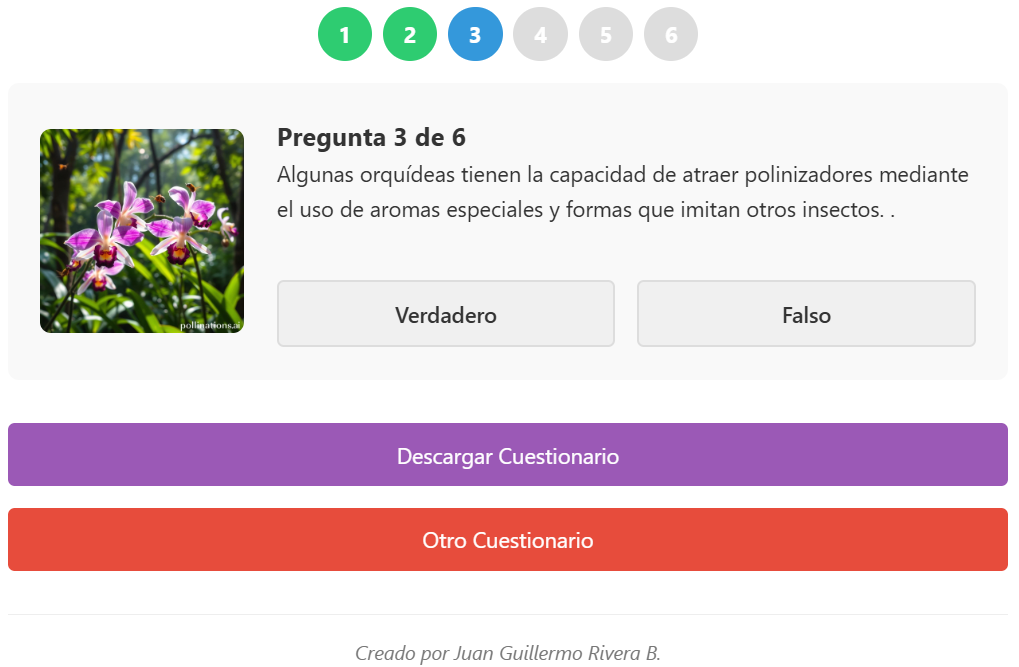 |
24. Generador de cuestionarios tipo falso o verdadero23 de marzo 2025 Esta herramienta, diseñada en WebSim, permite generar cuestionarios tipo falso o verdadero a partir de un tema ingresado por el usuario. Se pueden seleccionar, además, el número de preguntas y el modelo LLM (OpenAI, Mistral, DeepSeek, Llama o Gemini). El cuestionario obtenido incluye imágenes y textos generados por Pollinations. |
|
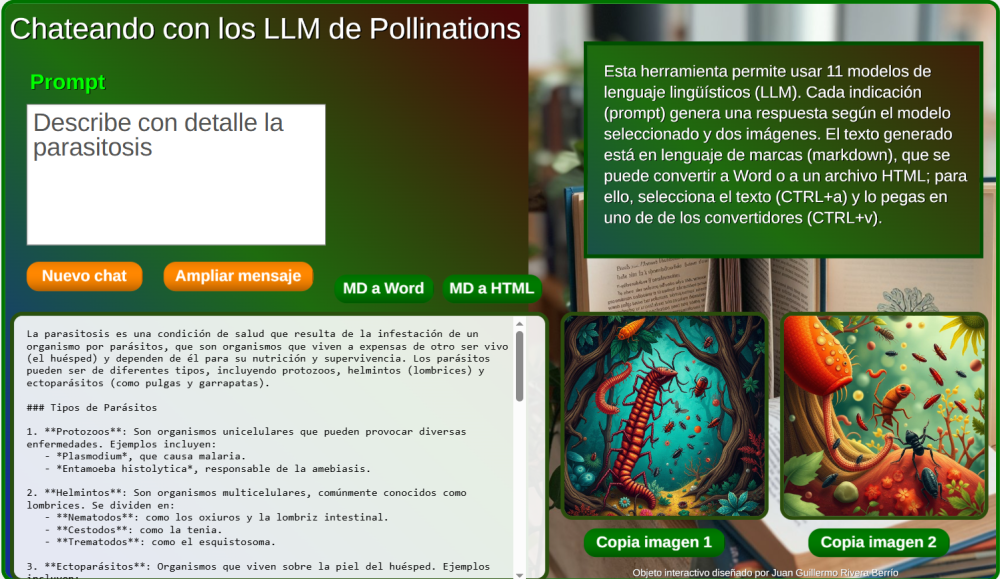 |
23. Chateando con varios modelos de lenguaje en Pollinations22 de marzo 2025 Esta herramienta permite usar 11 modelos de lenguaje lingüísticos (LLM) en Pollinations. Cada indicación (prompt) genera una respuesta según el modelo seleccionado y dos imágenes. El texto generado está en lenguaje de marcas (markdown), que se puede convertir a Word o a un archivo HTML. Herramienta útil para escribir un documento amplio, acompañado de excelentes imágenes. Ver video explicativo en https://youtu.be/4iy_D69EJ5A |
|
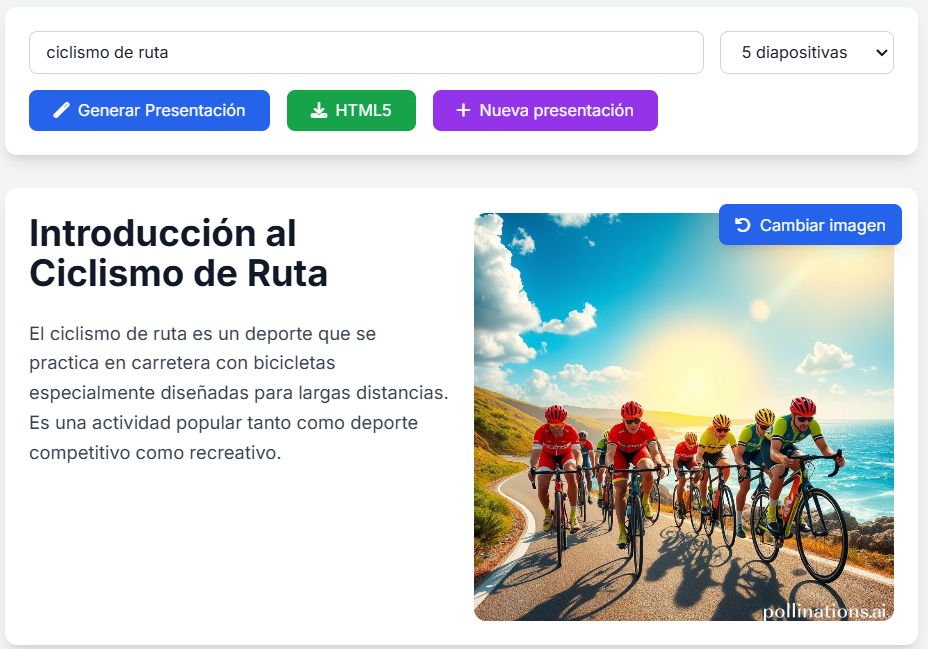 |
22. Generador de presentaciones con imágenes y texto (incluye cambio de imágenes)21 de marzo 2025 Esta herramienta permite crear presentaciones de diapositivas en HTML5, generando imágenes y textos con las API de pollinations.ai. Incluye la posibilidad de regenerar la imagen de una diapositiva. La app fue diseñada con ayuda de create.xyz, permitiendo generar entre tres 3 y 10 diapositivas. |
|
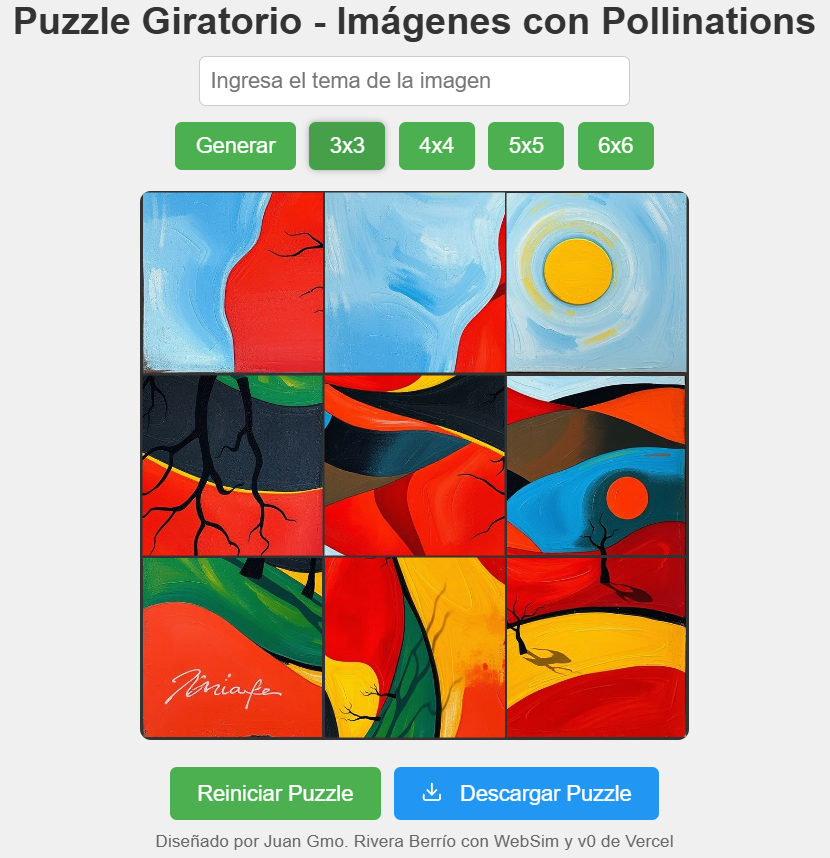 |
21. Generador de puzles giratorios con pollinations20 de marzo 2025 Esta herramienta permite crear puzles giratorios con imágenes generadas con Pollinations.ai, el usuario puede seleccionar puzles de 9, 16, 25 o 36 piezas. Una vez obtenido el puzle, se puede exportar a un archivo HTML, para compartir con estudiantes, colegas o familiares. El diseño del puzle se hizo con ayuda de herramientas de IA, como WebSim y v0 de Vercel. . |
|
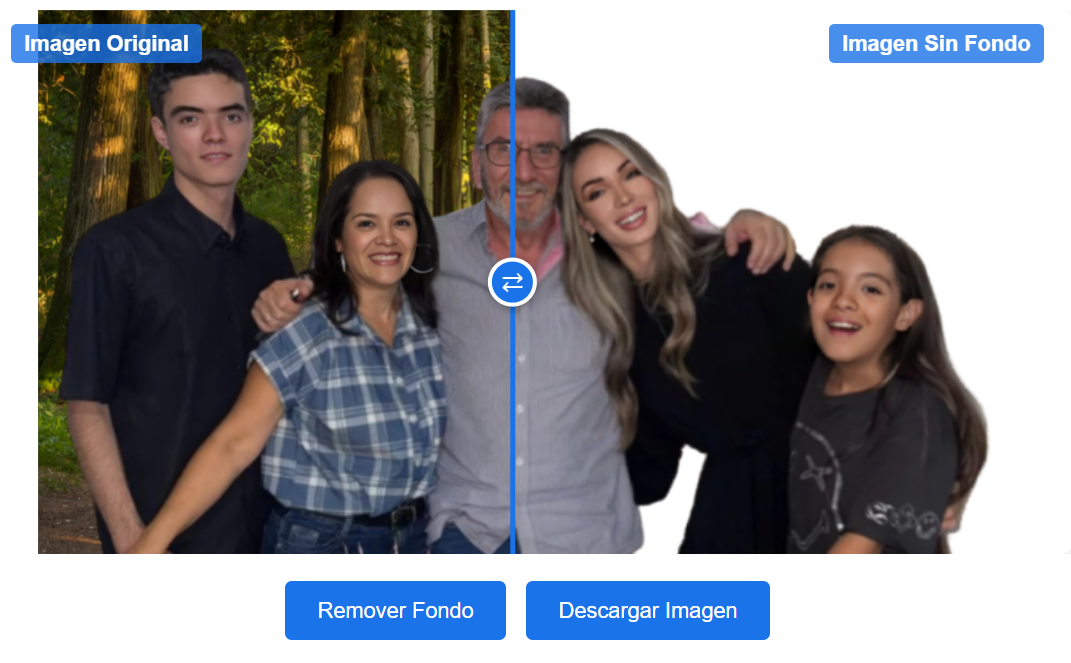 |
20. Removedor de fondos (acepta enlaces de pollinations)19 de marzo 2025 Excelente removedor de fondos diseñado con WebSim, permite subir imágenes en cualquier formato o ingresar la URL de la imagen, incluidas las de Pollinations.ai. Hemos incluido, también, un deslizador vertical para comparar la imagen original con la obtenida la remover el fondo. Adaptación realizada a partir de la aplicación "JCP Remove" de @Ellitox9201 . |
|
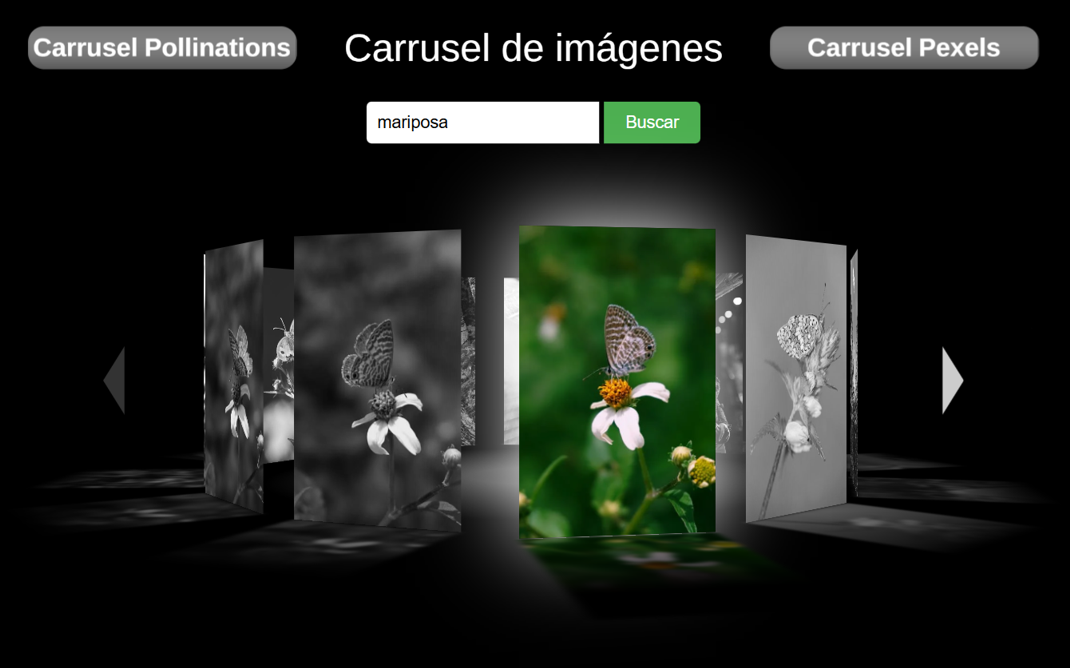 |
19. Carrusel de imágenes de Pollinations o Pexels19 de marzo 2025 Carrusel de 11 imágenes relacionadas con el tema ingresado por el usuario. Presenta dos opciones, la primera es un carrusel de imágenes generadas por Pollinations. La segunda opción es un carrusel de imágenes buecadas en Pexels. Los carruseles son una adaptación de la aplicación "3d carousel PURE CSS" en WebSim. |
|
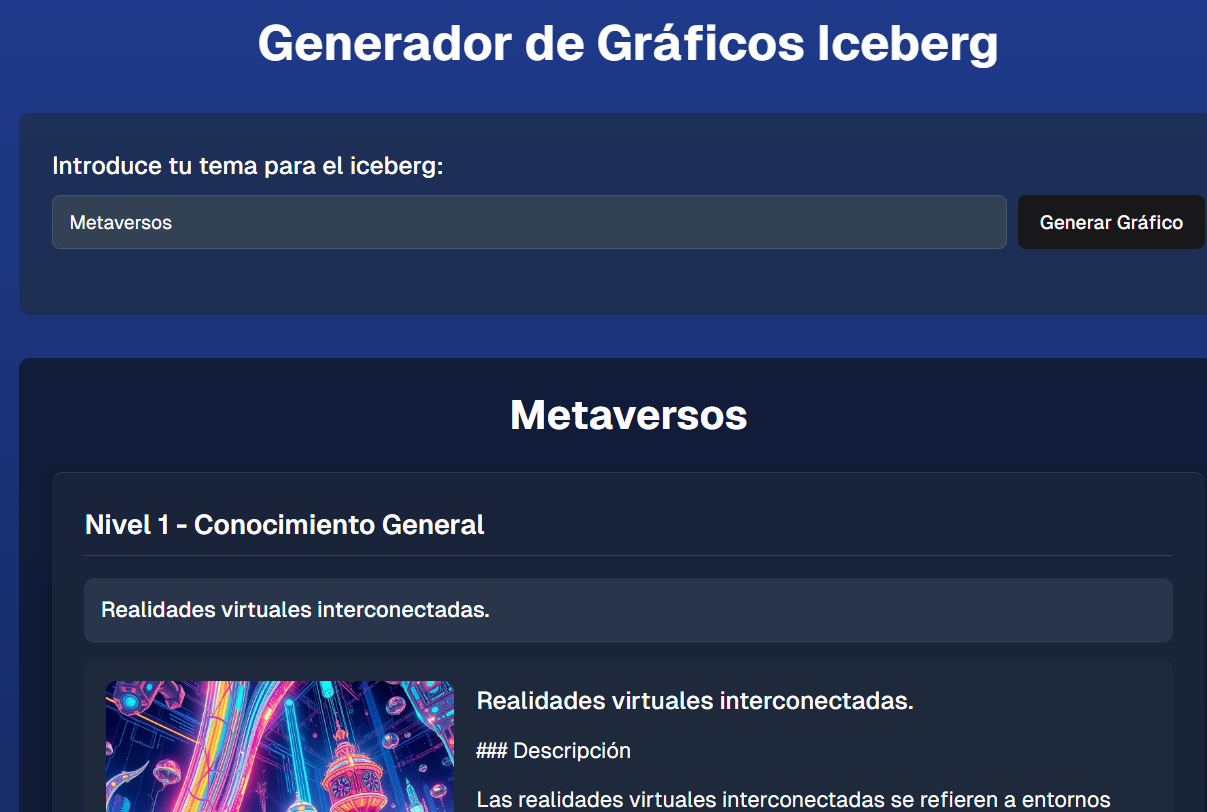 |
18. Generador de páginas ilustradas con Pollinations18 de marzo 2025 Herramienta de inteligencia artificial que genera páginas a partir de un tema ingresado por el usuario. Las páginas incluyen tres niveles, cada uno con tres apartados. En cada apartado se genera una imagen y un texto con las API de Pollinations. La idea original, se tomó de la aplicación "Iceberg Maker" de abandonemuse en WebSim. Una versión en inglés, la hemos publicado aquí. Luego de generar la página, es posible decargarla como un archivo en formato HTML para su uso en sitios web o simplemente compartirlo. |
|
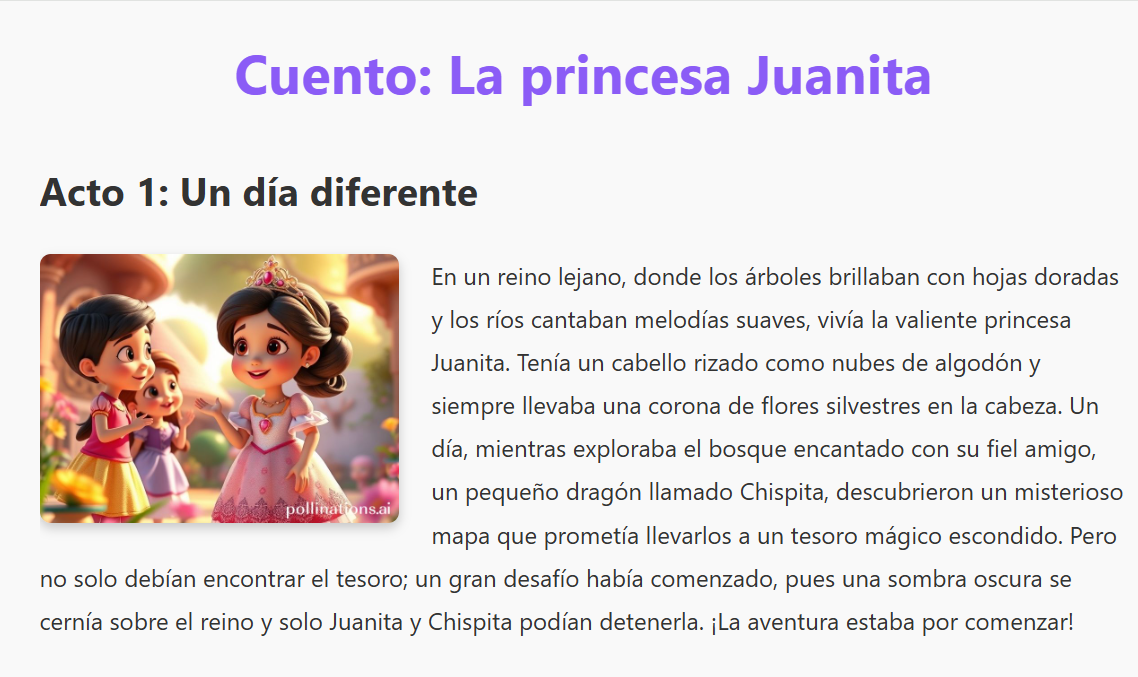 |
17. Crea tu cuento infantil con Pollinations17 de marzo 2025 Descripción:
|
|
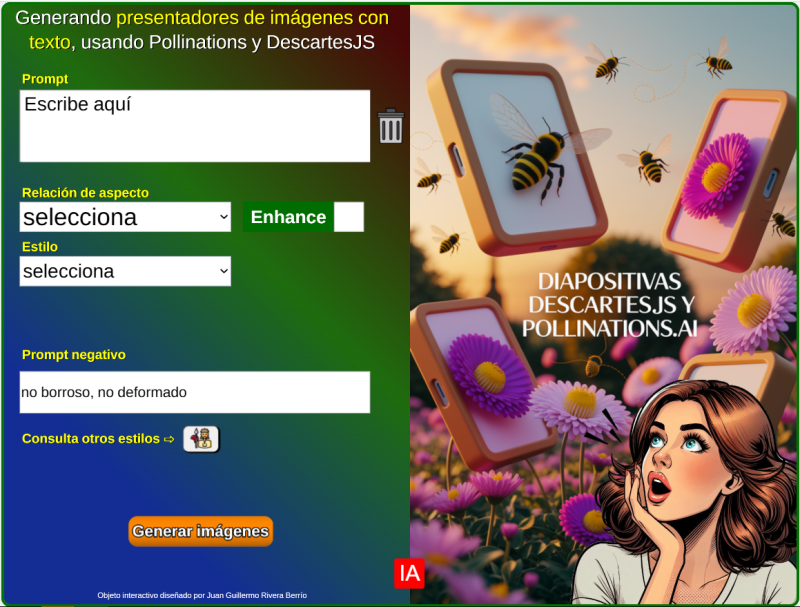 |
16. Generador de presentaciones de imágenes con texto, usando DescartesJS y Pollinations16 de marzo 2025 Descripción:
|
|
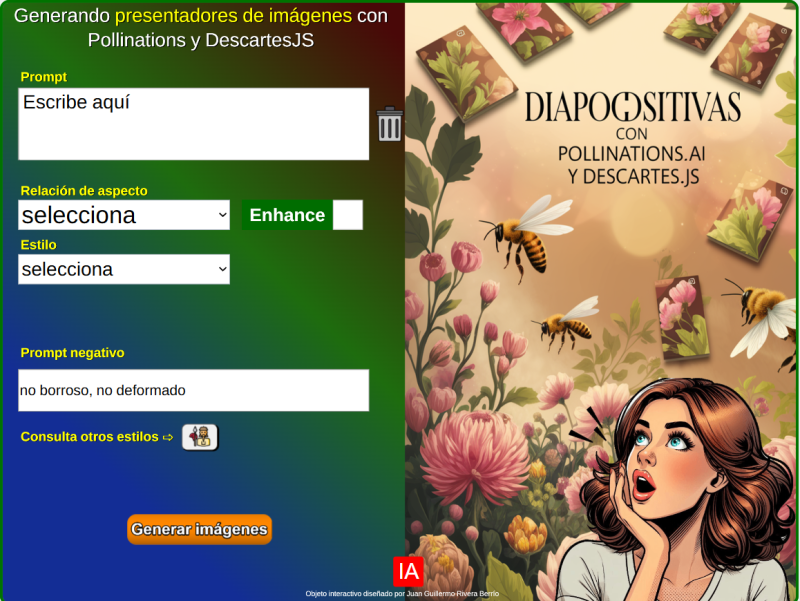 |
15. Generador de presentaciones de imágenes con DescartesJS y Pollinations15 de marzo 2025 Descripción:
|
|
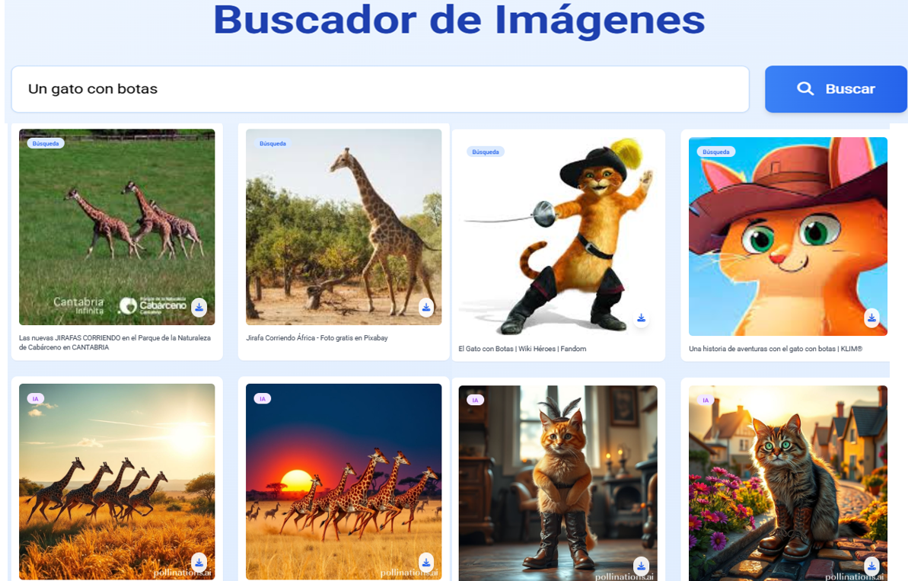 |
14. Buscador de imágenes en Google y Pollinations13 de marzo 2025 Descripción:
|
|
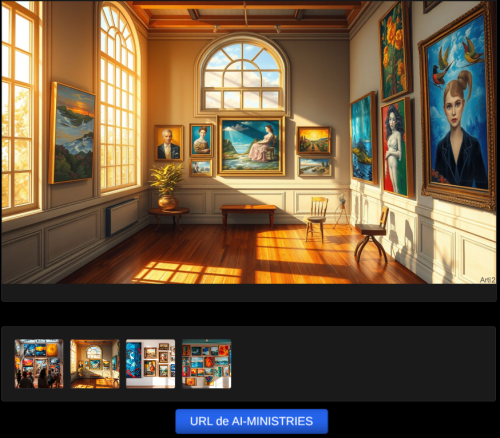 |
13. Generador de imágenes de AI-MINISTRIES12 de marzo 2025 Descripción: |
|
 |
12. Modelos e interfaces de AI-MINISTRIES11 de marzo 2025 Descripción: |
|
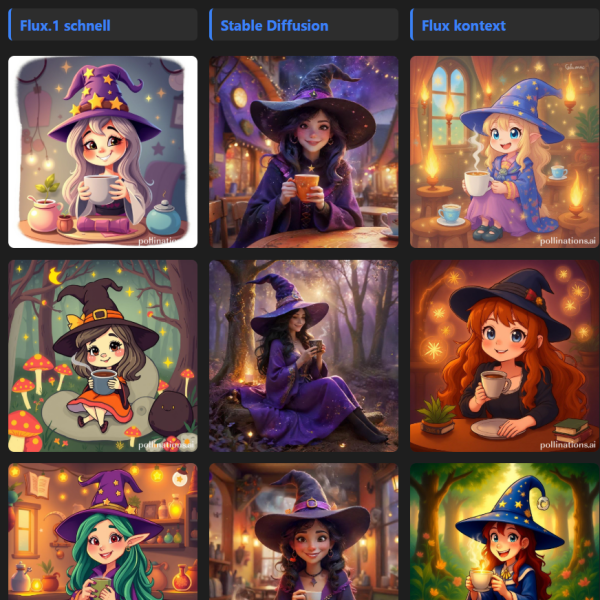 |
11. Modelos de imágenes de Pollinations10 de marzo 2025 (modificado el 15 de agosto de 2025) Descripción: La utilidad de la herramienta es poder evaluar y comparar la calidad de las imágenes obtenidas por cada modelo, usando diferentes estilos artísticos. Para descargar alguna imagen, haz clic sobre ella y se mostrará en una ventana emergente con el botón de descarga. |
|
 |
10. Generador de cuestionarios de selección múltiple - V110 de marzo 2025 (Actualizado el 15 de agosto de 2025) Esta herramienta permite generar cuestionarios de selección múltiple en español, inglés o francés, a partir de un tema ingresado por el usuario, con 5, 10, 10, 15 o 20 preguntas. Las preguntas del cuestionario van acompañadas de una imagen generada por Pollinations.AI (se sugiere esperar un tiempo prudencial, hasta que se generen las preguntas con sus respectivas imágenes). Una vez se genera el cuestionario, se habilta un botón para descargarlo y usarlo en local. Las imágenes se pueden regenerar al gusto del usuario. Algunos cuestionarios generados son: películas animadas, cuarta revolución industrial, insectos, AI generatives (inglés) y biologie (francés) El cuestionario fue diseñado por Juan Guillermo Rivera Berrío con tecnología Claude Sonnet 4.0 en Kiro y las API de Pollinations |
|
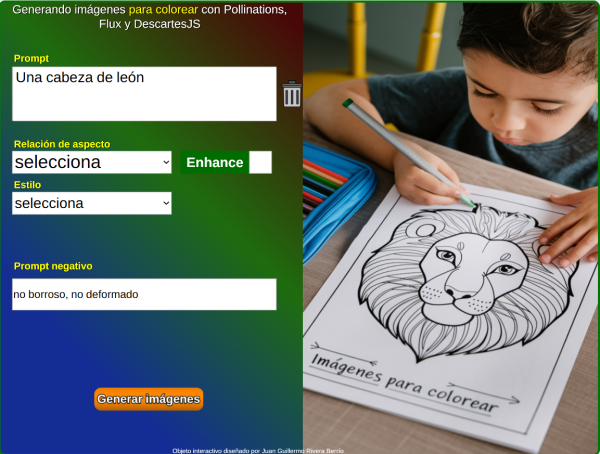 |
9. Generador de imágenes para colorear con Pollinations y DescartesJS9 de marzo 2025 Descripción: |
|
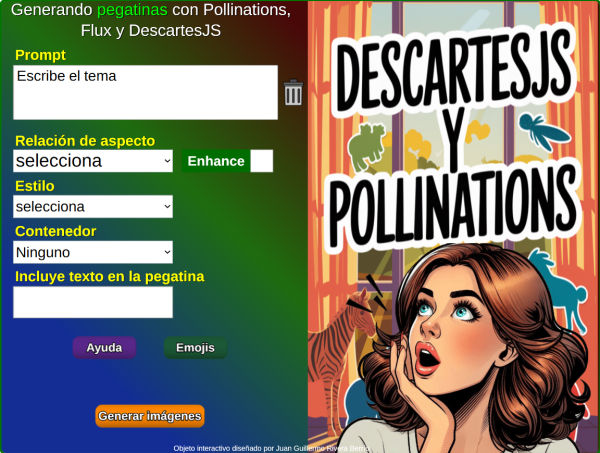 |
8. Generador de pegatinas con Pollinations y DescartesJS9 de marzo 2025 Descripción: |
|
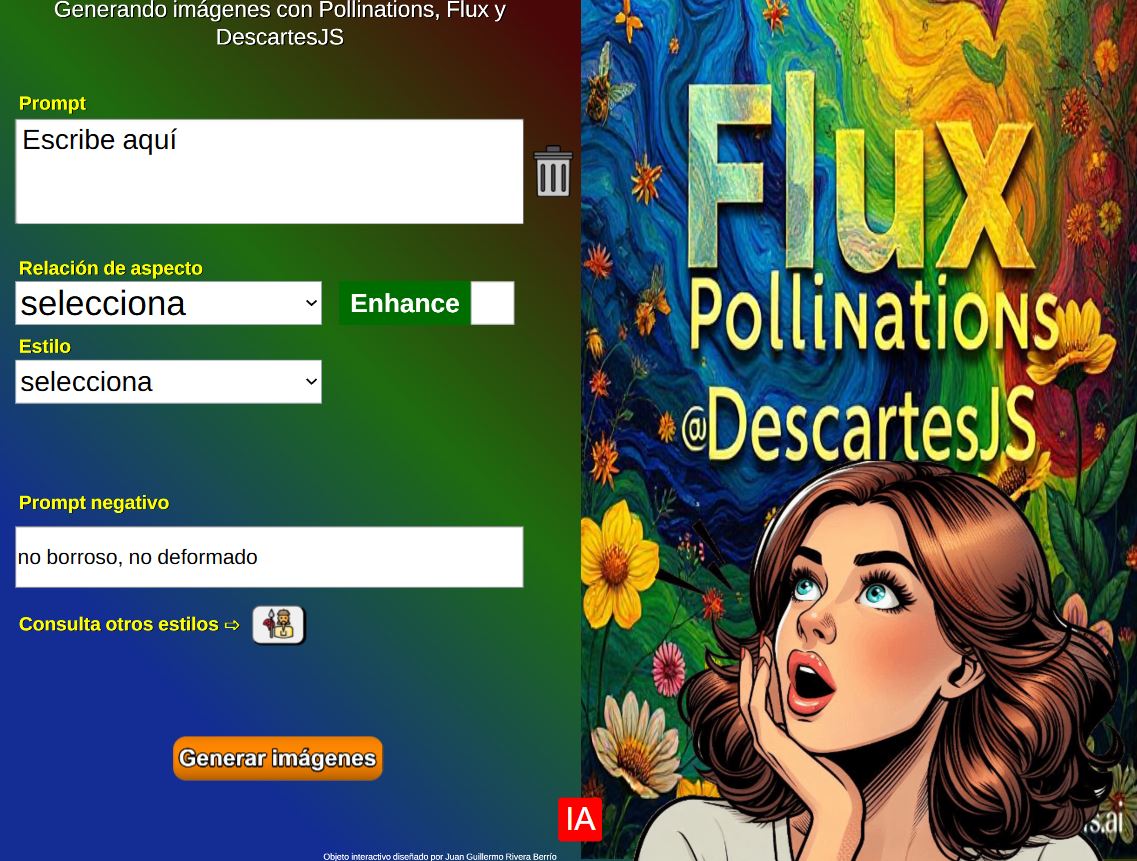 |
7. Generador de imágenes con Pollinations y DescartesJS8 de marzo 2025 Descripción: |
|
 |
6. ChatBot AI Assistant - Multimodal8 de marzo 2025 Descripción: |
|
 |
5. ChatBot Unity Lab AI8 de marzo 2025 Descripción: |
|
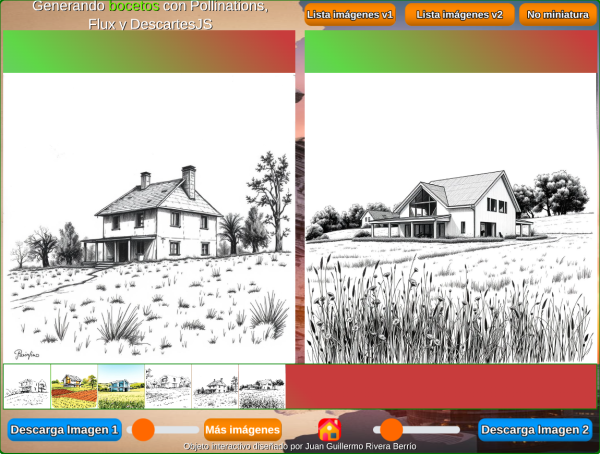 |
4. Bocetos arquitectónicos con Pollinations y DescartesJS7 de marzo 2025 Descripción: |
|
| |
3. Generando emoticones con Pollinations, Flux y DescartesJS6 de marzo 2025 Descripción: Herramientas usadas: DescartesJS, Pollinations, Flux, WebSim |
|
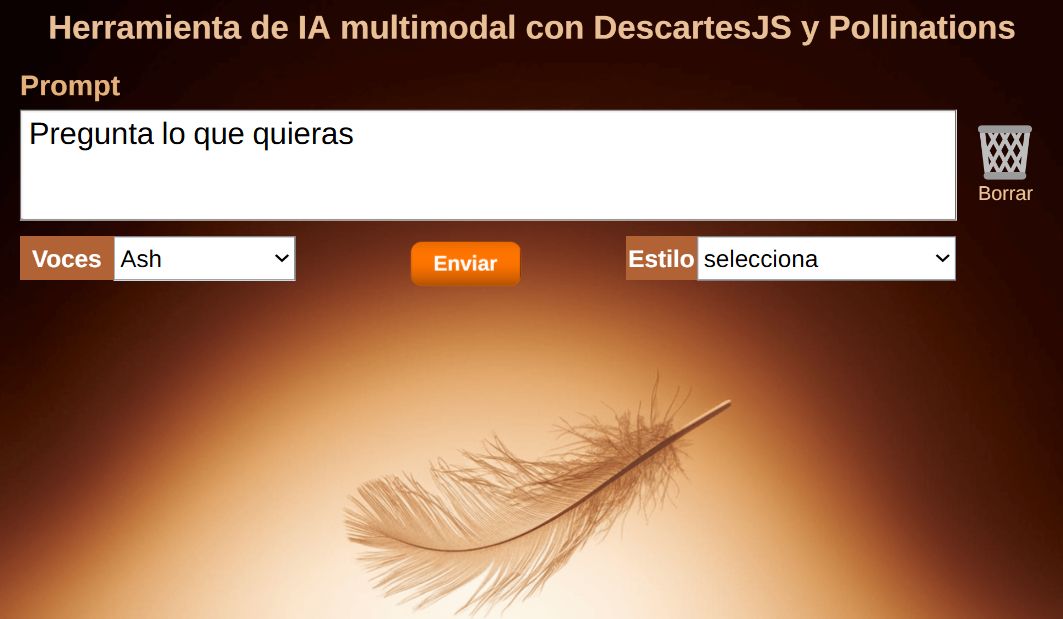 |
2. Herramienta de IA multimodal con DescartesJS y Pollinations5 de marzo 2025 Herramienta de inteligencia artificial multimodal basada en DescartesJS y Pollinations. La interfaz permite a los usuarios ingresar un prompt en un cuadro de texto y recibir respuestas generadas automáticamente. Las respuestas obtenidas son formato audio (mp3), texto (markdown) e imagen (jpg). En resumen, esta herramienta multimodal combina texto, voz e imágenes para ofrecer una experiencia de usuario más completa y enriquecedora, siendo útil en educación, consultas informativas y generación de contenido visual. |
|
;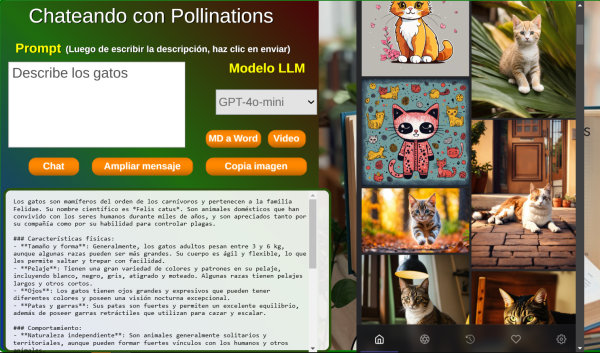 |
1. Chateando con Pollinations5 de marzo 2025 Herramienta de inteligencia artificial tipo ChatBot basada en DescartesJS y Pollinations. La interfaz permite a los usuarios ingresar un prompt en un cuadro de texto y recibir respuestas generadas automáticamente. Incluye, además, imágenes de la plataforma Lexica y la posibilidad de convertir el texto Markdown obtenido en formato Word. |
______________________________________
 |
A continuación, si lo deseas, puedes participar dejando un comentario para RED Descartes. También puedes escribirnos a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.. |
Boletín de Inteligencia Artificial
Escrito por Juan Guillermo Rivera Berrío

Boletín de Inteligencia Artificial
 |
Boletín 10 - Novedades IA Generativas1 de junio de 2025 |
|
 |
Boletín 9 - Novedades IA Generativas1 de mayo de 2025 |
|
 |
Boletín 8 - Novedades IA Generativas1 de abril de 2025 |
|
 |
Boletín 7 - Novedades IA Generativas1 de marzo de 2025 |
|
 |
Boletín 6 - Novedades IA Generativas1 de febrero de 2025 |
|
 |
Boletín 5 - Novedades IA Generativas2 de enero de 2025 |
|
 |
Boletín 4 - Novedades IA Generativas1 de diciembre de 2024 |
|
 |
Boletín 3 - Novedades IA Generativas1 de noviembre de 2024 |
|
 |
Boletín 2 - Novedades IA Generativas1 de octubre de 2024 |
|
 |
Boletín 1 - Novedades IA Generativas1 de septiembre de 2024 |
|
______________________________________
 |
A continuación, si lo deseas, puedes participar dejando un comentario para RED Descartes. También puedes escribirnos a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.. |
Diseño de libros interactivos con IA y DescartesJS
Escrito por José Antonio Salgueiro González
Vídeos del curso "Diseño de libros interactivos con IA y DescartesJS"
Vídeo de introducción
Recursos y tutoriales previos:
- Enlace a un archivo comprimido con la plantilla del libro. Las instrucciones se encuentran en el vídeo de bienvenida y presentación.
- Actividades previas a la primera sesión (19 minutos).
- Imágenes generadas por IA (5 minutos)
- Editores HTML (19 minutos)
- Contenido del curso y calendario:

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:
- Vídeo de la 1ª sesión (18 de octubre de 2024). Presentación de la 1ª sesión. Resumen sesión 1.ª
- Vídeo de la 2ª sesión (1 de noviembre de 2024). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (15 de noviembre de 2024). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (29 de noviembre de 2024). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (13 de diciembre de 2024). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (17 de enero de 2025). Presentación de la 6ª sesión .
- Vídeo de la 7ª sesión (7 de febrero de 2025). Presentación de la 7ª sesión .
- Vídeo de la 8ª sesión (14 de febrero de 2025).
Curso "Edición de libros interactivos" de la RED Descartes (5ª edición en línea)
Escrito por José R. Galo Sánchez|
Diseño de libros interactivos |
Vídeos de la quinta edición en línea del curso "Edición de libros interactivos"
Vídeo de introducción a la quinta edición en línea"
´- Vídeo de la 1ª sesión (13 de octubre de 2023). Presentación de la 1ª sesión.
- Vídeo de la 2ª sesión (27 de octubre de 2023). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (10 de noviembre de 2023). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (24 de noviembre de 2023). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (8 de diciembre de 2023). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (19 de enero de 2024). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (2 de febrero de 2024). Presentación de la 7ª sesión.
- Vídeo de la 8ª sesión, sesión final del curso (16 de febrero de 2024).
Novena y última sesión de la tercera edición del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezNovena y última sesión (24 de marzo de 2023)
|
1A.
|
Octava sesión de la tercera edición del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezOctava sesión (10 de marzo de 2023)
|
1A.
|
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
