Planifica el curso escolar 2023-2024 con los recursos del Proyecto AJDA
Este curso, el Proyecto AJDA, al igual que la Red Descartes a la que pertenece, cumple diez años y la mejor forma de celebrarlo, ha sido renovar el Proyecto en profundidad, mejorándolo notablemente. En este artículo vamos a comentar los principales cambios y progresos que se han llevado a cabo, con el objetivo de que todos los docentes que utilicen sus recursos puedan empezar este nuevo curso con un Proyecto más atractivo, actualizado, aplicable y funcional.
La mejora más destacada, y la que más ha costado, por el gran número de juegos existentes, ha sido la renovación total de los 514 juegos que actualmente contiene el Proyecto, mejorando la presentación, funcionalidades, programación y jugabilidad. Estas mejoras se han ido comentando en detalle a lo largo de este año, por lo que ahora simplemente pondremos algunas imágenes del resultado.
El nuevo juego 10x10 (IX)
Otras mejoras introducidas en los juegos ha sido en el terreno estético y visual, algunas de ellas gracias a la implementación de nuevas funcionalidades de Descartes en estos aspectos y que repercuten en una mejor apariencia y vistosidad de los mismos. Pasamos a comentar las más significativas.
- Utilización de degradados de color en elementos. También se pueden introducir imágenes de fondo. A continuación mostramos varios ejemplos:
- Mejora y uniformización de fondos en espacios, barras de navegación, escaletas, marcadores. A continuación mostramos algunos de ellos.
- Utilización de efectos en textos (bordes de letras, sombras, colores, alineaciones y justificaciones). Esto se puede apreciar, por ejemplo, en el título de los juegos. Otros ejemplos son textos con nombres de participantes o en marcadores.
- Empleo de estilos en botones y otros elementos. Dichos estilos incluyen: redondeado de bordes, sombras, estilos de color, estilos de textos, efectos de borde, activación y desactivación, efectos de ratón...
- Uso de imágenes, espacios y elementos animados. Estos recursos dan viveza y dinamismo a los juegos.
El nuevo juego 10x10 (VIII)
Hay juegos que necesitan cargar varios ficheros de preguntas al inicio de la partida, por ejemplo, juego "Minitrivial", que necesita cargar 6 ficheros, uno por cada uno de los seis temas que se utilizaran en el desarrollo de la partida.
Para mejorar este proceso de carga se ha diseñado un sistema para la selección de dichos ficheros al inicio de la partida (aunque también podrán ser cambiados durante el transcurso de la misma a través de la opción de configuración del menú superior desplegable).
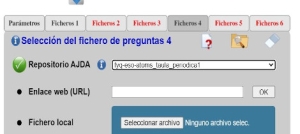
Al inicio de la partida se presenta una pantalla con una pestaña de configuración de los parámetros de la partida y tantas pestañas para carga de ficheros como sean necesarias. A través de cada una de las pestañas se introducirán los correspondientes ficheros.
Se podrá pasar de una pestaña pulsando en las propias pestañas a otra a través de los menús inferiores de navegación anterior y siguiente.
Cada ventana de selección de ficheros presentará su propio sistema de selección de ficheros, los datos y requisitos del mismo y las opciones de configuración.
Las pestañas en las que aun no se haya realizado la selección del fichero se mostrarán en rojo y pasarán a color negro cuando ésta haya sido realizada. Hasta que todos los ficheros hayan sido seleccionados no se podrá comenzar la partida (si se selecciona la modalidad de juego con introducción de preguntas a través de ficheros).
Configuración de la entrada Etiquetas Uso de juegos, No hay sugerencias que coincidan Publicada el 4/5/23 11:24 Enlace permanente Ubicación Opciones
El nuevo juego 10x10 (VII)
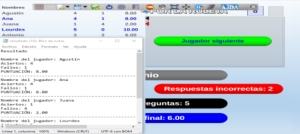
A continuación comentamos otra de las mejoras introducidas en los juegos didácticos y que afecta a la generación de ficheros de de texto con los resultados parciales o finales y que pueden ser solicitados en cualquier momento de la partida a través del menú de guardado de la barra superior desplegable, guardado de resultados (botón azul).
- Los datos de los ficheros de resultados se recuperan correctamente y de forma completa en partidas que han sido continuadas a partir de partidas guardadas en ficheros con anterioridad.
- Se ha mejorado la presentación y organización de los datos.
- Se han incluido nuevos datos de resultados en los ficheros.
- La opción de descargar el fichero de resultados está disponible en cualquier momento del juego.
- Se pueden descargar y archivar cuantos ficheros de resultados se quieran a lo largo de la partida.
El nuevo juego 10x10 (V)
Otro elemento introducido en el juego 10x10 en particular, y en otros muchos en general, es un espacio desplegable lateral en su zona izquierda. Se trata de un espacio de mayor tamaño que el menú superior desplegable y cuya función suele ser de marcador de resultados, escaleta, tabla de clasificación, etc.
Este espacio está disponible en todo momento del juego, salvo en las pantallas iniciales de configuración del mismo. Dado que es de mayor tamaño, dispone de dos controles de despliegue situados en el borde izquierdo y hacia la zona superior de la pantalla. Uno de ellos contiene una flecha negra y otro roja. La diferencia entre ambos es que la flecha roja provoca un despliegue instantáneo, mientas que la negra lo hace gradual. Dichos controles sirven tanto para abrir como para cerrar el espacio.
En el juego 10x10, este espacio lateral izquierdo presenta la escaleta del juego. En el juego Liguilla 6J, en este espacio se recogen los resultados de todos los partidos disputados en la "liguilla".
Finalmente, comentar que en el espacio que estamos tratando se podrían incluir, dependiendo de la naturaleza del juego, otra serie de contenidos, elementos u accesorios que mejoren el recurso didáctico.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)











































 CONTACTO
CONTACTO
