Título de la obra:
Valor del Dinero en el Tiempo. Modelos y aplicaciones
Parte 2
Autor:
José Benjamín Gallego Alzate
Instituto Tecnológico Metropolitano-ITM
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Imagen de portada: ilustración generada por Gemini
Imágenes de capítulos: ilustraciones generadas por Gemini
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-45-3

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
El conocimiento del valor del dinero en el tiempo, no es solo la adquisición de un saber disciplinar; es asimismo procurarse una habilidad fundamental para tomar decisiones financieras informadas, en los ámbitos profesional y de la vida personal.
Elementos conceptuales y prácticos básicos del valor del dinero en el tiempo, fueron abordados en el volumen uno de este libro. Conceptos y técnicas como los de valor futuro y valor presente bajo distintas modalidades de capitalización, las diferentes tasas de interés, el concepto de ecuación de valor, así como algunas herramientas de Excel, fueron allí tratados.
En este segundo volumen damos un paso adelante en el manejo del valor del dinero en el tiempo, al tratar sobre flujos de dinero que son modelados como anualidades o en series de gradientes. Estos temas encuentran aplicación en el diseño de diversos esquemas de amortización de empréstitos o créditos, en la valoración de activos financieros, así como en la evaluación de alternativas de inversión.
El estudiado de estos temas se realiza desde el escenario de la valoración compuesta, con tasa de interés generalmente constante, y en condiciones de certidumbre. Por ello, no se modelan la incertidumbre y el riesgo.
El capítulo uno está dedicado al estudio de las anualidades. Las anualidades son un conjunto de pagos (ingresos o egresos) de igual valor que ocurren con igual periodicidad y bajo la misma tasa de interés. Son de amplia aplicación las anualidades que capitalizan de modo vencido con pagos que pueden ocurrir al final del período (vencido), al inicio del período (anticipado), o diferido; también se presentan en forma de series finitas o perpetuas.
El capítulo uno también aborda el tema de las anualidades bajo capitalización continua y algunos casos con capitalización anticipadas. Este último tema es más “una curiosidad teórica” que una herramienta de amplia aplicación en los mercados financieros o de crédito; por esta razón el lector puede pasar por alto su estudio.
El capítulo dos trata de los flujos de dinero que crecen o decrecen en una magnitud constante y se presentan con igual periodicidad bajo una misma tasa de interés. Son los temas de las series de gradientes en los modos aritmético, geométrico o escalonado. Se conoce como gradiente a la medida del cambio que experimenta una serie de pagos, cambio que puede ser aritmético si éste es la suma o resta de una misma cantidad, o geométrico si lo hace en un porcentaje. Los gradientes aritmético, geométrico y escalonado se estudian desde las capitalizaciones vencida y continua, para casos de pagos vencido, anticipado, diferido y perpetuo.
Los temas estudiados en los dos capítulos anteriores se aplican en el capítulo tres en la elaboración de diferentes sistemas de crédito. Los sistemas de crédito son esquemas diseñados para la cancelación gradual de un capital tomado en préstamo. La cancelación gradual se puede llevar a cabo por medio de cuotas fijas, o por cuotas que crecen o decrecen de forma uniforme.
Se presenta una gran variedad de posibilidades para el diseño de sistemas de crédito. Empero, en este capítulo nos concentramos en el estudio de esquemas de amortización de mayor aplicación en el mercado colombiano, valorados en pesos y en Unidades de Valor Real (UVR). Los esquemas de amortización se diseñan para los casos de cuotas fijas vencida, anticipada, diferida, y con pago de cuotas extras. Se estudia además algunos sistemas de crédito en gradientes, así como el esquema de crédito con amortización constante y tasa de interés variable en DTF.
El cuarto capítulo está dedicado al asunto de las medidas de valor y alternativas de inversión. Por medida de valor entendemos el desarrollo y aplicación de un método o técnica que permita determinar la cantidad atribuida a la rentabilidad de diferentes alternativas de inversión bajo condiciones del valor del dinero en el tiempo. En este capítulo se estudia procedimientos básicos para obtener medidas de valor que se constituyen en criterios para tomar decisiones financieras, en particular de inversión, como son los métodos de: Valor Presente Neto (VPN), Tasa Interna de Retorno (TIR), Tasa Interna de Retorno Modificada (TIRM), Valor Anual Uniforme Equivalente (VAUE), Costo Anual Uniforme Equivalente (CAUE), así como otras medidas de valor que apoyan la toma de decisiones.
Previo al estudio de estos métodos, realizamos una breve introducción a las magnitudes y su estimación, que son requeridas en la determinación del valor de cada medida de valor.
El capítulo cinco sobre Conceptos matemáticos es un anexo donde se presenta de forma resumida los métodos de la regla de L'Hôpital y de la interpolación lineal, ambos procedimientos demandados en la estimación en algunas de las medidas de valor tratadas en este libro.
Expresamos nuestra gratitud con la Institución Universitaria ITM de la ciudad de Medellín por la oportunidad concedida para la escritura de este libro.
Especial gratitud tenemos con la profesional Kelly J. Londoño R., por la paciente y eficiente revisión de la primera versión de este libro. De igual manera con el Doctor y profesor Juan Guillermo Rivera Berrio de la Red Educativa Digital Descartes de España, por las enseñanzas en el diseño de libros interactivos aplicando herramientas de inteligencia artificial y el editor Descartes JS.
Las imágenes de este libro fueron diseñadas, a partir de la entrada de un prompt, por la inteligencia artificial Gemini de Google y el asistente de inteligencia artificial Copilot de Microsoft. En la elaboración de los cuestionarios incluidos al final de cada capítulo se utilizó las inteligencias artificiales generativas Websim y Copilot.
Las figuras del libro son realizadas por el autor. Al hacer un clic sobre cada una de ellas, éstas se expanden permitiendo una mejor observación y lectura.
Las anualidades son series uniformes, esto es, un conjunto de ingresos o egresos iguales (una cantidad fija de dinero) que ocurren periódicamente a lo largo del tiempo (con la misma frecuencia de tiempo, por ejemplo cada mes, cada trimestre, cada semestre o cada año) gestionados bajo la misma tasa de interés.
Representaremos a las anualidades con la letra A (en mayúscula) ya que es un signo tradicional en la literatura sobre el tema, y así mismo se hizo en el volumen uno de este libro. En ocasiones, se utilizan términos como pago periódico, cuota fija o abono, para referirse a la anualidad. En este volumen utilizamos las expresiones cuota fija o pago.
Cada pago está constituido por dos elementos. El primero es el interés (o rendimiento) sobre el saldo de un capital, representado por I, mientras que el segundo elemento es la amortización, R, entendida como la parte del pago que se dirige directamente a recuperar un capital invertido o, en el caso de un crédito, a reducir el saldo y cancelar la obligación financiera.
Con base en lo anteriormente dicho, tenemos que A=I+R y además R=A-I, o I=A-R
Existen diferentes tipos de series uniformes según se adopte algún criterio de clasificación. Si la clasificación de las anualidades se realiza bajo el criterio de la modalidad de capitalización, las anualidades pueden ser de capitalización vencida, capitalización anticipada o capitalización continua. Si el criterio es el momento de realizar el pago, existen anualidades con pago vencido, pago anticipado, pago diferido, o pago continuo.
Si el criterio de clasificación es la coincidencia, o no, del período de interés con el período del pago, las anualidades se clasifican en simples o generales, respectivamente. Las anualidades también son finitas y perpetuas. Con estos criterios, las permutaciones darían lugar a la existencia teórica de 48 tipos de anualidades, muchas de ellas no utilizadas en la práctica financiera.
Así por ejemplo, Aguilera y Díaz
En este capítulo estudiaremos las anualidades utilizando como primer criterio de identificación la modalidad de capitalización, en las formas vencida, continua y anticipada. Como segundo criterio de clasificación determinamos el momento en que ocurre la cuota fija, estudiando los casos de pago vencido, anticipado, diferido. Se incluye además algunos caos de pago perpetuo
Comenzamos el estudio de las anualidades con capitalización vencida, considerando que el pago puede darse, como ya se indicó, de modo vencido, anticipado, diferido; también el caso perpetuo. Determinaremos modelos que permitan calcular los valores presente y futuro de una anualidad, así como las ecuaciones para hallar el plazo y la tasa de interés de una operación financiera, y la misma cuota fija.
Un primer caso de anualidad con capitalización y pago vencidos se presenta en la siguiente Figura 1.1.
En la Figura, el principal $P$ está ubicado en el presente (en fecha focal cero, ff=0) y el primer pago ($A$) está un lugar a la derecha de $P$. Esta característica hace que la anualidad se clasifique como serie vencida o convencional. La tasa de interés $iv$ se incluye para indicar que es periódica vencida, y la serie está constituida por una cantidad $n$, finita, de pagos mensuales.
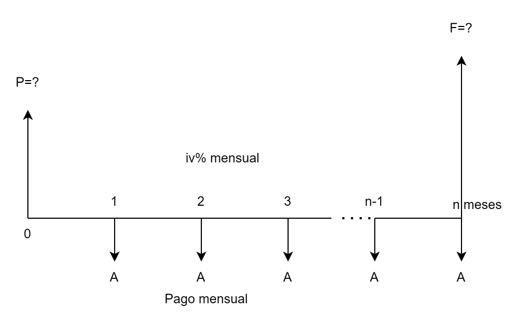
Es por lo tanto, una serie de cuotas fijas vencidas manejada con capitalización vencida. El valor futuro de la serie vencida, identificado con $F$, se calcula en la misma fecha focal donde se ubica la última $A$, esto es, en $n$.
Vamos a desarrollar un procedimiento matemático para hallar el valor presente de la serie uniforme representada en la Figura 1.1. El resultado obtenido servirá de base para alcanzar modelos matemáticos que posibiliten el cálculo del valor futuro, la cuota fija, el plazo y la tasa de interés de una situación financiera en específico.
La ejecución del procedimiento matemático es una aplicación de las progresiones geométricas estudiadas en el anexo al Vol 1 de este libro. También aplicamos el modelo de valor futuro de un valor presente bajo capitalización vencida, dado por la siguiente fórmula:
$$ F=P\left(1+i\right)^n$$De la anterior ecuación tenemos que:
$$P=\frac{F}{\left(1+i\right)^n}=F\left[\frac{1 }{\left(1+i\right)^n}\right] $$Son los factores $\left(1+i\right)^n$ y $\left[\frac{1}{\left(1+i\right)^n}\right]$, los que garantizan el manejo a valor equivalente de la serie uniforme bajo capitalización vencida.
Para obtener el valor presente de la serie uniforme representada en la Figura 1.1, identificamos a cada uno de los pagos como un valor futuro que descontamos (llevamos) a la fecha focal cero, al presente. El valor presente total del diagrama es, por lo tanto, la suma de todos los pagos descontados al instante cero. Utilizando en general $i$ como tasa de interés, tenemos:
$$P=\frac{A}{\left(1+i\right)}+\frac{A}{\left(1+i\right)^2}+\ldots+\frac{A}{\left(1+i\right)^{n-1}}+\frac{A}{\left(1+i\right)^n}\ (1.1)$$Observando el lado derecho de la ecuación (1.1) se nota como cualquier término de ésta, excepto el primero, es igual al término anterior multiplicado por $\frac{1}{1+i}$; esto es, se presenta una razón común y por tanto $P$ es la suma de los $n$ términos de una progresión geométrica (finita). Bajo esta condición tenemos:
$$a_1=\frac{A}{(1+i)}$$Podemos optar por dos caminos para simplificar la suma de los términos en progresión geométrica y obtener el valor presente $P$ de los pagos representados en Figura 1.1. El primero es utilizar las fórmulas de suma ya presentadas en el anexo del volumen 1 de este libro. El segundo es seguir el mismo algoritmo aplicado allí en la obtención de dichas fórmulas de suma. En este libro optamos por este segundo método y en los problemas propuestos pedimos al lector proceder desde las fórmulas de la suma de $n$ términos en progresión geométrica finita.
₪ Algoritmo
Tomar ecuación (1.1) y multiplicarla por la razón común, para obtener (1.2)
$$\frac{P}{(1+i)}=\frac{A}{\left(1+i\right)^2}+\frac{A}{\left(1+i\right)^3}+...+\frac{A}{\left(1+i\right)^n}+\frac{A}{\left(1+i\right)^{n+1}} (1.2)$$Restar (1.1)-(1.2):
$$P=\frac{A}{\left(1+i\right)^1}+\frac{A}{\left(1+i\right)^2}+...+\frac{A}{\left(1+i\right)^{n-1}}+\frac{A}{\left(1+i\right)^n} menos$$ $$\frac{P}{(1+i)}=\frac{A}{\left(1+i\right)^2}+\frac{A}{\left(1+i\right)^3}+...+\frac{A}{\left(1+i\right)^n}+\frac{A}{\left(1+i\right)^{n+1}} $$Los términos comunes se cancelan, resultando la ecuación (1.3), así:
Ahora solo falta simplificar esta última expresión matemática. Realizando la resta del lado izquierdo y tomando como factor común $\frac{A}{(1+i)}$ en lado derecho de la igualdad, tenemos:
$$\frac{P(1+i)-P}{(1+i)}=\frac{A}{(1+i)}\left[1-\frac{1}{\left(1+i\right)^n}\right]$$Realizando otros procediendo matemáticos, tenemos:
$$ \frac{P+Pi-P}{(1+i)}=\frac{A}{(1+i)}\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^n}\right]$$ $$Pi=\frac{A(1+i)}{(1+i)}\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^n}\right]$$ $$P=\frac{A}{i}\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^n}\right]$$Por lo tanto, la ecuación buscada es:
$$P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n}\right] (1.4)$$Dado que utilizamos el esquema presentado en la Figura 1.1 para la deducción de la ecuación (1.4), podemos indicar que el valor calculado de $P$ se ubica un lugar a la izquierda de la primera $A$ (como la primera anualidad está ubicada en ff=1, el valor calculado de $P$ se ubica en ff=0) . Esta observación es clave en el manejo adecuado de la ecuación (1.4) y posteriores aplicaciones.
Realicemos el siguiente ejercicio.
Solución
$P=?$
$A$= 1,500,000 pesos mensuales
$n$= 6 meses
$i$%=1.3% mensual
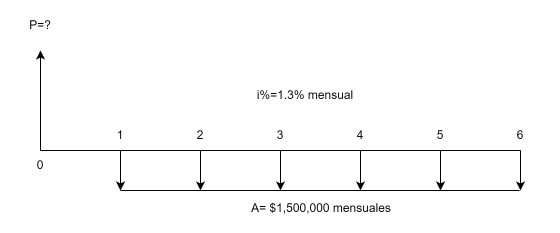
La Figura 1.2 es la representación gráfica del problema.
Las características de esta serie son las siguientes. En primer lugar, encontramos que la tasa de interés y los desembolsos por canon de arrendamiento comparten la misma unidad de tiempo, el mes; esta característica implica no tener que realizar conversión de tasa de interés, si ésta se enunciara, por ejemplo, en términos efectivos, nominal anual, o en otra unidad de tiempo. En segundo lugar, la obligación es cancelar un número finito de pagos (seis en total). Por estas dos condiciones, la serie uniforme del ejercicio 1.1 es, además, de naturaleza simple y finita.
.
La respuesta del ejercicio es:
$$P=1,500,000\left[\frac{\left(1+0.013\right)^6-1}{{0.013\left(1+0.013\right)}^6}\right]$$ $$P=8,604,291.31$$En la ecuación (1.4) además de la variable dependiente $P$, están las variables independientes de $A$, $i$, $n$, cada una con la posibilidad de ser una pregunta dentro de una situación financiera. Por ejemplo, si el propósito es calcular la serie uniforme vencida de un valor presente, solo basta con despejar $A$ de (1.4), obteniendo:
$$A=P\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right] (1.5)$$Debemos indicar que a partir del proceso de deducción de la ecuación (1.4), la serie a calcular con la fórmula (1.5) ubica la primera $A$ un lugar a la derecha de la posición de $P$. Con $P$ en ff=0, la primera $A$ se ubica en $ff=1$ y extiende pagos hasta el valor finito de $n$.
Solución
$A=?$
$P$= 4,230,000 pesos
$n= 1.5$ años; equivalentes a 6 trimestres
$ie$%= 22.0%EA
La representación del ejercicio en la Figura 1.3
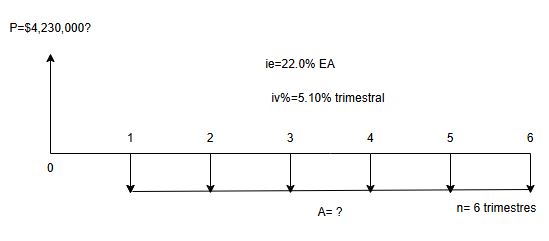
La diferencia de esta Figura 1.3 con la anterior, además de la tasa de interés, es la incógnita. En esta ocasión se pregunta por $A$
Observe en la Figura 1.3 que estando $P$ en la $ff=0$, la primera $A$ se dispone en $ff=1$ y derrama pagos hasta $n=6$. En este ejercicio los períodos de la cuota fija y de la tasa de interés no coinciden, por ello esta anualidad es además de tipo general.
Para resolver el ejercicio acudimos a lo aprendido de tasas equivalentes para hallar, en este caso, la tasa periódica trimestral equivalente a la efectiva anual dada en el problema. Para ello aplicamos el caso de efectiva mayor a efectiva menor.
Dicha tasa es:
$$i=\sqrt[4]{1+0.22}-1=0.0510$$La tasa de interés para el trimestre es de 5.10%, tasa que es equivalente a $J$=20.39% t.v. La respuesta al ejercicio es:
$$A=4,230,000\left[\frac{0.051\left(1+0.051\right)^6}{\left(1+0.051\right)^6-1}\right]=835,968.55$$Se debe cancelar la suma de 835,968.55 pesos trimestrales durante seis trimestres.
De cada pago, una parte se dirige a cancelar intereses sobre el saldo de lo adeudado al momento de realizar el pago; otra parte, el excedente de la cuota fija, es la amortización que se dirige a "matar" la deuda. Más adelante recordaremos la forma de calcular cada uno de los componentes del pago y su aplicación en sistemas de amortización.
Continuemos ahora con la determinación de una ecuación para el caso en que la variable dependiente es el plazo n, o cantidad de cuotas fija. Si:
$$P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n}\right]$$Ésta es igual a:
$$P=\frac{A}{i}\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^n}\right]$$Esto es:
$$\frac{Pi}{A}=\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^n}\right]$$Aplicando propiedad distributiva en lado derecho de la igualdad, tenemos:
$$\frac{Pi}{A}=\left[\frac{\left(1+i\right)^n}{\left(1+i\right)^n}-\frac{1}{\left(1+i\right)^n}\right]$$O sea:
$$\frac{Pi}{A}=1-\frac{1}{\left(1+i\right)^n}$$O también:
$$\frac{Pi}{A}-1=-\frac{1}{\left(1+i\right)^n}$$Multiplicando por (-1) la anterior ecuación, obtenemos:
Realizando la resta en lado izquierdo de la igualdad:
$$\frac{A-Pi}{A}=\frac{1}{\left(1+i\right)^n}$$Y es igual a:
$$\frac{A-Pi}{A}\left(1+i\right)^n=1$$ $$\left(1+i\right)^n\ =\frac{A}{A-Pi}$$Tomando logaritmo natural a ambos lados de la anterior expresión, tenemos:
$${ln\left(1+i\right)}^n\ =ln\left[\frac{A}{A-Pi}\right]$$ $$nln(1+i)\ =ln\left[\frac{A}{A-Pi}\right]$$En consecuencia, $n$ es: $$n=\frac{ln\left[\frac{A}{A-Pi}\right]}{ln(1+i)} (1.6)$$
O su equivalente:
$$n=\frac{ln(A)-ln(A-Pi)}{ln(1+i)} (1.6.1)$$Solución
$n=?$ en semestres
$P=23,245,300$
$A=3,709,358.20$ semestral
$ie=20.0$% EA
Debemos hallar la tasa periódica semestral vencida. Ésta es:
$i=9.54$% semestral.
En este ejemplo, la unidad de tiempo y la modalidad de tasa de interés (efectiva anual) no coinciden con el periodo de las cuotas (el semestre), implicando realizar modificación equivalente de tasa de interés. Para hallar la tasa efectiva del semestre (periódica vencida) se aplicó el caso de efectiva mayor a efectiva menor (ver capítulo 4 del Vol. 1)
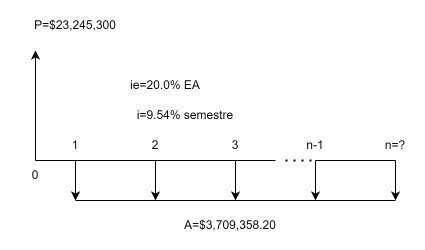
. $$n=\frac{ln\left[\frac{3,709,358.20}{3,709,358.2.-23,245,300\ast0.0954}\right]}{ln(1+0.0954)}$$La Cooperativa lechera deberá pagar 10 cuotas semestrales de $3,709,358.20$. Así mismo, 10 semestres equivalen a un plazo de 5 años. Ver en Figura 1.4 la representación del ejercicio desde el punto de vista de la Cooperativa Juan Queso.
De la ecuación inicial (1.4) solo nos resta preguntarnos por la tasa de interés (o de rendimiento) i. Contrario a lo realizado con las demás variables, para la tasa de interés, o rentabilidad, no existe procedimiento algebraico que permita determinar su ecuación: no es posible despejar de (1.4) la variable $i$. Lo anterior no significa la imposibilidad de predecir ésta; al contrario, las matemáticas han desarrollado métodos para realizar cálculos aproximados, como es el caso de la interpolación lineal.
A continuación procedemos a ilustrar la estimación de la tasa de interés $i$ desde la interpolación lineal. Para la conceptualización y operación de este método, invitamos al lector a consultar el anexo a este volumen.
Solución.
$P=485,000$ dólares
$A=35,000$ dólares trimestrales
$n= 5$ años, igual a 20 trimestres
$i=?$
Procedemos a reemplazar los datos en la ecuación (1.4), así:
$$485,000=35,000\left[\frac{\left(1+i\right)^{20}-1}{{i\left(1+i\right)}^{20}}\right]$$Y es igual a:
$$\frac{485,000}{35,000}=\left[\frac{\left(1+i\right)^{20}-1}{{i\left(1+i\right)}^{20}}\right]$$ $$13.8571429=\left[\frac{1}{i}-\frac{1}{{i\left(1+i\right)}^{20}}\right]$$Igualando a cero la anterior expresión, resulta:
$$13.8571429-\left[\frac{1}{i}-\frac{1}{{i\left(1+i\right)}^{20}}\right]=0$$La pregunta ahora es ¿cuál es la catidad de $i$ que hace que la igualdad se verifique? Nuestro problema es hallar la $i$ que hace cero la igualdad anterior. El resultado cero está al interior de valores extremos como por ejemplo -1 y 1, es decir en el intervalo abierto $(-1, 1)$.
Procedemos a ensayar con una tasa de interés $i$ tentativa y evaluamos si se verifica la igualdad. Ensayo #1: La tasa $i$ de 2% trimestral.
$$13.8571429-\left[\frac{1}{0.02}-\frac{1}{{0.02\left(1+0.02\right)}^{20}}\right]=-2.4942905$$La ecuación es diferente de cero, por lo que $i=0.02$ no es la tasa; tenemos un error. Procedemos a realizar un segundo ensayo aumentando la tasa $i$ y observamos que pasa con la ecuación. Ensayo #2: La tasa $i$ de 3.0% trimestral.
$$13.8571429-\left[\frac{1}{0.03}-\frac{1}{{0.03\left(1+0.03\right)}^{20}}\right]=-1.020332$$De nuevo el resultado es diferente de cero. Pero hay algo más: al aumentar la tasa $i$ de 2% a 3% el resultado de la ecuación pasa de $-2.49$ a -1.02$; es decir, nos estamos acercando a cero. Por lo tanto, realizamos un tercer ensayo. Ensayo #3: La tasa $i$ de 4% trimestral
$$13.8571429-\left[\frac{1}{0.04}-\frac{1}{{0.04\left(1+0.04\right)}^{20}}\right]=0.2668165$$De igual manera tenemos un resultado diferente de cero. Empero, en esta ocasión el resultado es positivo. La importancia de este último resultado es que nos permite afirmar que la tasa de interés buscada es mayor que 3.0% pero menor que 4.0%, porque el valor cero de la ecuación está entre -1.020332 y 0.2668165.
La pregunta ahora es: si con el 3.0% la ecuación es igual a -1.0203322 y con el 4.0% es de 0.2668165, ¿cuál es el valor de $i$ que la hace cero? Pues bien, es aquí donde utilizamos la interpolación lineal, al suponer que los puntos que hemos determinado pertenecen a una línea recta (de allí lo lineal).
Los puntos son: (0.03, -1.02032); ($i$%, 0); (0.04, 0.2668165). Recordemos además que conocidos tres números de una proporción geométrica podemos hallar el cuarto.
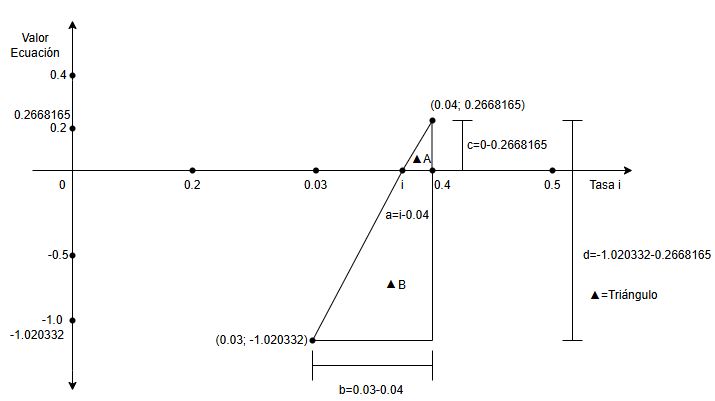
Para la interpolación disponemos los datos como en la siguiente Tabla 1.1, representados en el plano cartesiano en Figura 1.5
| $i$ | Ecuación |
|---|---|
| 0.04 | 0.2668165 |
| $i=?$ | 0 |
| 0.03 | -1.020332 |
Seguimos con el planteamiento de la ecuación de proporcionalidad:
$$\frac{a}{b}=\frac{c}{d}$$ En ella:
$a=i-0.04$
$b=0.03-0.04=-0.01$
$c=0-0.2668165=-0.2668165$
$d=-1.020332-0.2668165=-1.2871485$
De esta manera:
$$\frac{i-0.04}{-0.01}=\frac{-0.2668165}{-1.2871485}$$ $$i=\frac{-0.2668165}{-1.2871485}\ast{(-0.01)}+0.04=0.03792$$La tasa de interés es del 3.79% trimestre vencido.
Con esta tasa, la tasa nominal anual ($J=k*iv$) es $J=15.17$% y la efectiva anual, $ie=\left(1+iv\right)^k-1$, es $16.06$% E.A.
En la siguiente Figura 1.5, en perspectiva geométrica, se presentan los elementos para la interpolación lineal, apoyados en el concepto de semejanza de triángulos y en la ecuación de proporcionalidad que éste implica. La Tabla 1.1 no es más que la disposición en columnas de los valores de los ejes horizontal y vertical, respectivamente, del plano cartesiano (ver los valores de a, b, c y d; hacer clic sobre la figura).
₪ Valor Futuro
Continuamos con el estudio de las anualidades preguntándonos ahora por el valor futuro ($F$). El esquema del estudio sigue siendo la misma Figura 1.1. El valor futuro de la serie se calcula en el mismo lugar (ff) donde se halla la última anualidad (la última $A$). Para obtener la ecuación que nos permita realizar el cálculo, vamos a aprovechar resultados ya alcanzados. Recordemos que el valor futuro vencido pago único se calcula como:
Así mismo, ya sabes que:
$$P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n}\right]$$Ahora reemplacemos la segunda ecuación en la primera, y tenemos:
$$F=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n}\right]\left(1+i\right)^n$$ $$F=A\left[\frac{\left[\left(1+i\right)^n-1\right]\left(1+i\right)^n}{i{(1+i)}^n}\right]$$Cancelando $\left(1+i\right)^n$, la ecuación finalmente queda:
$$F=A\left[\frac{\left(1+i\right)^n-1}{i}\right] (1.7)$$La primera $A$ se ubica en $ff=1$ y su derrame es hasta la posición donde se ubicará el valor futuro. Veamos un ejemplo.
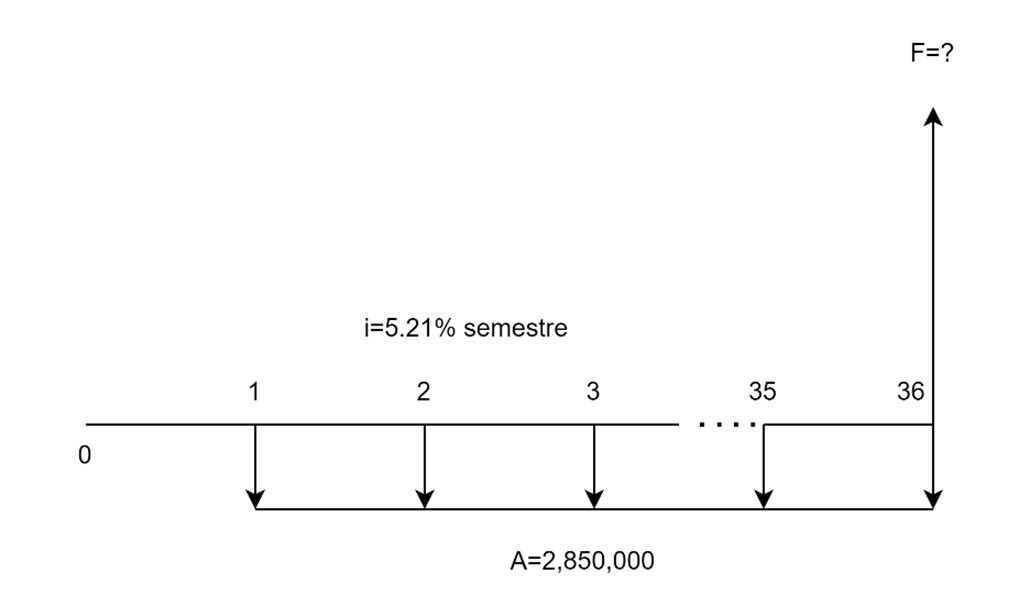
Ejercicio 1.5. Valor futuro de una anualidad vencida. Con el fin de tener recursos para la educación superior de su hijo, un padre de familia consignó durante 18 años la suma de $2,850,000 semestrales en un programa de ahorros que reconocía una tasa de interés 0.85% mensual. Hallar el valor acumulado al cabo de los 18 años.
Solución.
$F=?$
$A=2,850,000$
$i=0.85$% mensual
$n=18$ años
La tasa de interés es mensual y el plazo está dado en años, pero las cuotas se consignan cada semestre. Procedemos a realizar las transformaciones necesarias para resolver el ejercicio con la unidad de tiempo de la anualidad. Por ello, debemos hallar la tasa de interés semestral y el plazo convertirlo a semestres.
Para la tasa de interés, el asunto es pasar de una efectiva menor a una efectiva mayor. Esto es:
$ie=5.21$% semestral. El plazo, $n*k=18*2=36$ semestres.
El valor acumulado por el padre de familia es de:
$$F=2,850,000\left[\frac{\left(1+0.0521\right)^{36}-1}{0.0521}\right]=285,752,631.51$$Recordemos las características de esta anualidad. En primer lugar se trabaja bajo capitalización vencida. Es además convencional al tenerse pagos vencidos, finita pues son 36 consignaciones, y de carácter general al no coincidir el período de la tasa de interés con la unidad de tiempo de los pagos. En la ff=0 no hay anualidad, mientras que la última está ubicada en n=36, mismo lugar donde la fórmula ubica el valor F equivalente de la serie uniforme.
Con la ecuación (1.7) procedemos a determinar la fórmula para estimar la anualidad a partir de un valor futuro. Despejando $A$, tenemos:
$$A=F\left[\frac{i}{\ \left(1+i\right)^n-1}\right](1.8)$$La ecuación (1.8) convierte un valor futuro en serie uniforme, con derrame de pagos fijos desde el instante 1 hasta el sitio $n$ donde está ubicada $F$, como se ha indicado.
Resolvamos el siguiente ejemplo.
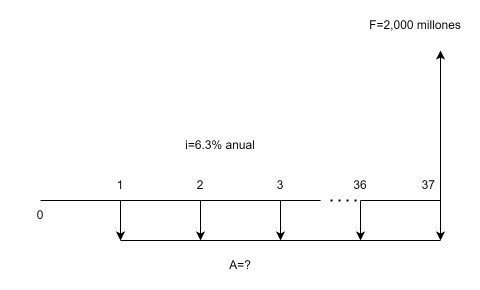
Ejercicio 1.6. Serie uniforme desde un valor futuro. Luego de terminar sus estudios de posgrado, un ingeniero financiero inicia su vida laboral a la edad de 25 años. Para su pensión de retiro, que en su caso es a los 62 años de edad, se vincula a un fondo privado para el manejo de sus ahorros durante 37 años. Si el ingeniero espera tener un ahorro de 2,000 millones de pesos al cabo de su vida laboral, ¿de cuánto debe ser la cuota fija anual de ahorro para lograr dicha meta, si el fondo ofrece un rendimiento del 6.3% anual? Ver Figura 1.7.
Solución.
$A=?$anual
$F=2,000$ millones de pesos
$i=6.3$% anual
$n=37$ años
Las variables tienen la misma unidad de tiempo, el año. Resolvemos directamente:
$$A=2,000,000,000\left[\frac{0.063}{\ \left(1+0.063\right)^{37}-1}\right]=14,067,153$$El lector ya podrá conjeturar sobre el ingreso anual que debe recibir el ingeniero financiero.
Estudiemos ahora el caso cuando n es la incógnita. Para ello, procedemos algebraicamente desde la fórmula (1.7), de la siguiente manera:
$$F=A\left[\frac{\left(1+i\right)^n-1}{i}\right]$$Y es igual a:
$$F=\frac{A}{i}\left[\left(1+i\right)^n-1\right]$$ $$\frac{Fi}{A}=\left(1+i\right)^n-1$$ $$\frac{Fi}{A}+1=\left(1+i\right)^n$$Tomando logaritmo natural a ambos lados de la igualdad:
$$ln\left[\frac{Fi+A}{A}\right]={ln\left(1+i\right)}^n$$ $$nln(1+i)=ln\left[\frac{Fi+A}{A}\right]$$Despejando $n$
$$n=\frac{ln\left[\frac{Fi+A}{A}\right]}{ln(1+i)} (1.9)$$O también
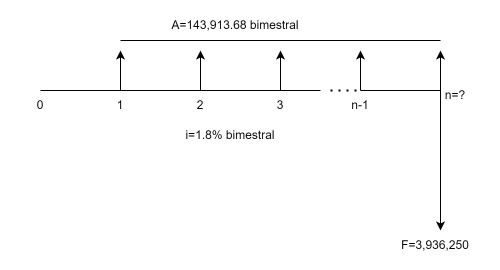
$$n=\frac{ln(Fi+A)-ln(A)}{ln(1+i)} (1.9.1)$$Ejercicio 1.7. El período $n$ desde un valor futuro. ¿En cuánto tiempo montos bimestrales de 143,913.68 pesos equivalentes a 3,936,250 pesos, genera renta del 1.8% bimestral?
Solución.
$n=?$
$A=143,913.68$ bimestral
$F=3,936,250$
$i=1.8$% bimestral
Ver la siguiente figura 1.8.
Con 1.9.1, tenemos:
$$n=\frac{ln(3,936,250*0.018+143,913.68)-ln(143,913.68)}{ln(1+0.018)}=38$$El plazo es de 38 trimestres. Se puede decir también que los 38 montos bimestrales de $143,913.68 equivalen a 3,936,250 pesos en 6.33 años
La interpolación para la tasa de interés i. Nos falta trabajar $i$ como variable dependiente. De nuevo igualamos a cero la fórmula (1.7) y nos orientamos con la determinación de un intervalo abierto que contenga al cero (-1,1).
Ejercicio 1.8. Interpolación lineal para i. Durante 2.5 años un carpintero artesanal recibió de un aserrador cinco rastras de maderaUna rastra de madera tiene dimensiones de 300 cm de largo* 50 cm de ancho * 10 cm de grueso semestrales para la elaboración de sus artesanías. Si al momento de recibir la última rastra, el carpintero cancela el equivalente a 30 rastras de madera, ¿qué tasa de interés en madera le reconoció al aserrador?
Solución.
$i=?$ semestral
$A=5$ rastra semestrales
$F=30$ rastras
$n=5$ semestres
Con:
$$\frac{F}{A}-\left[\frac{\left(1+i\right)^n-1}{i}\right]=0$$Ensayo #1: $i=5.0$%
$$\frac{30}{5}-\left[\frac{\left(1+0.05\right)^5-1}{0.05}\right]=0.4744$$Resultado diferente de cero. Realicemos un segundo ensayo subiendo la tasa.
Ensayo #2: $i=10$%
$$\frac{30}{5}-\left[\frac{\left(1+0.10\right)^5-1}{0.10}\right]=-0.1051$$Tenemos de nuevo un error, pero ya logramos un valor positivo y otro negativo como resultado de los ensayos. Procedemos a la interpolación. Ver Tabla 1.2
| $i$ | Ecuación |
|---|---|
| 0.10 | -0.1051 |
| $i=?$ | 0 |
| 0.05 | 0.4744 |
Con:
$a=i-0.10$
$b=0.05-0.10=-0.05$
$c=0-(-0.1051)=0.1051$
$d=0.4744-(-0.1051)=0.5795$
De esta manera:
$$i=\frac{0.1051}{0.5795}\ast{(-0.05)}+0.10$$ $$i=0.0909$$La tasa de interés es del 9.09% rastras de madera semestral vencido. Es aproximada porque se supone que los puntos hallados en los ensayos pertenecen a una línea recta, pero ecuación utilizada (1.7) no es ecuación de una línea recta.
Realicemos otro ejercicio para n, pero con algo adicional. Veamos el siguiente caso.
Ejercicio 1.9. El período $n$ con cuota inicial. Un vehículo con valor de 150 millones de pesos se adquiere con una cuota inicial de 50 millones y cuotas fijas mensuales de 2,539,343 al 1.5% mensual. ¿Cuántos pagos fijos son necesarios cancelar para saldar la deuda?
Solución.
$n=?$
$P=150,000,000$
Cuota inicial$=50,000,000$
$A=2,539,343$
$i=1.5$% mensual
En este ejercicio hay una cuota inicial de 50 millones. Ver Figura 1.9.
Iniciemos planteando la ecuación de valor del problema, ésta es:
$$150,000,000=50,000,000+2,539,343\left[\frac{\left(1+0.015\right)^n-1}{\left(1+0.015\right)^n*0.015}\right]$$Y es igual a:
$$150,000,000-50,000,000=2,539,343\left[\frac{\left(1+0.015\right)^n-1}{\left(1+0.015\right)^n*0.015}\right]$$Con este resultados y utilizando (1.6.1):
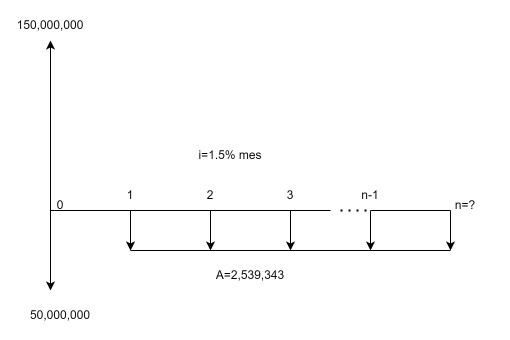
Se requieren de 60 cuotas fijas mensuales de $2,539,343
Continuando con el estudio de las anualidades con capitalización vencida, procedemos a abordar la situación de pagos diferidos o desplazados. Una anualidad es diferida cuando el primer pago de la serie uniforme se realiza en una fecha focal posterior al período uno (después de la ff=1); esto es, la serie de cuotas fijas inician su ocurrencia en cualquier instante posterior a ff=1.
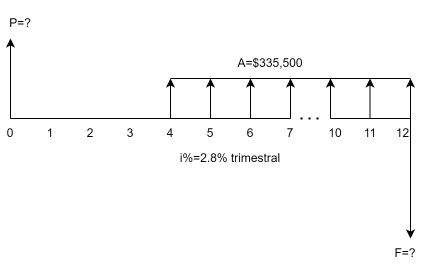
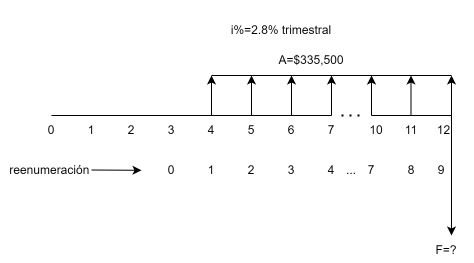
En la anterior Figura 1.10 se observa una serie uniforme desplazada respecto al valor presente P. Los pagos inician en la ff=4 y terminan en 12, para una serie uniforme con un total de nueve cuotas fijas; mientras el valor P se halla ubicado en ff=0, en su situación convencional. La primera A no está ubicada un lugar a la derecha de P, en su ubicación convencional, sino desplazada o diferida a la fecha focal cuatro(ff=4).
En cambio, observamos en la misma Figura 1.10 que el valor F está ubicado en el mismo instante donde ocurre la última cuota fija (en ff=12), por ello podemos proceder con el cálculo del valor futuro como se explicó en el tema anterior, procedimiento que más adelante ilustramos con un ejemplo.
Para calcular el valor presente de la serie en Figura 1.10, debemos combinar dos ecuaciones ya estudiadas. En particular, requerimos de $P=\frac{F}{\left(1+i\right)^n}=F\left[\frac{1}{\left(1+i\right)^n}\right]$ y de $P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n}\right]$, recordando que $P$ en la segunda ecuación ubica el valor calculado de la serie un lugar a la izquierda de la primera $A$.
Solución. Procedemos en dos pasos:
Paso #1. Hallar un valor presente provisional ($Pr.$) un lugar a la izquierda de la primera $A$ (en ff=3). Ver Figura 1.11
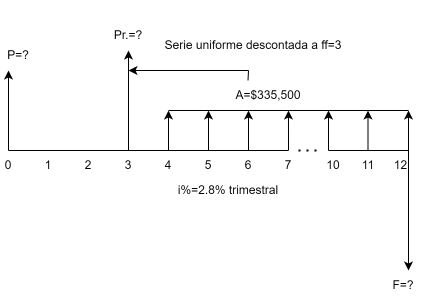
Desplazándonos desde la última $A$ ubicada en $ff=12$ hasta la $ff=3$, donde calculamos Pr, tenemos un total de nueve pagos. En este sentido, para el cálculo correspondiente, $n=9$. Veamos
$$Pr=335,500\left[\frac{\left(1+0.028\right)^9-1}{{0.028\left(1+0.028\right)}^9}\right]$$$Pr=2,636,773.70$ pesos
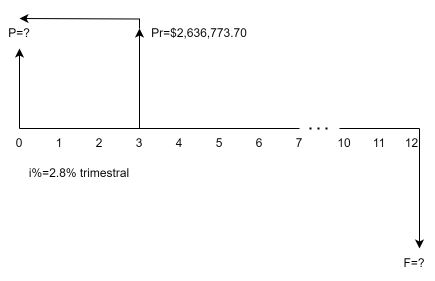
Paso #2. Hallar un valor presente P del valor provisional Pr. El problema ahora es como se representa en la Figura 1.12. En esta ocasión el $Pr$ lo asumimos como un valor futuro que debemos descontar desde $ff=3$ a cero. Para ello, hacemos un recorrido de derecha a izquierda de tres bimestres, esto es, $n=3$. Aplicando la ecuación del valor presente de un valor futuro pago único, tenemos:
$$P=2,636,773.70\left[\frac{1}{\left(1+0.028\right)^3}\right]=2,427,132.66$$En el paso #1, $n=9$ se obtiene por el recorrido en el diagrama de caja desde la última $A$ ubicada en $ff=12$ hasta un lugar a la izquierda de la primera $A$, hasta $ff=3$. En total, se hace un recorrido de nueve bimestres, o también sobre un total de nueve pagos.
En el paso #2, el valor $Pr$ es descontado a la ff=0, faltándose un recorrido en el tiempo de tres bimestres, $n=3$. Por lo tanto, el total del desplazamiento es de $9+3=12$ trimestres, que es el horizonte de tiempo total del problema.
En cada uno de los dos pasos hemos utilizado un valor diferentes para la $n$, sin utilizar un símbolo distinto en cada momento. En resumen, los pasos fueron:
$$P=2,636,773.70\left[\frac{1}{\left(1+0.028\right)^3}\right]$$ $$P=335,500\left[\frac{\left(1+0.028\right)^9-1}{{0.028\left(1+0.028\right)}^9}\right]\left[\frac{1}{\left(1+0.028\right)^3}\right]=2,427,132.66$$Nótese los distintos valores del exponente $n$. La ecuación general de equivalencia es:
. $$P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n}\right]\left[\frac{1}{\left(1+i\right)^n}\right] (1.10)$$En esta ecuación(1.10) y con la observación sobre sus valores, prestar atención a los valores de $n$ en cada uno de los pasos dados.
₪ Valor Futuro
Siguiendo con la misma Figura 1.10, en la que $F$ está ubicado en la misma fecha focal donde se halla la última $A$ (en ff=12), para realizar el cálculo del valor futuro procedemos a ubicarnos un lugar a la izquierda de la primera $A$.
La razón de la afirmación anterior está en que seguimos utilizando las ecuaciones de las series uniformes convencionales. Con respecto al tiempo, en total, tenemos un recorrido (desde $ff=3$ a $ff=12$) de nueve bimestres y una cantidad de nueve pagos, por ello $n=9$.
Para una mejor comprensión del problema ahora planteado, es recomendable realizar renumeración en el diagrama original, para identificar especialmente el valor de $n$. Ver la siguiente Figura 1.13.
Solución
Con la renumeración de la Figura 1.13 observamos que nos enfrentamos a un caso de serie uniforme convencional, por lo que directamente podemos utilizar la ecuación (1.7). Veamos:
$$F=335,500\left[\frac{\left(1+0.028\right)^9-1}{0.028}\right]=3,380,733.14$$El valor futuro en ff=12 de la serie uniforme diferida es de $3,380,733.14$ pesos.
Para constatar que los cálculos realizados son correctos, podemos trasladar (capitalizar) el valor presente obtenido anteriormente y hallar su valor futuro, en ff=12; o viceversa, el valor futuro de la Figura 1.13 descontarlo a ff=0 y obtener su valor presente. Realizando el primer procedimiento, tenemos:
$F=2,427,132.66\left(1+0.028\right)^{12}=3,380,733.14$. Igual valor futuro.
Ahora bien, si la situación del valor futuro es como se ofrece en la Figura 1.14, ya no se presenta una situación convencional y, por ello, no podemos utilizar directamente la ecuación (1.7) en su determinación. Estamos obligados a realizar dos pasos, dado que el valor futuro solicitado está desfasado.
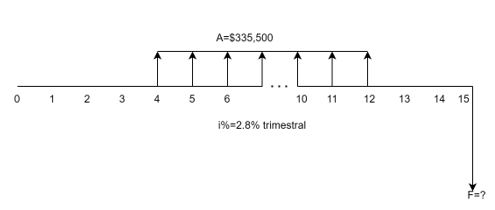
Paso #1. Hallar un valor futuro provisional ($Fp$.) en fecha focal 12. Este paso ya lo realizamos, obteniendo un monto de $3,380,733.14$ pesos.
Paso #2. Asumir el valor futuro obtenido en la ff=12 como un valor presente, que debemos trasladar (capitalizar) a la ff=15, donde se hace la pregunta por F.
El cálculo del segundo paso es:
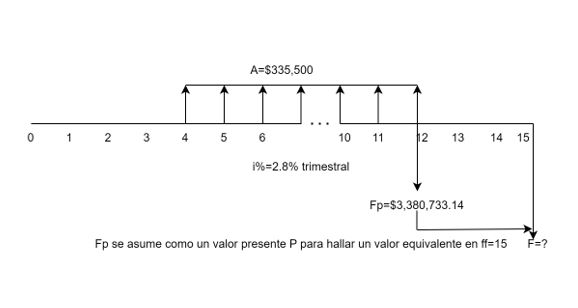
En consecuencia, los dos pasos dados son:
$$F=335,500\left[\frac{\left(1+0.028\right)^9-1}{0.028}\right]\left(1+0.028\right)^3=3,672,740,42$$De nuevo los exponentes, las $n$, son diferentes. La determinación de $n$ en cada paso es en el mismo sentido del caso para el valor presente. Empero, en esta ocasión utilizamos la ecuación $F=P\left(1+i\right)^n$, en el segundo paso y el exponente $n$ es igual al traslado en el tiempo que falta para llegar a la ff=15, del problema.
Por lo tanto, y en general, la ecuación de equivalencia es:
$$F={A\left[\frac{\left(1+i\right)^n-1}{i}\right]\left(1+i\right)}^n (1.11)$$Blank y Tarquin señalan lo necesario de una comprensión cabal de las fórmulas para el manejo de flujos de efectivos, que representamos en diagramas de caja o diagramas económico
La comprensión justa de como manipular los flujos de efectivos de diferentes situaciones financieras utilizando las ecuaciones estudiadas en este libro, ayudará al estudiante a enfrentar diferentes problemas financieros en su desempeño profesional, así como en la vida cotidiana.Los problemas que acompañan la aplicación de cada una de las fórmulas tienen el propósito de ilustrar algunas situaciones en este sentido.
Más adelante estudiaremos situaciones en las que experimentemos la aplicación de múltiples ecuaciones en la manipulación de flujos de efectivos más complejos. Por lo pronto estudiemos el siguiente ejercicio
Ejercicio 1.10. Valor presente y valor futuro de serie uniforme diferida. Ante la competencia del e-commerce, establecimientos de comercio tradicionales desarrollan estrategias para mantener cautivos a sus clientes, tales como "lleve hoy y pague después". El almacén "Tecno-facto al día" otorgó un crédito comercial para ser cancelado en 5 cuotas trimestrales iguales de $480,260, cancelando la primera dentro de seis meses, a una tasa de interés del 13.5% efectiva anual. ¿De cuánto fue el crédito otorgado? Si el cliente decide cancelar todo el crédito con un pago único al cabo de dos años, ¿Cuánto debe cancelar?
Solución.
$P=?$
$F=?$
$A=480,260$
$ie=13.5$% EA
$iv=3.216$% trimestre, es la tasa periódica
El problema se representa en la Figura 1.16, con la que es más expedito la identificación de las $n$ y manejar correctamente las fórmulas
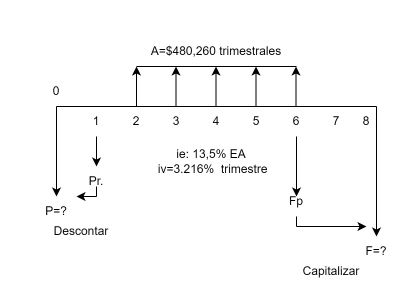
Para el valor presente, en el primer paso $n=5$ y el $Pr$ lo ubicamos en $ff=1$. Para el segundo paso, $n=1$ y con ello obtenemos el resultado final. Por lo tanto:
El resultado es $P=2,117,803.14$ pesos con un total de desplazamiento $n=5+1=6.$
En el valor futuro, para el primer paso $n=5$, y en el segundo $n=2$.
$$F=480,260\left[\frac{\left(1+0.03216\right)^5-1}{0.03216}\right]\left(1+0.03216\right)^2=2,728,207.85$$Al tiempo en el que no se hace pagos, sean estos de intereses, de abonos al capital adeudado, o de ambos, se le conoce como período de gracia. Éste es un tiempo en el que un deudor no hace pagos sobre su obligación (de intereses y/o capital). Sin embargo, lo anterior no significa que se le condonen, por ejemplo intereses, sino que estos se acumulan para ser cancelados en un momento posterior (se difiere el pago).
Las anualidades diferidas permiten manejar el valor del dinero en el tiempo bajo esta circunstancia de período de gracia. Veamos un caso.
Ejercicio 1.11. Valor de serie uniforme diferida. Como medida para el fomento del emprendimiento de base tecnológica, la Administración Distrital creó un fondo de inversión de riesgo para apoyar con capital semilla a iniciativas empresariales en la ciudad.
Es así como a la compañía "DataScience" se le otorga un crédito de fomentos por 500,000 dólares y un período de gracia de capital e intereses de dos años. La tasa de interés pactada es del 5.8% s.v., y pago de 10 cuotas semestrales fijas. Hallar el valor de la cuota.
Solución.
$A=?$
Período de gracias $=2$ años, igual a cuatro semestres
$i=5.8$% semestral
Número de cuotas fijas $=10$
$P=500,000$ dólares
La Figura 1.17 es la representación del problema. En ella se incluye un valor futuro provisional explicado con el desarrollo del ejercicio.
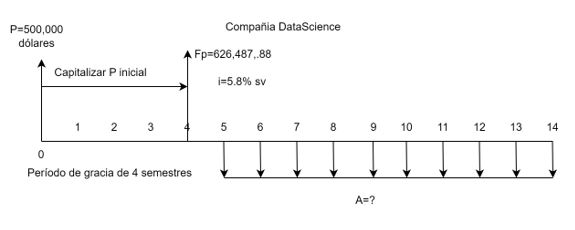
El período de gracia no significa condonación de deuda por intereses y de capital. Significa que se difiere el pago de éstos. Por ello en la Figura 1.17 no hay cuotas en los cuatro primeros semestres, equivalentes a los dos años de gracias. Es a partir del semestre cinco que inicia el pago de las diez cuotas semestrales iguales.
En el cálculo de las cuotas fijas, no podemos utilizar el capital inicial de 500,000 dólares, sino que debemos actualizar su valor, buscando un monto equivalente en la $ff=4$, que capitalice los intereses de los dos años de gracias, esto es, debemos hallar un valor futuro equivalente del capital inicial con fecha focal cuatro (de un $Fp$ ubicado un lugar a la izquierda de la primera $A$). Es decir:
$Fp=500,000\left(1+0.058\right)^4=626,487.88$ dólares, valor incluido en la Figura 1.17. Este valor futuro provisional, en segundo lugar, es identificado como un valor presente (el $P$ actualizado), requerido para hallar la serie uniforme.
La cuota fija por pagar asciende a: $$A=626,487.88\left[\frac{\left(1+0.058\right)^{10}0.058}{\left(1+0.058\right)^{10}-1}\right]=84,314.91$$
En resumen, el procedimiento es:
$$A=500,000\left(1+0.058\right)^4\left[\frac{\left(1+0.058\right)^{10}0.058}{\left(1+0.058\right)^{10}-1}\right]=84,314.91$$En general, tenemos:
$$A=P\left(1+i\right)^n\left[\frac{\left(1+i\right)^{n}i}{\left(1+i\right)^{n}-1}\right](1.12)$$De nuevo señalemos la necesidad de identificar correctamente las enes ($n$) en cada paso. En el primer paso tenemos a n=4 y en el segundo n=10, con un total de 14 semestres involucrados en el problema y el pago de 10 cuotas fijas de $84,314.91 dólares semestrales.
Al actualizar el capital para hallar las pagos fijos, constatamos que la expresión período de gracia no significa condonación de deuda, es diferir a valor equivalente los pagos de la obligación.
Una anualidad es perpetua cuando la serie de pagos, sean estos de ingresos o egresos, no tiene un último pago. Esta característica la sintetizamos indicando que $n$ tiende a infinito ($n\rightarrow\infty$).
Cuando se planean inversiones en proyectos productivos que tiene larga vida útil, tales como las obras públicas (centrales eléctricas, carreteras y puentes, suministro de agua potable y alcantarillado, etc.) o inversiones financieras con horizontes muy amplios (fondos permanentes), un método adecuado para el manejo de sus fondos y flujos de efectivo es la anualidad perpetua.
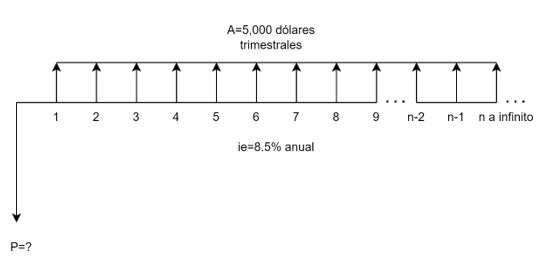
Si un fondo de inversión garantiza a perpetuidad la suma de 5,000 dólares trimestrales a un costo de oportunidad de 8.5% efectivo anual ¿De cuánto es el monto invertido en el fondo? Ahora bien, un capital de 1,000 millones de pesos al 8.9% efectivo anual ¿Qué renta perpetua mensual generaría? Estas son preguntas típicas que responderemos con el tema de las anualidades perpetuas.
Por lo pronto obtengamos la fórmula para hallar el valor presente de una anualidad perpetua. Para ello observar la Figura 1.18.
Desde la ecuación (1.4) tenemos:
$$P=\frac{A}{i}\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^n}\right]$$Aplicando propiedad distributiva
$$P=\frac{A}{i}\left[\frac{\left(1+i\right)^n}{\left(1+i\right)^n}-\frac{1}{\left(1+i\right)^n}\right]$$Siendo igual a:
$$P=\frac{A}{i}\left[1-\frac{1}{\left(1+i\right)^n}\right]$$Ahora con $n\rightarrow\infty$
La anterior ecuación es:
$$P=\frac{A}{i}\left[1-\frac{1}{\left(1+i\right)^\infty}\right]$$En el factor $\frac{1}{\left(1+i\right)^\infty}$, si $n\rightarrow\infty$, entonces éste tiende a cero; por ello:
$$P=\frac{A}{i}\left[1-0\right]$$ $$P=\frac{A}{i} (1.13)$$Resolvamos la pregunta sobre el monto invertido en el fondo.
Solución.
$P=?$
$A=5,000$ dólares
$ie=8.5$% E.A.
$iv=2.06$% trimestre
Se halla la tasa periódica trimestral de la efectiva anual, aplicando el caso de efectiva mayor a efectiva menor. El valor de $P$ es:
$$P=\frac{5,000}{0.0206}=242,667$$En el fondo hay invertidos 242,667 dólares.
Ahora pasemos a resolver la segunda inquietud, sobre la renta perpetua anual. Desde (1.13) despejamos $A$ y obtenemos:
$$A=P*i (1.14)$$La ecuación (1.14) indica que perpetuamente se recibe una renta igual a los rendimientos de un capital $P$ determinados con una tasa de interés fija $i$.
Solución
$A=?$
$P=1,000$ millones
$ie=8.9$% E.A.
Debemos hallar la tasa periódica, en este caso mensual. Aplicando el caso de efectiva mayor a efectiva menor, ésta es: $iv=0.714$%
Por lo tanto:
$$A=1,000*0.00714=7,130,287$$Se recibe una renta mensual perpetua de $7,130,287 pesos
Ejercicio 1.12. Anualidad Perpetua. Un fondo privado de pensiones, régimen de ahorro individual, pensionó a un usuario con una prima mensual de $4,500,000 a perpetuidad. Si el fondo reconoce una tasa de interés del 3% efectiva anual real ¿De cuánto fue el capital ahorrado por el usuario en su vida laboral? Suponga una inflación anual del 9%.
Solución.
Observamos que los porcentajes son anuales y la cuota fija mensual.
Por ello es necesario realizar ajustes a los datos, como se estudió en el capítulo 4 del Vol. 1. En particular, se requiere determinar la tasa de interés periódica mensual, para resolver el ejercicio. Los datos son:
$A=4,500,000$ de pesos
$\pi=9$% anual
${\rm ie}^\pi=3$% efectiva anual real
Realizando los cálculos, con estos datos tenemos que la tasa efectiva anual es $ie=12.27$%, la tasa nominal anual mes vencido es $J=11.63$%, y por último la tasa de interés periódica mes vencido es $iv=0.969$%. Como la anualidad perpetua es mensual, debemos utilizar esta última tasa en el cálculo. El resultado es:
$$P=\frac{A}{i}=\frac{4,500,000}{0.0097}=464,330,718$$El pensionado por el fondo privado logró ahorrar la suma de $464,330,178$ pesos. A una tasa de interés del $0.969$% compuesto mes vencido, podrá retirar como máximo al final de cada mes por siempre (a perpetuidad) la suma de $4,500,000$ pesos.
Ejercicio 1.13. Actualización del capital y Anualidad Perpetua. La acción comunal de la vereda la María del municipio de Yolombó (Antioquia) realizará obras de modernización de la maquinaria y equipos en el acueducto veredal, debido a las interrupciones frecuentes en el suministro de agua potable presentadas en los últimos años.
En su ejercicio estimaron una inversión inicial de 30 millones de pesos y, para poner a punto el suministro de agua, consideraron una inversión adicional de 5 millones de pesos acumulados al final del año uno, momento en que reiniciarían la operación. Si la Junta de la acción comunal estima el rendimiento bruto sobre la inversión total en 5%E.A. como mínimo, ¿De cuánto es el monto del valor anual que espera recibir la Junta como ingreso mínimo a perpetuidad?
Solución.
Inversión inicial=$30,000,000$ de pesos
Inversión adicional=$5,000,000$ de pesos
$i=5$% E.A.
Se presenta una inversión inicial en la $ff=$ y otra adicional en la $ff=1$, ver Figura 1.19. Como primer paso se debe actualizar la inversión del proyecto, para la $ff=1$; es hallar una valor equivalente al final del año uno. Si $Ip$ es la inversión del proyecto actualizada, su monto es:
$$Ip=30,000,000\left(1+0.05\right)+5,000,000=36,500,000$$Este monto de $36,500,000$ pesos, es la inversión total del proyecto a valor equivalente al final del año uno.
El segundo paso es hallar la anualidad perpetua; ésta es:
$$A=36,500,000*0.05=1,825,000$$
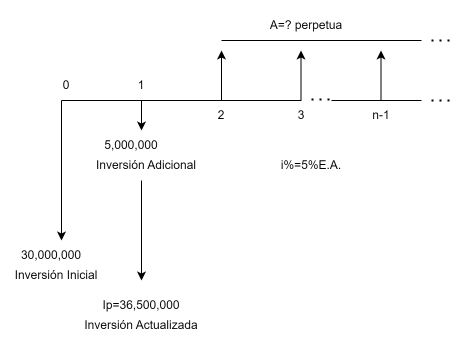
Los ingresos anuales son equivalentes a 1,825,000 pesos anuales "para siempre", al suministrar el agua potable a los actuales usuarios del servicio.
Continuando con el estudio de las series uniformes con capitalización vencida, procedemos a tratar el caso de las anualidades con pago anticipado, esto es, aquella situación en la que el primer pago (ingreso o egreso de efectivo fijo) se presenta en la fecha focal cero (la primera A se ubica en $ff=0$). El derrame de las cuotas fijas inicia, no en $ff=1$ como en las convencionales, sino en $ff=0$ o tiempo presente como también se le denomina. Ver figura 1.20
En dicha figura el derrame de $A$ se extiende hasta el instante de tiempo $n-1$. Por ejemplo, si debemos pagar diez cuotas fijas y la primera la realizamos en el presente (ff=0), en consecuencia el último pago lo realizaremos en $n=9$ (ff=n-1). Es claro entonces que lo anticipado se refiere al pago o cuota fija, no la capitalización, que sigue siendo vencida.
Como consecuencia de seguir aplicando el modelo de capitalización vencida, debemos observar además que tanto el valor presente de la serie uniforme, como su valor futuro, se determinan en los mismos lugares en el tiempo del caso convencional. Esto es $P$ en ff=0 y $F$ en ff=n.
Presentaremos dos procedimientos para hallar el valor presente equivalente de la serie representada en la Figura 1.20. Estos modelos son base para nuevas situaciones financieras, como son el valor futuro, la anualidad, la tasa de interés y el plazo (o número de cuotas).
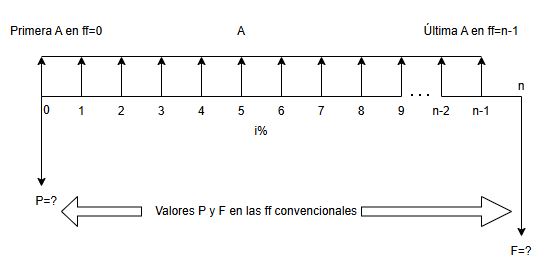
Los procedimientos son desarrollados siguiendo al profesor Meza Orozco.
Método 1.
En la Figura 1.20, la primera $A$ ya está ubicada en ff=0 o en tiempo presente. Debemos por lo tanto descontar al presente el resto de las anualidades en una cantidad total de $n-1$. Centrados en el resto de la serie, encontramos la primera $A$ en $ff=1$ y se extiende el derrame hasta $ff=n-1$, es decir, se ha identificado una serie uniforme convencional desde $n=1$ hasta $n-1$. Lo interesante de esta identificación es la posibilidad de aplicar directamente la ecuación (1.4) para hallar el valor presente de esta parte de la Figura 1.20. Con estas observaciones, el modelo de valor para la Figura 1.20 es: $$P=A+A\left[\frac{\left(1+i\right)^{n-1}-1}{i\left(1+i\right)^{n-1}}\right](1.15)$$Ahora, factorizando $A$, la ecuación queda como:
$$P=A\left[1+\frac{\left(1+i\right)^{n-1}-1}{i\left(1+i\right)^{n-1}}\right](1.16)$$Con los modelos (1.15) o (1.16) podemos calcular a valor equivalente, el monto presente de una serie uniforme con capitalización vencida y pago anticipado. Sin embargo, y dado el propósito pedagógico de este libro, la invitación a comprender los procesos lógico-matemáticos de los modelos, nos dirigimos a simplificar la ecuación (1.16).
Procedemos a realizar la suma de la expresión dentro del corchete de (1.16), con $i\left(1+i\right)^{n-1}$ como común denominador.
.Tenemos por lo tanto:
$$P=A\left[\frac{{i\left(1+i\right)^{n-1}+\left(1+i\right)}^{n-1}-1}{i\left(1+i\right)^{n-1}}\right]$$Tomando factor común $\left(1+i\right)^{n-1}$:
$$P=A\left[\frac{\left(1+i\right)^{n-1}(1+i)-1}{i\left(1+i\right)^{n-1}}\right]$$Igual base se suman exponentes:
$$P=A\left[\frac{\left(1+i\right)^{n-1+1}-1}{i\left(1+i\right)^{n-1}}\right]$$Por lo tanto:
$$P=A\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^{n-1}}\right](1.17)$$Ejercicio 1.14. Valor presente de anualidad anticipada. Un concesionario de la ciudad le ofrece a un cliente la posibilidad de adquirir un vehículo último modelo por medio del pago de sesenta cuotas mensuales fijas de 6,425,103.41 pesos, con cuota anticipada, financiado al 1.3% mensual. ¿Cuánto vale el vehículo de contado? Resolver con (1.15), (1.16) y (1.17).
Solución.
$P=?$
$A=6,425,103.41$
$n=60$
$i=1.3$% mes
Con (1.15)
$$P=6,425,103,41+6,425,103.41\left[\frac{\left(1+0.013\right)^{60-1}-1}{0.0130\left(1+0.013\right)^{60-1}}\right]$$ $$P=6,425,103.41+6,425,103.41\left[41.02266998\right]$$ $$P=6,425,103.41+263,574,896.59=270,000,000$$Con (1.16)
$$P=6,425,103.41\left[1+\frac{\left(1+0.013\right)^{60-1}-1}{0.013\left(1+0.013\right)^{60-1}}\right]$$ $$P=6,425,103.41\left[42.02266998\right]=270,000,000$$Con (1.17)
$$P=6,425,103.41\left[\frac{\left(1+0.013\right)^{60}-1}{0.013\left(1+0.013\right)^{60-1}}\right]$$ $$P=6,425,103.41\left[42.02266998\right]=270,000,000$$De contado, el vehículo vale 270 millones de pesos.
Método 2.
En la siguiente Figura 1.21 se presenta el segundo método del profesor Meza Orozco. Se desarrolla en dos pasos que describimos a continuación.
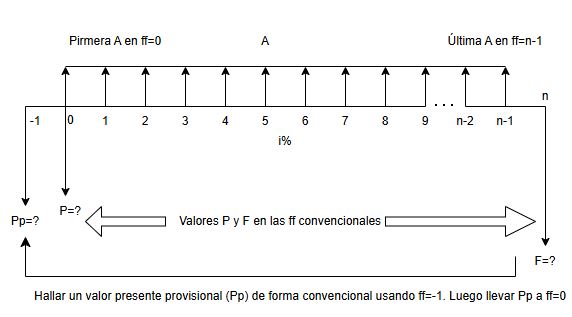
El primer paso es ubicarnos en una fecha focal anterior al presente (de cero) representada por menos uno (-1), y calcular allí un valor presente provisional (Pp), esto es, en ff=-1.
La conveniencia de este artificio es representar la serie uniforme anticipada como serie convencional, y aplicar directamente la ecuación (1.4) para hallar el valor presente provisional. El exponente de la ecuación, pasa de (n-1) a ser n. Por lo tanto, el paso uno es:
$$Pp=A\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^{n}}\right]$$
El segundo paso es trasladar el valor Pp calculado a la fecha focal cero y así hallar el valor presente $P$ como solución al problema. Para ello, Pp es un valor presente que llevamos al futuro con n=1. Por ello:
$$F=Pp\left(1+i\right)^n$$ $$F=Pp\left(1+i\right)^1$$De esta manera, el valor presente se determina como:
$$P=A\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^{n}}\right]*(1+i)(1.18)$$Resolvamos ahora el mismo problema 1.14. Tenemos:
$$P=6,425,103.41\left[\frac{\left(1+0.013\right)^{60}-1}{0.013\left(1+0.013\right)^{60}}\right]*(1+0.013)$$Es decir:
$$P=6,425,103,41(41.48339)(1+0.013)=270,000,000$$Arrojando igual resultado de 270 millones de pesos.
Ahora bien, (1.18) la simplificamos de la siguiente manera: $$P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^n\left(1+i\right)^{-1}}\right]$$Aplicando propiedad de exponentes:
Resultado que es la misma ecuación (1.17), modelo que será utilizando en adelante en el libro.
la anualidad. Obtengamos ahora la manera de hallar la serie uniforme finita con pago anticipado. Para ello solo es necesario despejar $A$ de (1.17).
La solución es:
$$A=P\left[\frac{i\left(1+i\right)^{n-1}}{\left(1+i\right)^n-1}\right](1.19)$$Ejercicio 1.15. Anualidad anticipada de un valor presente. En la ejecución de un proyecto productivo, los socios se comprometieron a financiar la inversión hasta la puesta en operación de la iniciativa, por valor de 5 millones de dólares. Dado que la inversión se ejecuta en horizonte de cinco años, los socios acuerdan el pago de una cuota fija anual bajo modalidad anticipada. Determinar el valor de la cuota fija si los socios comparten un costo de oportunidad de 8.3% anual.
Solución.
$A=?$
$P=5,000,000$ de dólares
$n=5$ años
$i=8.3$% anual
Solución para n. Procedemos a despejar $n$ de la ecuación (1.17), que iniciando extrayendo $i$ del corchete, tenemos:
Multiplicando a ambos lados de la igualdad por $\frac{i}{A}$, resulta:
$$\frac{Pi}{A}=\left[\frac{\left(1+i\right)^n-1}{\left(1+i\right)^{n-1}}\right]$$Aplicando propiedad distributiva al lado derecho de la igualdad, obtenemos:
$$\frac{Pi}{A}=\frac{\left(1+i\right)^n}{\left(1+i\right)^{n-1}}-\frac{1}{\left(1+i\right)^{n-1}}$$Y es igual a:
Es decir:
$$\frac{Pi}{A}=(1+i)-\frac{(1+i)}{\left(1+i\right)^n}$$Tomando factor común $(1+i)$:
$$\frac{Pi}{A}=(1+i)\left[1-\frac{1}{\left(1+i\right)^n}\right]$$Esto es:
$$\frac{Pi}{A(1+i)}=1-\frac{1}{\left(1+i\right)^n}$$Y es igual a:
$$\frac{Pi}{A(1+i)}-1=-\frac{1}{\left(1+i\right)^n}$$Multipliquemos la anterior igualdad por $-1$
$$1-\frac{Pi}{A(1+i)}=\frac{1}{\left(1+i\right)^n}$$Por lo que:
$$\frac{A(1+i)-Pi}{A(1+i)}=\frac{1}{\left(1+i\right)^n}$$En consecuencia:
$$\frac{A(1+i)-Pi}{A(1+i)}*\left(1+i\right)^n=1$$Así mismo
$$\left(1+i\right)^n=\frac{A(1+i)}{A(1+i)-Pi}$$Apliquemos logaritmo natural a ambos lados de la igualdad:
$${ln\left(1+i\right)}^n=ln\left[\frac{A(1+i)}{A(1+i)-Pi}\right]$$Al aplicar propiedad de logaritmos al lado izquierdo de la igualdad resulta la siguiente expresión:
$$nln(1+i)=ln\left[\frac{A(1+i)}{A(1+i)-Pi}\right]$$Y es igual a:
$$n=\frac{ln\left[\frac{A(1+i)}{A(1+i)-Pi}\right]}{ln(1+i)}(1.20)$$Al numerador del lado derecho de la igualdad, que es una división, podemos aplicar la propiedad logarítmica de la división.
Por lo tanto, la ecuación anterior es igual a:
$$n=\frac{ln\left[A(1+i)\right]-ln\left[A(1+i)-Pi\right]}{ln(1+i)}(1.20.1)$$Ejercicio 1.16. El cálculo de n bajo anualidad anticipada. Los socios del proyecto productivo del ejercicio anterior previeron dificultades financieras para cumplir con la programación de la cuota anticipada número cinco. Por ello, oportunamente gestionaron un crédito por el valor de 1,165,466 dólares para ser cancelado por medio de cuotas fijas anticipadas semestrales de 172,367.81 dólares al 10.52% E.A. Bajo este acuerdo financiero, ¿cuántas cuotas semestrales deben cancelar los socios?
Solución.
$n=?$
$P=1,165,466$ dólares
$A=172,367.81$ dólares
$ie=10.52$% E.A.
$iv=5.12$% semestral (tasa de interés $i$ periódica)
Se debe cancelar ocho cuotas iguales por el valor indicado.
El caso de la tasa de interés. En la ecuación (1.17) no es posible despejar la tasa de interés $i$, por ello, de nuevo acudimos a la interpolación lineal.
Ante alguna duda sobre el procedimiento con esta operación matemática, invitamos al lector a revisar el tema en el anexo a este libro.
Ejercicio 1.17. La tasa de interés bajo anualidad anticipada. ¿Qué tasa de interés hace equivalente el egreso de $3,659,200$ pesos con el flujo de ingresos mensuales representado por la serie uniforme $A=385,240$ pesos de la siguiente Figura 1.22?
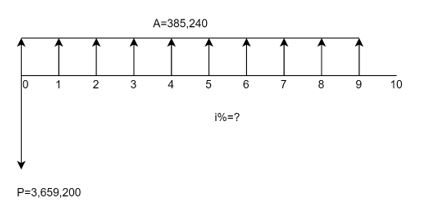
Solución.
Iniciamos planteando el asunto desde la ecuación (1.17); esto es, igualándola a cero:
$$3,659,200=385,240\left[\frac{\left(1+i\right)^{10}-1}{{i\left(1+i\right)}^{10-1}}\right]$$ $$\frac{3,659,200}{385,240}=\left[\frac{\left(1+i\right)^{10}-1}{{i\left(1+i\right)}^{10-1}}\right]$$ $$9.49849445-\left[\frac{\left(1+i\right)^{10}-1}{{i\left(1+i\right)}^9}\right]=0$$Continuamos con los ensayos. Ensayo #1. $i=1.0$%
$$9.49849445-\left[\frac{\left(1+0.01\right)^{10}-1}{{0.01\left(1+0.01\right)}^9}\right]=-0.067523$$Valor de la ecuación diferente de cero. Por ello, $i\neq 1.0$%. Ensayo #2. $i=2.0$%
$$9.49849445-\left[\frac{\left(1+0.02\right)^{10}-1}{{0.02\left(1+0.02\right)}^9}\right]=0.336258$$Valor de la ecuación diferente de cero. Por ello, $i\neq 2.0$%. Sin embargo, como cero está contenido entre $-0.67523$ y $0.336258$, la tasa de interés $i$ debe estar entre 1% y 2%.
Hagamos la disposición de los datos en una tabla y realicemos la interpolación. Ver figura 1.23
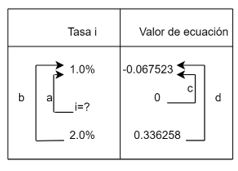
Los valores para establecer la ecuación de proporcionalidad son:
$a=i-0.01$
$b=0.02-0.01=0.01$
$c=0-(-0.067523)=0.067523$
$d=0.336258-(-0.067523)=0.403781$
Desde estos valores y con $\frac{a}{b}=\frac{c}{d}$ tenemos:
$$\frac{i-0.01}{0.01}=\frac{0.067523}{0.403781}$$ $$i=\frac{0.067523}{0.403781}*0.01+0.01$$ $$i=0.1672*0.01+0.01=0.011672$$La tasa de interés es del 1.167% mensual, recordado que este método ofrece un resultado aproximado.
₪ Valor futuro de serie uniforme anticipada
Para iniciar este tema, invitamos al lector a regresar a la Figura 1.20 y observe la ubicación de $F$. La variable $F$ está ubicado en la $ff=n$. Ahora bien, si con la ecuación (1.17) hallamos el valor presente ($P$) de esa serie uniforme anticipada, es correcto entonces utilizar este valor $P$ para hallar el valor futuro en la fecha focal n, utilizando para ello la fórmula del valor futuro pago único vencido. Es decir:
Desde esta intuición, procedemos a deducir la ecuación del valor futuro pretendido.
Como:
$$P=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^{n-1}}\right]$$Es cierto que $F=P\left(1+i\right)^n$ también es igual a:
$$F=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^{n-1}}\right]\left(1+i\right)^n$$Ecuación que perfectamente calcula el valor futuro deseado. Empero la podemos simplificar de la siguiente manera:
$$F=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^{n-1}\ \left(1+i\right)^{-n}}\right]$$Igual base se suman exponentes.
$$F=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^{n-1-n}\ }\right]$$ $$F=A\left[\frac{\left(1+i\right)^n-1}{{i\left(1+i\right)}^{-1}\ }\right]$$ $$F=A\left[\frac{\left(1+i\right)^n-1}{i}\right](1+i)$$Resultando finalmente:
$$F=A\left[\frac{\left(1+i\right)^{n+1}-(1+i)}{i}\right](1.21)$$En el ejercicio 1.14 se obtuvo como valor presente la suma de 270 millones de pesos, siendo el valor de contado del vehículo último modelo que paga 60 cuotas fijas bajo forma anticipada de 6,424,103.41 pesos al 1.3% mensual.
El valor futuro del vehículo, desde el valor de contado, es:
$$F=270,000,000\left(1+0.013\right)^{60}=\ 586,044,353.33$$Y con el modelo (1.21) es igual a:
$$F=6,424,103.41\left[\frac{\left(1+0.013\right)^{60+1}-(1+0.013)}{0.013}\right]$$ $$F=6,424,103.41*91.31166088=586,044,353.33$$Ejercicio 1.18. Valor futuro anualidad anticipada. Un inversionista estuvo ahorrando durante tres años la suma de 2,830,000 pesos al inicio de cada mes con el fin de lograr una meta de capital. El fondo de inversiones que recibe los depósitos le garantiza una tasa del 8.6% m.v. por sus ahorros. ¿Cuál será el monto alcanzado por el inversionista al cabo de los tres años?
Solución.
$A=2,830,000$
$n=3$ años, equivalentes a 36 meses
$J=8.6$% m.v
$iv=0.7166$% mensual, es la tasa de interés periódica
$F=?$
Ver la representación gráfica en la siguiente Figura 1.24
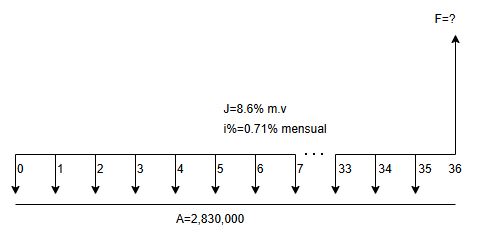
En total son 36 cuotas iguales, realizando la primera en $ff=0$ y la última en $ff=35$. El valor futuro se calcula en $ff=36$, por la razón ya antes mencionada
$$F=2,830,000\left[\frac{\left(1+0.007166\right)^{36+1}-(1+0.007166)}{0.007166}\right]$$ $$F=2,830,000*41.19758=116,589,155.55$$₪ La anualidad desde el futuro anticipado
De la ecuación(1.21) despejamos $A$ y obtenemos:
$$A=F\left[\frac{i}{\left(1+i\right)^{n+1}-(1+i)}\right](1.22)$$Dicha fórmula permite convertir un valor futuro en serie uniforme, iniciando el derrame de las $A$ en la $ff=0$ hasta un lugar antes de la posición o fecha focal de $F$, como se puede observar de nuevo en la Figura 1.24
Ejercicio 1.19. Anualidad anticipada desde un valor futuro. En diez años se logró acumular un capital de 850.000 dólares, mediante depósitos iguales al inicio de cada trimestre y tasa de interés del 18% E.A. Hallar el monto del depósito trimestral.
Solución.
$A=?$
$F=850,000$ dólares
$ie=18$% E.A.
$n=10$ años, equivalentes a 40 trimestres
Debemos hallar la tasa periódica, de efectiva mayor a efectiva menor. La tasa es $iv=4.22$% trimestral
Con (1.22), tenemos:
$$A=850,000\left[\frac{0.0422}{\left(1+0.0422\right)^{40+1}-(1+0.0422)}\right]=8,147.18$$La ecuación para n desde la fórmula de valor futuro. Desde (2.21) planteamos que:
Así mismo:
$$\frac{Fi}{A}=\left[\left(1+i\right)^{n+1}-(1+i)\right]$$En consecuencia:
$$\frac{Fi}{A}+(1+i)=\left(1+i\right)^{n+1}$$Por lo que:
$$\frac{Fi+A(1+i)}{A}=\left(1+i\right)^{n+1}$$O también
$$\left(1+i\right)^{n+1}=\left[\frac{Fi+A(1+i)}{A}\right]$$Tomando logaritmo natural en ambos lados de la igualdad anterior, tenemos:
Operando algebraicamente:
$$(n+1)ln(1+i)=ln\left[\frac{Fi+A(1+i)}{A}\right]$$ $$(n+1)=\frac{ln\left[\frac{Fi+A(1+i)}{A}\right]}{ln(1+i)}$$ $$n=\frac{ln\left[\frac{Fi+A(1+i)}{A}\right]}{ln(1+i)}-1 (1.23)$$Y es igual a:
$$n=\frac{ln\left[Fi+A(1+i)\right]-ln\left[A\right]}{ln(1+i)}-1 (1.23.1)$$Ejercicio 1.20. El cálculo de n desde un valor futuro. Una compañía desea invertir en un proyecto de infraestructura vial, por medio de una serie de pagos semestrales anticipados de 2,519,343 de dólares al 12% nominal anual mes vencido y alcanzar un monto total de 100 millones de dólares en n años . ¿Cuántas cuotas anticipadas debe depositarse para alcanzar la meta? ¿En cuántos años la empresa cumple la meta?
Solución.
$A=2.519,343$ millones
$F=100,000,000$ millones de dólares
$J=12$% m.v.
$iv=6.15$% semestral, es la tasa de interés equivalente del semestre
$n=?$ en semestres, el número de cuotas
Trabajando en millones y con (1.23.1) la respuesta es:
$$n=\frac{ln\left[100*0.0615+2.519(1+0.0615)\right]-ln\left[2.519\right]}{ln(1+0.0615)}-1$$ $$n=\frac{ln\left[6.152+2.674\right]-ln\left[2.519\right]}{ln(1.0615)}-1$$ $$n=\frac{ln(8.826)-ln(2.519)}{ln(1.0615)}-1$$ $$n=\frac{2.17742059-0.924000371}{0.059701985}-1=20.$$Se debe cancelar 20 cuotas al inicio de cada semestre de 2,519,343 dólares y la meta se cumple en 10 años.
Hasta este punto hemos abordado diferentes series uniformes que han compartido un elemento común: las de ser manejadas a valor equivalente por medio de la capitalización vencida. Esta característica común se identifica en la utilización de los factores siguientes:${(1+i)}^n$ y $\frac{1}{{(1+i)}^n}$.
En el siguiente punto vamos a tratar las anualidades con capitalización continua.
Como se trató en el volumen 1 de este libro, la capitalización continua, o a tiempo continuo, se capturó en la modelación por medio del número irracional $e$ (Euler).
La ecuación para calcular el valor futuro pago único al final de un plazo se determinó como $F=Pe^{nJ}$. De esta ecuación, se deriva para el valor presente la fórmula $P=\frac{F}{e^{nJ}}$, o también $P=Fe^{-nJ}$
Nos enfocamos en la deducción de las fórmulas para hallar los valores presente y futuro, de una serie uniforme con pago vencido y capitalización continua. De nuevo, un pago vencido indica que una cuota fija se genera al final de un período, ya sea este el mes, el trimestre, el semestre, etc. Por ello, las incógnitas $F$ y $P$ se ubican en el diagrama de caja de forma convencional. Ver Figura 1.25
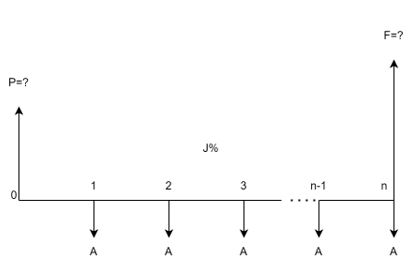
En el proceso de deducción de la fórmula para el valor presente, cada $A$ es asumida como un valor futuro que descontamos al presente, a la $ff=0$. Con $n$ identificamos los períodos iguales en los cuales se da el movimiento de las anualidades, sea cada mes, cada trimestres, etc. Descontando cada $A$, tenemos la siguiente ecuación para $P$:
$$P=Ae^{-J}+Ae^{-2J}+\ Ae^{-3J}+…Ae^{-(n-1)J}+Ae^{-nJ} (a)$$ La expresión anterior, es la suma de n términos en progresión geometría con razón común igual a ${e}^{-J}$. El primer término es $Ae^{-J}$ y el último término es $Ae^{-nJ}$.
Desde la constatación del carácter de la suma en la ecuación (a), multipliquemos la expresión anterior por la razón común para obtener (b):
$$Pe^{-J}=Ae^{-2J}+Ae^{-3J}+\ Ae^{-4J}+…Ae^{-nJ}+Ae^{-(n+1)J}(b)$$Restando (a)-(b):
$$P=Ae^{-J}+Ae^{-2J}+\ Ae^{-3J}+…Ae^{-(n-1)J}+Ae^{-nJ} (a) -$$ $$Pe^{-J}=Ae^{-2J}+Ae^{-3J}+\ Ae^{-4J}+…Ae^{-nJ}+Ae^{-(n+1)J} (b)$$Da como resultado:
$$P-Pe^{-J}=Ae^{-J}-Ae^{-(n+1)J} (c)$$Tomando factor común $P$ al lado izquierdo de (c) y de $Ae^{-J}$ en su lado derecho, tenemos:
$$P\left(1-e^{-J}\right)=Ae^{-J}\left[1-e^{-nJ}\right]$$Expresión que es igual a:
$$P\left(1-\frac{1}{e^J}\right)=Ae^{-J}\left[1-\frac{1}{e^{nJ}}\right]$$Realizando la resta en cada factor:
$$P\left(\frac{e^J-1}{e^J}\right)=Ae^{-J}\left[\frac{e^{nJ}-1}{e^{nJ}}\right]$$En consecuencia:
$$P=\frac{Ae^{-J}e^J}{{(e}^J-1)}\left[\frac{e^{nJ}-1}{e^{nJ}}\right]$$ $$P=Ae^{-J+J}\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]$$ $$P=Ae^0\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]$$ $$P=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right](1.24)$$En la ecuación (1.24), recordemos, $A$ es un flujo de anualidades o pagos que ocurren periódicamente de forma vencida; son por lo tanto, valores que ocurren de forma discreta ($A$ se da una sola vez en cada período, sea éste el mes, trimestre, semestre , año.).
$J$ es la tasa de interés nominal que hemos limitado como anual. Esta situación nos llevaría a pensar que las cuotas fijas solo se dan para períodos anuales; empero este no es el caso, como se ilustra más adelante con un ejemplo.
Ejercicio 1.21. El valor presente de anualidad vencida con capitalización continua. Una compañía ha emprendido el proyecto de introducir un nuevo producto al mercado que reporta ingresos brutos anuales de 500 mil dólares durante diez años. Si la expectativa de rendimiento sobre el capital invertido es de 35.0% anual continuo, ¿A cuánto asciende el capital invertido?¿Qué tasa efectiva anual continua rinde el capital?
Solución.
$A=500,000$ anual
$J=35.0$% anual continuo
$n=10$ años
$P=?$
La unidad de tiempo de las variables independientes es el año. Con (1.24 la solución es:
$$P=500,000\left[\frac{e^{10*0.35}-1}{e^{10*0.35}(e^{0.35}-1)}\right]$$ $$P=500,000\left[\frac{32.115452}{33.115452(0.41906755)}\right]=1,157,095.82$$La tasa efectiva anual continua es:
El capital es de $1,157,095.82 dólares y la rentabilidad de 41.91% E.A.
La anualidad desde el valor presente.
De la fórmula (1.24) despejamos $A$ y obtenemos:
$$A=P\left[\frac{e^{nJ}(e^J-1)}{e^{nJ}-1}\right]\ (1.25)$$Ejercicio 1.22. La anualidad con capitalización continua de un capital. Suponga ahora que la compañía del ejercicio anterior desea determinar la cuota fija mensual que durante diez años y con la misma expectativa de rendimiento de 35.0% anual continuo, le produce el capital invertido de 1,157,095.82 dólares. Hallar la cuota fija mensual, y las tasas de interés efectivas continuas mensual y anual
Solución.
Dado que la respuesta de $A$ se debe dar en meses, debemos realizar conversiones equivalentes a esta unidad de tiempo.
$A=?$ mensual
$J=35.0$% anual continuo
$n=10$ años
$P=1,157,095.82$
Conversiones: Para el plazo tenemos $n*k=10*12=120$ meses. Para la tasa de interés, como la tasa nominal de 35.0% es para un años, el valor equivalente de la tasa de interés para un mes (haciendo una regla de tres simple) es de 2.917%. Así entonces:
$$A=1,157,095.82\left[\frac{e^{120*0.02917}(e^{0.02917}-1)}{e^{120*0.02917}-1}\right]\ $$ $$A=1,157,095.82\left[\frac{33.115452(0.02959618-1)}{33.115452-1}\right]$$ $$A=1,157,095.82\left[\frac{0.98009086}{32.115452}\right]=35,311.94\ $$La cuota fija mensual asciende a 35,311.94 dólares.
Las tasas efectivas son:
Mensual. $ie=e^{0.02917}-1=1.02959618-1=0.02959618$, esto es 2.96% efectivo mes
Anual. $ie=e^{0.02917*12}-1=1.41906755-1=0.41906755$, esto es 41.91% efectivo anual, ya obtenida anteriormente.
La fórmula para n desde la ecuación (1.24). Iniciamos pasando la $A$ a dividir al lado izquierdo de la igualdad:
Luego pasamos la expresión $e^{nJ}(e^J-1)$ a multiplicar al lado izquierdo de la igualdad, obteniendo:
$$e^{nJ}(e^J-1)\ast\frac{P}{A}*=e^{nJ}-1$$Implicando que:
$$1=e^{nJ}\ -\ e^{nJ}(e^J-1)\ast\frac{P}{A}$$Tomando a $e^{nJ}$ como factor común, la ecuación queda igual a:
$$1=e^{nJ}\left[1-(e^J-1)\frac{P}{A}\right]$$O sea:
$$1=e^{nJ}\left[\frac{A-(e^J-1)P}{A}\right]$$Y es cierto que:
$$\left[\frac{A}{A-(e^J-1)P}\right]=e^{nJ}$$Tomando logaritmo natural a ambos lados de la igualdad anterior:
$$ln\left[\frac{A}{A-(e^J-1)P}\right]={lne}^{nJ}$$Como $lne^{nJ}=nJ\ast lne$, y recordando que $lne=1$, tenemos que $lne^{nJ}=nJ$; en consecuencia:
Por ello:
$$n=\frac{ln\left[\frac{A}{A-(e^J-1)P}\right]}{J} (1.26)$$Ejercicio 1.23. El cálculo de n desde capitalización continua. Una persona requiere urgentemente la suma de $1,002,526.06 euros comprometiéndose a cancelar cuotas trimestrales iguales de 38,200 euros con una tasa de interés de 3.2% el trimestre. ¿Cuál es el plazo solicitado para cancelar la obligación? o ¿cuántas cuotas se compromete a cancelar la persona? Hallar además la tasa nominal anual y la efectiva anual con capitalización continua de la situación.
Solución.
$P=1,002,526.06$
$A=38,200$
Tasa de interés del trimestre=$3.2$%
$n=?$
$J=?$
$ie=?$
Con (1.26), tenemos:
El plazo es 60 trimestres 0 15 años, o sesenta cuotas iguales de 38,200. La tasa nominal anual continua es de $J=4*0.032=0.128=12.8$%. La tasa efectiva anual continua es $ie=e^{0.032*4}-1=0.136553$, esto es, 13.66%.
¿Y para la tasa de interés J?
De nuevo recurrimos a la interpolación lineal y en ello se iguala a cero la ecuación (1.24).
$$\frac{P}{A}-\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]=0$$ ´Los datos para la interpolación los obtenemos con base en el procedimiento de ensayo y error, tratando de construir el intervalo adecuado, esto es, que contenga el valor de $J$ que haga cero la ecuación.
Ejercicio 1.24. El cálculo de la tasa de interés con capitalización continua. Un fondo de inversión recibe la suma de 20,753,476 pesos con el compromiso de cancelar 36 cuotas vencidas de 533,890 pesos mensuales. Si se asume capitalización continua, ¿qué tasa de interés nominal anual es la rentabilidad comprometida por el fondo?
Solución.
$P=20,753,476$
$A=533,890$ mensual
$n=36$ meses
$J=?$
Ensayo #1. Tasa de interés del 1.5% mensual.
$$\frac{20,753,476}{533,890}-\left[\frac{e^{36*0.015}-1}{e^{36*0.015}(e^{0.015}-1)}\right]=-27.2953$$La ecuación es diferente de cero. Procedemos a un segundo ensayo y observamos el comportamiento del resultado, si es cero, o se acerca a éste.
Ensayo #2. Tasa de interés del 2.0% mensual.
$$\frac{20,753,476}{533,890}-\left[\frac{e^{36*0.02}-1}{e^{36*0.02}(e^{0.02}-1)}\right]=-10.6290$$Al aumentar la tasa el resultado se aproxima a cero
Ensayo #3. Tasa de interés del 3.0% mensual.
$$\frac{20,753,476}{533,890}-\left[\frac{e^{36*0.03}-1}{e^{36*0.03}(e^{0.03}-1)}\right]=6.0364$$Con el 3%, el resultado de la ecuación es diferente de cero, pero en esta ocasión positivo. De esta manera, podemos afirmar que la tasa de interés que verifica la igualdad, es un valor comprendido entre 2.0% y 3.0%.
Continuamos por lo tanot a realizar la tabla de interpolación y desarrollar la ecuación de proporcionalidad para hallar la tasa indicada, que por la condición de tiempo de la cutoa fija, es mensual. Ver la siguiente Figura 1.26
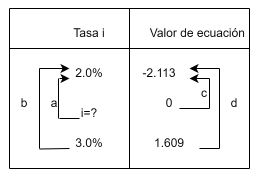
Los valores de la ecuación de proporcionalidad son:
$a=i-0.02$
$b=0.03-0.02=0.01$
$c=0-(-2.113)=2.113$
$d=1.609-(-2.113)=3.722$
Por tal razón:
$$\frac{i-0.02}{0.01}=\frac{2.113}{3.722}$$ $$i=0.56768*0.01+0.02=0.0257$$La tasa de interés estimada es 2.57% mensual y equivale a una $J=31.81$% anual continuo, resultado aproximado a su verdadero valor.
₪ El valor futuro con capitalización continua.
Aprovechando los resultados ya desarrollados sobre la capitalización continua, fácilmente logramos determinar la ecuación para calcular el valor futuro de la anualidad. El procedimiento es como a continuación se presenta.
Dado que:
$$F=Pe^{nJ}$$Y como ya sabemos:
$$P=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]$$Entonces:
$$F=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]\ e^{nJ}$$ $$F=A\left[\frac{(e^{nJ}-1)e^{nJ}}{e^{nJ}(e^J-1)}\right]$$Cancelando $e^{nJ}$, concluimos que:
$$F=A\left[\frac{e^{nJ}-1}{e^J-1}\right](1.27)$$Y de (1.27), la ecuación para la anualidad es:
$$A=F\left[\frac{e^J-1}{e^{nJ}-1}\right]\ (1.28)$$Ejercicio 1.25. El cálculo del valor futuro capitalización continua. Además de los aportes obligatorios al fondo privado de pensiones por nómina, usted se propone realizar un ahorro voluntario de 500,000 pesos mensuales durante los próximos 25 años que le faltan para cumplir la edad de retiro según la ley. Si la expectativa de rendimiento de los ahorros es 5% nominal anual continuo ¿Cuánto habrá acumulado si cumple el propósito?
Solución.
$F=?$
$A=500,000$ mensuales
$J=5$% nominal anual continuo
$n=25$ años
La unidad de tiempo de las cuotas es el mes, por lo que debemos realizar cambios en las demás variables a dicha unidad. Por ello, el plazo es equivalente a 300 meses y la tasa de interés mensual es de 0.417%. Por lo tanto:
$$F=500,000\left[\frac{e^{300*0.00417}-1}{e^{0.00417}-1}\right]$$ $$F=500,000\left[\frac{2.493835046}{0.001478707}\right]=298,397,963$$Los aportes de nómina y los recursos adicionales de ahorro constituyen el monto total de capital ahorrado para la jubilación.
Ejercicio 1.26. El cálculo de la anualidad desde un valor futuro. Suponga que usted requiere disponer de 100,000 dólares dentro de diez años, por lo que se propone ahorrar una cuota fija semestral en una entidad financiera que le ofrece un 5.8% nominal anual continuo. ¿De cuánto es el ahorro semestral a realizar?
Solución.
$A=?$ semestral
$F=100,000$ dólares
$J=5.8$% nominal anual continuo, y equivale al 2.9% semestral
$n=10$ años, y es igual a 20 semestres
Por lo tanto:
$$A=100,000\left[\frac{e^{0.029}-1}{e^{10*0.029}-1}\right]$$ $$A=100,000\left[\frac{0.029424594}{0.786038431}\right]=3,743.40$$Debe ahorrar semestralmente la suma de 3,743.40 dólares durante 10 años.
El modelo para n. Desde la ecuación (1.27), tenemos:
Es igual a:
$$\frac{F}{A}\left(e^J-1\right)=e^{nJ}-1$$De esta manera:
$$\frac{F}{A}\left(e^J-1\right)+1=e^{nJ}$$Así mismo
$$\frac{F\left(e^J-1\right)+A}{A}=e^{nJ}$$ $$e^{nJ}=\left[\frac{F\left(e^J-1\right)+A}{A}\right]$$Tomando logaritmo natural a ambos lados de la igualdad
$${ln(e}^{nJ})=ln\left[\frac{F\left(e^J-1\right)+A}{A}\right]$$O sea:
$$nJ=ln\left[\frac{F\left(e^J-1\right)+A}{A}\right]$$En consecuencia:
$$n=\frac{ln\left[\frac{F\left(e^J-1\right)+A}{A}\right]}{J} (1.29)$$y es igual a:
$$n=\frac{ln\left[F\left(e^J-1\right)+A\right]-ln\left[A\right]}{J}(1.30)$$Veamos un ejemplo.
Ejercicio 1.27. El cálculo de número de pagos desde un valor futuro. Una persona desea ahorrar la suma de 8,230,552 pesos anuales para comprar de contado un activo por valor de 500,000,000 de pesos. Si la tasa nominal de interés es de 10% anual capitalizable continuamente, ¿Cuánto tiempo necesitará?
Solución.
$n=?$ años
$F=500,000,000$ pesos
$A=8,230,552$ anuales
$J=10.0$% nominal anual continuo.
Con la ecuación (1.30), tenemos:
$$n=\frac{ln\left[500,000,000\left(e^{0.10}-1\right)+8,230,552\right]-ln\left[8,230,552\right]}{0.10}$$Necesita de 20 años. También podemos responder diciendo que requiere ahorrar 20 cuotas fijas anuales de 8,230,552 pesos.
Para terminar, ya el lector identifica que para hallar la tasa de interés se debe proceder con interpolación lineal. Para ello, igualamos a cero la ecuación (1.27), así:
$$F-A\left[\frac{e^{nJ}-1}{e^J-1}\right]=0$$O también como:
$$\frac{F}{A}-\frac{e^{nJ}-1}{e^J-1}=0$$Procedemos a desarrollar los modelos que permitan manejar los flujos de cajas diferidos, como los casos representados en las figuras 1.10, 1.13, 1.14, y 1.16, pero en esta ocasión con capitalización continua. En términos de procedimientos, son iguales a los modelos ya tratados, en cuanto ahora solo se modifica la modalidad capitalización.
Apoyados en la Figura 1.15 y con lo estudiado para el caso de anualidades diferidas con capitalización vencida, procedemos a presentar la fórmula para el caso continuo, resultado de los dos mismos pasos allí dados, para el cálculo de los valores presentes y futuros.
Invitando al lector a realizar las demostracione, el valor presente se determina como:
$$P=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]\left[\frac{1}{e^{nJ}}\right](1.31)$$Y para el valor futuro, tenemos:
$$F=A\left[\frac{e^{nJ}-1}{e^J-1}\right]e^{Jn}(1.32)$$Debemos tener de presente las mismas observaciones sobre los valores del exponente $n$ al aplicar las fórmulas.
Como ejercicios calculemos los valores presente y futuro de la Figura 1.10. Estos son:
El valor presente.
Obsérvese los exponentes $n$, con valores de 9 y 3.
$$P=335,500\left[\frac{0.28659604}{0.03653378}\right]\left[0.91943126\right]=2,419,844$$El valor futuro.
Resultado ubicado en la $ff=15$.
Para constatar que este valor es correcto, vamos a hallar el valor futuro de 2,419,844 del primer resultado. Éste es:
$$F=2,419,844e^{15*0.028}=3,682,909,96$$Obtenemos el mismo valor futuro, hecho que se explica por el manejo del dinero a valor equivalente.
₪ Las fórmulas para calcular la serie uniforme diferida.
Análogo a la capitalización vencida, la serie uniforme diferida de un valor presente, se calcula con el siguiente modelo:
$$A=Pe^{nJ}\left[\frac{e^{nJ}(e^J-1)\ }{e^{nJ}-1}\right](1.33)$$El primer componente de la ecuación (1.33), $Pe^{nJ}$, permite actualizar el monto del capital al cargar los intereses del período de gracia. En términos del diagrama de caja, ubica el valor actualizado un período antes del inicio del derrame de las anualidades. Con la segunda parte de la misma ecuación (1.33) se realiza el cálculo de la $A$.
Para el cálculo de la serie uniforme diferida desde un valor futuro, el modelo es:
$$A=F\frac{1}{e^{nJ}}\left[\frac{e^J-1}{e^{nJ}-1}\right]\ (1.34.)$$Y es igual a:
$$A=Fe^{-nJ}\left[\frac{e^J-1}{e^{nJ}-1}\right]\ (1.34.1)$$Los dos siguientes ejercicios ilustran sus aplicaciones.
Ejercicio 1.28. El cálculo de la serie uniforme diferida desde un valor presente. En el concesionario Speed-Time, la señora K.J.Londoño acaba de adquirir un vehículo de alta gama por valor de 350 millones de pesos, dando de contado la suma de 50 millones de pesos. Ella se compromete además a cancelar diez cuotas iguales semestrales, pero solicita un período de gracias en capital e intereses de dos años. Si la tasa de interés pactada es del 10% nominal anual continua, ¿Cuánto debe cancelar cada semestre para cumplir el acuerdo de pago?
Solución.
$A=?$
Valor vehículo=$350,000,000$ de pesos
Cuota inicial=$50,000,000$ de pesos
$P=300,000,000$ de pesos, capital neto financiado
$J=10.0$% nominal anual continuo, y equivale a 5% semestral
Período de gracias$= 2$ años, igual a cuatro semestres
Número de cuotas$= 10$ semestrales.
En la siguiente Figura 1.27 se presenta el diagrama del problema. En la $ff=0$ tenemos una entrada representada por el valor del vehículo y una salida por pago de contado. El resultado neto (entrada -salida) es la deuda de la señora Londoño por 300 millones, monto a cancelar por medio de 10 cuotas fijas diferidas.
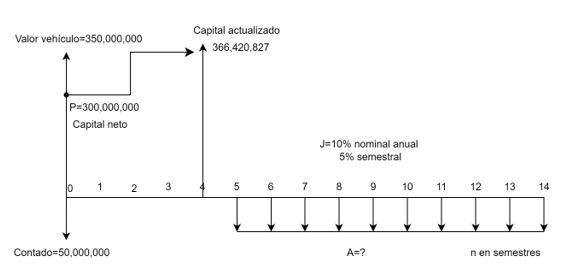
Procedemos a resolver el ejercicio en dos pasos para luego aplicar la ecuación (1.33) en su solución. Veamos:
Paso #1. Actualización de la deuda (como valor futuro del capital neto)
$$P=300,000,000e^{4*0.05}=366,420,827$$Se capitaliza continuamente durante cuatro semestres ( los 2 años de gracia), ubicando la deuda actualizada de la señora Londoño, un lugar a la izquierda de la primera $A$, que está en ff=5.
Paso #2. Hallar la anualidad. Se aplica el capital neto actualizado.
$$A=366,420,827\left[\frac{e^{10*0.05}(e^{0.05}-1)\ }{e^{10*0.05}-1}\right]=47,746,535$$En este segundo paso aplicamos $n=10$, por ser el total de cuotas acordadas. En total, el problema se ejecuta en 14 semestres, 7 años y diez pagos semestrales.
Identificando los dos valores para $n=$, con (1.33), la aplicación es:
$$A=300,000,000e^{4*0.05}\left[\frac{e^{10*0.05}(e^{0.05}-1)\ }{e^{10*0.05}-1}\right]=47,746,535$$Ejercicio 1.29. El cálculo de la serie uniforme diferida desde un valor futuro. En un proyecto de refinería de petróleo el gerente se comprometió a cancelar la suma de 500 millones de dólares en quince años. Con el propósito de cumplir la palabra empeñada, el gerente decide realizar un ahorro anual fijo por once años, que garantice acumular el monto adeudado al final del plazo. Si los ahorros anuales inician en el segundo año de operación del proyecto, determine el moto de éstos suponiendo como costo de oportunidad el 12.5% n.a. capitalizable de forma continua
Solución.
$A=?$ ahorro anual
$F=500$ millones de dólares
$J=12.5$% nominal anual continua
Número de cuotas iguales$= 11$ ($n=11$ años)
El futuro está diferido respecto a la última anualidad en tres años ($n=3$).
Tenemos identificadas dos valores de $n$ que podemos leer fácilmente en la siguiente Figura 1.28, que es la representación del problema.
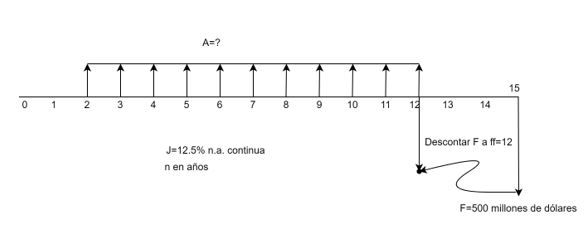
Resolvamos el ejercicio en dos pasos y luego con la ecuación (1.34.1)
Paso #1. Descuento del valor futuro. Debemos trasladar a valor equivalente, el monto de 500 millones de dólares de la $ff=15$ a la ff=12, lugar donde se realiza el último ahorro fijo (donde se ubica la última $A$), para ello $n=3$.
$$F=500,000,000e^{-3*0.125}=343,644,639.40$$Paso #2. Hallar la anualidad utilizando el monto futuro descontado. Para este segundo paso $n=11$, la cantidad de cuotas fijas a ahorrar.
$$A=343,644,639.40\left[\frac{e^{0.125}-1}{e^{11*0.125}-1}\right]=15,483,778$$De forma directa, con (1.34.1) tenemos:
$$A=500,000,000e^{-3*0.125}\left[\frac{e^{0.125}-1}{e^{11*0.125}-1}\right]=15,483,778\ $$Tratemos ahora de las anualidades perpetuas con capitalización continua. Como ya se indicó anteriormente, la característica básica consiste en que $n\rightarrow\infty$.
Para obtener el modelo correspondiente, partamos de la ecuación (1.24). $$P=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]$$
Siendo igual a:
$$P=\frac{A}{(e^J-1)}\left[\frac{e^{nJ}-1}{e^{nJ}}\right]$$Aplicando la propiedad distributiva:
$$P=\frac{A}{(e^J-1)}\left[\frac{e^{nJ}}{e^{nJ}}-\frac{1}{e^{nJ}}\right]$$Nos da:
$$P=\frac{A}{(e^J-1)}\left[1-\frac{1}{e^{nJ}}\right]$$Ahora bien, si $n\rightarrow\infty$, entonces la expresión del corchete $\frac{1}{e^{nJ}}\rightarrow0$ (tiende a cero). En consecuencia:
$$P=\frac{A}{(e^J-1)}\left[1-0\right]$$Es decir:
La ecuación (1.35) nos da el valor presente de una serie uniforme perpetua bajo capitalización continua. Si despejamos $A$, tenemos la ecuación para hallar la serie perpetua; ésta es:
$$A=P(e^J-1) (1.36)$$Del Vol. 1, capítulo 4, de este libro, el lector recordará que $e^J-1$ es la tasa de interés efectiva continua, que simbolizamos con $ie$. Es decir:
$$ie=e^J-1$$Podemos entonces concluir para las ecuaciones (1.35) y (1.36) que:
$$P=\frac{A}{ie} (1.35.1)$$ $$A=P*ie.\ (1.36.1)$$En 1.36.1, ininterrumpidamente se recibe los intereses sobre un capital.
Ejercicio 1.30. Valor presente de renta perpetua. Luego de un detallado estudio financiero, los socios de una compañía de base tecnológica concluyeron que ésta tiene el potencial de generar flujo de caja, y después de impuestos, por la suma de un millón de dólares anuales a perpetuidad.
Si el costo de oportunidad para la compañía es de 7.6% efectivo anual, ¿Qué valor tiene la empresa hoy?
Solución.
Este es un ejercicio simplificado sobre la valoración de empresas. Con el ejercicio solo se pretende aplicar la ecuación (1.35.1) en la determinación de un valor aproximado de la compañía, basados en la capacidad de generar flujo de caja o movimiento neto de efectivo para los socios.
$P=?$ El valor o precio de venta de la compañía
$A=1,000,000$ de dólares anuales
$ie=7.6$% efectiva anual continua
La compañía tiene un valor actual de $13,157,895 dólares.
Ejercicio 1.31. Estimación de la renta vitalicia. Se adquiere un local en zona franca con el fin de generar renta vitalicia por medio de su alquiler. En su adquisición se invierten 5,000 millones de pesos y el propietario exige como rendimiento mínimo el 0.95% mensual.
¿A cuánto asciende la renta perpetua mensual a la que se aspira alquilar el bien?
Solución.
$A=?$
$P=5,000$ millones de pesos
$ie=0.95$% mensual
El rendimiento mínimo deseado equivale a la suma de 47,500,000 pesos mensuales.
Para mantener por lo menos el poder adquisitivo constante de la renta fija vitalicia, se debe desarrollar acciones de reinversión que permita neutralizar los efectos de la inflación. Para ello, las reinversiones pueden partir de un parámetro de referencia como la tasa efectiva real.
Continuamos ahora con el estudio de las anualidades anticipadas (el pago $A$ es anticipado, al inicio del período) bajo capitalización continua. Para este propósito resultan útiles las Figuras 1.20 y 1.21.
El procedimiento es análogo al realizado en la sección 1.1.4 bajo capitalización vencida, en método y modelación matemática.
En tal sentido, y desde la Figura 1.20, el valor presente de la serie uniforme anticipada lo determinamos como:
$$P=A+A\left[\frac{e^{J(n-1)}-1}{e^{J(n-1)}(e^J-1)}\right](1.37)$$Ecuación que es análoga a (1.15). Procedamos a tomar factor común $A$.
$$P=A\left[1+\frac{e^{J(n-1)}-1}{e^{J(n-1)}(e^J-1)}\right](1.38)$$Ecuación semejante a (1.16). Realizando la suma del corchete tenemos:
$$P=A\left[\frac{e^{J(n-1)}(e^J-1)+e^{J(n-1)}-1}{e^{J(n-1)}(e^J-1)}\right]$$Tomando como factor común a $e^{J(n-1)}$, en el corchete, nos da:
$$P=A\left[\frac{e^{J(n-1)}(e^J-1+1)-1}{e^{J(n-1)}(e^J-1)}\right]$$Esto es:
$$P=A\left[\frac{e^{J(n-1)}(e^J)-1}{e^{J(n-1)}(e^J-1)}\right]$$En el numerador del corchete aplicamos propiedad de exponentes:
$$P=A\left[\frac{e^{J(n-1)+J}-1}{e^{J(n-1)}(e^J-1)}\right]$$Resultando:
O sea:
$$P=A\left[\frac{e^{Jn}-1}{e^{J(n-1)}(e^J-1)}\right](1.39)$$Siendo éste el resultado por el método 1. Ahora bien, para el método 2, tenemos que:
$$P=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)}\right]\ast e^J$$Ecuación análoga a (1.18). Procediendo algebraicamente tenemos:
$$P=A\left[\frac{e^{nJ}-1}{e^{nJ}(e^J-1)e^{-J}}\right]$$ $$P=A\left[\frac{e^{nJ}-1}{e^{nJ}e^{-J}(e^J-1)}\right]$$ $$P=A\left[\frac{e^{nJ}-1}{e^{nJ-J}(e^J-1)}\right]$$Para finalmente llegar a la misma ecuación (1.39)
$$P=A\left[\frac{e^{nJ}-1}{e^{J(n-1)}(e^J-1)}\right]$$Desde esta ecuación (1.39) es expedita la fórmula para la serie uniforme $A$. Ésta se determina como:
Ejercicio 1.32. Valor presente serie uniforme anticipada con capitalización continua. Resolver el ejercicio 1.14 bajo capitalización continua y comparar los resultados, incluyendo el cálculo de las respectivas tasas de interés efectivas.
Solución.
$P=?$
$ie=?$ caso vencido
$ie=?$ caso continuo
$A=6,425,103$
$n=60$ meses
$i=1.3$% mes
Con (1.39), tenemos:
$$P=6,425,103\left[\frac{e^{0.013*60}-1}{e^{0.013*(60-1)}(e^{0.013}-1)}\right]$$ $$P=6,425,103\left[41.93245977\right]=269,420,373$$El vehículo de contado tiene un valor de 269,420,373 pesos, monto inferior al caso de capitalización vencida en $579,627.
¿Por qué de contado es más barato por capitalización contínua? Antes de dar una respuesta a esta inquietud, obtengamos las tasas de interés efectivas anuales.
$$ie=\left(1+0.013\right)^{12}-1=0.1677$$ $$ie=e^{0.013*12}-1=0.1688$$La tasa de interés efectiva anual con capitalización vencida es del 16.77% y la tasa efectiva anual continua de 16.88%; la tasa de interés continua es mayor a la vencida. Por lo tanto, al descontar las cuotas fijas anticipadas con una tasa de interés mayor, que es el caso de la continua comparado con el vencido, el resultado es un valor presente más pequeño, ceteris paribus. Los datos son los mismos, solo se ha cambiado la modalidad de capitalización, de vencida a continua.
Ejercicio 1.33. Serie uniforme anticipada desde un valor presente y capitalización continua. Una aplicación algo extraña. Una comunidad aborigen posee hoy un capital productivo representado en una población de 522 cerdos (500 cerdas y 22 cerdos), en una relación de 22.7 cerdas por macho. De este capital esperan alimentar a toda la comunidad durante 15 años, partiendo de que la tasa neta de reproducción de los cerdos (es decir, restando a los nacimientos las muertes) es de 30.5% nominal anual continuo. Si la anterior es la realidad de la comunidad aborigen, ¿cuántos cerdos podrán sacrificar cada año iniciando hoy mismo?
Solución.
$A=?$anual
$J=30.5$% anual
$P=522$
$n=15$ años
Con (1.40), tenemos:
$$A=522\left[\frac{e^{0.30(15-1)}(e^{0.30}-1)}{e^{0.30*15}-1}\right]$$ $$A=522\left[0.26057467\right]=136$$La comunidad aborigen puede consumir 136 cerdos iniciando hoy mismo y por 14 años más.
₪ La situación para $n$, el número de cuotas.
Supongamos ahora que el líder de la comunidad aborigen considera la posibilidad de consumir la cantidad de 150 cerdos anuales. Con el capital representado en la población inicial de cerdos, desea saber en cuántos años se agota el inventario inicial, si se mantiene la misma tasa de crecimiento neto
Para responder la inquietud debemos desarrollar un modelo para el cálculo del número de cuotas. De (1.39) procedemos a despejar $n$.
$$P=A\left[\frac{e^{nJ}-1}{e^{J(n-1)}(e^J-1)}\right]$$Y es igual a:
De igual manera:
$$\frac{P(e^J-1)}{A}=\frac{e^{nJ}}{e^{J(n-1)}}-\frac{1}{e^{J(n-1)}}$$Desde propiedades de exponentes, tenemos:
$$\frac{P\left(e^J-1\right)}{A}=e^{nJ}\ast e^{-nJ+J}-\frac{1}{e^{nJ}e^{-J}}$$Que simplificando es:
$$\frac{P\left(e^J-1\right)}{A}=e^J-\frac{e^J}{e^{nJ}}$$ $$\frac{P\left(e^J-1\right)}{A}-e^J=-\frac{e^J}{e^{nJ}}$$Realizando la resta del lado derecho de la igualdad resulta:
$$\frac{P\left(e^J-1\right)-Ae^J}{A}=-\frac{e^J}{e^{nJ}}$$Pasando $e^J$ a dividir:
$$\frac{P\left(e^J-1\right)-Ae^J}{Ae^J}=-\frac{1}{e^{nJ}}$$Ahora, multiplicando por $-1$ y reordenando la ecuación, tenemos que:
Tomando logaritmo natural a ambos lados de la igualdad:
$$\ln{(e^{Jn})}=\ln{\left[\frac{Ae^J}{Ae^J-P(e^J-1)}\right]}$$Operando desde las propiedades de los logaritmos, tenemos:
$$nJ=\ln{\left[\frac{Ae^J}{Ae^J-P(e^J-1)}\right]}$$ $$nJ=ln\left(Ae^J\right)-\ln{\left[Ae^J-P\left(e^J-1\right)\right]}$$Para finalmente tener:
$$n=\frac{ln(Ae^J)-\ln{\left[Ae^J-P(e^J-1)\right]}}{J}(1.41)$$La solución para el lider de la comunidad aborigen es:
$$n=\frac{ln(150e^{0.305})-\ln{\left[150e^{0.305}-522(e^{0.305}-1)\right]}}{0.305}$$ $$n=\frac{ln(203.49)-\ln{\left[17.34\right]}}{0.305}$$ $$n=\frac{5.31563529-2.85275636}{0.305}=8.08$$Los cerdos alcanzan para 8 años. ¿Cómo entender el consumo anticipado en este caso? puede ser como sacrificio acelerado de cerdos al inicio del año y conservación del alimento bajo alguna técnica (secado al sol, ahumado, salazón).
Dado que el método para calcular la tasa de interés $J$ es por interpolación lineal (con ensayo y error) ya trabajado, procedemos a obtener la ecuación para el futuro de la anualidad anticipada bajo capitalización continua. En esta labor acudimos a resultados ya alcanzados. Veamos entonces el procedimiento.
Sabemos que:
$$F=Pe^{nJ}$$ $$P=A\left[\frac{e^{nJ}-1}{e^{J(n-1)}(e^J-1)}\right]$$Reemplazando la segunda ecuación en la primera:
$$F=A\left[\frac{e^{nJ}-1}{e^{J(n-1)}(e^J-1)}\right]e^{nJ}$$Y ya podemos continuar con la simplificación de la expresión.
$$F=A\left[\frac{e^{nJ}-1}{e^{Jn}e^{-J}(e^J-1)}\right]e^{nJ}$$Cancelando $e^{nJ}$
$$F=A\left[\frac{e^{nJ}-1}{e^{-J}(e^J-1)}\right]$$En consecuencia:
$$F=A\left[\frac{e^J(e^{nJ}-1)}{(e^J-1)}\right](1.42)$$Y de (1.42) se despeja $A$ para el cálculo de la serie uniforme anticipada de un valor futuro con capitalización continua. Veamos:
$$A=F\left[\frac{(e^J-1)}{e^J(e^{nJ}-1)}\right](1.43)$$Ejercicio 1.34. Futuro de anualidad anticipada y capitalización continua. Hallar el valor de $F$ de la Figura 1.29
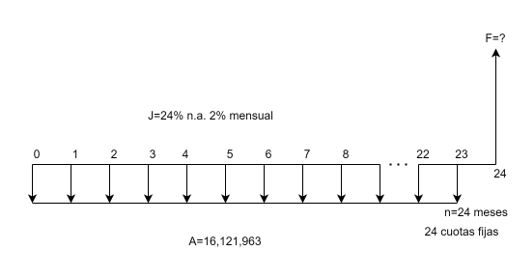
Solución. Aplicando directamente la ecuación , tenemos:
Ejercicio 1.35. Serie uniforme anticipada desde un valor futuro y capitalización continua. Una empresa desea acumular activos fijos por 4,500,000 dólares en 36 años. Si el costo de oportunidad de la compañía es del J=8.5% continuo ¿Cuánto debe invertir anualmente, iniciando hoy mismo, para lograr la meta de acumulación de activos?
Solución. Ver la Figura 1.30
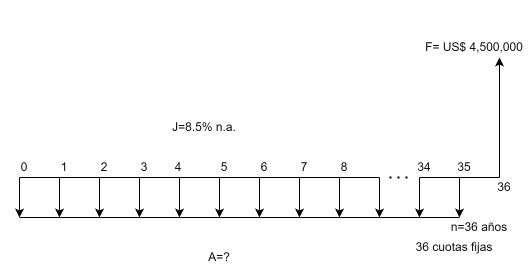
El ahorro anual es de 18,039.29 dólares.
Ahora de nuevo la fórmula para n. Partiendo de (1.42) tenemos:
Y esta última es igual a:
$$\frac{F{(e}^J-1)}{Ae^J}=e^{nJ}-1$$Pasando el 1 a sumar al lado izquierdo de la igualdad
$$\frac{F{(e}^J-1)}{Ae^J}+1=e^{nJ}$$Realizando la suma y reordenando la ecuación:
$$e^{nJ}=\frac{F{(e}^J-1)+Ae^J}{Ae^J}$$Aplicamos logaritmo a ambos lados de la igualdad, resulta:
$$nJ=ln\left[\frac{F{(e}^J-1)+Ae^J}{Ae^J}\right]$$Así entonces:
$$n=\frac{ln\left[F(e^J-1)+Ae^J\right]-ln\left[Ae^J\right]}{J}(1.44)$$Como ejercicios vamos a constatar que el resultado anterior para $A$ es correcto, asumiendo su valor como dato y a $n$ como la incógnita.
De esta manera tenemos la ventaja de conocer la respuesta. En el ejercicio 1.35, $n=36$ años.
Solución.
$F=4,500,000$
$A=18,039.29$
$J=8.5$% nominal anual
$n=?$
Como la tasa de interés es anual, $n$ es 36 años.
Continuamos el estudio de las series uniformes desde la óptica de la capitalización anticipada. Este tema es más una curiosidad teórica, producto de las posibilidades que genera el razonamiento conceptual (y por ello su estudio es opcional), que una presentación de modelos con amplia aplicación en los mercados financieros. Es una curiosidad académica, producto de la imaginación y el deseo de conjeturar combinaciones.
Dado este carácter, trabajamos solo las anualidades vencidas y las anualidades anticipadas, bajo la capitalización continua. El estudiante podrá intentar la modelación para los casos de anualidades diferidas y perpetuas aplicando el mismo raciocinio de las modalidades anteriores.
Recurramos de nuevo a la Figura 1.1, representación de una serie uniforme vencida. El asunto ahora es derivar los modelos matemáticos, las ecuaciones, para determinar los valores presente y futuro de dicha serie ahora con capitalización anticipada.
Ya estudiamos en el volumen uno la forma de calcular el valor futuro pago único de un valor presente con capitalización anticipada. Es:
$$F=P\left(\frac{1}{1-ia}\right)^n$$ $$F=P\left(1-ia\right)^{-n}$$Recordando que la tasa periódica de interés anticipada es $ia=\frac{J}{k}$. Así mismo, estudiamos que el valor presente de un monto futuro con capitalización anticipada, se determina como:
$$P=\frac{F}{\left(1-ia\right)^{-n}}$$ $$P=F\left(1-i_a\right)^n$$Para el valor presente, $P$ en $ff=0$, cada una de las $A$ de la figura 1.1 las tratamos como un valor futuro que descontamos al presente; utilizamos $P=F\left(1-i_a\right)^n$, con $F=A$.
Por ello, ahora tenemos:
$$P=A\left(1-ia\right)+A\left(1-ia\right)^2+\ldots+A\left(1-ia\right)^{n-1}+A\left(1-ia\right)^n (a)$$La ecuación (a) es la suma de n términos en progresión geométrica que tiene como razón común ($1-ia$). Por ello procedemos a multiplicarla por esta razón común para obtener la siguiente expresión matemática (b):
Restando $(a)-(b)$: $$P-P\left(1-ia\right)=A(1-ia)-A\left(1-ia\right)^{n+1}$$
Esto es:
$$P-P+P\ast ia=A\left(1-ia\right)-A\left(1-ia\right)^{n+1}$$ $$P\ast ia=A(1-ia)-A\left(1-ia\right)^{n+1}$$Tomando factor común $A$:
$$P\ast ia=A\left[(1-ia)-\left(1-ia\right)^{n+1}\right]$$En consecuencia:
$$P=A\left[\frac{(1-ia)-\left(1-ia\right)^{n+1}}{ia}\right](1.45)$$De nuevo, el valor $P$ calculado se ubica en el diagrama de caja un lugar a la izquierda de donde se halla la primera $A$, que en caso convencional está en $ff=1$. Veamos un ejemplo.
Ejercicio 1.36. Valor presente de anualidad vencida con capitalización anticipada. En el caso del ejercicio 1.1, suponga ahora que el costo de oportunidad del arrendador es el mismo 1.3% mensual, pero en esta ocasión de forma anticipada. ¿Cuánto debe cancelar de contado el arrendatario Cardeño?
Solución.
$P=?$
$A$= 1,500,000 pesos mensuales
$n$= 6 meses
$ia$=1.3% mensual
Bajo esta nueva condición el arrendatario paga de contado la suma de $8,599,258 y se ahorra, respecto a la forma vencida, la suma de 5,033 pesos (¿por qué ocurre este ahorro?).
Cambiemos de escenario y preguntemos qué tasa de interés periódica vencida es equivalente a esta tasa periódica anticipada.
Recordemos que $iv=ia/(1-ia)$. Desde esta ecuación, la tasa periódica vencida equivalente es:
$$iv=0.013/(1-0.013)=0.13171226=1.317$$la tasa de interés mes vencido equivalente es de 1.317%. Con esta tasa equivalente procedemos hallar el valor de contado a pagar por el arrendatario bajo capitalización vencida. Utilizando el modelo (1.4) el resultado es:
$$P=1,500,000\left[\frac{{(1+0.013171226)}^6-1}{{(1+0.013171226)}^6*0.013171226}\right]$$ $$P=1,500,000\left[5.7328\right]=8,599,258$$ Al ser la $ia$ del $1.3$% equivalente a $iv$ del $1.317$%, esta última debe arrojar igual valor económico al realizarse el cálculo de $P$ con capitalización vencida, como en efecto sucede. He aquí de nuevo ilustrado el concepto financiero de equivalencia.Recordemos además que en la equivalencia, las tasas efectivas deben ser iguales. Veamos si se cumple esta condición:
Tasa efectiva anticipada.
>Tasa efectiva vencida.
Ambas tasas son del 17% efectiva anual.
La equivalencia la podemos extender al caso continuo. Lo primero que vamos a realizar es hallar una tasa nominal anual continua equivalente a la efectiva anual del 17%. Para ello tenemos:
$$J=ln(1+0.17)=0.15700375$$Por lo tanto para el mes, la tasa es de 1.308% (en el cálculo de $P$ se incluyen más cifras decimales para mayor exactitud en el resultado).
Obtengamos ahora el valor de contado a cancelar por el arrendatario Cardeño bajo capitalización continua. Con el modelo (1.24), éste es:
$$P=1,500,000\left[\frac{e^{6*0.01308365}-1}{e^{6*0.01308365}(e^{0.01308365}-1)}\right]$$ $$P=1,500,000\left[\frac{0.08166538}{0.01424511}\right]$$ $$P=1,500,000\left[5.7328\right]=8,599,258$$Obtenemos de nuevo igual valor a pagar de contado.
Por lo tanto, el concepto de equivalencia nos permite expresar las condiciones de una operación financiera en términos de otras condiciones, obteniendo igual valor económico. Esto se refiere no solo a las modalidades de capitalización.
₪ La ecuación para la serie $A$.
De (1.45), tenemos:
$$A=P\left[\frac{ia}{(1-ia)-\left(1-ia\right)^{n+1}}\right] (1.46)$$
Ejercicio 1.37. Anualidad vencida con capitalización anticipada. Un emprendimiento de economía campesina requiere de financiación por 150,000,000 de pesos para la adquisición de maquinaria y equipos con el fin de producir y comercializar leche y ganado cebado, basado en ganado vacunos de doble propósito. La empresa Agro-Técnico acepta suministrar los requerimientos del emprendimiento, por medio del pago de una cuota fija semestral vencida, al 0.8% de interés mes anticipado y un plazo de quince años. Hallar la cuota a cancelar.
Solución.
$A=?$
$P$= 150,000,000 de pesos
$n$= 15 años, 30 semestres
$ia$=0.8% mensual
La tasa de interés semestral anticipada, necesaria para hallar la cuota semestral fija vencida, es:
$${\rm ia}_{semestre}=\left(\frac{1}{1-0.008}\right)^6-1=0.049373$$La tasa de interés $ia=0.8$% mes anticipado equivale a $ia=4.937$% semestre anticipado. Se aplicó el caso de efectiva menor a efectiva mayor y la fórmula para tasas de interés anticipadas.
Con (1.46) la cuota es:
El emprendimiento debe cancelar 30 cuotas iguales vencidas de $9,974,278.20 cada semestre al 4.937% semestre anticipado.
Proponemos al lector calcular la tasa de interés semestral vencida equivalente a la tasa de interés semestre anticipada de 4.937% y hallar la cuota fija semestre vencido. Constatar que el resultado de $A$ es el mismo.
De igual manera puede proceder para el caso de $A$ por capitalización continua.
₪ La ecuación para el plazo $n$.
Desde:
$$P=A\left[\frac{(1-ia)-\left(1-ia\right)^{n+1}}{ia}\right]$$ $$P=\frac{A}{ia}\left[(1-ia)-\left(1-ia\right)^{n+1}\right]$$Y es igual a:
$$\frac{P\ast i a}{A}=(1-ia)-\left(1-ia\right)^{n+1}$$Multiplicando por -1:
$$\frac{A\ (1-ia)-P\ast i a}{A}=\left(1-ia\right)^{n+1}$$Reordenando y tomando logaritmo natural en ambos lados de la expresión resulta:
$$ln\left(1-ia\right)^{n+1}=ln\left[\frac{A\ (1-ia)-P\ast i a}{A}\right]$$Es decir:
$$(n+1)ln(1-ia)=ln\left[\frac{A\ (1-ia)-P\ast i a}{A}\right]$$Por lo tanto, para $n$ tenemos:
$$n=\frac{ln\left[\frac{A\ (1-ia)-P\ast i a}{A}\right]}{ln(1-ia)}-1 (1.47)$$O también:
$$n=\frac{ln\left[A\ (1-ia)-P\ast i a\right]-ln\left[A\right]}{ln(1-ia)}-1 (1.47.1)$$Veamos a continuación un ejemplo para su aplicación.
Ejercicio 1.38. Cálculo de $n$ en Anualidad vencida con capitalización anticipada. Con los datos del ejercicio 1.3, suponga ahora que las cuotas fijas vencidas semestrales son bajo interés anticipado. Hallar $n$ y el plazo en años.
Solución.
$n=?$
$P= 23,245,300$ de pesos
$A= 3,709,358.20$
$ie=20.0$% E.A.
La tasa de interés del 20% E.A., equivale a una tasa de interés semestre anticipado de 8.71%. En consecuencia $n$ es igual a:
$$n=\frac{ln\left[\frac{3,709,358\ (1-0.087129)-23,245,300\ast0.087129}{3,709,258}\right]}{ln(1-0.087129)}-1$$ $$n=\frac{ln\left[\frac{1,360,823.88}{3,709,258}\right]}{ln(0.91287093)}-1$$ $$n=\frac{ln\left[0.366862\right]}{ln(0.91287093)}-1$$ $$n=\frac{-1.002768562}{-0.091160778}-1=10$$Se cancelan 10 cuotas iguales semestrales, para un total de 5 años. La respuesta es la misma que en el ejercicio original porque hemos utilizado una tasa de interés semestral anticipada equivalente a la semestral vencida.
La tasa de interés. Solución por interpolación lineal.
Ejercicio 1.39. Cálculo de la tasa de interés en Anualidad vencida con capitalización anticipada. Con una inversión inicial de 1,000 millones de dólares, una compañía carbonífera ha generado un proceso de explotación constante de carbón mineral en los últimos quince años, que le han implicado ingresos semestrales vencidos de 80 millones de dólares. Dada esta condición, la gerencia de la compañía se pregunta ¿qué tasa de rendimiento nominal y efectiva anual, semestre anticipado, está rindiendo la compañía?
Solución.
$J=?$ s.a.
$ie=?$ E.A.
$P= 1,000$ millones de dólares
$A= 80$ millones de dólares semestrales
$n=15$ años e igual a $30$ semestres
Para responder las dos preguntas de tasas de interés, es necesario previamente hallar la tasa periódica $ia$ semestre anticipado. En la solución aplicamos el modelo (1.45) igualado a cero. Es decir:
Ensayo #1. $ia=3.0$%
$$1,000-80\left[\frac{\left(1-0.03\right)-\left(1-0.03\right)^{30+1}}{0.03}\right]=-549.395 <0$$Ensayo #2. $ia=5.0$%
$$1,000-80\left[\frac{\left(1-0.05\right)-\left(1-0.05\right)^{30+1}}{0.05}\right]=-193.749 <0$$Ensayo #3. $ia=7.0$%
$$1,000-80\left[\frac{\left(1-0.07\right)-\left(1-0.07\right)^{30+1}}{0.07}\right]=57.636>0$$Ya tenemos un valor negativo y otro positivo para la ecuación de proporcionalidad, por ensayos con 5% y 7%, respectivamente.
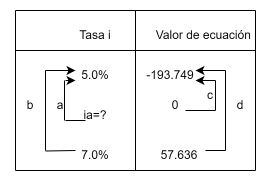
El valor de $ia$ que hace cero la ecuación está al interior de intervalo (5%,7%). Veamos la siguiente Figura 1.31.
$a=ia-0.05$
$b=0.07-0.05=0.02$
$c=0-(-193.749)$=193.749
$d=57.636-(-193.746)=251.385$
La ecuación de proporcionalidad es:
$$\frac{ia-0.05}{0.02}=\frac{193.749}{251.385}$$Por tanto, la tasa $ia$ es:
$$ia=\frac{193.749}{251.385}\ast0.02+0.05=0.0654$$Es decir, $ia=6.54$%. Con ella, la tasa nominal anual es de $13.08$% s.a. y la tasa efectiva anual de rentabilidad de $14.49$% E.A.
₪ La ecuación para el valor futuro.
Como hemos realizado en otras sesiones de este capítulo, para esta labor recurrimos a resultados obtenidos con anterioridad. En particular, sabemos que:
$$F=P\left(1-ia\right)^{-n}$$Y como el valor presente de una serie uniforme vencida con capitalización anticipada es la ecuación (1.45).
Reemplazando la ecuación (1.45) en la anterior ecuación, tenemos:
$$F={A\left[\frac{(1-ia)-\left(1-ia\right)^{n+1}}{ia}\right]\left(1-ia\right)}^{-n}$$Ecuación que es igual a:
Por lo tanto, igual a:
$$F=A\left[\frac{(1-ia)-\left(1-ia\right)^{n+1}}{{ia\left(1-ia\right)}^n}\right](1.48)$$De esta ecuación (1.48), el modelo para la serie uniforme, $A$, desde un valor futuro con capitalización anticipada es:
$$A=F\left[\frac{{ia\left(1-ia\right)}^n}{(1-ia)-\left(1-ia\right)^{n+1}}\right] (1.49)$$Desarrollemos a continuación dos ejercicios para ilustrar la aplicación de estos modelos.
Ejercicio 1.40. Cálculo del valor futuro de Anualidad vencida con capitalización anticipada. Un inmigrante accedió a un crédito de 500,000 dólares con el fin de adquirir vivienda propia en Palm Beach- Florida (USA) con el compromiso de cancelar 120 cuotas fijas vencidas mensuales de 7,208.63 dólares al 1% mes anticipado. A los cinco años de haber conseguido la propiedad, el propietario se pregunta cuál sería el precio de la casa en la eventualidad de requerir venderse una vez cancelada la deuda, determinando éste como el valor futuro equivalente a los 120 pagos fijos. Calcular dicho valor.
Solución.
$F=?$
$A= 7,208.63$ dólares mensuales
$n=120$ meses
$ia=1.0$% mensual
Para verificar que este resultado es correcto, procedamos a hallar el valor futuro del valor del crédito a 120 meses. Para ello aplicamos la fórmula de valor futuro pago único con capitalización anticipada, estudiada en el Vol. 1 de este libro.
$$F=500,000\left(\frac{1}{1-0.01}\right)^{120}$$ $$F=500,000\left(1.01010101\right)^{120}$$ $$F=500,000(3.340232123=1,670,116.10$$El precio base para negociar la casa en caso de venta es de 1,670,116.10 dólares, valor equivalente a los 500,000 dólares de hace 10 años atrás, cuando obtuvo el crédito al 1% mensual bajo modalidad de capitalización anticipada. Si se desea una ganancia adicional, el precio de venta debe ser mayor al base.
Ejercicio 1.41. Anualidad vencida desde un valor futuro con capitalización anticipada. Por circunstancias legales el inmigrante a USA debe regresar su país de origen por espacio de dos años. Decide arrendar la propiedad por cuota fija mes vencida, sin aumento entre años, con la esperanza de recaudar al cabo de los dos años la suma de 150,000 dólares. Si el costo de oportunidad es de ia=0.95% mensual, ¿De cuánto es el canon mensual del arriendo?
Solución.
$A=?$
$F= 150,000$ dólares
$n=24$ meses
$ia=0.95$% mensual
Se debe arrendar por 5,588 dólares mensuales fijos durante dos años.
El modelo para n. Desde (1.48):
Aplicamos la propiedad distributiva al lado derecho de la última igualdad, resulta
$$\frac{F\ast i a}{A}=\frac{(1-ia)}{\left(1-ia\right)^n}-\frac{\left(1-ia\right)^{n+1}}{\left(1-ia\right)^n}$$Por lo que:
$$\frac{F\ast i a}{A}=\left(1-ia\right)^{1-n}-(1-ia)$$ $$\frac{F\ast i a}{A}+(1-ia)=\left(1-ia\right)^{1-n}$$Realizando la suma al lado izquierdo de la última ecuación y aplicando propiedad de exponentes al lado derecho, tenemos:
$$\frac{F\ast i a+A(1-ia)}{A}=\frac{1}{\left(1-ia\right)^{n-1}}$$Esta última expresión es igual a:
$$\left(1-ia\right)^{n-1}=\frac{A}{F\ast i a+A(1-ia)}$$Tomando logaritmo natural a ambos lados de la igualdad:
$$(n-1)ln(1-ia)=ln\left[\frac{A}{F\ast i a+A(1-ia)}\right]$$Despejando $n$
$$n=\frac{ln\left[\frac{A\ }{F\ast i a+A(1-ia)}\right]}{ln(1-ia)}+1 (1.50)$$O también:
$$n=\frac{ln\left[A\right]-ln\left[F\ast i a+A(1-ia)\right]}{ln(1-ia)}+1 (1.50.1)$$Ejercicio 1.42. El cálculo de $n$. Una empresa manufacturera planea invertir la suma de 434,724 dólares en la adquisición de maquinaria para mejorar la eficiencia de su operación. Para tal fin, se propone realizar reserva de recursos financieros por la suma de 80,342 dólares semestrales con el fin de contar con el capital y realizar la adquisición de contado. El costo de oportunidad de la empresa es de 7.6% s.a, ¿En cuántos años puede hacer la inversión?
Solución.
$n=?$
$F= 434,724$ dólares
$A=80,342$ meses
$J=7.8$% s.a.
$ia=3.8$% semestre
El capital lo alcanza a disponer en cinco semestres, o dos años y medio (2.5 años), con ahorros semestrales de 80,342 dólares.
Siguiendo con la capitalización anticipada, entramos a estudiar las anualidades anticipadas. En esta ocasión se trata de anualidades que ocurren al inicio de un período pero gestionadas (manejadas a valor equivalente) con capitalización anticipada. De nuevo, es un desarrollo teórico, más que un tema común en los mercados de dinero y de capitales, resultado de las posibilidades que dan las variables de clasificación de las anualidades adoptadas en este libro. Además, dado el carácter académico de este libro, nos permite el planteamiento de estos modelos con libertad académica, siendo opcional para el estudiante.
Invitamos al lector a dirigirse a las Figuras 1.20, 1.22 y 1.24. Se trata ahora de la misma representación de los diagramas económicos pero manejados, gestionados, con capitalización anticipada (con la $ia$, como se observa en la siguiente Figura 1.32).
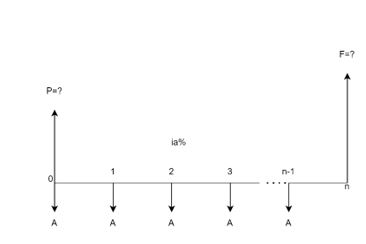
Iniciamos el estudio determinado el modelo para hallar el valor presente de la Figura 1.32. Todas las $A$, excepto las primera que ya se encuentra en la $ff=0$, debemos descontarla al presente. Para ello tenemos la siguiente expresión:
$$P=A+A\left(1-ia\right)+A\left(1-ia\right)^2+\ldots+A\left(1-ia\right)^{n-1} (a)$$La ecuación (a) tiene un derrame de $A$ desde la $ff=0$ hasta la $ff=n-1$. Es además la suma de n términos en progresión geométrica con razón común (1-ia), por ello vamos a multiplicarla por esta razón y conseguimos (b) así:
Restando (a)-(b), en la que se cancelan elementos comunes, resulta:
$$P-P\left(1-ia\right)=A-A\left(1-ia\right)^n$$Operando algebraicamente tenemos:
$$P-P+P\ast ia=\ A-A\left(1-ia\right)^n$$ $$P\ast ia=A-A\left(1-ia\right)^n$$Tomando factor común $A$.
$$P\ast ia=A\left[(1-\left(1-ia\right)^n\right]$$ $$P=A\left[\frac{1-\left(1-ia\right)^n}{ia}\right](1.51)$$ Del modelo (1.51) despejamos A, para la cuota fija anticipada bajo capitalización anticipada, como:
Así mismo, y dejando al lector la operación algebraica, la ecuación para n es:
Ejercicio 1.43. El cálculo del valor presente $P$. La compañía SUMINISTROS IA acaba de firmar un contrato para el suministro y mantenimiento al día de toda la infraestructura para los procesos informáticos y de conectividad con una empresa adscrita al gobierno municipal. ¿Cuál es el valor presente de dicho contrato si en una de sus cláusulas indica que se pagará, comenzando hoy mismo, 12 cuotas mensualesiguales de 5,245,300? La tasa de interés es de 1.0% mensual anticipado.
Solución.
$P=?$
$A=5,245,300$ mensual
$n=12$ meses y 12 cuotas
$ia=1.0$% mensual
El valor del contrato es de $59,594,543.
Ejercicio 1.44. El cálculo de la anualidad $A$. Un nuevo empresario ha realizado una inversión inicial en activos circulantes de 4.5 millones de dólares, con la esperanza de recuperarlos en cinco años por medio del ahorro de un monto fijo anticipado mensual. Si la tasa de rendimiento de proyecto es ie=20% E.A, ¿De cuánto es el valor mensual equivalente de la inversión?.
Solución.
$A=?$
$P=4,500,000$
$n=5$ años equivalentes a 60 meses
$ie=20$% E.A.
$ia=1.53$% mensual equivalente
Por tanto:
$$A=4,500,000\left[\frac{0.0153}{1-\left(1-0.0153\right)^{60}}\right]$$ $$A=4,500,000\left[\frac{0.0153}{0.60373505}\right]=114,110.68$$La inversión es equivalente a 60 cuotas fijas de 114,110.68 dólares mensuales, con el derrame de $A$ iniciando en la $ff=0$.
Invitamos al lector a deducirla ecuación para $n$. Ésta es:
O también:
$$n=\frac{ln\left[A-P\ast i a\right]-ln\left[A\right]}{ln(1-ia)} (1.54.1)$$Ejercicio 1.45. El cálculo de $n$. ¿Cuál es el valor de $n$ que hace equivalente 8,5 millones de hoy con pagos trimestrales anticipados de $589,440 al J=24% m.v? Ver Figura 1.33
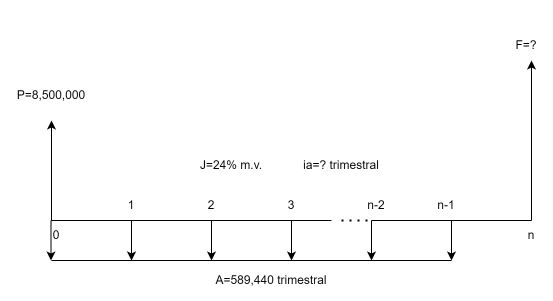
Debemos tener presente que la tasa nominal dada es mes vencido, mientras las cuotas $A$ son trimestrales. Por lo tanto, en primer lugar debemos hallar la tasa $ia$ trimestral equivalente, aplicando inicialmente el paso de nominal a efectiva y luego de efectiva mayor a efectiva menor (invitamos al lector a realizar los cálculos y constatar el resultado de 5.77% trimestre).
Solución.
$P=8,500,000$ millones
$A= 589,440$ pesos
$J=24$% m.v
$ia=5.77$% trimestre
Se requieren de 30 trimestres que son equivalentes a 7.5 años.
Ahora bien, ¿cómo podemos hallar el valor futuro de la anualidad representada en la anterior Figura 1.33? Invitamos al lector a que revise el procedimiento ejecutado en anteriores casos de valores futuros, y lo aplique en la obtención de la siguiente ecuación (1.55) para $F$.
Desde (1.55) es expedita la ecuación para la serie uniforme, ésta es:
$$A=F\left[\frac{\left(1-ia\right)^n\ast i a}{1-\left(1-ia\right)^n}\right] (1.56)$$Pasemos ahora a responder la pregunta pendiente de la Figura 1.33 sobre cuál es el valor futuro, que ubicamos gráficamente en la $ff=30$, pues el derrame anticipado de las $A$ inicia en $ff=0$ y termina en 29. El cálculo es:
$$F=589,440\left[\frac{1-\left(1-0.0577\right)^{30}}{\left(1-0.0577\right)^{30}\ast0.0577}\right]$$ $$F=589,440\left[\frac{0.83173861}{0.00970493}\right]$$ $$F=589,440\left[85.7027336\right]=50,516,639$$Para constatar si este resultado es correcto, hallemos el valor futuro del capital de 8.5 millones (el $P$); es decir:
$$F=8,500,000\left(\frac{1}{1-0.0577}\right)^{30}$$ $$F=8,500,000\left(1.06120801\right)^{30}$$ $$F=8,500,000(5.94313399)=50,516,639$$Concluimos con igual valor.
Ejercicio 1.46. El cálculo de la anualidad desde un valor futuro. Para el reemplazo de camiones de reparto, una fábrica de bebidas desea tener la suma de 2,000 mil millones de pesos en un fondo dentro de 7 años. Si la fábrica plantea realizar un ahorro uniforme mensual a partir de ahora a una tasa de interés de 18.0% m.v., hallar el monto del ahorro mensual.
Solución.
$A=?$
$F=2,000,000,000$
$n=7$ años equivalentes a 84 meses
$J=18.0$% m.v
$ia=1.478$% mensual equivalente
Para terminar este apartado nos falta tratar los temas de la tasa de interés y el plazo o número de cuotas desde un valor futuro. Procedemos a realizar la deducción de la fórmula para $n$.
Partiendo de (1.55), tenemos que.
$$F=\frac{A}{ia}\left[\frac{1-\left(1-ia\right)^n}{\left(1-ia\right)^n}\right]$$ $$\frac{F\ast i a}{A}=\left[\frac{1-\left(1-ia\right)^n}{\left(1-ia\right)^n}\right]$$Aplicando propiedad distributiva:
$$\frac{F\ast i a}{A}=\frac{1}{\left(1-ia\right)^n}-\frac{\left(1-ia\right)^n}{\left(1-ia\right)^n}$$ $$\frac{F\ast i a}{A}=\frac{1}{\left(1-ia\right)^n}-1$$ $$\frac{F\ast i a}{A}+1=\frac{1}{\left(1-ia\right)^n}$$ $$\frac{F\ast i a+A}{A}=\frac{1}{\left(1-ia\right)^n}$$Reordenando la ecuación:
$$\left(1-ia\right)^n=\frac{A}{F\ast i a+A}$$Aplicando logaritmo natural a ambos lados de la igualdad:
$$nln(1-ia)=ln\left[\frac{A}{F\ast i a+A}\right]$$ Obtenemos que:O también
$$n=\frac{ln\left[A\right]-ln\left[F\ast i a+A\right]}{ln(1-ia)} (1.57.1)$$Ejercicio 1.47. El cálculo de $n$ desde un valor futuro y anualidad. Una invención desarrollada por el departamento de I+D de una empresa de IA estima que en el mediano plazo podrá tener acumulado en utilidades netas la suma de 50 millones de dólares, por medio de diferentes esquemas de ventas de su invención. Si las utilidades netas se comportan como una anualidad anticipada de 998,625.28 dólares trimestrales gestionadas al 30% t.a. ¿En cuántos años se acumula el monto de utilidades netas?
Solución.
$n=?$
$F=50,000,000$
$A=998,625.28$ trimestrales
$J=30.0$% t.a.
$ia=7.5$% trimestral
Aplicando el modelo (1.57), los años son:
Se requieren de 20 trimestres o 5 años.
₪ La interpolación lineal para la tasa de interés.
Ejercicio 1.48. El cálculo de $ia$ desde un valor futuro y anualidad. Hallar la tasa de interés $ia$ que hace equivalente el valor futuro con el flujo de egresos representados en la siguiente Figura 1.34. Expresar además dicha tasas de interés en términos nominal y efectiva anual.
Además de serie uniforme, el diagrama incluye en $n=4$ y $n=12$ valores futuros de 5,000,000, que implica el manejo adicional de otros factores o ecuaciones.
Por lo tanto, en primer lugar planteamos la ecuación de valor para la equivalencia y luego igualamos a cero y resolvemos para $ia$
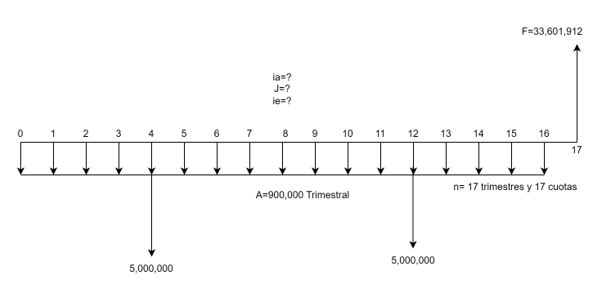
Ecuación de valor. Expresada como entradas iguales a salidas.
$33,601,912=900,000\left[\frac{1-\left(1-ia\right)^{17}}{\left(1-ia\right)^{17}}\right]+5,000,000\left(1-ia\right)^{-13}+5,000,000\left(1-ia\right)^{-5}$
Ecuación de valor igualada a cero.
$33,601,912-900,000\left[\frac{1-\left(1-ia\right)^{17}}{\left(1-ia\right)^{17}}\right]-5,000,000\left(1-ia\right)^{-13}-5,000,000\left(1-ia\right)^{-5}=0$
Procedemos a continuación con los ensayos, ofreciendo en los paréntesis $(1-ia)$ el resultado de la resta
Ensayo #1: $ia=1.5$%
.$33,601,912-900,000\left[\frac{1-\left(0.985\right)^{17}}{\left(0.985\right)^{17}\ast0.015}\right]-5,000,000\left(0.985\right)^{-13}-5,000,000\left(0.985\right)^{-5}=13,335,173$.
Resultado diferente de cero.
Ensayo #2: $ia=2.5$%
$33,601,912-900,000\left[\frac{1-\left(0.975\right)^{17}}{\left(0.975\right)^{17}\ast0.025}\right]-5,000,000\left(0.975\right)^{-13}-5,000,000\left(0.975\right)^{-5}=4,842,054$
Resultado diferente de cero.
Ensayo #3: $ia=3.5$%
$33,601,912-900,000\left[\frac{1-\left(0.965\right)^{17}}{\left(0.965\right)^{17}\ast0.035}\right]-5,000,000\left(0.965\right)^{-13}-5,000,000\left(0.965\right)^{-5}=-5,292,359$
Resultado diferente de cero, pero esta vez negativo. Procedemos a interpolar entre estos dos últimos valores.

El valor de la tasa de interés $ia$ está en el intervalo (1.5%,3.5%) sin ser estos valores extremos. Para establecer la ecuación de proporcionalidad tenemos:
$a=ia-0.025$
$b=0.035-0.025$
$c=0-4,842,054$
$d=-5,292,359-4,842,054$
Ecuación de proporcionalidad.
$$\frac{ia-0.025}{0.035-0.025}=\frac{0-4,842,054}{-5,292,359-4,842,054}$$ $$ia=\frac{-4,842,054}{-10,134,413}*0.01+0.025=0.02997778$$La tasa de interés es $ia=3.0$% trimestre anticipado. Con ésta, la tasa nominal anual es $J=k*ia=4*0.03=0.12$; del 12% t.a
La tasa efectiva anual es:
$ie=\left(\frac{1}{1-0.03}\right)^4-1=0.1296$. Es decir, del $12.96$% E.A.Hemos tratado las series uniformes desde el criterio de capitalización bajo las modalidades de vencida, continua y anticipada. Un segundo criterio se refiere al tipo de anualidad entendido como el momento en que ocurre la cuota fija, siendo posible los casos vencidos o convencional, diferidos, anticipados, donde se incluyó además el caso de anualidades perpetuas. Todas estas posibles anualidades, incluidas las "conjeturas teóricas", tienen una característica en común: son flujos de efectivo discretos (o anualidades discretas), es decir montos iguales que están separados por intervalos fijos de tiempo, tales como el mes, el trimestre, el semestres, el año.
Empero, ¿este conjunto de anualidades agota las posibilidades del tema? No.
Aunque no se trata en este libro, las anualidades también pueden ser continuas gestionadas bajo capitalización continua. Para el estudio de este tema, de "flujos de efectivo continuos uniformes con capitalización continua", invitamos al lector a consultar Sullivan, Wicks y Luxhoj
Con estos dos ejercicios que a continuación desarrollamos se tiene la intención de ilustrar el manejo de las diferentes ecuaciones sobre anualidades en situaciones particulares de flujos de caja (diagramas económicos). Por ejemplo, dada la siguiente Figura 1.36 hallar los valores presente y futuro equivalentes, resolviendo por capitalización vencida y continua; convertir además la Figura 1.36 en serie uniforme convencional.
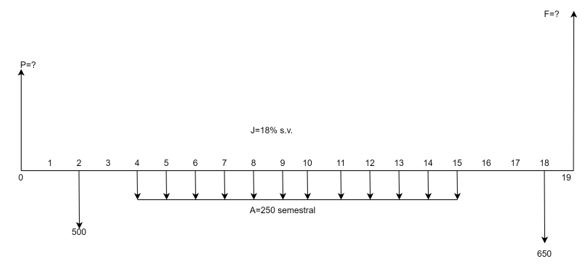
Solución. Valor presente capitalización vencida.
Con respecto a $P$ encontramos dos valores futuros en las $ff=2$ y $ff=18$, además de una serie uniforme desfasada con inicio en la $ff=4$ y termina en la $ff=15$. La ecuación de valor del problema y el resultado son:
$$P=\frac{500}{\left(1.09\right)^2}+250\left[\frac{\left(1.09\right)^{12}-1}{\left(1.09\right)^{12}*0.09}\right]*\frac{1}{\left(1.09\right)^3}+\frac{650}{\left(1.09\right)^{18}}$$ $$P=420.84+137.80+1,382.35=1,940.98$$Solución. Valor futuro capitalización vencida. La ecuación de valor y su resultado son:
Para constatar que la respuesta es correcta, llevemos $P$ de la primera solución a valor futuro. Esto es:
$$F=1,940.98\left(1+0.09\right)^{19}=9,979.88$$Para convertir la Figura 1.36 en serie uniforme convencional, es decir con la primera $A$ en la $ff=1$ y la última en 19, podemos utilizar el valor $P$ o del valor $F$, ya calculados. Veamos desde $P$:
$$A=1,940.98\left[\frac{\left(1.09\right)^{19}*0.09}{\left(1.09\right)^{19}-1}\right]=216.87$$Ahora desde $F$:
$$A=9,979.88\left[\frac{0.09}{\left(1.09\right)^{19}-1}\right]=216.87$$Debido a que los resultados de $P$ y $F$ son equivalentes, la respuesta para $A$ debe ser la misma con ambos valores.
Solución. Valor presente capitalización continua.
Solución. Valor futuro capitalización continua.
La anualidad convencional con capitalización continua es:
$$A=1,884.58\left[\frac{e^{0.09*19}\left(e^{0.09}-1\right)}{e^{0.09*19}-1}\right]=216.67$$Desde el valor futuro, tenemos:
$$A=10,419.79\left[\frac{e^{0.09}-1}{e^{0.09*19}-1}\right]=216.67$$
Ejercicio 1.49. Cálculo de capital con renta perpetua anticipada. Usted informa a su familia que ha invertido un capital $P$ con el propósito de generar una renta perpetua anticipada de 5,800,000 pesos. La tasa de interés pactada fue de 15.0% efectiva anual continua. ¿A cuánto asciende el capital invertido?
En este ejercicio tenemos dos situaciones especiales. En primer lugar, la tasa de interés es dada efectiva continua mientras las cuotas fijas son mensuales, por lo que debemos hacer ajuste de equivalencia en la tasa hallando la mensual. En segundo lugar, las cuotas fijas perpetuas son anticipadas, tema que se trata en este ejercicio por primera vez en el libro; por ello, desde el razonamiento para la solución se propone generar una ecuación para esta cuestión.
Solución.
$P=?$
$ie=15$% efectiva anual continua
$A=5,800,000$
Tasa de interés del mes. Podemos aplicar el procedimiento de efectiva a nominal para determinar la tasa nominal anual equivalente.
Luego, de la nominal anual obtenemos la mensual. Por lo tanto:
$$J=ln(1+0.15)=0.1398$$La tasa nominal es de 13.98% anual, equivalente a 1.164% nominal mes continuo
Valor presente de anualidad perpetua anticipada. En el punto 1.2.3 sobre anualidades perpetuas bajo capitalización continua, concluimos con las ecuaciones (1.35) y (1.35.1) para hallar el valor presente con anualidades vencidas, es decir con aquellas donde la primera $A$ se ubica en la $ff=1$. Empero, en este ejercicio la primera $A$ está ubicada en la $ff=0$, por lo que para su solución proponemos la siguiente alternativa:
O alternativamente
$$P=A+\frac{A}{ie}$$Siendo la primera $A$ después de la igualdad, la cuota fija que está ubicada en $ff=0$. Realizando operativas desde la primera ecuación:
$$P=A\left(1+\frac{1}{e^J-1}\right)$$ $$P=A\left(\frac{e^J-1+1}{e^J-1}\right)$$ $$P=A\left(\frac{e^J}{e^J-1}\right) (1.59)$$El capital invertido fue de:
$$P=5,800,000\left(\frac{e^{0.01164}}{e^{0.01164}-1}\right)$$ $$P=5,800,000\left(\frac{1.01166754}{1.01166754-1}\right)$$ $$P=5,800,000\left(\frac{1.01166754}{0.01166754}\right)$$Nótese que la tasa $ei$ del mes es 0.01166754, denominador del paréntesis
$$P=5,800,000\left(86.7078632\right)=502,905,607$$Aprovechamos este ejercicio para indicar que la anualidad perpetua anticipada bajo capitalización continua, su modelo se obtiene de la ecuación (1.59), como:
$$A=P\left(\frac{e^J-1}{e^J}\right)(1.60)$$O también:
$$A=P\left(\frac{ie}{e^J}\right) (1.60.1)$$Debemos estar atento a las tasas de interés utilizadas en el cálculo ya que deben corresponder a la unidad de tiempo de la anualidad.
Ejercicio 1.50. Valoración de bonos. Una sociedad anónima es autorizada a emitir bonos por valor de 10,000,000 de pesos cada uno con vencimiento en 5 años. Los cupones se pagan semestralmente a la tasa cupón de 7.6% nominal anual, con vencimiento del capital al quinto año. Determinar el monto de los cupones, realizar el diagrama económico del bono, determinar el precio del bono si los inversionistas exigen una rendimiento de 5.2% nominal anual.
Resolver el ejercicio con capitalizaciones vencida y continua
Solución.
Los bonos son contratos legales (tipo de pagaré, un título valor) por medio de los cuales los gobiernos y las empresas (públicas y privadas) acceden a financiación con terceros, con el fin de desarrollar sus planes o programas de inversión.
En este tipo de instrumento financiero se utiliza una jerga especial. A los rendimientos de un bono (los intereses del título) se les denominan cupón y a la tasa de interés utilizada para el cálculo del cupón, se le denomina tasa cupón. También se aplican conceptos como tasa de rentabilidad del inversionista, valor nominal del bono (Vn, y es el reembolso de una cantidad específica de dinero, como es el caso del capital al final del plazo), precio del bono (valor efectivo, Ve; es el descuento del flujo de efectivo del bono, o su valor presente), entre otros.
Valor nominal ($Vn$):10,000,000
Pago de cupón (pago de intereses):semestral
Tasa cupón: $J=7.6$% s.v., equivalente a $3.8$% semestral
Monto del cupón ($A$): $10,000,000*0.038=380,000$ semestral
Rentabilidad inversionistas: $J=5.2$% anual, y $2.60$% por semestre
Vencimiento $n=$ 5 años o 10 semestres
Precio del bono ($Ve$)=? Es el valor presente del flujo de efectivo del bono. Ver Figura 1.37.
Debemos aclarar que este es un ejemplo simplificado desarrollado con fines prácticos.
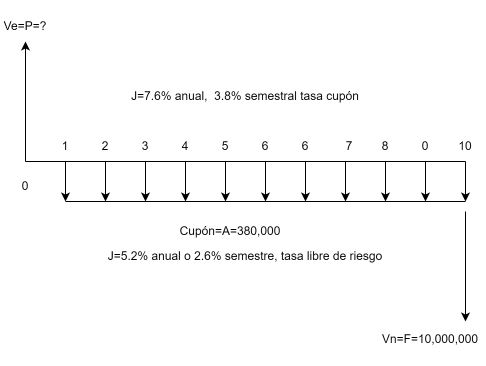
Valor presente con capitalización vencida.
Valor presente con capitalización continua. Supuesto: No se modifican la tasa y el cálculo del cupón; solo cambiamos la capitalización para el valor presente del bono.
Por ambos métodos, el precio del bono es mayor al valor nominal (valor residual de éste), y en ellos la tasa cupón es mayor, o se ubica por encima, a la tasa de rentabilidad del inversionista. En estas condiciones, se dice que el bono "cotiza sobre el par". Según Dumrauf,
₪ Cuestionario.
₪ Problemas.
R. $3,780,529.40R. 10.03% E.S. y 21.07% E.A.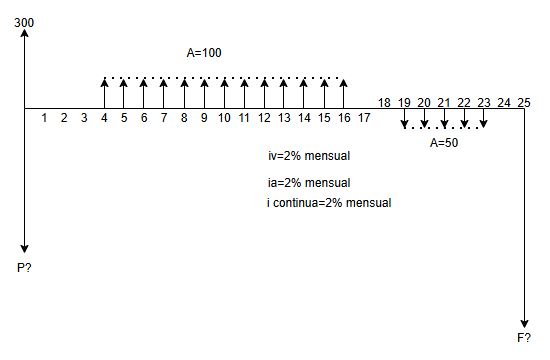
R. valor presente: 1,201.07; 1,198.26; 1,199.69. Valor futuro: 1,970.49; 1,985.64; 1,977.95. Tasa efectiva anual, 26.82%; 27.43%; 27.12%; respectivamenteR. $15,029,167.11 R. US$4,875.76R. Caso cuota anticipada: mes=0.610%, J=7.32% m.v., ie=7.57% E.A. Caso capitalización continua: mes=0.306%, J=3.67% m.v, ie=3.73%. R. Oferta 1:2,500,000; oferta 2: 2,525,000; diferencia:25,000.R. US$212,227,730.67 R. 60 semestres o 30 años en los tres casos.R. 45 semestres capitalización vencida, 52 semestres capitalización continua y 70 semestres capitalización anticipada. R. las alternativas son indiferentes.R. F=1,441,160.22 dólares, A= 54,871 dólares. R. A=55,043 dólares capitalización continua y A= 55,221 dólares capitalización anticipada. R. Continua 2.5% semestre y 5.20% E.A.; anticipada 2.5% semestre y 5.19% E.A. Los gradientes son series de flujos de efectivo (de ingresos o egresos) variables, esto es, series que representan movimientos periódicos de dinero que crecen o decrecen de manera uniforme (en una misma magnitud). Estos cambios se dan en períodos de tiempo iguales (mes, bimestre, trimestre, semestre, año, escalonado) y son manejados a valor equivalente bajo una misma tasa de interés.
Contrario a las series uniformes, las series en gradientes no son pagos iguales, sino que aumentan o disminuyen periódicamente y en una misma magnitud.
La magnitud a la que cambia la serie de flujo de efectivo, se le denomina gradiente. El gradiente es la medida del cambio (la variación) que experimenta periódicamente un flujo de efectivo, cambio que debe ser constante (siempre el mismo valor).
Si la magnitud a la que varía una serie es la suma (o resta) de una cantidad fija (constante), nos referimos a ella como serie en gradiente aritmético; en cambio si la magnitud a la que varía una serie (aumenta o disminuye) es un porcentaje constante (fijo o común), hablamos de serie en gradiente geométrico.
Estas series son análogas a las progresión aritmética y geométrica, estudiadas en el anexo al volumen 1 de este libro. Realmente, las series caracterizadas como de gradientes aritméticos son progresiones aritméticas, así como las series en gradiente geométrico son progresiones geométricas. La diferencia de estas series con las progresiones aritméticas y geométricas, estriba en que los valores que las constituyen están ubicados en el tiempo, se manejan bajo una misma tasa de interés y a valores equivalentes.
En este capítulo estudiaremos las series de flujo de efectivo en las formas de gradientes aritméticos y geométricos, bajo capitalizaciones vencida y continua.
Este apartado está dedicado al estudio de las series en gradientes que capitalizan al final del período de capitalización, iniciando con el caso aritmético.
En la siguiente Figura 2.1 observamos un flujo de ingresos mensuales en gradiente aritmético. El primer valor es de 30 pesos y de allí en adelante cada ingreso siguiente es igual al valor anterior más 10 pesos hasta llegar a un último monto de 110 pesos. En total son 9 ingresos mensuales, por lo que $n=9$, número total de ingresos que coincide con el plazo total. Es a la diferencia común que presenta los valores (la cantidad de cambio), de 10 pesos, la que se denomina gradiente aritmético, representado por la letra mayúscula $G$.
En la misma figura 2.1 se presentan las preguntas por el valor presente ($P=?$) y el valor futuro ($F=?$) de la serie. Procedemos a desarrollar la modelación para resolver ambas cuestiones, y para ello identificamos las variables de la siguiente manera:
$A_1=30$. Es el primer ingreso de la serie correspondiente a la $ff=1$
$A_2=40$. Es el segundo ingreso de la serie correspondiente a la $ff=2$
$A_3=50$. Es el tercer ingreso de la serie correspondiente a la $ff=3$
$A_9=110$. Es el noveno ingreso de la serie correspondiente a la $ff=9$; es además identificado como el enésimo valor de la serie (el monto que está en el lugar $n$)
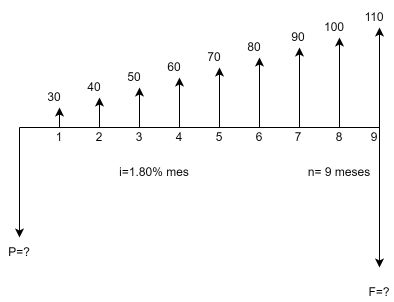
Nótese que la figura 2.1 es una serie de ingresos en progresión aritmética, con valores ubicados en fechas focales consecutivas de igual período (el mes), manejadas a valor equivalente por una misma tasa de interés, de $i=1.8$% mensual.
El $G$ se determina como la diferencia entre un número (o ingreso en específico en la Figura 2.1) y su inmediato antecesor, excepto para el primer valor. Es decir:
$G=40-30=10$
$G=50-40=10$
$G=110-100=10$
En general, para hallar el gradiente aritmético de una serie tenemos:
$G=A_n-A_{n-1}$ (2.1)
$G=60-50=10$.
El resultado puede ser positivo, como en el caso que traemos, o negativo.
Y para hallar el valor de un ingreso o egreso $n$, tenemos:
$A_n=A_1+\left(n-1\right)G$ (2.2)
$A_9=30+\left(9-1\right)10=110$
$A_{21}=30+\left(21-1\right)10=230$
Como consecuencia de (2.2), cada valor de la serie en gradiente aritmético está formada por dos componentes. Primero por $A_1$ que es una cantidad base; y el segundo por una cantidad de ($n-1$) veces $G$. El gradiente $G$ puede ser positivo (como en Figura 2.1) o negativo.
Por el hecho de que cada ingreso de la serie de la figura 2.1 se pueda obtener como $A_n=A_1+(n-1)G$, es posible separar de ésta los componentes: una serie uniforme de $A_1$ y una serie de los $G$.
En la figura 2.1 se identifican por lo tanto, las siguientes variables:
$P=?$
$F=?$
$A_1=30$
$G=10$
$i=1.8$%
$n=9$
Veamos gráficamente el asunto. El primer componente de la Figura 2.2, es una serie uniforme convencional, dado que el primer valor de $A=30$ está en la $ff=1$, y es una cantidad base que se extiende hasta la $ff=9$ (Ver Figura 2.2 primer componente).
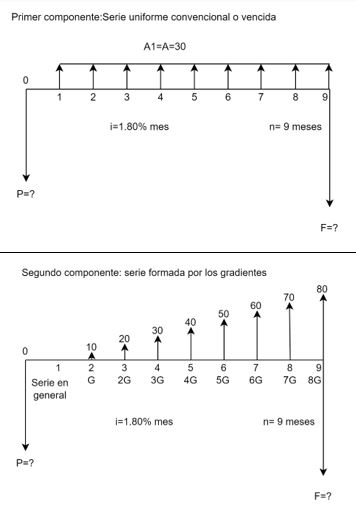
El segundo componente de la Figura 2.2, sin la base, es la serie de los cambios (el gradiente aritmético) de la serie de flujo de efectivo, cuyo primer valor está ubicado en la $ff=2$.
En la $ff=2$ tenemos $G=10$, en la $ff=3$ tenemos $2G=20$, y así sucesivamente para formar la serie de los cambios o segundo componente del flujo de ingreso en gradiente aritmético.
Ahora bien, cuando el primero valor del segundo componente (el gradiente) está en la $ff=2$, a dicha serie se le denomina convencional (ver Figura 2.2, segundo componente).
Por lo tanto, la serie de ingresos representada en la figura 2.1 es convencional porque la primera anualidad, A, está en la fecha focal uno y el primer gradiente aparece, está ubicado, en la fecha focal dos. Esta concreción es fundamental para el manejo correcto de los modelos matemáticos con gradientes y la realización de cálculos a valor equivalente.
El asunto ahora es cómo hallar los valores presente y futuro de la figura 2.1. Pues bien, para resolver la inquietud señalemos que el valor presente es igual a la suma de los valores presentes de los respectivos componentes especificados en la figura 2.2. Así mismo, para el valor futuro, éste es igual a la suma de los valores futuros de los dos componentes de la misma figura.
Es posible que el lector se esté preguntado por qué se suman los componentes de la Figura 2.2. Esto se debe a que el gradiente $G$ es positivo, y la serie original es creciente.
₪ Los valores presente y futuro del primer componente. La serie uniforme.
Este tema se trató en el primer capítulo de este volumen 2 (ver Anualidad vencida o convencional).
Por lo tanto los cálculos son:
Valor Presente
Valor Futuro
₪ El valor presente del segundo componente. Los gradientes.
Iniciamos con el tema del valor presente y más adelante desarrollamos el caso del valor futuro. Para el valor presente, un primer camino consiste en tratar o asumir a cada valor del diagrama del segundo componente, como un monto futuro que debemos descontar a la fecha focal cero. Esto es:
$$P=\frac{10}{{(1.018)}^2}+\frac{20}{{(1.018)}^3}+\frac{30}{{(1.018)}^4}+...+\frac{70}{{(1.018)}^8}+\frac{80}{{(1.018)}^9}$$ $P=319.83$Sin embargo, este método no es eficiente si pensamos en series en gradiente aritmético con un número grande, pero finito, de ingresos o egresos. Por ello, procedemos a generalizar la anterior expresión y realizar algunas operaciones matemáticas que permita su simplificación con el fin de obtener la ecuación con que alcanzar el mismo resultado de $P$, de manera más eficiente.
De la Figura 2.2, siendo $10=G$, $20=2G$, $30=3G$, etc., la ecuación en general nos queda como:
Tomando factor común $\frac{G}{(1+i)}$ en 2.1:
$$P=\frac{G}{(1+i)}\left[\frac{1}{(1+i)}+\frac{2}{\left(1+i\right)^2}+\frac{3}{\left(1+i\right)^3}+...+\frac{\left(n-1\right)}{\left(1+i\right)^{n-1}}\right]$$ $$P\left(1+i\right)=G\left[\frac{1}{(1+i)}+\frac{2}{\left(1+i\right)^2}+\frac{3}{\left(1+i\right)^3}+...+\frac{\left(n-1\right)}{\left(1+i\right)^{n-1}}\right] (2.2)$$Ahora restemos (2.2)-(2.1) habiendo tomado previamente factor común $G$ en esta última. Además, siendo $P(1+i)=P+Pi$ y luego de cancelar términos comunes, el resultado es:
$$Pi=G\left[\frac{1}{\left(1+i\right)}+\frac{1}{\left(1+i\right)^2}+\frac{1}{(1+i)^3}+...+\frac{1}{\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]$$ En esta última expresión extraer el término $\frac{n}{\left(1+i\right)^n}$ del corchete, obteniendo la ecuación siguiente: $$Pi=G\left[\frac{1}{\left(1+i\right)}+\frac{1}{\left(1+i\right)^2}+...+\frac{1}{\left(1+i\right)^{n-1}}+\frac{1}{\left(1+i\right)^n}\right]-\frac{Gn}{\left(1+i\right)^n}$$El anterior paso se justifica porque en el interior del corchete de la expresión anterior tenemos la suma de $n$ términos de una progresión geométrica, y cuya suma es como en (1.4). En consecuencia tenemos:
$$Pi=G\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}\right]-\frac{Gn}{\left(1+i\right)^n}$$Tomando factor común $G$ y pasando $i$ a dividir, tenemos finalmente que:
$$P=\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right] (2.3)$$La ecuación (2.3), es la fórmula para calcular el valor presente de la serie de gradientes aritméticos (segunda parte de figura 2.2). Por la condición de la Figura 2.2, el valor P calculado se ubica dos lugares a la izquierda de la primera G.
Ahora bien, como el $G$ es positivo, la ecuación para hallar el valor presente de la serie de ingresos en gradiente aritmético, como de la Figura 2.1, es:
$$P=A\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}\right]+\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right](2.4)$$El valor presente de dicha figura es:
$$P=30\left[\frac{\left(1.018\right)^9-1}{0.018\left(1.018\right)^9}\right]+\frac{10}{0.018}\left[\frac{\left(1.018\right)^9-1}{0.018\left(1.018\right)^9}-\frac{9}{\left(1.018\right)^9}\right]$$ $P=567.05$Para la situación en la que el gradiente aritmético sea negativo, reemplazamos el signo más $(+)$ por el menos $(-)$, dado que la serie es decreciente. La ecuación es como en (2.5).
$$P=A\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}\right]-\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right](2.5)$$Veamos el asunto en la siguiente Figura 2.3.
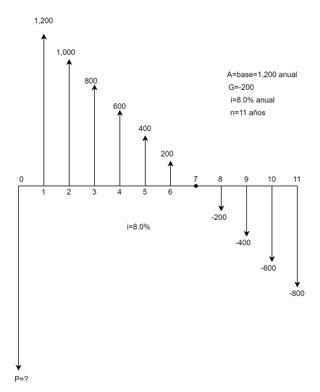
Con (2.5), tenemos: $$P=1,200\left[\frac{\left(1.08\right)^{11}-1}{0.08\left(1.08\right)^{11}}\right]-\frac{200}{0.08}\left[\frac{\left(1.08\right)^{11}-1}{0.08\left(1.08\right)^{11}}-\frac{11}{\left(1.08\right)^{11}}\right]$$ $P=2,513.63$
₪ El valor futuro del segundo componente. Los gradientes.
Así como en las anualidades, el valor futuro de un gradiente convencional se calcula en $n$, lugar donde está ubicada la última gradiente. El procedimiento para la fórmula es el siguiente:
Si $F=P(1+i)^n$ y a su vez $P=\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]$, reemplazando esta última expresión en la primera, tenemos que:
$$F={\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]\left(1+i\right)}^n$$Cancelando el factor $\left(1+i\right)^n$, obtenemos que:
$$F=\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i}-n\right] (2.6)$$Por lo tanto, el valor futuro de la serie representada en la Figura 2.1, en la que el gradiente es positivo, se obtiene con la siguiente ecuación (2.27):
$$F=A\left[\frac{\left(1+i\right)^n-1}{i}\right]+\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i}-n\right] (2.7)$$El cálculo de el valor futuro es por lo tanto:
$$F=30\left[\frac{\left(1+0.018\right)^9-1}{0.018}\right]+\frac{10}{0.018}\left[\frac{\left(1+0.018\right)^9-1}{0.018}-9\right]$$ $$F=290.28+665.54=665.54$$Con la ecuación (2.4) hallamos que $P=567.05$ de la misma Figura 2.1; si llevamos esta valor P al futuro en la $ff=9$, tenemos:
$$F=567.05\left(1+0.018\right)^9=665.54$$Igual valor. Este último procedimiento es una manera de constatar que se ha realizado el cálculo de modo correcto.
En la situación de un gradiente negativo, el modelo para el cálculo del valor futuro es:
$$F=A\left[\frac{\left(1+i\right)^n-1}{i}\right]-\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i}-n\right] (2.8)$$El valor futuro de la Figura 2.23 es:
$$F=1,200\left[\frac{\left(1+0.08\right)^{11}-1}{0.08}\right]-\frac{200}{0.08}\left[\frac{\left(1+0.018\right)^{11}-1}{0.08}-11\right]$$ $$F=19,974.58-14,113.72=5,860.86$$Para constatar el resultado realicemos:
$$F=2,513.63\left(1+0.08\right)^{11}=5,860.86$$Igual valor.
₪ El modelo para la anualidad. Convertir una serie de gradientes aritméticos en serie uniforme.
Para este proceso partimos de dos resultados ya alcanzados. El primero es la ecuación (1.5) del capítulo anterior:
$$A=P\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right]$$Y el segundo es la ecuación (2.3) de este capítulo
$$P=\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]$$Reemplazando (2.3) en (1.5), tenemos:
$$A=\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]*\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right]$$Simplificando:
$$A=\frac{G}{i}\left[1-\frac{ni}{\left(1+i\right)^n-1}\right]$$ $$A=G\left[\frac{1}{i}-\frac{n}{\left(1+i\right)^n-1}\right] (2.9)$$Ejercicio 2.1. Convertir en anualidad la serie de los gradientes Convertir la serie de la Figura 2.1 en serie uniforme convencional. Hallar además los valores presente y futuro de dicha anualidad y constatar la igualdad de valores.
Solución.
Por lo tanto la anualidad total es $A=30+38.81=68.81$. Los valores presente y futuro de esta nueva anualidad son:
Esta operación de convertir un gradiente aritmético nos es muy útil al intentar despejar $A$ de la ecuación (2.4). Dicha ecuación queda como:
$$P-\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]=A\left[\frac{\left(1+i\right)^n-1} {i\left(1+i\right)^n}\right]$$Pasando a realizar la operación contraria el factor de $A$ al lado izquierdo de la anterior igualdad, tenemos:
$$P\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right]-\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n }-\frac{n}{\left(1+i\right)^n}\right]\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right]=A$$Y por la anterior operación de convertir la serie de los gradientes a serie uniforme, resulta por lo tanto que:
$$A=P\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right]-G\left[\frac{1}{i}-\frac{n}{\left(1+i\right)^n-1}\right] (2.10)$$Si el caso tratado fuera como en el modelo (2.5) de la Figura 2.3, con gradiente decreciente, la ecuación sería:
$$A=P\left[\frac{i\left(1+i\right)^n}{\left(1+i\right)^n-1}\right]+G\left[\frac{1}{i}-\frac{n}{\left(1+i\right)^n-1}\right] (2.11)$$Invitamos al lector a que observe la situación de los signos que antecede al $G$, en las ecuaciones (2.10) y (2.11).
Ejercicio 2.2. Cálculo del primer valor (la base) de la serie gradiente La Administración Municipal de una pequeña ciudad ha constituido en el día hoy un fondo por 500 mil dólares con el fin de cubrir, durante cuatro años, los gastos mensuales de mantenimiento de jardines y parques del municipio. Los recursos son depositados en una entidad bancaria que reconoce el 12.68% E.A. Los ingenieros agrónomos responsables del mantenimiento sostienen que los gastos crecerán mensualmente en la suma de 500 dólares. ¿A cuánto asciende el gasto de mantenimiento del primer mes? Hallar además el monto de éstos para los meses 12, 24, 36 y 48.
Solución.
$A=?$ Primer valor y base de la serie
$P=500,000$ dólares
$n=4$ años o 48 meses
$ie=12.68$% equivalente a 1.0% mensual
$G=500$ mensuales
Con (2.10), el monto de $A$ es:
$$A=500,000\left[\frac{0.01\left(1+0.01\right)^{48}}{\left(1+0.01\right)^{48}-1}\right]-500\left[\frac{1}{0.01}-\frac{48}{\left(1+0.01\right)^{48}-1} \right]$$ $$A=13,116.92-10,789.79=2,368.12$$Para los demás valores aplicamos $A_n=A_1+(n-1)G$, siendo $A_1$ el valor base de la serie, acabado de calcular. Vamos:
$A_{12}=2,368.79+(12-1)500=8,868.12$
$A_{24}=2,368.79+(24-1)500=13,868.12$
$A_{36}=2,368.79+(36-1)500=19,868.12$
$A_{48}=2,368.79+(48-1)500=25,868.12$
Desde la ecuación (2.7) también podemos deducir una fórmula para $A$. Esta es:
$$F-\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i}-n\right]=A\left[\frac{\left(1+i\right)^n-1}{i}\right]$$ $$F\left[\frac{i}{\left(1+i\right)^n-1}\right]-\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i}-n\right]\left[\frac{i}{\left(1+i\right)^n-1}\right]=A$$Como la expresión:
$$\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i}-n\right]\left[\frac{i}{\left(1+i\right)^n-1}\right]=G\left[\frac{1}{i}-\frac{n}{\left(1+i\right)^n-1}\right]$$En consecuencia, para $A$ tenemos:
$$A=F\left[\frac{i}{\left(1+i\right)^n-1}\right]-G\left[\frac{1}{i}-\frac{n}{\left(1+i\right)^n-1}\right] (2.12)$$Ahora bien, si el desarrollo es desde la ecuación (2.8), el modelo para $A$ es:
$$A=F\left[\frac{i}{\left(1+i\right)^n-1}\right]+G\left[\frac{1}{i}-\frac{n}{\left(1+i\right)^n-1}\right] (2.13)$$Solo es asunto del signo que anteceda a $G$.
El lector puede además practicar sus matemáticas operativas despejando en cada fórmula estudiada la $G$, para hallar el gradiente aritmético.
Ejercicio 2.3. Cálculo del primer valor $A$ y la serie anual desde un valor futuro En los últimos cinco años, la Empresa Minera del Nordeste ha acumulado una producción total de 948,264 onzas de oro, cada onza con valor al día de hoy de 10,931,415.19 pesos. Se destaca que la producción anual ha seguido un gradiente aritmético de 10,000 onzas. Para sus proyectos, la Empresa Minera utiliza un costo de oportunidad de 5.0% anual. Bajo estas condiciones hipotéticas, hallar el volumen de producción en onzas de oro para cada uno los cinco años.
Solución. Con (2.12) tenemos:
$A=?$ Producción en onzas de año uno y base de la serie
$F=948,264$
$n=5$ años
$i=5.0$% anual
La producción del primer año fue de 152,586.78 onzas de oro. Los otro años son:
$A_2=152,586.78+(2-1)10,000=162,586.78$
$A_3=152,586.78+(3-1)10,000=172,586.78$
$A_4=152,586.78+(4-1)10,000=182,586.78$
$A_5=152,586.78+(5-1)10,000=192,586.78$
Para el estudio de este tema nos apoyamos en la siguiente Figura 2.4. En ella, la primera anualidad aparece en la $ff=4$ y el primer gradiente en la $ff=5$
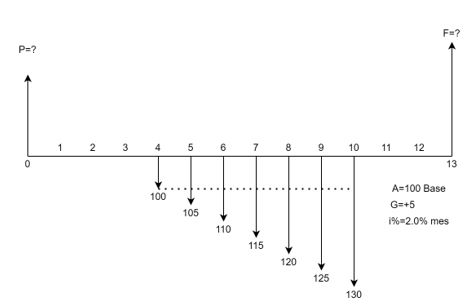
En la Figura 2.4 se solicita hallar $P$ en la $ff=0$ y a $F$ en ls $ff=13$. Como en el caso de las anualidades tratadas en el capítulo anterior, debemos realizar dos pasos para hallar los valores solicitados. En el primero aplicando directamente las respectivas fórmulas y, en el segundo, trasladando el valor obtenido en el paso anterior a la fecha focal solicitada. Recordemos además que en cada paso los exponentes $n$ tienen diferentes valores conforme al diagrama económico o flujo de efectivo de cada situación financiera.
₪ El El cálculo de $P$.
La primera $A$ está en la $ff=4$ y la fórmula directa corre un lugar a la izquierda por lo que tendríamos un valor provisional de $P$ ubicado en la $ff=3$, valor que debemos trasladar (descontar) a la $ff=0$ en un segundo paso. Ver Figura 2.5
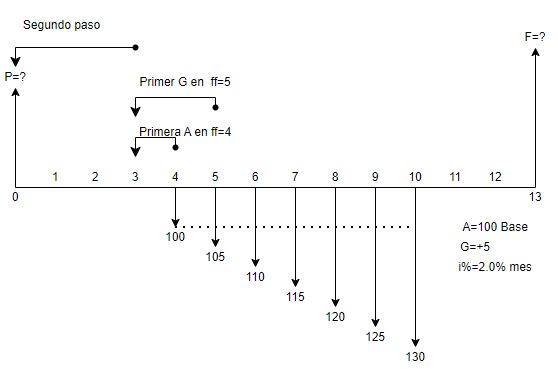
Ahora bien, el primer gradiente aparece en la $ff=5$ y como la fórmula directa para calcular $P$ corre dos lugares a la izquierda de éste, tenemos un valor provisional de $P$ en esa fecha focal que debemos descontar igualmente a la $ff=0$. En esta situación, e identificadas las $n$, tenemos por lo tanto:
$$P_A=100\left[\frac{\left(1+0.02\right)^7-1}{0.02\left(1+0.02\right)^7}\right]*\frac{1}{\left(1+0.02\right)^3}=609.87$$ $$P_G=\frac{5}{0.02}\left[\frac{\left(1+0.02\right)^7-1}{0.02\left(1+0.02\right)^7}-\frac{7}{\left(1+0.02\right)^7}\right]*\frac{1}{\left(1+0.02\right)^3}=89.07$$Como $P=P_A+P_G$, el resultado es:
$$P=609.87+89.07=698.94$$₪ El cálculo de $F$.
Como en el caso anterior, para hallar el valor futuro de la figura 2.4 se debe realizar dos pasos, que ilustramos a continuación. Ver Figura 2.6
$$F_A=100\left[\frac{\left(1+0.02\right)^7-1}{0.02}\right]\left(1+0.02\right)^3=788.93$$ $$F_G=\frac{5}{0.02}\left[\frac{\left(1+0.02\right)^7-1}{0.02}-7\right]\left(1+0.02\right)^3=115.22$$Siendo el resultado final:
$$F=F_A+F_G=788.93+115.22=904.15$$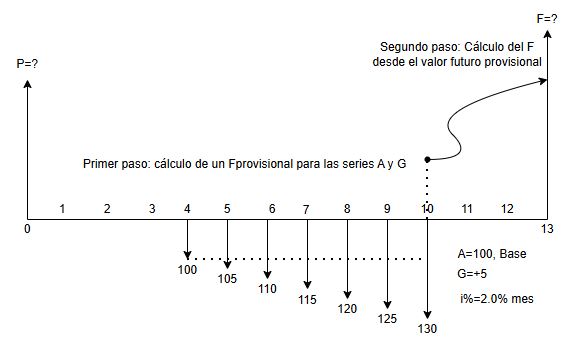
Si hallamos el valor presente de este valor futuro, en la $ff=0$, constatamos igual valor. Veamos:
$$P=\frac{904.15}{\left(1+0.02\right)^{13}}=698.94$$Ejercicio 2.4. Cálculo de la base $A$. Se adquiere maquinaria agrícola por valor de 200 millones para cancelarla por medio de 10 cuotas semestrales crecientes linealmente en 150,000 pesos, recibiendo además un año de gracia en intereses y capital. La tasa de interés pactada es de $J=8$% s.v. Hallar $A_1$ y $A_10$
Solución.
$P=200$ millones de pesos
$G=150,000$ pesos
$J=8$% anual o 4% semestral
$n=6$ años, siendo el primero de gracia. En total hay involucrado en el problema 12 semestres
Se cancelan en total 10 cuotas
Las preguntas son por:
$A=?$
$A_{10}=?$
El período de gracia significa diferir o posponer el pago, en este caso de las cuotas, un año. No es condonación de intereses ni de capital.
Debemos en primer lugar actualizar el capital, acumulando los intereses del año de gracias año, calculado al final del segundo semestre. Para ello hallamos el valor futuro del capital, capitalizado semestralmente. Este cálculo es:
Paso #1. Actualizar el capital
$$F=200,000\left(1.04\right)^2=216,320,000$$Al final del año uno se tiene una deuda acumulada de 216,320,000 pesos. Este valor es el nuevo $P$, y es empleado en el cálculo de la base de la serie de pagos, como segundo paso. Significa que los intereses capitalizados en el año uno genera intereses cubierto por las cuotas canceladas a partir del semestre tres. Entonces:
Paso #2. Hallar la primera cuota o base de la serie
Paso #3. Hallar el valor de la última cuota, $A_{10}$
$$A_{10}=26,043,707.49+(10-1)150,000=27,393,707.49$$Una serie de flujo de efectivo en gradiente aritmético es anticipada cuando la base $A$ está ubicada en la $ff=0$ y el primer cambio aritmético, denominado gradiente, está ubicado en la $ff=1$.
Para el manejo a valor equivalente de la serie, cálculos del valor presente y valor futuro, recurrimos al método 2 empleado en el caso de las anualidades anticipadas, del capítulo anterior, con el que se dedujo en modelo (1.17).
La situación a la que nos enfrentamos en este apartado, se representa en la siguiente Figura 2.7.
Para el valor de $P$, procedemos a hallar un valor provisional $Pp$ en la $ff=-1$, haciendo en primer momento que la serie de flujo de efectivo de la Figura 2.7 sea convencional; este movimiento implica que $n=13$. Luego, en segundo momento, se halla el valor solicitado en la $ff=0$. Veamos el primer momento:
$$P_p=10\left[\frac{({1.03)}^{13}-1}{0.03\left(1.03\right)^{13}}\right]+\frac{3}{0.03}\left[\frac{\left(1.03\right)^{13}-1}{0.03\left(1.03\right)^{13}}-\frac{13}{\left(1.03\right)^{13}}\right]$$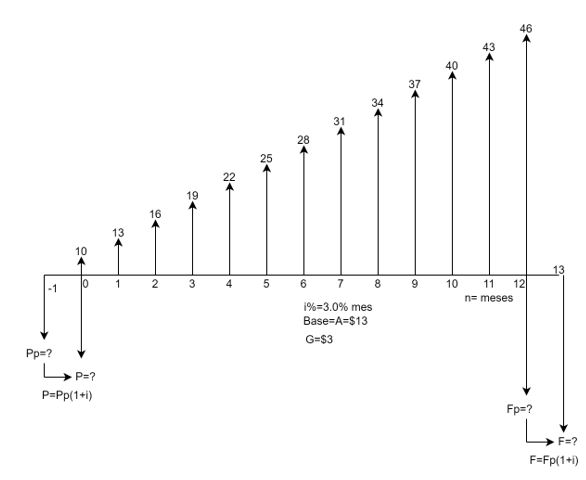
El segundo momento es trasladar el anterior valor a la $ff=0$, con $n=1$ y aplicando $P=P_p(1+i)$, como se indica gráficamente en la Figura 2.7. El resultado final es:
$P=284.61(1+0.03)=293.15$.
Generalizando el procedimiento, tenemos la ecuación (2.14):
$P=\left\{A\left[\frac{{(1+i)}^n-1}{{i(1+i)}^n}\right]+\frac{G}{i}\left[\frac{{(1+i)}^n-1}{i\left(1+i\right)^n}-\frac{n}{{(1+i)}^n}\right]\right\}*\left(1+i\right)(2.14)$
Si la serie hubiese sido decreciente, con $G$ negativo, en la ecuación 2.14 solo se requiere cambiar el signo $(+)$ por el signo $(-)$ antes de la misma $G$.
Para el valor futuro de la serie de la misma Figura 2.7, hallamos en primer lugar el futuro provisional, $Fp$, que garantiza un cálculo inicial convencional, utilizando $n=13$ y ubicando el valor hallado en la $ff=12$ (porque la primera anualidad está en cero). Luego el valor futuro se obtiene como $F=Fp(1+i)$. En general, este valor futuro lo calculamos con el siguiente modelo (2.15). Veamos:
$F={\left\{A\left[\frac{{(1+i)}^n-1}{{i(1+i)}^n}\right]+\frac{G}{i}\left[\frac{{(1+i)}^n-1}{i\left(1+i\right)^n}-\frac{n}{{(1+i)}^n}\right]\right\}*\left(1+i\right)}^n\left(1+i\right)$
Simplificando $(1+i)^n$:
$$F=\left\{A\left[\frac{{(1+i)}^n-1}{i}\right]+\frac{G}{i}\left[\frac{{(1+i)}^n-1}{i}-n\right]\right\}*\left(1+i\right)\ (2.15)$$la solución a la Figura 2.7 es:
$$F=\left\{10\left[\frac{{(1.03)}^{13}-1}{0.03}\right]+\frac{3}{0.03}\left[\frac{{(1+0.03)}^{13}-1}{0.03}-n\right]\right\}*\left(1.03\right)$$ $$F=\left\{10\left[15.618\right]+100\left[2.6178\right]\right\}*\left(1.03\right)=430.50$$Como prueba vemos que $F=293.15\left(1.03\right)^{13}=430.50$, igual valor
El flujo de efectivo en gradiente aritmético de la Figura 2.7 equivale a un valor presente de $293.15$ pesos y a un valor futuro de $430.50$ pesos. Empero, ¿Existen otras formas de resolver este ejercicio?
Si, existe varias formas de resolver el ejercicio de la figura 2.7, y todo depende de cómo asumamos el flujo de efectivo representado. Por ejemplo: vamos a suponer un pago anticipado de 10 pesos, una base (o serie uniforme) de 13 pesos que inicia en ff=1 sobre la que crece el flujo de efectivo con un gradiente aritmético de 3 pesos. Hallar de nuevo los valores $P$ y $F$. Ver representación en Figura 2.8
Con base en la Figura 2.8, el cálculo del valor presente es:
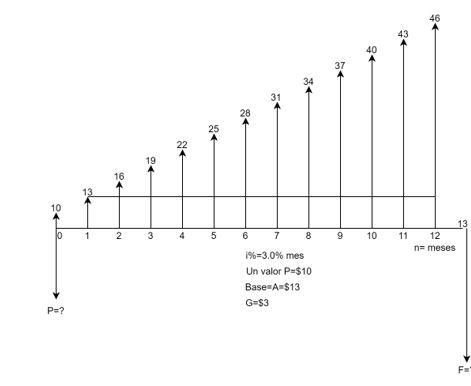
Ahora bien, la solución para el valor futuro es:
$F=10\left(1.03\right)^{13}+\left\{13\left[\frac{{(1.03)}^{12}-1}{0.03}\right]+\frac{3}{0.03}\left[\frac{{(1+0.03)}^{12}-1}{0.03}-12\right]\right\}1.03$
$$F=14.69+\left\{184.50+219.20\right\}\left(1.03\right)$$ $$F=14.69+(403.70)\left(1.03\right)$$ $$F=14.69+415.81=430.50$$Cálculo de la base A y la serie en gradiente aritmético. De la ecuación (2.14), con gradiente positivo, procedemos a despejar $A$; reescribiendo (2.14) tenemos:
Utilizando algunos resultados ya obtenidos, la expresión anterior queda como:
$$A=\frac{P}{\left(1+i\right)}\left[\frac{i{(1+i)}^n}{{(1+i)}^n-1}\right]-\frac{G}{i}\left[1-\frac{ni}{{(1+i)}^n-1}\right]$$Por lo tanto:
$$A=P\left[\frac{i{(1+i)}^{n-1}}{{(1+i)}^n-1}\right]-\frac{G}{i}\left[1-\frac{ni}{{(1+i)}^n-1}\right](2.16)$$Ejercicio 2.5. Cálculo de la base $A$ anticipada. Para apoyar la gestión de la Asociación de Juntas de Acción Comunal del municipio de Yolombó, el Consejo Municipal creó un fondo por $68,085,808 con el fin de realizar a la AJAC aportes anticipados trimestrales durante cinco años, pero decrecientes en 300,000 pesos, como iniciativa de promoción de la autonomía financiera. Si a nivel de recursos municipales se maneja un costo de oportunidad de 3% trimestral, hallar el valor de la primera cuota (la base de la serie), así como los valores de las cuotas 10, 15 y 20.
Solución.
$P=68,085,808$ de pesos
$G=-300,000$ pesos
$i=3$% trimestral
$n=5$ años e igual a 20 trimestres. Se cancelan en total 20 cuotas
$A=?$ Es la primera cuota y estaría ubicada en la $ff=0$
$A_{10}=?$ Estaría ubicada en la $ff=9$
$A_{15}=?$ Estaría ubicada en la $ff=14$
$A_{20}=$? Estaría ubicada en en $ff=19$
Se invita al lector a plantear el diagrama de caja de este problema, y realizar el cálculo de todas las cuotas para luego ubicar cada valor en la respectiva fecha focal del diagrama.
El valor de la cuota base de la serie y de las cuotas solicitadas, son:
$A=68,085,808\left[0.065257969\right]+10,000,000\left[0.255685848\right]$
$A=4,443,141,52+2,556,858,48=7,000,000$
$A_{10}=7,000,000+(10-1)(-300,000)=4,300,000$
$A_{15}=7,000,000+(15-1)(-300,000)=2,800,000$
$A_{20}=7,000,000+(20-1)(-300,000)=1,300,000$
Análogo a las anualidades (ver ecuación 1.13), la serie de gradiente aritmético perpetua es la situación en la que $n\rightarrow\infty$. En esta ocasión, el valor $P$ de la ecuación (2.3) es el límite cuando $n\rightarrow\infty$. Partiendo de esta ecuación, el desarrollo del modelo para dicho cálculo, es el siguiente:
$$P=\frac{G}{i}\left[\frac{\left(1+i\right)^n-1}{i\left(1+i\right)^n}-\frac{n}{\left(1+i\right)^n}\right]$$Multiplicando y dividiendo por $i$ el último factor del corchete, la ecuación anterior es equivalente a:
$$P=\frac{G}{i}\left[\frac{{(1+i)}^n-1}{i\left(1+i\right)^n}-\frac{ni}{{(1+i)}^ni}\right]$$En el corchete tomar factor común $i$ de denominadores:
$$P=\frac{G}{i^2}\left[\frac{{(1+i)}^n-1}{\left(1+i\right)^n}-\frac{ni}{{(1+i)}^n}\right]$$¿Qué sucede con esta ecuación cuando n se hace muy grande? Es decir, ¿cuál es el límite de la expresión cuando $n$ tiende a infinito?
Intuitivamente podemos pensar, como ya se hizo anteriormente en anualidades, que el $lim (n\to \propto)$ de $(1/(1+i){^n})$ es cero. Esto porque el uno ($1$) del numerador está siendo dividido por un número cada vez más grande. Por esta razón se reescribe la ecuación como:
$$P=\frac{G}{i^2}\left[1\ -0-\frac{ni}{{(1+i)}^n}\right]$$Ahora bien, intuitivamente también podemos afirmar que el $ lim (n\to \propto)$ de $\frac{ni}{{(1+i)}^n}$ también es cero. Podemos pensar que el denominador crecerá mucho más rápido que el numerador, debido a que el denominador está elevado a una potencia cada vez mayor, mientras que el numerador crece linealmente.
Sin embargo, para una demostración formal de éste y dado que tanto el numerador como el denominador tienden a infinito cuando $n$ tiende a infinito, podemos aplicar la regla de L'Hôpital. Esta regla permite calcular el límite de un cociente de funciones derivando tanto el numerador como el denominador (ver el concepto en el anexo a este libro).
Derivada del numerador.
Definamos el numerador como una función en la que $i$ es constante, es decir $f(n)=ni$. Recordando que la derivada de una constante es cero y la derivada de una variable respecto a si misma es uno, aplicamos la regla del producto a la anterior función y obtenemos:
$$ f'(n)=n'*i+n*i'$$Como la $n'=1$ y la $i'=0$, por consiguiente $f(n)'=i$
Derivada del denominador.
La función para el denominador es $g(n)=(1+i)^n$, de naturaleza exponencial. La derivada de una función exponencial de la forma $a^x$, donde $a$ es una constante, es:
$\frac{d}{dx}(a^x)=a^xln(a)$. Es decir, la derivada de una función exponencial es igual a la función original multiplicada por el logaritmo natural de la base. Aplicando dicha propiedad obtenemos:
$$\frac{dg(n)}{dn}={(1+i)}^n*ln(1+i)$$El resultado total de aplicar primeras derivadas es:
$$\frac{f'(n)}{g'(n)}=\frac{i}{{(1+i)}^n*ln(1+i)}$$Como $i$ es una constante (tasa de interés), cuando $n$ tiende a infinito, la expresión anterior tiende a cero (si se volviera a derivar, el numerador es cero y el denominador es un valor positivo que se hace más grande, por ello, la expresión en total tiende a cero).
Este resultado significa que, a medida que el número de períodos (n) tiende a infinito, el valor presente de un flujo de caja futuro se vuelve insignificante, sin importar el valor del flujo de caja inicial. Esto es coherente con la idea de que el dinero tiene un valor temporal y que los flujos de caja futuros se descuentan a una tasa de interés.
En consecuencia: $P=\frac{G}{i^2}\left[1\ -0-0\right]$, o sea $P=\frac{G}{i^2}(2.17.1)$
En términos perpetuos, la ecuación (2.4) para la serie de pagos en gradiente aritméticos positivo es ahora:
$$P=\frac{A}{i}+\frac{G}{i^2}(2.17.2)$$Ahora, si el gradiente es negativo, se cambia el signo (+)por (-).
Ejercicio 2.6. Cálculo del valor presente serie perpetua. Una empresa está evaluando la inversión en un fondo que promete rendimientos crecientes a lo largo del tiempo. Se estima que el primer año el fondo generará dividendos de 10,000 dólares, y que estos dividendos aumentarán en 500 dólares cada año posterior de forma indefinida. Si la tasa de descuento adecuada para este tipo de inversión es del 8% anual, ¿Cuál es el valor presente de esta inversión perpetua?
Solución.
$P=?$
$G=500$ dólares anuales
$i=8$% anual
$A=10,000$ dólares.
El valor presente obtenido representará el monto máximo que la empresa estaría dispuesta a pagar hoy por esta inversión, considerando la tasa de descuento y el crecimiento esperado de los dividendos.
En el caso de gradiente geométrico, las series aumentan o disminuyen de un período a otros en un porcentaje constante. A esta tasa constante de cambio de la serie la denominamos gradiente geométrico y la representamos por $g$.
Supongamos que una compañía comercial estima para el próximo año un ingreso por venta de 5,800 millones dólares. Por la ampliación de la oferta de productos, espera además que las ventas aumenten durante los 4 años siguientes al 6% anual con respecto al año anterior. El gerente financiero está interesado en conocer la equivalencia en valor presente de este flujo de ingresos, para lo que aplica como tasa de oportunidad el 5% anual. La representación del problema se realiza en la Figura 2.9
Como las ventas del año siguiente son el 6% más que el año anterior, la serie de flujo de ventas se calcula como: $A_n=A_1\left(1+g\right)^{n-1}$, con $g=6$%. Por ello:
$A_1=5,800$ millones de dólares
$A_2=5,800\left(1+0.06\right)^{2-1}=6,148$
$A_3=5,800\left(1+0.06\right)^{3-1}=6,517$
$A_4=5,800\left(1+0.06\right)^{4-1}=6,908$
$A_5=5,800\left(1+0.06\right)^{5-1}=7,322$
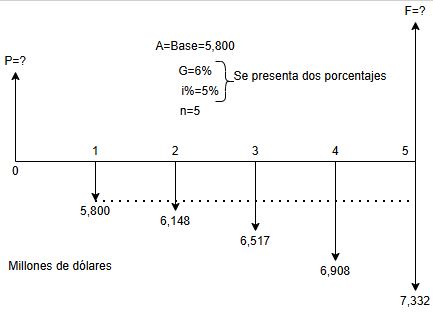
Iniciamos hallando el valor presente de dicho diagrama. Para ello planteamos la siguiente expresión, en la que cada cuota geométrica se descuenta a la $ff=0$. Ver la siguiente Figura 2.10
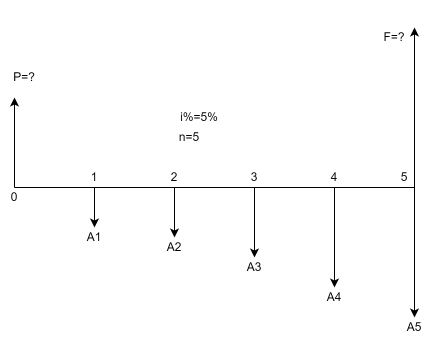
Utilizando $A$ como base y generalizando, tenemos:
$$P=\frac{A}{\left(1+i\right)}+\frac{A(1+g)}{\left(1+i\right)^2}+\frac{A\left(1+g\right)^2}{\left(1+i\right)^3}+...+\frac{A\left(1+g\right)^{n-1}}{\left(1+i\right)^n} (a)$$Tomado factor común $A$
$$P=A\left[\frac{1}{\left(1+i\right)}+\frac{\left(1+g\right)}{\left(1+i\right)^2}+\frac{\left(1+g\right)^2}{\left(1+i\right)^3}+...+\frac{\left(1+g\right)^{n-1}}{\left(1+i\right)^n}\right] (b). $$En la ecuación (2), la expresión entre corchetes es la suma de n-términos en progresión geométrica, con razón común $\frac{\left(1+g\right)}{\left(1+i\right)}.$ Por lo tanto multipliquemos (2) por dicha razón común:
$$P\frac{\left(1+g\right)}{\left(1+i\right)}=A\left[\frac{\left(1+g\right)}{\left(1+i\right)^2}+\frac{\left(1+g\right)^2}{\left(1+i\right)^3}+\frac{\left(1+g\right)^3}{\left(1+i\right)^4}+...+\frac{\left(1+g\right)^n}{\left(1+i\right)^{n+1}}\right] (c)$$Restemos ahora (b) – (c) y obtenemos:
$$P\frac{\left(1+g\right)}{\left(1+i\right)}-P=A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^{n+1}}-\frac{1}{\left(1+i\right)}\right]$$Y es igual a:
$$P\left[\frac{\left(1+g\right)}{\left(1+i\right)}-1\right]=A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^{n+1}}-\frac{1}{\left(1+i\right)}\right]$$ $$P\left[\frac{1+g-1-i}{\left(1+i\right)}\right]=A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^{n+1}}-\frac{1}{\left(1+i\right)}\right]$$ $$P\frac{\left(g-i\right)}{\left(1+i\right)}=A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^{n+1}}-\frac{1}{\left(1+i\right)}\right]$$Tomando factor común $(1+i)$ del lado derecho de la última expresión:
$$P\frac{\left(g-i\right)}{\left(1+i\right)}=\frac{A}{(1+i)}\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]$$ $$P(g-i)=\frac{A(1+i)}{(1+i)}\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]$$En consecuencia:
$$P=\frac{A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]}{(g-i)}(2.18)$$O también:
$$A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]\ast(g-i)^{-1} (2.18.1)$$Ahora bien, el modelo (2.18) lo podemos también simplificar, así:
$$P=\frac{A\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^n}\right]}{(g-i)}$$Y aplicando la multiplicación de extremos y medios, tenemos finalmente:
$$P=A\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^n(g-i)}\right](2.18.2)$$El valor presente de las ventas de la empresa comercial en los cinco años, es:
$$P=5.800\left[\frac{\left(1+0.06\right)^5-\left(1+0.05\right)^5}{\left(1+0.05\right)^5(0.06-0.05)}\right]$$ $$P=5.800\left[\frac{0.06194402}{0.01276282}\right]=28.150$$El valor exacto es de $28,150,158.878.44$ dólares en los cinco años.
Ejercicio 2.7. Cálculo del valor presente gradiente geométrico negativo. Suponga ahora que por alguna eventualidad, la expectativa de la anterior empresa comercial no es que sus ventas crezcan un 6% anual respecto al año anterior, sino que lo hace al $-1$%. Hallar de nuevo el valor presente equivalente de las ventas.
Solución.
$P=?$
$A=5.800$ millones de dólares
$g=-1.0$%
$i=5$%
$n=5$ años
Con (2.18.2): $$P=5.800\left[\frac{\left(1-0.01\right)^5-\left(1+0.05\right)^5}{\left(1+0.05\right)^5(-0.01-0.05)}\right]$$
Nótese en la anterior expresión los cambios de signos por tener (-g). El valor de las ventas es:
$$P=5.800\left[\frac{-0.32529151}{-0.07657689}\right]=24.638$$El valor de las ventas es de $24,637,859.812.38$ dólares en los cinco años.
Los modelos (2.18.1) y (2.18.2) se pueden utilizar cuando el gradiente geométrico es un porcentaje negativo ($-g$); solo es necesario estar atento con la multiplicación de los signos al emplear las fórmulas, como se realizó en el ejercicio anterior. Por ejemplo en:
$$(1+(-g))^n=(1-g)\ ^n$$ $$(1+(-0.01))^5=(1-0.01)\ ^5$$En los dos anteriores ejercicios existe una característica común: la de $ g\neq i$. Sin embargo, ¿qué sucede si se presenta que $g=i$?
Para abordar esta inquietud resolvamos el ejercicio suponiendo ahora que las ventas crecen el 5% anual. Por ello:
Solución.
$P=?$
$A=5.800$ millones de dólares
$g=5.0$%
$i=5.0$%
$n=5$ años
Con (2.18.2): $$P=5.800\left[\frac{\left(1+0.05\right)^5-\left(1+0.05\right)^5}{\left(1+0.05\right)^5(0.05-0.05)}\right]$$ $$P=5.800\left[\frac{0}{0}\right]=\frac{0}{0}$$
El resultado está indeterminado. Para resolver esta indeterminación un camino es aplicar de nuevo la regla L'Hôpital (que se deja para el lector. Ver anexo). Otro camino es desde la ecuación (b), así:
$$P=A\left[\frac{1}{\left(1+i\right)}+\frac{\left(1+g\right)}{\left(1+i\right)^2}+\frac{\left(1+g\right)^2}{\left(1+i\right)^3}+...+\frac{\left(1+g\right)^{n-1}}{\left(1+i\right)^n}\right] $$Como $g=i$, ésta queda igual a:
$$P=A\left[\frac{1}{\left(1+i\right)}+\frac{\left(1+i\right)}{\left(1+i\right)^2}+\frac{\left(1+i\right)^2}{\left(1+i\right)^3}+...+\frac{\left(1+i\right)^{n-1}}{\left(1+i\right)^n}\right]$$Simplificando:
$$P=A\left[\frac{1}{\left(1+i\right)}+\frac{1}{\left(1+i\right)}+\frac{1}{\left(1+i\right)}+...+\frac{1}{\left(1+i\right)}\right]$$Como desde la generalización tenemos planteado $n$ pagos o flujo de efectivo (serie finita), el término común dentro del corchete se repite $n$ veces. En consecuencia, la ecuación para este caso es:
$$P=A\frac{n}{\left(1+i\right)}\ (2.19)$$Solución.
El resultado exacto es de $27,619,047,619$ dólares
En Conclusión:
Aplicamos los modelos $(2.18)$, $(2.18.1)$ o $(2.18.2)$, si y sólo si $g\neq i$
Aplicamos el modelo $(2.19)$ si y sólo si $g=i$
₪ El modelo para la anualidad.
Del modelo (2.18.2) despejamos $A$ y obtenemos la ecuación que permite obtener la base para construir la serie de flujo de efectivo en gradiente geométrico. Ésta es:
$$A=\left[\frac{\left(1+i\right)^n(g-i)}{\left(1+g\right)^n-\left(1+i\right)^n}\right](2.20)$$
Ejercicio 2.8. Cálculo del valor de $A$ gradiente geométrico. La tienda PC al DÍA vende una computadora en 5,200,000 pesos para ser cancelada en 12 cuotas mensuales que crecen al 1.5% mensual. Hallar el valor de las cuotas 1, 6 y 12, si la tasa de interés pactada es del 24% m.v.
Solución.
$A=?$
$P=5,200,000$
$g=1.5$% mensual
$J=24$% o $i=2$% mensual
$n=1$ año o $12$ meses
Solución.
Con (2.20):
$$A=5,200,000\left[\frac{\left(1+0.02\right)^{12}(0.015-0.02)}{\left(1+0.015\right)^{12}-\left(1+0.02\right)^{12}}\right]$$ $$A=5,200,000\left[\frac{-0.00634121}{-0.07262362}\right]=454,043.54$$Los $454,043.54$ pesos, son el valor de la primera cuota ($A_1$) y la base para la determinación de los siguientes pagos. Para $A_6$ y $A_{12}$, con $A_n={A_1\left(1+g\right)}^{n-1}$, tenemos:
$$A_6=454,043.54\left(1+0.015\right)^{6-1}=489,133.84$$ $$A_6=454,043.54\left(1+0.015\right)^{12-1}=534,840.10$$Resolvamos el mismo ejercicio, pero esta vez con $g=-1.5$%. Los valores de las cuotas 1, 6 y 12 son:
$$A=5,200,000\left[\frac{\left(1+0.02\right)^{12}(-0.015-0.02)}{\left(1-0.015\right)^{12}-\left(1+0.02\right)^{12}}\right]$$ $$A=5,200,000\left[\frac{-0.0443886}{-0.43410983}\right]=531,708.78$$ $$A_6={531,708.78\left(1-0.015g\right)}^{6-1}=493,009.16$$ $$A_{12}={531,708.78\left(1-0.015g\right)}^{12-1}=450,269.33$$₪ El valor futuro de la serie de flujo de efectivo en gradiente geométrico.
Este valor se calculó en el mismo lugar donde está el último pago de la serie en gradiente geométrico. Recordemos que:
$$F=P\left(1+i\right)^n$$Ahora bien, en el modelo(2.18.2) tenemos a $P$ en función de $A$. Reemplazando (2.18.2) en la ecuación de $F$, resulta:
$$F=A\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^n(g-i)}\right]\left(1+i\right)^n$$ $$F=A\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{(g-i)}\right]\ (2.21)$$Ejercicio 2.9. Cálculo del valor futuro de serie en gradiente geométrico. Un inversionista del sector de la construcción tiene en un centro comercial cinco locales para alquilar, cada uno con un canon de 30 millones de pesos anuales. En los últimos años, el alquiler de locales en dicho centro comercial ha crecido al 5% anual y se espera que esta tendencia continue. Se desea conocer el valor acumulado por arrendamiento de dichos locales en diez años, sobre la base de una tasa de oportunidad del 8% anual.
Solución.
$F=?$
$A=150,000,000$
$g=5.0$% anual
$i=8$% anual
$n=10$ años
Es una situación en la que $g\neq i$
Con (2.21):
$$F=150,000,000\left[\frac{\left(1+0.05\right)^{10}-\left(1+0.08\right)^{10}}{\left(0.05-0.08\right)}\right]$$ $$F=150,000,000\left[\frac{-0.53003037}{\left(-0.03\right)}\right]=2,650,151,852$$Ejercicio 2.10. Valor futuro de dos alternativas de inversión. Se tiene la posibilidad de invertir un capital en dos alternativas de inversión con diferentes plazos. La alternativa A consiste en adquirir acciones de empresa de base tecnológica emergente, en la que se proyecta ganancias con crecimiento del 15% anual durante los próximos cinco años. La opción B es invertir en un fondo que actúa en el mercado en bienes raíces comerciales, con estimación de rendimientos crecientes al 8% anual sostenible durante 9 años. Hallar los valores futuros si para las inversiones se disponen de 10,000 dólares; la tasa de interés es del 10% anual.
Solución.
En ambas opciones $g\neq i$.
Opción A
$g=15$% anual
$A=10,000*0.15=1,500$ dólares
$n=5$ años
$i=10$% anual
Opción B
$g=8$% anual
$A=10,000*0.08=800$ dólares
$n=9$ años
$i=10$% anual
La opción A resulta se más rentable debido al mayor gradiente de crecimiento de los rendimentos aplicado en un plazo más corto de la inversión. En cinco años esta opción logra acumular ganancias de 12,025 dólares.
A este nivel, nos podemos estar preguntado por la situación de la tasa de interés $i$ y del gradiente $g$ como incógnita en una situación financiera, bajo la condición de $ g\neq i$. Para esta inquietud, y desde las ecuaciones de los diferentes modelos matemáticos estudiados, el método de solución es la interpolación lineal.
Si la situación fuera con $g=i$, el asunto es despejar la $i$ desde el modelo (2.19); es decir no se requiere de interpolación. Veamos un caso para $g\neq i$.
Ejercicio 2.11. Cálculo del gradiente geométrico. Una bodega comercial que importa productos chinos misceláneos para surtir emprendedores que los comercializan utilizando internet (ecommerce), realizó ventas en efectivo durante el primer mes de funcionamiento de 100 millones de pesos. El gerente comercial de la bodega ha observado que durante los meses siguientes las ventas han venido creciendo geométricamente alcanzando un acumulado al cabo del año (a los 12 meses) de 2,825.41 millones de pesos. Si la empresa maneja un costos de oportunidad del 3% mensual, ¿En qué porcentaje mensual crecieron las ventas?
Solución.
$g=?$
$A=100$ millones
$F=2,825.41$ millones
$n=12$ meses
$i=3.0$%
Desde el modelo representado por la ecuación (2.21), pasando $A$ a dividir $F$ e igualando a cero, tenemos:
$$\frac{F}{A}-\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{(g-i)}\right]=0$$Ensayo #1: $g=5$%
$$\frac{2,825.4}{100}-\left[\frac{\left(1+0.05\right)^{12}-\left(1+0.03\right)^{12}}{(0.05-0.03)}\right]=9.75$$Diferente de cero. Ensayo #2: $g=10$%
$$\frac{2,825.4}{100}-\left[\frac{\left(1+0.10\right)^{12}-\left(1+0.03\right)^{12}}{(0.10-0.03)}\right]=3.787$$Diferente de cero. Ensayo #3: $g=15$%
$$\frac{2,825.4}{100}-\left[\frac{\left(1+0.15\right)^{12}-\left(1+0.03\right)^{12}}{(0.15-0.03)}\right]=-4.45$$El valor de $g$ está contenido en el intervalo (10%,15%). Procedemos a establecer la ecuación de proporcionalidad.
$$\frac{g-0.10}{0.15-0.10}=\frac{0-3.787}{-4.45-3.787}$$ $$g=\frac{(0.15-0.10)(0-3.787)}{(-4.45-3.787)}+0.10=0.125$$La tasa de crecimiento mensual de la ventas es del 12.5%.
₪ La situación para $n$.
Desde los modelos para las variables $P$, $A$, $F$, es posible despejar $n$ aplicando operaciones de logaritmos. Veamos el caso para $n$, partiendo de la ecuación (2.18).
$$P=\frac{A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]}{(g-i)}$$Es igual a:
$$P(g-i)=A\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]$$ $$\frac{P(g-i)}{A}=\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1$$ $$\frac{P(g-i)}{A}+1=\left(\frac{1+g}{1+i}\right)^n$$ $$\frac{A+P(g-i)}{A}=\left(\frac{1+g}{1+i}\right)^n$$Tomando logaritmo natural en ambos lados de la igualdad:
$$\ln{\frac{A+P(g-i)}{A}}=\ln{\left(\frac{1+g}{1+i}\right)^n}$$ $$n*\ln{\left[\frac{(1+g)}{(1+i)}\right]=\ln{\left[A+P(g-i)\right]-\ln{\left[A\right]}}}$$Ejercicio 2.12. Cálculo de n en serie gradiente geométrico. ¿En cuántos años una cuota trimestral de 1,5 millones de pesos que crece al 2.3% trimestral equivale a un capital inicial de 28,99 millones de pesos? Suponga una tasa de interés del 1.3% mensual.
Solución.
$n=?$
$A=1,5$ millones
$g=2.3$% trimestral
$i=1.3$% mensual y es equivalente a $i=3.95$% trimestral
$P=28.99$ millones de pesos
En total son 24 trimestres que corresponden a 6 años.
Para el manejo a valor equivalente de flujos de efectivo en gradiente geométrico anticipado, podemos aplicar los dos mismos métodos desarrollados para las series en gradiente aritmético. Con el siguiente ejemplo ilustramos la situación; ver Figura 2.11.
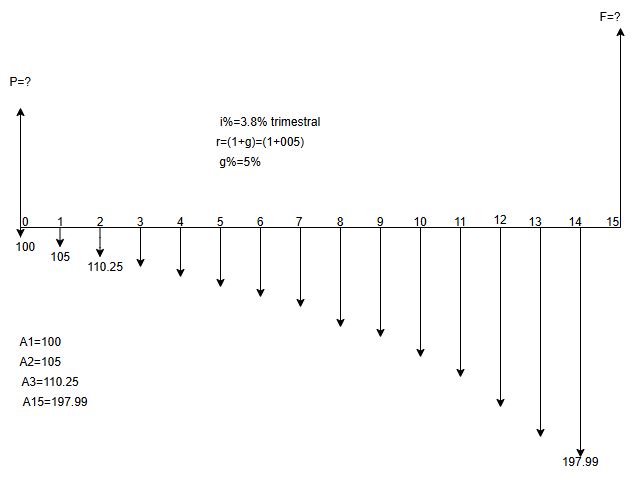
Teniendo de presente la metodología empleada para el caso de gradientes aritméticos, procedemos a plantear la ecuación de solución y el cálculo respectivo, para luego generalizar con el modelo.
Método #1.
$$P=100+105\left[\frac{\left(1+0.05\right)^{14}-\left(1+0.038\right)^{14}}{\left(1+0.038\right)^{14}*(0.05-0.038)}\right]=1,627.68$$En general:
$$P=A_1+A_2\left[\frac{\left(1+g\right)^{n-1}-\left(1+i\right)^{n-1}}{\left(1+i\right)^{n-1}*(g-i)}\right](2.23)$$Empero, como $A_2=A_1(1+g)$, entonces (2.23) es también:
$$P=A_1+A_1(1+g)\left[\frac{\left(1+g\right)^{n-1}-\left(1+i\right)^{n-1}}{\left(1+i\right)^{n-1}*(g-i)}\right]$$ $$P=A_1\left\{1+(1+g)\left[\frac{\left(1+g\right)^{n-1}-\left(1+i\right)^{n-1}}{\left(1+i\right)^{n-1}*(g-i)}\right]\right\}(2.24)$$Considerando que $n-1=15-1$, el resultado es:
$$P=100\left\{1+(1+0.05)\left[\frac{\left(1+0.05\right)^{14}-\left(1+0.038\right)^{14}}{\left(1+0.038\right)^{14}*(0.05-0.038)}\right]\right\}$$ $$P=100\left\{1+15.2768471\right\}=1,627.68$$El modelo (2.24) es más general dado que parte de la base de la serie, $A_1$. Desde esta ecuación, las fórmulas para $A_1$ y $F$, son respectivamente:
$$A_1=P\left[\frac{1}{1+\left(1+g\right)}\right]\left[\frac{\left(1+i\right)^{n-1}\left(g-i\right)}{\left(1+g\right)^{n-1}-\left(1+i\right)^{n-1}}\right]\left(2.25\right)$$ $$F={A_1\left\{1+(1+g)\left[\frac{\left(1+g\right)^{n-1}-\left(1+i\right)^{n-1}}{\left(1+i\right)^{n-1}*(g-i)}\right]\right\}\left(1+i\right)^n}$$Simplificando $(1+i)^n$, tenemos:
$$F=A_1\left\{{(1+i)}^n+(1+g)\left[\frac{\left(1+g\right)^{n-1}-\left(1+i\right)^{n-1}}{\left(1+i\right)^{-1}*(g-i)}\right]\right\}$$Para finalmente obtener:
$$F=A_1\left\{{(1+i)}^n+(1+g)\left[\frac{\left(1+g\right)^{n-1}(1+i)-\left(1+i\right)^n}{(g-i)}\right]\right\} (2.26)$$El valor futuro de la Figura 2.11 es:
$$F=100\left\{{(1.038)}^{15}+(1.05)\left[\frac{\left(1.05\right)^{14}(1.038)-\left(1.038\right)^{15}}{(0.05-0.038)}\right]\right\}$$ $$F=100\left\{(1.74968175)+(1.05)\left[25.4568543\right]\right\}$$ $$F=100\left\{1.74968175+26.729697\right\}=2,847.94$$Para constatar que este valor es correcto, hallemos el valor futuro del valor presente ya calculado de la misma Figura 2.11. Éste es:
$$F=1,627.68\left(1+0.038\right)^{15}=2,847.94$$Método #2.
$$P=100\left[\frac{\left(1+0.05\right)^{15}-\left(1+0.038\right)^{15}}{\left(1+0.038\right)^{15}(0.05-0.038)}\right](1+0.038)$$ $$P=100\left[15.6809703\right](1.03)=1,627.68$$En general la ecuación es:
$$P=A_1\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^n(g-i)}\right](1+i)$$Simplificando:
De igual manera, los modelos para la base de la serie y el valor futuro, son:
$$A_1=P\left[\frac{\left(1+i\right)^{n-1}(g-i)}{\left(1+g\right)^n-\left(1+i\right)^n}\right] (2.28)$$Para $F$:
$$F=A_1\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^{n-1}(g-i)}\right]\left(1+i\right)^n$$
Simplificando $(1+i)^n$:
$$F=A_1\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^{-1}(g-i)}\right]$$ $$F=A_1\left[\frac{\left(1+g\right)^n-\left(1+i\right)^{n}}{(g-i)}\right](1+i) (2.29)$$El valor futuro de la Figura 2.11 es:
$$F=100\left[\frac{\left(1+0.05\right)^{15}-\left(1+0.038\right)^{15}}{(005-0.038)}\right](1+0.038)$$ $$F=100\left[\frac{0.32924143}{0.012}\right]1.038=2,847.94$$Los flujos de efectivo en gradiente geométrico diferidos nos permiten modelar situaciones financieras y de inversiones productivas en las que existe períodos de gracias o en la realización de inversiones que generan ingresos netos después de cierto tiempo con variaciones exponenciales crecientes o decrecientes constantes.
Para el manejo a valor equivalente de los flujos de efectivo en gradiente geométrico diferido aplicamos el mismo procedimiento empleado en el caso de gradiente aritmético. Ver Figura 2.12
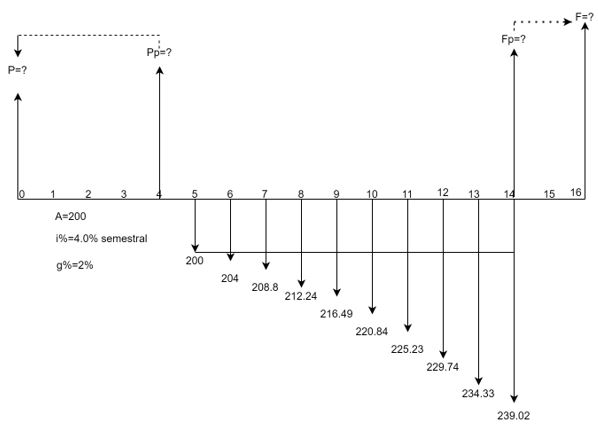
Valor presente. El primer valor está ubicado en la $ff=5$ y el último en la $ff=14$. Debemos calcular un valor presente provisional en $ff=4$, como se indica en la Figura.
Luego, en un segundo paso, descontamos el valor provisional a la $ff=0$ y así hallar el valor presente pretendido. Por lo tanto, realizando simultáneamente los dos pasos, el resultado es:
$$P=200\left[\frac{\left(1+0.02\right)^{10}-\left(1+0.04\right)^{10}}{\left(1+0.04\right)^{10}(0.02-0.04)}\right]\frac{1}{\left(1+0.04\right)^4}$$ $$P=200\left[\frac{-0.26124986}{-0.02960489}\right]*0.85480419=1,508.65$$
Para el primer paso tenemos a $n=10$, que corresponde a los movimientos crecientes de efectivo semestral, y en el segundo paso $n=4$, para un total de desplazamiento de $n=14$. En general, la fórmula queda como:
$$P=A\left[\frac{\left(1+g\right)^n-\left(1+i\right)^n}{\left(1+i\right)^n(g-i)}\right]\frac{1}{\left(1+i\right)^n} (2.30)$$Valor futuro. Para este caso debemos hallar un valor futuro provisional en la $ff=14$ y luego trasladar dicho valor a la $ff=16$. El cálculo es:
$$F=200\left[\frac{\left(1+0.02\right)^{10}-\left(1+0.04\right)^{10}}{(0.02-0.04)}\right]\left(1+0.04\right)^2$$ $$F=200\left[\frac{-0.36124986}{-0.02}\right](1.0816)=2,825.68$$Observar la aplicación de los exponentes. Además invitamos al lector a descontar a la $ff=0$ este valor futuro para obtener de nuevo el valor $P$.
Ejercicio 2.13. Valores presente y futuro de serie diferida en gradiente geométrico. Luego de cinco años de la siembra, un pequeño productor cafetero del suroeste antioqueño comenzó a generar ingresos por la venta de su producto en valor de 20 millones de pesos al final del quinto año. Considerando el crecimiento de la producción y del precio de venta en los mercados internacionales, el productor ha proyectado un crecimiento de los ingresos por venta del 5% anual constante durante 9 años más, momento en que el cultivo alcanza su máxima producción. Si se tiene una rentabilidad del 7% anual, hallar los valores presente y futuro de los ingresos por ventas en el tiempo considerado.
Solución.
$P=?$
$F=?$
$A=20$ millones
$g=5.0$% anual
$i=7.0$% anual
$n=14$ años.
El primer ingreso es n $n=5$ y el último en $n=14$, para un total de 10 ingresos anuales.
$$P=20,000,000\left[\frac{{(1.05)}^{10}-\left(1.07\right)^{10}}{\left(1.07\right)^{10}(0.05-0.07)}\right]\frac{1}{\left(1.07\right)^4}$$En esta salución empleamos en total $n=14$. En el primer factor tenemos a $n=10$, en el segundo factor $n=4$).
El valor futuro se halla en el mismo instante donde está el último ingreso. En este caso $n$ es igual a $10$.
Por lo tanto:
$$F=20,000,000\left[\frac{\left(1+0.05\right)^{10}-\left(1+0.07\right)^{10}}{(0.05-0.07)}\right]$$ $$F=20,000,000\left[\frac{-0.338253}{-0.02}\right]=338,256,731$$Ejercicio 2.14. Anualidad desde serie diferida en gradiente geométrico. Un estudiante inicia este año 2026 estudios doctorales en ingeniería en una universidad pública de la ciudad, con duración de ocho semestres y financiado con recursos públicos. Para el año 2026, el costo semestral es de 10,227,200 pesos, valor que crece cada año en un 7%.
El crédito estudiantil tiene un costo efectivo anual equivalente a la inflación, asumida en 5.2%. Además, al estudiante se le da un año de gracias para iniciar los pagos del crédito, una vez terminado el octavo semestre, y cinco años adicionales para cancelar 60 cuotas mensuales crecientes al 0.1% mensual.Hallar la primera y última cuota.
Es necesario realizar varios pasos para resolver este ejercicio. En primer lugar debemos calcular los desembolsos semestrales que realiza la entidad pública que financia al estudiante, siendo pagos al inicio del semestre. En segundo lugar actualizar el valor de la deuda del estudiante una vez terminado el período de gracia. En tercer lugar, hallar las cuotas.
En el primer año, cada semestre es financiado en un valor de:
$Semestre 1= 10,227,200$, en la ff=0
$Semestre 2= 10,227,200$, en la ff=1
En el segundo año, cada semestre es financiado en un valor 7% mayor que el año anterior. Por ello el nuevo valor semestral es de $10,227,200*1.07=10,943,104$, para las $ff= 2, 3$.
Y así sucesivamente para los restantes dos años. Ver siguiente Figura 2.13 para los demás valores.
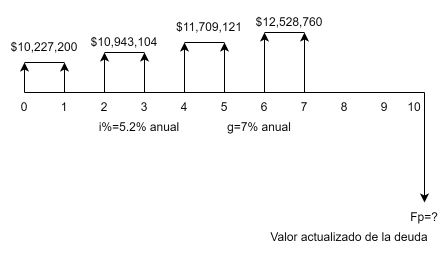
El segundo paso es hallar el valor actualizado de la deuda al $i=5.2$% anual, aplicando el equivalente semestralmente de 2.57% La figura 2.13 es la representación de un gradiente geométrico escalonado, tema que trataremos más adelante en este capítulo.
Para resolver el asunto, cada valor semestral lo asumimos como un valor presente que debemos trasladar (capitalizar) a la fecha focal 10.
$F=10,227,200\left(1.0257\right)^{10}=13,177,573.52$
$F=10,227,200\left(1.0257\right)^9=12,847,764.82$
$F=10,943,104\left(1.0257\right)^8=13,4.3,045.31$
$F=10,943,104\left(1.0257\right)^7=13,067,593.49$
$F=11,709,121\left(1.0257\right)^6=13,632,374.99$
$F=11,709,121\left(1.0257\right)^5=13,291,183.50$
$F=12,528,760\left(1.0257\right)^4= 13,865,628.55$
$F=12,528,760\left(1.0257\right)^3=13,518,599.18$
Para una deuda total de $106,803,763.37 pesos luego del año de gracia. Es sobre este valor que se calcula los pagos mensuales crecientes geométricamente en 0.1%
Como tercer paso tenemos que calcular el primer pago ($A_1$) mensual. Para este cálculo la tasa mes equivalente es de 0.423% y el gradiente geométrico mensual de 0.1%; el valor de la deuda actualizada en este paso es un valor presente $P$. Con la ecuación (2.20) obtenemos:
$$A=106,803,763.37\left[\frac{\left(1+0.00423\right)^{60}*\left(0.001-0.00423\right)}{\left(1+0.001\right)^{60}-\left(1+0.00423\right)^{60}}\right]$$ $$A=106,803,763.37\left[\frac{-0.0041661}{-0.226678305}\right]=1,962,951.56$$El valor de la primera cuota $A_1$ o base $A$ de la serie en gradiente geométrico es de 1,962,951.56 pesos. Para hallar el valor a pagar en la cuota sesenta (último pago), como para cualquier otro cuota deseada, lo realizamos con: $A_n=A_1{(1+g)}^{n-1}$.
Por lo tanto, el último pago es: De cada cuota cancelada, una parte cubre los intereses sobre el saldo y el excedente se dirige a amortizar el capital. Este tema lo estudiaremos en el próximo capítulo sobre sistemas de crédito
$$A_n=A_{60}=1,962,951.56{(1+0.001)}^{60-1}=2,082,189.03$$Con base en la ecuación (2.18) procedemos a obtener el modelo para determinar el valor presente equivalente de una serie perpetua en gradiente geométrico. De nuevo la situación de perpetuidad se representa con $n \to \infin$. En la ecuación (2.18):
$$P=A\frac{\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]}{g-i}$$que reescribimos como: $$P=\frac{A}{g-i}\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]$$
el valor presente $P$ cuando n tiende a infinito depende de si la serie en gradiente geométrico converge, ya que ésta es condición para que el límite exista. Veamos con detalle este asunto.
Pretendemos hallar $P$ como el:
$$\lim_{n\rightarrow\infty}{\frac{A}{g-i}\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]}$$En esta ecuación, la clave de la convergencia está en el cociente $\frac{\left(1+g\right)^n}{\left(1+i\right)^n}$; cociente que reescribimos como:
$$\left(\frac{1+g}{1+i}\right)^n$$¿Qué condición se debe cumplir en el anterior cociente para que la serie en gradiente geométrico converja y el límite exista?.
Todo depende del resultado de la razón (cociente) entre $\frac{1+g}{1+i}$, en la que $i>0$.
Es decir:
En esta situación, la ecuación para $P$ es: $$P=\lim_{n\rightarrow\infty}{\frac{A}{g-i}\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]}$$ $$P={\frac{A}{g-i}\left[0-1\right]}$$ $$P={-\frac{A}{g-i}}$$ $$P={\frac{A}{i-g}}(2.31)$$
La ecuación (2.30) nos sigue siendo útil para este caso, dado que solo debemos prestar atención porque $g$ ahora es negativa, ($-g$).
$$P={\frac{A}{i-(-g)}}$$Estos resultados significan que aunque los flujos de efectivo crezcan o decrezcan a una tasa gradiente constante, el valor presente de todos éstos, descontados a la tasa de interés $i$, es finito. Lo anterior es posible porque la razón ($r$) es menor que uno.
Lo anterior lo podemos observar de la siguiente manera:
$$P=\lim_{n\rightarrow\infty}{\frac{A}{g-i}\left[\frac{\left(1+g\right)^n}{\left(1+i\right)^n}-1\right]}$$ $$P=\frac{A}{g-i}\left[1^n-1\right]$$ $$P={\frac{A}{g-i}\left[0\right]}$$Empero este caso, de hallar $P$ cuando $g=i$, ya se estudió al desarrollar el modelo de la ecuación (2.19). Aplicando derivada, la ecuación con $n \to \infin$ tiene un límite.
Ejercicio 2.15. Valor presente de serie perpetua en gradiente geométrico. El progreso vial del Departamento de Antioquia ha implicado la construcción de diferentes túneles, y la planeación de otros, dada la condición montañosa de la región. Estas obras permiten acortar la longitud de las carreteras, reducir los tiempos de viaje y del consumo de combustible, mejorando la eficiencia del transporte, entre otros efectos positivos. Sin embargo, estos túneles requieren de mantenimiento anual para su correcto funcionamiento.
Suponga que se desea constituir con un depósito único, un fondo para el mantenimiento a perpetuidad del Túnel de Occidente, que estima para el primer año un valor de 500 millones de pesos, valor que crece anualmente en 7.5%. Si la gestión del fondo ofrece rendimientos al 10% anual, determinar el monto del depósito único.
Solución.
$P=?$
$A_1=500$ millones
$g=7.5$%
$i=10$%
El fondo para el mantenimiento del Túnel de Occidente se debe constituir con 20,000 millones de pesos.
Nos vamos a apoyar de nuevo en las Figuras 2.1 y 2.2, así como de la metodología aplicada para obtener las ecuaciones (1.24) y (2.4). El valor presente de los valores que forman el gradiente aritmético bajo capitalización continua, es:
$$P=Ge^{-2J}+2Ge^{-3J}+\ {3Ge}^{-4J}+…+{(n-1)Ge}^{-nJ} (a)$$ $$P=G\left[e^{-2J}+2e^{-3J}+\ {3e}^{-4J}+\ldots+{(n-1)e}^{-nJ}\right] (b)$$Multiplicar (b) por $e^J$:
$$Pe^J=G\left[e^{-J}+2e^{-2J}+\ {3e}^{-3J}+\ldots+{(n-1)e}^{-(n-1)J}\right] (c)$$Restando (c)-(b), tenemos:
$$Pe^J-P=G\left[e^{-J}+e^{-2J}+\ e^{-3J}+\ldots+e^{-(n-1)J}-{(n-1)e}^{-nJ}\right] $$ $$P(e^J-1)=G\left[e^{-J}+e^{-2J}+\ e^{-3J}+\ldots+e^{-(n-1)J}-{(n-1)e}^{-nJ}\right] $$ Como la expresión $-{(n-1)e}^{-nJ}$ es igual a:$-{ne}^{-nJ}+e^{-nJ}=e^{-nJ}-{ne}^{-nJ}$, la última ecuación es ahora:
$$P(e^J-1)=G\left[e^{-J}+e^{-2J}+\ e^{-3J}+\ldots+e^{-(n-1)J}+e^{-nJ}-{ne}^{-nJ}\right] $$Es decir:
$P(e^J-1)=G\left[e^{-J}+e^{-2J}+\ e^{-3J}+\ldots+e^{-(n-1)J}+e^{-nJ}\right]-G{ne}^{-nJ} (d)$
En la ecuación (d), los términos dentro del corchete forman una progresión geométrica con:
$r=e^{-j}$
$a_1=e^{-j}$
$a_n=e^{-nj}$
Recordando que la suma de n términos en progresión geométricamente es:
$$S_n=\frac{a_1-a_n*r}{1-r}$$Ésta es igual a:
$$S_n=\frac{e^{-j}-e^{-nj}*e^{-j}}{1-e^{-j}}$$Simplificando, dicha suma es igual a:Invitamos al lector a realizar el procedimiento operativo para llegar a dicho resultado.
$$S_n=\frac{e^{nj}-1}{e^{nj}(e^j-1)}$$Integrando este resultado en la expresión (d), tenemos en consecuencia:
$$P(e^J-1)=G\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}\right]-G{ne}^{-nJ} $$Tomando factor común $G$
$$P(e^J-1)=G\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}-{ne}^{-nJ}\right]$$ $$P(e^J-1)=G\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}-\frac{n}{e^{nJ}}\right] $$ Para finalmente concluir que el valor presente de las variaciones aritméticas denominadas gradientes (segundo componente de la Figura 2.2), es: $$P=\frac{G}{(e^J-1)}\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}-\frac{n}{e^{nJ}}\right] (32)$$El modelo matemático completo para hallar el valor presente de la Figura 2.2, es por lo tanto:
$$P=A\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}\right]\ +\frac{G}{(e^J-1)}\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}-\frac{n}{e^{nJ}}\right] (33)$$Y si el gradiente aritmético es negativo, $-G$, el modelo es:
$$P=A\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}\right]\ -\frac{G}{(e^J-1)}\left[\frac{e^{nj}-1}{e^{nj}(e^j-1)}-\frac{n}{e^{nJ}}\right] (34)$$El valor presente de la Figura 2.1 ( o de los dos componentes de la Figura 2.2) bajo capitalización continua es:
Así, el valor presente es por lo tanto:
$$P=30\left[\frac{0.17586024}{0.02135712}\right]\ +\frac{10}{0.01816298}\left[\frac{0.17586024}{0.01235712}-\frac{9}{1.75586024}\right]$$ $$P=30\left[8.23426691\right]\ +\frac{10}{0.01816298}\left[8.23426691-7.65397084\right]$$ $$P=30\left[8.23426691\right]\ +550.75055\left[0.58029607\right]=566.52$$₪ El valor futuro
Procedamos a determinar el valor futuro de la misma Figura 2.1. Para ello aplicamos resultados que ya hemos obtenido. Conocemos de (1.27) que $F=A\left[\frac{e^{nj}-1}{e^j-1}\right]\ $, y sabemos también que $F=Pe^{nJ}$.
Ahora bien, siendo además $P$ igual a (32), tenemos que el valor futuro continuo de la serie de las variaciones aritméticas (segundo componente de la Figura 2.2) es en consecuencia:
De esta manera, el valor futuro de la figura 2.1 ( o de los dos componentes de 2.2), es:
$$F=A\left[\frac{e^{nj}-1}{e^j-1}\right]\ +\frac{G}{(e^J-1)}\left[\frac{e^{nj}-1}{e^j-1}-n\right](36)$$Si el gradiente aritmético es negativo, el modelo queda como en $(37)$:
$$F=A\left[\frac{e^{nj}-1}{e^j-1}\right]\ -\frac{G}{(e^J-1)}\left[\frac{e^{nj}-1}{e^j-1}-n\right](37)$$Para el diagrama en cuestión, el valor futuro es:
$$F=30\left[\frac{e^{9*0.018}-1}{e^{0.018}-1}\right]\ +\frac{10}{(e^{0.018}-1)}\left[\frac{e^{9*0.018}-1}{e^{0.018}-1}-9\right]$$ $$F=30\left[\frac{0.17586024}{0.01816298}\right]\ +\frac{10}{0.01816298}\left[\frac{0.17586024}{0.01816298}-9\right]$$ $$F=30\left[9.68234704\right]\ +550.570555\left[9.68234704-9\right]=666.15$$Para constatar si este valor es correcto aplicamos $F=Pe^{nJ}$:
$$F=566.52e^{9*0.018}=666.15$$Igual valor futuro
El valor presente continuo es menor al valor presente con capitalización vencida, mientras que el valor futuro continuo es mayor al respectivo valor futuro vencido. Estos resultados son consistentes con lo estudiado en el tema de las tasas de interés efectivas bajo diferentes modalidades de capitalización
Ejercicio 2.16. Modelos para las anualidades. Se invita al lector a realizar las operaciones algebraicas necesarias para obtener los modelos matemáticos que permitan:
Convertir la serie de gradiente aritmético en serie uniforme
Hallar la anualidad base ($A_1$) a partir de las ecuaciones (33) y (34)
Hallar la anualidad base ($A_1$) a partir de las ecuaciones (36) y (37)
Solución. Las respuestas en su orden son:
Centraremos ahora la atención en el manejo a valor equivalente de los flujos de efectivo, de series de ingresos o egresos, bajo la forma de gradiente geométrico con capitalización continua. De nuevo, los modelos de interés son aquellas ecuaciones que permiten determinar el valor presente, el valor futuro, y la base (anualidad) para hallar la serie geométrica en tiempo finito.
Nos referiremos a la serie en gradiente geométrico vencido y para ello acudimos de nuevo a la Figura 2.10. En términos generales el valor presente es:
$P=Ae^{-J}+A(1+g)e^{-2J}+\ A{\left(1+g\right)^2e}^{-3J}+…+A{\left(1+g\right)^{(n-1)}e}^{-nJ}(a)$
siendo (a) la suma de n términos en progresión geométrica cuya razón común es $r=(1+g)e^{-j}.$
Procedemos a multiplicar la ecuación $(a)*r$, así:
$P(1+g)e^{-j}=A(1+g)e^{-2J}+A\left(1+g\right)^2e^{-3J}+\ A{\left(1+g\right)^3e}^{-4J}+…+A{\left(1+g\right)^ne}^{-(n+1)J} (b)$
Restando $(a)-(b)$:
$$P-P(1+g)e^{-j}=Ae^{-J}-A{\left(1+g\right)^ne}^{-(n+1)J} $$Tomando los respectivos factores comunes en ambos lados de la igualdad:
Desarrollando operativamente, tenemos:
$$P\left[1-\frac{(1+g)}{e^j}\right]=A\left[\frac{1}{e^j}-\frac{\left(1+g\right)^n}{e^{(n+1)j}}\right]$$ $$P\left[\frac{e^j-(1+g)}{e^j}\right]=\frac{A}{e^j}\left[1-\frac{\left(1+g\right)^n}{e^{nj}}\right]$$ $$P\left[e^j-(1+g)\right]=\frac{Ae^j}{e^j}\left[1-\frac{\left(1+g\right)^n}{e^nj}\right]$$ $$P\left[e^j-(1+g)\right]=A\left[\frac{{e^{nj}-\left(1+g\right)}^n}{e^{nj}}\right]$$ $$P=A\left[\frac{{e^{nj}-\left(1+g\right)}^n}{e^{nj}\left[e^j-(1+g)\right]}\right](43)$$Hallemos ahora el valor presente del problema planteado en la figura 2.9. con el modelo (43). Éste es:
$$P=5,800\left[\frac{{e^{5*0.05}-\left(1+0.06\right)}^5}{e^{5*0.05}\left[e^{0.05}-(1+0.06)\right]}\right]$$ $$P=5,800\left[\frac{1.2840-1.3382}{1.2840\left[-0.087289\right]}\right]$$ $$P=5,800\left[\frac{-0.05420016}{-0.0112089}\right]$$Para finalmente:
₪ El valor $A_1$
Desde la ecuación (43) es expedito el modelo para hallar la base de la serie de gradiente geométrico con capitalización continua. Ésta es:
$$A=P\left[\frac{e^{nj}\left[e^j-(1+g)\right]}{{e^{nj}-\left(1+g\right)}^n}\right](44)$$Ejercicio 2.17. Anualidad base de serie en gradiente geométrico capitalización continua . Coro-Tech es una empresa de productos electrónicos que ha acumulado un inventario de 20 millones de dólares al día de hoy. Su gerente Donald Trump se ha propuesto como meta rotar dicho inventario en un plazo de dos años, partiendo de un incremento mensual de las ventas del 2.5% a partir del segundo mes. Si la rentabilidad media de Coro-Tech es de39.29% E.A., ¿De cuánto debe ser las ventas del primer mes?¿de cuánto las ventas en los meses 12 y 24?
Solución.
$A_1=?$
$A_{12}=?$
$A_{24}=?$
$n=24$ meses
$g=2.5$% mensual
$ie=39.29$% E.A., equivalente a $2.8$% mensual
$P=20,000,000$ de dólares
Las ventas del primer mes $A_1$, y base de la serie, es de 889,986.79 dólares. Los otros valores son:
$A_{12}=889,986.79\left(1+0.025\right)^{12-1}=1,167,739.79$
$A_{24}=889,986.79\left(1+0.025\right)^{24-1}=1,570,480.19$
₪ El valor futuro
Si $F=Pe^{nJ}$ y $P=A\left[\frac{{e^{nj}-\left(1+g\right)}^n}{e^{nj}\left[e^j-(1+g)\right]}\right]$, entonces:
$$F=A\left[\frac{{e^{nj}-\left(1+g\right)}^n}{e^{nj}\left[e^j-(1+g)\right]}\right]e^{nJ}$$Cancelando $e^{nJ}$:
$$F=A\left[\frac{{e^{nj}-\left(1+g\right)}^n}{e^j-(1+g)}\right](45)$$Y por lo tanto:
$$A=F\left[\frac{e^j-(1+g)}{{e^{nj}-\left(1+g\right)}^n}\right](46)$$Ejercicio 2.18. El valor de una finca. Hace 20 años se compró una finca de 26 hectáreas por la suma de 10 millones de pesos, dedicada a la producción de leche y productos lácteos. En el primer trimestre de actividades después de la compra, el balance entre ingresos y egresos generó un saldo positivo de 540,000 pesos que, en los trimestres consecutivos creció al 2% neto. Si la rentabilidad media trimestral de la finca ha sido de 2.8%, ¿en cuánto se puede vender la finca hoy?
Solución.
$F=?$
$A_{1}=540,000$
$P=10,000,000$
$n=20$ años u 80 trimestres
$g=2$% trimestral
$J=33.6$% nominal anual, equivalente a 2.8% trimestral
En el problema tenemos un valor presente representado por el capital destinado a la compra de la propiedad, y un flujo de efectivo que crece geométricamente a una tasa del 2% sobre un valor inicial de 540,000 pesos. Así entonces, la solución de:
Es el valor actual de la propiedad desde las variables aquí involucradas. Es un caso simple de valorización al no considerar otras variables que pueden determinar el precio del bien tangible.
Terminamos el desarrollo de modelos para el manejo a valor equivalente de flujos de efectivo, con los gradientes (aritmético y geométrico) escalonados, pero en esta ocasión solo bajo la modalidad de capitalización vencida.
En general, un gradiente escalonado es una secuencia de flujos de efectivo (pagos, ingresos o egresos, de flujos netos) en la que sus valores permanecen constantes durante períodos específicos, para luego cambiar en una cantidad fija en el siguiente período, ver Figura 2.14. Los nuevos valores, como los de $A_2$, se mantiene fijo durante el nuevo período, que tiene duración igual al período anterior; y así sucesivamente.
En Figura 2.14, El comportamiento de la serie de pagos describe una forma de “escalón”, por ello su denominación de escalonado. En ella, $t$ son los períodos, y hacen también referencia al número de escalones.
En cada período $t$ (escalón) existe un número finito de cuotas fijas, siendo su cantidad total identificada con la letra $n$.
Las cuotas pueden ser valores mensuales, trimestrales, etc.
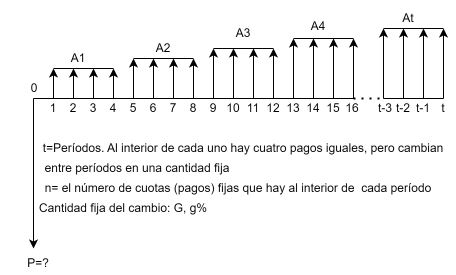
Por ejemplo, en cada período de la figura 2.14, hay cuatro cuotas fijas. Si estas cuotas son trimestrales entonces $n=4$ y cada $t$ es un año.
Para hacer el cálculo del valor presente de la serie escalonada, sea aritmética o geométrica, es necesario definir dos variables adicionales, además de las ya conocidas $G$ y $g$
Apoyados en la Figura 2.14, así como en modelos y procedimientos ya presentados, vamos a proceder con la determinación de la ecuación para hallar el valor presente equivalente de un flujo de efectivo como el representado en señalada Figura. Procederemos indicando varios pasos.
Paso 1. Hallar el valor futuro de cada serie uniforme al final de cada período. Ver figura 2.15.
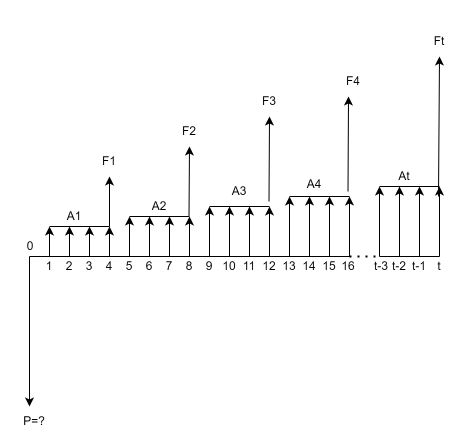
Los valores Futuros son:
$$F_1=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]$$ $$F_2=A_2\left[\frac{\left(1+i\right)^n-1}{i}\right]$$ $$F_3=A_3\left[\frac{\left(1+i\right)^n-1}{i}\right]$$ $$F_t=A_t\left[\frac{\left(1+i\right)^n-1}{i}\right]$$Así es posible escribir una primera ecuación para $P$, como la siguiente:
$$P=\frac{F_1}{(1+ie)}+\frac{F_2}{\left(1+ie\right)^2}+\frac{F_3}{\left(1+ie\right)^3}+...+\frac{F_t}{\left(1+ie\right)^t}$$Paso 2. Expresar la anterior ecuación en términos del equivalente de cada $F$.
$P=\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}+\frac{A_2\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+\frac{A_3\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^3}+...+\frac{A_t\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$
Ahora bien, desde la definición de progresión aritmética estamos habilitados para escribir que:
$$A_2=A_1+G$$ $$A_3=A_1+2G$$Y en general:
Empleando lo anterior, la ecuación del paso 2 es igual a:
$P=\frac{A_1\left[\frac{{(1+i)}^n-1}{i}\right]}{\left(1+ie\right)}+\frac{\left[A_1+G\right]\left[\frac{{(1+i)}^n-1}{i}\right]}{\left(1+ie\right)^2}+...+\frac{\left[A_1+(t-1)G\right]\left[\frac{{(1+i)}^n-1}{i}\right]}{\left(1+ie\right)^t}$
Paso 3. Aplicando propiedad distributiva:
$A_2\left[\frac{\left(1+i\right)^n-1}{i}\right]=\left[A_1+G\right]\left[\frac{\left(1+i\right)^n-1}{i}\right]=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]+G\left[\frac{\left(1+i\right)^n-1}{i}\right]$
$A_3\left[\frac{\left(1+i\right)^n-1}{i}\right]=\left[A_1+2G\right]\left[\frac{\left(1+i\right)^n-1}{i}\right]=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]+2G\left[\frac{\left(1+i\right)^n-1}{i}\right]$
$A_t\left[\frac{\left(1+i\right)^n-1}{i}\right]=\left[A_1+(t-1)G\right]\left[\frac{\left(1+i\right)^n-1}{i}\right]$, siendo además igual a:
$A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]+(t-1)G\left[\frac{\left(1+i\right)^n-1}{i}\right]$.
Procedemos a determinar el valor presente para la serie uniforme $A_1$, y luego el valor presente para la serie de gradientes $G$.
Paso 4. Valor presente de la serie uniforme ($A_1$).
La ecuación es:
$P_A=\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}+\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^3}+...+\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$
Tomando factor común $\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}:$
Al interior del corchete de la anterior ecuación, tenemos la suma de $t$ términos en progresión geométrica con:
Por lo tanto, y siendo $S_t=\frac{a_1-a_t*r}{1-r}$, tenemos:
$$S_t=\frac{1-\frac{1}{\left(1+ie\right)^{t-1}}*\frac{1}{(1+ie)}}{\frac{1+ie-1}{\left(1+ie\right)}}$$ $$S_t=\frac{1-\frac{1}{\left(1+ie\right)^t}}{\frac{1+ie-1}{(1+ie)}}$$ $$S_t=\frac{\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^t}}{\frac{ie}{(1+ie)}}$$Realizando multiplicación de extremos y medios:
$$S_t=\left[\frac{\left[\left(1+ie\right)^t-1\right](1+ie)}{\left(1+ie\right)^tie}\right]$$Así obtenemos que:
$$P_A=\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}\left[\frac{\left(1+ie\right)^{t+1}-(1+ie)}{\left(1+ie\right)^tie}\right]$$ $$P_A=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^{t+1}-(1+ie)}{\left(1+ie\right)^tie(1+ie)}\right]$$Para finalmente lograr que:
$$P_A=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}\right]$$Paso 5. Valor presente de la serie de $G$.
En lo básico, para este componente se realiza el mismo procedimiento para $P_A$. La ecuación de partida, (a),es:
$P_G=\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+\frac{2G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^3}+\frac{3G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^4}+...+\frac{(t-1)G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$
Multipliquemos la ecuación $(a)$ por $(1+ie)$, y obtenemos (b):El lector notará que no se incluye todos los elementos que explícitamente se presentaron en la ecuación anterior. Esto se debe a cuestiones de espacio para dar una mejor presentación a la ecuación obtenida.
$$P_G(1+ie)=\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}+\frac{2G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+...+\frac{(t-1)G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^{t-1}}$$Restando las ecuaciones (b)-(a):
Al lado izquierdo de la nueva igualdad tendríamos la resta de: $P_G(1+ie)-P_G=P_G(1+ie-1)$, siendo igual a $P_G*ie$
Entonces:
$P_G*ie=\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}+\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+...-\frac{(t-1)G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$(c)
Ahora bien, como el último factor de la ecuación $(c)$:
$$-\frac{(t-1)G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}=-\frac{tG\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}+\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t} $$E igual a:
$$-\frac{(t-1)G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}=\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}-\frac{tG\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$$Obtenemos de nuevo la ecuación (c) como:
$P_G\ast ie=\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)}+\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+\ldots+\frac{G\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}-\frac{tG\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$
Agrupando términos comunes:
$P_G*ie=G\left[\frac{\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}+\frac{\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^2}+...+\frac{\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}\right]-\frac{tG\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^t}$
En el corchete de la ecuación anterior se encuentra la suma de $t$ términos en progresión geométrica. Basados en los procedimientos realizados para el componente $P_A$, en esta ocasión resulta que:
Tomando factor común $G\left[\frac{\left(1+i\right)^n-1}{i}\right]$
$$P_G\ast ie=G\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}-\frac{t}{\left(1+ie\right)^t}\right]$$Para finalmente:
$$P_G=\frac{G}{ie}\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}-\frac{t}{\left(1+ie\right)^t}\right]$$Así entonces, el valor presente de la Figura 2.14 es:
$${P=P}_A+P_G (47)$$$P=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}\right]+\frac{G}{ie}\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}-\frac{t}{\left(1+ie\right)^t}\right]$
Y si el gradiente aritmético es negativo ("los escalones descienden"), el modelo es la siguiente ecuación (48):
$P=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}\right]-\frac{G}{ie}\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}-\frac{t}{\left(1+ie\right)^t}\right]$
En las ecuaciones (47) y (48) se presentan dos porcentajes. El primero es la tasa de interés $i$, tasa periódica; que se utiliza para hallar los valores futuros de las series uniformes incluidas en cada período o "escalón”. El segundo es la tasa de interés $ie$, generalmente anual y empleada para descontar cada uno de los valores futuros.
Además, en los componentes las tasas de interés ($i$, $ie$) comparten la unidad de tiempo que tienen $A_1$ y $F$. Recordar además la relación de equivalencia que hay entre ellas.
Ejercicio 2.19. El valor presente de serie escalonada aritméticamente. Un capital fue prestado con una cuota mensual vencida del 800.000 para el primer año al 1.5% mensual y un plazo de 8 años. El sistema de pago se determinó por cuota escalonada aritméticamente con un incremento de 50,000 pesos anuales. ¿A cuánto asciende el capital prestado? y ¿de qué valor es la cuota mensual en el año 8?
Solución.
$P=?$
$A_{1}=800,000$
$G=50,000$
$t=8$ años (escalones)
$n=12$ (cuotas mensuales de cada escalón)
$i=1.5$% mensual (cuotas mensuales)
$ie=(1+0.015)^{12}-1=19.56$%. Esta tasa es efectiva anual y se corresponde con $t$ en años (escalones anuales).
₪ El valor presente de las anualidades
$$P_A=800,000\left[\frac{\left(1+0.015\right)^{12}-1}{0.015}\right]\left[\frac{\left(1+0.1956\right)^8-1}{\left(1+0.01956\right)^80.1956}\right]$$₪ El valor presente de los gradientes
$P_G=\frac{50,000}{0.1956}\left[\frac{\left(1+0.015\right)^{12}-1}{0.015}\right]\left[\frac{\left(1+0.1956\right)^8-1}{\left(1+0.1956\right)^80.1956}-\frac{8}{\left(1+0.1956\right)^8}\right]$
$$P_G=255,600\left[13.04\right]\left[1.972\right]=6,573,351$$ $$P=40,561,340+6,573,351=47,134,691$$Para el año 8, se tiene 12 cuotas mensuales de:
$$A_8=800,000+(8-1)50,000=1,150,000$$Se invita al lector a realizar los cálculos para los demás escalones y ubicarlos en el diagrama de caja de la Figura 2.16.
Desde el modelo (47) despejamos $A_1$ para hallar la base del flujo de efectivo. En el modelo (47) el gradiente es positivo. Con un poco de matemáticas operativas obtenemos:
$$A_1=P\left[\frac{i}{\left(1+i\right)^n-1}\right]\left[\frac{\left(1+ie\right)^tie}{\left(1+ie\right)^t-1}\right]-G\left[\frac{1}{ie}-\frac{t}{\left(1+ie\right)^t-1}\right](49)$$Ejercicio 2.20. Anualidad y gradiente aritmético escalonado. A última hora, el estudiante de doctorado del ejercicio 2.14 decide cancelar en crédito por medio de cuotas mensuales que crecen cada año en 10,000. Si la tasa de interés es el mismo 5.2% efectivo anual y el plazo de cinco años, hallar la cuota mensual a cancelar por año, recordando que la deuda acumulada es de $106,803,763.
Solución.
$A_1=?$
$P=106,803,763$
$ie=5.2$% anual
$i=0.4233$% mes equivalente
$n=12$ meses
$t=5$ años
$G=10,000$ anual
Con modelo (49), tenemos:
$A_1=106,803,763\left[\frac{0.004233}{\left(1+0.004233\right)^{12}-1}\right]\left[\frac{\left(1+0.052\right)^50.052}{\left(1+0.052\right)^5-1}\right]-10,000\left[\frac{1}{0.052}-\frac{5}{\left(1+0.052\right)^5-1}\right]$
$$A_1=106,803,763.37\left[0.018908\right]-10,000\left[1.89073\right]=2,000,450.04$$El primer año pagará doce cuotas mensuales iguales de $2,000,450$ pesos. Para el segundo año, la cuota mensual se incrementa en $10,000$, quedando en un monto de $2,010,450$ pesos; y así sucesivamente para los restantes tres años. Ver flujo de efectivo en Figura 2.17
₪ El valor futuro de serie en gradiente escalonado
Partamos de la definición de valor futuro como $F=P(1+ie)^t$, es decir determinándolo con base en los escalones y la tasa de interés respectiva del período. Es posible también resolver el valor futuro empleando la tasa de interés periódica, la $i$ del período de la anualidad, pero para ello es requerido redefinir la variable $n$.
En este último caso, $n$ debe ser tratado, no como la cantidad de anualidades al interior de un escalón, sino como equivalente al plazo total de la operación financiera involucrada. Si $t=8$ años y $n=12$ cuotas mensuales, para el problema del valor futuro se redefine como $n=12*8=96$ meses. Veamos el primer caso:
Con la anterior ecuación del valor futuro y reemplazando en ella la ecuación (47), con gradiente aritmético positivo, la fórmula para el valor futuro de flujo de efectivo en gradiente aritmético escalonado es:
$F=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{ie}\right]+\frac{G}{ie}\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(ie\right)}-t\right]$(50)
Ejercicio 2.21. Valor futuro de gradiente aritmético escalonado. Hallar el valor futuro con los datos del ejercicio 2.19, constatando además las afirmaciones sobre las formas de hallar dicho valor futuro indicadas en párrafos anteriores.
Solución.
$F=?$
$P=47,134,691$
$A_{1}=800,000$
$G=50,000$
$t=8$ años
$n=12$ meses, o 12 cuotas por escalón
$i=1.5$% mensual
$ie=(1+0.015)^{12}-1=19.56$%.
Método 1. Solución aplicando la ecuación (50). Reemplazando los valores y realizando cálculos, tenemos:
$$F=800,000\left[13.04\right]\left[16.2347\right]+255,600\left[13.04\right]\left[8.2347\right]$$ $$F=169,337,187.67+27,449,020.29=196,825,207.96$$Método 2. Aplicando la fórmula de futuro vencido pago único con las variables $t$ e $ie$ (en el ejercicio son datos anuales). Para este caso, y el siguiente, conocemos a $P$.
$$F=47,134,691(1+0.195618171)^8=196,825,207.96$$Método 3. Aplicando $n$ e $i$ (en el ejercicio datos mensuales).
$$F=47,134,691(1+0.015)^{96}=196,825,207.96$$Por los tres métodos, el resultado para $F$ es el mismo.
En este tópico, la serie de flujo de efectivo escalonado cambia sus valores entre períodos con base en un porcentaje, que ya hemos representado por la letra $g$. La variación entre períodos de la serie es, por esta razón geométrica; la serie crecen o decrecen escalonadamente de modo exponencial.
El procedimiento para hallar el modelo que posibilite el cálculo del valor presente es similar al caso aritmético. Conservamos las mismas definiciones de las variables, pero ahora trabajamos con $g$. Con base en las Figuras 2.14 y 2.15 podemos plantear inicialmente que:
Haciendo explícito la equivalencia de cada $F$, tenemos:
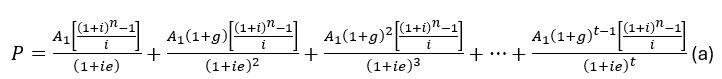
La anterior ecuación es la expresión de la suma de $t$ términos en progresión geométrica cuya razón es $r=\frac{\left(1+g\right)}{\left(1+ie\right)}.$ Multiplicando $(a)*r$, obtenemos:
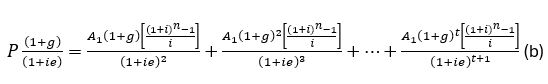
Restando $(a)-(b)$, en la que términos intermedios se anulan, resultando:
$$P-P\frac{\left(1+g\right)}{\left(1+ie\right)}=\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}-\frac{A_1\left(1+g\right)^t\left[\frac{\left(1+i\right)^n-1}{i}\right]}{\left(1+ie\right)^{t+1}}$$Realizando la resta en el lado izquierdo de la anterior igualdad y tomando factor común en su lado derecho, obtenemos:
$$\frac{P(1+ie)-P\left(1+g\right)}{\left(1+ie\right)}=\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}\left[1-\frac{\left(1+g\right)^t}{\left(1+ie\right)^t}\right]$$Y es igual a:
$$\frac{P(ie-g)}{\left(1+ie\right)}=\frac{A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]}{(1+ie)}\left[1-\frac{\left(1+g\right)^t}{\left(1+ie\right)^t}\right]$$ $$P(ie-g)=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{{\left(1+ie\right)^t-\left(1+g\right)}^t}{\left(1+ie\right)^t}\right]$$Y así finalmente concluir con:
$$P=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{{\left(1+ie\right)^t-\left(1+g\right)}^t}{\left(1+ie\right)^t(ie-g)}\right] (51)$$Para $ g\neq ie$.
Para una gradiente geométrico negativo, como ($-g$), tenemos:
$$P=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{{\left(1+ie\right)^t-\left(1-g\right)}^t}{\left(1+ie\right)^t(ie+g)}\right](52)$$Ejercicio 2.22. El valor presente. El presupuesto de ingresos netos de una compañía estimó 4,800 dólares mensuales para el primer año. Para los cuatro años siguientes, se supone que el flujo de ingresos crecerá de manera geométrica en un 6.5% anual respecto al año anterior. Si el costo de oportunidad es 10% E.A, hallar el valor presente de este presupuesto.
Solución.
$P=?$
$A_{1}=4,800$
$g=6.5$%
$t=5$ años
$n=12$ meses o cuotas del escalón
$ie=10$% anual, tasa equivalente a $i=0.797$% mensual
₪ La base de la serie gradiente; $A_1$.
De la ecuación (51), tenemos que:
$$ A_1=P\left[\frac{i}{\left(1+i\right)^n-1}\right]\left[\frac{\left(1+ie\right)^t(ie-g)}{\left(1+ie\right)^t-\left(1+g\right)^t}\right](53)$$₪ El valor futuro
Si $F=P(1+ie)^t$ y reemplazamos $P$ por la ecuación (51), tenemos que:
$$F=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{{\left(1+ie\right)^t-\left(1+g\right)}^t}{(ie-g)}\right](54)$$Se deja al lector la obtención de las mismas dos fórmulas anteriores en el caso de gradiente geométrico negativo, o sea con (-g).
Ejercicio 2.23. La anualidad. La siderúrgica Steel.LLC necesita 2,5 millones de dólares de capital externo a la compañía para financiar el desarrollo de la producción de aceros de baja aleación. Para ello se compromete a cancelar cuotas fijas trimestrales que crecen anualmente en 4.5% como compensación media por pérdida del poder adquisitivo del capital por inflación. La tasa de interés ofrecida es de 8.5% efectiva anual por el monto solicitado. Si el plazo de la operación es de diez años, hallar el valor de las cuotas trimestrales del primer y último año.
Solución.
$A_{1}=?$
$A_{10}=?$
$P=2,500,000$
$g=4.5$% anual
$t=10$ años
$n=4$ trimestre, y número de cuotas del escalón
$ie=8.5$% E.A., tasa equivalente a $i=2.06$% trimestral
Para $A_{10}$:
Ejercicio 2.24. El valor futuro. Hallar el valor futuro de las cuotas obtenidas en el anterior ejercicio y constatar si también se aplican las diferentes formas de hallar dicho valor futuro, como se realizó en el ejercicio 2.21 .
Método 1: Aplicando ecuación (54)
$$F=77,409.90\left[\frac{\left(1.0206\right)^4-1}{0.026}\right]\left[\frac{{\left(1.085\right)^{10}-\left(1.045\right)}^{10}}{(0.085-0.045)}\right]$$ $$F=72,879.58\left[4.125333287\right]\left[17.7003505\right]=5,652,458.60$$Método 2. Aplicando $t$ e $ie$ (en el ejercicio datos anuales).
$$F=2,500,000(1+0.085)^{10}=5,652,458.60$$Método 3. Aplicando $n$ e $i$ (en el ejercicio datos trimestrales).
$$F=2,500,000(1+0.020604396)^{40}=5,652,458.60$$Estos métodos son modos como el estudiante puede desarrollar habilidades para confirmar las respuestas y estar seguro de sus resultados, traduciéndose este hecho en camino para la autonomía en el aprendizaje y la formación profesional.
₪ Cuestionario.
₪ Problemas.
R. P=376,931,111 pesos, F=879,247,269 pesos, A=4,673,406 pesos. R. Crédito:140,708,788, de contado:201,012,555; crédito:141,205,007, de contado:201,721,439; respectivamente. R. Opción #1: 22,473, 23,663, 3,934,303; opción #2 19,533, 27,898, 3,934,303; respectivamente. R. $$P=\frac{A}{e^j-1}+\frac{G}{{{(e}^j-1)}^2}$$
$$P=\frac{A}{ie}+\frac{G}{{\rm ie}^2}$$R. G=100,000, g=0.57%, G=100,783, respectivamente. R. Opción #1: 141,240,483 y 135,540,483. Opción #2: 149,763,015 y 123,729,504; respectivamente.R. Aritmético: 145,207,049 y 139,570,049. Geométrico: 154,041,033 y 127,263,868; respectivamente. R. Gradiente: g=0.442%; ecuación:
$$P=\frac{A}{e^j-(1+g)}$$ R. P=1,626,187 dólares; F=2,502,091 dólares. R. P=1,472,490 dólares, F=2,204,061 dólares.Por sistemas de crédito nos queremos referir al diseño de diferentes esquemas para cancelar o amortizar un capital tomado en préstamo (una obligación financiera).
Para Plaza V.
...consiste en un desembolso por parte del prestamista y una serie de pagos denominadas cuotas, por parte del prestatario, y una tasa de interés. Cada cuota tiene dos componentes: primero, el interés que sería el costo del crédito o ingreso del prestamista, y segundo, la amortización, que es el pago del préstamo propiamente dicho, que es denominado el capital o el principal.
Según Aguilera y Díaz,
Es por lo tanto, la cancelación gradual de un crédito por medio de cuota fija. Sin embargo, también existe esquemas de amortización de deudas que aplican pagos con valores que crecen o decrecen de manera uniforme, por ejemplo en gradiente.
Para los profesores González y Medina
...denominar un proceso financiero mediante el cual se disminuye, gradualmente, una deuda por medio de pagos periódicos, que pueden ser iguales o diferentes. Por lo tanto se puede aplicar diversos sistemas de amortización y dentro de cada uno hay numerosas variantes.
Una manera práctica de representar los diferentes sistemas de crédito, es por medio de tablas de amortización.Recordemos que cada pago realizado en la cancelación de una deuda, ya sea por cuota fija o cuota variable en gradiente, tiene dos componentes: intereses sobre el saldo y la amortización, es decir que $A=I+R$, como ya estudiamos en el volumen uno de este libro.
Para observar lo que sucede con las cuotas, los intereses, la amortización y el saldo de la deuda a medida que pasa el plazo otorgado en el préstamo, es que acudimos a la representación por medio de tablas de amortización, de las que a su vez obtenemos algunas gráficas.
La base de estos esquemas es lo estudiado en el capítulo uno de este libro. Hallar una cuota fija, es aplicar un modelo de los estudiados para calcular $A$. Estudiaremos diferentes esquemas de amortización bajo capitalización vencida, para pagos realizados de forma vencido, anticipado o diferido.
Veamos la siguiente situación:
Ejercicio 3.1 Sistema de amortización con cuota fija vencida. Una computadora Personal con valor de $4,800,000 se compra a crédito por medio de 4 cuotas trimestrales iguales al 5.8% trimestre. Hallar el valor de la cuota y elaborar la tabla de amortización.
Solución
$A=?$
$P=4,800,000$
$i=5.8$% trimestre
$n=4$ trimestres y cuatro cuotas
Debemos hallar el pago o cuota fija desde un valor presente, por ello:
$$A=4,800,000\left[\frac{\left(1+0.058\right)^4*0.058}{\left(1+0.058\right)^4-1}\right]=1,378,901$$Los intereses y amortización de la primera cuota son:
$$I_1=4,800,000*0.058=278,400$$ $$R_1=1,378,901-278,400=1,100,501$$De esta manera, el saldo insoluto al final del primer trimestres es de:
$$S_1=4,800,000-1,100,501=3,699,499$$Los intereses y la amortización de la segunda cuota, así como el nuevo saldo, son:
$$I_1=3,699,499*0.058=214,571$$ $$R_1=1,378,901-214,571=1,164,330$$ $$S_1=3,699,499-1,165,330=2,535,170$$Procedemos de igual manera hasta completar los cuatros trimestres y culminar con saldo igual a cero. Ver la siguiente Tabla 3.1.
| $n$ | Cuota | Interés | Amortización | Saldo |
|---|---|---|---|---|
| 0 | - | - | - | -4,800,000 |
| 1 | 1,378,901 | 278,400 | 1,100,501 | 3,699,499 |
| 2 | 1,378,901 | 214,571 | 1,164,330 | 2,535,170 |
| 3 | 1,378,901 | 147,040 | 1,231,861 | 1,303,309 |
| 4 | 1,378,901 | 75,592 | 1,303,309 | 0 |
₪ Solución del ejercicio en hoja de cálculo Excel
En la elaboración de la tabla de amortización del anterior ejercicio podemos acudir a la funciones predefinidas de Excel, como se presentan en la siguiente Figura 3.1
En la función PAGO, el argumento tipo puede tomar dos valores. Cuando tipo es igual a cero el PAGO se calcula como cuota vencida; en cambio sí tipo es uno, el cálculo de la cuota $A$ se realiza de modo anticipado; empero recordemos que la capitalización es vencida en ambos casos.
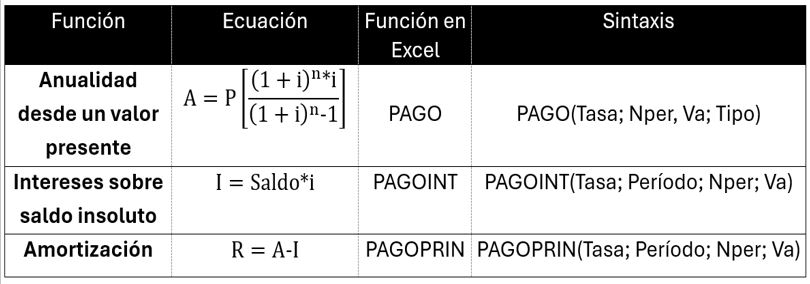
En las funciones PAGOINT y PAGOPRIN, el argumento Período permite identificar al pago específico (cuota o anualidad) objeto del cálculo de los respectivos intereses sobre el saldo y del excedente que se destina a amortización. Por ejemplo, si en ambas funciones el argumento período es dos, a la cuota dos se determina cuánto es por intereses sobre el saldo, y cuánto se destina a amortización.
El cálculo de la cuota es como en la siguiente Figura 3.2.
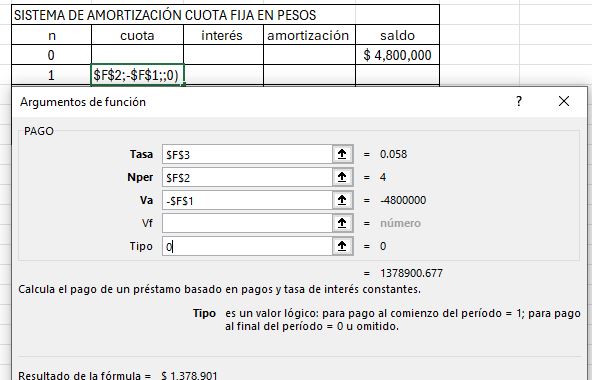
Obsérvese que se ha usado celdas absolutas en el cálculo.
De esta cuota una parte se destina a pagar intereses sobre el saldo de la deuda y su excedente para amortización, como ya se indicó. Para los intereses del primer trimestre ver Figura 3.3.
Los argumentos de la función PAGOINT: Tasa, Nper y Va, están en celdas absolutas. El argumento Período está en celda relativa y con valor 1 indicando los intereses a cubrir con la primera cuota.
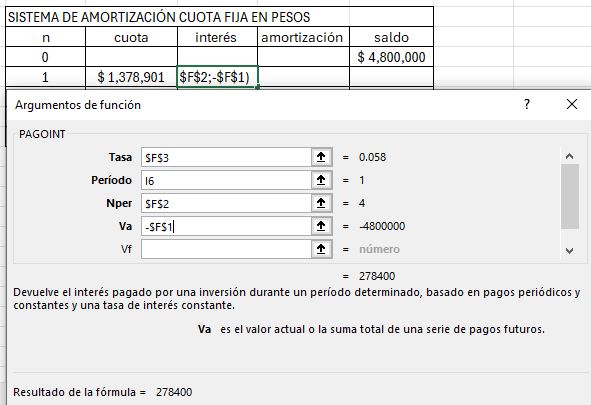
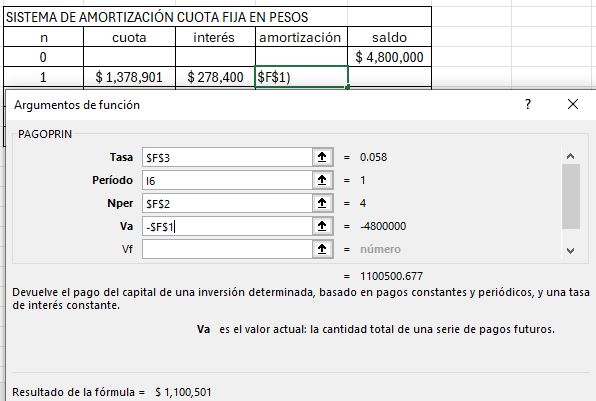
La función PAGOPRIN tiene los mismos argumentos y características de la función PAGOINT. Ver anterior Figura 3.4
Para el saldo insoluto, en Excel restamos al saldo anterior el monto de la amortización, usando celdas relativas. Ver Figura 3.5
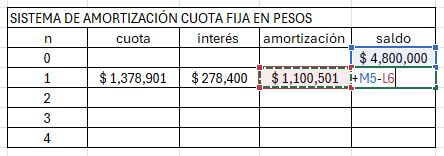
Hemos así terminado la programación de la primera fila de la tabla de amortización, aplicando celdas absolutas y relativas. Para completar la tabla solo resta señalar toda la fila programada y dar doble clic en el vértice inferior derecho (punto amarillo), como en Figura 3.6.
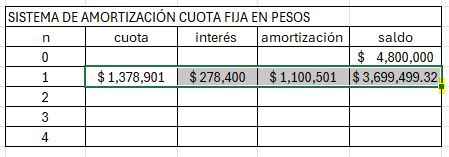
La tabla completa se puede observar en la siguiente Figura 3.7.
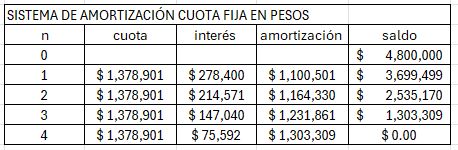
Tenemos por lo tanto un sistema de cancelación de deuda por medio de cuotas fijas vencidas (serie uniforme o anualidad) con intereses decrecientes sobre el saldo insoluto y amortización o abonos al capital crecientes. Desde la cancelación de la primera cuota el saldo de la deuda comienza a disminuir. Por esta característica, este sistema es ampliamente utilizado en diferentes créditos, como es por ejemplo en la compra de vivienda, vehículos, crédito comercial, en la adquisición de maquinaria y equipos, entre otros.
En los créditos de vivienda, que se hacen generalmente a largo plazo, a 10, 15, 18 o más años, la programación es la misma. Si los pagos son cuotas mensuales, un crédito de vivienda a 15 años implica que $n=15*12=180$ meses o cuotas, haciendo más extensas (más filas) la tabla; pero la metodología para la elaboración del esquema de amortización es la misma que acabamos de describir.
Sobre las formas de determinar el saldo de un préstamo sin necesidad de elaborar la tabla de amortización, Meza Orozco
Así por ejemplo, en el ejercicio 3.1 una vez cancelada la cuota dos quedan por cancelar otros dos pagos. Por ello, el saldo en $ff=2$ es:
$$P=1,378,901\left[\frac{\left(1+0.058\right)^2-1}{\left(1+0.058\right)^20.058}\right]=2,535,170$$Resultado igual al valor del saldo en la fila dos ($n=2$) de la tabla de amortización de Figura 3.7.
Valor futuro de la deuda en n=2:
$F=4,800,000(1+0.058)^{2}=5,372,947$
Valor futuro de las cuotas canceladas hasta n=2:
$F=1,378,901\left[\frac{\left(1+0.058\right)^2-1}{0.058}\right]=2,837,777$
Saldo insoluto:
El anterior sistema se aplica en créditos para compra de vivienda que se cancelan por intermedio de cuotas fijas en UVR. En el capítulo 4 del volumen uno de este libro, se estudió el tema de la tasa remunerativa, efectiva anual y periódica, y la tasa efectiva anual de operaciones en UVR.
Dichos conceptos son aplicados en este sistema de crédito. Veamos el asunto con un ejercicio.
Ejercicio 3.2 Sistema de amortización con cuota fija en UVR. Se solicita un crédito por 200 millones de pesos destinados a la adquisición de vivienda y ser cancelado por medio de cuota fija mensual, con plazo de quince años. Para el ejercicio se supone que el valor de la UVR al momento de simular el crédito es de 378.61 pesos la unidad; además se supone como inflación el 7% E.A. y la tasa remunetativa del 11% E.A. Elaborar la tabla de amortización para este crédito.
Solución
$A=?$ Cuota mensual
$P=200,00,000$
$\pi_{anaul}=7.0$% E.A., la inflación
${\rm ie}_r=11.0$% E.A., es la tasa remunerativa
$n=15$ años y equivalente a 180 meses, también es el número de cuotas
${\rm UVR}_0=378.61$, es la UVR base (del día de la simulación del crédito)
Con estas información procedemos a calcular los valores equivalentes de las siguientes variables:
Ahora bien, como las cuotas son mensuales, estos datos anuales los debemos convertir a equivalente mensual. Por lo tanto:
Con estos nuevos valores mensuales procedemos a realizar las proyecciones de las diferentes columnas de la tabla de amortización. En cada momento de la elaboración se irá especificando la aplicación en concreto de cada tasa. En la tabla de Excel disponemos de toda la información como se presenta en la siguiente Figura 3.8
₪ Proyección de la UVR.
Para la proyección del valor de la UVR en el plazo del préstamo, realizamos la estimación mensual de ésta considerando su valor base, la inflación mensual y el momento o mes específico para el que se hace la proyección. En esta tarea recurrimos a la siguiente fórmula:
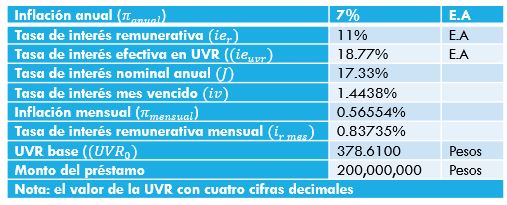
${\rm UVR}_t={\rm UVR}_0\left(1+\pi_{mensul}\right)^t$, con $t=1,2,3...n$
Por lo tanto, la proyección de los valores de la UVR para $n=1,20,150,180$, son:
${\rm UVR}_1=378.6100\left(1+0.005654\right)^1=380.7507$
${\rm UVR}_{20}=378.6100\left(1+0.005654\right)^{20}=433.8040$
${\rm UVR}_{150}=378.6100\left(1+0.005654\right)^{150}=882.0829$
${\rm UVR}_{180}=378.6100\left(1+0.005654\right)^{180}=1,044.5969$
La inflación mensual se aplica en la estimación del valor mensual de la UVR, desde n=1,...,180.
₪ El monto del préstamo expresado en UVR.
Para convertir el capital tomado en préstamo a Unidades de Valor Real, procedemos a dividir dicho capital por el valor base de la UVR:
$$P_{UVR}=\frac{200,000,000}{378.6100}=528,248.0653\ UVR$$₪ La anualidad, los intereses sobre el saldo, la amortización y el saldo insoluto, en UVRs
El procedimiento para determinar en UVRs las magnitudes de estas variables es el mismo aplicado en el ejercicio 3.1. Sin embargo, la tasa de interés a utilizar en los cálculos es la remunerativa mensual. Recordemos que la tasa remunerativa efectiva anual es la tasa de interés que se aplica al capital en UVR y, como los pagos en el ejercicios son mensuales, se emplea la tasa remunerativa mensual equivalente; es decir el 0.8735% mensual.
Para su cálculo en Excel, ver la siguiente Figura 3.9
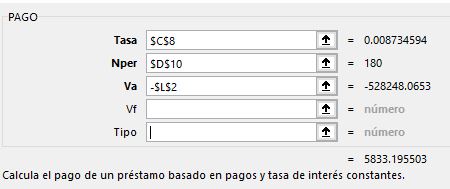
El cálculo de los intereses en Excel se presenta en la Figura 3.10
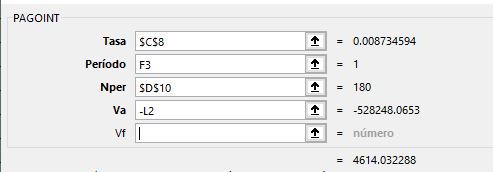
El cálculo de la amortización en Excel se presenta en la Figura 3.11
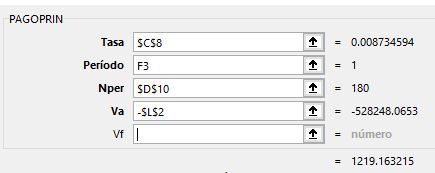
El cálculo del saldo insoluto en Excel se presenta en la Figura 3.12. La operación es, al saldo anterior restar la amortización.

₪ Conversión de la cuota fija UVR a pesos.
Como la UVR es solo una unidad de cuenta, no es empleada como medio de pago. Por ello debemos convertirla a su valor equivalente en pesos. Lo anterior lo alcanzamos multiplicando la cuota número uno por el valor estimado de la UVR en la misma fecha focal, $n=1$.
$$A_{pesos}=5,833.1955*380,7507=2,220,993$$El cálculo de la cuota en pesos en Excel se presenta en la Figura 3.13.

₪ El saldo insoluto expresado en pesos.
Para este cálculos desarrollamos la siguiente ecuación:
Si para la cuota uno el saldo anterior es $S_0$, entonces:
$$S_1=S_0+S_0*i_{pesos}-\ A_{pesos}$$En general, al cancelarse una cuota $A_t$, tenemos:
$$S_t=S_{t-1}+S_{t-1}*i_{pesos}-\ A_{pesos}$$ $$S_t=S_{t-1}(1+i_{pesos})-\ A_{pesos}$$Esta fórmula exige conocer el saldo anterior, en la realización del cálculo pretendido. Luego de cancelar la cuota uno en pesos, el saldo insoluto en pesos es:
$$S_1=200,000,000(1+0.014438)-2,220,993=200,666,632$$En la siguiente Figura 3.14 se presenta en cálculo en Excel.

Para la cuota dos:
$$S_2=200,666,632(1+0.014438)-2,233,551=201,330,331$$Y así sucesivamente. Es en el cálculo de los intereses sobre el saldo de la deuda en pesos cuando aplicamos la tasa de interés mensual para el capital en pesos.
De esta manera, ya hemos aplicado las tres tasas mensuales, calculadas previamente, en el diseño de la tabla de amortización de este crédito en UVR.
₪ Tabla de amortización de crédito en UVR.
En la siguiente Figura 3.15 se presenta la tabla de amortización completa. En ella se han ocultado filas dado lo extenso del plazo.
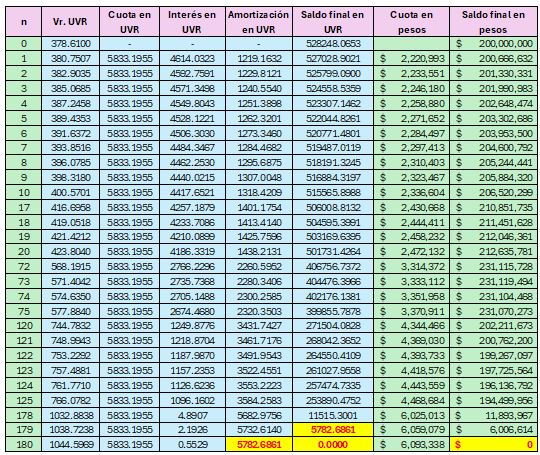
En la tabla, las columnas en azul son estimaciones de valores en UVR.
Las otras columnas en verde, además de $n$, son para valores en pesos.
Al cancelarse la cuota 180, los saldos en UVR y en pesos son cero (ver al final de la tabla en colores amarillo y rojo). Obsérvese además como al pagar la cuota número 180, la amortización en UVR es exactamente igual al valor del saldo insoluto en UVR en la $ff=179$ (de 5,782.6861), y por ello el saldo es cero (observar la misma situación con saldo en pesos).
El comportamiento en pesos del saldo de la deuda en el tiempo, lo podemos observar en la siguiente Figura 3.16.
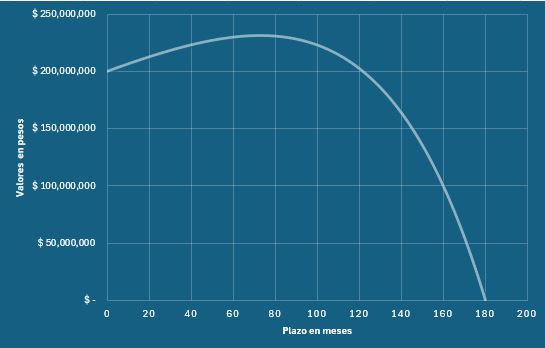
Al inicio, el saldo en pesos presenta en su gráfica una pendiente positiva, alcanzando su valor máximo, de 231,119,494 pesos, en $ff=73$ (a los seis años y un mes). Este crecimiento ocurre porque la cuota en pesos no alcanza a cubrir los intereses en pesos generados por el saldo anterior.
Al generarse un excedente de intereses, éstos son integrados al saldo insoluto en pesos.
En la cuota 74 esta tendencia cambia. La razón: la cuota en pesos alcanza a cubrir los intereses sobre el saldo en pesos y abona una pequeña parte al saldo adeudado. Veamos:
Esto es, la cuota en pesos número 74 posibilitó cubrir los intereses sobre el saldo adeudado al momento y, por primera vez, amortizar a dicho saldo un valor en pesos de 15,026. Esto ha sido posible porque el valor de la UVR crece a un ritmo geométrico (tiene un comportamiento exponencial).
Tenemos igual valor. Ahora bien, es entre las cuotas 121 y 122 (es decir algo más de 10 años) que el saldo en pesos vuelve a su nivel, corrientes, de los 200 millones de pesos, para ser cero con el pago de la cuota 180
Al cancelar la última cuota en UVR de 5,833.1955 con valor de cada unidad de 1,044.5969, se debe cancelar al prestamista la suma de 6,093,338 pesos. Con esta pago se cubre el saldo pendiente, de 6,006,614 de pesos, y los intereses sobre el saldo. Dichos intereses son:
$$I_{180}=6,006,614*0.014438=86,724$$Así las cosas, el valor en pesos de la última cuota se distribuye en intereses y amortización de la siguiente manera:
Este ejercicio se ha realizado con un dato de inflación que se supone constante durante los 15 años del crédito; esto es necesario para construir el esquema de amortización. Empero, el prestatario debe ser consciente que en la práctica de cancelar el crédito esto no es así; el nivel anual o mensual de la variación general de los precios seguramente será diferente al supuesto en la simulación, con consecuencia sobre el valor de la UVR al momento de cancelar una cuota y su respectivo equivalente en pesos.
Veamos el asunto con los siguientes escenarios.
En este escenario el valor de la UVR para cancelar la primera cuota fija en UVR, así como el valor de la cuota en pesos, son:
$${\rm UVR}_1=378.6100\left(1+0.008\right)=381.6339$$ $$A_{1\ en\ pesos}=5,833.1955*381.6339=2,226,174$$El resultado es un sobre costo con respecto a lo simulado de 5,181 pesos. En cambio, si la variación mensual de los precios es de 0.4%, los resultados en este caso son:
$${\rm UVR}_1=378.6100\left(1+0.004\right)=380.1244$$ $$A_{1\ en\ pesos}=5,833.1955*380.1244=2,217,340$$En consecuencia la cuota en pesos disminuye en 3,653 pesos, reduciéndose el costo del crédito en dicha cuota. Así entonces, el primer escenario desfavorece al prestatario y el segundo lo favorece
En realidad existe un riesgo en cuanto no hay certeza sobre el comportamiento de la variable $\pi$ en el tiempo. Este riesgo es para ambas partes de la transacción, el prestamista y el prestatario, pero en sentido contrario.
Este esquema se aplica en créditos diferidos, modalidad que resulta atractiva para diferentes agentes económicos, en la creación o consolidación unidades de producción. Un caso específico son los créditos de fomento, con tasa de interés baja y período de gracia que ayudan con la estabilidad financiera de los negocios.
En el emprendimiento de un nuevo negocio, el posponer el inicio de los pagos de un crédito da respiro sobre la necesidad inmediata en la generación de ingresos y liquidez para su cubrimiento, permitiendo al nuevo negocio establecerse sin presión por el pago de la financiación externa. Sin embargo, la desventaja consiste en que los intereses se acumulan, haciendo crecer el monto de la deuda; las cuotas fijas se determinan sobre el capital actualizado (capitalizado los intereses del período de gracia).
Como ejemplo de esta modalidad de crédito, vamos a desarrollar el esquema de amortización para el ejercicio 1.11 del capítulo 1.
Solución.
$A=?$
Período de gracias $=2$ años, igual a cuatro semestres
$i=5.8$% semestral
$n=7$ años, dos años de gracia y 5 adicionales para 10 cuotas semestrales
$P=500,000$ dólares
La tabla de amortización muestra, al no existir cancelación de cuotas en los cuatro primeros semestres (en los que escribimos valor cero), la acumulación de los intereses y la actualización del capital al final de cuarto semestre, para luego realizar el cálculo de la cuota fija de los próximos 10 semestres.
El proceso de acumulación de intereses y actualización de saldo de la deuda, semestre a semestre, es:
$F_1=500,000\left(1.058\right)=529,000$
$F_2=529,000\left(1.058\right)=559,682$
$F_3=559,682\left(1.058\right)=592,144$
$F_4=592,144\left(1.058\right)=626,488$
Ahora bien, con la fórmula general tenemos:
$F=500,000\left(1.058\right)^4=626,488$, de los cuales 126,488 dólares son los intereses acumulados del período de gracia. Es sobre este valor futuro que se calcula, como ya se indicó, la cuota fija. Aproximando decimales, ésta es:
$$A=626,488\left[\frac{\left(1+0.058\right)^{10}0.058}{\left(1+0.058\right)^{10}-1}\right]=84,315$$Aplicando la misma metodología y funciones de Excel, el plan de amortización se presenta en la siguiente Figura 3.17
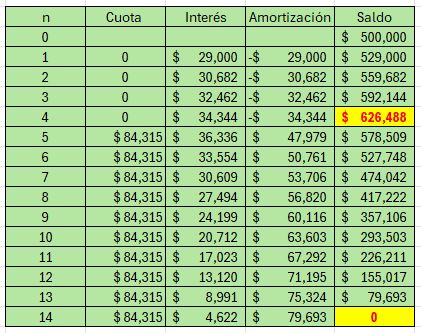
En este esquema de amortización debemos recordar de nuevo que lo anticipado es la cuota, no los intereses, porque continuamos trabajando con capitalización vencida. Como consecuencia de esta condición, la primera cuota fija a cancelarse al inicio del período (en $ff=0$), no incluye el componente de intereses y todo el monto de $A$ se destina a la amortización. En este sistema de crédito el primer pago se realiza inmediatamente después de recibir el préstamo y, como no ha pasado tiempo desde que se recibió el dinero, no se ha generado intereses vencidos.
Por lo anterior, estaríamos tentados a pensar en una operación financiera de crédito bajo un monto neto de capital, al restar el primer pago fijo; pero ello no es correcto. En este esquema, se parte de la determinación de una cuota fija que se pacta cancelar al inicio del período de pago y, por ello, tendrá efectos sobre el total de intereses a cancelar. Para ver este asunto en términos numéricos, resolvamos por medio de cuota anticipada el ejercicio 3.1.
Solución.
$A=?$ anticipada
$P=4,800,000$
$i=5.8$% trimestre
$n=4$ trimestres y cuatro cuotas
Para el cálculo de la cuota fija anticipada recurrimos a la ecuación (1.19):
$$A=4,800,000\left[\frac{{0.058\left(1.058\right)}^{3-1}}{\left(1.058\right)^4-1}\right]$$En Excel, el cálculo de la cuota fija anticipada es con la misma función PAGO, pero debemos tener la precaución de ingresar en el argumento tipo, el uno (1) para indicar su calidad de anticipada. Veamos:
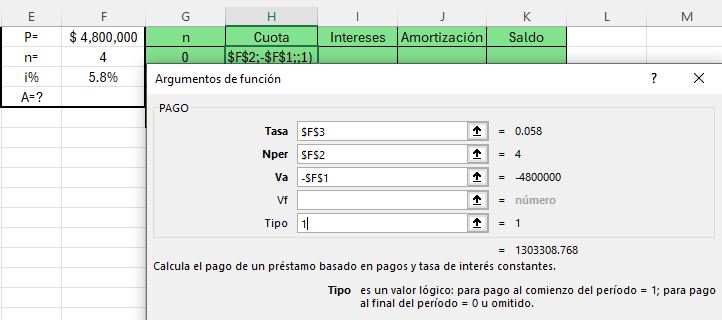
Se obtiene igual valor.
En Excel, las funciones PAGOINT y PAGOPRIN están diseñadas para cuotas vencidas, es decir con pagos al final de período y no al inicio (además de la capitalización vencida); estas dos funciones no tienen en el argumento tipo forma para indicar el pago anticipado.
Para utilizar estas funciones predefinidas de Excel, propongo la siguiente metodología: modificar los argumentos $va$ y $Nper$ de dichas funciones, utilizando a partir de la $ff=1$ el valor neto de la deuda y para Nper igual a 3, que son las cuotas restantes.
Lo anterior, para que se refleje el saldo neto después de cancelar la primera cuota anticipada en $ff=0$ y el número de cuotas que restan por cancelar. Por ello, en vez de utilizar 4,800,000 de pesos en el argumento $va$ aplicamos 3,496,691), y en el argumento Nper utilizar 3 (las cuotas restantes por cubrir), al aplicar las funciones PAGOINT y PAGOORIN.
Los cálculos para los conceptos de interés y amortización son:
En un diagrama de caja, este saldo está ubicado en la $ff=0$. Por ello cancelar una cuota anticipada en el segundo período es prácticamente igual a pagarla en el último día del período uno, es decir, vencida con respeto al saldo neto. Los $3,496,691$ pesos son el valor propuesto para utilizar como ajuste en las funciones PAGOINT y PAGOPRIN.
$I_1=3,496,691*0.058=202,808$
$R_1=1,303,309-202,808=1,100,501$
$S_1=3,496,691-1,100,501=2,396,191$
$I_2=2,396,191*0.058=138,979$
$R_2=1,303,309-138,979=1,164,330$
$S_3=2,396,191-1,164,330=1,231,861$
$I_3=1,231,861*0.058=71,448$
$R_3=1,303,309-71,448=1,231,861$
$S_3=1,231,861-1,231,861=0$
Una vez calculada la cuta fija anticipada en Excel, y de haber programado en la tabla de amortización la fila de $n=0$ como en Figura 3.19, la aplicación de las funciones PAGOINT y PAGOPRIN son:
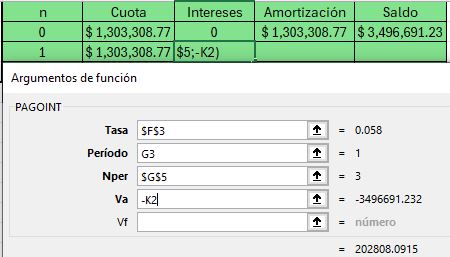
Siendo el resultado de 202,808 pesos, monto ya obtenido como $I_1$. El cálculo de la amortización en la segunda cuota, con $ff=1$, es:
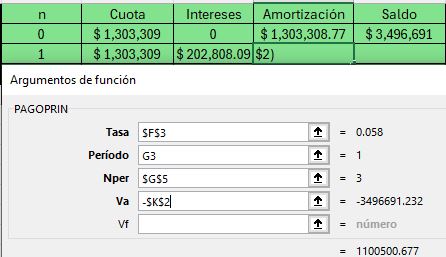
Se obtiene el resultado de 1,100,501 pesos. Finalmente, la tabla de amortización se presenta en la siguiente Figura 3.21
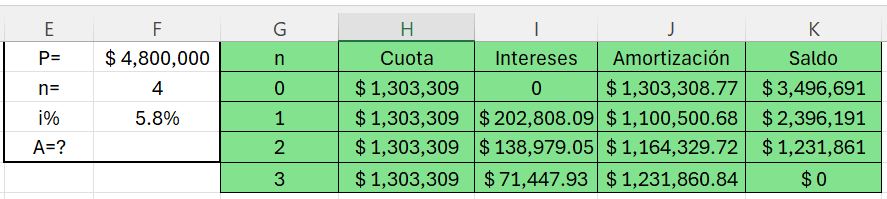
Con el pago de la última cuota, al inicio del cuarto período, el saldo de la deuda es cero. La suma total de las amortizaciones es de 4,800,000 pesos igual al capital tomado en préstamo representado en un PC.
Con el pago de la última cuota se cubre el saldo pendiente y los intereses que este saldo ocasiona. En este sistema el total de intereses cancelados son de $413,235.
En el esquema de cuota fija vencida, ésta es mayor que la cuota anticipada, y el total de intereses ascienden a 715,603 pesos, ver Tabla 3.1 o Figura 3.7. Al ser la cuota anticipada, pero la capitalización de intereses vencida, la primera cuota no ha acumulado aún intereses y toda ella se dirige a la amortización del crédito; ver Figura 3.21 fila para $n=0$, que es el inicio del período uno. La segunda, cancelada al inicio del período dos, es decir $n=1$, cubre los intereses del primer período, calculados sobre el saldo insoluto de 3,496,691 pesos, no de 4.8 millones, implicando menores intereses que en el caso de cuota vencida.
En esta ocasión presentaremos un esquema de amortización en el que la contratación de un empréstito se realiza con pagos fijos vencidos y se acuerda el pago de cuotas extras en determinados momentos dentro del plazo. En este escenario, para calcular la cuota fija debemos considerar los pagos extraordinarios que afectan al monto del capital o valor $P$ sobre el cual se calcula ésta. Veamos un ejemplo que resolvemos planteando una ecuación de valor.
Ejercicio 3.3 Sistema de amortización con cuota fija y cuotas extras pactadas. Se toma en préstamo un capital de 10,000,000 de pesos con plazo de 10 años, para ser cancelado por medio de cuotas fijas vencidas semestrales al 4.5% semestral. Se acuerda además la cancelación de dos cuotas extras, la primera de 1,000,000 de pesos en el semestre cinco, la segunda de 1,500,000 en el semestre quince. Hallar el valor de la cuota semestral y elaborar la tabla de amortización.
Solución
$A=?$
$P=10,000,000$
$i=4.5$% semestre
$n=10$ años e igual a 20 semestres
Cuota extra en $n=5$ de 1,000,000
Cuota extra en $n=15$ de 1,500,000
Semestralmente se debe cancelar la suma de 647,487 pesos, además en el mes cinco se debe pagar la cuota extra de 1,000,000 para un total de 1,647,487, y en el mes quince 1,500,000 pesos extra para un total de 2,147,487.
$I_1=10,000,000*0.045=450,000$
$R_1=647,487-450,000=197,487$
$S_1=10,000,000-197,487=9,802,513$
$I_2=9,802,513*0.045=441,113$
$R_2=647,487-441,113=206,374$
$S_2=9,802,513-206,374=9,596,139$
En la siguiente Figura 3.22 se presenta el esquema completo de amortización, en la que se señala los pagos extras en los semestres cinco y quince.
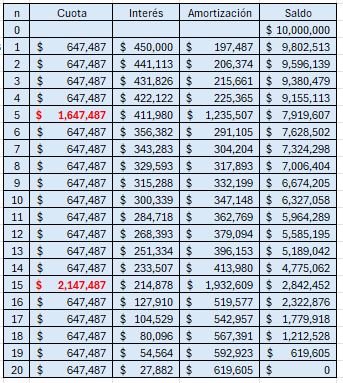
En Excel, este problema se resuelve con la herramienta buscar objetivo.
Dicha herramienta se estudió en el vol. 1 de este libro a propósito de la ecuación de valor.
¿Es posible en Colombia realizar pagos extras en las operaciones de crédito sin acuerdo previo? La respuesta es sí.
La Ley 1555 de 2012 adiciona el literal g) a la Ley 1320 de 2009 para autorizar efectuar "pagos anticipados en toda operación de crédito en moneda nacional sin incurrir en ningún tipo de penalización o compensación por lucro cesante, de las cuotas o saldos en forma total o parcial, con la consiguiente liquidación de intereses al día del pago".
Los usuarios de crédito pueden en cualquier momento realizar abonos, o cancelar la deuda pendiente, de un empréstito. En el caso de realizar un abono al saldo insoluto, se presenta dos situaciones:
Para ilustrar estas situaciones, procedemos con los datos del ejercicio 3.3 pero suponiendo que no hubo un pacto inicial sobre cuotas extraordinarias en el crédito. La nueva cuota fija, por valor de 768,761 pesos, y el esquema de amortización en la siguiente Figura 3.23.
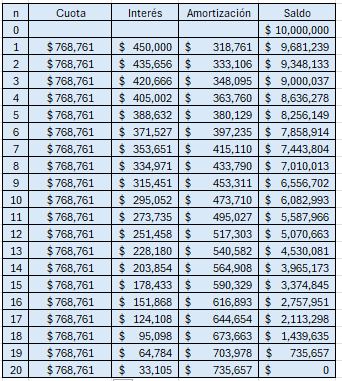
Caso #1: Abono al capital conservando la misma cuota fija. Supongamos que con el pago de la cuota 10, el prestatario realiza un abono a la deuda de 3,000,000 de pesos, cancelando en total la suma de 3,768,761. Aplicando este hecho al esquema de amortización de Figura 3.23, tenemos que el saldo insoluto es de 3,082,993, como se observa para $n=10$ en la Figura 3.24. El crédito se cancelaría al pagar la cuota 15, reduciendo el plazo de pago en cinco semestres (en la Figura 3.24 se ha conservado $n=20$, pero se ajusta en Figura 3.25). 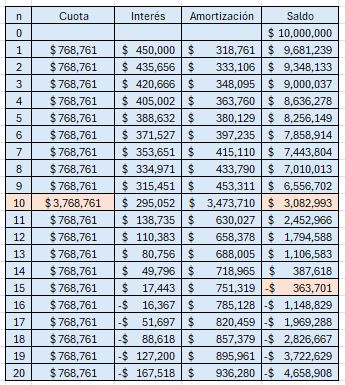
$A_{15}=387,618+387,618*0.045$
$A_{15}=387,618+17,443=405,060$
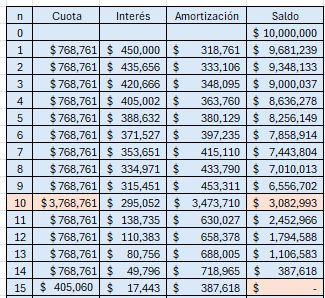
Caso #2: Abono al capital conservando el plazo original. Con la cancelación de la décima cuota se abona los mismos 3,000,000, haciéndose necesario reliquidación del crédito. Para ello, con el saldo insoluto de 3,082.993 pesos y diez cuotas por pagar al 4.5% semestral, la nueva cuota fija es de:Ver el esquema de amortización ajustado en la siguiente Figura 3.26.
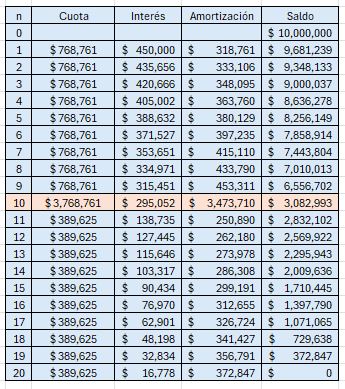
En esta sesión estudiaremos sistemas de amortización con cuotas variables, que crecen o decrecen en forma aritmética, geométrica o escalonada. La presentación de estos esquemas se fundamenta en la naturaleza académica de este texto, más que ser modelos ampliamente aplicados en la economía colombiana. La metodología de elaboración de estos sistemas conservan básicamente los mismos elementos conceptuales y de estructura de la tabla de amortización del caso en series uniformes o anualidades
En los casos de gradientes aritmético y geométrico, existe una característica básica: La variación de la cuota respecto al pago inmediatamente anterior (con excepción de la primera cuota que actúa como base de la serie de pagos). En este primer modelo, dicha variación es una suma fija positiva, el denominado gradiente aritmético o lineal creciente. Veamos un ejemplo.
Ejercicio 3.4 Sistema de amortización en gradiente aritmético. La suma de 10,000,000 de pesos se acuerda cancelar por medio de cuotas bimestrales que crecen en 40,000 pesos bimestral. Si la tasa de interés es de 4 años y la tasa de interés es del 18% b.v., hallar el monto de la primera cuota (La base de la serie o $A$), las cuotas 2, 10 y 15 y el saldo de la deuda al cancelarse la cuota 15.
Solución.
$P=10,000,000$
$G=40,000$
$J=18$% b.v., equivalente al 3% bimestral
$n=4$ años, equivalentes a 24 bimestres
$A=?$ La solución para $A$ con la ecuación (2.10):
La segunda cuota, la diez y la quince son:
$A_2=186,658.14+40,000=226,658.14$
$A_{10}=186,658.14+(10-1)40,000=564,658.14$
$A_{15}=186,658.14+(15-1)40000=746,658.14$
La aplicación de la primera cuota. Consiste en determinar los intereses sobre el saldo ($I_1$) y el monto del abono al capital ($R_1$). Con la cancelación de la primera cuota no se alcanza a cubrir los intereses causados del primer bimestre, por lo que el saldo de la deuda aumenta en el monto no cubierto (los $113,342). La aplicación de la segunda cuota. La amortización: $R_2=226,658-303,400=-76,742$.
El nuevo saldo: $S_2=10,113,342-(-76,742)=10,190,084$. Con la cancelación de la segunda cuota aún no se alcanza a cubrir los intereses causados del período y el saldo de la deuda sigue creciendo.
Los aspectos hasta aquí ejemplificados en el cálculo de las diferentes cuotas, los intereses, la amortización y el saldo insoluto, son los elementos metodológicos para el diseño del sistema de amortización en una hoja de cálculo como Excel. En la siguiente Figura 3.27 se puede observar dicho diseño, en el que se ha incluido en valor de la primera cuota calculada con el modelo (2.10).
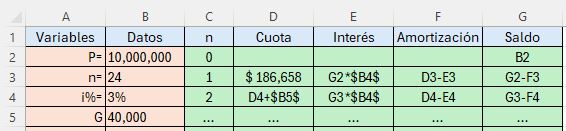
Señalamos las columnas pertinentes y con doble clic en vértice inferior derecho, se completa la tabla de amortización. Ver Figura 3.28.
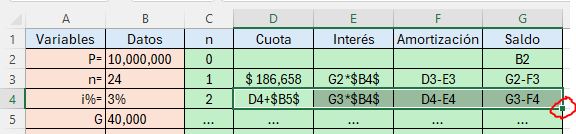
₪ Elaboración desde la herramienta Buscar Objetivo.
Sin embargo, por medio de la herramienta Buscar objetivo, Excel ofrece la posibilidad de realizar el cálculo de este sistema de amortización en gradiente, incluida la cuota base de la serie de pagos. En ello, como hipótesis indicamos un valor tentativo de la primera cuota, para luego realizar el cálculo verdadero de ésta y de todo el esquema de amortización, con base en la programación de las diferentes columnas para, básicamente, las dos primeras filas de la tabla.
Realizando como hipótesis $A=100$, la programación sería como en la siguiente Figura 3.29; resultados en Figura 3.30.
La programación de la columna Cuota, se ejecuta bajo el siguiente concepto: cualquier término de una progresión aritmética, excepto el primero, se forma sumando al anterior una cantidad fija, que llamamos gradiente aritmético; así cualquier cuota es igual a la anterior más la cantidad fija que constituye el gradiente.
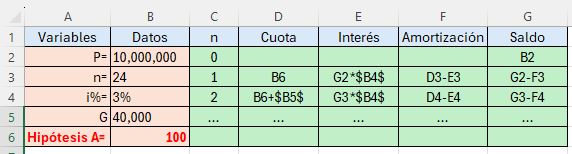
Ahora debemos proceder con el cálculo del verdadero esquema de amortización. Para ello, el saldo en $n=24$ debe ser cero, que por ahora no ocurre en Figura 3.30.
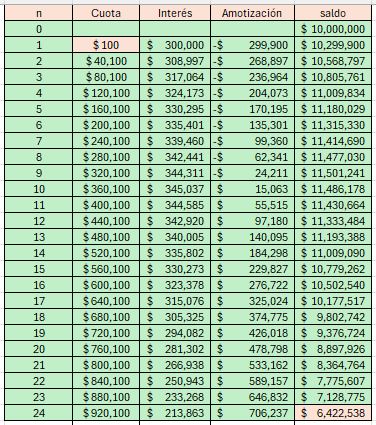
Procedemos a aplicar la herramienta de Excel. La pregunta es ¿cuál es el verdadero valor de $A$ que hace cero el saldo al realizarse el último pago en el esquema de amortización? Para ello aplicamos buscar objetivo, así:
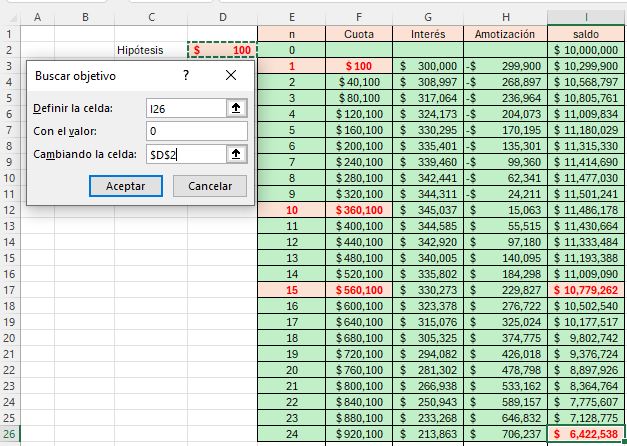
De la figura 3.31, en Definir la celda se tiene activa la celda I26 con un saldo de $6,422,530, pero este valor debe ser cero al cancelarse la última cuota en gradiente; por ello en el argumento con el valor ingresamos cero. Por último, en el argumento cambiando la celda damos clic en la celda D2, que contiene la hipótesis inicial. Finalmente aplicamos aceptar para realizar el cálculo de la primera cuota y recalcular la tabla de amortización, ver dicho resultado en Figura 3.32.
En la tabla de amortización constatamos los valores ya calculados de las cuotas uno, dos, diez y quince. También tenemos igual valor de la cuota 16 empleada como base para el cálculo del saldo en $ff=15$.
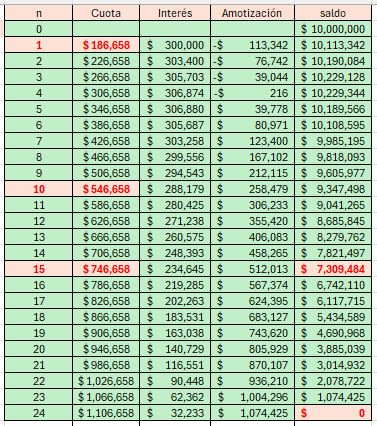
Es con la cancelación de la cuota quinta cuando el saldo de la deuda cambia de tendencia. Dicha cuota permite cubrir los intereses sobre el saldo acumulado y realizar un abono a éste. Con la cancelación de la cuota 24, se cubre el saldo pendiente de $1,074,425 y sus respectivos intereses, de 32.233 pesos, para así "matar la deuda".
En la siguiente Figura 3.33 podemos observar la evolución de la cuota y el saldo insoluto.
El crecimiento de la cuota es lineal con pendiente positiva (linealmente creciente); el saldo alcanza un valor máximo en $n=4$ para descender hasta hacerse cero con la cancelación de la última cuota.
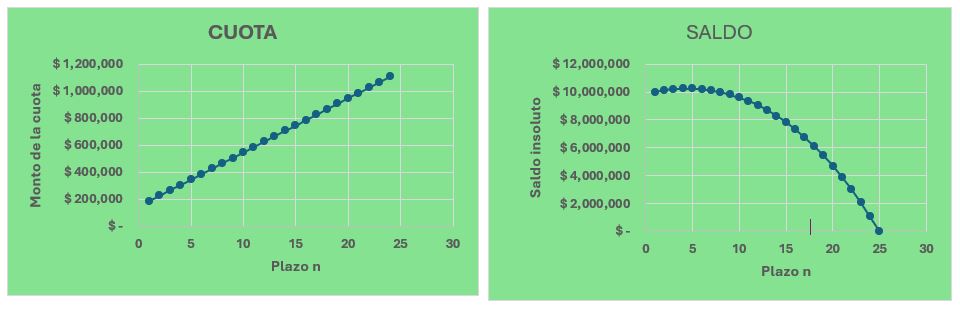
₪ Esquema de amortización con gradiente linealmente decreciente.
Trabajaremos con las mismas variables y datos del ejercicios anterior, pero en esta ocasión el gradiente aritmético es negativo; esto es, tendremos que $G=-40,000$ (cambiamos el signo a la cantidad de $G$, ceteris paribus).
Para hallar la primera cuota, o base de la serie, acudimos a la ecuación (2.11). El cálculo es el siguiente:
$$A=10,000,000\left[\frac{{1.03}^{24}*0.03}{{1.03}^{24}-1}\right]+40,000\left[\frac{1}{0.03}-\frac{24}{{1.03}^{24}-1}\right]$$ $$A=10,000,000\left[0.05905\right]+40,000\left[33.333-23.2379\right]=994,290.18$$La segunda cuota, la diez y la quince son:
$A_2=994,290-40,000=954,290$
$A_{10}=994,290+(10-1)(-40,000)=634,290$
$A_{15}=994,290+(15-1)(-40000)=434,290$
El saldo en $S_{15}$. Para éste, hallamos primero la cuota 16, así $A_{16}=994,290+(16-1)(-40000)=394,290$. Por el método del valor presente de las cuotas que restan por pagar (9) en la misma fecha focal del último pago, el saldo es:
$$S_{15}=394,290\left[\frac{{1.03}^9-1}{{1.03}^9*0.03}\right]-\frac{40,000}{0.03}\left[\frac{{1.03}^9-1}{{1.03}^9*0.03}-\frac{9}{{1.03}^9}\right]$$ $$S_{15}=3,069,986-1,184,478=1,885,509$$La primera cuota es muy superior al caso anterior, ello porque debe soportar en cada pago sucesivo la resta del gradiente aritmético, por monto de $40,000.
Para la tabla de amortización procedemos con la programación postulando de nuevo la hipótesis sobre la primera cuota y ejecutar luego la herramienta de Buscar objetivo.
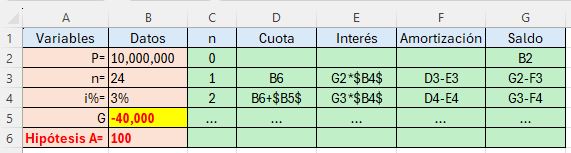
El resultado de este ejercicio, el nuevo esquema de amortización, en la siguiente Figura 3.35, en la que se resaltan los cálculos realizados previamente con las diferentes ecuaciones.
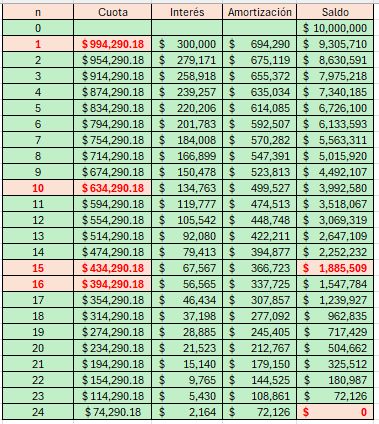
Por el sistema lineal creciente, los intereses cancelados suman 5,519,795 de pesos; en cambio por el sistema lineal decreciente, los intereses totales son de 2,822,964 pesos. Solo por elegir este último sistema, en la financiación se ahorraría en intereses, respecto al creciente, la suma de 2,696,831.
Los comportamientos de la serie de pagos y del saldo insoluto, los podemos observar en la siguiente Figura 3.36
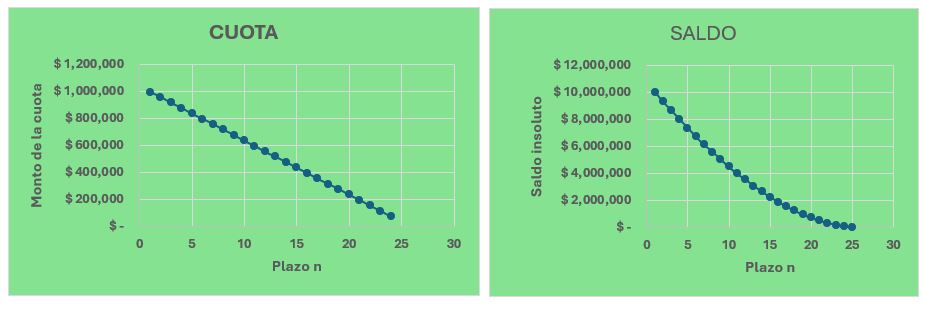
En gradiente geométrico, los esquemas de amortización presentan cuotas que crecen o decrecen en un porcentaje, ya sea éste positivo o negativo. Para ilustrar la elaboración de la tabla de amortización, utilicemos los mismos datos del caso aritmético, pero suponiendo ahora que la variación de la cuota es de 2%; es decir, iniciamos con un gradiente geométrico positivo.
Solución.
$A=?$
$P=10,000,000$
$J=18$% b.v., equivalente al 3% bimestral
$n=4$ años, equivalentes a 24 bimestres
$g=2.0$%
La solución para $A$ es por medio de la ecuación (2.20), así:
$$A=10,000,000\left[\frac{\left(1+0.03\right)^{24}(0.02-0.03)}{\left(1+0.02\right)^{24}-\left(1+0.03\right)^{24}}\right]$$ $$A=10,000,000\left[\frac{-0.02032794}{-0.42435686}\right]=479,029$$Valor que sería para $A_1$. Las cuotas 2, 10, 15 y 16 son:
$$A_2=479,029\left(1+0.02\right)^{2-1}=488,610$$ $$A_{10}=479,029\left(1+0.02\right)^{10-1}=572,484$$ $$A_{15}=479,029\left(1+0.02\right)^{15-1}=632,069$$ $$A_{16}=479,029\left(1+0.02\right)^{16-1}=644,711$$Determinemos ahora el saldo insoluto una vez se haya cancelado la cuota 15. Por el método del valor presente, éste es:
$$P=644,711\left[\frac{\left(1+0.02\right)^9-\left(1+0.03\right)^9}{\left(1+0.03\right)^9\left(0.02-0.03\right)}\right]$$ $$P=644,711\left[\frac{-0.10968062}{-0.01304773}\right]$$ $$P=644,711\left[8.40610587\right]=5,419,505$$En la siguiente Figura 3.37 se presenta la programación del esquema de amortización, en Excel. Obsérvese que se aplica $g=2$%.
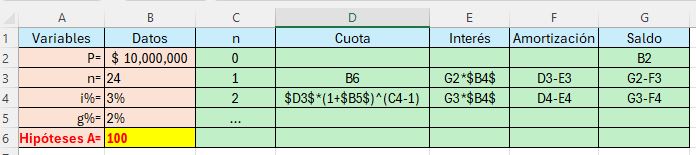
De nuevo la hipótesis es A=100. Aplicando la herramienta de buscar objetivo a la anterior programación, ver el esquema de amortización resultante en la siguiente Figura 3.38
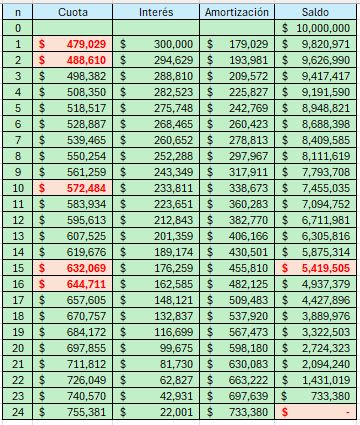
₪ Esquema de amortización con gradiente geométrico decreciente.
Para este ejercicio vamos a definir $g=-2$% y seguiremos con los mismos datos y cálculos. Trabajando con el mismo modelo (2.20) y tomando en consideración el signo negativo del gradiente geométrico, la cuota ahora es:
$$A=10,000,000\left[\frac{\left(1+0.03\right)^{24}\ast(-0.02-0.03)}{\left(1-0.02\right)^{24}-\left(1+0.03\right)^{24}}\right]$$ $$A=10,000,000\left[\frac{-0.10163971}{-1.41701377}\right]=717,281$$Los valores de las cuotas 2, 10, 15 y 16 son:
$$A_2=229,935\left(1-0.02\right)^{2-1}=702,935$$ $$A_{10}=717,281\left(1-0.02\right)^{10-1}=598,031$$ $$A_{15}=717,281\left(1-0.02\right)^{15-1}=540,573$$ $$A_{16}=717,281\left(1-0.02\right)^{16-1}=529,762$$El saldo luego de pagar la cuota 15 es de:
$$P=529,762\left[\frac{\left(1-0.02\right)^9-\left(1+0.03\right)^9}{\left(1+0.03\right)^9\left(-0.02-0.03\right)}\right]\ $$ $$P=529,762\left[\frac{-1.41701377}{-0.10163971}\right]$$ $$P=529,762\left[13,54153757\right]=7,385,691$$La programación de la tabla de amortización en la siguiente Figura 3.39. Se resalta en rojo el gradiente geométrico con un porcentaje de -2.0%, que es el cambio con respecto al ejercicio inmediatamente anterior.
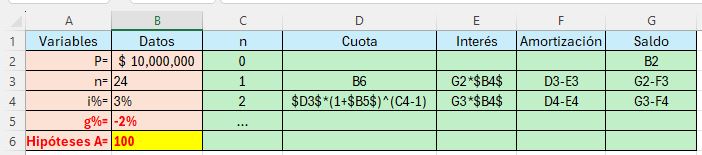
En la celda D4, como B5=-2%, la expresión entre paréntesis resulta $\left[(1+(-0.02)=(1-0.02)=0.98\right]$; las cuotas decrecen con razón de 0.98 respecto a la inmediatamente anterior, excepto para la primera; es decir cada cuota después de la primera es el 98% de la cuota anterior.
En la figura 3.40 podemos observar el esquema de amortización. La suma total de las amortizaciones es de 10,000,000 de pesos; con la cancelación de la última cuota se cubre el saldo pendiente de la deuda de 437,574 pesos y sus respectivos intereses de 13,127 pesos.
Bajo este sistema de gradiente geométrico decreciente, los intereses en el plazo ascienden a la suma de 3,779,673, mientras que por el sistema de cuota creciente geométricamente son de 4,572,967, implicando el sistema decreciente un ahorro de intereses por el monto de 793,294 pesos.
Con cuota decreciente geométricamente, se inicia cancelando montos más altos que permiten abonar un mayor valor al capital tomado en préstamo, reduciendo así más rápidamente el monto del saldo insoluto.
Es así como en fecha focal 15, el saldo insoluto en el esquema de la Figura 3.38 es de 5,419,505 mientras que para el esquema de cuota decreciente geométricamente de la Figura 3.40 es de 3,824,897 pesos. Esta diferencia se refleja en la reducción del monto total de intereses con respecto al esquema de amortización con cuota creciente geométricamente. Mientras menos capital ajeno tenga en su manos el prestatario, menor son los intereses a cubrir.
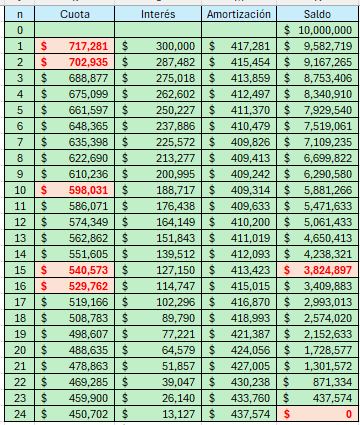
A pesar de ser escasamente utilizados en la economía colombina para la cancelación de deudas de capital financiero, los esquemas de amortización bajo la modalidad de gradiente escalonado, en las formas aritmética o geométrica, presentan características deseables para la gestión de los empréstitos. En particular, las cuotas se pueden programar en gradiente creciente, por ejemplo, con periodicidad anual, respondiendo a los ritmos de variables económicas como la inflación y/o el aumento en el nivel de ingresos (como son los sueldos y salarios), acorde con las capacidades de pago de los prestatarios y generando estabilidad de la cuota al interior de la periodicidad acordada.
Con el fin de ilustrar la metodología de elaboración de la tabla de amortización, seguimos trabajando con los datos del ejercicio que traemos, pero suponiendo el plazo de cuatro años y periodicidad semestral para el cambio de la cuota. Por lo tanto, en cuatro años del problema tenemos ocho semestres y al interior de cada semestre hay tres bimestres.
₪ Esquema de amortización con gradiente escalonado linealmente creciente.
Para este caso, los datos quedan de la siguiente manera:
Solución.
$A_1=?$
$P=10,000,000$
$t=8$ escalones semestrales (en 4 años 8 semestres)
$J=18$% b.v.
$i=3$% bimestral
$ie=9.27$% tasa efectiva semestral que se corresponde con $t$ en semestres
$n=3$ bimestres, o tres cuotas en cada escalón
$G=40,000$ semestrales
El valor de $A_1$, con:
$$A_1=P\left[\frac{i}{\left(1+i\right)^n-1}\right]\left[\frac{\left(1+ie\right)^tie}{\left(1+ie\right)^t-1}\right]-G\left[\frac{1}{ie}-\frac{t}{\left(1+ie\right)^t-1}\right]$$Es:
$$A_1=10,000,000\left[\frac{0.03}{0.0927}\right]\left[\frac{0.18849}{1.03279}\right]-40,000\left[\frac{1}{0.0927}-\frac{8}{1.03279}\right]$$ $$A_1=10,000,000\left[0.059047416\right]-40,000\left[3.038679\right]=468,939$$Tres cuotas bimestrales de $468,939 constituyen los tres pagos del primer semestre o escalón uno. Para los demás escalones, las cuotas bimestrales son:
Segundo Semestre:Tercer Semestre:Cuarto Semestre:Quinto Semestre:Sexto Semestre:Séptimo Semestre:Octavo Semestre:Cada cuota, como ya es conocido se aplica en intereses sobre el saldo y abono al capital o amortización. Para el primer escalón, los intereses, la amortización y el saldo insoluto son:
Primer semestre cuota uno:Primer semestre cuota dos:Primer semestre cuota tres:El proceso se repite para las demás cuotas de los restantes escalones, hasta completar los ocho semestres.
La programación en la hoja de Excel para realizar los cálculos del esquema de amortización, es como se observa en la siguiente Figura 3.41. Se hace de nuevo la hipótesis de $A_1=100$ y se resuelve con la herramienta buscar objetivo de análisis de hipótesis.
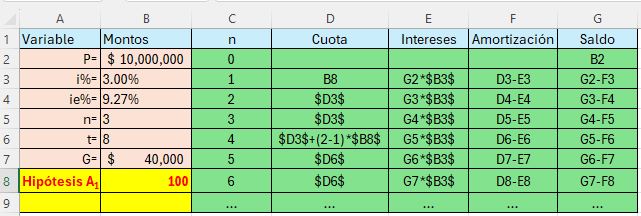
En la siguiente Figura 3.42 podemos observar la programación de los primeros tres semestres bajo la hipótesis de $A_1=100$.
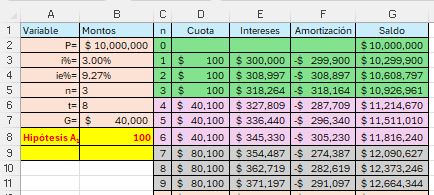
Las columnas siguen el desarrollo operacional descripto en la anterior Figura 3.41.
Solo resta aplicar la herramienta de Excel para hacer el cálculo correcto del esquema de amortización. Veámoslo:
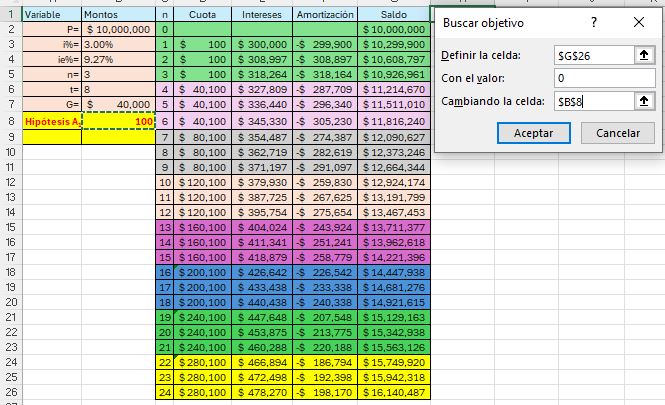
Damos aceptar y se efectúa el cálculo de la tabla de amortización. Ver siguiente Figura 3.44. Cada escalón de tres cuotas fijas bimestrales está resaltado con un color. La cuota 10 es de 588,939 pesos, perteneciente al cuarto semestre; la cuota 15 es de 628,939 pesos perteneciente al escalón o semestre cinco. El saldo una vez cancelada la cuota 15 es de 5,501,492 pesos.
Dicho saldo se calcula con la ecuación 47, así:
$P=A_1\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}\right]+\frac{G}{ie}\left[\frac{\left(1+i\right)^n-1}{i}\right]\left[\frac{\left(1+ie\right)^t-1}{\left(1+ie\right)^tie}-\frac{t}{\left(1+ie\right)^t}\right]$
Pero siendo $A_1$ la cuota 16.
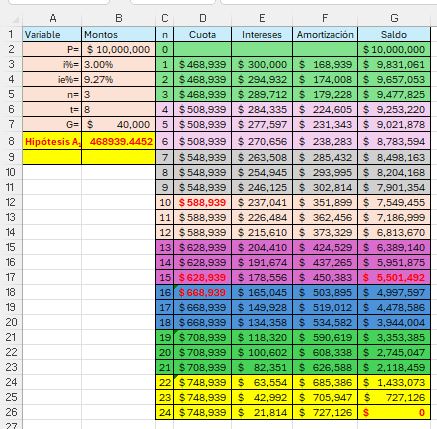
En la solución, $n=3$ y $t=3$ porque faltan tres escalones o semestres para que el saldo sea cero, y $A_1$ es como ya se indicó.
Para el saldo, hallaremos primero el valor presente de la serie uniforme y luego la serie gradiente. Recordando que $P=P_A+P_G (47)$, entonces:
Componente de serie uniforme:Componente de serie de gradientes:En consecuencia:Invitamos al lector a realizar el mismo ejercicio pero con gradiente lineal decreciente, es decir con $G=-40,000$
₪ Esquema de amortización con gradiente escalonado geométricamente creciente.
En su solución el gradiente del 2% ahora es semestral; por lo tanto los datos son como se dispone a continuación.
Solución.
$A_1=?$
$P=10,000,000$
$t=8$ escalones semestrales ( en 4 años 8 semestres)
$J=18$% b.v.
$i=3$% bimestral
$ie=9.27$% tasa efectiva semestral que se corresponde con $t$ en semestres
$n=3$ cuotas en cada escalón
$g=2.0$% semestral
El valor de $A_1$, con:
$$ A_1=P\left[\frac{i}{\left(1+i\right)^n-1}\right]\left[\frac{\left(1+ie\right)^t(ie-g)}{\left(1+ie\right)^t-\left(1+g\right)^t}\right]$$Por ello:
$$A_1=10,000,000\left[\frac{0.03}{{1.03}^3-1}\right]\left[\frac{{1.0927}^8(0.0927-0.02)}{{1.0927}^8-{1.02}^8}\right]$$ $$A_1=10,000,000\left[\frac{0.03}{0.0927}\right]\left[\frac{0.147839}{0.86113473}\right]$$ $$A_1=10,000,000\left[0.32353035\right]\left[0.171679312\right]=555,435$$En el primer semestre se debe cancelar tres cuotas bimestrales de 555,435 pesos. Para los otros semestres las cuotas son:
Segundo Semestre:Tercer Semestre:Cuarto Semestre:Quinto Semestre:Sexto Semestre:Séptimo Semestre:Octavo Semestre:Aplicación de las cuotas y saldo insoluto
Primer semestre cuota uno:Primer semestre cuota dos:Primer semestre cuota tres:Con la hipótesis de una cuota inicial igual a 100, en la Figura 3.45 se presenta la programación en la hoja de Excel para aplicar la herramienta Buscar Objetivo. En cada escalón, o cambio de semestre, la cuota crece un 2% respecto al escalón anterior.
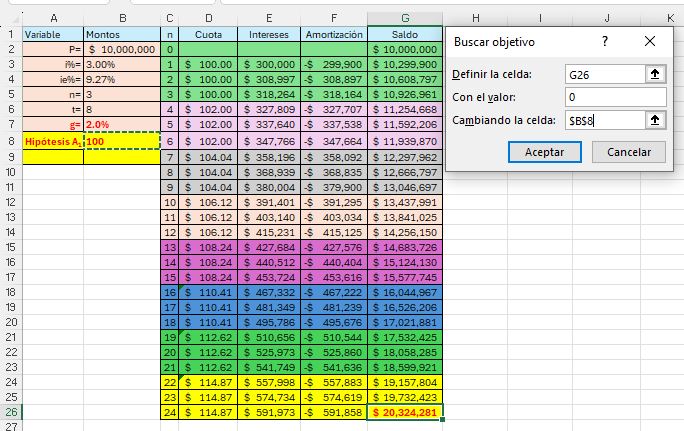
Una vez dado aceptar se calcula el esquema de amortización pretendido, que se presenta en la siguiente Figura 3.46. Con la cancelación de la última cuota, en $n=24$, de 638,020 pesos, se cubren el saldo insoluto de 619,437 pesos y sus respectivos intereses de 18,583 pesos.
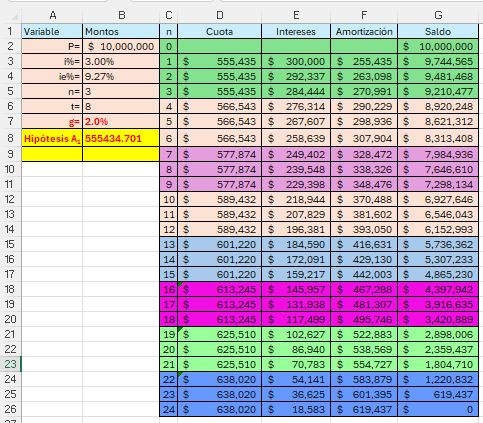
Son dos las características esenciales que describen la naturaleza de este esquema de amortización. En primer lugar, en vez de cuota fija se tiene ahora un monto fijo de amortización, determino como el resultado de dividir el capital tomado en préstamo por la cantidad de cuotas periódicas a cancelar.
La amortización fija: Se resuelve como $R=\frac{P}{n}$, siendo $n$ el número de cuotas periódicas.Tasa de interés: Dado que para la entidad financiera que otorga un crédito se trata de una tasa de colocación, ésta se expresa como $DTF+ Margen$%; haciéndose necesario el cálculo de la tasa de interés periódica equivalente para liquidar los intereses al momento de cancelar cada una de las cuota.Se utiliza este esquema en créditos hipotecarios y de consumo. Veamos un ejemplo de consumo.
Ejercicio 3.5 Sistema de amortización DTF y abono constante a capital. El 11 de febrero de 2024, un habitante de la ciudad de Medellín tomó un crédito de consumo con el fin de realizar mejoras en su casa, por valor de 8,400,000 para ser cancelado con cuotas mensuales vencidas y plazo de un año. Se pactó como tasa de interés DTF+5.0% t.a. Elaborar el esquema de amortización que fue cancelado por el habitante de la ciudad.
Solución.
$A_1=?$ mensual
$P=8,400,000$
i%= $DTF+5.0$% t.a.
$n= 1$ año, equivalente a 12 meses
La amortización fija:Tasa de interés periódica (mensual):Debemos hallar una tasa de interés mensual vencida equivalente. Para ello, en marzo 11 de 2024 la $DTF=10.86$% E.A.Paso #1. Convertir la DTF a nominal trimestre anticipado
$$J=4\left[1-\frac{1}{\sqrt[4]{1+0.1086}}\right]=0.1018\ t.a.$$Paso #2. Sumar las tasas nominales trimestre anticipado
$$J=0.1018 t.a.+0.05 t.a.=0.1518 t.a.$$Paso #3. Hallar la tasa efectiva anual ($ie$)
$$ie=\left(\frac{1}{1-\frac{0.1518}{4}}\right)^4-1=0.167349$$Paso #4. Hallar periódica mensual vencida ($iv$, en general $i$)
$$iv=\sqrt[12]{1+0.1673}-1=0.0129781$$La tasa mensual es de 1.2978% para la primera cuota.
El monto de los intereses: Con la anterior tasa de interés efectiva periódica calculamos el monto de los intereses sobre el saldo insoluto a cubrir con la primera cuota (del mes de marzo).En consecuencia, el tomador del préstamo canceló en el mes de marzo de 2024 una cuota igual a:
$$A_1=190,061+700,000=809,061$$En la siguiente Figura 3.47 columna G, se presenta el cálculo de las tasas de interés periódicas de los meses que comprenden el plazo del ejercicio, cuya metodología es la descrita para el mes de marzo ya realizado.
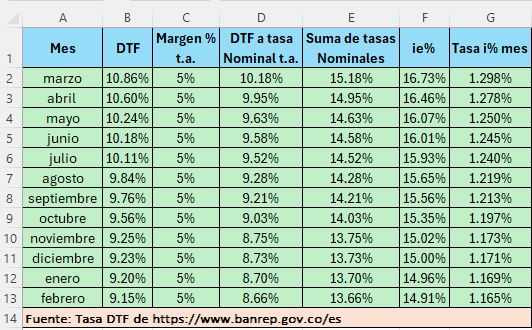
El saldo resultante luego del abono al capital por la primera cuota es de:
$$S_1=809,061-700,000=7,700,000$$Realicemos ahora los cálculos para el mes de abril y practicar de nuevo la metodología para determinar la tasa de interés periódica y el cálculo de la cuota dos. La DTF para la fecha es 10.60% E.A.
La amortización fija:Tasa de interés periódica (mensual):Paso #1. Convertir la DTF a nominal trimestre anticipado
$$J=4\left[1-\frac{1}{\sqrt[4]{1+0.1060}}\right]=0.0995\ t.a.$$Paso #2. Sumar las tasas nominales trimestre anticipado
$$J=0.0995 t.a.+0.05 t.a.=0.1495 t.a.$$Paso #3. Hallar la tasa efectiva anual ($ie$)
$$ie=\left(\frac{1}{1-\frac{0.1495}{4}}\right)^4-1=0.1646$$Paso #4. Hallar periódica mensual vencida ($iv$)
$$iv=\sqrt[12]{1+0.1646}-1=0.01278$$La tasa mensual es de 1.278% para determinar los intereses de la segunda cuota.
Intereses, cuota y saldo para cuota dos:$I_2=7,700,000*0.01278=98,385$
$A_2=98,385+700,000=798,385$
$S_2=7,700,000-700,000=7,000,000$
Este proceso se repita hasta el mes 12, fin del plazo. También, es la base de la programación en Excel para el cálculo de la tabla de amortización. Ver tabla en Figura 3.48
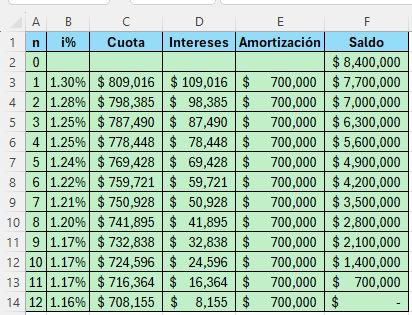
₪ Cuestionario.
₪ Problemas.
R.3,309,434; 51,107,295; 1,328,790; 1,930,453; respectivamente. Realizar el esquema de amortización.R. 3,225,569; 47,881,726; 1,244,925; 1,980,644; respectivamente. Realizar el esquema de amortización.R.16,649,845; 3,860,450; 59,616,580; 1,550,031; 2,310,419; respectivamente. Realizar el esquema de amortización. R. Esquema 1=98,566,050; esquema 2= 93,534,164; esquema 3= 114,977,144. R. $UVR_1$=389.6494; Cuota $UVR_1$=5,299.9322; intereses $UVR_1$=3,795.8272; amortización $UVR_1$= 1,504.1050; cuota en pesos= 2,065,115.23; saldo en pesos= 280,510,017.56.R.991.2949 UVRs; 5,299.9322 UVRs ; 27.7407 UVRs; 5,272.1915 UVRs; 5,253,795.65 pesos; 0.00 pesos; respectivamente. R. Para la fecha focal 1: 389.6494 UVRs; 4,350.4090 UVRs ; 3,795.8272 UVRs; 554.5819 UVRs; 1,695,134.16 pesos; 280,879,997.66 pesos; respectivamente. Para la fecha focal 240: 991.2949 UVRs; 6,740.4090 UVRs ; 35.2803 UVRs; 6,705.1287 UVRs; 6,681,732.99 pesos; 0.00 pesos; respectivamente. Resp. Para la fecha focal 1: UVR1=389.6494; 1,634,5300 UVRs ; 3,795.8272 UVRs; -2,161.2979 UVRs; 636,893.58 pesos; 281,938,238.25 pesos; respectivamente. Para la fecha focal 240: 991.2949 UVRs; 17,627.9260 UVRs ; 92.2673 UVRs; 17,535.6587 UVRs; 17,474,472.85 pesos; 0.00 pesos; respectivamente. R. Para la fecha focal 1: 389.6494 UVRs; 4,913.2423 UVRs ; 3,795.8272 UVRs; 1,117.4151 UVRs; 1,914,441.79 pesos; 280,660,690.03 pesos; respectivamente. Para la fecha focal 240: 991.2949 UVRs; 5,935.7320 UVRs ; 31.0685 UVRs; 5,904.6634 UVRs; 5,884,060.75 pesos; 0.00 pesos; respectivamente.R. Problema 5: Sistema de amortización por cuota fija en UVRs; intereses de 539,813,180.27 pesos. Problema 7: sistema de amortización por cuota creciente en 10 UVRs mensual; intereses de 606,376,078.36 pesos. Problema 8: sistema de amortización por cuota UVR creciente en 1.0% mensual; intereses de 944,144,708.29 pesos. Problema 9 : sistema de amortización por cuota UVR creciente escalonada al 1.0% anual; intereses de 569,543,177 pesos. En este problema el más conveniente es el sistema de cuota fija en UVR dado que presenta menor pago de intereses en total. R.1.098%; 1.081%; 1.061%; 1.071%; 1.054%; 1.068%, respectivamente. R. Ver siguiente Figura 3.49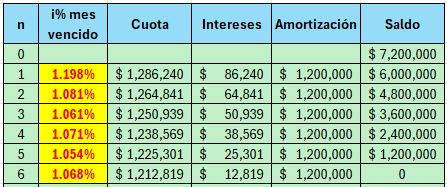
En términos generales, la medición es el proceso que permite determinar y atribuir cantidades a una magnitud; esto es, asignar un número a una variable, propiedad o atributo, de una cosa u objeto de estudio. Las magnitudes son variables (propiedades o atributos) susceptibles de medición. Según Díez y Moulines
En nuestro contexto, por medida de valor entendemos el desarrollo de una forma (método o técnica) para cuantificar el valor de la rentabilidad de alternativas de inversión bajo condiciones de valor del dinero en el tiempo. El resultado obtenido, "la cantidad de algo", es expresado en términos de unidades monetarias, por ejemplo en pesos, o en porcentaje como es la tasa de rentabilidad. La medida de valor obtenida se constituye en elemento de juicio para tomar decisiones sobre la realización de inversiones.
En el análisis y evaluación de alternativas de inversión, debemos realizar estimaciones de diferentes magnitudes como son, por ejemplo, el monto de la inversión inicial y de la inversión en capital de trabajo, los flujos de ingresos y egresos derivados de la iniciativa de inversión y el tiempo en que estos se proyectan, la rentabilidad mínima deseada (expresada en términos de costo de oportunidad, de tasa de retorno, o de costo promedio ponderado del capital), el valor de salvamento, o de rescate, de un activo. Las magnitudes se emplean en el diseño de flujos de caja.
Con esta información (estimaciones) procedemos a desarrollar las medidas de valor para determinar (evaluar) la rentabilidad de la alternativa de inversión.
Según Blank y Tarquin las medidas de valor son criterios para elegir una alternativa para un conjunto específico de estimaciones.
En este capítulo estudiaremos algunos procedimientos básicos para obtener medidas de valor que toman en cuenta el valor del dinero en el tiempo y en condiciones de certidumbre, medidas que a su vez son denominadas criterio de evaluación de alternativas de inversión. Como criterios, son bases para emitir juicios sobre la conveniencia financiera de llevar a cabo una idea de inversión.
En este punto haremos una breve descripción de las magnitudes, ya reseñadas, que se requieren para desarrollar y estimar las diferentes medidas de valor presentadas en este capítulo. Un tratamiento amplio de estas variables se puede consultar en textos sobre formulación y evaluación de proyectos, por ejemplo en Sapag, et al. ₪ Las inversiones del proyecto. En términos de capital productivo, la inversión hace referencia a los requerimientos de activos (fijos y diferidos, o tangibles e intangibles) y de capital de trabajo, para la puesta en marcha y operación del proyecto productivo.
En ocasiones, los estudios de las inversiones de un proyecto productivo determinan y programan inversiones después del inicio de la operación, encaminadas al reemplazo de activos, o por la planeación de la ampliación de la escala de producción.
Son tres componentes de inversión los que determinan la cuantía de la inversión total, $I_t$, en un proyecto productivo. Estos son: Inversión inicial, inversión en capital de trabajo e inversión en la operación.
Inversión inicial.Inversión en capital de trabajo.Inversión en la operación.En consecuencia, la inversión total de un proyecto productivo, $I_t$, está resumida por la siguiente expresión matemática:
$$I_t=I_0+I_{ct}+I_r (4.1)$$
Aunque las depreciaciones y las amortizaciones de la inversión inicial hacen parte de los costos y gastos de la operación del proyecto, estos no ocasionan salidas o egresos de efectivo (dado que son movimientos contables de pérdida de valor de los activos, es decir, gastos no desembolsables), y por ello en la evaluación de la rentabilidad del proyecto se hace un tratamiento especial de estos, como veremos más adelante.
₪ Los ingresos y egresos derivados de la iniciativa de inversión.
La operación del proyecto de inversión genera flujos de ingresos, de costos y de gastos. Los ingresos básicos de la iniciativa de inversión productiva son aquellos derivados directamente de las ventas de los bienes y servicios objeto de la operación del proyecto. En los proyectos, existen además ingresos indirectos (no operacionales) que se ocasionan, por ejemplo, por la venta de los activos reemplazados, por el logro de beneficio tributario, como por la venta de materiales secundarios o de desechos generados durante la producción.
En relación con los costos y gastos, es necesario determinar la cuantía de los costos de producción y de los gastos que el proyecto implica, dado sus nivel de inversión total, la escala de producción y las metas de ventas e ingresos programadas. Los costos de producción se agregan en las categorías de: Mano de Obra Directa, Materia Prima (directa) y los Costos Indirectos de Fabricación. Esta última categoría incluye la mano de obra indirecta, los materiales indirectos, y otros costos indirectos ( como la depreciación de los activos fijos de la producción, y las amortizaciones de activos intangibles relacionados con la producción, como es el caso de la licencia de software que controla maquinaria).
Los gastos son aquellos egresos que se ocasionan por la administración y la gestión de las ventas. Estos gastos incluyen también la asignación por depreciación de equipos de oficina, por ejemplo, y de amortizaciones de intangibles debido, por ejemplo, a las licencias de software para la gestión administrativa y contable, al registro de marcas, o por obtener los derechos de autor de pauta publicitaria, etc.
Los elementos de ingresos directos de la operación ($ID$), los costos de producción ($CP$) y los gastos de administración y venta (GAV), permiten elaborar el siguiente balance denominado Utilidad Operativa ($UO$) de la iniciativa de inversión:
$$UO=ID-CP-GAV (4.2)$$Para financiar la inversión del proyecto, los recursos de capital tienen origen en los aportes de los inversionistas (recursos propios en efectivo, colocación de acciones), y el capital de deuda (por crédito bancario, colocación de bonos, hipotecas, etc. ), realizando una mezcla de ambas fuentes de recursos. También se puede acudir a fuentes internas del proyecto, como son los recursos acumulados de depreciaciones y amortizaciones, y la retención de utilidades. Los recursos de deuda dan lugar al pago de intereses, que ocasionan gastos financieros, y egresos por la amortización del capital con el fin de saldar la deuda. Considerando los gastos financieros, $GF$, y los ingresos no operacionales, $INO$, tenemos ahora un balance entre ingresos y egresos denominado Utilidad Antes de Impuesto, $UAI$.
Este balance se resume en la siguiente ecuación (4.3):
$$UAI=UO+INO-GF (4.3)$$Al conjunto de las fuentes de financiación de la inversión total del proyecto, se denomina estructura de capital, y cada una de ellas tiene asociado un costo para el proyecto.
En el caso de los recursos propios, es común hacer referencia al costo de oportunidad de los inversionistas, como el costo asociado a esta fuente de financiación.
₪ La tasa de referencia. La expectativa de una tasa de retorno atractiva
La realización de una inversión, sea esta de naturaleza financiera o productiva, tiene su venero en lo que se espera ganar en forma de rendimiento futuro, en el retorno del capital incrementado por los rendimientos. Es decir, el inversionista espera obtener una cantidad de dinero en un monto superior al capital invertido, siendo así la inversión rentable.
Por ende, cada inversionista tiene una previsión (esperanza o expectativa) sobre la rentabilidad apropiada que debe cumplir una iniciativa de inversión para asignar sus recursos financieros en forma de capital productivo, previsión que es expresada en términos de una tasa de retorno sobre la inversión realizada. A esta expectativa porcentual de rendimiento, se le ha identificado como Tasa Mínima Atractiva de Retorno (TMAR;
Dicha expectativa se constituye en tasa de referencia en la evaluación de las alternativas de inversión. Pero, ¿cómo forma el inversionista la expectativa de rentabilidad?, es decir, ¿sobre qué base se llega a definir una TMAR para un proyecto de inversión en particular?
Debemos indicar claramente que no hay una receta, fórmula o modelo, que nos permita determinar con certeza la tasa mínima de retorno atractiva.
Según Sullivan, W. G., et.al.
El mismo J.M. Keynes
las consideraciones en que se basan las expectativas sobre los rendimientos probables son, por una parte, los hechos que podemos dar por conocidos con más o menos certeza y, por otra parte, los conocimientos futuros que solo pueden preverse con relativa seguridad...El hecho más destacado es lo extremadamente precario de las bases de conocimiento en que ha de basarse nuestros cálculos de los rendimientos probables.
Algunas consideraciones que fundamentan el establecimiento de la TMAR, son:
Tasa de interés libre de riesgo.En los Estados Unidos, se utiliza como tasa de interés libre de riesgo a la tasa de los Bonos o Letras del Tesoro. Es libre de riesgo porque los anteriores títulos valores son deudas del gobierno, y por ello, con escasa probabilidad de incumplimiento de pago con sus acreedores.
En Colombia, se utiliza como tasa de interés "segura" a la tasa de los Títulos de Tesorería (TES), valores de deuda pública que son respaldados por el Gobierno Nacional y el Banco de la República. Estos títulos son emitidos con diferentes plazos por lo que se ocasiona diferentes tasas de interés.
Disponiendo de una tasa de interés libre de riesgo, como guía para la determinación de la TMAR se establece que: $$TMAR>i_{lr}$$El costo de oportunidad (CO).En la toma de decisiones de inversión sobre diferentes alternativas, se recurre a la determinación y análisis del costo de oportunidad del inversionista. Este se define como el valor de la opción que es sacrificada, esto es, el beneficio que se deja de percibir al destinar los recursos de capital financiero a una alternativa de inversión en lugar de otra. El costo de oportunidad pretende medir la bondad de una alternativa de inversión en términos de lo que se deja de ganar en su mejor uso alternativo (los recursos financieros invertidos ya no están disponibles para otros fines).
Supongamos que un empresario se enfrenta a tres alternativas de inversión mutuamente excluyentes: Invertir en TES con rendimiento esperado de $9.86$% E.A., ampliar la planta de producción de su empresa con tasa de retorno esperada $11.0$% E.A. y, por último, optimizar un portafolio de títulos de renta variable con rendimiento probable del $13.5$% E.A. Desde las tasas de retornos planteadas, el empresario elige la alternativa del portafolio de títulos de renta variable y descarta las demás; así mismo, el mejor uso alternativo de los recursos es la opción de ampliar la planta de producción y, por ello, el costo de oportunidad de este empresario es el $11.0$% E.A.
La tasa de retorno de la segunda mejor opción no tomada, es el costo de oportunidad. Ahora bien, si por alguna circunstancia el empresario se decidiera por la opción de ampliar la planta, y no por el portafolio de títulos valores con tasa de retorno del $13.5$%, el costo de oportunidad es de $0.11-0.135=-0.025$; es decir $-2.5$%. Estaríamos en presencia de una mala (irracional) elección.
Para futuras inversiones, estas se realizarán si la rentabilidad es mayor al $13.5$%; esto es, el empresario ha formado un nuevo costo de oportunidad. En consecuencia, una orientación para la toma de decisiones sobre alternativas de inversión es:
$$TMAR>CO$$No obstante, Blank y Tarquin
El costo promedio ponderado del capital (CPPC).Como ya se ha indicado, las fuentes de los recursos para financiar la inversión total de un proyecto, tienen origen en los recursos propios y de deuda, y en conjunto constituyen la estructura de capital del proyecto.
Cada fuente de financiación tiene para el proyecto un costo. De manera general, en cuanto a recursos propios, el costo se relaciona con la expectativa de rendimiento de la inversión. Para los recursos de deuda, el costo está representado por la tasa de interés con la que se contrata los préstamos y empréstitos.
Igual situación se presenta en el caso de las recursos externos o de deuda. Las fuentes posibles de recursos de deuda son la colocación de bonos, los préstamos bancarios e hipotecas, los pagarés, las letras de cambio, entre otros. Cada uno de ellos tiene un costo para el proyecto, haciéndose necesario igualmente el cálculo del costo promedio ponderado del capital de deuda, costo que se puede calcular antes o después de impuestos (incluyendo o no, los intereses ocasionados por las deudas, ya que afectan la utilidad antes de impuestos).
Lo común en la financiación de los proyectos, es una mezcla de ambas fuentes, por ejemplo un 60% de recursos propios y un 40% de recursos de deuda. En esta situación, debemos determinar el costo promedio ponderado del capital (CPPC) o WACC, por su denominación en inglés (Weighted Average Cost of Capital).
En la Figura 4.2 se presenta el modelo para el cálculo después de impuesto. Las variables son:
$E=$ Total de recursos propios
$D=$ Total de recursos de deuda
$V=E+D=$ Total estructura de capital
$R_e=$ costo promedio ponderado de los recursos propios
$R_d=$ costo promedio ponderado de los recursos de deuda
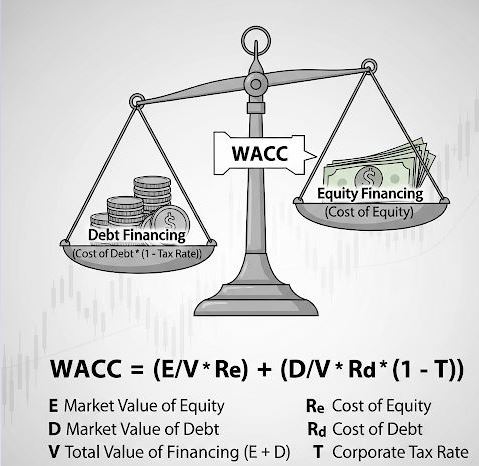
$T=$ Tasa impositiva.
Ejercicio 4.1. El CPPC. Determinar el costo promedio ponderado del capital de una inversión financiada con recursos propios en un 60% y costo promedio de 25% efectivo anual, y el restante 40% es financiada con recursos de deuda con costo promedio de 20% efectivo anual. Si $T=35$% E.A., hallar CPPC antes y después de impuestos
Solución.
Esto es, $23.0$% y $20.2$% efectivo anual, respectivamente.
Ejercicio 4.2. El CPPC de recursos propios, de deuda y CPPC de mezcla. Para la financiación de un proyecto productivo se determinó la siguiente estructura de capital: Aportes de socios 300 millones de pesos al 25% efectivo anual por costo de oportunidad, emisión de bonos a largo plazo por 200 millones al 18% efectivo anual, préstamos bancario por 100 millones de pesos al 20% efectivo anual, en total 600 millones de pesos. Hallar el costo promedio ponderado de los recursos propios, el costo promedio ponderado del capital de deuda y el costo promedio ponderado de la estructura del capital (mezcla), después de impuestos.
Solución.
Es decir, del $18.67$% y $12.13$% respectivamente. El CPPC después de impuestos es menor porque los intereses pagados por compromisos de deuda son deducibles de impuesto, ocasionado un ahorro fiscal y, con ello, un ahorro al proyecto.
Y después de impuestos:
$$CPPC=0.5\ast0.25+0.5\ast0.1867(1-0.35)=0.1857$$El $21.83$% y $18.57$% respectivamente.
Resolvamos el ejercicio aplicando la fórmula del CPPC directamente, es decir sin el cálculo previo del CPPCD, pero solo después de impuestos. Con valores en millones, el cálculo es:
$$CPPC=\frac{300}{600}\ast0.25+\frac{200}{600}\ast0.18(1-0.35)+\frac{100}{600}0.20(1-0.35)$$ $$CPPC=0.5\ast0.25+0.33\ast0.18(0.65)+0.17*0.20(0.65)=0.1857$$Igual valor de $18.57$%. Nótese además: en todos los ejercicios la suma de las ponderaciones es igual a uno (o el 100%). En este último ejemplo la suma es: $0.50+0.33+0.17=1$.
¿Qué relación guarda el CPPC con la TMAR? Como orientación para la determinación de la TMAR, tenemos:
$$ TMAR\geq CPPC$$¿En qué situación $TMAR>CPPC$? Cuando en el análisis para la determinación del rendimiento mínimo se incluya el factor prima de riegos del proyecto (como son los riesgos sistemático y de mercado). Esta afirmación también es válida para el caso de la tasa de interés libre de riesgo, la TMAR se puede ajustar por el factor de riesgo del proyecto. Empero, en este texto no se modela el problema del riesgo en el análisis de alternativas de inversión.
En conclusión, el costo promedio ponderado del capital, es la tasa que se paga por los recursos requeridos para cubrir la inversión total de un proyecto, tales como los activos fijos y diferidos, de capital de trabajo. En cambio, la tasa mínima atractiva de retorno, es la rentabilidad mínima exigida a un proyecto para invertir en él; es la concreción numérica de la expectativa de rendimiento sobre la inversión, y por ello referente en la evaluación de alternativas de inversión.

La TMAR puede ser expresada en términos reales o corrientes. Análogo a la tasa de interés efectiva real, y definiendo a ${\rm TMAR}^\pi$ como la real, tenemos que la tasa mínima atractiva de retorno a precios constantes del año base es:
$${\rm TMAR}^\pi=\frac{TMAR-\pi}{1+\pi}(4.4)$$Para expresarla en términos corriente, despejamos de (4.4) a TMAR, obteniendo:
$$TMAR={\rm TMAR}^\pi+\pi+{\rm TMAR}^\pi\ *\ \pi(4.5.1)$$Es decir:
$$TMAR={(1+TMAR}^\pi)(1+\pi)-1(4.5.2)$$La utilización de las fórmulas (4.5.1) y (4.5.2) implicaría realizar pronósticos sobre el nivel de inflación para el horizonte de planeación del proyecto productivo.
₪ El valor de salvamento o de rescate (VS). El supuesto de liquidación del proyecto.
Todo proyecto se formula en un horizonte de planeación de $n$ años, dependiendo de su naturaleza. Es posible realizar estudios de proyectos con estimaciones a cinco, diez, o veinte años. En la práctica proyectos con naturaleza perpetua, como son la generación de energía eléctrica, los servicios básicos de acueducto y alcantarillado, los bonos perpetuos, etc, se pueden evaluar en un horizonte de tiempo de 30 años.
La metodología de evaluación de proyectos supone que al final del último año del estudio del proyecto de inversión (el año $n$), éste se liquida. Se hace un "corte artificial" y se supone la venta de los activos, por un monto que se debe estimar desde la preparación del proyecto, ocasionando una entrada adicional denominada valor de salvamento, $VS$.
La dificultad de esta estimación está en el hecho de determinar el precio de venta para dentro de $n$ años de un activo que aún no se ha adquirido. Un método empleado en esta labor de estimación, es el contable que dice: el $VS$ es igual al valor neto en libros de los activos, es decir, igual al valor de compra del activo menos la depreciación acumulada en el año $n$ de liquidación del proyecto. Es por ello, un valor residual.
Otros métodos posibles son el valor del mercado del activo y el valor económico del activo (ver Sapag, et. al.

₪ Sistematización de la información por medio del Flujo de Caja.
La información requerida para la evaluación del proyecto se sistematiza por medio del estado de flujo de caja libre (también conocido como flujo de caja o de efectivo). Como su nombre lo indica, se incluye todos aquellos movimientos de dinero en efectivo, en su calidad de entradas (ingresos operacionales, por venta de activos, ahorros tributarios, etc.) y de egresos (como los costos de producción, gastos, pagos financieros).
En este capítulo haremos referencia a dos tipos de flujo de caja libre: al flujo de caja puro o del proyecto, y al flujo de caja libre del inversionista. El soporte para la elaboración de dichos flujos, es el estado de resultados del proyecto que en su forma simple se presenta a continuación.
Estado de resultados.Ingreso de operación
-Costos de producción=Utilidad Bruta
-Gastos de administración
-Gastos de venta=Utilidad operativa
+Otros ingresos no operativos
-Otros gastos no operativos
-Gastos financieros=Utilidad antes de impuestos
-Impuestos
=Utilidad Neta
Flujo de caja libre del proyecto.Este flujo es libre porque sus excedentes están dirigidos a cubrir las exigencias de rentabilidad de los inversionistas y las obligaciones derivadas de la financiación de la inversión por deudas.
A la estructura del estado de resultados anterior se le debe realizar varios ajustes para obtener el flujo de caja libre. En primer lugar, no se incluye la carga financiera por intereses de las deudas. En segundo lugar, la depreciación de tangibles y la amortización de intangibles no son costos y gastos desembolsables, y por tanto no son movimiento de efectivo.
Por lo tanto, y al estar incluidos en los costos de producción y en los gastos de administración y ventas, debemos reincorporarlos para obtener el flujo de caja libre. Además, al final del horizonte $n$ se recupera el total del capital de trabajo. Con estos ajustes, el flujo de caja libre queda de la siguiente manera:
Ingreso de operación
-Costos de producción=Utilidad Bruta
-Gastos de administración
-Gastos de venta=Utilidad operativa
+Otros ingresos no operativos
-Otros gastos no operativos=Utilidad antes de impuestos
-Impuestos=Utilidad Neta
+Depreciaciones
+Amortizaciones
+Recuperación del capital de trabajo=FNE del proyecto
El flujo neto de efectivo (FNE) es el excedente que entra a participar en el cubrimiento de las obligaciones con los acreedores y de la rentabilidad de los inversionistas.
El flujo de caja libre del inversionista.La estructura de este flujo de efectivo es la siguiente:
Ingreso de operación
-Costos de producción=Utilidad Bruta
-Gastos de administración
-Gastos de venta=Utilidad operativa
+Otros ingresos no operativos
-Otros gastos no operativos
-Gastos financieros=Utilidad antes de impuestos
-Impuestos=Utilidad Neta
+Depreciaciones
+Amortizaciones
+Recuperación del capital de trabajo
-Abonos al capital de deuda=FNE del inversionista
Los flujos de efectivo se estiman a precios corrientes o del año en curso, así como a precios constantes o de un año base. Bajo el primer enfoque, es necesaria realizar el pronóstico de la inflación promedio anual para el horizonte de tiempo $n$ del proyecto de inversión, y aplicar en la evaluación la TMAR corriente de la ecuación (4.51) o (4.5.2).
En cambio, si se trabaja los flujos de efectivo con los precios de un año base, por ejemplo cuando $ff=0$, la TMAR consistente con este proceder es la real, como en la ecuación (4.4). Bajo esta situación, los cambios en el valor de las magnitudes del flujo de efectivo se deben exclusivamente al cambio en los volumenes, por ejemplo de producción y venta de mercancías, y no a cambios de los precios.
Este proceder hace innecesario la elaboración de una conjetura sobre la inflación futura. Adoptaremos este método para el resto del libro.
En la siguiente Figura 4.5 se presenta un ejemplo de flujo de caja libre del proyecto. En él no se ha incluido el año cero como base ($ff=0$). La inversión fija y diferida es de 900 millones de pesos y la inversión en capital de trabajo es de 100 millones de pesos, no se plantea inversiones de reemplazo ni de modificación del tamaño de la operación. La inversión total es de 1,000 millones de pesos.
El capital se financia con un 60% de recursos propios y el restante 40% con recursos de deuda; el costos de estas fuentes de recursos son 20.5% y 15.0% efectivo anual, respectivamente. En consecuencia, el WACC de este proyecto, es de:
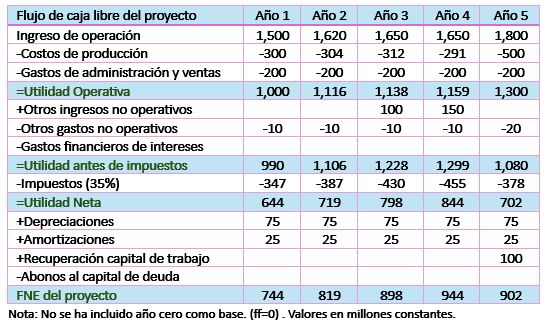
Después de impuesto, el WACC es:
$$WACC=0.60*0.205+0.40*0.15*(1-0.35)=0.162$$Del 18.3% efectivo anual real antes de impuestos y del 16.2% después de impuestos. Este último valor lo asumimos como la TMAR del proyecto, adicionando un 5% efectivo anual por prima de riesgo del proyecto; por lo tanto, la TMAR= 21.2% efectiva anual real. El valor de salvamento es igual a 400 millones correspondientes al monto neto en libros de los activos. La representación gráfica de este proyecto se ofrece en la Figura 4.6.
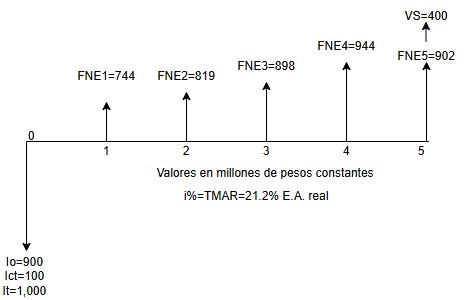
En el diagrama se hace explicito la inversión, representada como salidas, y el valor de salvamento como una entrada adicional en $ff=5$.
El flujo de caja desde el punto de vista del inversionista se presenta en la siguiente Figura 4.7.
La financiación se cancela por medio de una cuota fija anual de 119 millones. De esta cuota, el primer año se cancela intereses de 60 millones y abona al capital 59 millones (se aplica el caso de sistema de amortización con cuota fija). Ver Figura 4.7 para los demás pagos, señalados en amarillo.
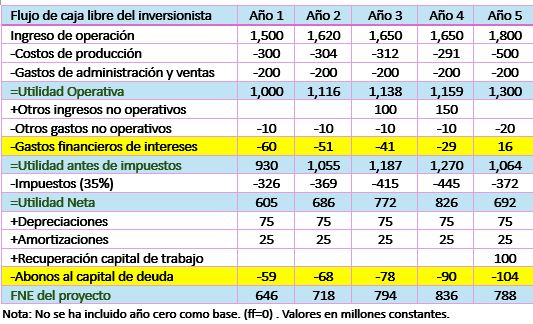
En este modelo, la inversión asumida como relevante para el análisis de la rentabilidad es la financiada por los recursos propios, es decir de 600 millones (el 60% de la inversión total); así mismo, la TMAR pertinente es el CPPC de recursos propios, el 20.5% al que le sumamos el 5% por prima de riesgo (debido por ejemplo al riesgo sistemático). El diagrama de este caso, en Figura 4.8.
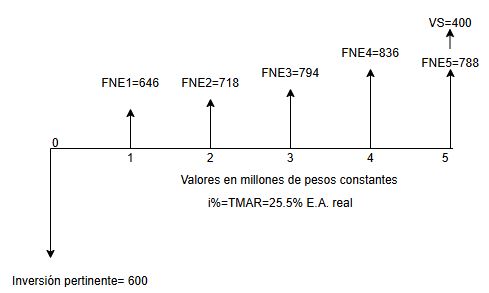
Deseamos llamar la atención sobre el siguiente hecho: el CPPC, y con él la TMAR, no es constante en el horizonte de tiempo en el que se formula el proyecto. El fundamento de esta afirmación está en que los abonos al capital de deuda cambian la composición en la estructura de capital, entre los recurso propios y los de deuda. Veamos un ejemplo.
La composición inicial de la estructura de capital de 1,000 millones, de los cuales 60% son recursos propios y 40% de deuda, es decir de 600 millones y 400 millones respectivamente, al final del primer año cambia, al asistir un abono total al capital de deuda de 59 millones, a 659 millones de recursos propios y 341 de recursos de deuda. Por ello, la nueva composición de la estructura de capital es de 65.9% de recursos propios y 34.1% de deuda. Con ello, el CPPC al final del año uno es:
$$CPPC=0.659*0.205+0.341*0.15(1-0.35)=0.1683$$Del $16.83$% E.A., y el CPPC antes de impuestos es:
$$CPPC=0.659*0.205+0.341*0.15=0.1862$$Del $18.62$% E.A. En la composición porcentual de la estructura de capital, gana participación los recursos propios y disminuyen los de deuda, con las amortizaciones de estos últimos recursos. El CPPC total, se acerca cada vez más al CPPC de los recursos propios.
Con la información desarrollada en el punto anterior procedemos a presentar el procedimiento para calcular la medida de valor conocida como valor presente neto, ($VPN$), y la pauta para decidir sobre la aceptación o el rechazo de una alternativa de inversión. En este procedimiento, la TMAR actúa como tasa de interés y se emplea para descontar todos los flujos de efectivos al momento presente (a la $ff=0$).
El procedimiento para el cálculo del valor presente neto, se concreta en la siguiente ecuación (4.6): $$VPN(tmar)=-I_0-I_{ct}+\sum_{j=1}^{n}{\frac{{\rm FNE}_j}{\left(1+tmar\right)^j}+\frac{VS}{\left(1+tmar\right)^n}}(4.6)$$La pauta para decidir sobre la implementación de una alternativa de inversión es:
Si $VPN(tmar)\geq0$, el proyecto cumple la condición financiera de rentabilidad para su aceptación; el proyecto es viable financieramente.
En la situación de $VPN(tmar)=0$, el proyecto rinde exactamente lo mínimo exigido para su aceptación. Desde la óptica financiera, en ocasiones se señalan a estos proyectos como indiferentes.
En cambio, si el resultado es $VPN(tmar)<0$, el proyecto se rechaza, porque no cumple con lo mínimo exigido. Es decir, el proyecto con las entradas no está en condiciones de cubrir las salidas (inversión y rentabilidad), a la tasa TMAR.
Hallemos ahora el valor presente neto de las Figuras 4.6 y 4.8
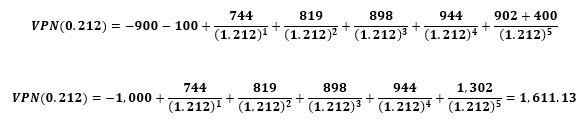
Al descontar los primeros $744$ al $21.2$%, se obtiene un valor presente de $613.86$. Este valor es el resultado de extraer, descontar, del valor inicial la rentabilidad deseada, y su destino es contribuir con la recuperación de la inversión total de 1,000 millones de pesos. Así ocurre con los demás ingresos netos.
Tenemos el siguiente balance entre entradas y salidas de efectivo:
$$VPN(0.212)=-1,000+2,611.13=1,611.13$$Con los flujos netos de efectivos más el valor de salvamento, el proyecto cubre la rentabilidad deseada, la inversión inicial de 1,000 (millones de pesos) y genera una rentabilidad extra (sobre la ordinaria o solicitada) de 1,611.13 (millones). El proyecto financieramente se debe ejecutar.
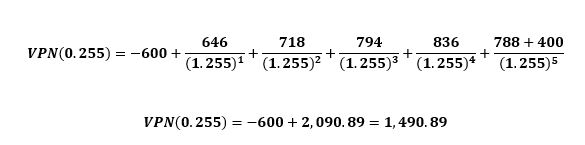
Recordemos que en la obtención de los flujos netos de efectivo (FNE) se han incluido los pagos de intereses y los abonos al capital de duda. Por ello, los FNE y el valor de salvamento, se destinan a cubrir la inversión total de proyecto financiada con recursos propios y las ganancias mínimas esperadas. El resultado para el inversionista es una utilidad excedente de 1,490.89 millones. Igualmente, el proyecto financieramente se debe aceptar.
₪ Alternativas de inversión mutuamente excluyentes con igual vida útil.
Las alternativas de inversión mutuamente excluyentes son aquellas cumplen el mismo propósito, son sucedáneas, y por ello compiten entre sí. Al tomar la decisión por una de ellas, hace innecesaria las demás.
Se debe elegir la alternativa que tenga el mayor valor presente neto, a una TMAR determinada, ya que ofrece el mayor beneficio o retorno al inversionista. Veamos el siguiente ejemplo.
Ejercicio 4.3. VPN de alternativas excluyentes con igual vida útil. Una empresa de logística nacional está pensando en la adquisición de nueva tecnología que le permita realizar en mejores condiciones la gestión de la empresa. Para ello se propone implementar un sistema de Autonomous Mobile Robot (AMR, conocida como vehículos autónomos inteligentes) para la automatización de tareas de transporte internos recibiendo dos ofertas de empresas locales, que compiten entre sí. La primera es de un sistema AMR Modular para logística interna, de rápida instalación y puesta en funcionamiento y reduce accidentes de trabajo; el valor es de 1,100,000 de dólares. La segunda opción es un sistema AMR de robots colaborativos (Cobots ), con valor de 1,500,000 dólares. Ambas alternativas se estudian bajo la misma vida útil de cinco años. El estudio de los efectos financieros de las propuestas, arrojan los siguientes resultados:
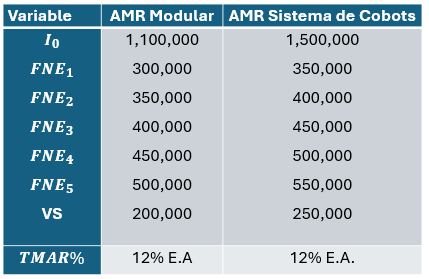

Solución. Con valores en miles de dólares:
Alternativa ModularAlternativa Sistema de CobotsEl sistema AMR Modular ofrece los mejores rendimientos financieros para la empresa logística, por lo que se aceptaría esta opción. Esta aceptación anula la posibilidad de seleccionar la alternativa sustituta.
₪ Alternativas mutuamente excluyentes con diferentes vidas útiles.
La determinación de la medida de valor VPN para este caso, requiere de la comparación bajo el mismo número de años o igual período. Para subsanar esta situación se procede a determinar el mínimo común múltiplo con las vidas útiles de las alternativas consideradas, y es el utilizado como período común en la evaluación de las alternativas de inversión.En el siguiente ejercicio 4.4 se plantea dos alternativas con vidas útiles de 6 y 9 años. Para compararlas en igual período, el mínimo común múltiplo (MCM) es 18 años.
Ejercicio 4.4. VPN de alternativas excluyentes con diferentes vidas útiles. Como gerente de una empresa manufacturera de equipos inteligentes necesitas determinar una línea de producción. Para ello tienes dos alternativas mutuamente excluyentes La línea de Producción Semi automatizada (LPSA) con vida útil de 6 años, requiere de una inversión inicial de 500 mil dólares y genera FNE desde al año uno al año seis de 160 mil dólares, con valor de salvamento de 20 mil dólares. Línea de Producción Automatizada (LPA) con vida útil de 9 años, requiere de una inversión inicial de 800 mil dólares, y genera FNE desde el año uno al año nueve de 265 mil dólares, y un valor de salvamento de 50 mil dólares. Con una TMAR de 20% E.A., determinar financieramente la mejor propuesta.
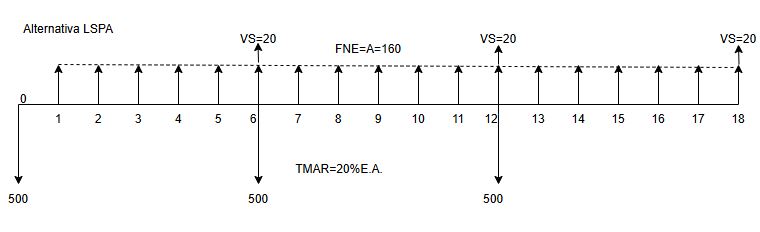
La alternativa LPA repite el ciclo de vida dos veces en 18 años. En las fechas focales cero y nueve se hace inversión inicial de 800 mil dólares; Los valores de salvamente se dan en los años 9 y 18. Ver Figura 4.11
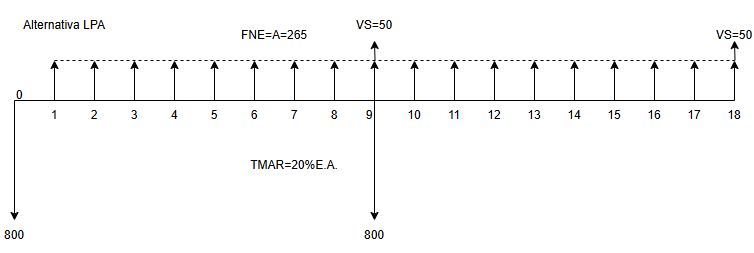
Solución. Con valores en miles de dólares.
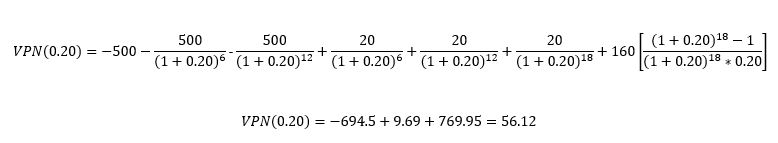
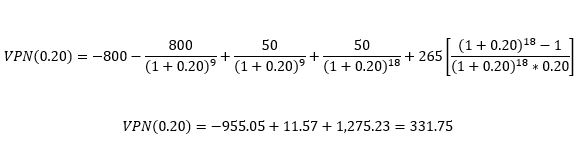
Se define a la tasa interna de retorno (TIR) como aquella tasa que hace al valor presente neto de una alternativa de inversión igual a cero. Si identificamos a la TIR con $i^*$, desde la ecuación (4.6), esta definición se expresa como:
Desde la ecuación (4.7), también podemos indicar que la TIR es la tasa que hace igual a las entradas de un proyecto con sus salidas (igualdad de ingresos y egresos); veamos:
$$I_0+I_{ct}=\sum_{j=1}^{n}{\frac{{\rm FNE}_j}{\left(1+i^*\right)^j}+\frac{VS}{\left(1+i^*\right)^n}}\ (4.8)$$La TIR es una tasa que se cobra (o se paga) sobre el saldo, en nuestro caso, de la inversión no recuperada. Así como en los sistemas de amortización la tasa de interés se aplica sobre el saldo insoluto, la TIR se aplica al saldo no recuperado de la inversión. La definición de TIR, como en la ecuación (4.7), conserva el supuesto de reinversión automática, supuesto ya señalado desde el modelo del valor futuro pago único.
Para hallar esta medida de valor, recurrimos al método de la interpolación lineal, ya ampliamente ilustrado en capítulos anteriores. Más adelante utilizaremos la hoja del cálculo Excel para este propósito.
La pauta para la aceptación o rechazo de una iniciativa de inversión por esta medida de valor es:
Se acepta la iniciativa si: Se rechaza la iniciativa si:Como ejemplo procedemos a estimar la TIR para el proyecto representado en las figuras 4.6 y 4.8.
Ya sabemos que con una tasa del $21.2$% el VPN es de 1,611.13, monto indicativo de alta rentabilidad. Realicemos un primer ensayo con tasa de 50% y la vamos aumentando en 15% hasta hallar un VPN negativo. Los resultado son:
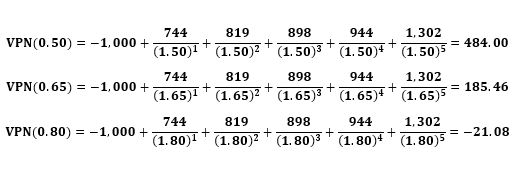
Conforme con los resultados, la TIR es un valor que está entre $65$% y $80$%. Desde la ecuación de proporcionalidad, TIR es:
$$i^\ast=\frac{0-(-21.08)}{185.45-(-21.08)}\ast(0.65-0.80)+0.80=0.7821$$TIR del $78.21$% y es mayor que la TMAR. El proyecto se acepta
Ensayemos con una tasa del 80% y vamos aumentando en 20%. Los resultados son:
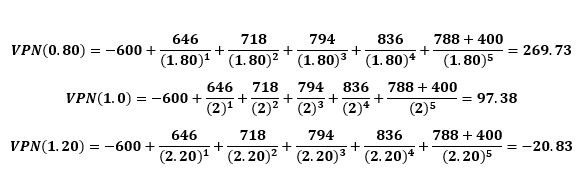
La TIR del inversionista se halla entre 100% y 120%. Desde la ecuación de proporcionalidad, TIR es:
$$i^\ast=\frac{0-(-20.83)}{97.38-(-20.83)}\ast(1.0-1.20)+1.20=1.1594$$La TIR es de $115.94$% y mayor que la TMAR. El proyecto se acepta financieramente. Los resultados son consistentes con los de la medida de valor por VPN: con ambas medidas el proyecto, puro y del inversionista, se acepta financieramente.
La siguiente figura 4.12 presenta la relación entre el VPN y diferentes tasas mínimas atractivas de retorno para el caso del proyecto puro.
En dicha Figura se observa la existencia de una pendiente negativa entre el VPN y la TMAR, al unir los punto de la tabla $i$% vs. $VPN$. A medida que aumenta la $i$% (TMAR) el VPN disminuye, incluso con valores negativos a tasas altas del $85$% y $100$%.
Por lo tanto, se hace necesario un proceso argumentado, informado, para la definición de la TMAR y su relación con TIR. Una TMAR muy alta puede llevar a rechazar proyecto de inversión muy atractivo financieramente, y viceversa, con una TMAR baja.
En la Figura 4.12, con TIR igual a $78.21$% el $VPN=0$. Este es el rendimiento interno (o sea propio) y máximo que ofrece esta alternativa de inversión, desde el caso puro. Los rendimientos son sobre el saldo de la inversión no recuperada.
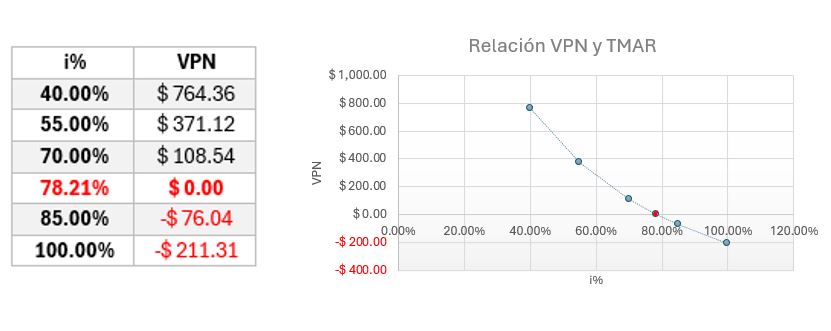
Para observar el proceso de TIR sobre saldo de la inversión no recuperadas, nos apoyamos en la siguiente Figura 4.13, del flujo de caja libre puro.
En este caso, $n$ es el horizonte de planeación del proyecto definido para cinco años. Las cuotas de cada año son los respectivos flujos netos de efectivo (FNE). Los intereses de cada año resultan de aplicar al saldo no recuperado de la inversión la tasa interna de retorno. La amortización anual resulta de restar a cada cuota los intereses; el excedente obtenido se destina a cubrir el saldo de la inversión. En resumen, es el mismo proceder de los planes de amortización trabajados en el capítulo anterior.
Para el año $n=1$, los intereses son de $I=1000*0.7821=782$ miles de dólares. Con un FNE de 744 miles de dólares, no se alcanza a cubrir los intereses en valor de $38$ mil dólares.
Por lo anterior, ese valor se acumula en el saldo de $I_t$ siguiente.
Con el $FNE_1$, no se alcanza a cubrir estos intereses, y por lo tanto el saldo de la inversión total, $I_t$, crece. En cambio, con el $FNE_5$ se logra cubrir los intereses y el saldo de la inversión. En el año 5 se recupera la inversión total con rendimiento interno del 78.21%. El excedente de rendimiento sobre la TMAR, son recursos del capital propio. Los recursos de origen externo participan en el resultado financiero del proyecto por medio del CPPC de deuda.
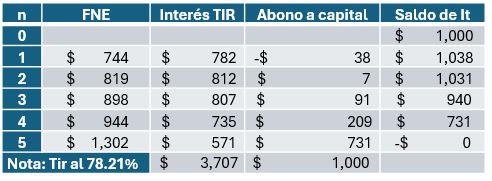
Ejercicio 4.5. TIR de alternativas excluyentes con diferentes vidas útiles. Hallar la TIR para las alternativas tecnológicas LPSA y LPA de las Figuras 4.10 y 4.11.
Solución.

Como el $VPN(0.25$) es negativo, la TIR es un valor entre 20% y 25%. Desde la ecuación de proporcionalidad, TIR es:
$$i^\ast=\frac{0-(-20.83)}{97.38-(-20.83)}\ast(1.0-1.20)+1.20=0.2304$$TIR de $23.04$% E.A.

La TIR de esta alternativa está entre 25% y 35%. Desde la ecuación de proporcionalidad el resultado es:
$$i^\ast=\frac{0-(-96,401.71)}{141,142.16-(-96,401.71)}\ast(0.25-0.35)+0.35=0.3022$$La TIR de $30.22$% E.A. Se confirma el resultado obtenido por el VPN, en cuanto ${\rm TIR}_{LPA}>{\rm TIR}_{LPSA}$.
Ahora bien, si el $VPN(tmar)>0$ entonces $TIR>TMAR$. La TIR indica por lo tanto hasta cuánto puede el inversionista aumentar el rendimiento mínimo deseado.
Sin embargo, sobre la TIR debemos llamar la atención en tres aspectos:
Aplicación del método de la TIR con alternativas mutuamente excluyentes.Para ilustrar esta metodología, en la Figura 4.14 se presenta el flujo de efectivo incremental de las alternativas LPSA y LPA, identificadas como (A) y(B) respectivamente. El flujo de efectivo incremental se obtiene como (B)-(A), siendo (B) la de mayor inversión inicial.
Se trata de constatar si se justifica la mayor inversión que implica (B), con respecto a la opción (A). Se realiza ensayos con 30% y 40%, obteniendo los siguientes resultados:
$$VPN(0.30)=96,476.86$$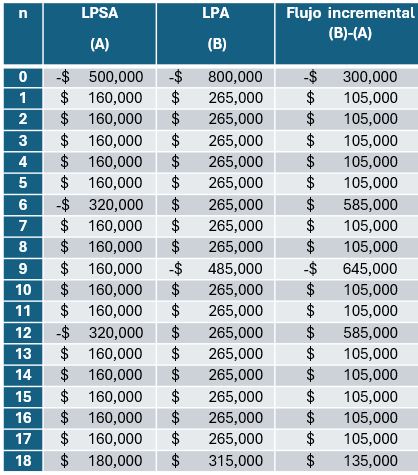
La TIR es en consecuencia:
$$i^\ast=\frac{0-(-2,129.38)}{96,476.86-(-2,193.38)}\ast(0.30-0.40)+0.40=0.3972$$Del $39.72$%. Y como $39.72$% > $20.0$%, se justifica la inversión incremental de $(B)$ de $300,000$, sobre la opción $(A)$; es correcto elegir la iniciativa de mayor inversión.
La presencia de múltiples TIR.la siguiente situación es la posibilidad de existencia de múltiples TIR para una alternativa de inversión. Observando la ecuación (4.7) encontramos que esta es un polinomio de grado $n$, que inicia con un elemento negativo y luego cambia en el siguiente elemento a signo positivo para sostenerse hasta el final; es decir presenta un cambio de signo.
Conforme a la regla de los signos de Descartes, un polinomio de grado $n$ tiene tantas raíces (es decir soluciones y, en nuestro caso TIR) como cambios de signos. Varias raíces, incluso con resultados negativos, son soluciones; hallándonos así ante soluciones múltiples.
Esta situación hace que la medida de valor TIR sea menos confiable para la toma de decisiones, al no poderse determinar cuál de las tasas posibles es la verdadera.
En el Diagrama de caja del ejercicio 4.6, se observa dos cambios de signos. En $ff=0$ hay una entrada, luego en las fechas 1 y 2 los valores son negativos, para luego en $ff=3$ ser de nuevo positivo; los signos cambian así: $(+,-,-,+)$.
Estos dos cambios de signo son evidencia de la existencia de dos TIR. Para el cálculo procedemos a evaluar el VPN del diagrama con diferentes tasas para luego interpolar. Según la figura 4.15, entre las tasas $i$ de 5% y 10% el VPN=0, evento que ocurre de igual manera entre las tasas $i$ de 40% y 45%. Se hace entonces interpolación en esos intervalos para obtener las dos TIR.
$$i^\ast=\frac{0-138.74}{-103.17-138.74}\ast(0.10-0.05)+0.05=0.07468$$Una primera tasa interna de retorno de $7.5$% E.A.
Ejercicio 4.6. TIR múltiples. Un proyecto de inversión ha generado el siguiente diagrama de caja. Determinar cuántas TIR existen y hallar el valor de estas.
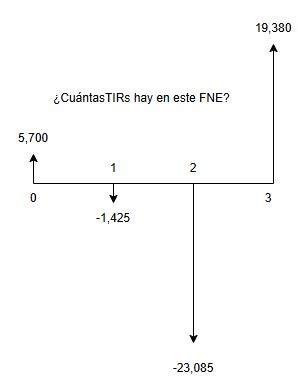
La segunda TIR es del $41.34$% E.A. ¿Con cuál tasa tomamos la decisión de aceptar o rechazar el proyecto?
Suponiendo una TMAR del 25%, tendríamos:
No es posible entonces decidir sobre la base de TIR, cuando existe dos o más tasas que hacen al $VPN=0$. Esta situación es una desventaja de esta medida de valor con respecto al Valor Presente Neto.
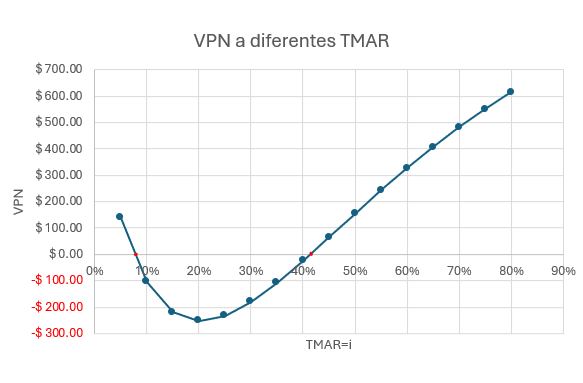
El supuesto de reinversión a la tasa TIR.Ambas medidas de valor, el $VPN(tmar)$ y la $TIR$, suponen reinversión de los flujos de caja del proyecto de inversión. El $VPN$ supone reinversión a la misma $TMAR$, la $TIR$ supone reinversión a la misma tasa de retorno $i^\ast$.
Para los proyectos de las Figuras 4.6 y 4.8, ¿es realista suponer reinversión de los $FNE$ a las tasas de internas de retorno de $78.21$% y $115.94$%, respectivamente?
La respuesta es no, las $TIR$ son sustancialmente mayor a la $TMAR$. Es más realista reinvertir los recursos a tasas como el $CPPC$, el $CO$, a la $i_{lr}+$ prima de riesgo, a la misma $TMAR$.
Son dos las consideraciones críticas presentes en la medida de valor de la TIR. En primer lugar, el supuesto implícito de reinversión de los flujos de efectivo a tasas de rentabilidad interna, muy superiores a la $TMAR$, no es realista. En segundo lugar, el cambio de signo de los flujos de efectivo genera tasas internas múltiples. Estas dos deficiencias de la medida de valor, la hace menos confiable como método de evaluación de alternativas de inversión. Bajo estas circunstancias, se recomienda la utilización de otros métodos para determinar la aceptación o rechazo de un proyecto de inversión.
Con esta medida de valor se resuelve las dos deficiencias señaladas para la $TIR$: reinversión a tasas realista y generación de una sola tasa de rentabilidad, también llamada Tasa Externa de Rendimiento, $TER$.
El procedimiento para hallar la $TIRM$ es el siguiente:
Todos los flujos netos de efectivo negativos (salidas) son descontados a $ff=0$ (valor presente) utilizando como tasa de descuento el CPPC de deuda después de impuestos (ver
Con los resultados de estos dos primeros pasos, es decir con el valor futuro en $ff=n$ de los FNE positivos y el valor presente de los FNE negativos, se elimina la posibilidad de varios cambios de signo de los FNE, y por ello se garantiza una sola tasa interna de retorno. También nos podemos hacer la siguiente pregunta: ¿cuál es la tasa que hace a estas dos cantidades, el valor futuro y el valor presente, equivalentes?, es decir, cuál es la $TER$ o $TIRM$. Si a la TIRM la representamos con $i'$, la respuesta a la cuestión es:
$$F=P(1+i')^n$$Despejando $i'$, la TIRM es: $$i'=\sqrt[n]{\frac{F}{P}}-1 (4.9)$$
Una ecuación ya conocida desde el tema del valor futuro vencido pago único.
La pauta general para aceptar un proyecto de inversión es que $TIRM$ es mayor o igual a la $TMAR$. Es decir:
$$TIRM\geq TMAR$$Es rechazado cuando $TIRM< TMAR$. Veamos un ejemplo
Ejercicio 4.7. El cálculo de la TIRM . Un proyecto de inversión para la implementación de la tecnología Gemelos Digitales y Simulación 3D , empleando software de simulación digital para diseñar, validar y operar almacenes inteligentes, ha generado el siguiente diagrama de caja.
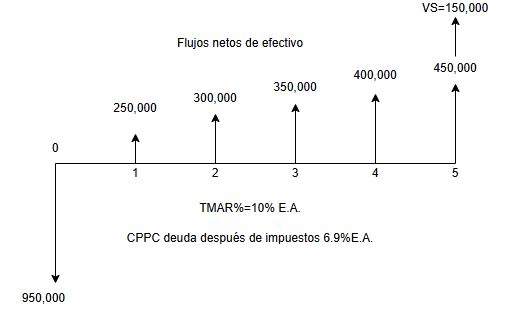
Usando el 10% como tasa de reinversión, hallar la TIRM
El flujo de caja solo presenta un cambio de signo, por lo que no existe el problema de tasas múltiples. Realizando los ensayo e interpolando, la TIR de este ejercicio es de 24.18% E.A. Para la TIRM procedemos a realizar el proceso de los tres pasos.
Los flujos netos positivos presentan la forma de una gradiente aritmético, con base de $250,000$ y gradiente de $50,000$. Aplicando $\epsilon=10$% obtenemos:
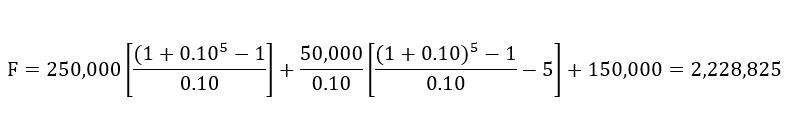
Solo existe un valor negativo de 950,000 correspondiente a la inversión inicial, ya en $ff=0$. Por ello no hay necesidad de descontar y usar Rho
TIRM del $18.6$% E.A. Como $TIRM> TMAR$ se acepta el proyecto.
Ejercicio 4.8. El cálculo de la TIRM con FNE positivos y negativos. A un ángel inversor le presentan la posibilidad de invertir en el proyecto que se sintetiza en el diagrama económico. Ver siguiente figura.
La $TMAR$ es determinada en 10.0%, La tasa de reinversión, definida como el CPPC propio, es de 8.0%, mientras que la tasa de financiación es de 5.8% después de impuestos; todas son tasas efectivas anuales. El proyecto debe evaluarse por el método de la TIRM
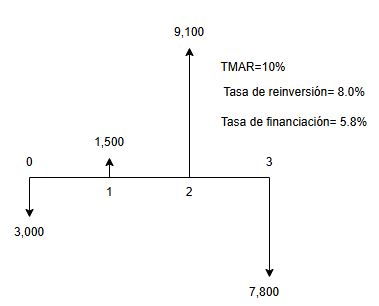
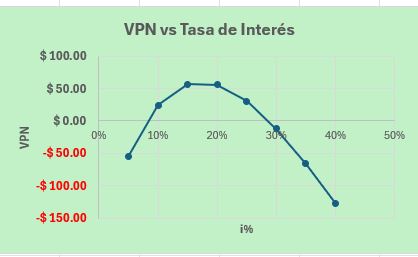
Interpolación entre 5% y 10%TIR de 8.08% menor que TMAR del 10%.
Interpolación entre 25% y 30%$TIR$ de 28.6% mayor que $TMAR$ del 10%.
¿Cuál es la TIR del proyecto?, ¿A qué tasa se reinvierten los recursos? Ante esta situación se acude a la medida de valor de $TIRM$Solución.
$TIRM$ de 6.49%, resultado menor que la $TMAR$ ($10.0$%). El proyecto se rechaza.
Esta medida de valor consiste en calcular, a partir de la información financiera del proyecto, un valor anual uniforme equivalentes (VAUE). Para ello, todos los valores de las variables determinadas en la iniciativa de inversión se transforman en anualidad (A), en serie uniforme, utilizando como tasa de interés la TMAR. El VAUE, también conocido como Valor Anual (VA), es el balance entre las anualidades de entrada y las anualidades de salidas.
Las pautas para aceptar o rechazar un proyectos son:
La interpretación del resultado es en el mismo sentido del VPN. Un VAUE>0, genera anualmente ganancias extraordinarias; un VAUE=0, se recupera la inversión y genera excedentes iguales a lo mínimo exigido; con VAUE<0, no se alcanza a recuperar la inversión del proyecto.
Supongamos que un proyecto de inversión ha generado el diagrama económico que se presenta en la Figura 4.17. En ella están explícitos, los valores de la inversión inicial, el valor de salvamento, los flujos de ingresos y los de egresos, bajo una TMAR del 15%.
La tarea consiste en convertir el diagrama en anualidad, en un valor equivalente para cada año. Para ello procedemos así:
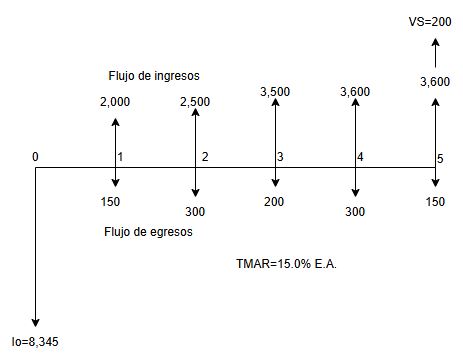
Para ello hallamos primero el valor presente de los ingresos y luego el resultado, lo convertimos a anualidad. Estos son:
$$P=\frac{2,000}{1.15}+\frac{2,500}{{1.15}^2}+\frac{3,500}{{1.15}^3}+\frac{3,600}{{1.15}^4}+\frac{3,600}{{1.15}^5}=9,778.94$$ $$A_{ingreso}=9,778.94\left[\frac{{1.15}^5*0.15}{{1.15}^5-1}\right]=2,917.21$$Para ello, procedemos a hallar primero el valor presente de los egresos y luego el resultado, lo convertimos a anualidad. Estos son:
$$P=\frac{150}{1.15}+\frac{300}{{1.15}^2}+\frac{200}{{1.15}^3}+\frac{300}{{1.15}^4}+\frac{150}{{1.15}^5}=734.88$$ $$A_{egreso}=734.88\left[\frac{{1.15}^5*0.15}{{1.15}^5-1}\right]=219.23$$El VAUE es mayor que cero, ofrece ganancias extraordinarios. Se acepta el proyecto
El balance de las entradas es 2,946.87 (valores positivos). El balance de salidas es de 2,708.67. Por lo tanto:
$$VAUE(0.15)=2,946.87-2,708.67=238.20$$El diagrama económico de la Figura 4.17 se puede plantear en términos netos, como en la siguiente Figura 4.18.
Recordemos que los valores ubicados en una misma fecha focal, se pueden sumar o restar, dependiendo del caso (si son entradas o salidas).
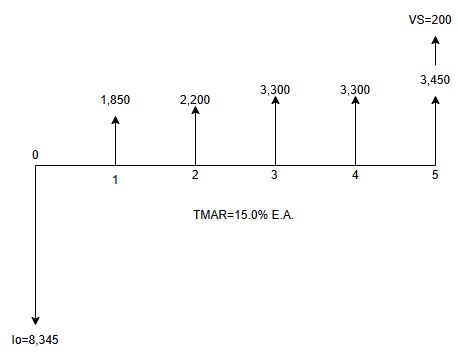
El resultado del VAUE no debe cambiar, pero se hace más corto su cálculo. Este es:
Aprovechemos la figura anterior Y hallemos el VPN y la TIR de dicho problema. Tenemos:
El valor presente neto al 15% de rentabilidad mínima.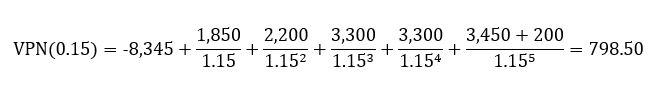
El VPN(15%) es mayor que cero. El proyecto se acepta.
El caso de la TIR.Como al 15% el VPN es positivo, procedemos a realizar un ensayo con el 20%, así:
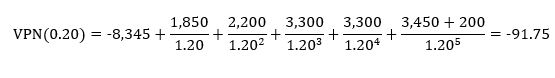
Resultado negativo. Por lo tanto, la TIR es una valor entre 15% y 20%. Desde la ecuación de proporcionalidad la TIR es:
$$i^\ast=\frac{0-\left(-91.75\right)}{798.50-\left(-91.75\right)}\ast(0.15-0.20)+0.20=0.185079$$TIR del 18.51% y mayor que la TMAR. El proyecto se acepta.
El resultado de la evaluación por tres medidas de valor, es la aceptación del proyecto. Los resultados son consistentes.
Además, la TIR es cercana a la TMAR, siendo así realista suponer la reinversión de los flujos de efectivo liberados por el proyecto a la misma tasa interna de rendimiento.
¿Qué resultado se obtiene al convertir el VPN anterior en serie uniforme? Resolvamos la inquietud:
$$A=798.50\left[\frac{{(1+0.15)}^5*0.15}{{(1+0.15)}^5-1}\right]=238.20$$El resultado es el VAUE. Por lo tanto:
$$VAUE=VPN\left[\frac{{(1+i)}^n*i}{{(1+i)}^n-1}\right](4.10)$$O también:
$$VPN=VAUE\left[\frac{{(1+i)}^n-1}{{(1+i)}^n*i}\right](4.11)$$La medida de valor VAUE se realiza sobre la vida útil del proyecto, no requiriendo la aplicación de iguales plazos por medio del MCM, con iniciativas mutuamente excluyentes.
Un caso especial del VAUE es el método del Costo Anual Uniforme Equivalente (CAUE). Esta medida de valor se aplica para proyectos de inversión donde priman los salidas (inversión, costos y gastos). En estos proyectos los ingresos son prácticamente inexistentes, ya que solo se incluye como entrada al valor de salvamento al final de la vida útil del proyecto.
Es común descubrir en la literatura sobre el tema, que los costos y gastos se agreguen en una anualidad denominada Costo Anual de Operación (CAO). De esta manera, son básicamente tres variables las que se incluyen en la medida de valor de CAUE: La inversión inicial, el valor de salvamento y los costos anuales de operación.
La medida de valor consiste en convertir todos los valores de las variables anteriores en un valor anual equivalente, resultado que representa un flujo de pagos anuales (de salidas de efectivo anualizadas). Por ello, dicha medida de valor se calcula del siguiente modo:
$$CAUE(i)=I_0\left[\frac{{(1+i)}^n-1}{{(1+i)}^n*i}\right]+CAO-VS\left[\frac{i}{{(1+i)}^n-1}\right] (4.12)$$Siendo i% la TMAR del proyecto. Como priman las salidas, en la ecuación (4.12) se han dejado a estos con signo positivo, en cambio el valor del salvamente, única entrada, se le asigna el signo negativo.
La pauta en la evaluación de proyectos con el método del CAUE, es seleccionar la alternativa con el menor valor (menor pago anualizado) entre opciones mutuamente excluyentes, evaluadas según sus vidas útiles.
Ejercicio 4.9. El cálculo del CAUE . Una empresa considera renovar sus procesos en la planta de producción, obteniendo para ello dos propuestas tecnológicas mutuamente excluyentes. La Alternativa A es un sistema de robots colaborativos; la Alternativa B es un sistema de robots tradicionales. Los costos de ambas propuestas son:
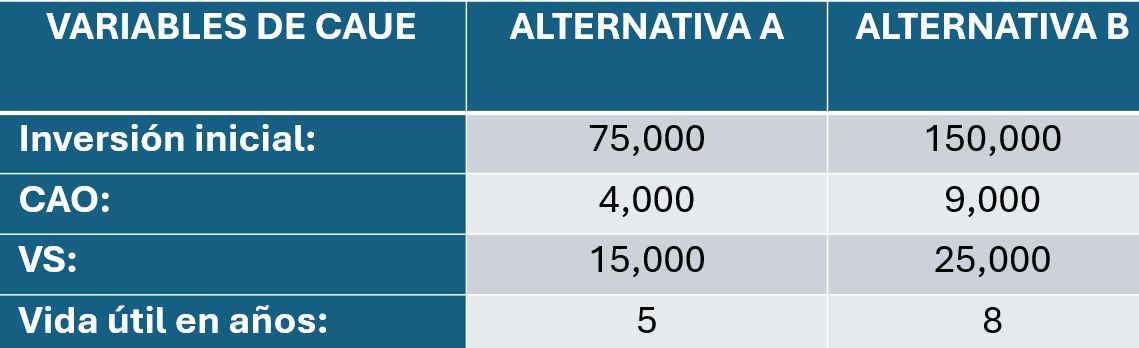
Con TMAR=15%, seleccionar la alternativa económicamente viable para la empresa.
Solución:
Se selecciona la Alternativa A por ser la de menor costo anual equivalente.
La ecuación de valor de la medida VPN, modelo (4.6) permite obtener varios indicadores que complementan el análisis de evaluación y toma de decisiones sobre proyectos de inversión. Los indicadores son coeficientes que por su origen relacionan valores equivalentes en una fecha focal determinada, en particular en el presente ($ff=0$).
Indicador de rendimiento (IR)Este indicador es el cociente del valor presente neto de todas las entradas de un proyecto ( los FNES y el VS) con la inversión del proyecto (inversión inicial y de capital de trabajo). Como cociente, el IR puede ser mayor, igual o menor a uno; el resultado indica el número de veces que con las entradas se cubre la inversión. Su cálculo es:
$$IR=\frac{\sum_{j=1}^{n}{\frac{{FNE}_j}{\left(1+TMAR\right)^j}+\frac{VS}{\left(1+TMAR\right)^n}}}{I_0+I_{ct}} (4.13)$$Para el ejercicio de la Figura 4.18, y aprovechando cálculos realizados, el IR es:
$$IR(0.15)=\frac{9,044.06+\frac{200}{{1.15}^5}}{8,345}=1.09569$$Se cubre la inversión en 1.096 veces. Como el indicadore es mayor que uno, el proyecto genera ganancias extras. Se acepta financieramente.
Tasa Beneficio/Gasto (B/G)Este indicador no es más que la expresión en porcentaje de IR. Es decir:
$$ B/G=(IR-1)$$Por lo tanto:
$$B/G=\left[\frac{\sum_{j=1}^{n}{\frac{{FNE}_j}{\left(1+TMAR\right)^j}+\frac{VS}{\left(1+TMAR\right)^n}}}{I_0+I_{ct}}-1\right]$$Los resultados posibles son B/G mayor que cero, igual a cero o menor que cero.
Para el mismo ejercicio, la tasa B/G es:
$$B/G=\left[\frac{9,044.06+\frac{200}{{1.15}^5}}{8,345}-1\right]$$ $$B/G=(1.09569-1)=0.09569$$Es decir, el $9.57$%. Debido a que $B/G>O$, se acepta el proyecto.
En esta sesión utilizamos funciones de Microsoft Excel, en adelante Excel, para el cálculo de las medidas de valor VPN, TIR y TIRM. Nos limitamos a estas medidas de valor debido al hecho de existir en Excel la función que posibilita ágilmente obtener el resultado buscado.
Ejercicio 4.10. Aplicación en hoja de cálculo de Excel. Hallar las medidas de valor de VPN, TIR y TIRM para el proyecto representado en el siguiente diagrama de caja.
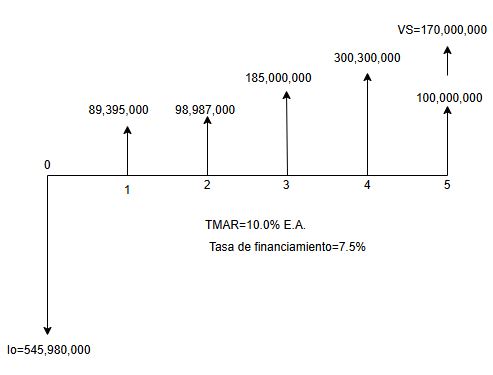
Asuma la TMAR=10% y la tasa de financiamiento de 7.5%
El valor presente netoPara esta medida de valor empleamos de Excel la función VNA. En el campo Tasa de la función digitamos la TMAR%. En los campos valor1, valor2, etc., digitamos los valores futuros de los FNE, desde el período 1 (ff=1) hasta el 5, que incluye además el VS. Otra opción para ingresar los valores es por medio de rango de celdas en el campo valor1, como en la Figura 2.19. Sin embargo, la función VNA no incorpora en sus campos a la inversión inicial, que está ubicada en la fecha focal cero ($ff=0$).
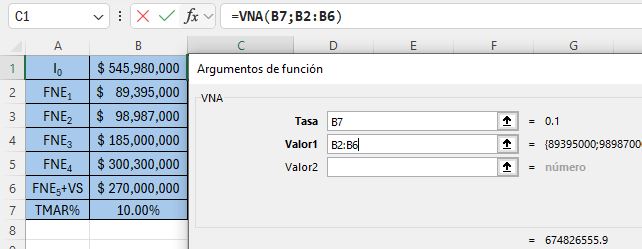
Por lo anterior, para obtener el VPN de un proyecto, debemos restar al resultado del VNA, la inversión inicial. Para esta operación ver Figura 4.20
Es decir:
$$VPN(tmar)=VNA-I_0$$ $$VPN(0.10)=674,826,555.87-545,980,000=128,846,555.87$$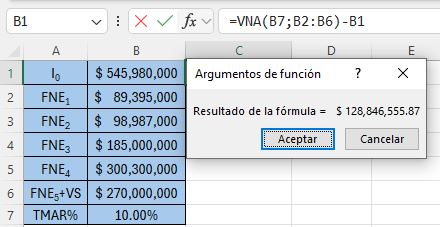
La tasa interna de retornoContrario a la función VNA, la función TIR de Excel incorpora a la inversión inicial en su campo de valores. Son dos los argumentos necesarios para resolver la función. El campo valores, es un rango que contiene el flujo de caja del proyecto, desde la inversión inicial (ingresada con signo negativo) hasta el último FNE y el VS.
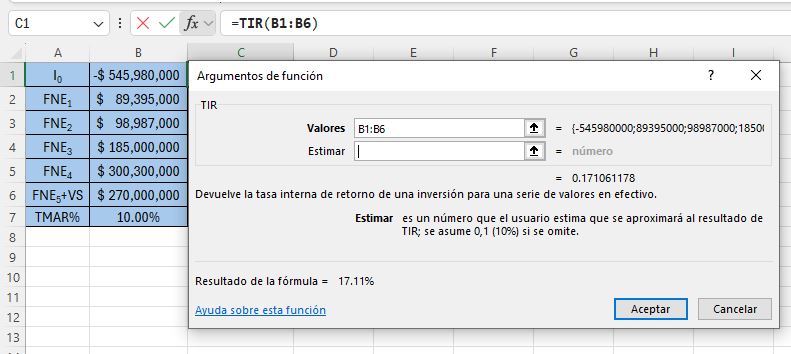
En el ejercicio que traemos, estos datos están en el rango de celdas B1:B6. El campo estimar contiene una tasa aproximada de la TIR, que por defecto es del 10%; si lo deseamos, podemos ingresar la tasa que consideremos. Una vez completa la información en los argumentos, damos aceptar para obtener el resultado pretendido. La TIR del proyecto es de 17.11%; ver Figura 4.21
La tasa interna de retorno modificadaEn Excel la función es TIRM y sus campos incluyen: Valores, como rango de celdas para el flujo de caja del proyecto ($I_o$, FNE, VS, en rango B1:B6), la tasa de financiación (TF), y la tasa de reinversión que asumimos del 10%, la misma TMAR. Ver Figura 4.22.
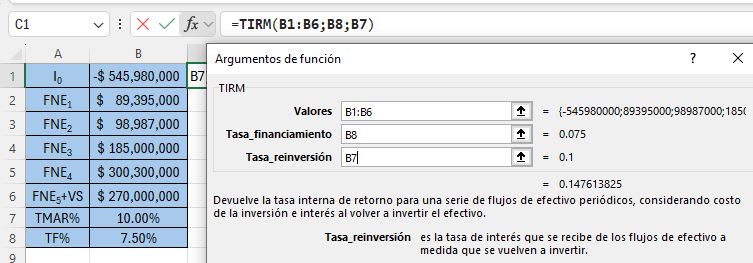
El resultado es $TIRM=14.76$%. Para el ejercicio obtuvimos:
$$VPN(0.10)>0$$ $$TIR>TMAR$$ $$TIRM>TMAR$$ R. Inversión inicial: $I_0 =1,983,808.19$; inversión total: $I_t=I_0+I_{ct}=2,463,808.19$R. CPPC antes de impuesto=14.5% E.A.; CPPC después de impuesto=12.73% E.A.R. Inversión pertinente total= 1,500 millones de pesos, siendo 500 millones por capital de trabajo. En la evaluación del proyecto se aplicaría como TMAR el 15.5% E.A.R. La diferencia es de 60 en UAI por gastos financieros de intereses; la diferencia en el monto de impuestos es por el escudo fiscal al permitirse la deducción de los intereses para liquidar el monto de impuestos; el ahorro tributario es de 21 y se obtiene multiplicando el gasto deducible (de intereses) por la tasa impositiva, esto es 60*0.35=21; los ahorros tributarios anuales son respectivamente: 21, 17.85, 14.35, 10.15, 5.6, para un total de 68.95 en cinco años. 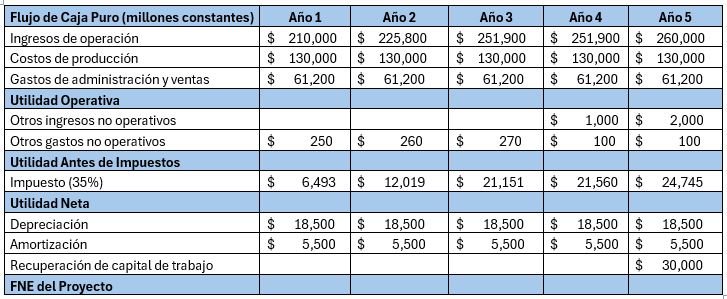
R. Para el año 1 y respectivamente: 18,800; 18,550; 12,058; 36,058
R. 3,726; 23%; 22.90%; 1.02 ; 2.33%; respectivamente. 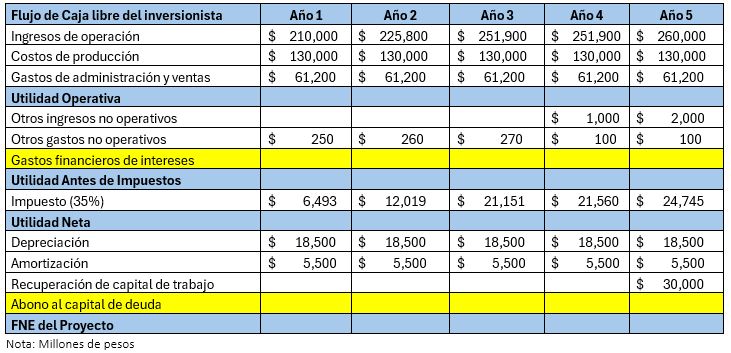
Para el año 1. R. cuota: 23,475; intereses: 14,820; abono al capital de deuda: 8,655; utilidad operativa:18,800; utilidad antes de impuestos:3,730; utilidad neta:2,425; FNE:17,769; CPPC antes de impuesto: 22.33%; CPPC después de impuestos:19.09%
R. Inversión apropiada:82,000; TMAR apropiada es el CPPC del inversionista:25.5%; VPN=12,391; TIR:31%; TIRM:29%; VAUE:4,655; IB:1.15;B/G:15.11%. R. Los ahorros anuales son respectivamente: 5,187; 4,611; 3,848; 2,859; 1,599. El total del escudo fiscal es de 18,100. R. Sistema #1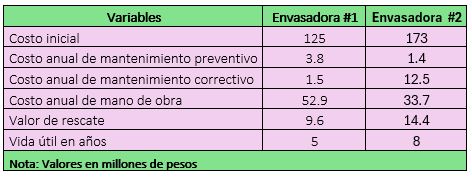
Para resolver límites de funciones que presentan formas indeterminadas, se ha desarrollado la herramienta matemática conocida como Teorema de la regla L'Hôpital. Formas indeterminadas son situaciones en las que el resultado obtenido al tomar el límite de una función es de $0/0$, $\infty /\infty $, como en los siguientes casos:
La regla dice que si tenemos una función $f(x)$ diferenciable de la forma $f(x)=\frac{g(x)}{h(x)}$, con derivada de $h(x)\neq 0$, y $ a\neq 0$, si al tomar los límites:
$$\displaystyle \lim_{x \to a}f(x)=\displaystyle \lim_{x \to a}g(x)/\displaystyle \lim_{x \to a}h(x)=0/0,$$ $$\displaystyle \lim_{x \to \infty }f(x)=\displaystyle \lim_{x \to \infty }g(x)/\displaystyle \lim_{x \to \infty }h(x)=\infty /\infty, $$el límite se obtiene derivando la función $f(x)$, aplicando las reglas de la derivada de manera independiente al numerador y al denominador; si el límite existe, $L$, es su solución. $$f'(x)=g'(x)/h'(x)=L$$
Si persiste la indeterminación, aplicamos la segunda derivada y así sucesivamente. Para los dos ejemplos anteriores, los límites son:
Esta regla se aplica en el tema de gradiente geométrico cuando $g=i$
La interpolación es el procedimiento matemático que consiste en hallar un valor dentro de un intervalo en el que se conoce los valores extremos; es estimar valores intermedios entre valores conocidos. Con el término lineal se indica que los datos o valores conocidos se ajustan a una línea recta (polinomio de primer orden); si los datos se ajustan a una forma parabólica, la interpolación es cuadrática (polinomio de segundo orden); etc.
Si tenemos dos puntos en un plano cartesiano, datos suficientes y necesarios para trazar una línea recta, tales como $(x_0,f(x_0)$ y $(x_1,f(x_1))$, la interpolación lineal consiste en determinar o estimar el valor de $f(x)$ para un valor de $x$ tal que $x_{0}< x< x_{1}$ (o sea, intervalo $x_0,x_1$), por lo que el valor a estimar de $f(x)$ debe cumplir con $f(x_{0})< f(x)< f(x_{1})$.
Teniendo en cuenta que la ecuación de la recta que pasa por eso dos puntos extremos es:
$$f(x)-f(x_0)=\frac{f(x_1)-f(x_0)}{x_1-x_0}(x-x_0),$$al despejar $f(x)$, tenemos la fórmula para la interpolación, así:
Esta ecuación se soporta geométricamente en el concepto de semejanza de triángulos, concepto que a su vez se establece desde la proporción geométrica.
Recordemos que razón matemática es el cociente que se obtiene al dividir dos números (por ejemplo $100/20=5$; la razón es 5). Ahora, la proporción geométrica es la igualdad de dos razones (por ejemplo 100/20=350/70; la razón común es 5). En general, podemos escribir para la proporción geométrica que:
$$\frac{a}{b}=\frac{c}{d}$$Igualdad empleada en la determinación de los triángulos semejantes. Además, si en esta igualdad son conocidos tres elementos, es posible hallar el cuarto, así:
$$a=\frac{c}{d}*b$$Esta expresión es la estructura que básicamente soporta la ecuación (A1)
Para que dos triángulos sean semejantes se debe cumplir que sus lados correspondientes guarden entre ellos una proporcionalidad, las razones sean iguales. Para ilustrar el asunto veamos un ejemplo.
Los siguientes triángulos DEF y ABC son semejantes si:
$$\frac{d}{a}=\frac{e}{b}=\frac{f}{c}$$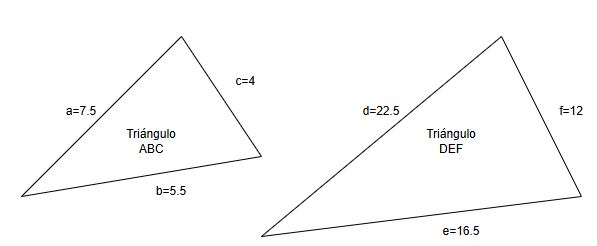
Veamos:
$$\frac{22.5}{7.5}=\frac{16.5}{5.5}=\frac{12}{4}=3$$Los triángulos presentan en sus lados correspondientes una razón común de 3, y por ello semejantes.
Al graficar una función, a partir de dos punto, podemos hallar un tercer punto por medio de interpolación lineal, utilizando la semejanza de triángulos. En la siguiente Figura 5.1 hemos dibujado dos punto para la función $f(x)=5+x^{2}$, deseamos saber cuánto vale $f(x)$, cuando $x=2.5$
Al unir los dos puntos conocidos con una línea recta, de ahí lo lineal de la interpolación (aunque $f(x)$ no es lineal), es posible establecer dos triángulos a los que aplicamos el concepto de igualdad de razones, es decir, establecer una ecuación de proporcionalidad.
Dicha ecuación de proporcionalidad, es la herramienta para hallar el valor desconocido, como realizamos a continuación. Ver Figura 5.2
.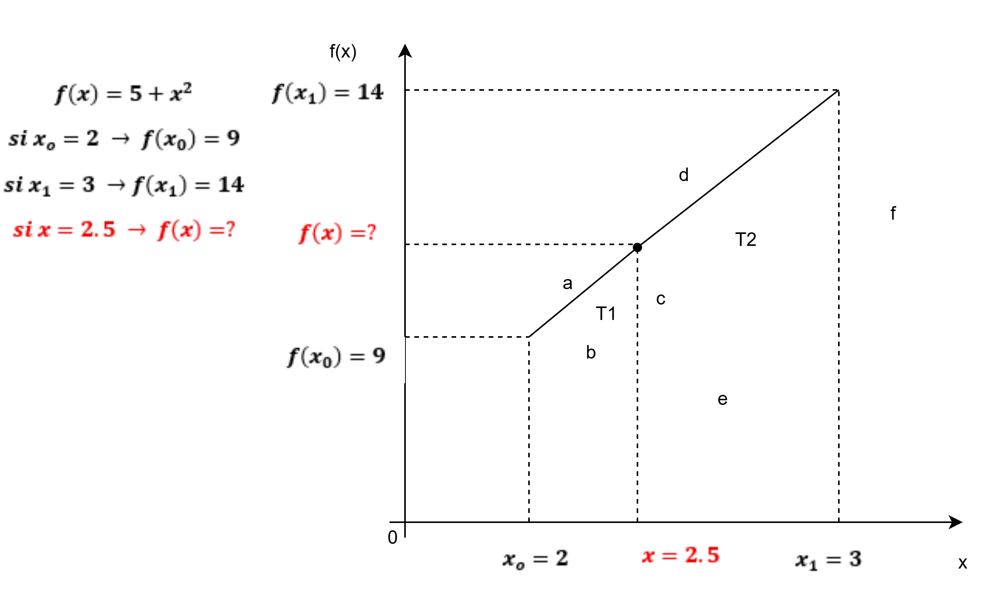
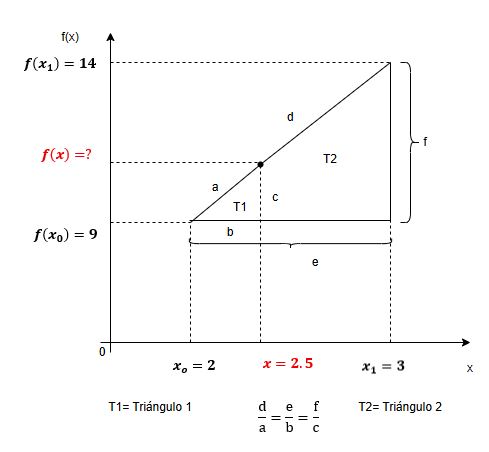
Si en la expresión de proporcionalidad se cumple la igualdad de razones para dos relaciones, en la tercera también se cumple. Así tenemos que si $e/b=f/c$ entonces asimismo se cumple para $d/a$.
Trabajando con $e/b=f/c$, tenemos:
$$e=x_1-x_0$$ $$b=x-x_0$$ $$f=f(x_1)-f(x_0)$$ $$c=f(x)-f(x_0)$$Por lo tanto:
$$\frac{x_1-x_0}{x-x_0}=\frac{f(x_1)-f(x_0)}{f(x)-f(x_0)}$$Despejando $f(x)$, resulta:
$$f(x)=\frac{(x-x_0)}{{(x}_1-x_0)}*[f(x_1)-f(x_0)]+\ f(x_0)$$Que se puede reescribir como:
$$f(x)=\frac{[f(x_1)-f(x_0)]}{{(x}_1-x_0)}*(x-x_0)+f(x_0)$$La misma ecuación A1. Por interpolación, el valor de $f(x)$ es:
$$f(x)=\frac{(14-9)}{(3-2)}*(2.5-2)+9=11.5$$Con la ecuación original el resultado es:
$$f(x)=5+{(2.5)}^2=11.25$$Se obtuvo una buena aproximación al valor real de la ecuación. La razón está en que mientras más pequeño es el intervalo para la interpolación, $(x_0,x_1)$, más exacta es la estimación.
El factor $\frac{f(x_1)-f(x_0)}{(x_1-x_0)} $, además de representar la pendiente de una línea recta, $m=\frac{\Delta f(x)}{\Delta x}$, es una aproximación a la primera derivada. Por ello, y en general, mientras más reducido sea el intervalo para la estimación por interpolación lineal, más exacto será el valor calculado.En el texto se aplica la interpolación lineal en problemas de cálculo de la tasa de interés, en anualidades y gradientes por ejemplo, y la tasa interna de retorno, TIR.
