Memorias del curso "Diseño de objetos interactivos con DescartesJS e IA"
Título: Memorias del curso "Diseño de objetos interactivos con DescartesJS e IA"
Sección: iCartesiLibri
Bloque: Formación
Unidad: Formación docente
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autores: Carlos Alberto Rojas Hincapié, Juan Guillermo Rivera Berrío y Jesús Manuel Muñoz Calle
ISBN: 978-84-10368-26-2
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Xadrez. Regras básicas
Título: Xadrez. Regras básicas.
Sección: iCartesiLibri
Bloque: Juegos
Unidad: Juegos de mesa. Ajedrez
Nivel/Edad: Cualquier nivel/Todas la esdades
Idioma: Gallego
Autor: Emilio Pazo Núñez
ISBN: 978-84-10368-25-5
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
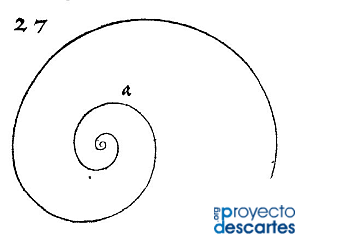
Crítica de la pseudoespiral de Durero
Título: Crítica de la pseudoespiral de Durero
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad/ 18 años o más
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Métodos numéricos. Ejemplos prácticos con Matlab.
Título: Métodos numéricos. Ejemplos prácticos con Matlab.
Sección: iCartesiLibri
Bloque: Análisis numérico
Unidad: Métodos numéricos
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autor: Elena E. Álvarez Saiz
ISBN: 978-84-10368-24-8
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Electrónica Digital. Ejemplos y Ejercicios. Segunda parte.
Título: Electrónica Digital. Ejemplos y Ejercicios. Segunda parte.
Sección: iCartesiLibri
Bloque: Ingeniería
Unidad: Electrónica
Nivel/Edad: Bachillerato y universidad (16 años o más)
Idioma: Castellano
Autores: Oscar Ignacio Botero Henao
ISBN: 978-84-10368-23-1
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional