¿Conoces lo que es la simetría axial? @prende.mx
Escrito por Montserrat Gelis BoschEsta semana presentamos la unidad interactiva Simetría, un recurso educativo para la introducción de este concepto en los últimos cursos de primaria.
Este objeto digital pertenece al subproyecto aprende.mx de la RED. Las unidades de este subproyecto han sido desarrolladas con la herramienta DescartesJS y se han realizado en colaboración con el gobierno mejicano para su proyecto aprende.mx.
El proyecto aprende.mx es una iniciativa de la Secretaría de Educación Pública del gobierno mejicano. Consta de aplicaciones, recursos educativos y programas digitales para los últimos cursos de primaria. Algunas de estas actividades han sido desarrolladas con la herramienta DescartesJS, y se divulgan desde la Red Educativa Digital Descartes dentro del subproyecto aprende.mx.
Los materiales están clasificados en tres bloques: matemáticas, ciencias y castellano. En el bloque de matemáticas encontramos actividades sobre distintos contenidos: números, medida, geometría, estadística y probabilidad.
En este vídeo se muestran con detalle las actividades de la unidad simetría.
EDAD 3º ESO Académicas - Movimientos en el plano
Escrito por Alfonso Saura EspínEste mes vamos a ver los movimientos en el plano, correspondientes a 3ºESO Académicas:
1.Vectores
Concepto de vector. Coordenadas
Vectores equipolentes
Suma de vectores
2.Traslaciones
Traslación según un vector
Composición de traslaciones
3.Giros
Giro de centro O y ángulo α
Simetría central
Figuras invariantes de orden n
4.Simetría axial
Simetría de eje e
Figuras con eje de simetría
Composición de simetrías axiales
PISA 2017. Objetos interactivos para la formación en competencias
Escrito por Montserrat Gelis BoschDentro del Proyecto Competencias de la RED encontramos una serie de materiales que forman el grupo PISA 2017. Estas unidades se basan en los objetos liberados PISA 2015 y han sido desarrolladas con la herramienta Descartes.
Por su diseño y construcción añaden interactividad, aleatoriedad y posibilidad de corrección automática con el fin de facilitar el autoaprendizaje y la formación en competencias.
Estas unidades están agrupadas en cinco categorías: ciencias, comprensión lectora, finanzas, matemáticas y resolución de problemas.
Una vez realizadas todas las actividades de una unidad cualquiera, se puede optar por la revisión y modificación de las respuestas o seguir para su corrección. Se presentan cuatro opciones de corrección, la corrección directamente de la actividad, descargar las respuestas, imprimir o enviar por correo electrónico.
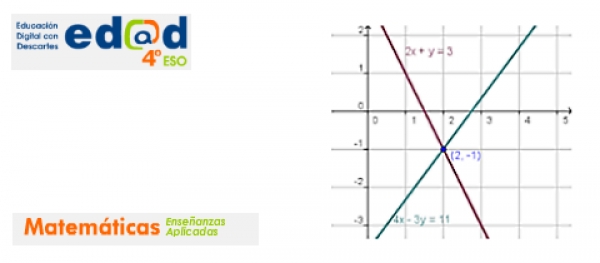
EDAD 4º ESO Aplicadas - Sistemas de ecuaciones
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad de "Sistemas de ecuaciones" de 4ºESO Aplicadas:
De forma muy breve hemos tratado los siguientes temas:
1.Sistemas de ecuaciones lineales
Ecuación lineal con dos incógnitas
Sistemas de ecuaciones lineales
Clasificación de sistemas
2.Métodos de resolución
Reducción
Sustitución
Igualación
3.Aplicaciones prácticas
Resolución de problemas
4.Sistemas de inecuaciones con una
incógnita
Resolución
Más...
Subproyecto Misceláneas.
El subproyecto Misceláneas está de enhorabuena, que se recuerde, pocas veces, en tan poco tiempo, un grupo tan reducido de personas ha aportado tanta cantidad de objetos de tan elevada calidad y tan alto potencial educativo a cualquiera de los subproyectos de la Red Descartes. Y no es la intención desmerecer al resto, muy al contrario; si no la de dar merecida notificación de un hito tan memorable. La excepcionalidad se justifica a si misma nada más visualizar cualesquiera de las últimas escenas incorporadas al subproyecto, lo que ya ha sido posible gracias a las reseñas que tanto José R. Galo Sánchez como Ángel Cabezudo Bueno han expuesto recientemente en el apartado Últimos materiales del blog y al artículo que el primero de ellos acaba de publicar, también en este blog, donde justifica el proceso de creación, creando a su vez nuevas escenas relacionadas con el tema de proporcionar una ayuda inestimable a la capacidad de visualización de las transformaciones dinámicas en el espacio tridimensional. Por otro lado la buena salud del subproyecto también se debe a la infatigable tarea de adaptación de materiales obsoletos, al nuevo editor DescartesJS, de las profesoras Elena E. Álvarez Sáiz y María José García Cebrian, los profesores ya mencionados y otros/as que aunque no se indican están en la mente de todos los usuarios del portal. Relativo a las aportaciones más recientes caben destacar:
- De la profesora Rita Jiménez Igea, quien nos ha sorprendido con un nuevo diseño de las escenas, más funcional, interactivo, armonioso y desde luego con un potencial instructivo y didáctico encomiable, seleccionamos una muestra de sus aportaciones:
De las que destacamos:

Matemáticas, joyería y mezclas.
- Seleccionar parte de las aportaciones del profesor José R. Galo Sánchez al subproyecto Misceláneas o casi a cualquier otro subproyecto es una tarea ardua, así que seleccionaré cronológicamente las siete últimas aportaciones relacionadas con el desarrollo del cubo y de entre ellas destacaré las tres más recientes; no obstante quisiera aprovechar la ocasión para documentar la génesis de la creación de las siete últimas y extraordinarias aportaciones de nuestro presidente para dar valor al ejercicio de la colaboración entre socios a tenor de los frutos obtenidos.
En el año 2001 la profesora Ángela Nuñez Castaín publicó la miscelánea Partición de un cubo en seis pirámides triangulares iguales, en el año 2017 se adaptó a DescartesJS dicha miscelánea, la adaptación fué realizada conjuntamente por la profesora y nuestro presidente. A continuación se muestra el resultado obtenido. Las misceláneas más recientes que se han publicado sobre el tema han sido:- Partición de un cubo en pirámides de base cuadrada. Caso general.
- Partición de un cubo en 4 pirámides cuadradas iguales dos a dos
- Partición de un cubo en seis pirámides triangulares congruentes
- Partición de un cubo en cinco pirámides triangulares
- Partición de un cubo en seis pirámides cuadradas iguales
- Partición de un cubo en cinco pirámides cuadradas
- Partición de un cubo en tres pirámides cuadradas iguales
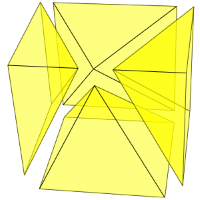
- A la hora de cerrar este artículo nos vemos sorprendidos por una nueva y brillante aportación del profesor José R. Galo Sánchez que aunque aún no hemos tenido tiempo de analizar en profundidad consideramos de interés prioritario su exposición. Partición no prismática de un cubo en seis pirámides triangulares equivalentes
De las anteriores destacamos:
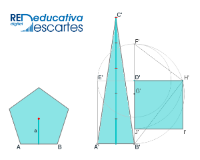
- A continuación, también a modo de resumen, exponemos tres misceláneas: la primera, que muestra la cuadratura de un polígono regular, elaborada por el profesor Ángel Cabezudo Bueno y el autor de este artículo y las otras dos, de este último, relativas a los patrones de teselación tipo mitad del cuadrado.
- Pentágono regular: Cuadratura. Método clásico
- Teselas del plano. Patrones: Mitad del cuadrado
- Teselas del plano. Patrones: Mitad del cuadrado II
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una presentación de los cuerpos platónicos diferente a lo habitual.
Ildefonso Fernández Trujillo. 2018
Hoy presentamos la unidad Operaciones con números racionales, perteneciente al proyecto Miscelánea de la RED.
Se trata de un objeto didáctico interactivo con una serie de actividades para practicar las operaciones con números racionales. Las actividades de esta unidad son adecuadas para los primeros cursos de la ESO y facilitan el aprendizaje y consolidación de dichos cálculos ya que en cada ejercicio el alumno puede comprobar si su respuesta es correcta o no y seguir así la evolución de su aprendizaje.
El siguiente vídeo consta de dos partes, en primer lugar se analizan las actividades que forman parte de dicha unidad y, en segundo lugar, se propone la inserción de este objeto en un curso Moodle para el trabajo en el aula, mediante el código para embeber.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)










 CONTACTO
CONTACTO
