Entre los proyectos de la RED Descartes se encuentra un grupo de actividades creadas a partir de unidades liberadas de PISA y de Pruebas de Evaluación Diagnóstico utilizadas en diferentes Comunidades autónomas. Se trata del Proyecto Competencias.

Las unidades digitales pertenecientes a este proyecto se basan en situaciones y contextos cotidianos. Las actividades que se proponen son interactivas y autoevaluables y permiten que un mismo alumno puede realizar muchas veces la misma actividad, que presentará pequeñas variaciones. Esta característica convierte a las unidades de este proyecto en un recurso importante para la formación en competencias del estudiante.

En el siguiente vídeo se han seleccionado una serie de objetos en los cuales se deben utilizar propiedades geométricas y equivalencias entre medidas para resolver situaciones reales. Una vez seleccionadas las actividades, se muestran los pasos a seguir para insertar estas actividades en nuestra aula virtual Moodle.  

Proporcionalidad. Las Espirales XIV

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación e iCartesiLibri.

Como muestra enlazamos la unidad sobre Como se mueven las cosas. Aceleración, del subproyecto TELESECUNDARIA,

la GEOevaluación de SurAmérica,

y el libro interactivo Paletización y Empaque.

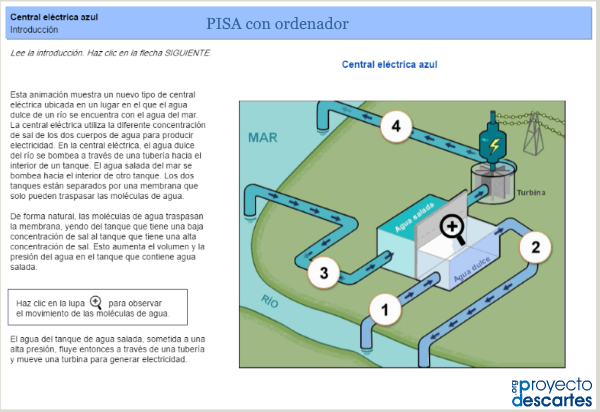
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D cuyos materiales pueden enlazarse desde este espacio web mediante los botones MATEMÁTICAS y FÍSICA Y QUÍMICA y los contenidos del subproyecto Competencias en general y en particular los referidos como PISA con ordenador. De entre ellos enlazamos, con la siguiente imagen, el extraordinario trabajo sobre la generación de energia Central eléctrica azul

Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el instrumento ideado por la escuela platónica para duplicar un cubo, esto es, dado un cubo de arista a y volumen V halla de forma mecánica y basandose en los razonamientos de Hipócrates, el segmento de longitud a'= a·2^1/3 que será la arista del cubo de volumen V' = 2·V.

La escena permite, con cierta facilidad, determinar el segmento OD pero si el usuario no está familiarizado con el uso del instrumento puede pulsar el botón de información, , que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la construcción de Platón, o atribuida a la escuela platónica, del hecho de la duplicidad.

La utilidad es facilmente adaptable y admite las modificaciones y/o ampliaciones que el usuario considere convenientes para su uso personal.

En el siguiente trabajo presentamos el instrumento conocido como Mesolabio de Eratóstenes y la manera de encontrar, con su uso virtual, el segmento que sirva de arista al cubo que doble en volumen a uno inicial dado.

Repetimos lo dicho anteriormente: la escena permite, con cierta facilidad, determinar la arista del cubo con volumen doble a uno dado, pero si el usuario no está familiarizado con el uso del instrumento puede pulsar el botón de información, , que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la semejanza de triángulos, del hecho de la duplicidad.

En esta ocasión, en la sección de vídeo, hemos elegido la tercera parte de los que se han mostrado en las últimas entradas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales".

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Compleja" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

• Se ha creado la siguiente escena: Espiral compleja. El crecimiento de esta espiral, tal y como se ha construido, es extremadamente rápido debido al factor rⁿ el lector puede modificar facilmente el comportamiento de la escena añadiendo más controles y/o modificando el rango de valores de los actuales.
  La demostración de las fórmulas (teoremas) de Moivre y Euler están disponibles en la wikipedia.
• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Compleja incluida.

Con el siguiente trabajo realizado con GeoGebra, tendremos la oportunidad de manejar, virtualmente, un mesolabio para hallar la arista de un cubo que tenga doble volumen que uno dado. Esto es, partiremos de esta situación

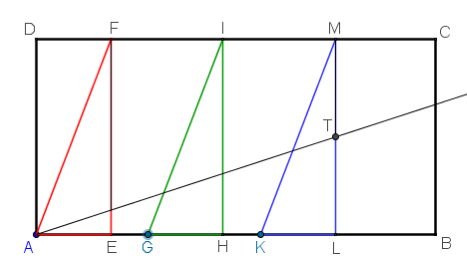
y trataremos de llegar a esta otra

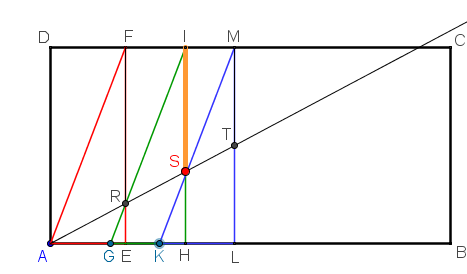
solución

al manipular los controles gráficos G y K y conseguir el objetivo, se muestran las dos medias proporcionales, FR e IS, propuestas por Hipócrates, entre dos segmentos, MT y DA, de longitudes a y 2·a respectivamente, donde a es la longitud de la arista del cubo inicial. La recta determina el segmento que se usará de arista del cubo de volumen doble al primero. 
Con ayuda de los cursores y seleccionando alternativamente con el ratón los puntos G y K el ajuste puede ser bastante exacto tal y como muestra la imagen solución.

Se ha creado el recurso en la web de GeoGebra: 'Las espirales complejas.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.

Bibliografia:

• Documentación de Yuli Andrea Rodríguez Rodríguez y Benjamin R. Sarmiento Lugo
• El problema de la Duplicación del cubo de Juana Contreras S. y Claudio del Pino O. Instituto de Matemática y Física. Universidad de Talca.
• Una aproximación a la curva de transición Clotoide vista desde Mathematica de:
  Luís Blanch, Emilio Checa, Josefa Marín
  Universitat Politecnica de Valencia
  Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
• Problema de la duplicación del cubo de Juan Pablo Mora.
• Consideraciones sobre los complejos y las espirales de:
  Miguel Ángel Morales Medina
• Otros documentos buscados en Internet.

Ildefonso Fernández Trujillo